-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2022; 12(1): 120-129
doi:10.5923/j.ajfd.20221201.03
Received: Jul. 11, 2022; Accepted: Jul. 26, 2022; Published: Jul. 27, 2022

High Reynolds Number Investigation of Lid Driven Cavity Flow
Jay P. Narain
Retired, Independent Research Person
Correspondence to: Jay P. Narain, Retired, Independent Research Person.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

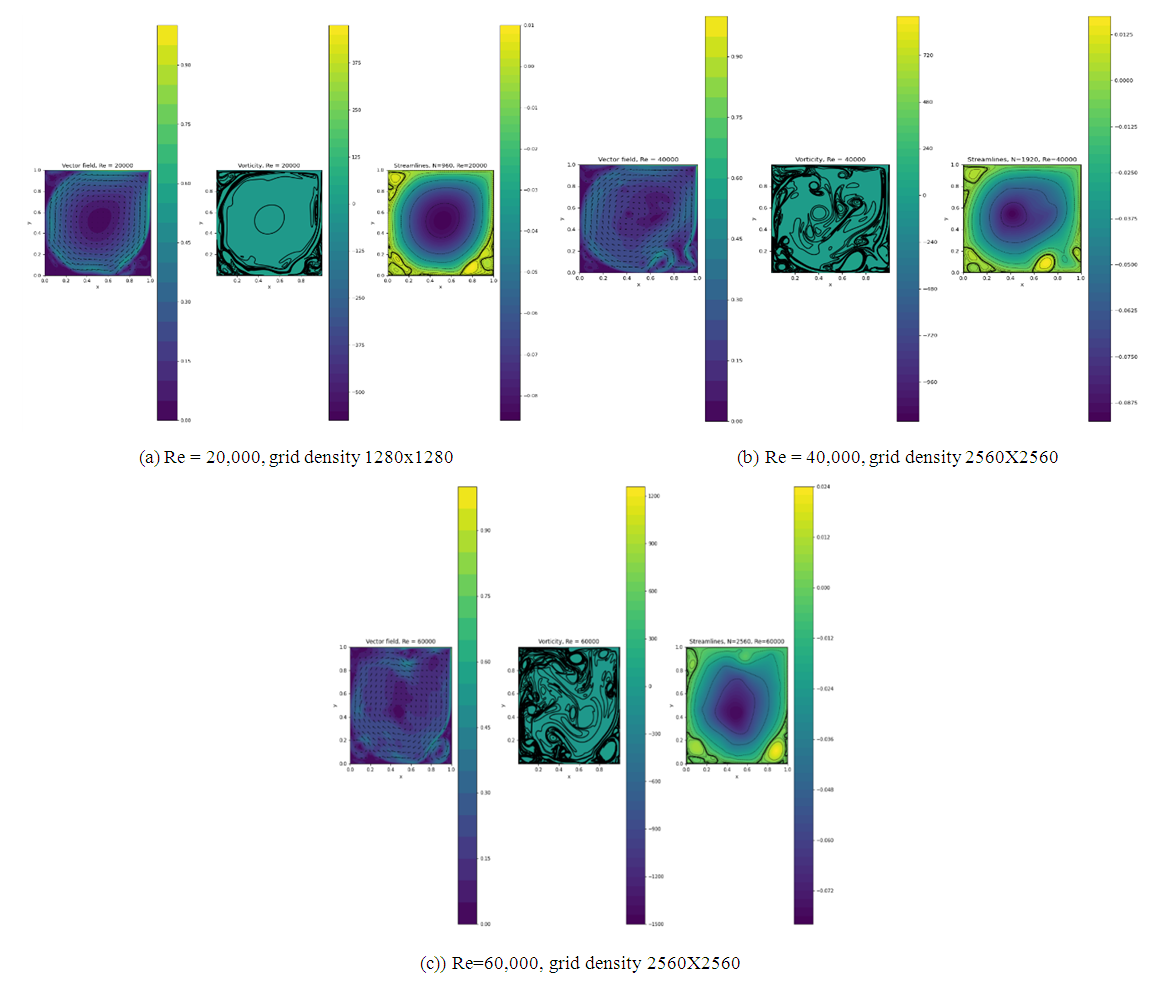
Lattice Boltzmann method (LBE) has attracted enormous interest to analyze this two-dimensional incompressible Navier-Stokes flow in a Lid Driven square cavity. A few papers have applied it to deep aspect ratio cavities. For the most part, the Reynolds number (Re) have been limited to 5,000. The aspect ratio (Ar) has also been limited to four. In most of the analyses, single relaxation time model (SRT) known as, Bhatnagar, Gross and Krook [8] model (LGBK) is used. The present work extends the Re capability beyond 10,000 for cavities with Ar up to six. It also uses two relaxation time (TRT) approach and half way bounce back boundary conditions. For square cavities, results were obtained for Re up to 60,000.
Keywords: Lid driven cavity flow, LBE solver with SRT or TRT relaxation
Cite this paper: Jay P. Narain, High Reynolds Number Investigation of Lid Driven Cavity Flow, American Journal of Fluid Dynamics, Vol. 12 No. 1, 2022, pp. 120-129. doi: 10.5923/j.ajfd.20221201.03.
1. Introduction
- The lid driven flow inside a square cavity has drawn considerable numerical and experimental interest for decades. Theoretically, Batchelor [1] pointed out that lid driven cavity flows exhibit almost all the phenomenon that can possibly occur in incompressible flows: eddies, secondary flows, complex flow patterns, chaotic particle motions, instability, and turbulence. Practical applications are in material processing, dynamics of lakes, metal casting, galvanizing and some airport runways. AbdelMigid et. al. [2] have given a concise review of the developments of various numerical schemes, starting from finite-difference [3,4], finite-volume [5] to Lattice Boltzmann (LBM) methods [6,7,8]. Several new publications [13,14] propose adding additional dissipation without loss of any accuracy. They show the results for very high Reynolds number with highly vectorized GPU code running three to four times faster than the code without modifications. Presently we think that a standard LBE code with SRT or TRT relaxation capability can be run for high Reynolds numbers by just increasing grid density inside the cavity. A GPU vectorized LBGK code [9] will be used to study the high Reynolds number cases, the effect of aspect ratio for deep cavities, and the partial slip conditions.
2. Discussions
- Unlike CFD methods that solve the conservation equations of macroscopic properties (i.e., mass, momentum, and energy) numerically, Lattice Boltzmann method (LBM) models the fluid consisting of fictive particles, and such particles perform consecutive propagation and collision processes over a discrete lattice. Due to its particulate nature and local dynamics, LBM has several advantages over other conventional CFD methods, especially in dealing with complex boundaries, incorporating microscopic interactions, and parallelization of the algorithm. A different interpretation of the lattice Boltzmann equation is that of a discrete-velocity Boltzmann equation. The numerical methods of solution of the system of partial differential equations then give rise to a discrete map, which can be interpreted as the propagation and collision of fictitious particles. For two dimensional flows D2Q9 model is used. For collision (relaxation) step, Bhatnagar, Gross and Krook [8] model is used. The model assumes that the fluid locally relaxes to equilibrium over a characteristic timescale. This timescale determines the kinematic viscosity, the larger it is, the larger is the kinematic viscosity. The streaming step is merely the forward motion in time. The whole model is known as LBGK model. The details of lattice density propagation, equilibrium state, numerical scheme can be found in published papers [6,7]. Here we will start with a GPU vectorized LBGK code [9,10]. The code has Single relaxation time (SRT) due to BGK model, as well as two relaxation time model (TRT) [10]. It also has Half-way bounce-back boundary condition model. The equations, boundary conditions, and initial conditions are adequately discussed in the cited references [6,7,8,9,10]. In general SRT model is good for relaxation time equal to one. For high Re cases, relaxation time is lower. The TRT model handles such cases with stability.The cavity problem will be solved for two vertical stationary walls, and with top wall moving with a velocity u0 and bottom wall moving or stationary. The code will be used to analyze flow inside cavities of several aspect ratio (Ar or K).Case A: The flow inside a square cavity with top wall moving with velocity u0 to the right. The author [9] showed the case for Reynolds number 1000. He showed excellent correlation with Ghia et al [4] bench mark data. Ghia et al solved this case up to Re = 10,000 with a mix of finite difference for dissipation, finite volume for advection with an efficient multi-grid schemes [4]. A finite volume code on staggered mesh [11] was used in our past investigation [12] up to Re = 3,200. With slight increase in grid dimension, we were able to run it up to Re 10,000. These methods introduce numerical viscosity which enables them to run at high Reynolds numbers. We tested the present code for Reynolds Numbers (Re) of 400, 1,000, 5,000, 10,000 and 15,000, All the intermediate Re in the test range can be run without any problem. The following streamline plots have Reynolds number (Re) and number of grid points(N) shown on title. The actual grid dimension will be N times (N times Ar). For example, for a square cavity it will be 128x128, since Ar is 1.
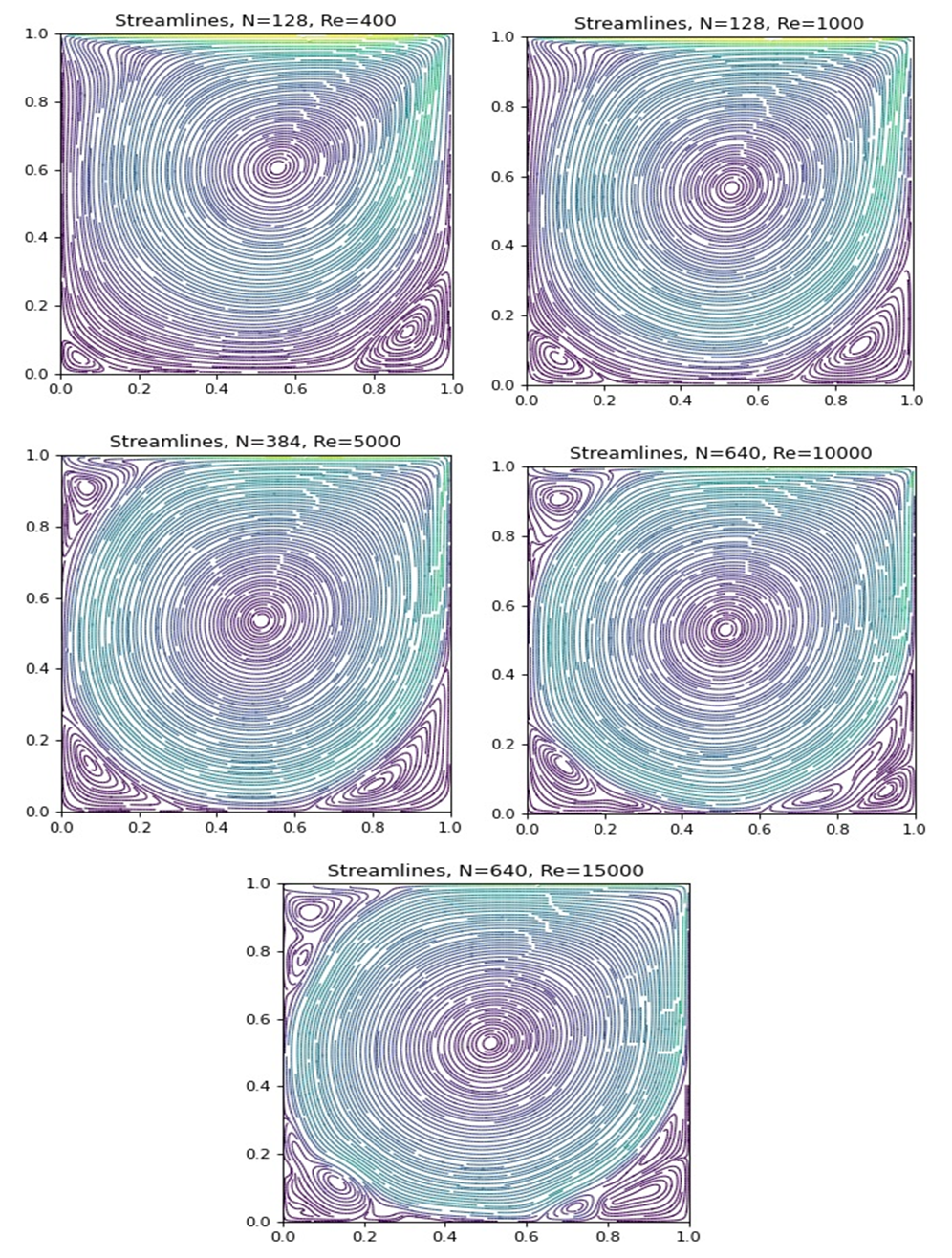 | Figure 1. Plots of stream function for various Re. N on title denotes NxN grid requirement |
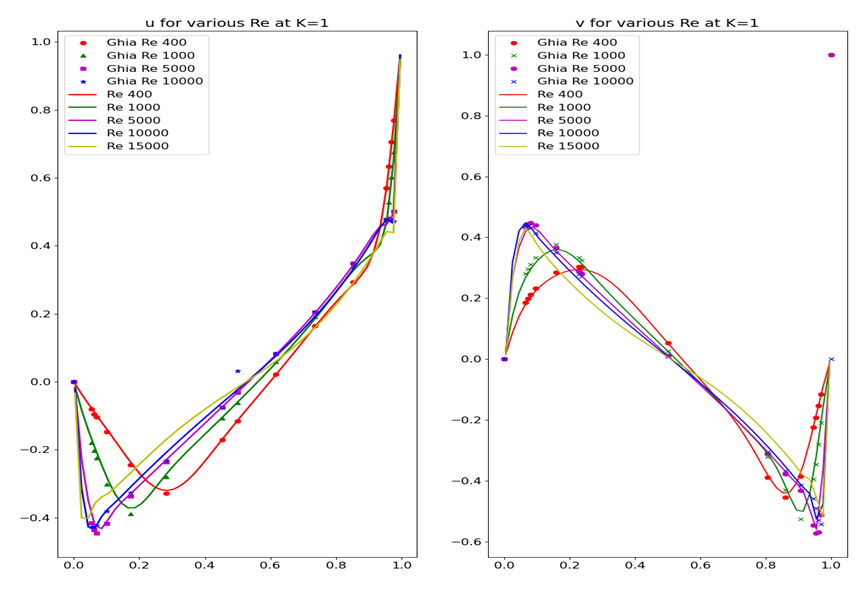 | Figure 2. Mid Plane velocity prediction and correlation with bench mark data |
 | Figure 3. Total velocity, vorticity, and streamlines for several Re |
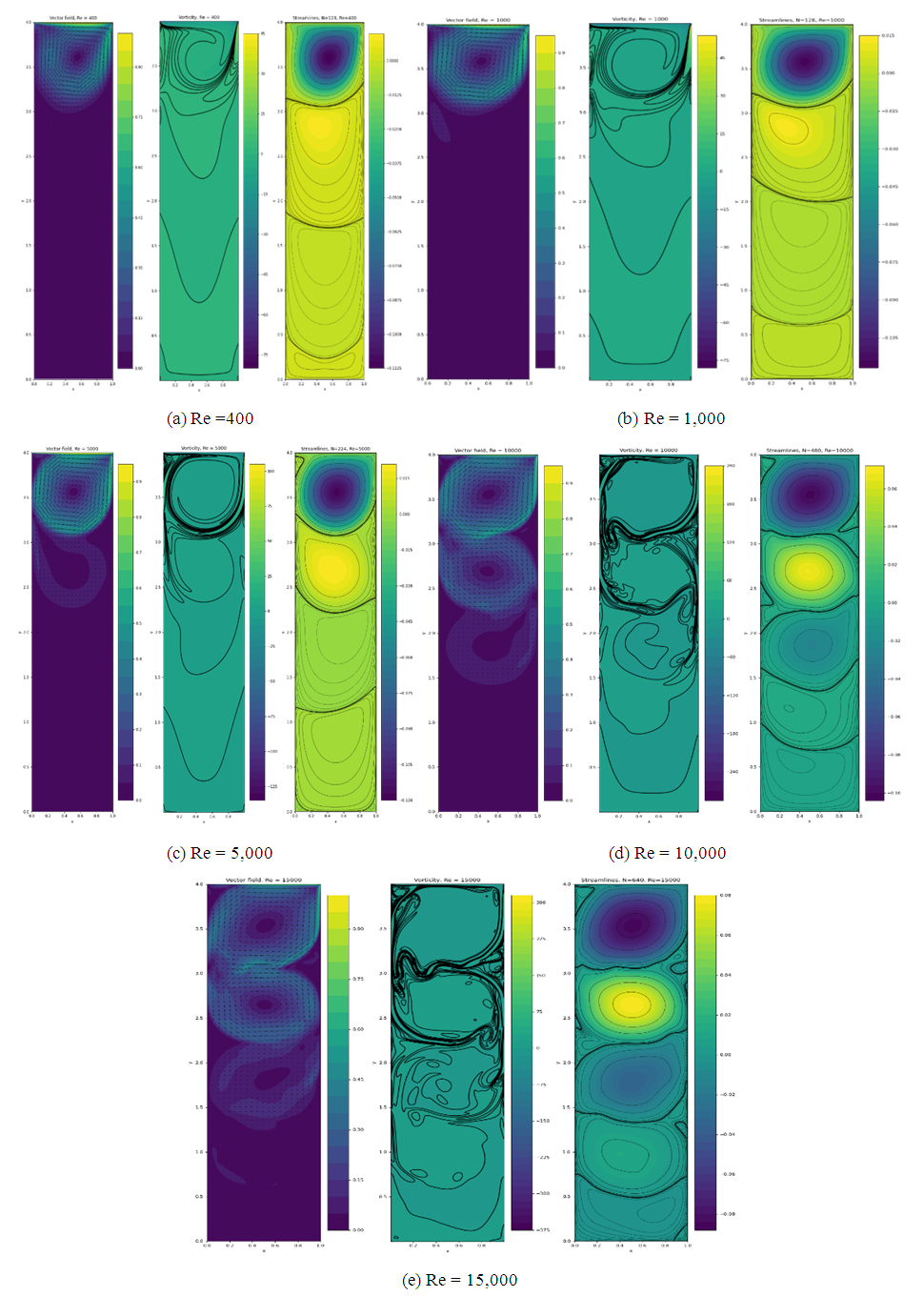 | Figure 4. Plots of total velocity, vorticity and stream function for various Reynolds numbers and Ar = 4 |
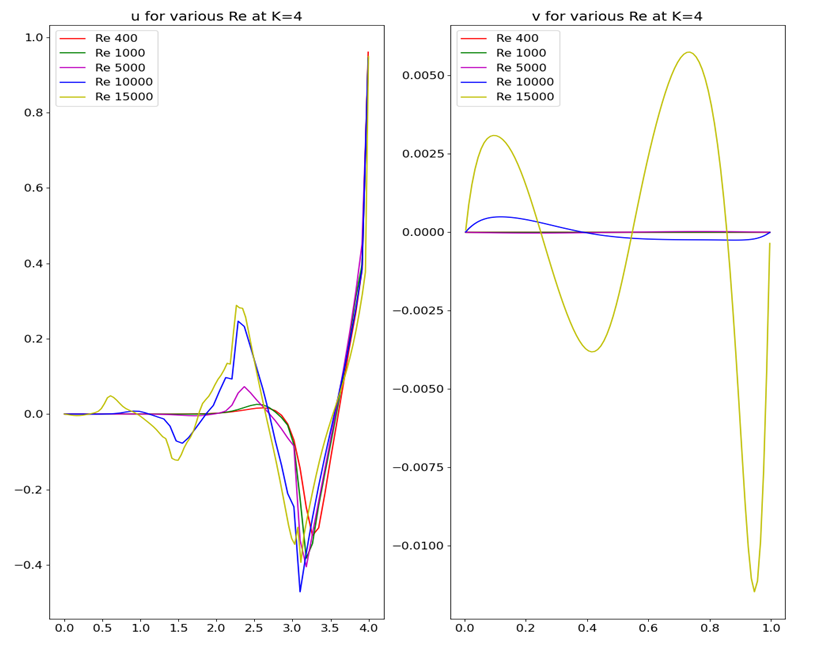 | Figure 5. Mid Plane velocity predictions for Ar = 4 |
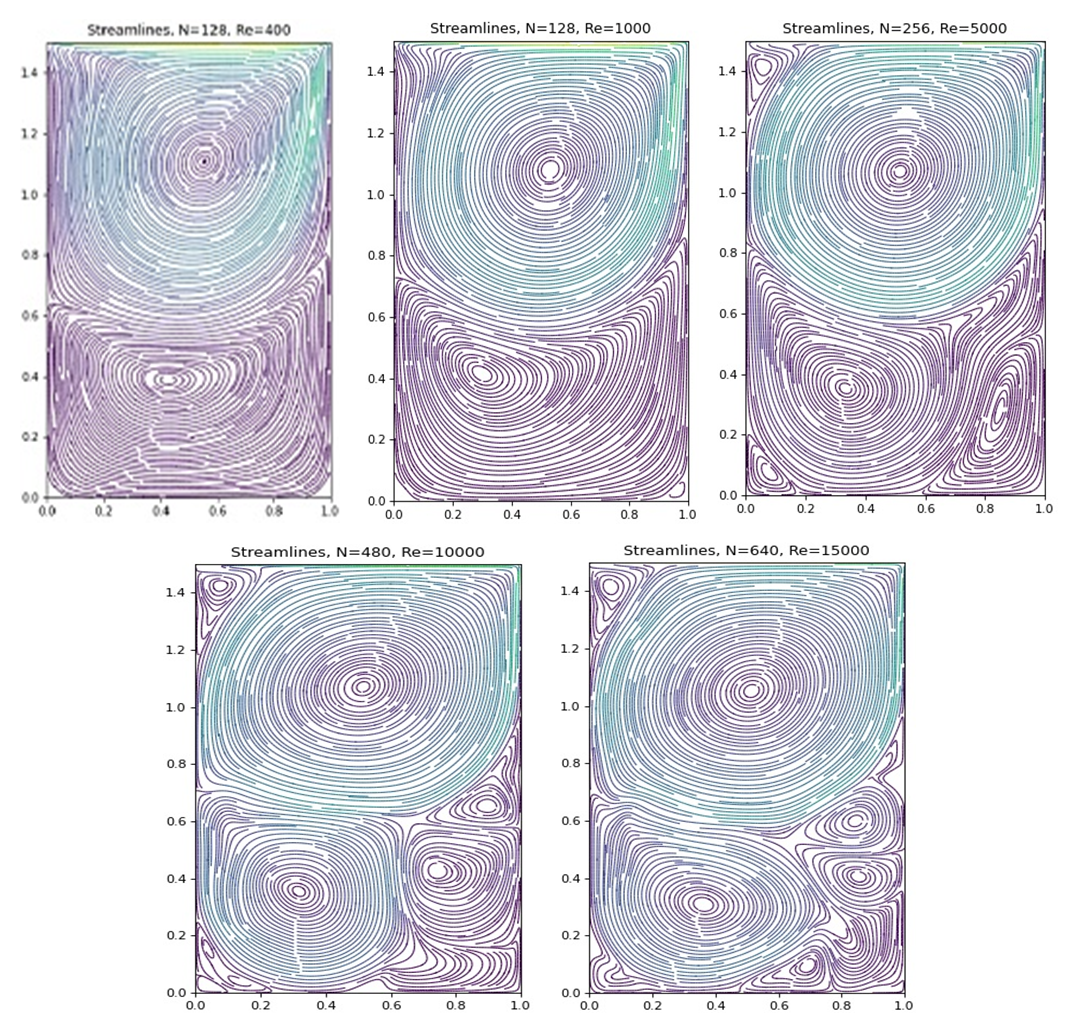 | Figure 6. Plots of stream function for various Re |
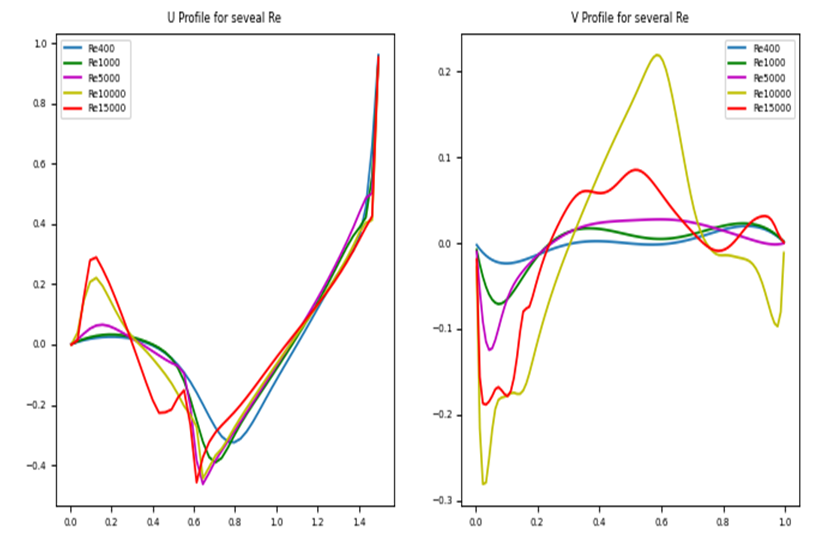 | Figure 7. Mid Plane velocity predictions for Ar = 1.5 |
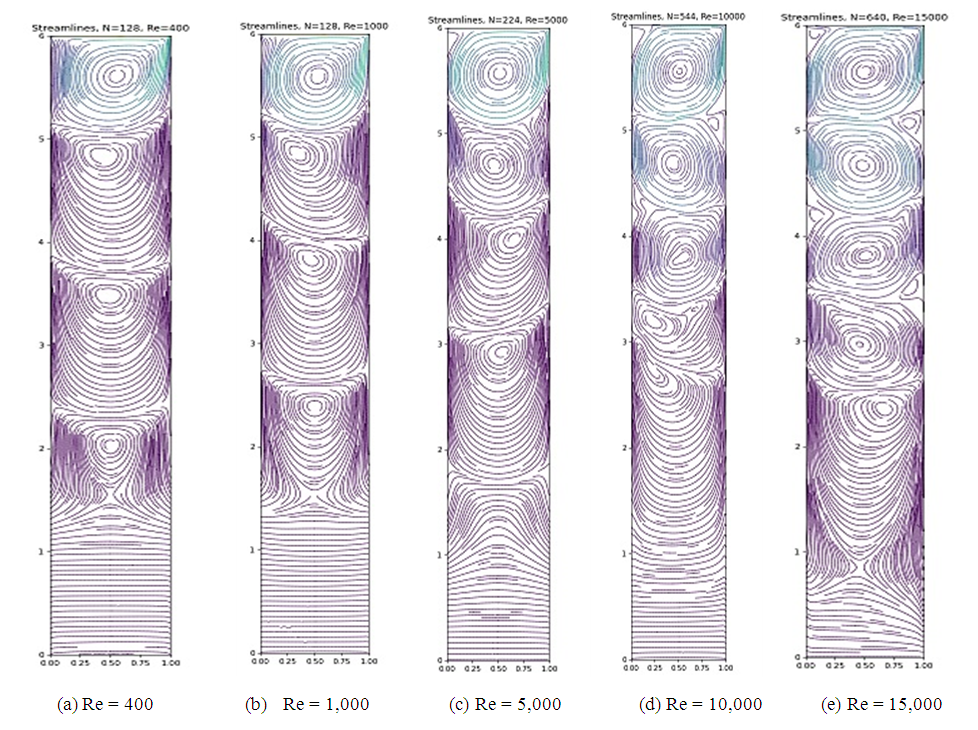 | Figure 8. Streamlines predictions for Ar = 6 |
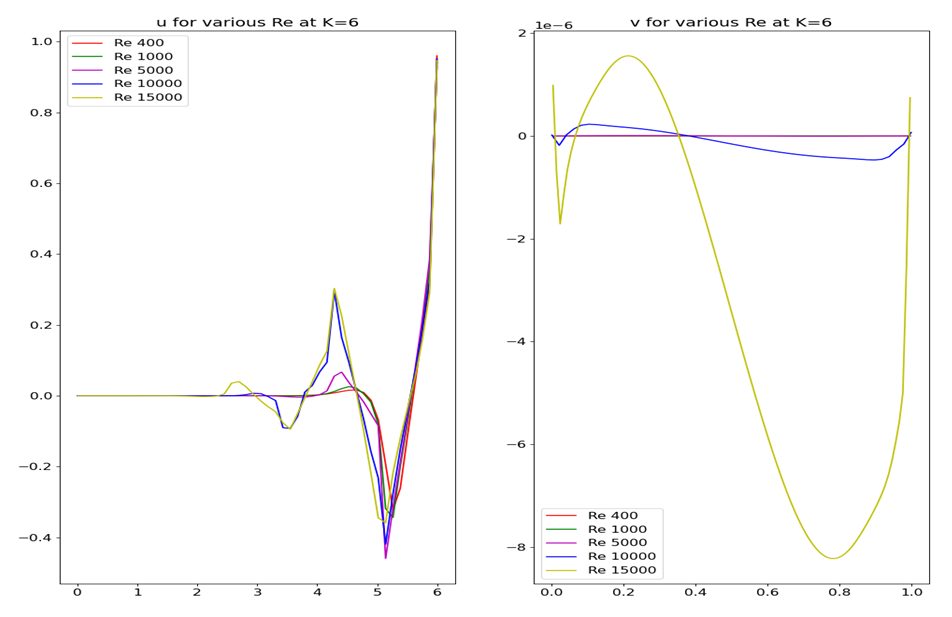 | Figure 9. Mid Plane velocities predictions for Ar = 6 |
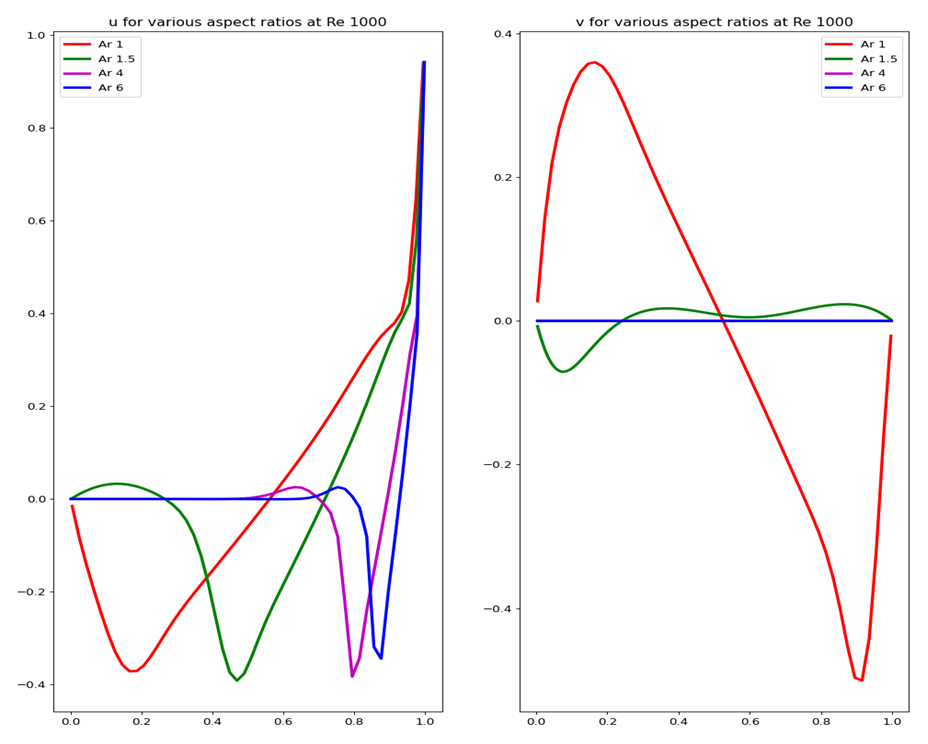 | Figure 10. Mid Plane velocity predictions for various Ar and Re = 1000 |
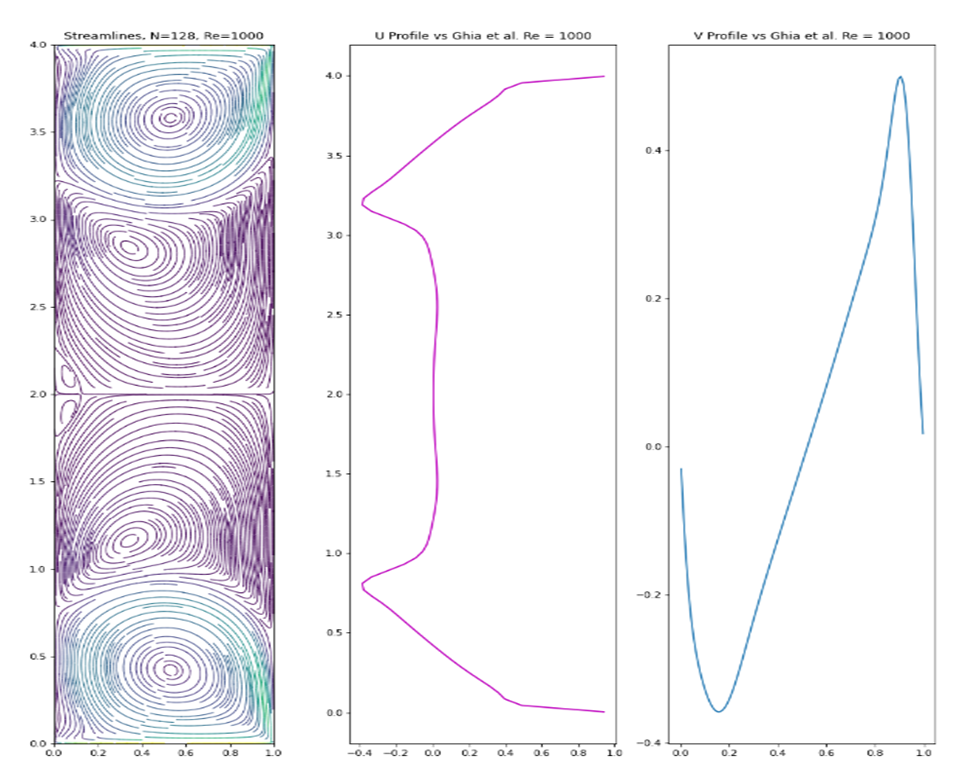 | Figure 11. Walls moving in same direction |
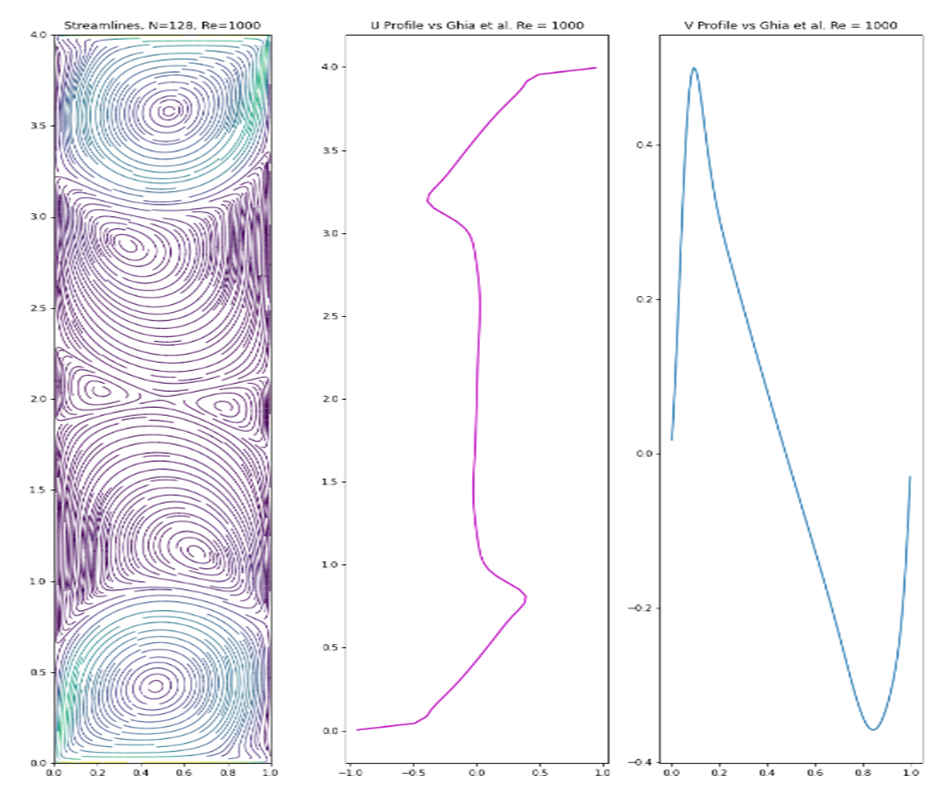 | Figure 12. Walls moving in opposite direction |
3. Conclusions
- The present LBE solver with TRT scheme seems to be capable of running the cavity flow problem from moderate to high Reynolds numbers. For square cavity, results shown for Re up to 60,000 exceed those of previous investigations up to 5,000. The results compare well with existing benchmark data for square cavity flow. The code was very stable and can run low to high aspect ratio cavity flows. The velocity data will be put in https://github.com/narain42/Poission-s-Equation-Solver-Using-ML as velocity data folder for future correlation purposes by inspiring new authors.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML