-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2022; 12(1): 1-15
doi:10.5923/j.ajfd.20221201.01
Received: Mar. 23, 2022; Accepted: Apr. 6, 2022; Published: Apr. 22, 2022

Lid Driven Cavity Flow: Review and Future Trends
Jay P. Narain
Retired, Independent Research Person
Correspondence to: Jay P. Narain , Retired, Independent Research Person.
| Email: |  |
Copyright © 2022 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The lid driven cavity flow has been of considerable interest for decades [1]. A number of numerical methods have been developed to analyze this two-dimensional incompressible Navier-Stokes flow problem [2]. Presently, a finite volume solver will be used to solve this problem for cavities of various aspect ratios. The cases for various slip configurations and various Reynolds numbers will be investigated. Next, a number of physics informed neural network solvers will be evaluated. The status of physics informed neural network will be presented.
Keywords: Lid driven cavity flow, Finite volume schemes, Physics informed neural networks
Cite this paper: Jay P. Narain , Lid Driven Cavity Flow: Review and Future Trends, American Journal of Fluid Dynamics, Vol. 12 No. 1, 2022, pp. 1-15. doi: 10.5923/j.ajfd.20221201.01.
1. Introduction
- The lid driven flow inside a square cavity has drawn considerable numerical and experimental interest for decades. Theoretically, Batchelor [1] pointed out that lid driven cavity flows exhibit almost all the phenomenon that can possibly occur in incompressible flows: eddies, secondary flows, complex flow patterns, chaotic particle motions, instability, and turbulence. Practical applications are in material processing, dynamics of lakes, metal casting, galvanizing and some airport runways. Tamer et. al. [2] have given a concise review of the developments of various numerical schemes, starting from finite-difference [3,4], finite-volume [5] to Lattice Boltzmann(LB) methods [6,12,13,14]. Although so many remarkable methods have been outlined in the review [2], we will use a modified version of finite-volume code [7] to present several scenarios and compare them with current LB method. The physics informed deep learning (PINN)method [8] revolutionized neural network application to several fluid-dynamics problems. We will use two newer PINN methods [9,10] to analyze and assess the current status of the PINN scheme. The deep cavity flow with aspect ratio greater than one has also drawn considerable attention using LB scheme [12] as well as Fluent commercial software [16]. We will show deep cavity results with the finite volume and PINN solvers. The present PINN methods can not analyze high Reynolds number scenarios. Some insight into this problem will be presented.
2. Discussions
- We will start with a finite volume solver. During our assessment, it was found to be superior to basic finite difference methods and gave consistently remarkable results compared to results from any published work. It is quite fast, takes only a few seconds for low Reynolds numbers and increasing minutes for high Reynolds number flows on a basic home computer. The stream function or psi, vorticity and pressure equations for a two-dimensional incompressible flow are given by [11];
 | (1) |
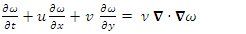 | (2) |
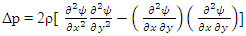 | (3) |
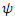 is the stream function,
is the stream function, 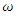 is the vorticity, p is the pressure, and ρ is the density.The cavity problem will be solved for two vertical stationary walls, and with top wall moving with a velocity u0=1. The slip conditions for the bottom wall will be stationary, or moving in same direction with velocity u0=1, or in opposite direction with velocity uo=-1. A schematic cavity is shown as follows;
is the vorticity, p is the pressure, and ρ is the density.The cavity problem will be solved for two vertical stationary walls, and with top wall moving with a velocity u0=1. The slip conditions for the bottom wall will be stationary, or moving in same direction with velocity u0=1, or in opposite direction with velocity uo=-1. A schematic cavity is shown as follows;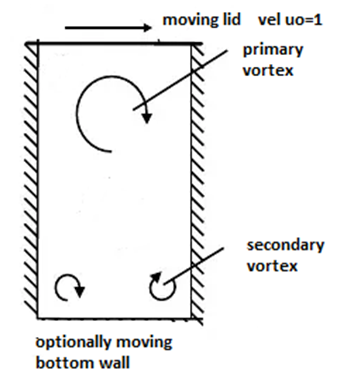 | Sketch 1. A cavity with top and moving wall concepts |
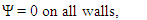 | (4) |
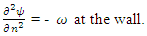 | (5) |
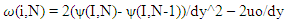 | (6) |
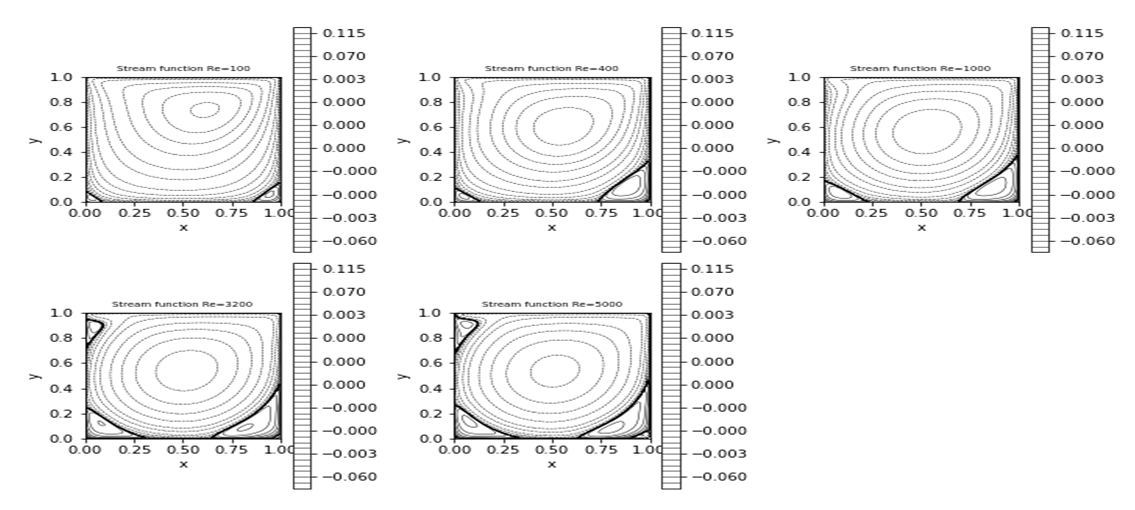 | Figure 1. Plots of stream function for various Reynolds numbers |
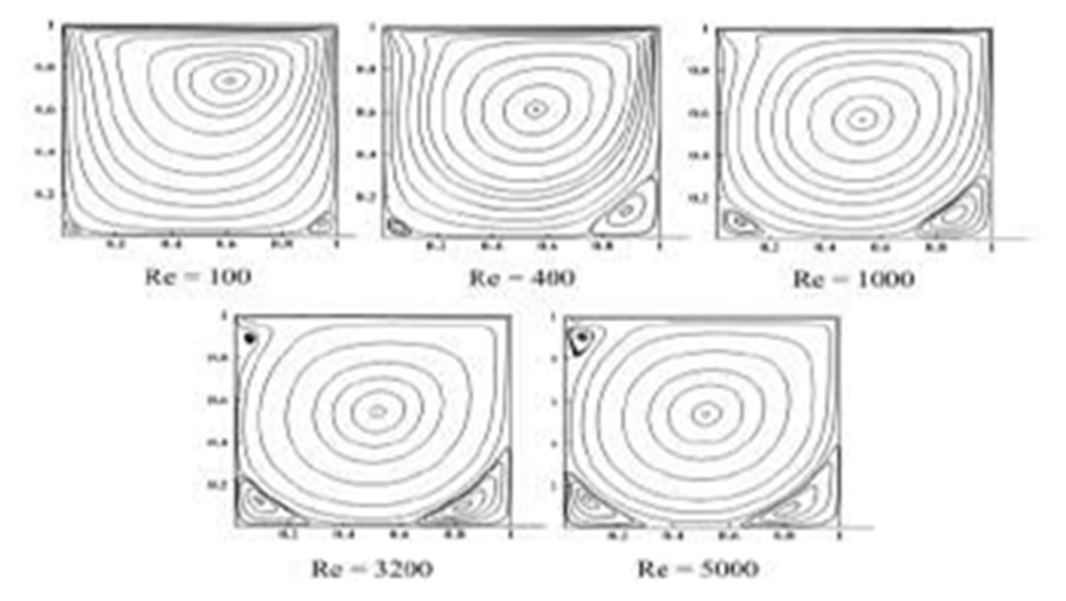 | Figure 2. Plots of stream function for various Reynolds numbers from a Lattice Boltzmann solver [12] |
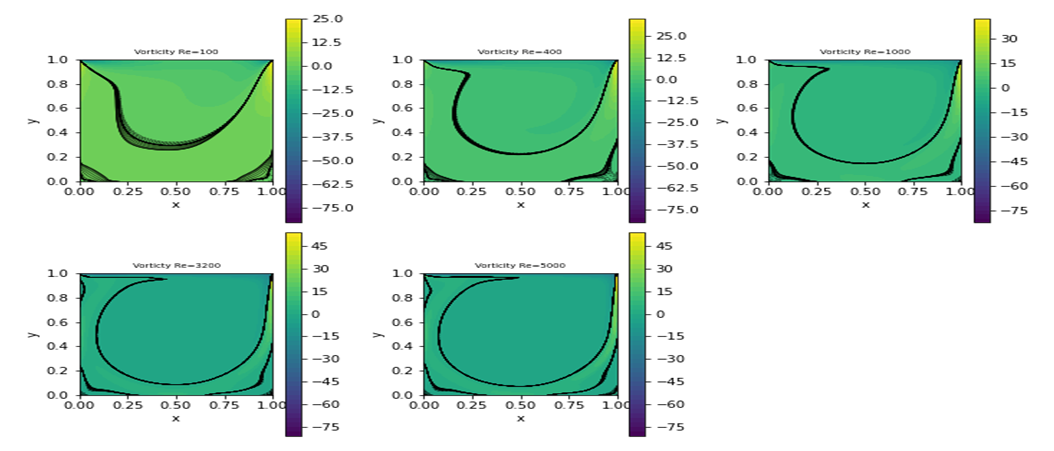 | Figure 3. Plots of vorticity for various Reynolds numbers from the present fv solver |
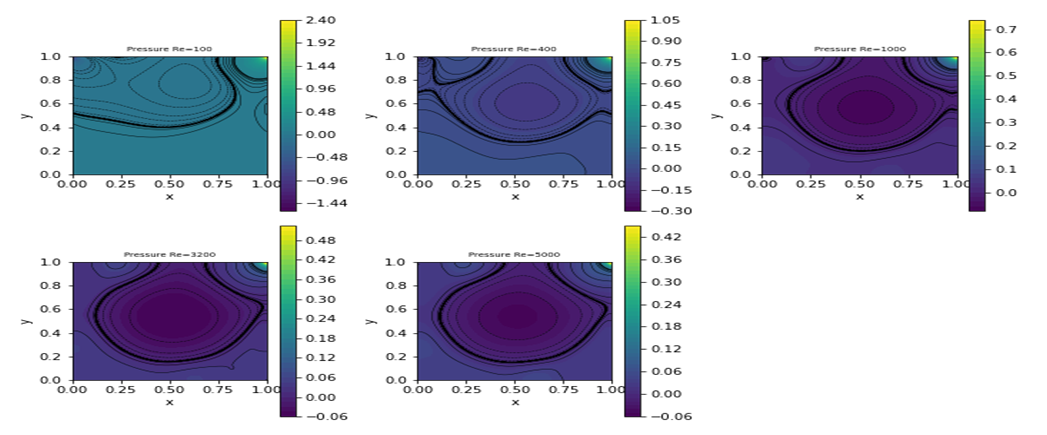 | Figure 4. Plots of pressure for various Reynolds numbers from the present fv solver |
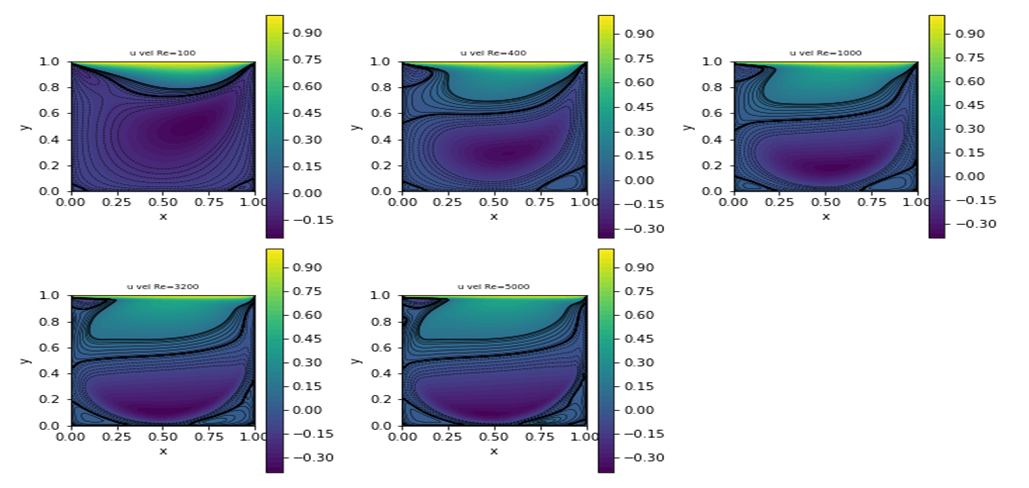 | Figure 5. Plots of streamwise velocity u for various Reynolds numbers from the present fv solver |
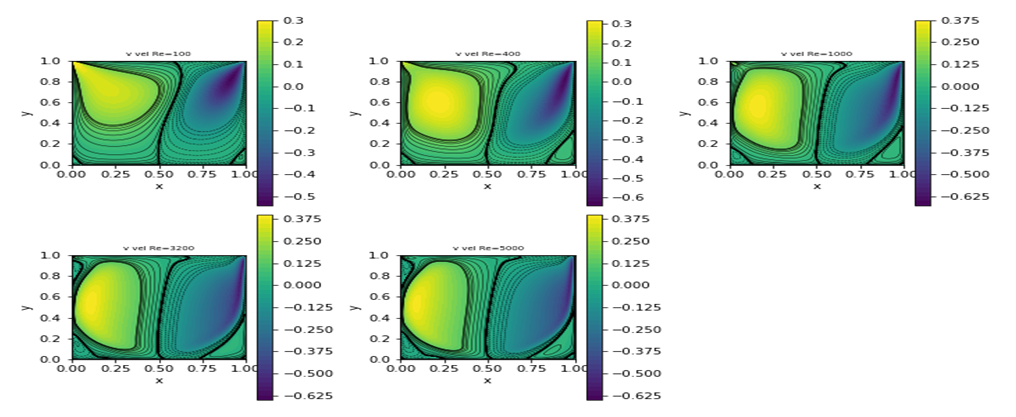 | Figure 6. Plots of transverse velocity v for various Reynolds numbers from the present fv solver |
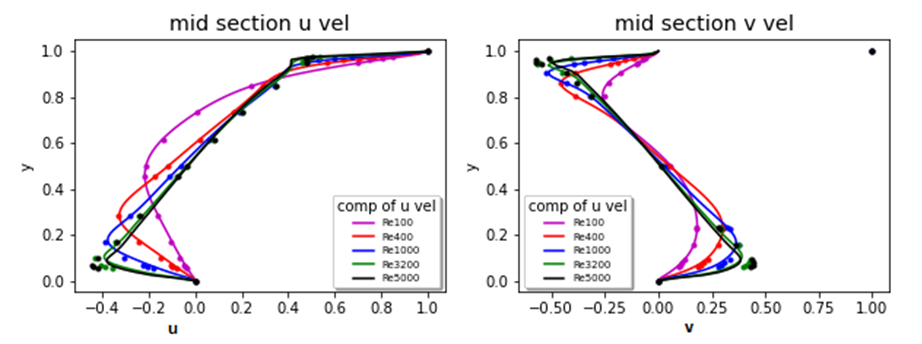 | Figure 7. A comparison of centerline u, v velocities for all analyzed Reynolds numbers |
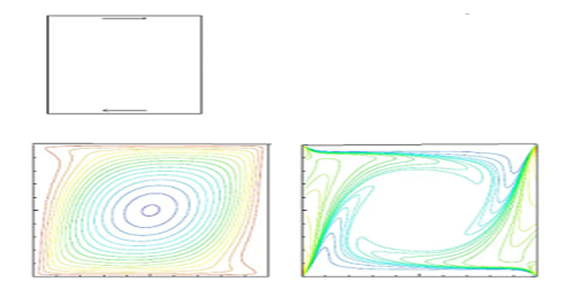 | Figure 8. Plots of cavity configuration, stream function and vorticity at Re=400 from a Lattice Boltzmann solution paper [13] |
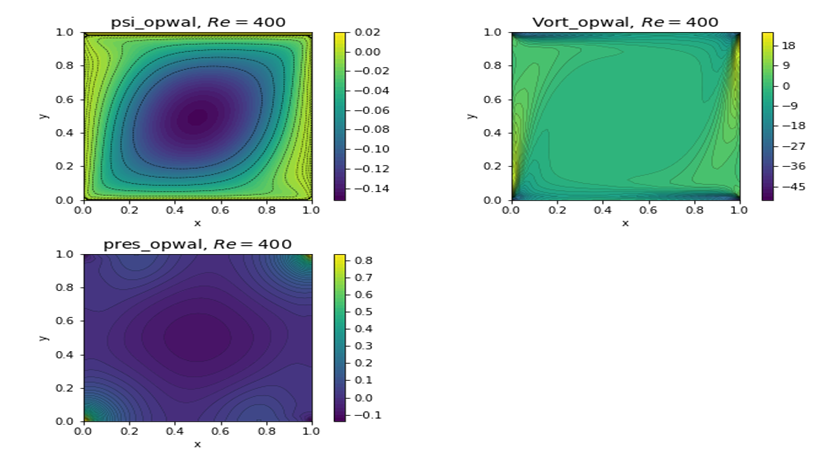 | Figure 9. Plots of stream function, vorticity, and pressure at Re=400 from a present finite volume solver |
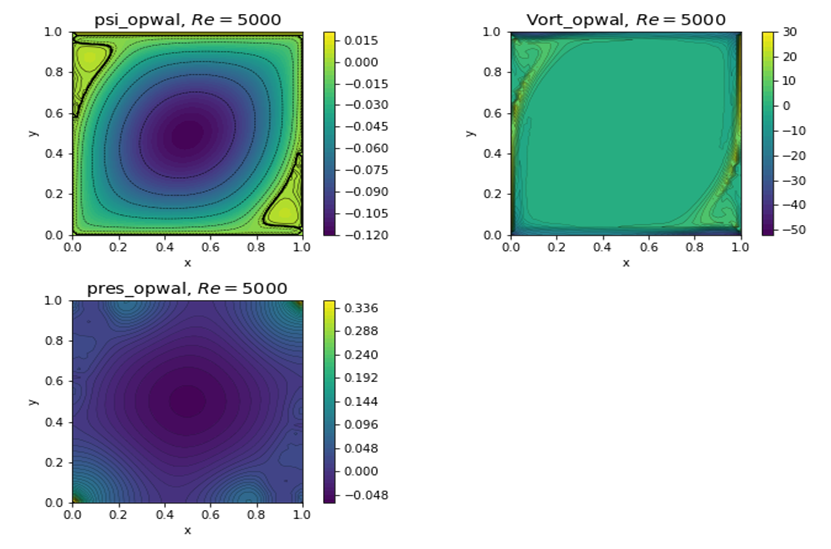 | Figure 10. Plots of stream function, vorticity, and pressure at Re=5000 from a present finite volume solver |
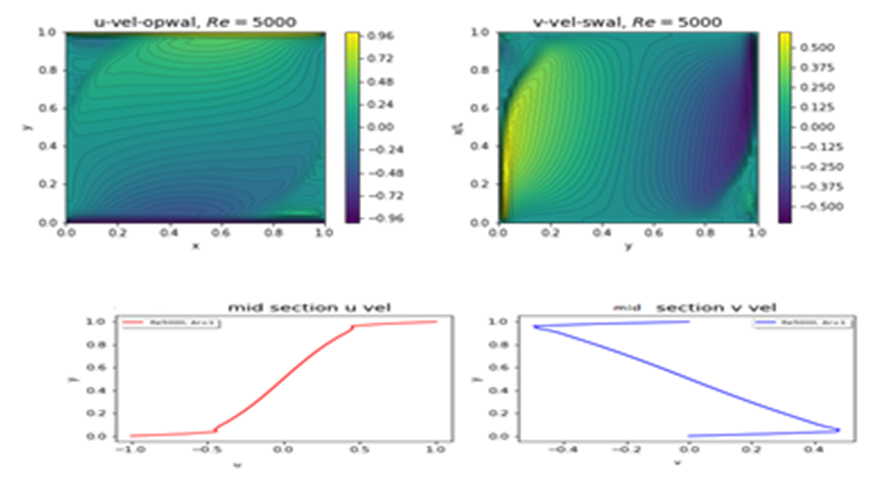 | Figure 11. Plots of u and v velocity components and their mid-section values at Re=5000 |
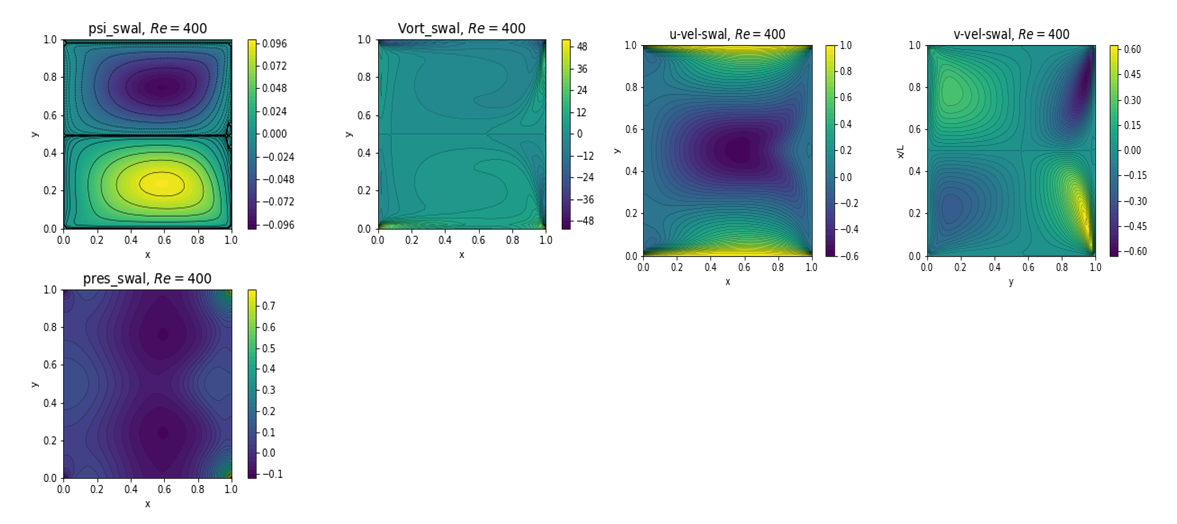 | Figure 12. Plots of psi, vorticity, pressure, u and v velocity for Re=400 from fv solver |
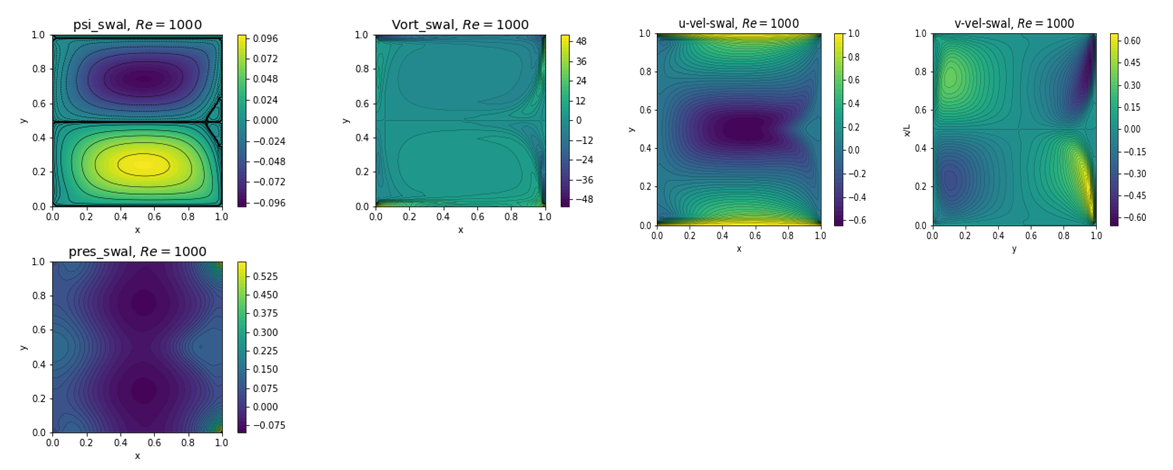 | Figure 13. Plots of psi, vorticity, pressure, u and v velocity for Re=1000 from fv solver |
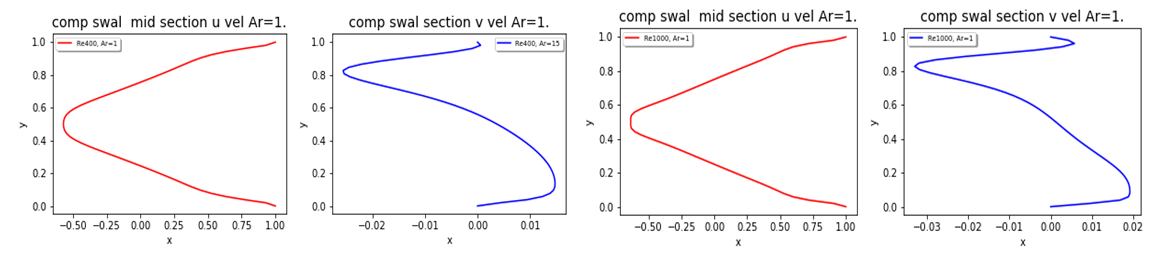 | Figure 14. Plots of u and v velocity components at mid-section for Re=400 and Re=1000 from fv solver |
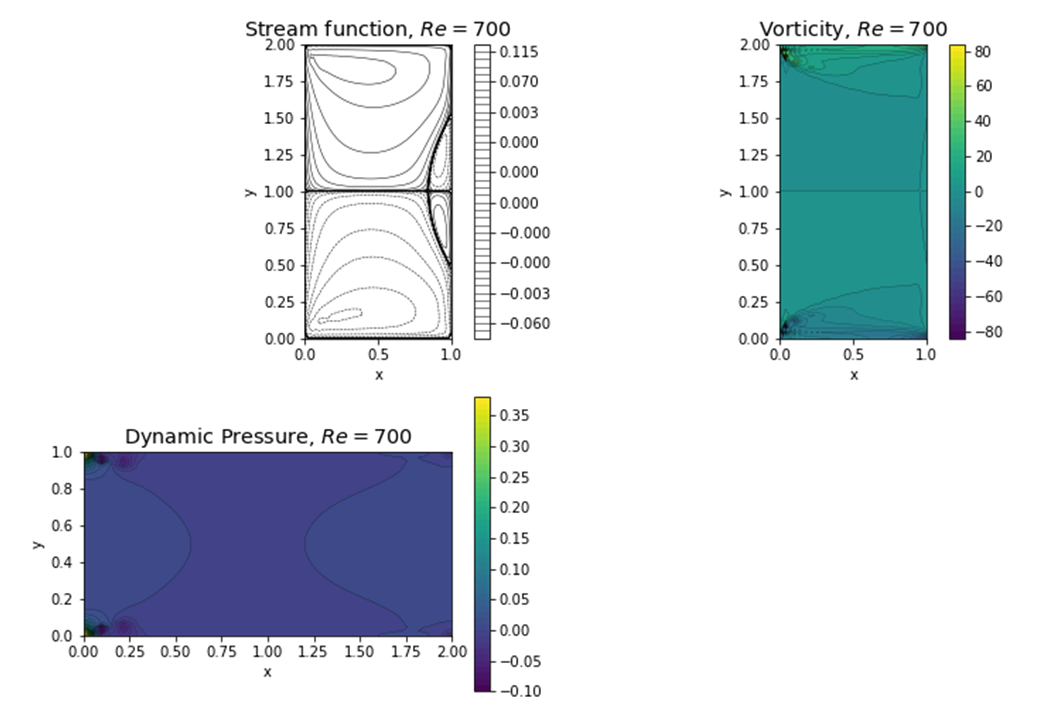 | Figure 15. Plots of psi, vorticity, pressure, u and v velocity for Re=700, Ar=2 from fv solver |
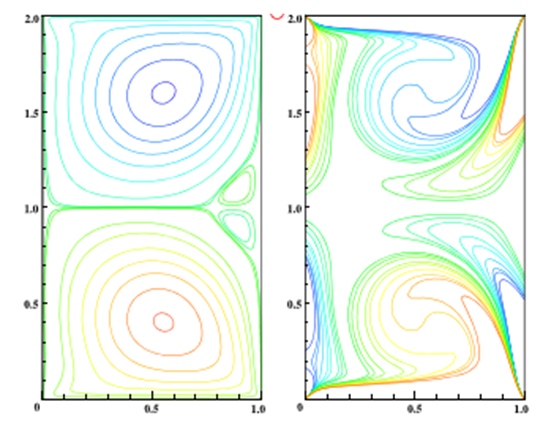 | Figure 16. Plots of psi, and vorticity for Re=700, Ar=2 from LB method |
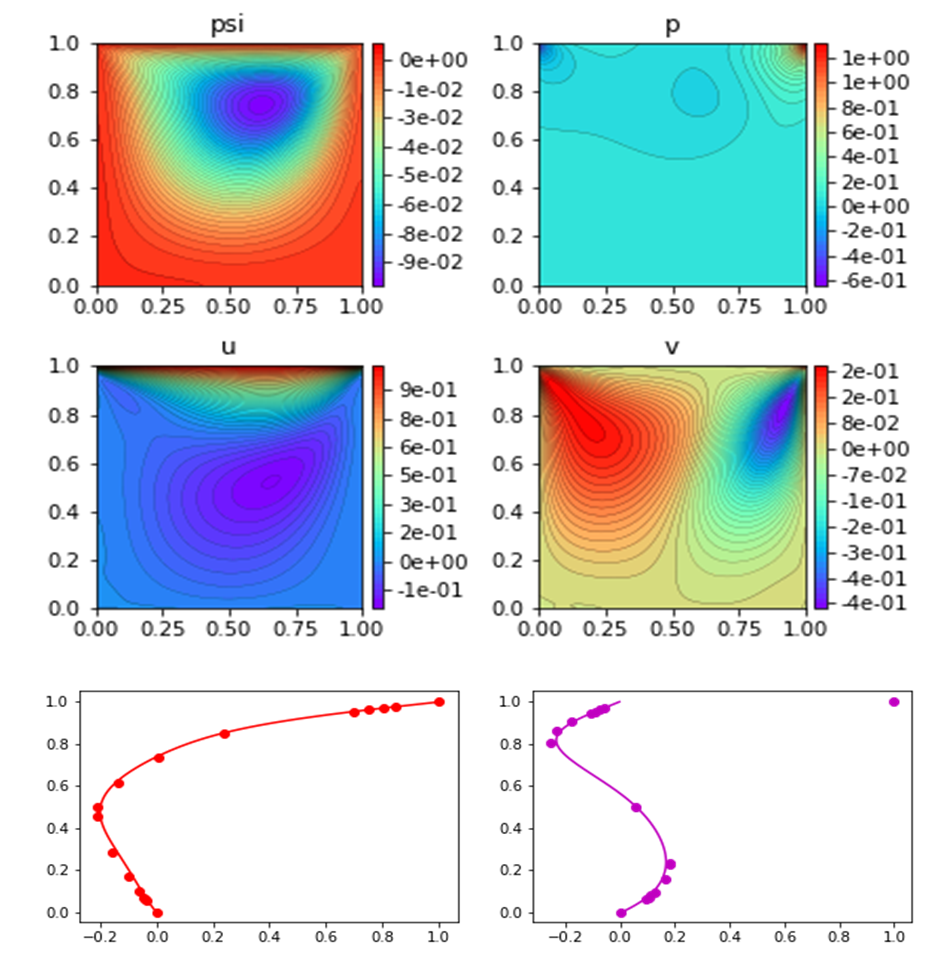 | Figure 17. Plots of psi, p, u, v, and u-, v- velocity components at mid-section for Re=100 |
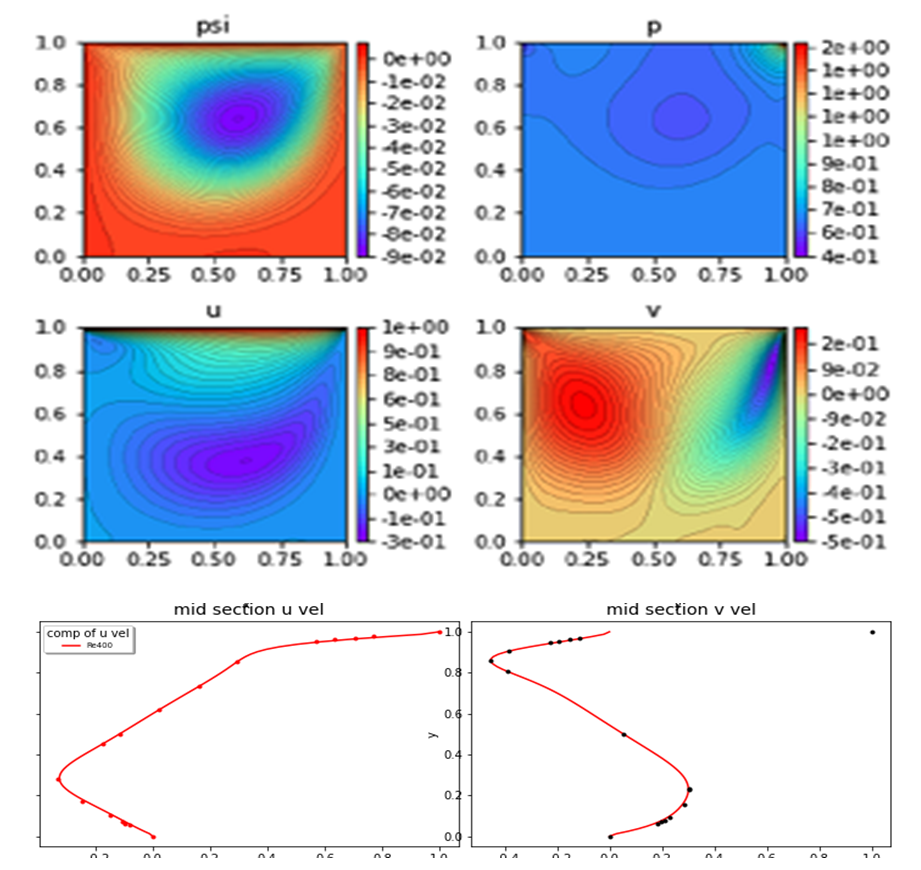 | Figure 18. Plots of psi, p, u, v, and u-, v- velocity components at mid-section for Re=400 |
 | Figure 19. Plots of u, v, and p for Re=400 |
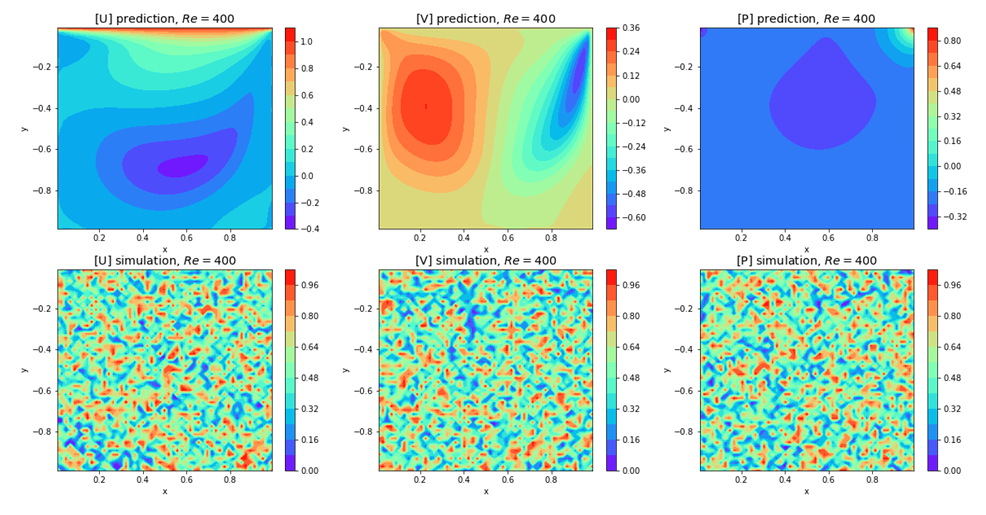 | Figure 20. Plots of u, v, and p for Re=400 with random predictive samples |
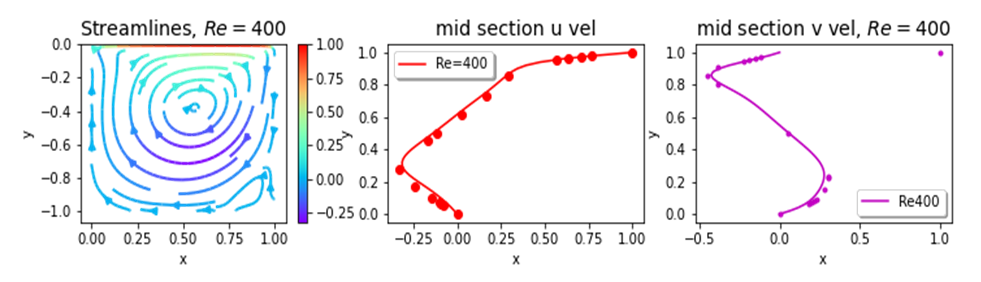 | Figure 21. Plots of psi, u, v at mid sections for Re=400 |
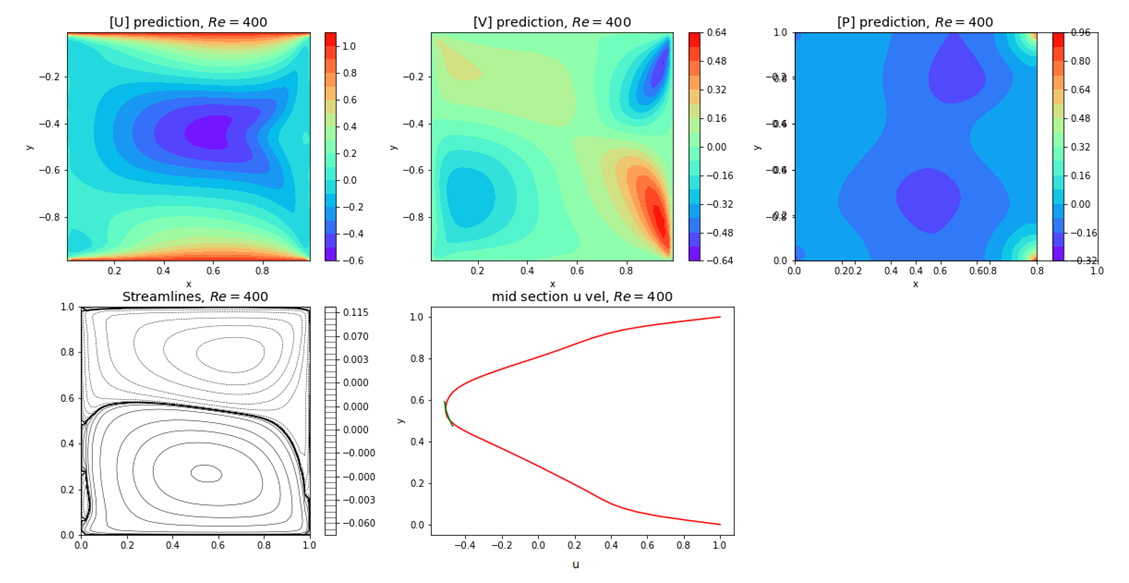 | Figure 22. Plots of u, v, p, psi and u-, v- velocity components at mid-section for Re=400 and for top and bottom walls moving in same direction with unit velocity |
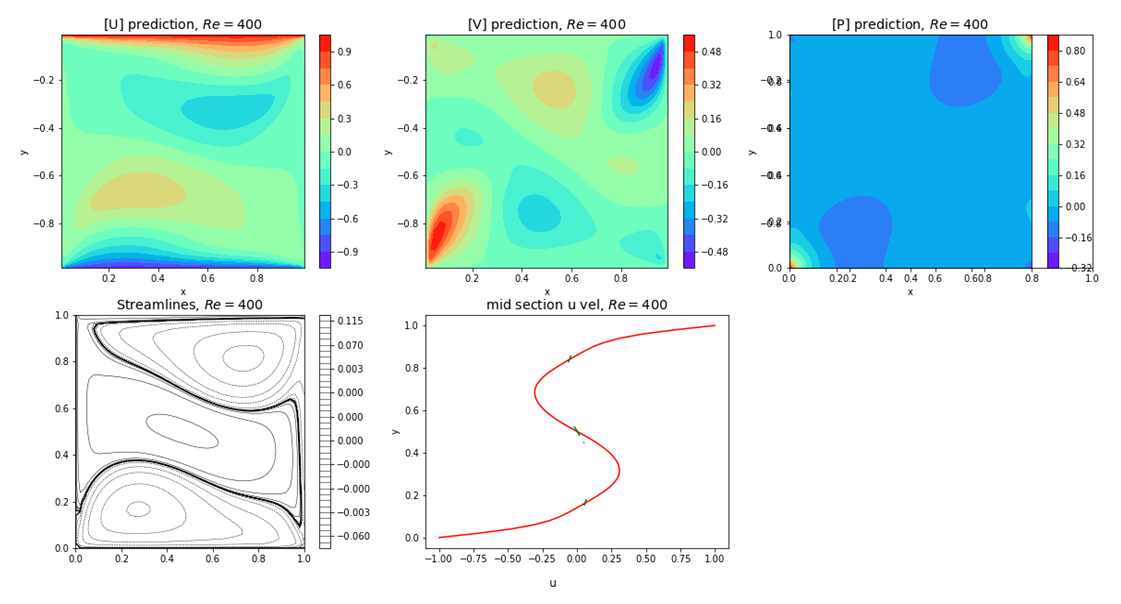 | Figure 23. Plots of u, v, p, psi and u-, v- velocity components at mid-section for Re=400 and for top and bottom walls moving in opposite directions with unit velocity |
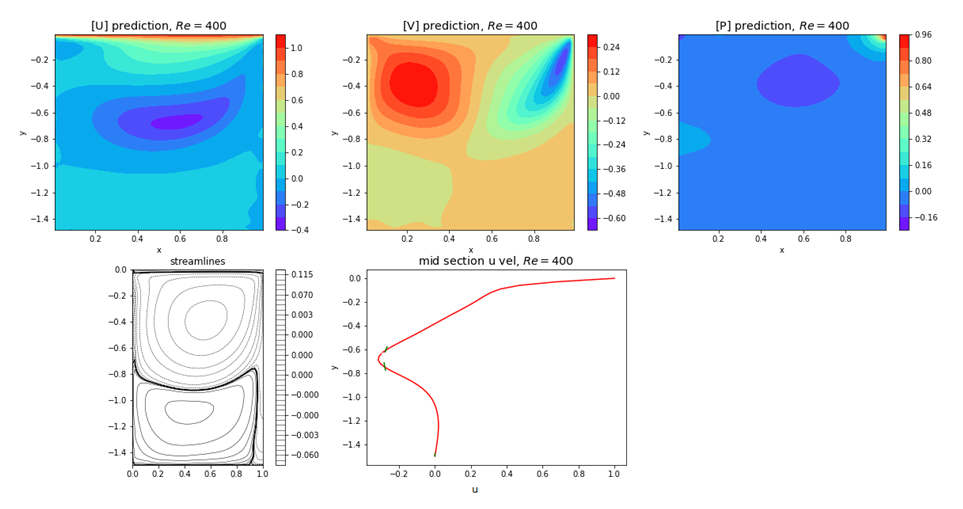 | Figure 24. Plots of u, v, p, psi and u-, v- velocity components at mid-section for Re=400 and for Ar=1.5 |
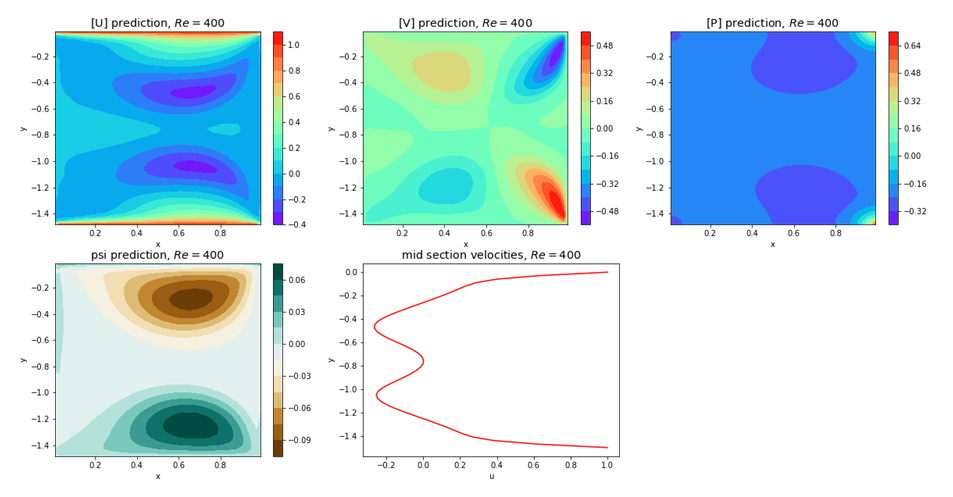 | Figure 25. Plots of u, v, p, psi and u-, v- velocity components at mid-section for Re=400 and for Ar=1.5, and top and bottom walls moving in same direction |
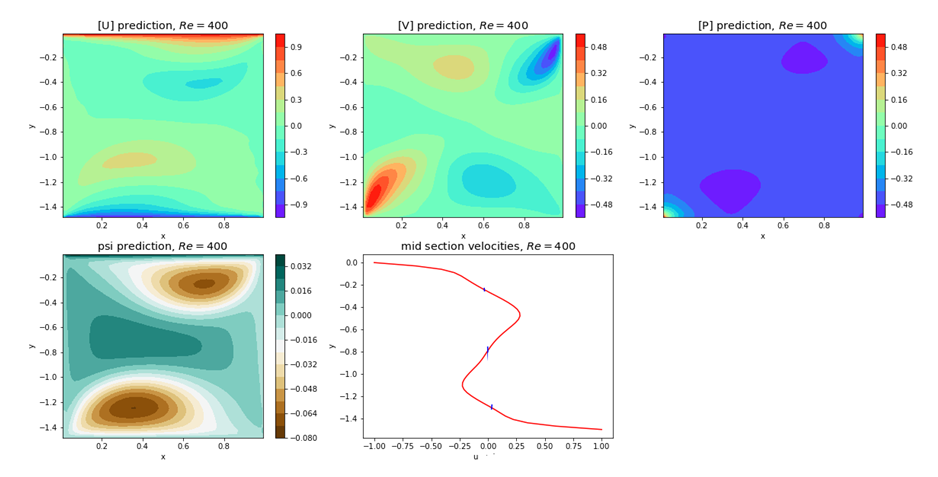 | Figure 26. Plots of u, v, p, psi and u-, v- velocity components at mid-section for Re=400 and for Ar=1.5, and top and bottom walls moving in opposite direction |
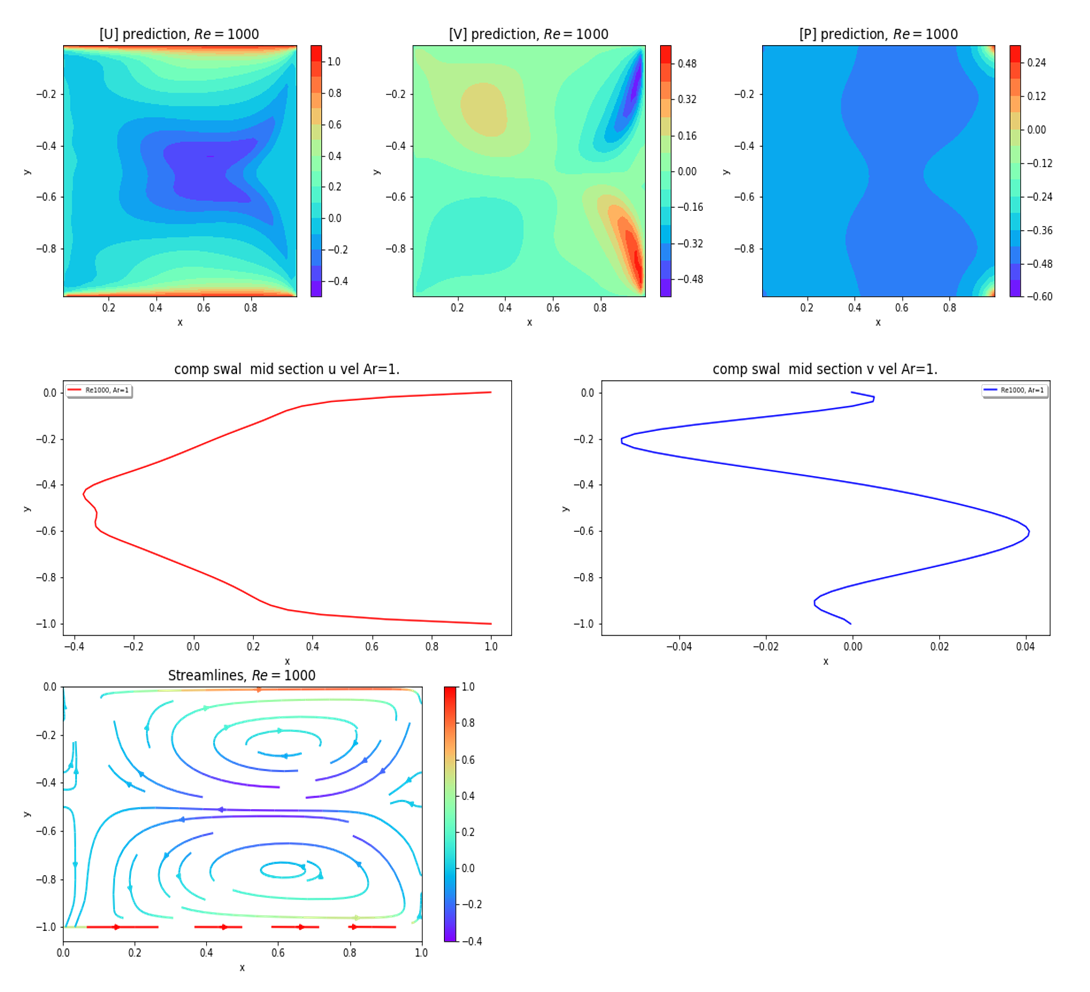 | Figure 27. Plots of u, v, p, psi and u-, v- velocity components at mid-section for Re=1000 and for top and bottom walls moving in the same direction with unit velocity |
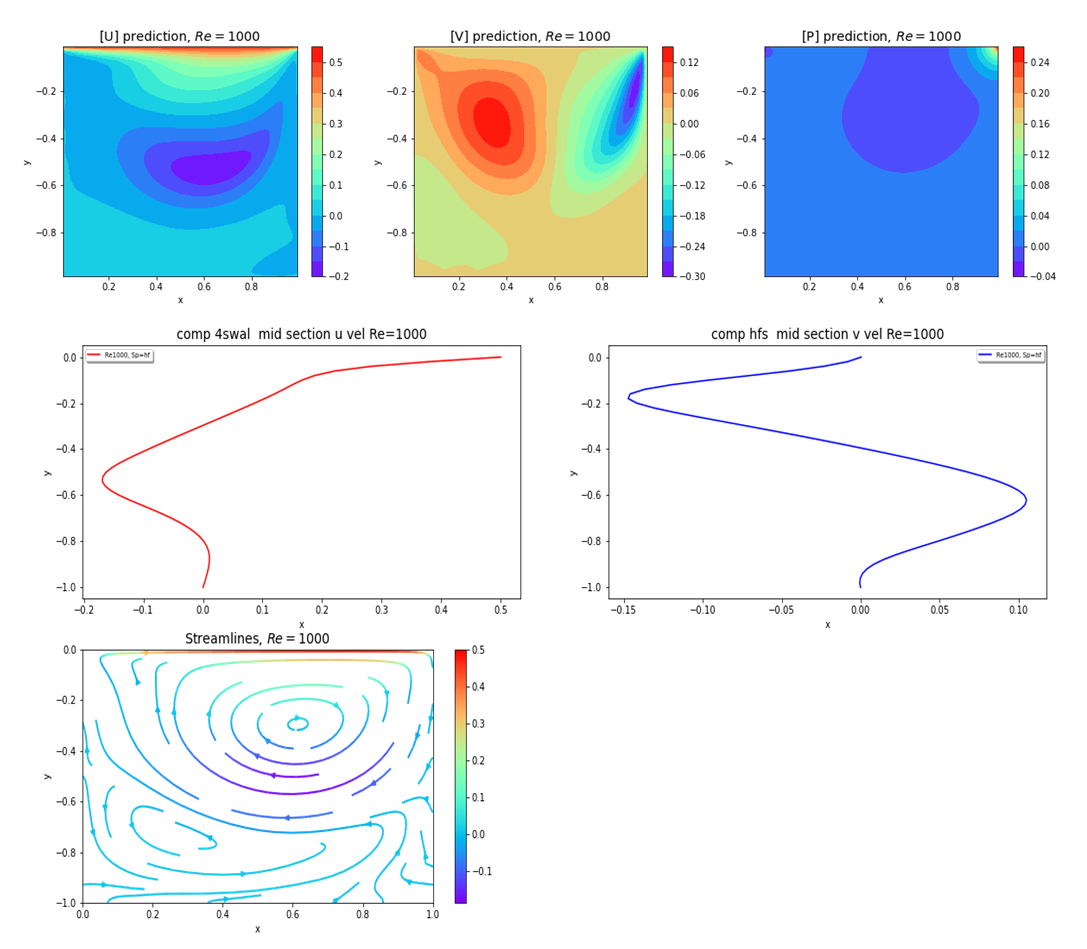 | Figure 28. Plots of u, v, p, psi and u-, v- velocity components at mid-section for Re=1000 and for top wall moving with half speed |
3. Conclusions
- The present finite volume solver seems to be capable of running the cavity flow problem from moderate to high Reynolds numbers. The results compare well with finite volume and LB results which seem to be a good benchmark for cavity flow analysis. A few physics informed neural network works were reviewed. The use of external CFD solution seems to be unwarranted. Since machine learning is based on random simulations, so random simulation is the best way to go. The ability of PINN codes to run at high Reynolds number was examined. A few cases were run for Re=1000 where additional viscosity was induced by wall motions. This was just a preliminary concept. More work needs to be done by Academicians to overcome this issue.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML