-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2021; 11(1): 5-12
doi:10.5923/j.ajfd.20211101.02
Received: Mar. 14, 2021; Accepted: Apr. 2, 2021; Published: May 15, 2021

Confluence Flow of Two Mixing Rivers: A Hydrodynamic View
Ighoroje W. A. Okuyade1, Tamunoimi M. Abbey2, Aloysius T. Gima-Laabel3
1School of Applied Sciences, Federal Polytechnic of Oil and Gas, Bonny Island, Nigeria
2Applied Mathematics and Theoretical Physics Group, Department of Physics, University of Port Harcourt, Port Harcourt, Nigeria
3Department of Applied Mathematics, CypherCrescent Limited, Port Harcourt, Nigeria
Correspondence to: Ighoroje W. A. Okuyade, School of Applied Sciences, Federal Polytechnic of Oil and Gas, Bonny Island, Nigeria.
| Email: |  |
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A magneto-hydrodynamic model of the merging flow of two rivers is presented. The governing non-linear partial differential equations are reduced to single independent variable problems using the similarity transformation. The resulting equations are linearized using the regular perturbation series expansion solutions, and solved for the velocity characteristic. Expressions for the velocity are quantified and presented graphically. The analyses of results show that increase in the magnetic field strength and merging angle reduce the flow velocity, whereas the increase in the Grashof number increases it. The concurrencies of the parameter effects make some to cushion the others. The results have some significant implications on transport of the bed-loads/sediments in the rivers courses toward standing water bodies.
Keywords: Confluence flow, Hydrodynamic, Mixing rivers
Cite this paper: Ighoroje W. A. Okuyade, Tamunoimi M. Abbey, Aloysius T. Gima-Laabel, Confluence Flow of Two Mixing Rivers: A Hydrodynamic View, American Journal of Fluid Dynamics, Vol. 11 No. 1, 2021, pp. 5-12. doi: 10.5923/j.ajfd.20211101.02.
1. Introduction
- A confluence is a place where two flows with the same or different characteristics merge. The flow may be natural or artificial. Specifically, two or more water bodies (rivers, streams, lakes, or canals) may collide, conflux, or merge to form a new single flowing water body. When two rivers merge to become the source of a new one, in some cases, the waters may mix, as in the confluences of Rivers Ilz, Danube, and Inn in Passau, Germany; Jialing and Yangtze in Chongqing, China; Thompson and Frazer in Lytton, British Columbia, Canada; Benue and Niger in Nigeria. In other cases, they may not mix, as in the confluences of Rivers Ohio and Mississipi at Cairo, Illinois in the USA; Rio Negro and Rio Solimoes, near Manaus, Brazil; see [1].The merging of rivers takes many forms. In some, a small river (the lateral flow) enters a large one (the main flow) to form an open channel flow, as in tributaries; in others, two non-parallel rivers flowing in approximately the same direction meet at a point to form a single stream. The merging rivers rising from mountains whose gradients, the chemical composition of the source rocks, and environmental climatic conditions are different are bound to have different velocities, chemical compositions, temperature and colours, geological properties, etc. Similarly, river confluence flows are characterized by significant changes in flow dynamics, sediment transport, and bed morphology. Merging flow problems have been studied in a diversified manner. Some studied the merging flow of blood in arteries, and many others, the confluence flow of rivers and streams. On merging blood flow, [2] considered the flow through a straight channel with an upstream splitter plate; [3], neglecting the effects of pulsatility, investigated a two-dimensional merging blood flow in a basilar artery using geometrical transformation, conformal mapping, and numerical approaches. More so, on a general note, [4] numerically examined a steady two-dimensional asymmetric merging flow of micro-polar fluid in a rectangular channel. Similarly, the merging flow of two rivers has been studied from different perspectives. Some studied it ecologically [5], some hydro-dynamically [6] - [14]); some sedimentologically ([15] - [17]); some through laboratory experiments ([18], [19]), and others by field survey ([20] - [23]). Importantly, on a hydro-dynamic review of reports, [24] studied the flow dynamics of an open confluence flow for several merging angles and discharge ratios, and noticed that the flow has six hydro-dynamic regions: flow deflection, flow stagnation, flow separation, maximum velocity, shear layer, and flow recovery; the flow is characterized by helical flow cells. [9] studied the mixing processes in laboratory and field confluences using a 3-D Re-Normalization Group Theory (RNG)
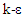 turbulence model and showed the difference between concordant (equal bed levels) and discordant (uneven bed levels) rivers, and the effects of the channels curvatures on the flow mixing. [12] investigated the combined hydrodynamic, sediment transport, and mixing processes in large confluences using a field study approach, water quality, and seismic profile measurement, and observed the key hydrodynamic features of large confluences. [14] gave a review of the flow dynamics and sediment transport at open channel confluences, but with a focus on the link between flow dynamics, sediment transport, and bed morphology.Upon the above reports, it is evident that many of the studies on the confluence flow of rivers were carried out using field surveys, experiments, simulations, and otherwise. This paper presents an analytic model of the hydrodynamic behaviour of the mix-merging flow of two rivers with different flow characteristics. We investigate among others, the effects of some important hydro-dynamic parameters on the flow and transport of bed-loads/sediments. This paper is organized as follows: section 2 is the Methodology; section 3 is the Conclusion.
turbulence model and showed the difference between concordant (equal bed levels) and discordant (uneven bed levels) rivers, and the effects of the channels curvatures on the flow mixing. [12] investigated the combined hydrodynamic, sediment transport, and mixing processes in large confluences using a field study approach, water quality, and seismic profile measurement, and observed the key hydrodynamic features of large confluences. [14] gave a review of the flow dynamics and sediment transport at open channel confluences, but with a focus on the link between flow dynamics, sediment transport, and bed morphology.Upon the above reports, it is evident that many of the studies on the confluence flow of rivers were carried out using field surveys, experiments, simulations, and otherwise. This paper presents an analytic model of the hydrodynamic behaviour of the mix-merging flow of two rivers with different flow characteristics. We investigate among others, the effects of some important hydro-dynamic parameters on the flow and transport of bed-loads/sediments. This paper is organized as follows: section 2 is the Methodology; section 3 is the Conclusion.2. Methodology
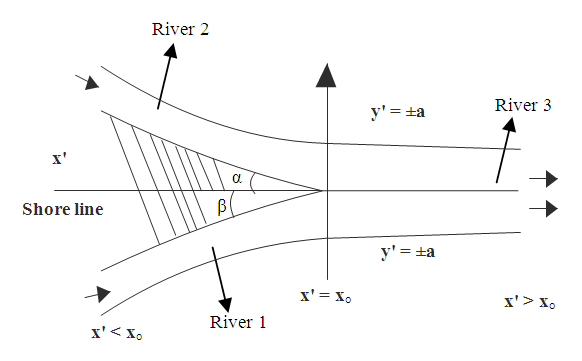 | Figure 1. A physical model of symmetrical confluxing flowing rivers (α=β) |
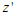 -axis. Therefore, if
-axis. Therefore, if 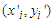 and
and 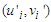 are mutually orthogonal axes and the associated velocity components;
are mutually orthogonal axes and the associated velocity components; 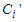 and
and 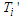 are the concentration and temperature of the waters in the merging channels,
are the concentration and temperature of the waters in the merging channels, 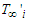 and
and 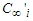 are the equilibrium concentration and temperature of the waters in the merging channels, then by the Boussinesq approximations, the equation of mass balance, momentum, energy, and diffusion guiding the flow are as follows:
are the equilibrium concentration and temperature of the waters in the merging channels, then by the Boussinesq approximations, the equation of mass balance, momentum, energy, and diffusion guiding the flow are as follows: | (1) |
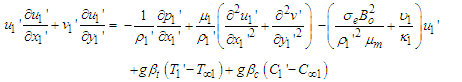 | (2) |
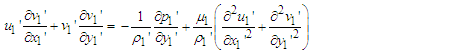 | (3) |
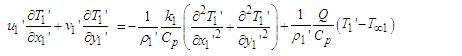 | (4) |
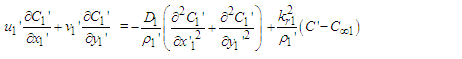 | (5) |
 | (6) |
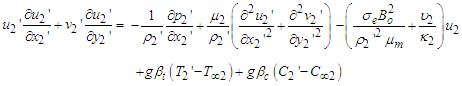 | (7) |
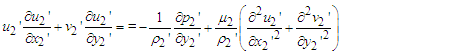 | (8) |
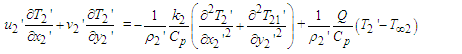 | (9) |
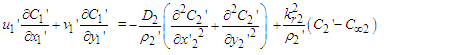 | (10) |
 | (11) |
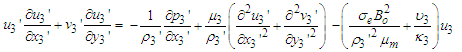 | (12) |
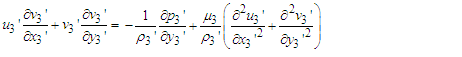 | (13) |
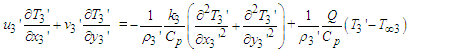 | (14) |
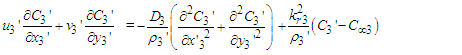 | (15) |
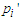 are the flow pressures;
are the flow pressures; 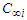 are the concentrations of the waters at equilibrium;
are the concentrations of the waters at equilibrium; 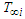 are the waters temperatures at equilibrium;
are the waters temperatures at equilibrium; 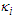 are the permittivity of the rivers channel;
are the permittivity of the rivers channel; 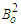 is the applied uniform magnetic field strength due to the nature of the waters;
is the applied uniform magnetic field strength due to the nature of the waters; 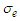 is the electrical conductivity of the waters;
is the electrical conductivity of the waters; 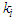 are the thermal conductivities of the waters.
are the thermal conductivities of the waters. 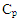 is the specific heat capacity of the waters at constant pressure;
is the specific heat capacity of the waters at constant pressure; 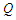 is the heat absorption coefficient;
is the heat absorption coefficient; 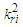 are the rates of chemical reaction of the waters;
are the rates of chemical reaction of the waters; 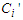 are the concentrations (quantities of material being transported);
are the concentrations (quantities of material being transported); 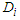 are the diffusion coefficient of the waters; g is gravitational field vector;
are the diffusion coefficient of the waters; g is gravitational field vector; 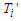 are the waters temperatures;
are the waters temperatures; 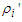 are the densities of the waters.
are the densities of the waters. 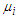 are the viscosities of the waters;
are the viscosities of the waters; 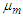 is the magnetic permittivity of the waters;
is the magnetic permittivity of the waters; 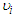 are the kinematic viscosities of the waters. River 3 is flowing with the combined flow variables of rivers 1 and 2 such that
are the kinematic viscosities of the waters. River 3 is flowing with the combined flow variables of rivers 1 and 2 such that 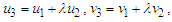
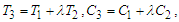
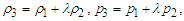
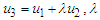 is a positive fraction.The physical model of the merging/confluence problem is given in Fig. 1. Rivers 1 and 2 are flowing from different sources/mountains
is a positive fraction.The physical model of the merging/confluence problem is given in Fig. 1. Rivers 1 and 2 are flowing from different sources/mountains 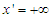 , merge at
, merge at 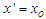 , and continued towards a standing water body
, and continued towards a standing water body 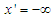 . Upon this, the model is divided into two regions: the upstream region
. Upon this, the model is divided into two regions: the upstream region 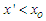 and downstream region
and downstream region 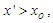 with
with 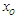 as the nodal or merging point. More so, for the geometric transition occurring between the merging rivers and the confluent river, the problem of the wall curvature effect exists. To cater for this, we take a simple transition wherein the breadths of each of the rivers are assumed equal to half that of the confluent river, that is,
as the nodal or merging point. More so, for the geometric transition occurring between the merging rivers and the confluent river, the problem of the wall curvature effect exists. To cater for this, we take a simple transition wherein the breadths of each of the rivers are assumed equal to half that of the confluent river, that is, 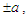 and
and 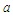 is non-dimensionally taken to be unity such that the merging angle is directly used (see [25]). Upon this, the boundaries become
is non-dimensionally taken to be unity such that the merging angle is directly used (see [25]). Upon this, the boundaries become 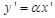 in the upstream and
in the upstream and 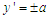 the downstream. Similarly, we assume the velocity of the merger-river to be
the downstream. Similarly, we assume the velocity of the merger-river to be 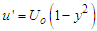 .Now, the boundaries conditions are:
.Now, the boundaries conditions are: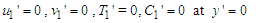 | (16) |
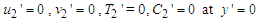 | (17) |
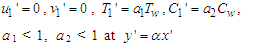 | (18) |
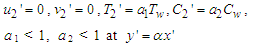 | (19) |
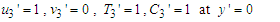 | (20) |
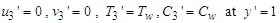 | (21) |
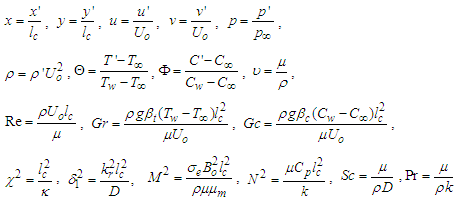 | (22) |
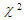 is the local Darcy number; M2 is the Hartmann’s number; Pr is the Prandtl number; Sc is the Schmidt number;
is the local Darcy number; M2 is the Hartmann’s number; Pr is the Prandtl number; Sc is the Schmidt number; 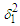 is the rate of a chemical reaction, and N2 is the heat exchange parameter;
is the rate of a chemical reaction, and N2 is the heat exchange parameter; 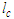 is the scaled length,
is the scaled length, 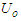 is the characteristic velocity, which is maximum at the centre and zero at the wall,
is the characteristic velocity, which is maximum at the centre and zero at the wall, 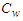 and
and 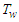 are concentration and temperature, respectively at which the river walls are maintained,
are concentration and temperature, respectively at which the river walls are maintained,  and
and 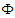 are the dimensionless temperature and concentration,
are the dimensionless temperature and concentration, 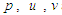 and
and 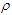 are dimensionless pressure, velocity in the x-axis, velocity in the y-axis and density, respectively;
are dimensionless pressure, velocity in the x-axis, velocity in the y-axis and density, respectively; 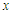 and
and 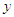 are the dimensionless x- and y- axes, respectively, and
are the dimensionless x- and y- axes, respectively, and 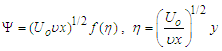 | (23) |
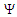 is the stream function, and
is the stream function, and 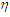 is the independent variable of the stream function, and
is the independent variable of the stream function, and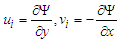 | (24) |
 | (25) |
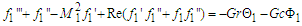 | (26) |
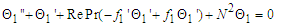 | (27) |
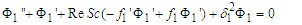 | (28) |
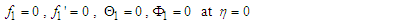 | (29) |
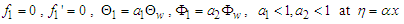 | (30) |
 | (31) |
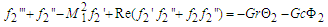 | (32) |
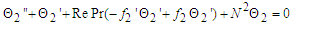 | (33) |
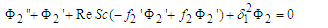 | (34) |
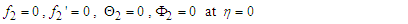 | (35) |
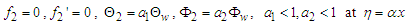 | (36) |
 | (37) |
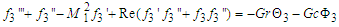 | (38) |
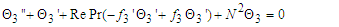 | (39) |
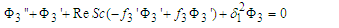 | (40) |
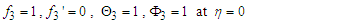 | (41) |
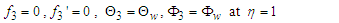 | (42) |
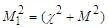 Equations (25) - (28), (32) - (34) and (37) - (40) are non-linear and coupled. Making them tractable, we seek for the perturbation series expansion solutions of the form:
Equations (25) - (28), (32) - (34) and (37) - (40) are non-linear and coupled. Making them tractable, we seek for the perturbation series expansion solutions of the form: 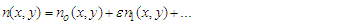 | (43) |
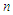 represents the flow dependent variables,
represents the flow dependent variables, 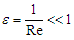 is the perturbation parameter. The choice of this parameter is based on the fact that, at the merging point, the interaction of the two rivers creates a sort of turbulence, implying an increase in the Reynolds number.
is the perturbation parameter. The choice of this parameter is based on the fact that, at the merging point, the interaction of the two rivers creates a sort of turbulence, implying an increase in the Reynolds number. 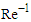 will therefore give a very small value by which the problem is perturbed. It is interesting to note that the turbulence effects decay away some distances from the merging point and the flow normalizes.Substituting equation (43) into equations (25) - (42) yields a set of equations that require some analysis. On the analysis of flow, we shall invoke the Kirchhoff Law of the flow of materials at the junction wherein the quantity of materials entering the junction is said to be equal to the total quantity of materials leaving the junction. Impliedly, the quantity of water/materials leaving Rivers 1and 2 for the junction is equal to the total quantity of water/materials in River 3. This tends to explain the fact that River 3 is the combined continuation of Rivers 1and 2. On this premise, we seek for approximate solutions to describe the problem. We choose the order zero equations as the equations describing the flow characteristics of Rivers 1 and 2 in the unperturbed state of flow, and the order one equations for River 3 as those describing the perturbed state of the flow downstream. Following this, the order one equations for the upstream flow and order zero equations for the downstream flow are played down. So, our working equations are reduced to
will therefore give a very small value by which the problem is perturbed. It is interesting to note that the turbulence effects decay away some distances from the merging point and the flow normalizes.Substituting equation (43) into equations (25) - (42) yields a set of equations that require some analysis. On the analysis of flow, we shall invoke the Kirchhoff Law of the flow of materials at the junction wherein the quantity of materials entering the junction is said to be equal to the total quantity of materials leaving the junction. Impliedly, the quantity of water/materials leaving Rivers 1and 2 for the junction is equal to the total quantity of water/materials in River 3. This tends to explain the fact that River 3 is the combined continuation of Rivers 1and 2. On this premise, we seek for approximate solutions to describe the problem. We choose the order zero equations as the equations describing the flow characteristics of Rivers 1 and 2 in the unperturbed state of flow, and the order one equations for River 3 as those describing the perturbed state of the flow downstream. Following this, the order one equations for the upstream flow and order zero equations for the downstream flow are played down. So, our working equations are reduced to | (44) |
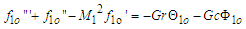 | (45) |
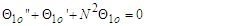 | (46) |
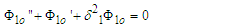 | (47) |
 | (48) |
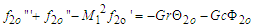 | (49) |
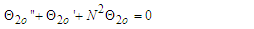 | (50) |
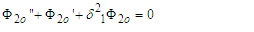 | (51) |
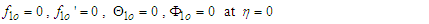 | (52) |
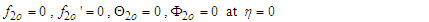 | (53) |
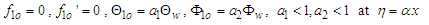 | (54) |
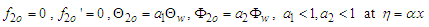 | (55) |
 | (56) |
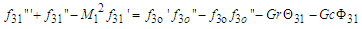 | (57) |
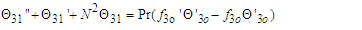 | (58) |
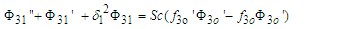 | (59) |
 | (60) |
 | (61) |
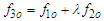 , we get
, we get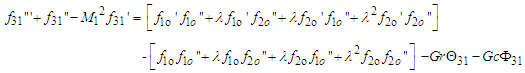 | (62) |
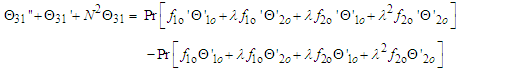 | (63) |
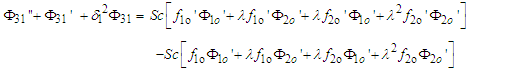 | (64) |
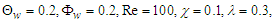
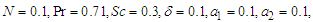 and varied values of
and varied values of 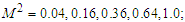
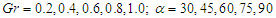 we obtained the graphs shown below. The figures show that the flow velocity is decreased by the increase in the magnetic field strength and merging angles but increases by the increase in the convective currents.
we obtained the graphs shown below. The figures show that the flow velocity is decreased by the increase in the magnetic field strength and merging angles but increases by the increase in the convective currents. 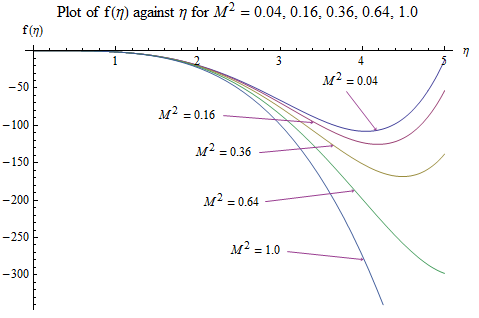 | Figure 2. Velocity (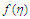 )-Magnetic field ( )-Magnetic field (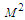 ) profiles for ) profiles for 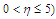 |
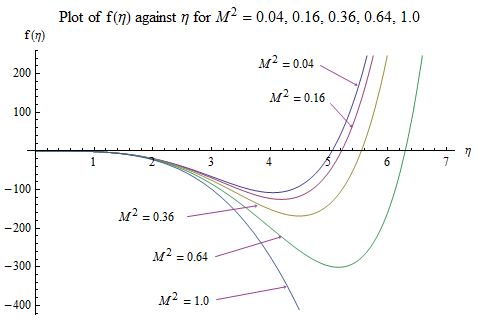 | Figure 3. Velocity (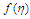 )-Magnetic field ( )-Magnetic field (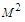 ) profiles for ) profiles for 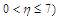 |
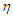 has some effects on the flow patterns; as can be seen in Fig. 2 and Fig. 3.In a similar development, the porosity of the river channels has the same effects on the velocity as the magnetic field parameter.
has some effects on the flow patterns; as can be seen in Fig. 2 and Fig. 3.In a similar development, the porosity of the river channels has the same effects on the velocity as the magnetic field parameter. | Figure 4. Velocity (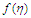 )-Grashof number ( )-Grashof number ( ) profiles for ) profiles for 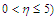 |
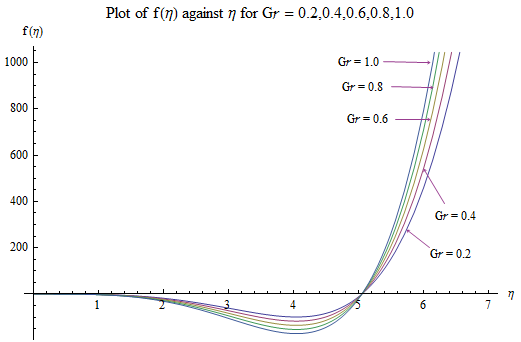 | Figure 5. Velocity (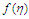 )-Grashof number ( )-Grashof number (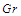 ) profiles for ) profiles for 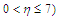 |
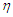 on the flow pattern are seen in Fig. 4 and Fig. 5. For
on the flow pattern are seen in Fig. 4 and Fig. 5. For 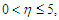 the profiles tends to converge at
the profiles tends to converge at 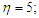 for
for 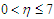 , the profiles converge at
, the profiles converge at 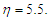 At this point, a flow separation, which may be due to an adverse flow condition, wherein
At this point, a flow separation, which may be due to an adverse flow condition, wherein 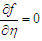 is noticed. A short distance from this point, the profiles become distinct.More so, the results here are applicable when the Grashof number which is due to the chemical concentration of the water is considered.
is noticed. A short distance from this point, the profiles become distinct.More so, the results here are applicable when the Grashof number which is due to the chemical concentration of the water is considered.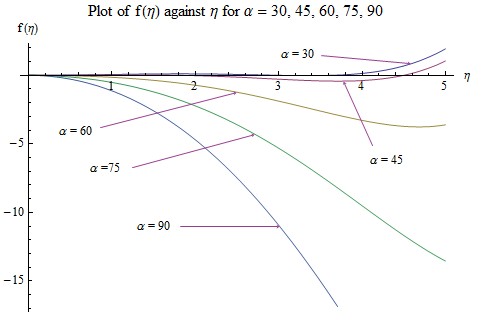 | Figure 6. Velocity (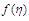 )-Confluence angle ( )-Confluence angle ( ) profiles for ) profiles for  |
 | Figure 7. Velocity (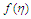 )-Confluence angle ( )-Confluence angle (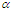 ) profiles for ) profiles for 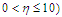 |
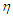 on the flow pattern, in the presence of the merging angle can be seen in Fig. 6 and Fig. 7.The results show that, apart from the existing gradient/slope between the river and the source mountain, mass volume of the water, depth of the river, gravity, amidst others, hydrodynamic parameters affect the river flow, and subsequently affect the transport of the bed-loads/sediments. Usually, as the river flows downwards from the mountains, the particles eroded are carried along with them as bed-loads/sediments. The gradient effect highly enhances their transport in the upper and middle zones of the river, where velocities are high and moderate, respectively. The gradient effects subside or are decayed in the depositional zone. Naturally, the other factors and hydro-dynamic parameters effects take sway completely. Specifically, the decrease in the velocity by the increase in the magnetic field and porosity parameters and merging angle retard the transport of the bed-loads/sediments, thus causing early deposition of the materials and shallowing-up of the river. On the other hand, the increase in velocity through the increase in the convective currents and Reynolds number enhances the transport of the bed-loads/sediments, thus delaying the shallowing-up of the river in its course towards a standing water body.
on the flow pattern, in the presence of the merging angle can be seen in Fig. 6 and Fig. 7.The results show that, apart from the existing gradient/slope between the river and the source mountain, mass volume of the water, depth of the river, gravity, amidst others, hydrodynamic parameters affect the river flow, and subsequently affect the transport of the bed-loads/sediments. Usually, as the river flows downwards from the mountains, the particles eroded are carried along with them as bed-loads/sediments. The gradient effect highly enhances their transport in the upper and middle zones of the river, where velocities are high and moderate, respectively. The gradient effects subside or are decayed in the depositional zone. Naturally, the other factors and hydro-dynamic parameters effects take sway completely. Specifically, the decrease in the velocity by the increase in the magnetic field and porosity parameters and merging angle retard the transport of the bed-loads/sediments, thus causing early deposition of the materials and shallowing-up of the river. On the other hand, the increase in velocity through the increase in the convective currents and Reynolds number enhances the transport of the bed-loads/sediments, thus delaying the shallowing-up of the river in its course towards a standing water body.3. Conclusions
- A hydro-dynamic confluence flow model of two rivers is presented. The effects of some parameters: magnetic field strength, convective currents and merging angle on the flow velocity structure are investigated. The analysis of results shows that the increase in• magnetic field decreases the velocity, • Grashof number increases the velocity, and • merging angle decreases the velocity. The effects of these parameters on the flow have attendant implications on the transport of river bed-load/sediments.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML