-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2019; 9(1): 1-12
doi:10.5923/j.ajfd.20190901.01

Theoretical Study of the Behavior of a Hydraulic Ram Pump with Springs System
Andriamahefasoa Rajaonison, Hery Tiana Rakotondramiarana
Institute for the Management of Energy (IME), University of Antananarivo, Antananarivo, Madagascar
Correspondence to: Andriamahefasoa Rajaonison, Institute for the Management of Energy (IME), University of Antananarivo, Antananarivo, Madagascar.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A new type of hydraulic ram pump, called Raseta pump, was invented, patented and crafted in Madagascar. The peculiarity of this hydram pump over conventional ones is that there is a spring in each of the waste and delivery valves. In addition, the usual air balloon is replaced by a balloon with 4 springs. Thus, this paper aims at theoretically studying the behaviour of this hydram pump equipped with a system of springs. For that purpose, a model associated with the studied hydram pump was developed and coded on Matlab. Then, a global sensitivity analysis was carried out for identifying the most influential parameters of this model while successively considering as the surveyed model outputs: the amount of wasted water, the amount of pumped water and the efficiency of the pump. As results, the most dominating parameters are relatively the same as those found by previous works on the conventional hydram pump without springs: height of the water column in the delivery pipe, the height of supply tank, the weight of the waste valve, and the length of the waste valve stroke. However, there are 3 other parameters that the present study exceptionally found as among the most influential ones as well, namely: the stiffness of the spring in the waste valve, the modulus of elasticity of the fluid, and the radius of the waste valve disk. In addition, similar to the case of air balloon, the effect of the spring balloon is not relevant. An extension work could be a techno-economic investigation of a pump system constituted by a number of hydram pumps similar to the one studied here for increasing water head in a pico hydropower plant.
Keywords: Hydram pump, Water supply, Bernoulli equation, Raseta pump, Modelling, Global sensitivity analysis
Cite this paper: Andriamahefasoa Rajaonison, Hery Tiana Rakotondramiarana, Theoretical Study of the Behavior of a Hydraulic Ram Pump with Springs System, American Journal of Fluid Dynamics, Vol. 9 No. 1, 2019, pp. 1-12. doi: 10.5923/j.ajfd.20190901.01.
Article Outline
1. Introduction
- The hydraulic ram pump, which is simply called hydram pump from now on, was invented by Joseph Michel Montgolfier by the end of the 18th century [1]. Used as a water supply machine, this pump uses the energy of water to raise a certain water amount to a height much higher than that of the initial watercourse [1]. This process is based on a phenomenon known as "water hammer" [2] which is a shock wave created by the sudden stop of moving water [3]. In other words, the kinetic energy of a water column having taken a certain speed is stopped suddenly by a valve which creates an overpressure [4, 5]. This harmful phenomenon for pipelines [6] is used in the hydram pump to raise water without any other source of energy than that of the water itself [7]. Several studies were carried out on hydram pump which generally has six main components [5, 8, 9] as can be seen from Figure 1.
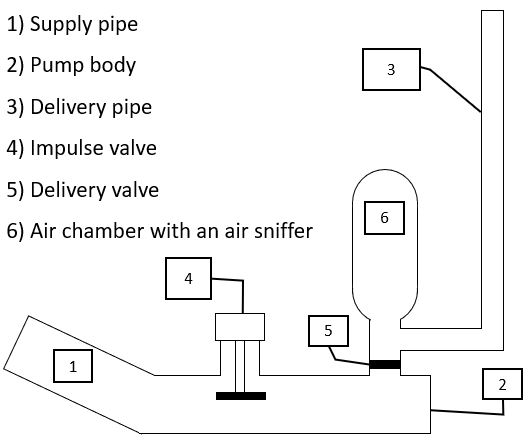 | Figure 1. Components of a conventional hydram pump |
2. Materials and Methods
2.1. Description of the Functioning of Hydram Pump System to Model
- The hydram is fed by a source which is a tank or stabilization tank itself fed by a river, a watercourse, etc. The pumped water is then stored in a tank for later use (Figure 2).
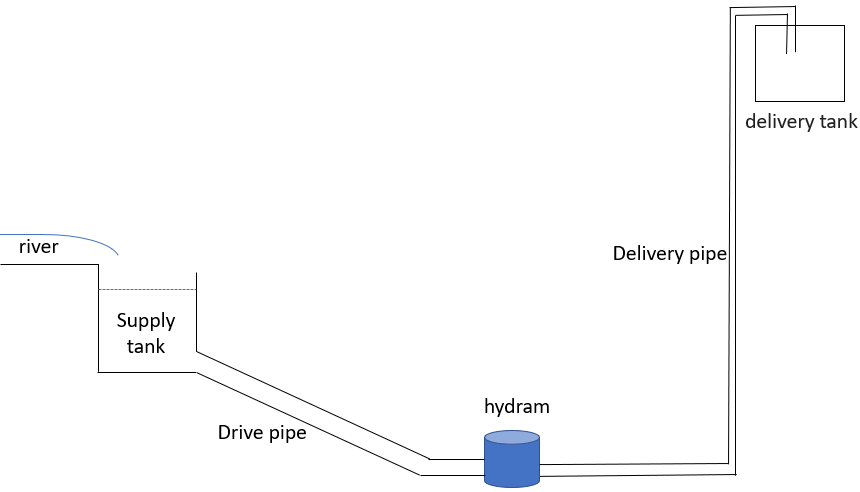 | Figure 2. Overview of the pumping system |
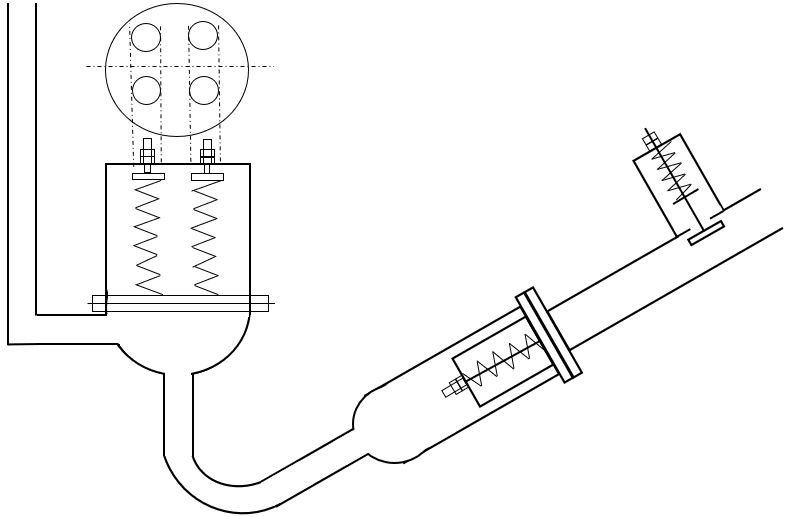 | Figure 3. Scheme of the studied hydram pump with system of springs [22] |
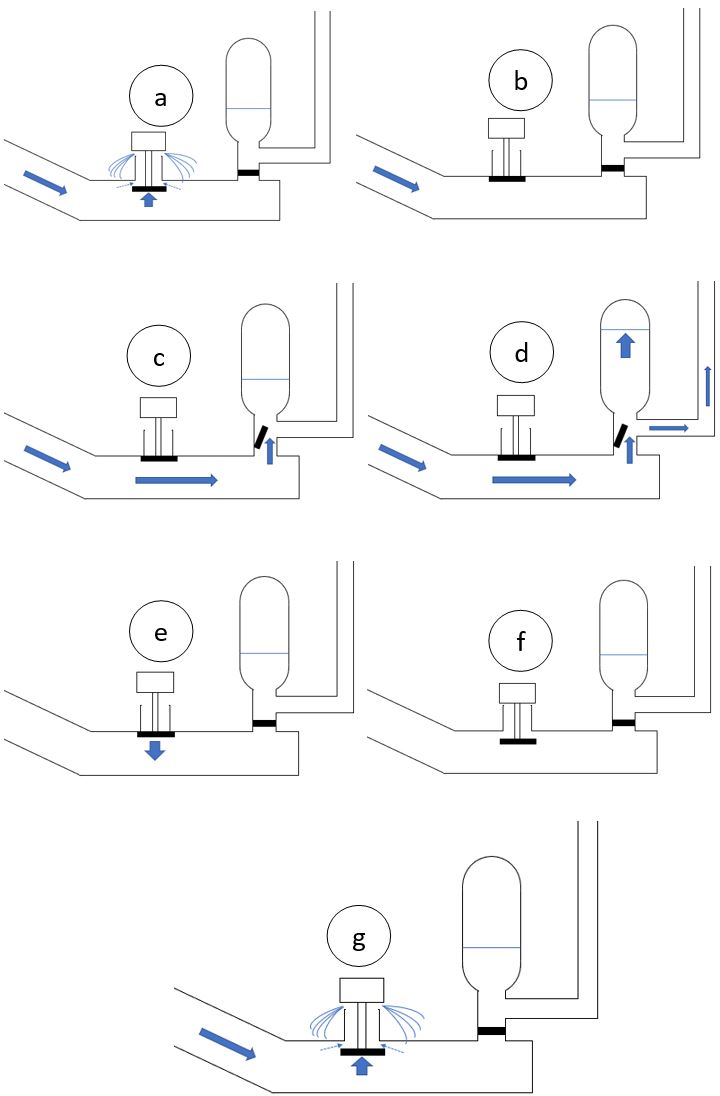 | Figure 4. Functioning of the studied hydram pump |
2.2. Mathematical Formulation
- A step-by-step analysis will assist in establishing the model that gives the amount of lost water, the amount of pumped water per cycle, and the efficiency of the hydram pump.
2.2.1. Simplifying Assumptions
- The following simplifying assumptions are adopted for modelling the studied hydram pump:I. The quantity of water in the supply tank is constant, that is, the flow of water entering it from a river, or any other form of watercourse is greater than the flow of water coming out through the supply pipe. An overflow is also installed.II. The waste valve is assumed to be elastic [1].III. The 4 springs in the balloon are identical and the sum of their masses is neglected.IV. The initial position of the valve in the balloon is at the same level as that of the waste valve.V. The weight of the delivery valve is negligible compared to the return force of its spring. VI. The supply pipe has no obstacle such as a fitting, a bend or other obstacles. The head loss in the supply pipe is only due to the roughness of the pipe.VII. In the study of period 2, the friction in the supply pipe is neglected because the pressure change caused by this friction is not significant compared to the other pressure changes for a well installed pump [1].VIII. The waste valve disk is considered to be a circular plate whose bending is assumed as being due to a point load applied to its centre.IX. The disk of the waste valve is assumed to rest all around its circumference.X. Frictions during study of period 5 are neglected [1]XI. The valve attached to the ends of the springs in the balloon is well sealed so that no water can overflow outside during operation of the studied hydram pump.XII. The air in the balloon containing the four springs is in contact with the outside air.XIII. The head loss at the elbow at the base of the hydram pump is neglected.XIV. The relaxation of the springs in the balloon at the end of the period 3 is instantaneous and, therefore, does not influence the duration of a cycle.
2.2.2. Mathematical Model Relating to Period 1
- Period 1 represents the duration (s) of the closure of the waste valve [21] and is determined by equation (1):
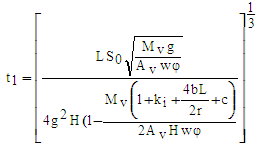 | (1) |
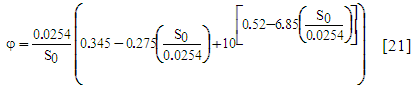 | (2) |
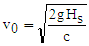 | (3) |
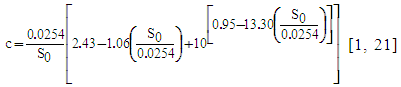 | (4) |
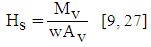 | (5) |
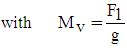 | (6) |
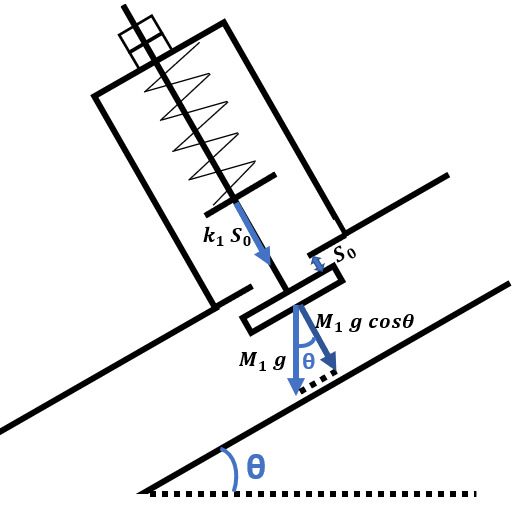 | Figure 5. Forces applied on the waste valve |
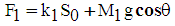 | (7) |
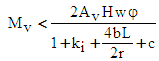 | (8) |
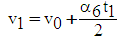 | (9) |
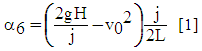 | (10) |
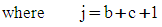 | (11) |
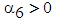 | (12) |
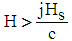 | (13) |
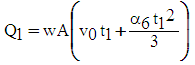 | (14) |
2.2.3. Mathematical Model Relating to Period 2
- The duration of period 2 can be computed as follows [1]:
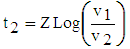 | (15) |
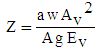 | (16) |
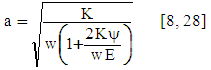 | (17) |
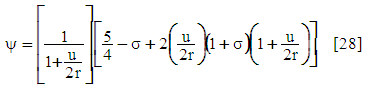 | (18) |
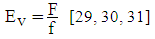 | (19) |
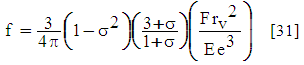 | (20) |
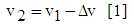 | (21) |
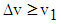 | (22) |
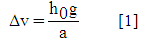 | (23) |
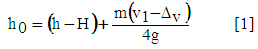 | (24) |
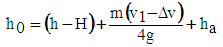 | (25) |
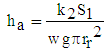 | (26) |
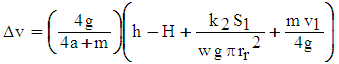 | (27) |
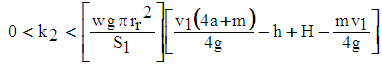 | (28) |
2.2.4. Mathematical Model Relating to Period 3
- It is during the third period that the water is pumped. However, the pumping of water is not done in one go or continuously but by discontinuous pushes induced by pressure waves. The water velocity in the supply pipe gradually decreases until the water can no longer be pumped through the delivery pipe [1].The duration of period 3 can be computed as follows [1]:
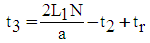 | (29) |
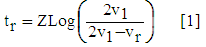 | (30) |
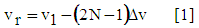 | (31) |
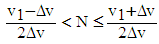 | (32) |
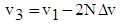 | (33) |
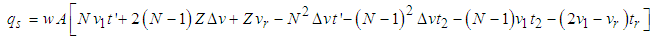 | (34) |
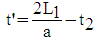 | (35) |
2.2.5. Modeling of the Spring Balloon
- The previous study of period 3 does not take into account the spring balloon. Thus, a modeling procedure similar to an air balloon proposed by Krol [10, 21] was adopted for the modeling of our spring balloon. During period 3, water is temporarily stored in the balloon [10, 21] before being ejected into the delivery pipe. In order to compute this amount of additional pumped water, the level of water in the spring balloon should first be known by means of the following energy balance [21]:
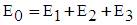 | (36) |
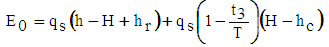 | (37) |
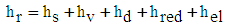 | (38) |
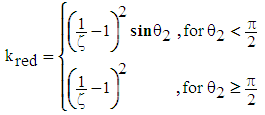 | (39) |
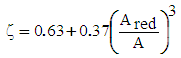 | (40) |
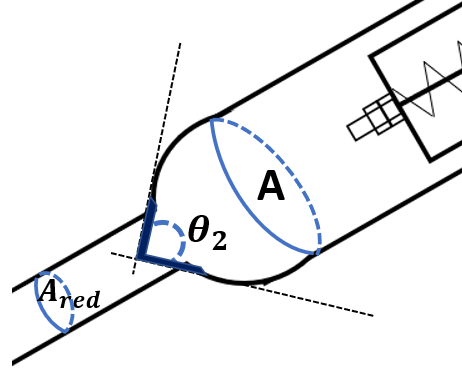 | Figure 6. Progressive shrinkage of the supply pipe |
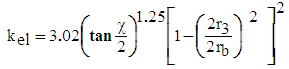 | (41) |
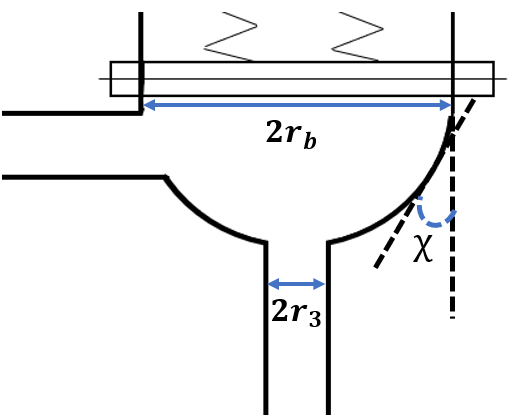 | Figure 7. Gradual enlargement of the pipe |
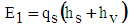 | (42) |
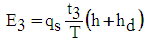 | (43) |
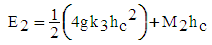 | (44) |
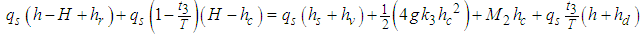 | (45) |
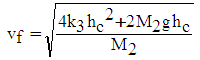 | (46) |
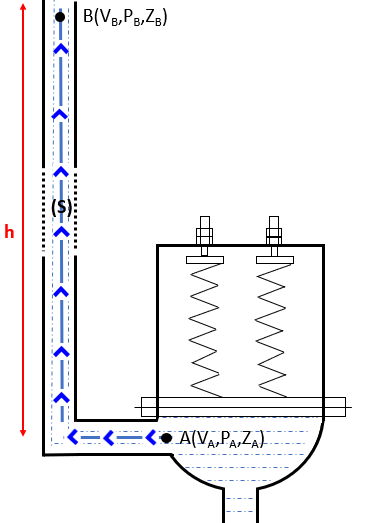 | Figure 8. Elevation of water along the delivery pipe during the thrust of the balloon membrane |
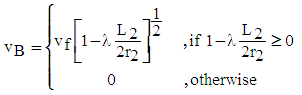 | (47) |
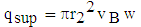 | (48) |
2.2.6. Mathematical Model Relating to Period 4
- The duration of period 4 is given by equation (49) [1]:
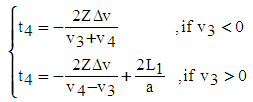 | (49) |
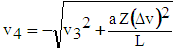 | (50) |
2.2.7. Mathematical Model Relating to Period 5
- The friction is neglected during this period because they have little influence on the values of the duration and the velocity of the water. Then, the duration of period 5 [1] is computed with equation (51):
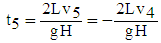 | (51) |
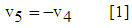 | (52) |
2.2.8. Mathematical Model Relating to Period 6
- Equation (53) enables to calculate the duration of period 6 [1]:
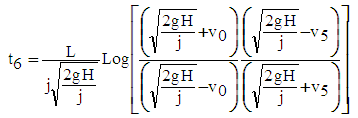 | (53) |
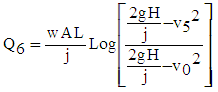 | (54) |
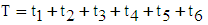 | (55) |
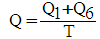 | (56) |
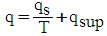 | (57) |
2.3. Calculation Procedure
- Figure 9 presents the successive steps for the calculation procedure:
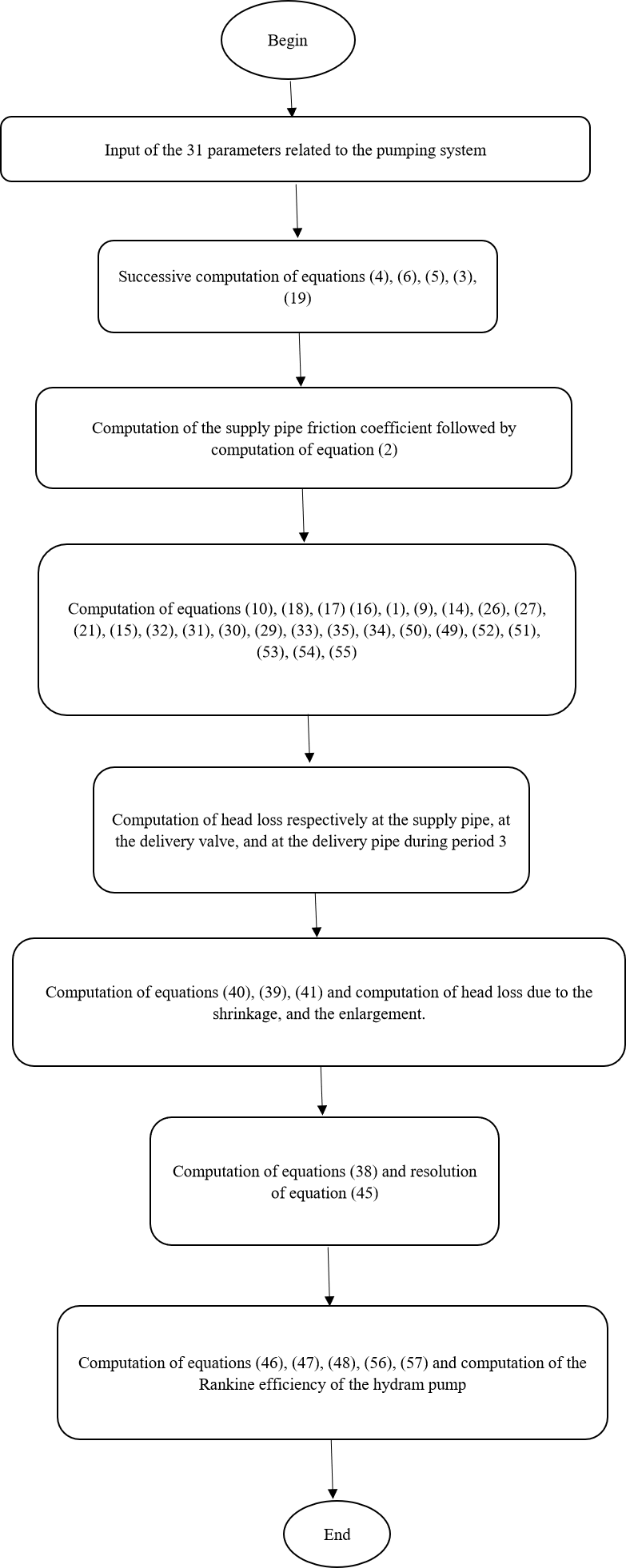 | Figure 9. Successive steps for the calculation procedure |
2.4. Work Tools
- The model associated with the studied system was coded on Matlab [38] while the global sensitivity analysis of this model was conducted with the help of a Matlab coded tool named GoSAT (Global sensitivity analysis tool) [39] which is an algorithm using a derived method FAST (Fourier Amplitude Sensitivity Test) for automatically ranking in downward order in a bar chart the main effects and the second interaction effects of various parameters of a model [40]. In the present work, 3 model outputs were successively surveyed, namely: the amount of pumped water, the amount of lost water and the efficiency of the hydram pump; while inputting 31 parameters for each surveyed model output.
3. Results and Discussion
3.1. Adequate Stiffness Values of the Delivery Valve Spring and the Balloon Springs
- Before carrying out the global sensitivity analysis of the model, the ideal value ranges of stiffness of the delivery valve spring and the balloon springs are determined. While taking the stroke length of the waste valve S0 equal to 0.002 (m), its spring stiffness k1 equal to 100 (N.m-1) and the value of the balloon membrane stroke S2 equal to 0.15 (m), the values of k2 and k3 were respectively varied between [0, 6500] and [0, 3], we computed the water height in the balloon of which contours are presented in Figure 10 according to values of k2 and k3. In fact, the value ranges of these two parameters have to be chosen such that the level of water in the balloon should not exceed the stroke length of the valve in the balloon. As can be seen from Figure 10, the suitable value ranges of k2 and k3 that meet the abovementioned condition are respectively [0, 100] and [0.5, 2].
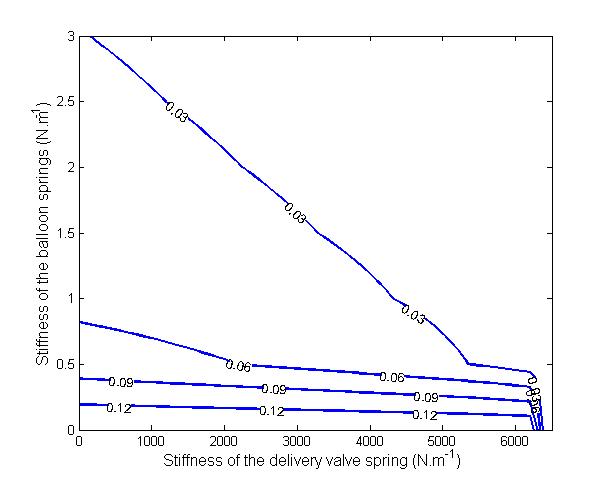 | Figure 10. Contours of water height in the balloon according to the values of k2 and k3 |
3.2. Results of the Global Sensitivity Analysis of the Developed Model
- Figures 11, 12 and 13 present the most influential parameters of the developed model while respectively taking the amount of pumped water, the amount of lost water, and the hydram pump efficiency as surveyed model outputs.
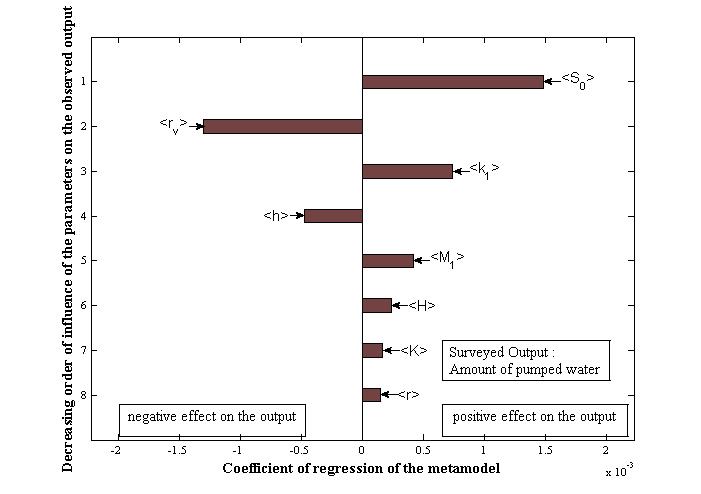 | Figure 11. Classification of the most dominating factors of the model, pumped water |
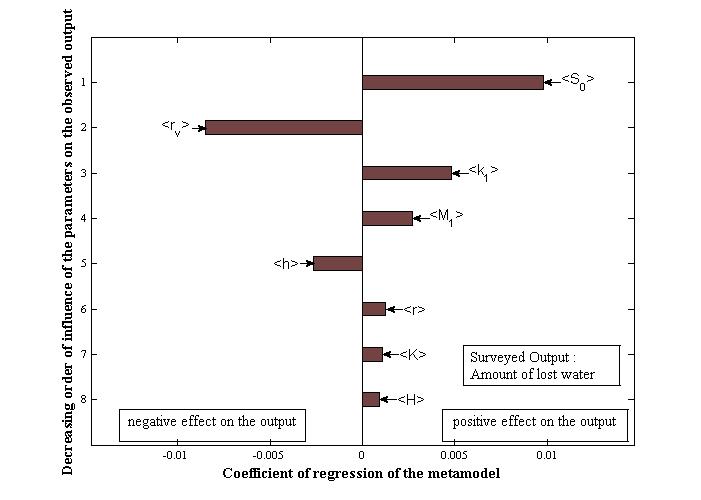 | Figure 12. Classification of the most dominant factors of the model, lost water |
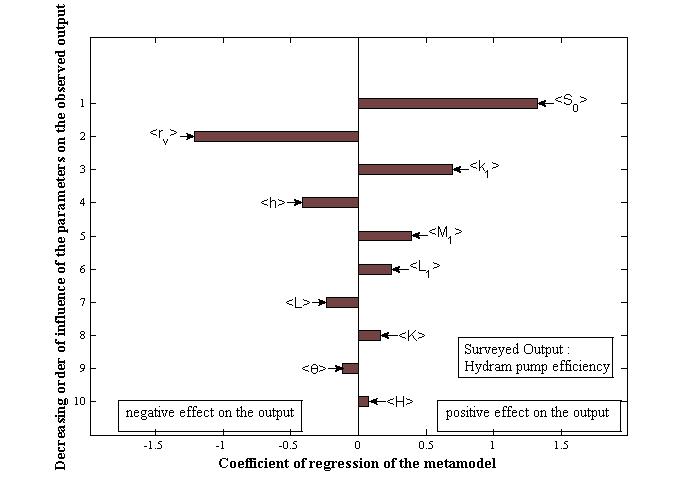 | Figure 13. Ranking of the most dominant factors of the model, efficiency |
4. Conclusions
- After modelling and the sensitivity analysis of the parameters of the hydraulic ram pump with springs system, the parameters which influence both the amount of pumped water, the amount of lost water and the efficiency of the pump are the same, namely: the length of the waste valve stroke; the radius of the waste valve disc, the stiffness of the waste valve spring, the height of the water column in the delivery pipe, and the waste valve weight.These results are the same as those of previous studies on the hydraulic ram pump [1, 9, 21]. But if it has been shown that the weight of the waste valve plays an important role on the operation of the pump, this parameter is less important than the stiffness of the waste valve spring in our case.Therefore, if one wants to have good results for each output independently, it is necessary to act on additional parameters. Those parameters are the same for the amount of pumped and lost water which are: the supply tank height and the supply pipe radius as shown in Figures 11 and 12. For the efficiency of the pump, those parameters are: the length of the supply pipe from the source to the center of the delivery valve, the length of the supply pipe from the source to the center of the waste valve, and the slope of the hydram pump relative to the horizontal as shown in Figure 13.As for the balloon containing the four springs, it was shown that it has no influence on the operation of the pump. Indeed, for a classic hydram pump with an air balloon, previous study deduced that compared to the kinetic energy in the supply pipe, the potential energy due to the balloon effect is small and may be neglected [21]. So, as obtained from the global sensitivity analysis of the model, the spring balloon has no effect on the operation of the studied hydram pump. In fact, the balloon is mainly used only to eliminate the noise of the water hammer [17, 41].The studied spring hydram pump was invented and crafted in Madagascar by Rasetarivelo who applied a patent at the Malagasy Office of Industrial Property (OMAPI) in 2004; the patent is entitled "Pompe à eau à système de ressorts sans autre source d’énergie que l’eau" (hydram pump with springs system without any other source of energy but water), and the application number is 2004/012 [22].As a follow-up to this study, the techno-economic aspect of the pump could be interesting in case of a small hydropower plant to increase water head. Moreover, a comparison between experimental and simulation results can be carried out too.
Nomenclature
- a : velocity of pressure-wave transmission in the supply pipe (m.s-1), given by equation (17)A : cross section of the supply pipe (m2)Av : area of the waste valve (m2)Ared : cross section of the shrinked pipe (m2)b : linear head loss coefficient of the supply pipe (-)c : friction coefficient of the waste valve (-), given by equation (4)e : thickness of the disk of the waste valve (m)E : modulus of elasticity or Young's modulus of the supply pipe (N.m-2)E0 : energy received by the balloon (kg.m), given by equation (37)E1 : energy lost in the supply pipe and in the delivery valve (kg.m), given by equation (42)E2 : potential energy due to the compression of the four springs (kg.m), given by equation (44)E3 : energy of the water directly pumped on the head (h+hd) (kg.m), given by equation (43)Ev : average stiffness of the waste valve disc (kg.m-1), given by the equation (19)f : bending of the disk of the waste valve (m), given by equation (20)F : point charge (N)F1 : sum of the forces exerted on the waste valve (N), given by equation (7)g : acceleration of gravity (m.s-2)h : height of the water column in the delivery pipe (m)h0 : increase of the pressure head necessary to open the delivery valve (m), given by equation (25)hc : level of water in the balloon (m)hd : linear head loss in the delivery pipe during period 3 (m)hel : singular head loss by progressive expansion of the pipe (m)hs : head loss in the supply pipe during the period 3 (m)hv : singular head loss due to the delivery valve during period 3 (m)ha : height of the water column necessary to oppose the pressure force of the delivery spring for a full opening (m), given by equation (26)hred : singular head loss by the progressive reduction of the pipe (m)hr : the sum of the head losses during period 3 (m), given by (38)H : height of the supply tank (m)Hs : static head for closing of the waste valve (m), given by equation (5)k1 : spring stiffness constant of the waste valve (N.m-1)k2 : spring stiffness constant of the delivery valve (N.m-1)k3 : stiffness of each spring in the spring balloon (N.m-1)ki : sum of the singular head loss coefficients due to obstacles: fitting, elbow and others (-)ks : coefficient de perte de charge de la conduite d’alimentation (-)K : modulus of elasticity of water (N.m-2)kel : head loss coefficient by progressive expansion of the pipe (-), given by equation (41)kred : head loss coefficient by the progressive reduction of the pipe (-), given by equation (39)L : length of the supply pipe from the supply tank to the center of the waste valve (m)L1 : length of the supply pipe from the source to the center of the delivery valve (m)L2 : length of the delivery pipe (m)m : friction constant of the delivery valve (m.s-1)M1 : weight of the moving part of the waste valve (kg)M2 : weight of the disc in the balloon (kg)Mv : equivalent weight of the waste valve (valve + spring) (kg), given by equation (6)N : number of pushes between period 2 and period 3, given by equation (32)q : amount of pumped water per cycle (kg.s-1), given by equation (57)qs : amount of pumped water during the period 3 (kg.cycle-1), given by equation (34)qsup: quantity of extra pumped water (kg.s-1), given by equation (48)Q : amount of lost water in a cycle (kg.s-1), given by equation (56)Q1 : amount of lost water during period 1 (kg.cycle-1), given by equation (14)Q6 : amount of water lost during the period 6 (kg.s-1), given by equation (54)r : radius of the supply pipe (m)r2 : radius of the delivery pipe (m)r3 : radius of the shrinked pipe (m)rb : radius of the disc in the balloon (m)rr: radius of the disc of the delivery valve (m)rv : radius of the disk of the waste valve (m) S0 : length of the waste valve stroke (m)S1 : length of the delivery valve stroke (m)S2 : length of the balloon membrane stoke (m)ti : duration of the period i (i=1 to 6) (s)tr : the duration of the last push at the end of the period 3 (s), given by equation (30)T : duration of a complete cycle (s), given by equation (55)u : thickness of the supply pipe (m)v0 : value of the water minimum velocity at which the waste valve begins to close (m.s-1), given by equation (3)vf : velocity of the spring balloon membrane at the end of period 3 (m.s-1), given by equation (46)vi : water velocity in the supply pipe at the end of the period i (i = 1 to 6) (m.s-1)vr : velocity of the water in the supply pipe near the end of period 3 (m.s-1), given by equation (31)vB : water velocity at the outlet of the delivery pipe (m.s-1), given by equation (47)w : water density (kg.m-3)
Greek Letters
- α6 : acceleration of the water column in the supply pipe at the end of Period 6 or at the beginning of Period 1 (m.s-2), given by equation (10)ζ : contraction coefficient (-), given by equation (40)∆v: reduction in velocity (m.s-1), given by equation (27)θ: inclination angle of the pump from the horizontal (°)θ2 : solid angle in the shrinkage (°)λ : linear head loss coefficient of the delivery pipe during the pumping of the extra pumped water (-)σ : Poisson’s ratio of the supply pipe material (-)φ : coefficient of drag of the waste valve (-), given by equation (2)χ : angle at the enlargement (°)ψ : factor related to the speed of the pressure-wave transmission, given by equation (18)
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML