-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2018; 8(4): 105-111
doi:10.5923/j.ajfd.20180804.01

Onset of Magnetoconvection in a Rotating Darcy Porous Layer Heated from Below with Temperature Dependent Heat Source
E. O. Odok1, C. Israel-Cookey2, E. Amos1
1Department of Mathematics, Rivers State University, Port Harcourt, Nigeria
2Department of Physics, Rivers State University, Port Harcourt, Nigeria
Correspondence to: C. Israel-Cookey, Department of Physics, Rivers State University, Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The onset of stationary and oscillatory magnetoconvection in a rotating infinitely horizontal porous layer filled with electrically conducting Newtonian fluid heated from below with temperature – dependent heat source within the Darcy limit using linear stability analysis is investigated for free – free boundaries. The effects of heat source, magnetic field and rotation parameters on the onset of convection are presented graphically and analyzed in detail. It is found that increases in magnetic and rotation parameters delayed the onset of stationary and oscillatory convection, thereby stabilizing the system. The heat source parameter increment accelerates the onset of convection and the system is more unstable; while Prandtl number slowed the onset of oscillatory convection.
Keywords: Magnetoconvection, Rotating Darcy porous layer, Temperature– dependent heat source, Free- free boundaries
Cite this paper: E. O. Odok, C. Israel-Cookey, E. Amos, Onset of Magnetoconvection in a Rotating Darcy Porous Layer Heated from Below with Temperature Dependent Heat Source, American Journal of Fluid Dynamics, Vol. 8 No. 4, 2018, pp. 105-111. doi: 10.5923/j.ajfd.20180804.01.
Article Outline
1. Introduction
- The study of fluid convection in a rotating porous layer heated from below has received considerable attention due to many applications in its many applications in geophysics, oceanic flows, astrophysics, and in engineering. Such applications in engineering include among others chemical processing, food processing, solidification and centrifugal casting of metals, and rotating machinery. Excellent reviews of the problem of thermal convection in a rotating porous medium can be found in [1-7]. In particular, Vadasz [5] investigated the effect of the Coriolis force in the thermal convection when the Darcy model is extended by including the acceleration term in the momentum equatiom. Vadasz and Govender [8] considered the influence of gravity and centrifugal forces on the onset of convection in a rotating porous layer. Recently, Falsaperla et al. [9] considered the problem of classical Benard system, with and without rotation under the Newton-Robin boundary conditions and fixed heat fluxes for temperature field. More recently, Kang et al. [10] investigated high Rayleigh number steady state thermal convection in a rotating porous half space in which rotation led to rise in downward flow in contrast to the upward thermal convection.It is important to recognize that many convective instability problems of practical importance involve electrically conducting fluids. In such cases, the influence of external fields like electric and magnetic fields become important. Comprehensive account of the linear theory of Rayleigh-Benard magnetoconvection can be found in Chandrasekhar [1], where the onset of instability affected by vertically imposed magnetic field. In particular, the effects of magnetic field become dominant when the fluid is highly electrically conducting. The study of the effects of externally imposed magnetic field is important in understanding the dynamics of the system under consideration. In such situations the electric current, J is induced when a flow of electrically conducting liquid crosses a magnetic field B which in then generates a Lorentz force proportional to
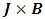 [11, 12]. It is important to mention that the Lorentz force changes the force balance in the momentum equation, making the behaviour different from flows in situations without external magnetic fields. There are a number of practical situations in which the onset of convection is induced by internal heating in areas such as geophysics and engineering under situations in nuclear heat cores, nuclear waste disposal, oil extraction, weak exothermic reactions and crystal growth within the porous media [13-18]. Alex and Patil [19] investigated the problem of thermal instability with combined effects of centrifugal acceleration and anisotropy for both Darcy and Brinkman limits. Although sufficient literature exists on thermal convection in porous medium, very little has been devoted to the study of the effects of internal heating and magnetic field in a rotating Darcy layer, nor in the case of combined effects rotation and internal heating in isotropic porous medium. Yu and Shih [20] investigated the problem of convection induced by internal heating in electrically conducting fluid in the presence of a magnetic field, and found that magnetic field increases the stability of the fluid layer. To the best of our knowledge, in all the investigations mentioned above, there is no study on the combined effects of magnetic field and heat source on the onset of thermal convection in a rotating porous medium with an externally imposed magnetic field. Therefore, in this present paper, we analyze the onset of stationary and oscillatory convection in a rotating fluid layer heated from below under simultaneous effects of magnetic field and temperature dependent heat source.
[11, 12]. It is important to mention that the Lorentz force changes the force balance in the momentum equation, making the behaviour different from flows in situations without external magnetic fields. There are a number of practical situations in which the onset of convection is induced by internal heating in areas such as geophysics and engineering under situations in nuclear heat cores, nuclear waste disposal, oil extraction, weak exothermic reactions and crystal growth within the porous media [13-18]. Alex and Patil [19] investigated the problem of thermal instability with combined effects of centrifugal acceleration and anisotropy for both Darcy and Brinkman limits. Although sufficient literature exists on thermal convection in porous medium, very little has been devoted to the study of the effects of internal heating and magnetic field in a rotating Darcy layer, nor in the case of combined effects rotation and internal heating in isotropic porous medium. Yu and Shih [20] investigated the problem of convection induced by internal heating in electrically conducting fluid in the presence of a magnetic field, and found that magnetic field increases the stability of the fluid layer. To the best of our knowledge, in all the investigations mentioned above, there is no study on the combined effects of magnetic field and heat source on the onset of thermal convection in a rotating porous medium with an externally imposed magnetic field. Therefore, in this present paper, we analyze the onset of stationary and oscillatory convection in a rotating fluid layer heated from below under simultaneous effects of magnetic field and temperature dependent heat source.2. Mathematical Formulation
- We consider an infinite electrically conducting horizontal fluid saturated porous layer confined between two parallel boundaries located at
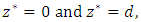 and are maintained at temperatures
and are maintained at temperatures 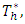 and
and 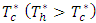 , respectively. The porous layer is rotating uniformly about the vertical axis at a constant angular velocity
, respectively. The porous layer is rotating uniformly about the vertical axis at a constant angular velocity 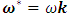 . A uniform magnetic field
. A uniform magnetic field 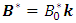 is applied across the fluid layer in the vertically upward direction, where the induced magnetic field is neglected on the account of small magnetic Reynolds number. A Cartesian coordinate system
is applied across the fluid layer in the vertically upward direction, where the induced magnetic field is neglected on the account of small magnetic Reynolds number. A Cartesian coordinate system 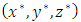 is chosen such that the origin is at the bottom of the porous layer and the gravity force acting in the negative
is chosen such that the origin is at the bottom of the porous layer and the gravity force acting in the negative 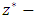 direction. The schematic diagram of the system considered is shown in Fig. 1.
direction. The schematic diagram of the system considered is shown in Fig. 1.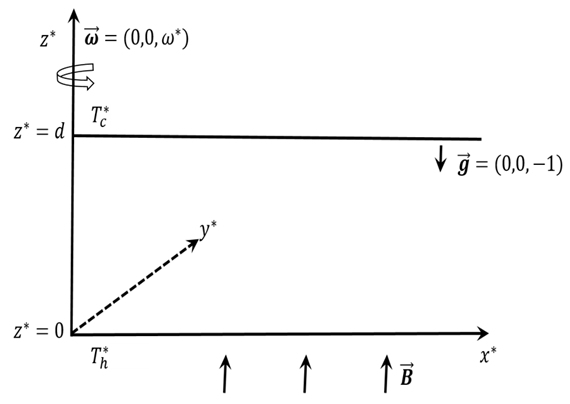 | Figure 1. Physical model and coordinate system |
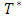 , and taking into account the Coriolis force and acceleration coefficient terms, the governing equations of the fluid motion in a homogeneous and isotropic medium follow Darcy model under Bousssinesq approximation together with Lorentz force are [1, 6, 18, 21, 22]
, and taking into account the Coriolis force and acceleration coefficient terms, the governing equations of the fluid motion in a homogeneous and isotropic medium follow Darcy model under Bousssinesq approximation together with Lorentz force are [1, 6, 18, 21, 22] 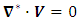 | (1) |
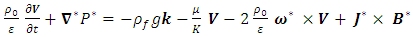 | (2) |
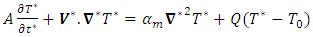 | (3) |
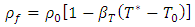 | (4) |
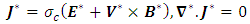 | (5) |
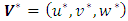 is the velocity,
is the velocity, 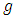 is the acceleration due to gravity,
is the acceleration due to gravity, 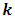 is the unit vector in the vertical direction,
is the unit vector in the vertical direction, 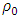 is the reference temperature,
is the reference temperature, 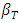 is the cofficient of thermal expansion,
is the cofficient of thermal expansion, 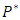 is the pressure, K is the permeability of the porous medium,
is the pressure, K is the permeability of the porous medium, 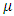 is the fluid viscosity,
is the fluid viscosity, 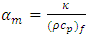 is the thermal diffusivity, where
is the thermal diffusivity, where 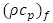 is the volumetric heat capacity of the fluid,
is the volumetric heat capacity of the fluid, 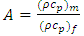 is the ratio of heat capacities,
is the ratio of heat capacities, 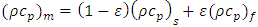 is volumetric heat capacity of the porous medium,
is volumetric heat capacity of the porous medium, 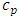 is the specific heat capacity,
is the specific heat capacity, 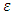 is the porosity parameter where the subscripts f, s and m denotes the properties of the fluid, solid and porous matrix, respectively. Further,
is the porosity parameter where the subscripts f, s and m denotes the properties of the fluid, solid and porous matrix, respectively. Further, 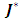 is the current density,
is the current density, 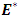 is the electric field,
is the electric field, 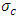 is the electrical conductivity, and
is the electrical conductivity, and 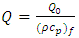 is constant of proportionality.The electric field given in Eq. (5) can be written in terms of the electrostatic potential,
is constant of proportionality.The electric field given in Eq. (5) can be written in terms of the electrostatic potential, 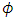 as
as 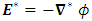 . Now assuming that the boundaries are electrically insulated for which
. Now assuming that the boundaries are electrically insulated for which 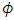 is a constant. Based on this assumption, the current density,
is a constant. Based on this assumption, the current density, 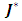 reduces to
reduces to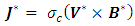 | (6) |
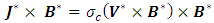 | (7) |
2.1. Boundary Conditions
- Since the field is bounded by two horizontal parallel plates located at
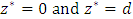 , the following boundary condition are assumed for the velocity field
, the following boundary condition are assumed for the velocity field 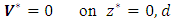 | (8a) |
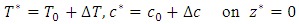 | (8b) |
 | (8c) |
2.2. Non - dimensionalization
- Using Eqs. (4) and (7) together with the following scaling
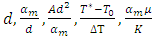 for length, velocity, time, temperature, and pressure respectively, where
for length, velocity, time, temperature, and pressure respectively, where 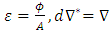 , respectively, the governing equations and the boundary conditions (8) in dimensionless form are
, respectively, the governing equations and the boundary conditions (8) in dimensionless form are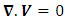 | (9) |
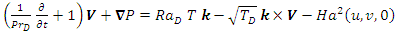 | (10) |
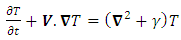 | (11) |
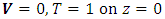 | (12a) |
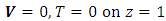 | (12b) |
2.3. Basic State
- The basic state of the system is assumed to be independent of time (quiescent). They vary only in the
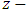 direction, and are described by
direction, and are described by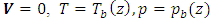 | (13) |
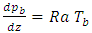 | (14) |
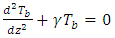 | (15) |
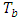 are
are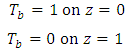 | (16) |
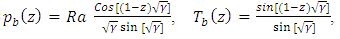 | (17) |
2.4. Perturbation Equations
- To study the stability of the basic state, we superimpose perturbations on the basic state in the form
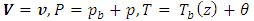 | (18) |
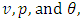 are the perturbed quantities over their equilibrium counterparts and are assumed small. On substituting Eq. (18) into Eqs. (9) – (12), and linearize by neglecting products of perturbed quantities yield, the following equations
are the perturbed quantities over their equilibrium counterparts and are assumed small. On substituting Eq. (18) into Eqs. (9) – (12), and linearize by neglecting products of perturbed quantities yield, the following equations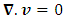 | (19) |
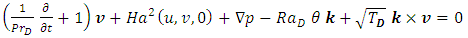 | (20) |
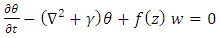 | (21) |
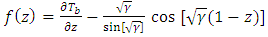 is the basic temperature gradient distribution.Since the flow is confined between two parallel plates, located at z = 0 and 1, the temperature is maintained at fixed values at the plate walls. Therefore, the temperature perturbations vanish at the plate walls. Hence, the boundary conditions for the temperature perturbation is now
is the basic temperature gradient distribution.Since the flow is confined between two parallel plates, located at z = 0 and 1, the temperature is maintained at fixed values at the plate walls. Therefore, the temperature perturbations vanish at the plate walls. Hence, the boundary conditions for the temperature perturbation is now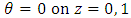 | (22a) |
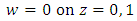 | (22b) |
3. Linear Stability Analysis
- To facilitate the analysis, we perform the operations
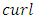 and
and 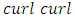 on Eq. (20), using the continuity equation (Eq. (19)), the identity
on Eq. (20), using the continuity equation (Eq. (19)), the identity 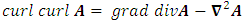 and keeping only the z components yield
and keeping only the z components yield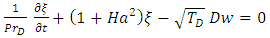 | (23) |
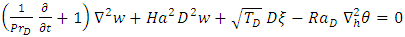 | (24) |
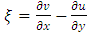 is the z – component of the vorticity,
is the z – component of the vorticity, 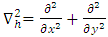 is the Laplacian in the horizontal plane and
is the Laplacian in the horizontal plane and 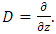 In order to predict the threshold of convection, we assume all fields to be two dimensional time periodic wave with wave number a in the horizontal plane. Then, we set
In order to predict the threshold of convection, we assume all fields to be two dimensional time periodic wave with wave number a in the horizontal plane. Then, we set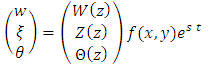 | (25) |
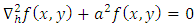 and
and 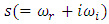 is the growth rate of disturbances. The substitution of Eq. (25) into Eqs. (21), (23) and (24) yield
is the growth rate of disturbances. The substitution of Eq. (25) into Eqs. (21), (23) and (24) yield 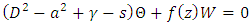 | (26) |
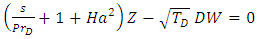 | (27) |
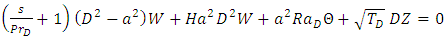 | (28) |
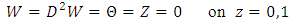 | (29) |
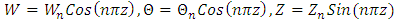 | (30) |
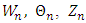 and n an integer. From now on, we restrict our analysis to the lowest mode (idealized mode)
and n an integer. From now on, we restrict our analysis to the lowest mode (idealized mode) 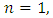 which corresponds to the most dangerous mode. On using Eq. (30) the eigenvalue problem Eqs. (26) – (28) in matrix form become
which corresponds to the most dangerous mode. On using Eq. (30) the eigenvalue problem Eqs. (26) – (28) in matrix form become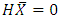 | (31) |
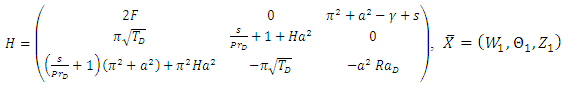 and
and 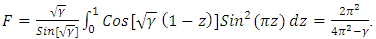 The solvability of the system Eq. (31) requires that the determinant of H vanish, that is
The solvability of the system Eq. (31) requires that the determinant of H vanish, that is 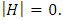 This condition yields the expression for the Rayleigh number,
This condition yields the expression for the Rayleigh number, 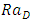 as
as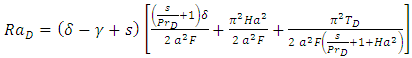 | (32) |
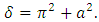 Since the growth rate
Since the growth rate 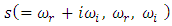 is in general a complex quantity. The system with
is in general a complex quantity. The system with 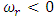 is always stable, while for
is always stable, while for 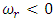 , it will be unstable. For neutral (marginal) stability
, it will be unstable. For neutral (marginal) stability 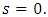
3.1. Onset of Stationary Convection
- For the validity of the principle of exchange of stabilities to hold, the growth rate must vanish. That is,
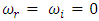 at the marginal stability. Setting
at the marginal stability. Setting 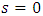 in Eq. (32) and simplifying yields the Rayleigh number,
in Eq. (32) and simplifying yields the Rayleigh number, 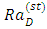 for the onset of stationary convection as
for the onset of stationary convection as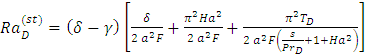 | (33) |
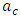 and the corresponding critical Rayleigh number,
and the corresponding critical Rayleigh number, 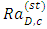 for the onset of convection. By setting
for the onset of convection. By setting 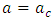 and
and 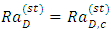 in Eq. (33) and minimizing according to [1]
in Eq. (33) and minimizing according to [1]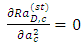 | (34) |
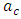 given by
given by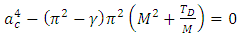 | (35) |
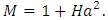 The solution of Eq.(35) yields the critical wave number,
The solution of Eq.(35) yields the critical wave number, 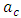 as
as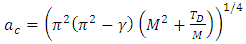 | (36) |
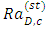 for the onset of stationary convection as
for the onset of stationary convection as 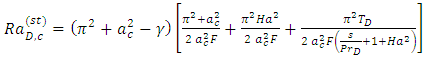 | (37) |
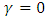 and magnetic field parameter
and magnetic field parameter 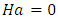 in Eq. (36), we obtain the critical wave number as
in Eq. (36), we obtain the critical wave number as 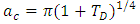 | (38) |
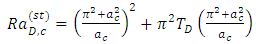 | (39) |
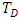 ), Eqs. (38) and (39) reduce to
), Eqs. (38) and (39) reduce to 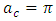 | (40) |
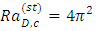 | (41) |
3.2. Onset of Oscillatory Convection
- For the onset of oscillatory convection, we set
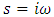 and
and 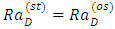 in Eq. (32). The result gives the oscillatory Raleigh number,
in Eq. (32). The result gives the oscillatory Raleigh number, 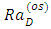 as
as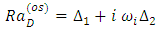 | (42) |
 | (43) |
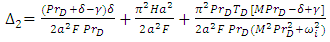 | (44) |
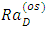 is a physical quantity, it must be real. Hence, for the validity of oscillatory convection
is a physical quantity, it must be real. Hence, for the validity of oscillatory convection 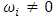 and
and 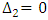 . Setting
. Setting 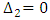 in Eq. (42) and simplifying gives the expression for the frequency,
in Eq. (42) and simplifying gives the expression for the frequency, 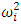 as
as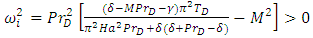 | (45) |
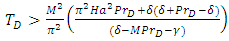 | (46) |
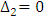 yields the expression for oscillatory number,
yields the expression for oscillatory number, 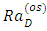 as
as 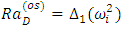 | (47) |
4. Results and Discussion
- The onset of magnetoconvection in a rotating Darcy porous layer saturated with electrically conducting fluid heated from below with temperature dependent heat source with free – free boundaries has been studied analytically. In this section, we discuss the effects of the parameters in the governing equations on the basic temperature distribution, basic temperature gradient and on the onset of both stationary and oscillatory convections numerically and graphically. Figure 2 shows the effect of heat source parameter
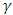 on the distribution of basic temperature,
on the distribution of basic temperature, 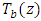 of the system across the fluid layer. It is observed that increases in the heat source
of the system across the fluid layer. It is observed that increases in the heat source 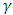 amounts to increase in the basic temperature distribution,
amounts to increase in the basic temperature distribution, 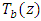 . This is an indication that increase in
. This is an indication that increase in 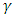 may lead to some instabilities in the system. To know effect of the heat source
may lead to some instabilities in the system. To know effect of the heat source 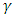 on the basic temperature gradient of the system, the calculated basic temperature gradient distribution,
on the basic temperature gradient of the system, the calculated basic temperature gradient distribution, 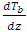 for different values of heat source
for different values of heat source 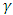 is shown in Fig.3. As expected, it is observed that for the stability problem all the values are negative. Also, it is observed from Fig. 3 that increase in heat source amounts to increase in the basic temperature profile which in turn enhances the disturbances in the fluid layer and the system becomes more unstable.
is shown in Fig.3. As expected, it is observed that for the stability problem all the values are negative. Also, it is observed from Fig. 3 that increase in heat source amounts to increase in the basic temperature profile which in turn enhances the disturbances in the fluid layer and the system becomes more unstable.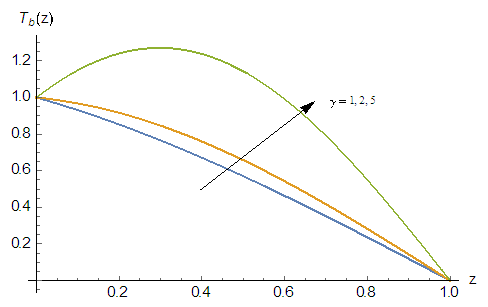 | Figure 2. Effect of heat source, γ on the distribution of basic temperature, |
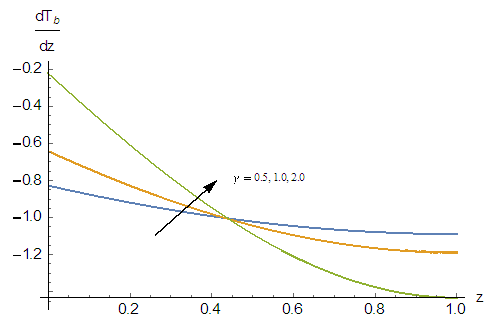 | Figure 3. Effect of heat source, γ on the distribution of basic temperature gradient, 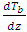 |
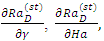 and
and 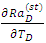 analytically. From Eq. (33), it follows that
analytically. From Eq. (33), it follows that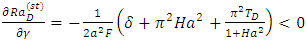 | (48a) |
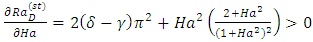 | (48b) |
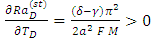 | (48c) |
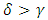 . From Eq. (48a), it worth noting that
. From Eq. (48a), it worth noting that 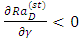 , which indicates that the heat source parameter,
, which indicates that the heat source parameter, 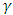 has destabilization effect on the system. This is in agreement with the earlier result obtained by Israel-Cookey et al. [22] in the absence of solute concentration Rayleigh number. Also, from Eqs. (48b) and (48c), it follows that magnetic field and rotation parameters inhibit the onset of stationary convection. Hence, magnetic field and rotation have stabilizing effects to make the system more stable. This may be due to the fact that magnetic field and rotation tend to suppress the vertical motion and hence convection, by restricting the motion to the horizontal plane. These results are in agreement with Vadasz [5, 22]. The stability curves in
has destabilization effect on the system. This is in agreement with the earlier result obtained by Israel-Cookey et al. [22] in the absence of solute concentration Rayleigh number. Also, from Eqs. (48b) and (48c), it follows that magnetic field and rotation parameters inhibit the onset of stationary convection. Hence, magnetic field and rotation have stabilizing effects to make the system more stable. This may be due to the fact that magnetic field and rotation tend to suppress the vertical motion and hence convection, by restricting the motion to the horizontal plane. These results are in agreement with Vadasz [5, 22]. The stability curves in 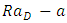 plane for the onset of both stationary and oscillatory convection for various values of heat source, magnetic field, and rotation parameters are depicted in Figs. (4) – (7), respectively. From Figs. (4a) and (4b) it is observed that the Raleigh number for both stationary and oscillatory convections decreases with increase in heat source parameter, which indicates that the heat source parameter has a destabilizing effect to make the system more unstable.
plane for the onset of both stationary and oscillatory convection for various values of heat source, magnetic field, and rotation parameters are depicted in Figs. (4) – (7), respectively. From Figs. (4a) and (4b) it is observed that the Raleigh number for both stationary and oscillatory convections decreases with increase in heat source parameter, which indicates that the heat source parameter has a destabilizing effect to make the system more unstable.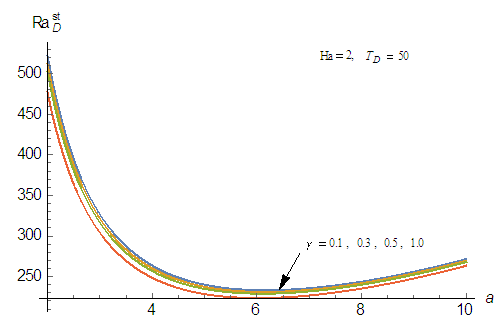 | Figure 4(a). Effect of heat source, γ on thermal Rayleigh number, 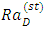 with respect to wave number, a for stationary convection for different values of parameters with respect to wave number, a for stationary convection for different values of parameters |
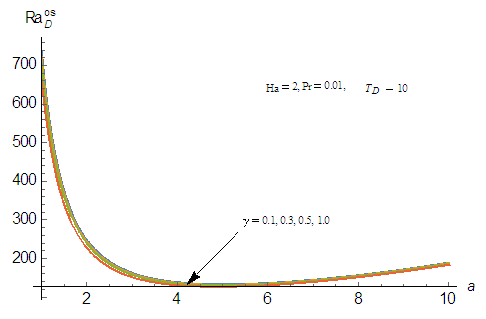 | Figure 4(b). Effect of heat source, γ on thermal Rayleigh number,  with respect to wave number, a for oscillatory convection for different values of parameters with respect to wave number, a for oscillatory convection for different values of parameters |
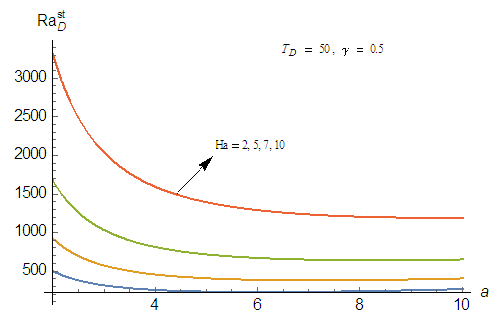 | Figure 5(a). Effect of magnetic field, Ha on thermal Rayleigh number,  with respect to wave number, a for stationary convection for different values of parameters with respect to wave number, a for stationary convection for different values of parameters |
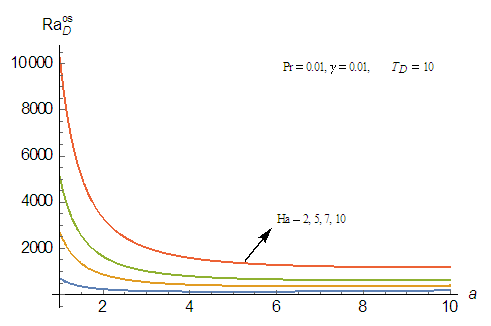 | Figure 5(b). Effect of magnetic field, Ha on thermal Rayleigh number, 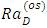 with respect to wave number, a for oscillatory convection for different values of parameters with respect to wave number, a for oscillatory convection for different values of parameters |
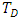 on the onset of both stationary and oscillatory convection on the system. It is observed from these figures that increases in the rotation parameter,
on the onset of both stationary and oscillatory convection on the system. It is observed from these figures that increases in the rotation parameter, 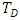 results in increase in the Rayleigh number for both stationary and oscillatory convection, which is an indication that the effect of rotation is to enhance the stability of the system. This results are in good agreement with Vadasz [5].
results in increase in the Rayleigh number for both stationary and oscillatory convection, which is an indication that the effect of rotation is to enhance the stability of the system. This results are in good agreement with Vadasz [5].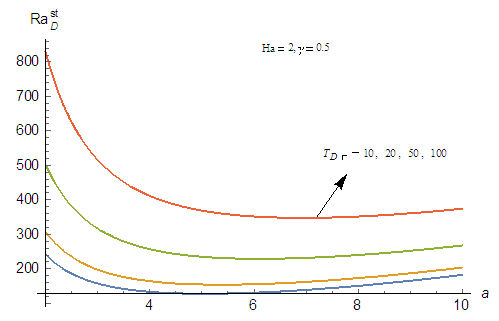 | Figure 6(a). Effect of rotation, 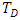 on thermal Rayleigh number, on thermal Rayleigh number, 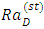 with respect to wave number, a for stationary convection for different values of parameters with respect to wave number, a for stationary convection for different values of parameters |
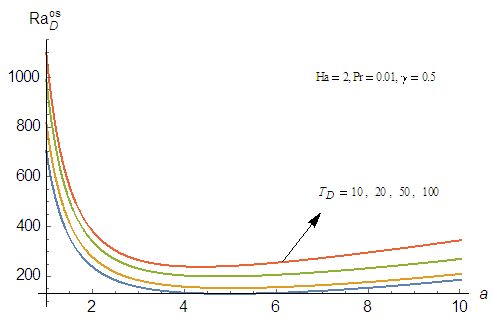 | Figure 6(b). Effect of rotation, 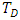 on thermal Rayleigh number, on thermal Rayleigh number, 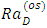 with respect to wave number, a for oscillatory convection for different values of parameters with respect to wave number, a for oscillatory convection for different values of parameters |
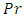 on the stability of the system, the variation of oscillatory convection as a function of wave number, a for fixed values of
on the stability of the system, the variation of oscillatory convection as a function of wave number, a for fixed values of 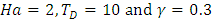 is depicted in Fig. 7. It is observed, the Prandtl number affects only the oscillatory convection and from Fig. 7 it is observed that the oscillatory Rayleigh number,
is depicted in Fig. 7. It is observed, the Prandtl number affects only the oscillatory convection and from Fig. 7 it is observed that the oscillatory Rayleigh number, 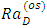 is increased with increase in the Prandtl number,
is increased with increase in the Prandtl number, 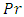 which means that Prandtl number has a stabilizing effect on the system.
which means that Prandtl number has a stabilizing effect on the system. 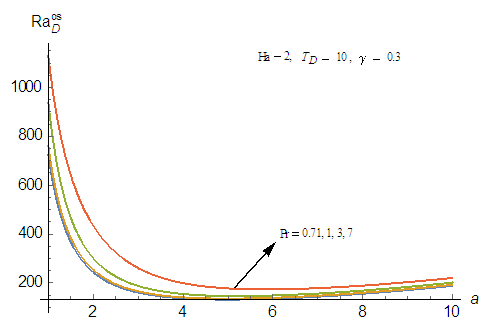 | Figure 7. Effect of Prandtl number, Pr on thermal Rayleigh number, 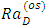 with respect to wave number, a for oscillatory convection for different values of parameters with respect to wave number, a for oscillatory convection for different values of parameters |
5. Conclusions
- The criterion for the onset of magnetoconvection in a rotating Darcy layer filled with electrically conducting fluid with temperature – dependent heat source, which is heated from below for free – free boundaries has been investigated. The linear stability analysis is used for establishing the criteria for onset of both stationary and oscillatory convections in the system. The effects of physical parameters in the governing equations, such as heat source parameter,
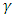 , magnetic field parameter, Ha, rotation parameter,
, magnetic field parameter, Ha, rotation parameter, 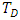 , and the Prandtl number, Pr are shown graphically. The effects of increasing magnetic field and rotation parameters slow down the onset of both stationary and oscillatory convection, while the Prandtl number delays the onset of oscillatory convection. This means that magnetic field parameter, Ha, rotation parameter,
, and the Prandtl number, Pr are shown graphically. The effects of increasing magnetic field and rotation parameters slow down the onset of both stationary and oscillatory convection, while the Prandtl number delays the onset of oscillatory convection. This means that magnetic field parameter, Ha, rotation parameter, 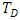 , and the Prandtl number, Pr are stabilizing factors. On the other hand, the heat source parameter,
, and the Prandtl number, Pr are stabilizing factors. On the other hand, the heat source parameter, 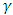 accelerates the onset of convection.
accelerates the onset of convection. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML