-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2018; 8(2): 47-62
doi:10.5923/j.ajfd.20180802.02

On the Hydrodynamic Effects of Humpback Whale’s Ventral Pleats
Arash Taheri
Ph.D., Division of Applied Computational Fluid Dynamics, Biomimetic and Bionic Design Group, Tehran, Iran
Correspondence to: Arash Taheri, Ph.D., Division of Applied Computational Fluid Dynamics, Biomimetic and Bionic Design Group, Tehran, Iran.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper, hydrodynamic effects of ventral pleats covering mouth and bell parts of humpback whales are studied for the first time. In this regard, turbulent flows over a simplified model of the animal body as a half grooved ellipsoid are numerically simulated using Lam-Bremhorst low Reynolds turbulence model resolving to the wall at different angles of attack and sideslip. The results show that presence of the ventral pleats leads to formation of low speed strips and shear layer/vortex on the bottom surface of the animal, which in turn results in a relatively higher pressure region on the bell and higher drag coefficient compared to a case without grooves. In this way, pleats generate lift and contribute to buoyancy force and also increase tendency of flow separation. The results also depict superior performance of the grooved body at sideslip angles. Furthermore, results of cavitating flow simulation over the grooved model showed a suppression of lift generation contribution of the ventral grooved surface in cavitating conditions, the most similar situations to bubbly flows experienced by humpback whales in bubble net fishing environment.
Keywords: Hydrodynamics, Humpback whale body, Ventral pleats, CFD, Cavitation, Bionics
Cite this paper: Arash Taheri, On the Hydrodynamic Effects of Humpback Whale’s Ventral Pleats, American Journal of Fluid Dynamics, Vol. 8 No. 2, 2018, pp. 47-62. doi: 10.5923/j.ajfd.20180802.02.
Article Outline
1. Introduction
- Humpback whales (Megaptera novaeangliae) are remarkable swimmers in oceans. These animals belong to rorquals (Balaenopteridae) under a broader group of cetacean mammalian marine animals. These giant swimmers possess a knobby head, a dorsal fin placed on two-third of the animal back surface, a powerful fluke and a streamlined body along with a long length about 12-18 m and a medium weight range among rorquals from 30 to 40 tons, compared to other heavy weight species like blue whales with about 140 tons [1, 2]. Humpback whales also exhibit a high level of swimming manoeuvrability in the ocean partially linked with their powerful flukes [1] and also superior hydrodynamic performance of their flippers with an approximate length of 0.3 of the body length and with special tubercled topology shown in Fig.1 [3, 4]. As one can observe in the figure, humpback whales have evolved tubercles on the leading edge and the trailing edge of their flippers representing a special pattern involving peaks and troughs with varying amplitude and wavelength [4]. Turbulent and transitional flows over tubercled wings have been extensively studied in the literature. As a short summary, wings with wavy leading edge planform depict superior lift coefficient performance in the after-stall region compared to the clean planforms [3, 5 and 6]. Streamwise vortex generation is a crucial factor to explain flow characteristics over a humpback whale flipper. In this case, wavy leading edge generates two counter-rotating vortices with different vorticity signs at different sides of the trough of each individual protuberance and secondary- spanwise flows are generated in the leading edge region. It is postulated that higher amount of momentum induced by streamwise vortices originating from protuberances results in a softer/ flatter post-stall behaviour for wings with leading edge undulations [5, 6]. Caused by the ecological constrains of life in oceans, humpback whales have also developed some unique individual and social behavioural features, like breaching behaviour (Fig.1), generation of the most complex sound among the swimming animals in general and in their group foraging process [7, 8] and utilization of a smart bubble net hunting technique [9], to name a few [2].
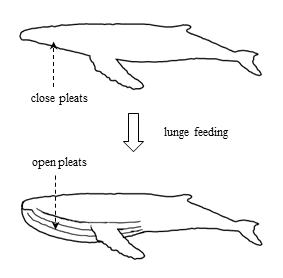 | Figure 2. Humpback whale lunge feeding process |
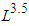 , where
, where 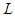 is the body length of the whale. For instance, for a whale with total length of 14 and 16 m, amount of engulfed mass of prey-laden ocean water would be approximately equals to 15 and 24 tons, respectively. It is also worth mentioning that by increasing the body length, engulfed mass capacity of the aquatic animal increases; furthermore, oxygen carrying capacity of these air-breathing marine animals improves by increasing the size of these breath-hold divers, providing them more time at foraging depth [13]. There exist many interesting lessons considering humpback whale swimming hydrodynamics; however in this paper, hydrodynamics of external turbulent flow passing over the humpback whale ventral pleats is studied. In this regard, flow fields around a simplified model of the animal body are numerically simulated at different angles of attack (AoA, hereafter) and a prescribed sideslip angle. In the following, details are presented.
is the body length of the whale. For instance, for a whale with total length of 14 and 16 m, amount of engulfed mass of prey-laden ocean water would be approximately equals to 15 and 24 tons, respectively. It is also worth mentioning that by increasing the body length, engulfed mass capacity of the aquatic animal increases; furthermore, oxygen carrying capacity of these air-breathing marine animals improves by increasing the size of these breath-hold divers, providing them more time at foraging depth [13]. There exist many interesting lessons considering humpback whale swimming hydrodynamics; however in this paper, hydrodynamics of external turbulent flow passing over the humpback whale ventral pleats is studied. In this regard, flow fields around a simplified model of the animal body are numerically simulated at different angles of attack (AoA, hereafter) and a prescribed sideslip angle. In the following, details are presented. 2. Humpback Whale Body Model
- Ellipsoid can be considered as a good approximation to represent the streamlined body shape of many cetaceans. As shown in the top view of a humpback body sample in Fig. 3, a 3:1 ellipsoid can be adopted to model main features of the humpback whale body, as hired in this paper.
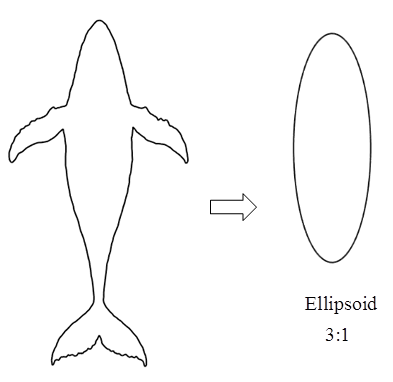 | Figure 3. Humpback whale body approximation |
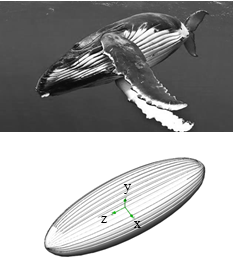 | Figure 4. Humpback whale body; Top: non-lunge swimming (modified from the original picture [16]), Bottom: simplified body model as an ellipsoid with ventral pleats on the half of the body surface |
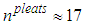 ventral pleats each with a depth of
ventral pleats each with a depth of 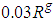 and a width equals to
and a width equals to 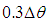 , where
, where 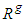 is the local radius of a circle formed by intersection of the vertical planes perpendicular to z-axis and the ellipsoid, while
is the local radius of a circle formed by intersection of the vertical planes perpendicular to z-axis and the ellipsoid, while 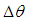 is equal to
is equal to 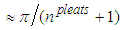 . To construct the geometry a total number of 20 intersection curves and 2 guide curves forming the external shape of the ellipsoid in the plane, defined by y=0, are generated by high resolution and imported into the SolidWorks CAD environment. Then, the resulting half- grooved ellipsoid model resembling humpback whale body is majorly constructed by utilizing a lofting process, i.e. stitching the guide curves by surfaces, as shown in Fig. 4.
. To construct the geometry a total number of 20 intersection curves and 2 guide curves forming the external shape of the ellipsoid in the plane, defined by y=0, are generated by high resolution and imported into the SolidWorks CAD environment. Then, the resulting half- grooved ellipsoid model resembling humpback whale body is majorly constructed by utilizing a lofting process, i.e. stitching the guide curves by surfaces, as shown in Fig. 4.3. Numerical Methodology
- To study flow field details over the grooved and non-grooved ellipsoids, numerical simulations are conducted at different AoAs and a given sideslip angle. In all simulations, the body model is kept at a fixed position in space, i.e. in y-z and x-z planes and effects of AoA,
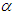 , (Fig. 5-a) and sideslip angle,
, (Fig. 5-a) and sideslip angle, 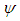 , (Fig. 5-b) are included via setting freestream blowing angles, i.e.
, (Fig. 5-b) are included via setting freestream blowing angles, i.e. 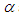 and
and 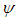 (Fig. 5).
(Fig. 5).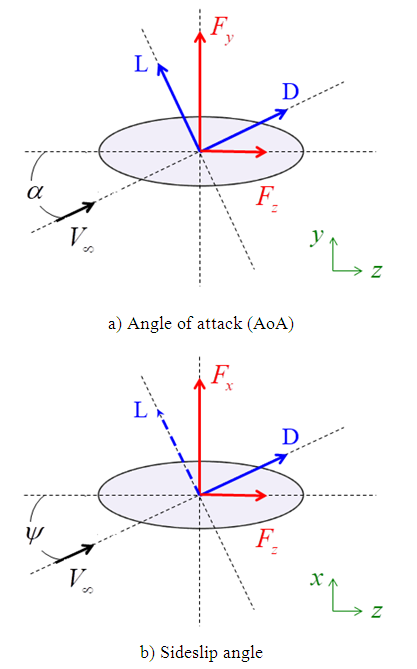 | Figure 5. Coordinate system utilized for the ellipsoid simulations |
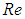 . For inflow setting with AoA in y-z plane, freestream uniformly flows in x-direction by imposing null lateral velocity at the inlet plane, as below:
. For inflow setting with AoA in y-z plane, freestream uniformly flows in x-direction by imposing null lateral velocity at the inlet plane, as below: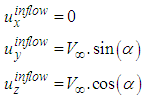 | (1) |
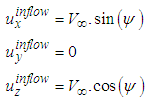 | (2) |
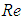 . Humpback whales with a body length about 12-18 m, experience turbulent flows on their body, with high
. Humpback whales with a body length about 12-18 m, experience turbulent flows on their body, with high 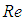 easily reaching to orders of magnitude equal to 107-108. To have an idea, maximum swimming speed of the humpback whales while singing is about 4 m/s [17] and in general with maximum about 7 m/s and minimum of about 0.55-2.0 m/s in the feeding phase; in addition, ocean current speed is fastest near the ocean surface with about 2.5 m/s and gulf currents speed is about 1.8 m/s [18]. As an example, for a humpback whale with a typical length of 15 m, swimming with speed of about 1 m/s,
easily reaching to orders of magnitude equal to 107-108. To have an idea, maximum swimming speed of the humpback whales while singing is about 4 m/s [17] and in general with maximum about 7 m/s and minimum of about 0.55-2.0 m/s in the feeding phase; in addition, ocean current speed is fastest near the ocean surface with about 2.5 m/s and gulf currents speed is about 1.8 m/s [18]. As an example, for a humpback whale with a typical length of 15 m, swimming with speed of about 1 m/s, 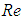 is equal to
is equal to 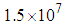 , defined based on the body length. In this paper, all upcoming ellipsoid simulations are performed at this Reynolds number, i.e.
, defined based on the body length. In this paper, all upcoming ellipsoid simulations are performed at this Reynolds number, i.e. 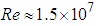 .
.3.1. Computational Domain and Mesh Generation
- To investigate hydrodynamic effects of the humpback whale ventral grooves, two series of simulations are performed on the constructed models in this study: first, a 3:1 ellipsoid without grooves, namely ‘clean’ ellipsoid hereafter, and second a 3:1 ellipsoid with pleats on half-surface of the body namely ‘grooved’ ellipsoid hereafter, resembling ventral pleated body of humpback whales (Fig. 4- bottom). As mentioned in the previous section, both geometries have been numerically constructed in SolidWorks CAD Environment [19]. Computational grids for these external flow simulations were also constructed using SolidWorks meshing tools with Cartesian-base grid coupled with an adaptive mesh- clustering to capture complex geometrical features like ventral pleats and also boundary layer zone, with minimum 10 nodes close to the wall in the boundary layer [20]. Fig. 6 depicts grid generation around the clean ellipsoid along with the computational domain. For the grooved ellipsoid, computational domain is exactly the same as Fig. 6-top, except in the near body zone, where mesh is modified by ventral grooves, as shown in Fig. 7. The latter figure shows front and side views of the generated grid for the grooved ellipsoid in the middle sections of the ellipsoid which exhibits clustering to the wall. As shown in both Fig. 6 and Fig. 7, near wall zone is completely well-captured to the wall due to the computational demand of the utilized turbulence treatment in the present study (soon explained in the next subsection). After performing grid convergence test, two well-converged grids with about 1.5 and 2 million elements have been utilized for the clean and grooved ellipsoid simulations, respectively. It is worth mentioning that running simulations resolving to the wall for multiple operating points adopted in this study is computationally costly; therefore, there always exists a trade-off between size of the computational domain, mesh resolution and the desired achievable accuracy.
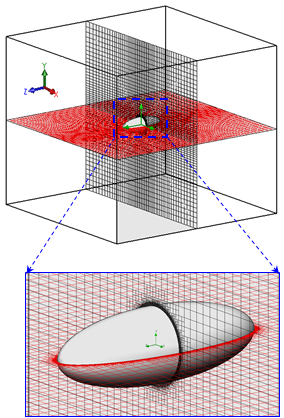 | Figure 6. Clean ellipsoid grid and computational domain |
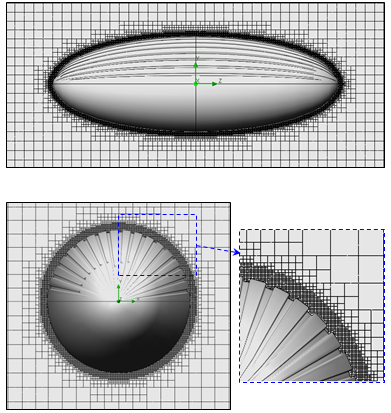 | Figure 7. Grooved ellipsoid cross-sectional grids at the middle planes: side view (top) and front view (bottom) |
3.2. Flow Solver, Turbulence Treatment and Settings
- In unsteady Reynold averaged Navier-Stokes (URANS) approach, governing equations of fluid motions including Navier-Stokes, continuity and also turbulence model equations are numerically solved in the case of turbulent flow simulations. In this paper, the governing equations of non- cavitating and cavitating turbulent flows over the humpback whale body model are solved using SolidWorks Flow Simulation (SFS) solver [19, 20] with Lam-Bremhorst low- Reynolds number version of
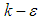 model (LB LRN
model (LB LRN 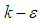 , hereafter), resolving to the wall [21]. In general, fluid flow governing equations of the problem can be expressed as below [20, 22]:
, hereafter), resolving to the wall [21]. In general, fluid flow governing equations of the problem can be expressed as below [20, 22]: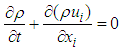 | (3) |
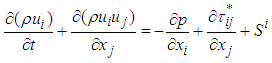 | (4) |
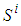 , is the source term and total stress tensor
, is the source term and total stress tensor 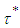 , including Reynolds stress tensor, is defined as the following:
, including Reynolds stress tensor, is defined as the following: 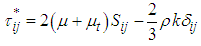 | (5) |
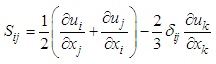 | (6) |
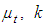 and
and 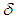 denote turbulent eddy viscosity, turbulent kinetic energy and Kronecker delta, respectively. The above set of equations suffers from a so-called ‘closure problem’; therefore, the extra variable, i.e. turbulent eddy viscosity, should be estimated in a way. In LB LRN
denote turbulent eddy viscosity, turbulent kinetic energy and Kronecker delta, respectively. The above set of equations suffers from a so-called ‘closure problem’; therefore, the extra variable, i.e. turbulent eddy viscosity, should be estimated in a way. In LB LRN 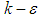 like the original
like the original 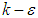 model, this is done by solving two extra transport equations for turbulent kinetic energy
model, this is done by solving two extra transport equations for turbulent kinetic energy 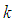 and turbulent eddy dissipation
and turbulent eddy dissipation 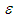 coupled with the aforementioned governing equations, as below [20, 21 and 22]:
coupled with the aforementioned governing equations, as below [20, 21 and 22]: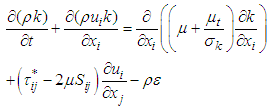 | (7) |
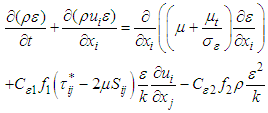 | (8) |
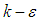 similar to the original
similar to the original 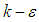 are empirically set, as below:
are empirically set, as below: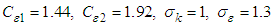 Having on hand both
Having on hand both 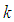 and
and 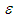 values at each computational node, turbulent eddy viscosity is calculated as:
values at each computational node, turbulent eddy viscosity is calculated as: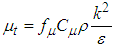 | (9) |
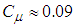 and LB damping function
and LB damping function 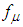 , also
, also 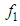 and
and 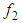 parameters (Eq. 8) in the LB LRN version of the
parameters (Eq. 8) in the LB LRN version of the 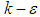 model are defined as below:
model are defined as below: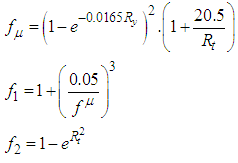 | (10) |
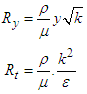 | (11) |
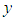 is defined as the shortest distance to any solid surface. Finally time and length scales of the representative turbulent eddy at each computational node can be computed using the following relations [23]:
is defined as the shortest distance to any solid surface. Finally time and length scales of the representative turbulent eddy at each computational node can be computed using the following relations [23]: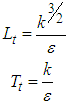 | (12) |
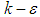 model utilized here is different with the original
model utilized here is different with the original 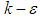 turbulence model; in LB LRN
turbulence model; in LB LRN 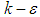 approach, damping functions,
approach, damping functions, 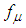 and also
and also 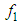 and
and 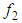 functions are introduced and calculated as functions of the minimum distance to the wall. In addition, it is worth mentioning that SFS needs at least 10 nodes in the direction normal to the wall-surface in the boundary layers to efficiently approximate these high gradient zones with LB LRN
functions are introduced and calculated as functions of the minimum distance to the wall. In addition, it is worth mentioning that SFS needs at least 10 nodes in the direction normal to the wall-surface in the boundary layers to efficiently approximate these high gradient zones with LB LRN 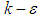 method [19, 20]. In non-cavitating cases, finite-volume SFS solver numerically solves governing equations of the fluid flow motions by an operator-splitting technique and uses a SIMPLE-like approach to treat pressure-velocity decoupling issue [19, 20]. Furthermore, the solver solves asymmetric linear system of the discretised equations coming from the momentum/ turbulence with a preconditioned conjugate gradient method along with an incomplete LU factorization preconditioning; while symmetric pressure-correction system of equations is solved by the aid of a multigrid technique [20].In cavitating cases, SFS uses another all-speed solver developed based on a hybrid density- and pressure-based splitting technique proposed by Alexandrikova et al. [22]. The underlying method adopts a separate density-based approach for compressible flow zones, while uses a pressure-based treatment for incompressible zones without cavitation simultaneously in a single computational domain [22]. Furthermore, the solver uses the same LB LRN
method [19, 20]. In non-cavitating cases, finite-volume SFS solver numerically solves governing equations of the fluid flow motions by an operator-splitting technique and uses a SIMPLE-like approach to treat pressure-velocity decoupling issue [19, 20]. Furthermore, the solver solves asymmetric linear system of the discretised equations coming from the momentum/ turbulence with a preconditioned conjugate gradient method along with an incomplete LU factorization preconditioning; while symmetric pressure-correction system of equations is solved by the aid of a multigrid technique [20].In cavitating cases, SFS uses another all-speed solver developed based on a hybrid density- and pressure-based splitting technique proposed by Alexandrikova et al. [22]. The underlying method adopts a separate density-based approach for compressible flow zones, while uses a pressure-based treatment for incompressible zones without cavitation simultaneously in a single computational domain [22]. Furthermore, the solver uses the same LB LRN 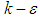 turbulence model as explained before along with a barotropic state equation as
turbulence model as explained before along with a barotropic state equation as 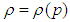 , derived with thermodynamic equilibrium assumption [22]. With the aid of the smart underlying splitting technique, SFS is capable to handle a broad range of time scale, density and speed of sound variations, arising in a single domain in cavitating flow conditions. As mentioned earlier, for numerical simulations three components of the inflow velocity (Eq. 1 or 2) are set at the inflow section. Other boundaries are treated as ‘outflows’. For simulation convergence, predefined goals as
, derived with thermodynamic equilibrium assumption [22]. With the aid of the smart underlying splitting technique, SFS is capable to handle a broad range of time scale, density and speed of sound variations, arising in a single domain in cavitating flow conditions. As mentioned earlier, for numerical simulations three components of the inflow velocity (Eq. 1 or 2) are set at the inflow section. Other boundaries are treated as ‘outflows’. For simulation convergence, predefined goals as 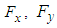 and
and 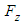 forces (or equivalently lift and drag forces) are monitored on top of the velocity and pressure variables to achieve a converged state; in SFS solver, convergence criteria is automatically set by the solver based on dynamic calculation of dispersion of the goal functions, which guarantees the lowest convergence residual level [19]. In the next section, simulation results are presented in details.
forces (or equivalently lift and drag forces) are monitored on top of the velocity and pressure variables to achieve a converged state; in SFS solver, convergence criteria is automatically set by the solver based on dynamic calculation of dispersion of the goal functions, which guarantees the lowest convergence residual level [19]. In the next section, simulation results are presented in details.4. Results and Discussion
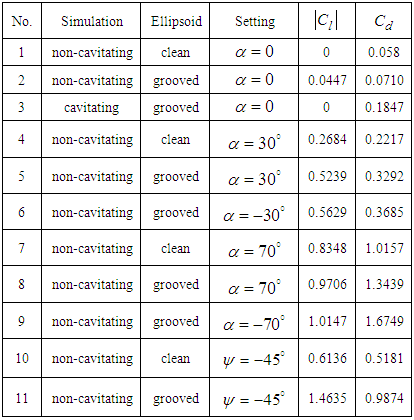
- In this section, turbulent flows over the humpback whale pleated body model, i.e. the grooved ellipsoid, are simulated at high Reynolds number,
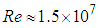 . There is no experimental data available in this case; therefore the effects of ventral pleats are studied by comparison to results of the turbulent flow simulations over the clean 3:1 ellipsoid model. To perform flow simulations over the clean and grooved ellipsoids, first of all effects of applied surface roughness is considered to adjust the parameter for the upcoming simulations. Table 1 depicts drag coefficient
. There is no experimental data available in this case; therefore the effects of ventral pleats are studied by comparison to results of the turbulent flow simulations over the clean 3:1 ellipsoid model. To perform flow simulations over the clean and grooved ellipsoids, first of all effects of applied surface roughness is considered to adjust the parameter for the upcoming simulations. Table 1 depicts drag coefficient 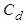 values obtained from turbulent flow simulations on the clean ellipsoid at null AoA,
values obtained from turbulent flow simulations on the clean ellipsoid at null AoA, 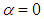 , for different applied averaged roughness values. As it is clear in the table, a roughness equals to 10 microns results in a drag coefficient close to the ellipsoid experimental value, i.e.
, for different applied averaged roughness values. As it is clear in the table, a roughness equals to 10 microns results in a drag coefficient close to the ellipsoid experimental value, i.e. 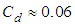 [24, 25]. For both clean and grooved ellipsoids in all upcoming simulations, an averaged roughness value of 10 microns is applied.
[24, 25]. For both clean and grooved ellipsoids in all upcoming simulations, an averaged roughness value of 10 microns is applied.
|
4.1. Streamwise Humpback Whale Swimming
- In this subsection, streamwise swimming of humpback whale is modelled by non-cavitating turbulent flow simulations of the grooved body along with the clean body for comparison purposes at
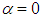 . Due to the symmetry exists in the case of clean ellipsoid at
. Due to the symmetry exists in the case of clean ellipsoid at 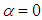 , one can expect to have null lift force in this case. Fig. 8 shows
, one can expect to have null lift force in this case. Fig. 8 shows 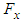 and
and 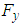 force oscillations around zero as convergence history of the goal function for the clean ellipsoid. Fig. 9 similarly shows lateral forces variations for the grooved ellipsoid compared to the clean one. As one can see in the latter figure, in contrast to the previous case, the grooved ellipsoid generates noticeable amount of
force oscillations around zero as convergence history of the goal function for the clean ellipsoid. Fig. 9 similarly shows lateral forces variations for the grooved ellipsoid compared to the clean one. As one can see in the latter figure, in contrast to the previous case, the grooved ellipsoid generates noticeable amount of 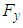 force and contributes to lift generation (here like buoyancy force in the negative-y direction) of the animal. The difference observed between the clean and grooved ellipsoids are expected a-priori, due to symmetry breakdown existing in the grooved case in y-direction.
force and contributes to lift generation (here like buoyancy force in the negative-y direction) of the animal. The difference observed between the clean and grooved ellipsoids are expected a-priori, due to symmetry breakdown existing in the grooved case in y-direction. 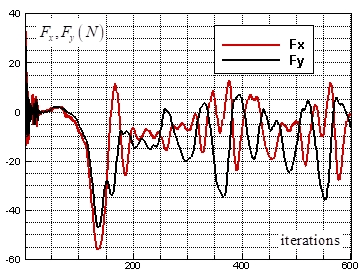 | Figure 8. Lateral force goal function history for the clean ellipsoid at 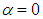 |
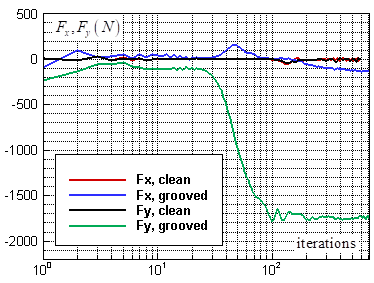 | Figure 9. Lateral force goal function history for the grooved and clean ellipsoids at 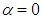 |
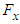 is also generated for the grooved ellipsoid, due to the dissymmetry imposed in x-direction to partially mimic the natural dissymmetry existing in the real ventral groove pattern of a humpback whale (Fig. 7). Fig. 10 shows variations of the axial force for both clean and grooved ellipsoids.
is also generated for the grooved ellipsoid, due to the dissymmetry imposed in x-direction to partially mimic the natural dissymmetry existing in the real ventral groove pattern of a humpback whale (Fig. 7). Fig. 10 shows variations of the axial force for both clean and grooved ellipsoids.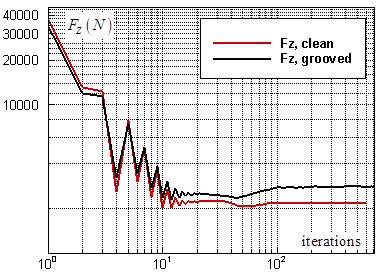 | Figure 10. Axial force goal function history for the grooved and clean ellipsoids at 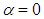 |
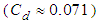 compared to the clean one
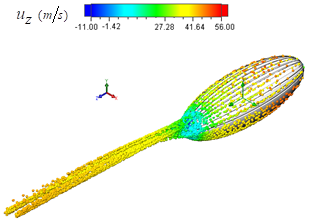
compared to the clean one 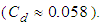 In Fig. 11, front view of axial velocity field along with pathlines in the middle section, defined by z=0, is shown.
In Fig. 11, front view of axial velocity field along with pathlines in the middle section, defined by z=0, is shown. 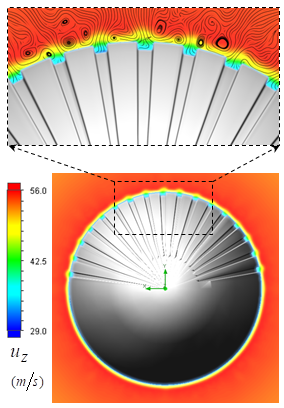 | Figure 11. Axial velocity field around the body at 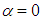 in the middle plane at z=0: pathlines close to the body (top), front view (bottom) in the middle plane at z=0: pathlines close to the body (top), front view (bottom) |
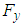 contributes to buoyancy force and should be interpreted as a lift force, i.e. opposite to the animal weight force. By comparing top and bottom surfaces of the body in Fig. 11, one can obviously observe that ventral grooves modify the velocity field pattern compared to the clean surface in the bottom; in fact, strip of low velocity form on the bottom surface of the animal body. Fig. 12 also shows axial velocity field in the longitudinal middle plane defined as x=0.
contributes to buoyancy force and should be interpreted as a lift force, i.e. opposite to the animal weight force. By comparing top and bottom surfaces of the body in Fig. 11, one can obviously observe that ventral grooves modify the velocity field pattern compared to the clean surface in the bottom; in fact, strip of low velocity form on the bottom surface of the animal body. Fig. 12 also shows axial velocity field in the longitudinal middle plane defined as x=0.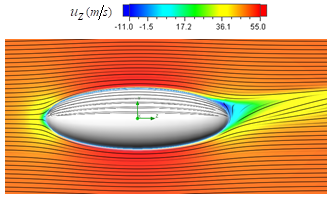 | Figure 12. Axial velocity field around the body at 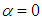 in the middle plane defined as x=0 in the middle plane defined as x=0 |
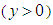 and bottom
and bottom 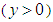 regions breaks due to presence of the ventral pleats on the top surface. As expected, a stagnation point at the ellipsoid nose is present and also an asymmetric recirculation zone forms at the aft-body zone of the grooved ellipsoid. To capture hidden structures in the flow field like vortical structures/shear layers,
regions breaks due to presence of the ventral pleats on the top surface. As expected, a stagnation point at the ellipsoid nose is present and also an asymmetric recirculation zone forms at the aft-body zone of the grooved ellipsoid. To capture hidden structures in the flow field like vortical structures/shear layers, 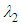 -criterion is utilized here [26]. The
-criterion is utilized here [26]. The 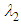 -criterion method links the minimum extrema of pressure occurring in vortex core regions or shear layers in the case of shear contamination to the eigenvalues of the Hessian of pressure, i.e.
-criterion method links the minimum extrema of pressure occurring in vortex core regions or shear layers in the case of shear contamination to the eigenvalues of the Hessian of pressure, i.e. 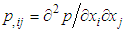 ; in the method vortex cores with/without shear contamination can be identified by
; in the method vortex cores with/without shear contamination can be identified by 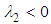 . In fact, the threshold level utilized for capturing the structures is case-dependent and is typically selected by try and error. Fig. 13 depicts hidden structures generated on the humpback whale body simplified model obtained via
. In fact, the threshold level utilized for capturing the structures is case-dependent and is typically selected by try and error. Fig. 13 depicts hidden structures generated on the humpback whale body simplified model obtained via 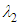 -criterion with threshold as
-criterion with threshold as 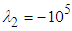 .
. 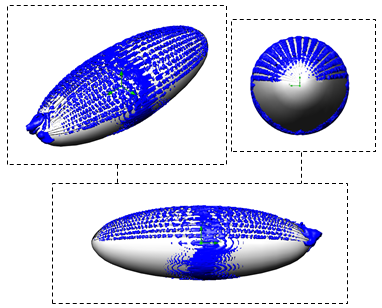 | Figure 13. Vortical structures/shear layers developed on the humpback whale body model captured by 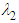 -criterion at -criterion at  : isometric view (top-left), front view (top-right) and side view (bottom) : isometric view (top-left), front view (top-right) and side view (bottom) |
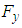 is generated that contributes to buoyancy force in humpback whale swimming at the expense of more energy consumption due to higher level of drag force (table 2).
is generated that contributes to buoyancy force in humpback whale swimming at the expense of more energy consumption due to higher level of drag force (table 2).
|
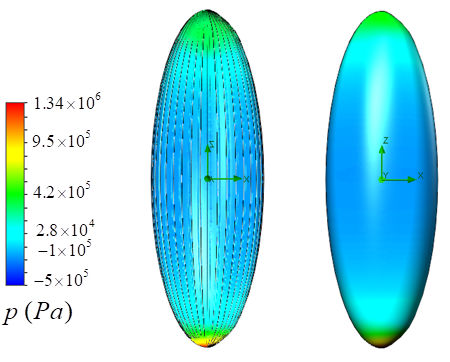 | Figure 14. Pressure field on the clean (right) and grooved (left) surfaces of the humpback whale body at  |
 | Figure 15. Isometric view of tracer particle dynamics over the humpback whale body in the streamwise swimming  |
4.2. Effects of AoA
- Despite having a giant body and mass, humpback whales unexpectedly exhibit high level of manoeuvrability in rolling, banking and turning; as mentioned this is majorly linked to their unique tubercled flipper [3, 4]. These swimming animals experience a broad range of AoA and sideslip in their manoeuvres in the oceans; to complete the picture and to study hydrodynamic effects of the pleated body in the flow field a set of different AoA and a sideslip angle are considered for simulations in the present and next subsections, respectively, as
 and
and 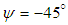 . Table 2 summarizes numerical performance coefficients, i.e. lift and drag coefficients covering all numerical simulations performed in this paper. As one can see in the table, for all AoA, lift coefficient obtained from the grooved body is higher than the corresponding coefficient of the clean ellipsoid, while the grooved body results in a higher level of drag coefficient, majorly due to the formation of low-speed shear strips in the grooves. It is also observed in the table that by increasing AoA, lift and drag coefficients increase as expected. The symmetry also breaks for positive and negative AoA, due to presence of the ventral pleats on the half-surface of the body and as a result of geometrical symmetry breakdown in y- direction with respect to the plane, defined by
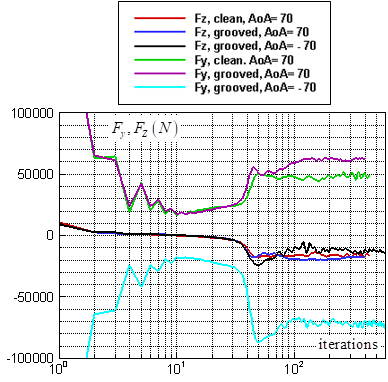
. Table 2 summarizes numerical performance coefficients, i.e. lift and drag coefficients covering all numerical simulations performed in this paper. As one can see in the table, for all AoA, lift coefficient obtained from the grooved body is higher than the corresponding coefficient of the clean ellipsoid, while the grooved body results in a higher level of drag coefficient, majorly due to the formation of low-speed shear strips in the grooves. It is also observed in the table that by increasing AoA, lift and drag coefficients increase as expected. The symmetry also breaks for positive and negative AoA, due to presence of the ventral pleats on the half-surface of the body and as a result of geometrical symmetry breakdown in y- direction with respect to the plane, defined by 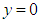 . In Fig. 16 and Fig. 17, convergence history of the axial and lateral forces for different AoA values,
. In Fig. 16 and Fig. 17, convergence history of the axial and lateral forces for different AoA values, 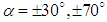 , are shown. As one can see in the figures, behaviour of the grooved and clean ellipsoids is different at the same AoA, as expected. In addition, in the case of grooved ellipsoid resembling humpback whale body, there is no symmetry between
, are shown. As one can see in the figures, behaviour of the grooved and clean ellipsoids is different at the same AoA, as expected. In addition, in the case of grooved ellipsoid resembling humpback whale body, there is no symmetry between 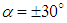 cases; the same dissymmetry is also observed between
cases; the same dissymmetry is also observed between 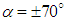 cases; as stated before, this difference comes from presence of the ventral grooves on the half of the wetted surface. As one can see in the both figures, for the clean ellipsoid,
cases; as stated before, this difference comes from presence of the ventral grooves on the half of the wetted surface. As one can see in the both figures, for the clean ellipsoid,  and
and  are also generated at both positive and negative AoA, although absolute values of the forces are obviously less than the corresponding values in the case of the grooved ellipsoid. It is trivial that positive and negative AoA in the case of clean ellipsoid have the same behaviour due to its geometrical symmetry (not shown).
are also generated at both positive and negative AoA, although absolute values of the forces are obviously less than the corresponding values in the case of the grooved ellipsoid. It is trivial that positive and negative AoA in the case of clean ellipsoid have the same behaviour due to its geometrical symmetry (not shown). | Figure 16. Axial and lateral force goal function monitoring for the grooved and clean ellipsoids at 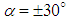 |
 | Figure 17. Axial and lateral force goal function monitoring for the grooved and clean ellipsoids at 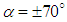 |
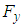 and
and 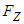 increase by increasing AoA. In table 2, all ultimate converged force data are translated to the lift and drag coefficients. Fig. 18 shows topology of the flows at different AoA.As one can see in Fig. 18, at higher AoA more complicated flow pattern is illustrated by flow pathlines bundling around the grooved body, due to formation of vortical structures in the wake of the body. As also shown in the figure, there is no symmetry between
increase by increasing AoA. In table 2, all ultimate converged force data are translated to the lift and drag coefficients. Fig. 18 shows topology of the flows at different AoA.As one can see in Fig. 18, at higher AoA more complicated flow pattern is illustrated by flow pathlines bundling around the grooved body, due to formation of vortical structures in the wake of the body. As also shown in the figure, there is no symmetry between 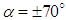 cases; in the negative AoA, pathlines are getting more bundled than in the positive AoA and forms a heavy wake due to presence of ventral pleats on the top surface. The effect is less pronounced in the
cases; in the negative AoA, pathlines are getting more bundled than in the positive AoA and forms a heavy wake due to presence of ventral pleats on the top surface. The effect is less pronounced in the  cases, although still exists.
cases, although still exists.  | Figure 18. 3D pathlines over the grooved body along with the axial velocity field in the middle plane defined as x=0, at different AoA |
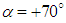 ; as shown in the figure, a region of high velocity forms on top of the body. Two counter-rotating vortices are also generated on the grooved surface.
; as shown in the figure, a region of high velocity forms on top of the body. Two counter-rotating vortices are also generated on the grooved surface.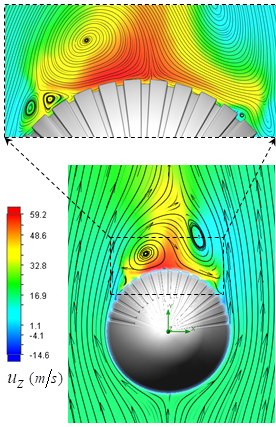 | Figure 19. Axial velocity field around the body at  in the middle plane at z=0: pathlines close to the body (top), front view (bottom) in the middle plane at z=0: pathlines close to the body (top), front view (bottom) |
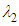 -criterion is applied. Threshold levels as
-criterion is applied. Threshold levels as 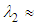
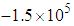 and
and 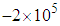 are applied for
are applied for 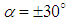 and
and 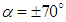 , respectively. As one can observe in Fig. 20, different structures form on the grooved surface at different AoA. At
, respectively. As one can observe in Fig. 20, different structures form on the grooved surface at different AoA. At 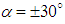 , two attached tail-like vortical structures with positive and negative angle with respect to the longitudinal axis of the body, i.e. z-direction are generated at positive and negative AoA, respectively. For both
, two attached tail-like vortical structures with positive and negative angle with respect to the longitudinal axis of the body, i.e. z-direction are generated at positive and negative AoA, respectively. For both 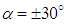 cases, structures form on the grooved surface; although at
cases, structures form on the grooved surface; although at 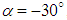 , structures are extended to the clean surface as well. By increasing AoA to
, structures are extended to the clean surface as well. By increasing AoA to 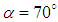 , few scattered and shorter tails are generated at the aft-body. In addition, an attached structure forms originating from the ellipsoid nose. At
, few scattered and shorter tails are generated at the aft-body. In addition, an attached structure forms originating from the ellipsoid nose. At 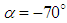 , tail structures are efficiently omitted and only covering structures on the grooved surface are generated along with two relatively short spikes at the ellipsoid nose, as shown in Fig. 20.
, tail structures are efficiently omitted and only covering structures on the grooved surface are generated along with two relatively short spikes at the ellipsoid nose, as shown in Fig. 20. | Figure 20. Vortical structures/shear layers developed on the humpback whale body model (side view) captured by 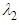 -criterion at different AoA -criterion at different AoA |
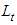 , defined in Eq. 12) on the body surface; smaller turbulent structures are typically generated on the grooved surface on the top compared to the clean surface of the body on the bottom, as shown in Fig. 21 for
, defined in Eq. 12) on the body surface; smaller turbulent structures are typically generated on the grooved surface on the top compared to the clean surface of the body on the bottom, as shown in Fig. 21 for  as an example.Fig. 21 also shows shear stress variation on the humpback whale body model at
as an example.Fig. 21 also shows shear stress variation on the humpback whale body model at  ; as it is obvious in the figure, high shear stress strips form on the grooved surface on the top, while the clean surface possesses very low values of the shear stress due to formation of large separation zone on the bottom at this AoA.
; as it is obvious in the figure, high shear stress strips form on the grooved surface on the top, while the clean surface possesses very low values of the shear stress due to formation of large separation zone on the bottom at this AoA. | Figure 21. Turbulent length scale (top) and shear stress (bottom) fields on the humpback whale body surface at 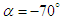 (side view) (side view) |
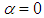 . Like before, spherical ethane particles with 0.0001 m diameter are released from the humpback whale body surface and convected downstream by the background flow field. Ideal reflection has also been applied for fluid particle-solid interactions, e.g. in the recirculation zones. As an example, Fig. 22 depicts a snapshot of tracer particle motions at
. Like before, spherical ethane particles with 0.0001 m diameter are released from the humpback whale body surface and convected downstream by the background flow field. Ideal reflection has also been applied for fluid particle-solid interactions, e.g. in the recirculation zones. As an example, Fig. 22 depicts a snapshot of tracer particle motions at  . As one can see in the figure and also in a movie generated by the present particle study, tracer particles majorly follow vortical structures arising on the grooved surfaces and pass downstream.
. As one can see in the figure and also in a movie generated by the present particle study, tracer particles majorly follow vortical structures arising on the grooved surfaces and pass downstream.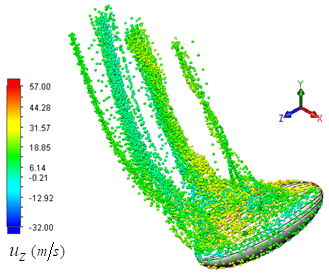 | Figure 22. Particle dynamics study over the humpback whale body at  |
4.3. Effects of Sideslip Angle
- Humpback whales experience high angles of sideslip in their manoeuvers in the oceans. In this subsection, turbulent flow over the body is simulated at high sideslip angle, i.e.
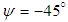 , as shown in Fig. 23.
, as shown in Fig. 23.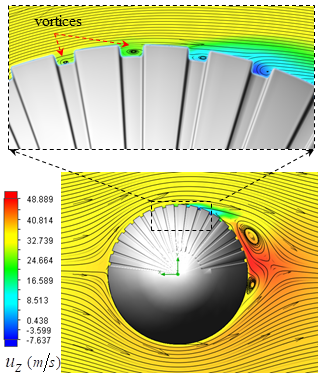 | Figure 23. Axial velocity field around the body at 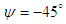 in the middle plane at z=0: pathlines close to the body (top), front view (bottom) in the middle plane at z=0: pathlines close to the body (top), front view (bottom) |
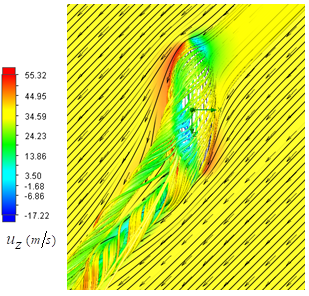 | Figure 24. 3D pathlines over the grooved body along with the axial velocity field in the middle plane defined as y=0, at 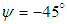 |
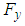 and component projections of
and component projections of 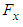 and
and 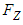 . Fig. 25 shows convergence history of forces in the case of flow over the grooved ellipsoid at
. Fig. 25 shows convergence history of forces in the case of flow over the grooved ellipsoid at 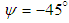 .
.  | Figure 25. Axial and lateral force goal function monitoring for the grooved and clean ellipsoids at  |
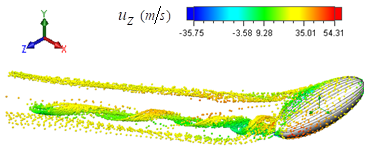 | Figure 26. Isometric view of tracer particle dynamics over the humpback whale body at sideslip angle as 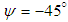 |
 , turbulent length scales are also modified on the clean and grooved surfaces as shown in Fig. 27. As one can see in the figure, at x+ larger turbulent eddies are generated compared to the turbulent structures at x- on the clean surface. In general, finer turbulent eddies are generated on the grooved surface compared to the clean one, similar to the typical cases investigated in this paper at other AoAs; a strip of large vortices is also generated at x- in the aft-body zone on the grooved surface as shown in Fig. 27.
, turbulent length scales are also modified on the clean and grooved surfaces as shown in Fig. 27. As one can see in the figure, at x+ larger turbulent eddies are generated compared to the turbulent structures at x- on the clean surface. In general, finer turbulent eddies are generated on the grooved surface compared to the clean one, similar to the typical cases investigated in this paper at other AoAs; a strip of large vortices is also generated at x- in the aft-body zone on the grooved surface as shown in Fig. 27.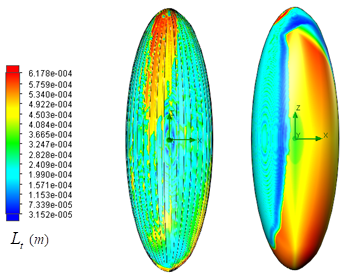 | Figure 27. Turbulent length scale field on the clean (right) and grooved (left) surfaces of the humpback whale body at  |
4.4. Swimming in Cavitating Conditions
- As mentioned earlier, some groups of humpback whales learned to use a social foraging technique, called bubble net feeding, for prey haunting [7, 8, 9, and 27]. In the process, they move in a shrinking helical/circular path, with a dimeter of about 3 to 30 meters, towards the surface blowing air rings/cloud at different instants from beneath of a prey school via two blowholes of these breath-hold swimming animals to make the prey more concentrated. They basically control pattern of the bubble column cylinder via bubble generation characteristics; in general, there is a continuous trade-off between net depth and bubble generation characteristics due to different rise rates of small and large bubbles, as showed in details by F. A. Sharpe [27]. After fish schooling provided by the resulting bubble net and forcing the prey to concentrate moving upward, at the next step humpback whales swim upward in a drag-based feeding fashion, i.e. mouth open, to engulf the prey colony. In this process, humpback whales basically swim in an air and water mixture, not in a pure-water condition. On the other hand, there always exist some sorts of dissolved gas in the ocean/sea water [28]. In general, flow simulation in multiphase flow conditions is a challenging task due to existence of a broad range of Mach number and time scales of the phenomena involved. In fact, sonic speed dramatically drops in air-bubble and water mixture; as an example, speed of sound in liquid sea water is about 1500 m/s and in water-vapour is about 450 m/s depending on the temperature; for liquid-vapour mixture, speed of sound drops to about 3.2 m/s at volume fraction of 0.5 [29]. In the case of air-water mixture with air volume fraction of 0.4, sonic speed drops to about 20 m/s [30]. By local decreasing of sonic speed in different regions of a single computational domain, solver encounters to local Mach number increase and even presence of shock waves in the solution domain. As explained in section 3.2, to handle cavitating flows, an all-speed solver developed based on a hybrid density- and pressure-based splitting technique along with LB LRN
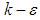 turbulence treatment are hired in the solver. In this section, to have an idea about hydrodynamic effects of ventral pleats on the humpback whale body in a bubble net environment, a cavitating flow simulation is performed at
turbulence treatment are hired in the solver. In this section, to have an idea about hydrodynamic effects of ventral pleats on the humpback whale body in a bubble net environment, a cavitating flow simulation is performed at 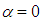 with
with 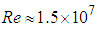 having inflow dissolved gas mass fraction of 0.001. Fig. 28 shows density variation around the humpback whale body model along with tracer particle dynamics coloured by axial velocity quantity.
having inflow dissolved gas mass fraction of 0.001. Fig. 28 shows density variation around the humpback whale body model along with tracer particle dynamics coloured by axial velocity quantity.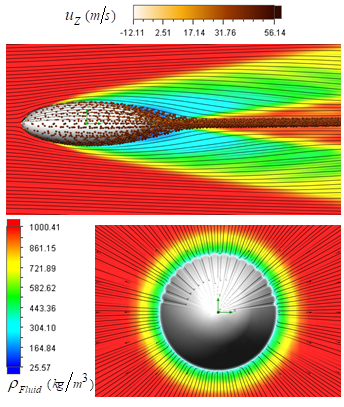 | Figure 28. Cavitating flow field around the body: fluid density superimposed with tracer particle dynamics, side view (top), front view (bottom) |
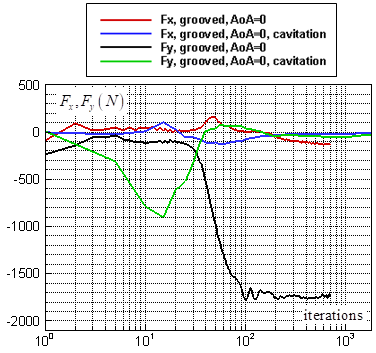 | Figure 29. Lateral force goal function monitoring for the grooved ellipsoid in the cavitating flow condition at  |
 -criterion in the cavitating flow simulation at
-criterion in the cavitating flow simulation at  . As one can see in the figure, a similar but noisier structure pattern to the non-cavitating case (Fig. 13) is generated on the grooved ellipsoid in the cavitating condition. Here, density of the structures is higher in front-body region and less in the aft-body zone.
. As one can see in the figure, a similar but noisier structure pattern to the non-cavitating case (Fig. 13) is generated on the grooved ellipsoid in the cavitating condition. Here, density of the structures is higher in front-body region and less in the aft-body zone. | Figure 30. Developed structures on the humpback whale body model identified by 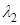 -criterion in cavitating flow simulation at -criterion in cavitating flow simulation at  |
4.5. Predicted Separation Zones
- To see the effects of ventral grooves on the separation zone fomation, separated flow regions, defined as
 , on the clean and grooved ellipsoids are shown in Fig. 31 and Fig. 32, respectively. As one can see in the both figures, by increasing AoA, larger separation zone form on the body.
, on the clean and grooved ellipsoids are shown in Fig. 31 and Fig. 32, respectively. As one can see in the both figures, by increasing AoA, larger separation zone form on the body. 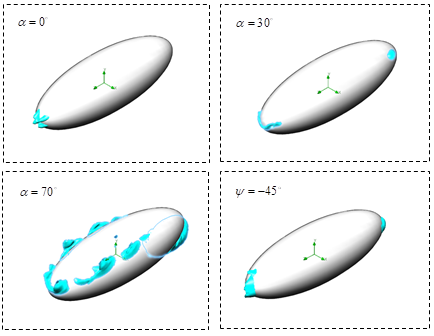 | Figure 31. Separation zones on the clean ellipsoid body at different AoA and a sideslip angle |
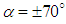 , due to the geometrical dissymmetry in the y-direction generated by presence of the ventral grooves. By comparing Fig. 31 and Fig. 32 at
, due to the geometrical dissymmetry in the y-direction generated by presence of the ventral grooves. By comparing Fig. 31 and Fig. 32 at 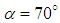 , a long separated tail detached to the body is seen for the grooved ellipsoid, which is not present in the case of the clean ellipsoid; this reverse-flow zone is induced in the core filament of the strong vortical structure seen in Fig. 20 and also in the tracer particle dynamic study presented in Fig. 22. As one can also see in Fig. 32 at
, a long separated tail detached to the body is seen for the grooved ellipsoid, which is not present in the case of the clean ellipsoid; this reverse-flow zone is induced in the core filament of the strong vortical structure seen in Fig. 20 and also in the tracer particle dynamic study presented in Fig. 22. As one can also see in Fig. 32 at 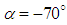 , a large separation zone is generated under the body on the clean surface due to presence of the ventral grooves on the top surface. In the case of cavitating flow condition on the grooved ellipsoid at
, a large separation zone is generated under the body on the clean surface due to presence of the ventral grooves on the top surface. In the case of cavitating flow condition on the grooved ellipsoid at 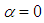 , separation zone depicts a very small reverse-flow region at the aft-body zone; the region is smaller compared to the non-cavitating case (Fig. 32). By comparing cases at
, separation zone depicts a very small reverse-flow region at the aft-body zone; the region is smaller compared to the non-cavitating case (Fig. 32). By comparing cases at 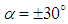 , very close patterns are obtained for these positive and negative AoA; although small differences is still visible in Fig. 32. At
, very close patterns are obtained for these positive and negative AoA; although small differences is still visible in Fig. 32. At 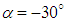 , a relatively larger separation zone is generated at the aft-body zone; while small separations exist on the top at
, a relatively larger separation zone is generated at the aft-body zone; while small separations exist on the top at 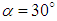 .
. 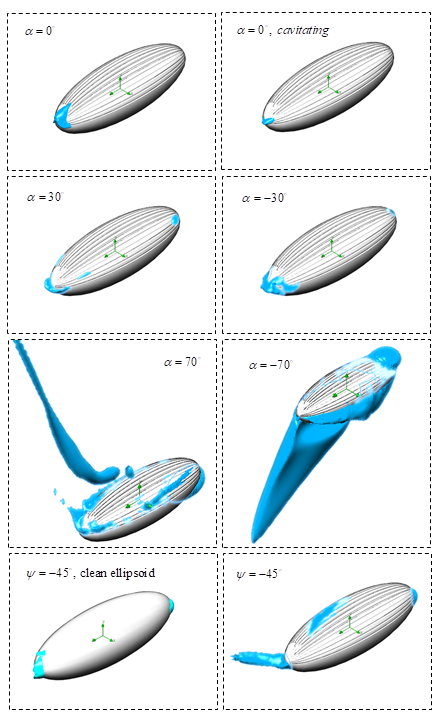 | Figure 32. Separation zones on the grooved ellipsoid body at different positive and negative AoA and a sideslip angle |
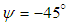 , a relatively similar pattern of separation lakes is obtained for the clean and grooved ellipsoids; although a deflected tail forms in the case of the grooved ellipsoid (Fig. 32), which is not present in another case (Fig. 1). Furthermore, a separation zone is generated on top of the body on the grooved ellipsoid (Fig.32), which does not exist on the clean ellipsoid body surface (Fig. 31).It is also interesting to notice that due to a typical streamlined body developed by humpback whales under necessity of life in oceans, as modelled by a 3:1 grooved ellipsoid, large separation formation is only limited to high AoA.
, a relatively similar pattern of separation lakes is obtained for the clean and grooved ellipsoids; although a deflected tail forms in the case of the grooved ellipsoid (Fig. 32), which is not present in another case (Fig. 1). Furthermore, a separation zone is generated on top of the body on the grooved ellipsoid (Fig.32), which does not exist on the clean ellipsoid body surface (Fig. 31).It is also interesting to notice that due to a typical streamlined body developed by humpback whales under necessity of life in oceans, as modelled by a 3:1 grooved ellipsoid, large separation formation is only limited to high AoA. 5. Conclusions
- In the present study, hydrodynamic effects of the ventral pleats covering bottom surface of the humpback whale body were studied for the first time. Although, the focus was put on the humpback whales in this paper, many other rorqual whale species also possess ventral pleats on the bottom surface of the body; therefore a similar conclusion can be made in those cases as well. Fig. 33 shows a schematic summary of the essential hydrodynamic effects of the ventral peats. As it is clear in the figure, ventral grooves on the right-hand side of the body are virtually removed to create an imaginary- smooth belly surface for comparison purposes only; offcourse in real species, ventral pleat net covers the entire humpback whale bottom surface.
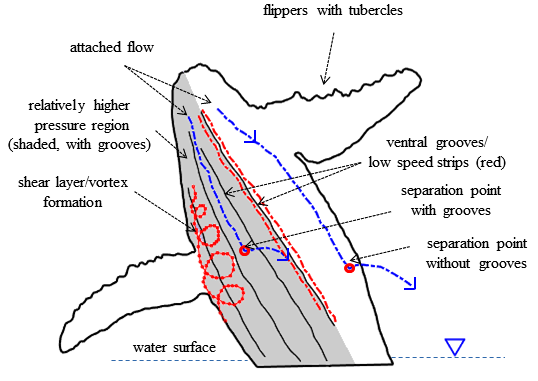 | Figure 33. Summary of hydrodynamic effects of humpback whale ventral pleats in the animal swimming |
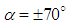 . As shown in the paper, the grooved body exhibits a superior lift generation performance compared to the clean ellipsoid for flows with sideslip angle, e.g.
. As shown in the paper, the grooved body exhibits a superior lift generation performance compared to the clean ellipsoid for flows with sideslip angle, e.g. 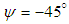 ; at this sideslip angle, lift and drag coefficients increases about 138% and 90%, respectively, due to presence of the ventral grooves on the half of the body surface. Relative symmetry of the turbulent length scale in the lateral direction, i.e. x-direction, also breaks in the turbulent flow over the body with a sideslip angle. It was also observed that turbulent length scale reduces on the grooved surface compared to the clean surface of the grooved ellipsoid for all AoA; in other words, smaller turbulent eddies are generated on the grooved surface. Particle studies performed at high AoA and at a predefined sideslip angle also showed complicated tracer particle motions in the separated zone and under vortical structures attached and detached to the body, induced due to the presence of ventral grooves on the body. In the cavitating flow condition, resembling bubble net environment in this paper, swimming of humpback whales governed by their powerful fluke motion was considered at
; at this sideslip angle, lift and drag coefficients increases about 138% and 90%, respectively, due to presence of the ventral grooves on the half of the body surface. Relative symmetry of the turbulent length scale in the lateral direction, i.e. x-direction, also breaks in the turbulent flow over the body with a sideslip angle. It was also observed that turbulent length scale reduces on the grooved surface compared to the clean surface of the grooved ellipsoid for all AoA; in other words, smaller turbulent eddies are generated on the grooved surface. Particle studies performed at high AoA and at a predefined sideslip angle also showed complicated tracer particle motions in the separated zone and under vortical structures attached and detached to the body, induced due to the presence of ventral grooves on the body. In the cavitating flow condition, resembling bubble net environment in this paper, swimming of humpback whales governed by their powerful fluke motion was considered at 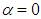 . Results showed that lift generation by the grooved surface is majorly suppressed under cavitating flow conditions; in other words, lift coefficient approaches zero and effects of grooves are effectively omitted in lift coefficient, although drag coefficient considerably increases in this situation; this provides a better directional control for the animal in the hunting final step by cancelling the lateral forces. As also shown, separation zone formation is modified by presence of ventral grooves on the humpback whale body.
. Results showed that lift generation by the grooved surface is majorly suppressed under cavitating flow conditions; in other words, lift coefficient approaches zero and effects of grooves are effectively omitted in lift coefficient, although drag coefficient considerably increases in this situation; this provides a better directional control for the animal in the hunting final step by cancelling the lateral forces. As also shown, separation zone formation is modified by presence of ventral grooves on the humpback whale body.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML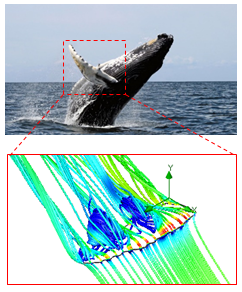
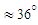 [3]
[3]