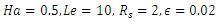-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2018; 8(2): 41-46
doi:10.5923/j.ajfd.20180802.01

Soret and Magnetic Field Effects on Thermosolutal Convection in a Porous Medium with Concentration Based Internal Heat Source
Chigozie Israel-Cookey1, Emeka Amos2, Liberty Ebiwareme2
1Department of Physics, Rivers State University, Port Harcourt, Nigeria
2Department of Mathematics, Rivers State University, Port Harcourt, Nigeria
Correspondence to: Emeka Amos, Department of Mathematics, Rivers State University, Port Harcourt, Nigeria.
| Email: |  |
Copyright © 2018 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

This paper investigates the effects of Soret and magnetic field on thermosolutal convection in a porous medium with concentration based internal heat source. In formulating the leading equations we assume that the Boussinesq approximation is valid and the Darcy law is governing the flow. Linear stability analysis was employed to determine the onset of instability. The influence of Soret, Hartmann number and internal heat are shown in figures and tables. Increase in Hartmann number delays the onset of instability while increase in Soret hastens the onset of instability for both stationary and oscillatory convection. The study established that the stability of the system occurred for values of internal heat, 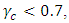 while instability sets in for
while instability sets in for 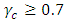 for all values of Hartmann number,
for all values of Hartmann number, 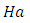 and Soret,
and Soret, 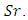
Keywords: Magnetic field, Soret, Concentration Based Internal Heat, Linear Stability Analysis
Cite this paper: Chigozie Israel-Cookey, Emeka Amos, Liberty Ebiwareme, Soret and Magnetic Field Effects on Thermosolutal Convection in a Porous Medium with Concentration Based Internal Heat Source, American Journal of Fluid Dynamics, Vol. 8 No. 2, 2018, pp. 41-46. doi: 10.5923/j.ajfd.20180802.01.
Article Outline
1. Introduction
- The phenomena of combined heat and mass transfer has been an active area of research for many years. In a system where two species with different diffusivities are present, variety of interesting convective phenomena can occur. Understanding of the phenomena has attracted the attention of researchers because of its application in geothermal reservoirs, metallurgy, migration of solutes in water-saturated soils, migration of moisture through air contained fibrous insulations and many others. A comprehensive review of studies in double diffusive convection can be found in [1-4].There are situations in which convection can be driven by internal heat sources in porous media and such applications can be found to occur in nuclear reactions and high quality crystal production. Multiconstituent liquids subjected to long-lasting temperature gradients are liable to experience thermal diffusion flows and modification of the specie concentration. The effect can be useful in elaboration of high-technology materials (solidification of semiconductors), optimization of petroleum extraction, Montel [5]. In view of utilization of molten semi-conducting materials in the control of molten iron flow in steel industry, knowledge of Soret and Magnetic field is needed in above application.Tveitereid [6] studied thermal convection with internal heat and obtained steady solutions in the form of hexagons and two-dimensional rolls. The result show that down-hexagons are stable for Rayleigh numbers up to 8 times the critical value, while up-hexagons are unstable for all values of the Rayleigh number. Gaikwad and Dhanraj [7] investigated the effect of internal heat source on the onset of double-diffusive reaction-convection where the linear stability analysis is based on the usual normal mode method. Hill [8], in his study of double diffusive convection in a porous medium, showed that internal heat source advances the onset of convection.Studies of the magnetic effect on convection is relevant in technological processes and has been considered. Rudraiach [9] studied the effect of an externally imposed vertical magnetic field on double diffusive convection principally in a Boussinesq fluid. Shlioris [10] considered the linearized relation for magnetized perturbed qualities at the limit of instabilities. Amos and Israel-Cookey [11] showed that stabilization of convective flow can be achieved on the application of magnetic field. Rakoto- Ramambason and Vasseur [12] considered analytical and numerical investigation on the effect of magnetic field on natural convection in a horizontal shallow porous cavity. The result shows that magnetic field decreases the flow velocity. Cheng [13] studied the effect of magnetic field on natural convection using an integral approach. The results show that the application of transverse magnetic field normal to the flow direction decreases the Nusselt number and Sherwood number. In the study also, the thickness ratio of the thermal boundary layer to the concentration boundary layer is found to be independent of the intensity of the magnetic field. Takhar [14] studied free convection heat transfer due to simultaneous action of buoyancy radiation and transverse magnetic field in a semi-infinite plate and showed that the magnetic field exerts a strong influence on the velocity of the flow. Bhadauria and Sherani [15] considered onset of double diffusive convection in a sparsely packed porous medium under modulated temperature at the boundaries using linear stability analysis. Gupta and Singh [16] also used linear stability analysis to study double diffusive reaction-convection in a fluid layer with viscous fluid heated and salted below subject to chemical equilibrium on the boundaries. Benacer et al [17] studied Soret effect on convection in a horizontal porous medium submitted to a concentration based internal energy. Platen and Costesque [18] studied experimentally the Soret coefficient in a pure fluid and in a porous medium and concluded that the coefficient is the same for both media. It is, therefore, the subject of this study to consider the simultaneous effects of Soret and magnetic field field on thermosolutal convection in a porous medium with concentration based internal heat source.
2. Mathematical Formulation
- We consider an electrically conducting fluid-saturated porous layer of height
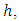 bounded by two horizontal parallel planes
bounded by two horizontal parallel planes 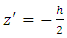 and
and 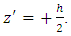 The porous layer is heated and salted from below in such a way that the greater salt concentration is towards the bottom of the layer. The temperature
The porous layer is heated and salted from below in such a way that the greater salt concentration is towards the bottom of the layer. The temperature 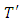 at the lower and upper planes are maintained at
at the lower and upper planes are maintained at 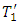 and
and 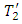 respectively such that
respectively such that 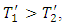 while the salt concentration
while the salt concentration 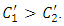 A magnetic field of strength
A magnetic field of strength 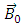 is applied on the
is applied on the 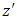 direction. We assume that the Boussinesq approximation is valid and that the Darcy law is governing the flow. We also assume that the magnetic Reynold’s number is small so that the induced magnetic field is neglected. Under the flow configurations and assumptions, the governing equations are,
direction. We assume that the Boussinesq approximation is valid and that the Darcy law is governing the flow. We also assume that the magnetic Reynold’s number is small so that the induced magnetic field is neglected. Under the flow configurations and assumptions, the governing equations are, 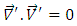 | (1) |
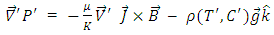 | (2) |
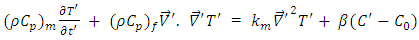 | (3) |
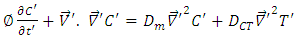 | (4) |
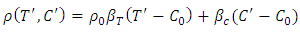 | (5) |
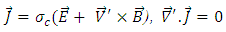 | (6) |
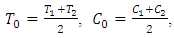 are reference temperature and concentration respectively,
are reference temperature and concentration respectively, 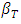 is the thermal expansion coefficient,
is the thermal expansion coefficient, 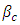 is the solutal expansion,
is the solutal expansion, 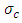 ii electrical conductivity,
ii electrical conductivity, 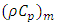 and
and 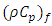 are heat capacity of the porous medium and the fluid respectively,
are heat capacity of the porous medium and the fluid respectively, 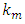 is the thermal conductivity of the porous medium,
is the thermal conductivity of the porous medium, 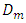 and
and 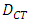 are mass diffusivity and thermal diffusion coefficient respectively, K is permeability of the porous medium,
are mass diffusivity and thermal diffusion coefficient respectively, K is permeability of the porous medium, 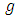 is acceleration due to gravity,
is acceleration due to gravity, 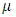 is dynamic viscosity,
is dynamic viscosity, 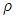 is density,
is density, 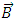 is the magnetic field,
is the magnetic field, 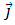 is electric density,
is electric density, 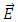 is the electric field,
is the electric field, 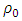 is a reference density,
is a reference density, 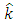 is a unit vector in the
is a unit vector in the 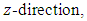
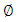 is a porosity parameter, P is the pressure.The boundary conditions are
is a porosity parameter, P is the pressure.The boundary conditions are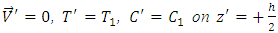 | (7a) |
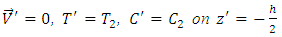 | (7b) |
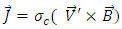 and the electromagnetic force
and the electromagnetic force 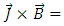
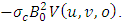 Hence the governing equations take the form
Hence the governing equations take the form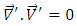 | (8) |
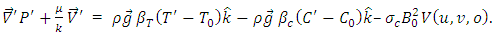 | (9) |
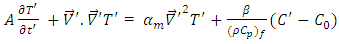 | (10) |
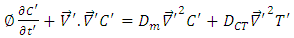 | (11) |
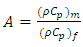 and
and 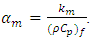 We introduce the following non dimensional variables:
We introduce the following non dimensional variables: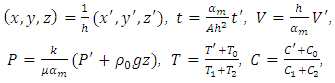 | (12) |
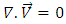 | (13) |
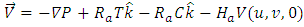 | (14) |
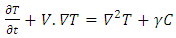 | (15) |
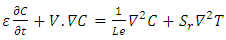 | (16) |
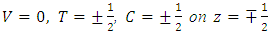 | (17) |
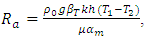 is the thermal Rayleigh number,
is the thermal Rayleigh number, 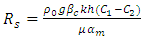 is the solutal Raleigh number,
is the solutal Raleigh number, 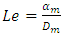 is the Lewis number,
is the Lewis number, 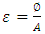 is a constant parameter,
is a constant parameter,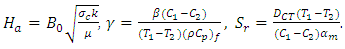
3. Method of Solution
3.1. Steady State Solution
- We admit a steady state solution in the infinite layer. The basic or motionless state of the system is given by
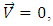
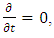 so that equations (13-17) becomes
so that equations (13-17) becomes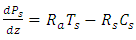 | (18) |
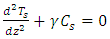 | (19) |
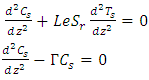 | (20) |
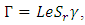 and the subscript s denote steady state,subject to the conditions
and the subscript s denote steady state,subject to the conditions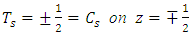 | (21) |
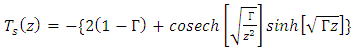 | (22) |
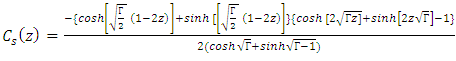 | (23) |
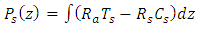 | (24) |
3.2. Linear Stability Analysis
- To access the stability of the steady state solutions, we define perturbations of the form
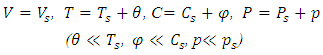 | (25) |
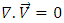 | (26) |
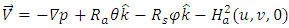 | (27) |
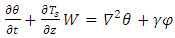 | (28) |
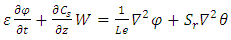 | (29) |
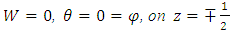 | (30) |
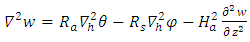 | (31) |
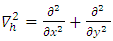 is the Laplacian in the horizontal plane,We now consider the reaction of the system to all possible disturbances by taking normal modes of the form
is the Laplacian in the horizontal plane,We now consider the reaction of the system to all possible disturbances by taking normal modes of the form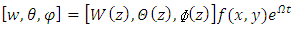 | (32) |
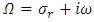 is the growth rate and is in general complex.
is the growth rate and is in general complex. 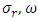 are real and
are real and 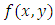 varies periodically and satisfies
varies periodically and satisfies 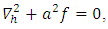 (Drazin and Reid [19]), so that
(Drazin and Reid [19]), so that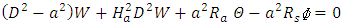 | (33) |
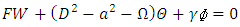 | (34) |
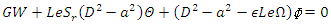 | (35) |
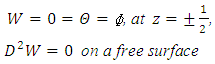 | (36) |
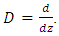 Now, assuming the solutions to be periodic of the form
Now, assuming the solutions to be periodic of the form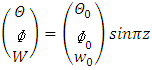 | (37) |
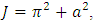 we obtain the following eigenvalue problem
we obtain the following eigenvalue problem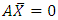 | (38) |
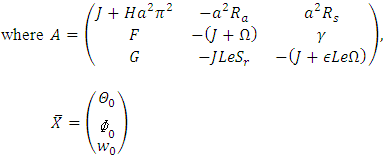 Equation (38) is solvable if the determinant of
Equation (38) is solvable if the determinant of 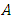 is equal to zero, that is
is equal to zero, that is 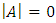 . Letting
. Letting 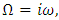 and separating the real and imaginary parts yields
and separating the real and imaginary parts yields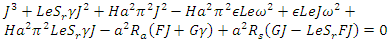 | (39) |
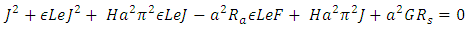 | (40) |
3.2.1. Stationary Convection
- For stationary convection, we set
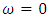 in equation (39) and obtain the Rayleigh number,
in equation (39) and obtain the Rayleigh number, 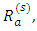 for stationary convection as
for stationary convection as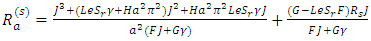 | (41) |
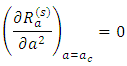 Performing the operation, we obtain the critical wave number as
Performing the operation, we obtain the critical wave number as 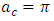 and the corresponding critical Rayleigh number as
and the corresponding critical Rayleigh number as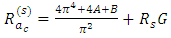 | (42) |
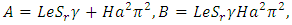
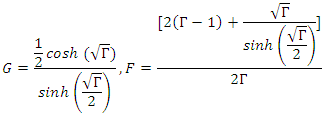 Setting
Setting 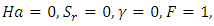
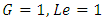 on equation (41) yields
on equation (41) yields 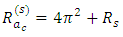 | (43) |
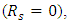 our result is consistent with Nield [22]. That is
our result is consistent with Nield [22]. That is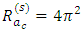 | (44) |
3.2.2. Oscillatory Convection
- When the growth rate,
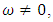 we obtain the thermal Rayleigh number for oscillatory convection from equation (40) in the form
we obtain the thermal Rayleigh number for oscillatory convection from equation (40) in the form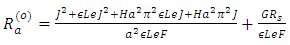 | (45) |
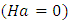 and
and 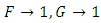 we obtain the critical Rayleigh number for oscillatory convection as
we obtain the critical Rayleigh number for oscillatory convection as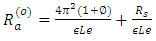 | (46) |
4. Results and Discussion
- In order to understand the physical situation, we have computed numerical values of the critical wave number for the onset of instability for various values of Soret, Hartmann number, porosity and radiation using the arithmetic built -in-function of the software Mathematica (Wolfram, [25]). Figure 1 shows results for stationary convection for
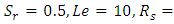
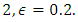 It is observed that increase in Hartmann number delays the onset of instability with higher values of the Hartmann number leading to a greater stabilization of the system.
It is observed that increase in Hartmann number delays the onset of instability with higher values of the Hartmann number leading to a greater stabilization of the system.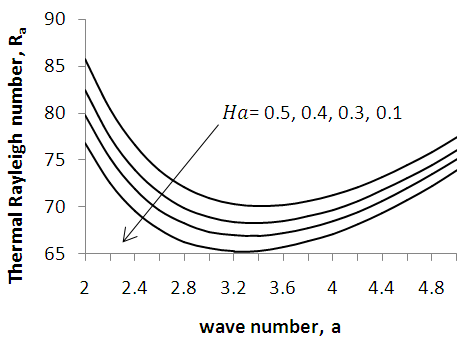 | Figure 1. Variation of thermal Rayleigh number on stationary convection for different values of Hartmann number, 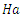 |
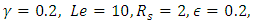
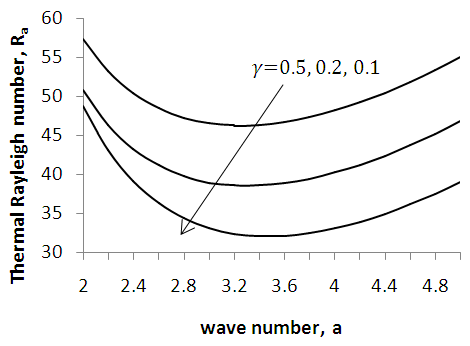
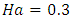 for stationary convection, it is observed from Figure 2 that increase in Soret hastens the onset of instability and leads to destabilization of the system. Figure 3 shows that, for fixed values
for stationary convection, it is observed from Figure 2 that increase in Soret hastens the onset of instability and leads to destabilization of the system. Figure 3 shows that, for fixed values 
 increase in the heat parameter decreases the thermal Rayleigh number, indicating that the internal heat parameter hastens the onset of instability for stationary convection.
increase in the heat parameter decreases the thermal Rayleigh number, indicating that the internal heat parameter hastens the onset of instability for stationary convection. | Figure 2. Variation of the thermal Rayleigh number on stationary convection for different values of Soret, 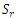 |
 | Figure 3. Variation of the thermal Rayleigh number on stationary convection for different values of the internal heat, 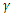 |
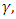 and Hartmann number,
and Hartmann number, 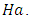 The thermal Rayleigh number,
The thermal Rayleigh number, 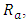 increases as the Hartmann number increases for the values of the internal heat parameter considered. Furthermore for
increases as the Hartmann number increases for the values of the internal heat parameter considered. Furthermore for 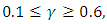 increase in
increase in 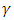 results in decrease in
results in decrease in 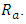 This implies that increase in
This implies that increase in 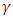 leads to instability in the system. For all values of the Hartmann number, instability sets in at the critical internal heat parameter,
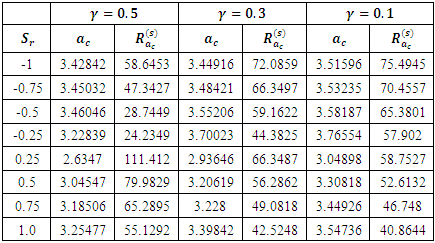
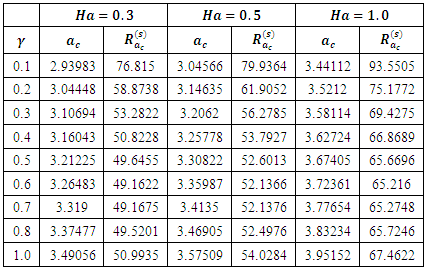
leads to instability in the system. For all values of the Hartmann number, instability sets in at the critical internal heat parameter, 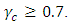 We considered the thermal Rayleigh values for the oscillatory case in Table 2. It is observed that increase in the magnetic field parameter increases the thermal Rayleigh number value while increase in the internal heat parameter decreases the thermal Rayleigh number value. This implies that
We considered the thermal Rayleigh values for the oscillatory case in Table 2. It is observed that increase in the magnetic field parameter increases the thermal Rayleigh number value while increase in the internal heat parameter decreases the thermal Rayleigh number value. This implies that 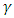 is a destabilizing parameter while
is a destabilizing parameter while 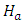 is a stabilizing parameter for fixed Soret parameter,
is a stabilizing parameter for fixed Soret parameter, 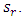
|
|
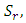 and Hartmann number,
and Hartmann number, 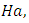 for fixed
for fixed 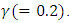 It is observed that increase in Soret decreases the critical thermal Rayleigh value but simultaneous increase in Soret and magnetic field intensity increases the thermal Rayleigh number. Therefore, increase in
It is observed that increase in Soret decreases the critical thermal Rayleigh value but simultaneous increase in Soret and magnetic field intensity increases the thermal Rayleigh number. Therefore, increase in 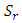 destabilizes but sustained increase in
destabilizes but sustained increase in 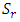 and
and 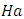 stabilizes the system. The variation of Soret and internal heat parameter for stationary convection is depicted in Table 4. Increase in the internal heat parameter,
stabilizes the system. The variation of Soret and internal heat parameter for stationary convection is depicted in Table 4. Increase in the internal heat parameter, 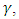 decreases the critical thermal Rayleigh number value,
decreases the critical thermal Rayleigh number value, 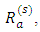 for different values of Soret,
for different values of Soret, 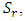 considered. This, therefore, hastens the onset of instabilities.
considered. This, therefore, hastens the onset of instabilities.
|
|
5. Conclusions
- Soret and magnetic effects on thermosolutal convection in a porous medium with concentration based internal heat source is investigated using linear stability analysis. The roles of Soret, magnetic field and internal heat in the onset of convection has been deduced. The findings reveals that increase in magnetic field intensity delays the onset of instabilities in stationary convection. The internal heat hastens the onset of instabilities. For all values of the Hartmann number, instability sets in at the critical internal heat value,
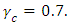 In the oscillatory case, internal heat source produces the same effect as for the oscillatory case. The analysis also show that Soret hastens the onset of instabilities for both stationary and oscillatory convection. In the limiting case when Soret, magnetic field and internal heat were set at zero, our results is in agreement with earlier studies on related areas of double diffusive convection.
In the oscillatory case, internal heat source produces the same effect as for the oscillatory case. The analysis also show that Soret hastens the onset of instabilities for both stationary and oscillatory convection. In the limiting case when Soret, magnetic field and internal heat were set at zero, our results is in agreement with earlier studies on related areas of double diffusive convection.  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML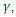 and Hartmann number,
and Hartmann number, 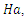 for stationary convection for
for stationary convection for 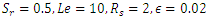
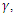 and Hartmann number,
and Hartmann number,  for oscillatory convection for
for oscillatory convection for 
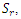 and Hartmann number,
and Hartmann number,  for oscillatory convection for
for oscillatory convection for 
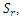 and internal heat,
and internal heat, 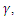 for stationary convection for
for stationary convection for