1. Introduction

The study of magnetohydrodynamic (MHD) fluid flow in tubes under the effect of transverse magnetic field is encountered in mechanism of pumps, accelerators, and MHD generators, geothermal system, petroleum industry, nuclear reactors, filtration process and biomechanics. In the recent years, a considerable growth in the study of MHD flow of biofluids is observed. Human blood flow dynamics is an emerging field in biofluids which has drawn attention from researchers due to its wide range of applicability in the arena of normal and pathological conditions. Various mathematical models and methods, including analytical, experimental and numerical, have been developed to understand the blood flow behaviour in arteries.

Blood behaves as a Newtonian fluid in large vessels when the shear rate is greater than 100 s^-1 and its behaviour changes to non-Newtonian for shear rate lower than 100 s^-1 [1]. Several features in blood blow dynamics such as vessel wall elasticity, non-Newtonian viscosity, slurry particles in blood, although are physiologically relevant but can be neglected justifiably in most arterial flows [2]. Blood is considered as a magnetic fluid due to erythrocytes, the major constituent of blood, which are oxides of iron and are present with uniquely high concentration in mature erythrocytes. Several attempts have been made [3-5] to study the effect of magnetic field on blood flow in arteries. An experimental and numerical study was carried out by Taylor and Draney [6] to quantify the blood flow velocity and pressure field in human arteries.

In the circulatory system, blood from heart is carried by the arteries to different parts of the body and veins carry impure blood from different parts of the body to the heart. This cyclic flow of blood due to the pumping action of heart results in a pulsatile pressure gradient throughout the system. The pulsatile pressure gradient is a superimposition of the steady state pressure gradient and the transient state pressure gradient. Under various circumstances, such as, travelling in aircrafts and high speed vehicles, during sports activities the whole body experiences external body acceleration. It is observed that prolonged exposure to these external body acceleration factors disturb the normal blood flow and may result in headache, abdominal pain, loss of vision, haemorrhage of certain body parts and abnormal increase in pulse rate [7]. Chaturani and Palanisamy [8] studied the pulsatile flow of blood under the effect of periodic body acceleration by treating blood as a power-law fluid. Siddiqui et. al. [9] analysed, mathematically, the flow of blood through narrow arteries by considering both Herschel-Bulkley model as well as the Casson fluid model. Blood flow in large and small arteries under the effect of periodic external acceleration is studied in [10] by considering the effect on vessel wall. The pulsatile flow of blood in porous medium is analysed in [11, 12] by treating blood as a Newtonian fluid. The pulsatile flow of blood as a modified second-grade fluid is studied in [13]. Majhi and Nair [14] studied analytically the pulsatile flow of blood as a third grade fluid under the influence of body acceleration. Blood flow in arteries under periodic body acceleration is studied in [15-17].

In the present study, a numerical investigation is carried out to analyse the pulsatile flow characteristics of blood through an artery under the combined effect of an external periodic body acceleration and applied magnetic field. In addition, we have considered the flow in an inclined tube which pertains to the cases of several arteries which are not parallel to the body or in other words make a non-zero angle with the body axis. The motivation of this study is to investigate the role of applied magnetic field, periodic body acceleration, permeability of the medium and inclination angle of artery in blood flow dynamics and discussing its clinical significance.

2. Problem Formulation

Let us consider the fully developed unsteady, axisymmetric MHD flow of blood, modelled as a viscous incompressible Newtonian fluid, in a porous tube of radius R₀ inclined horizontally with angle δ. Let (u*, v*, w*) denote the velocity components in the cylindrical polar coordinate system (r*, θ*, z*). The flow is considered to be symmetric about the z*-axis which is assumed to be the centreline of the artery. The flow in the tube is driven by pulsatile pressure gradient. A constant magnetic field of strength B₀ is applied in the r*-direction, perpendicular to the direction of fluid flow. The induced magnetic field is neglected under the assumption of very small magnetic Reynold number.

For time t*>0, a periodic body acceleration acts in the axial direction and is given by

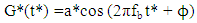(1)

where a* is the amplitude, f_b is the frequency and ϕ is the lead angle of G*(t*) with respect to the action of heart.

With the above considerations, the governing equations for the unsteady MHD flow of blood, using Brinkman-extended Darcy model are

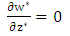(2)

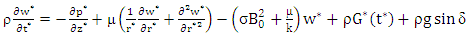(3)

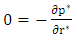(4)

with the following boundary and initial conditions

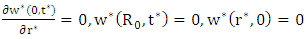(5)

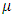where is the coefficient of dynamic viscosity, 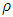is the blood density, 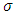is the electrical conductivity, k is the intrinsic permeability of the medium and g is the acceleration due to gravity.

The pulsatile pressure gradient is given by

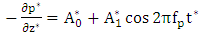(6)

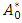where p* is the pressure, is the constant component of pressure gradient, 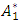is the amplitude of the fluctuating component of pressure gradient and 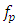is the pulse frequency.

Introducing the following non-dimensional variables

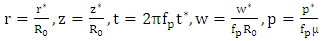(7)

in Eq.(3), we obtain the dimensionless momentum equation of the problem as

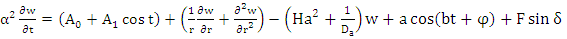(8)

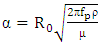Where is the Womersley number, 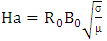is the Hartmann number, 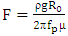is the gravity parameter and 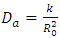is the permeability parameter. The corresponding boundary conditions are

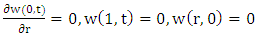(9)

3. Numerical Methods

The momentum equation governing the unsteady pulsatile flow of blood modeled as a MHD Newtonian fluid in an inclined porous tube subject to external magnetic field and periodic body acceleration is a second order partial differential equation. An attempt is made to solve the time-dependent PDE by using a suitable combination of the weighted residual Galerkin finite element method and Crank-Nicholson scheme. The computational domain is partitioned into N equal intervals such that 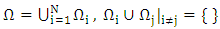where .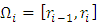

The weighted residual Galerkin scheme is derived by multiplying the non-dimensional momentum equation by a weight function 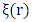and integrating the expression over 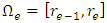as given below

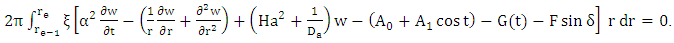(10)

Integrating the above equation by parts, we obtain the weak form of the momentum equation as

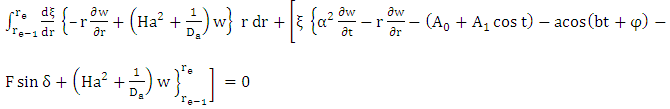(11)

The finite element model of the problem is formulated by substituting the approximation function

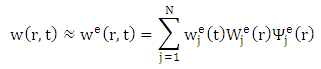for w, where 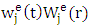is the approximation of w over 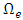at the jth node, 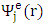is the approximation function having Lagrangian property and 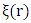is approximated by 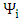which is defined in the following way

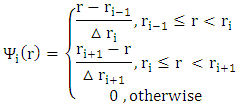with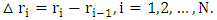

The finite element model of the problem thus becomes

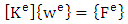(12)

where

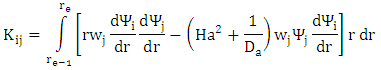
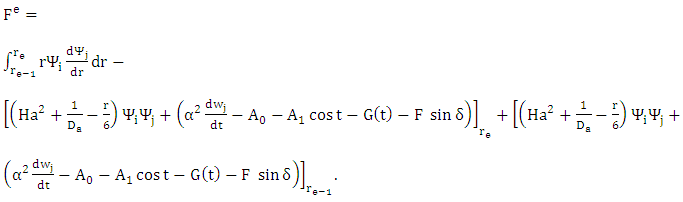This is a system of N algebraic equations in N variables and after applying the boundary conditions we get a system of N-2 equations with N-2 unknowns {w}={w₂, w₃, …, w_N-1} at all the nodes. The right hand side vector {F^e} of size (N-2)×1 contains first order time derivatives of the function w at the same nodes. The Crank-Nicholson scheme is implemented to handle the resulting system of ordinary differential equations with time derivative of w.

4. Results and Discussion

The result of our mathematical investigation on the unsteady pulsatile blood flow in an inclined porous artery under the combined influence of periodic body acceleration and externally applied magnetic field is discussed in his section. Our study is concerned with the effect of different governing flow parameters on the axial velocity distribution along the radial distance and time. The computation is carried out by using the following standard values of the parameters: α= 3.0, Ha=2.0, 1/D_a=3.0, a=1.0, b=2.0, F=2.0, A₀=1.0, A₁=1.0, ϕ=π/4 and δ=π/2. For the sake of comparison we have examined the flow profile for other values of the parameters and those are mentioned in the figures. Figures (1)-(6) present the axial velocity distribution along the radial distance for various flow parameters.

Figure 1 gives the effect of amplitude of the periodic body acceleration on the flow profile. It is observed that with the increase in amplitude of body acceleration a there is a remarkable rise in the flow velocity. The behavior gets reversed for variation in frequency of body acceleration as shown in Fig. (2).

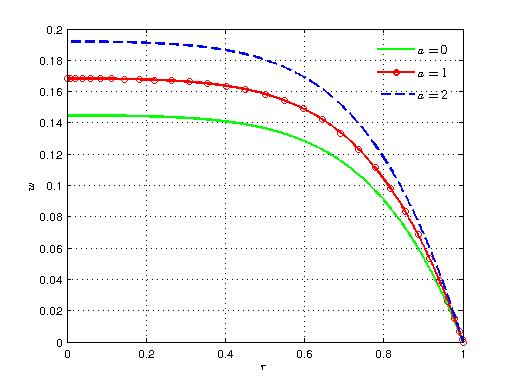Figure 1. Variation of axial velocity with radial distance for different values of a

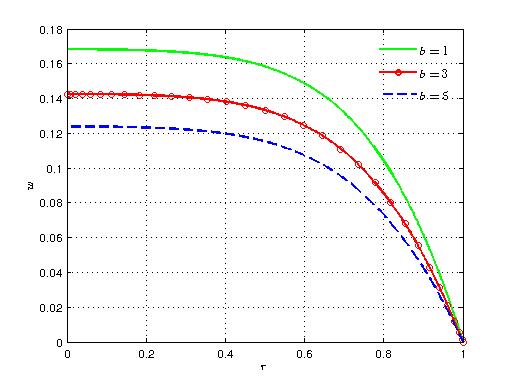Figure 2. Variation of axial velocity with radial distance for different values of b

Figures 3 and 4 present the velocity distribution for different values of the permeability parameter 1/D_a and the magnetic parameter Ha. The figures depict that velocity decreases with increasing values of both the parameters. This result for the magnetic parameter can be implemented as a control measure in the case of surgeries where blood flow needs to be checked. As the porous permeability increases, there is a cross flow which increases the viscosity of the fluid and hence the velocity decreases. The effect of gravitational parameter F and angle of inclination δ can be visualized from figures 5 and 6, respectively. In both the cases velocity increases monotonically with elevated values of these parameters. This result gives an idea about the varying flow characteristics in different arteries with varying angles that they make with the body axis.

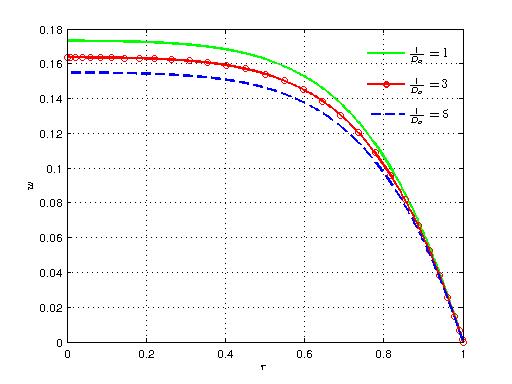Figure 3. Variation of axial velocity with radial distance for different values of 1/Da

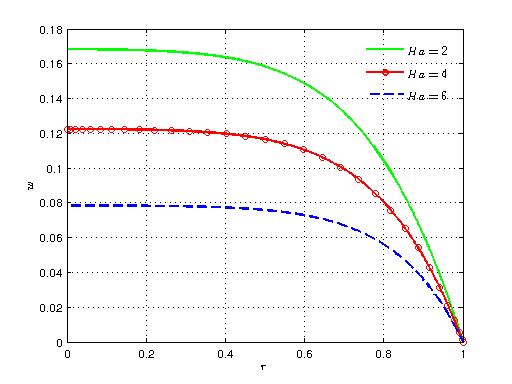Figure 4. Variation of axial velocity with radial distance for different values of Ha

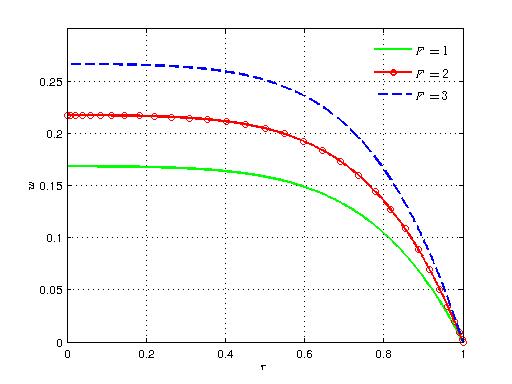Figure 5. Variation of axial velocity with radial distance for different values of F

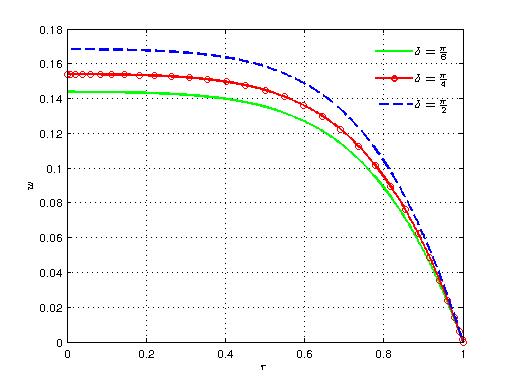Figure 6. Variation of axial velocity with radial distance for different values of δ

Figures 7 and 8 show the effect of amplitude and frequency of body acceleration parameters, respectively.

Figures 9 and 10 show the velocity distribution with time for different values of porous permeability parameter and magnetic parameter, respectively. It is observed that the velocity decreases for increasing values of these parameters. Figures 11 and 12 present the variation of axial velocity for varying values of F and δ. Both the plots show an increasing trend for increasing values of the respective parameters. Figure 13 gives the flow profile with time for different values of the Womersley number. An increase in the Womersley number decreases the fluid velocity.

Figure 14 depicts the flow dependence on the pulsatile pressure gradient. As the amplitude of the transient state pressure gradient A₁ increases, velocity increases.

Figure 15 shows the velocity profile for different values of the lead angle of body acceleration.

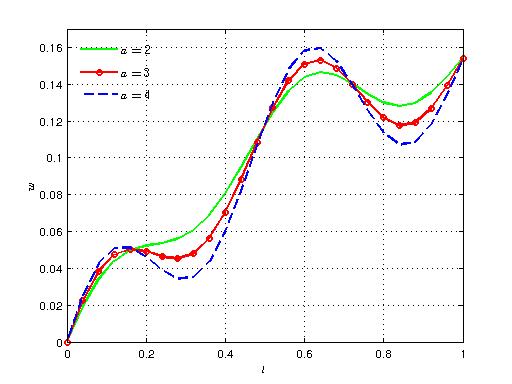Figure 7. Variation of axial velocity with time for different values of a

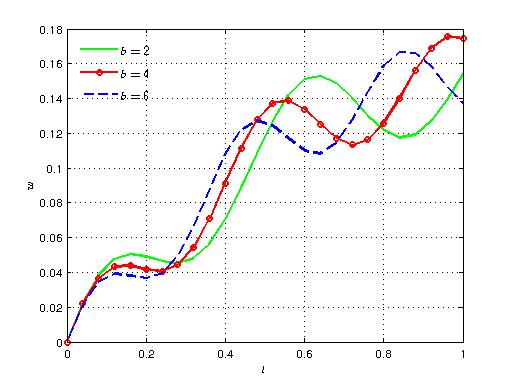Figure 8. Variation of axial velocity with time for different values of b

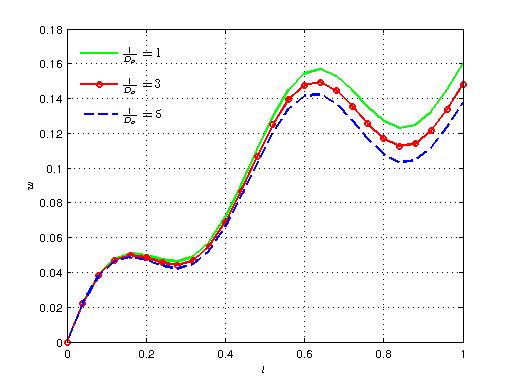Figure 9. Variation of axial velocity with time for different values of 1/Da

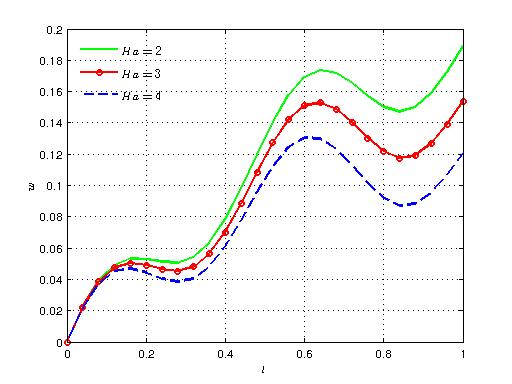Figure 10. Variation of axial velocity with time for different values of Ha

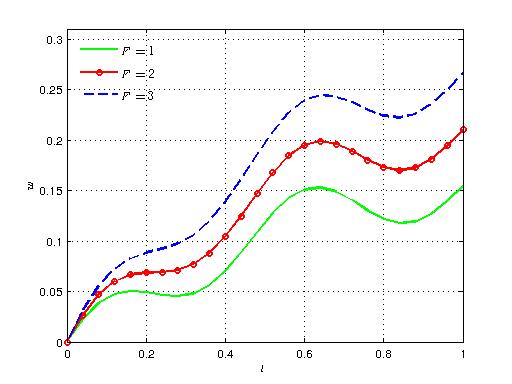Figure 11. Variation of axial velocity with time for different values of F

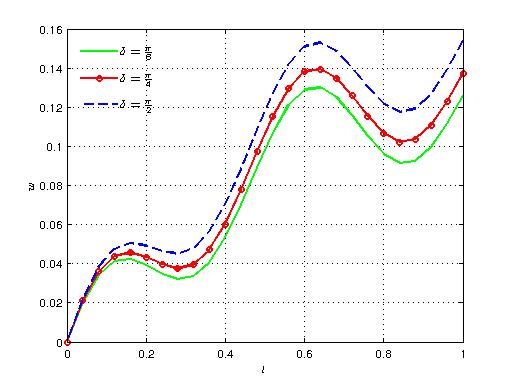Figure 12. Variation of axial velocity with time for different values of δ

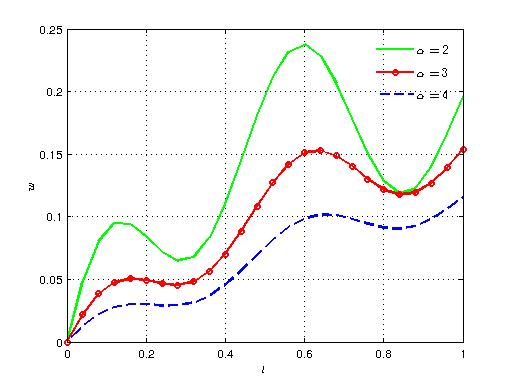Figure 13. Variation of axial velocity with time for different values of α

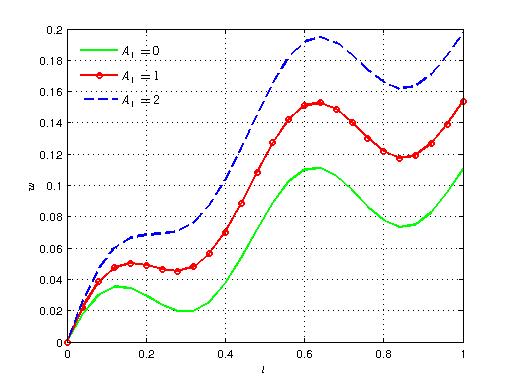Figure 14. Variation of axial velocity with time for different values of A1

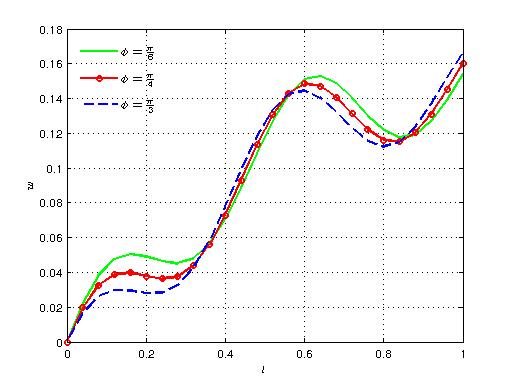Figure 15. Variation of axial velocity with time for different values of ϕ

5. Conclusions

This paper is devoted to the finite element modeling of the pulsatile transport of blood in an artery under the combined effect of periodic body acceleration and an external magnetic field applied in the transverse direction of the fluid flow. In this analysis, blood is considered to be a viscous, incompressible and electrically conducting Newtonian fluid and the artery is taken as a rigid porous cylindrical tube. The governing momentum equation is modeled using Ohm’s law, Brinkman-extended Darcy law and pulsatile pressure gradient, periodic body acceleration, effect of gravity and horizontal inclination factors are taken into account. The resulting partial differential equation is solved by weighted residual Galerkin finite element method and for dealing with the transient condition we use Crank-Nicholson scheme. The analysis of this real world problem is carried out by computational and visualization technique. The study reveals that there is a strong impact of the flow parameters associated with the flow problem on the velocity distribution.