Rowsanara Akhter1, Mohammad Mokaddes Ali2, Md. Babul Hossain2, Md. Musa Miah2
1Department of Mathematics, International University of Scholars, Dhaka, Bangladesh
2Department of Mathematics, Mawlana Bhashani Science and Tech. University, Tangail, Bangladesh
Correspondence to: Rowsanara Akhter, Department of Mathematics, International University of Scholars, Dhaka, Bangladesh.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
This work examines the effect of thermal radiation on convective heat transfer in viscous, incompressible and electrically conducting fluid of low Prandtl number over an inclined heated flat plate in presence of transverse magnetic field. The governing equations are converted into non-dimensional forms containing Prandtl number, magnetic field parameter, inclination parameter and thermal radiation parameter and the obtained non-linear partial differential equations subject to appropriate boundary conditions are solved numerically using finite-difference method and then discussed in detail for the effects of pertinent parameters. A comparison with earlier work shows the excellent agreement.
Keywords:
Thermal Radiation, MHD, Inclined Flat Plate, Finite Difference Method
Cite this paper: Rowsanara Akhter, Mohammad Mokaddes Ali, Md. Babul Hossain, Md. Musa Miah, MHD Free Convection Boundary Layer Flow over an Inclined Heated Flat Plate with Thermal Radiation Effect, American Journal of Fluid Dynamics, Vol. 7 No. 2, 2017, pp. 41-48. doi: 10.5923/j.ajfd.20170702.01.
1. Introduction
The study of heat transfer analysis is an interesting research area due to its potential applications in engineering, such as nuclear plants, combustion modeling, heat exchangers, cooling systems design, various propulsion devices for air craft’s, chemical engineering and electronics etc. Moreover, heat transfer by thermal radiation plays a significant role on the heat transfer characteristics where high temperature is occurred. Furthermore, the flow field is influenced noticeably with the effect of magnetic field. Considering its wide applications in science and engineering, a large number of theoretical, numerical and experimental works have been conducted by many investigators. Pop and Na [1] developed a mathematical model in free convection flow for arbitrary inclined flat plate embedded in a porous medium to analyze the behavior of the flow and heat transfer characteristics. The effects of conduction-radiation on natural convection boundary layer flow of viscous incompressible fluid over an isothermal horizontal plate studied by Hossain and Takhar [2]. Hossain et al. [3] analyzed the effect of radiation on natural convection flow in incompressible fluid along a uniformly heated vertical plate. Abdel-Naby et al. [4] investigated radiation effects on MHD unsteady free convection flow over a vertical plate with variable surface temperature. Ali et al. [5] employed the implicit finite difference method to analyze the effect of radiation and viscous dissipation on conjugate free convection flow over a vertical flat plate. Chamkha et al. [6] analyzed the effect of natural convection boundary-layer flow of an electrically-conducting fluid over a semi-infinite inclined flat plate embedded in a porous medium with variable porosity due to solar radiation effect. Aydin and Kaya [7] studied magnetohydrodynamic mixed convection heat transfer for an inclined plate. Siddiqa et al. [8] carried out a numerical study of the effect of internal heat generation and variable viscosity on natural convection flow over an inclined flat plate. In this analysis the effect of thermal radiation on free convection flow over an inclined flat plate has been studied numerically when a transverse magnetic field is incorporated. The governing equations are obtained in non-dimensional forms which are solved numerically employing finite difference method. This numerical simulation has significant importance in many practical systems. The results obtained for the various values of physical parameters in terms of velocity and temperature profiles as well as the skin friction coefficient and Nusselt number and then discussed in the following sections.
2. Mathematical Analysis
We consider steady free convection boundary layer flow of viscous, incompressible and electrically conducting fluid over an inclined flat plate of length l and thickness b. It is assumed that heat is transferred from the outside surface of the plate, which is maintained at the constant temperature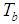 , where
, where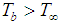 ,
, 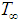 is the ambient temperature. A uniform magnetic field of strength is applied in the y-direction. The physical model and coordinate system is presented in Fig.1.
is the ambient temperature. A uniform magnetic field of strength is applied in the y-direction. The physical model and coordinate system is presented in Fig.1.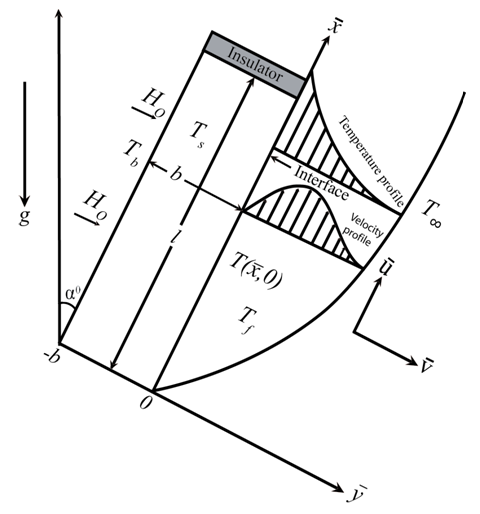 | Figure 1. Physical model and coordinate system |
The energy equation for a solid plate is formulated as 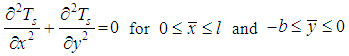 | (1) |
where the conditions of the temperature and heat flux are continuous at the solid fluid interface, namely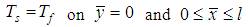 | (2) |
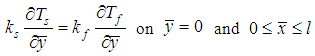 | (3) |
The axial heat conduction along the wall is negligible when compared with the normal conduction across the wall which is consistent with the boundary layer theory. Thus the equation (1) reduces to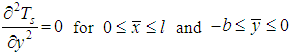 | (4) |
As 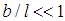 and applying
and applying 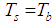 on
on 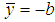 in equation (1) we obtain
in equation (1) we obtain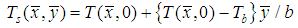 | (5) |
Here 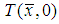 is the unknown temperature at the solid fluid interface which is calculated using the solution of the governing equations. Thus the condition (3) can be written as the following form
is the unknown temperature at the solid fluid interface which is calculated using the solution of the governing equations. Thus the condition (3) can be written as the following form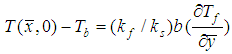 | (6) |
Applying the Boussinesq approximation, the governing equations within the usual boundary layer can be written as follows: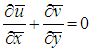 | (7) |
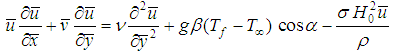 | (8) |
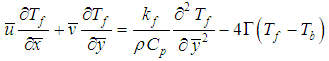 | (9) |
In the above equations, 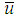 and
and 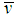 are the dimensional velocity components in the
are the dimensional velocity components in the 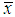 and
and 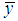 directions, respectively;
directions, respectively; 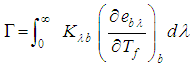 ,
, 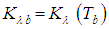 is the mean absorption coefficient,
is the mean absorption coefficient, 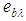 is Plank’s function and
is Plank’s function and 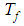 is the temperature of the fluid within the boundary layer,
is the temperature of the fluid within the boundary layer,  is the kinematic viscosity,
is the kinematic viscosity, 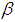 is the thermal expression co-efficient,
is the thermal expression co-efficient, 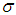 is the electrical conductivity, Cp is the specific heat due to constant pressure. The boundary conditions are given as follows:
is the electrical conductivity, Cp is the specific heat due to constant pressure. The boundary conditions are given as follows: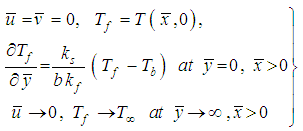 | (10) |
Now we introduce the following set of dimensionless variables to convert the governing equations into the dimensionless forms: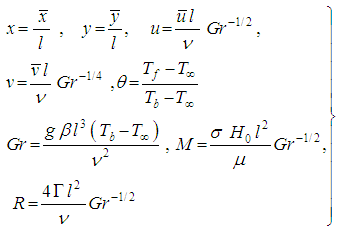 | (11) |
Where 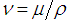 is the kinematic viscosity, Gr is the Grashof number and
is the kinematic viscosity, Gr is the Grashof number and 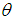 is the non-dimensional temperature. With the help of equation (11), the non-dimensional governing equations are:
is the non-dimensional temperature. With the help of equation (11), the non-dimensional governing equations are: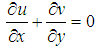 | (12) |
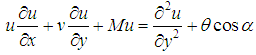 | (13) |
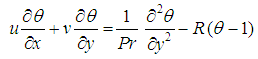 | (14) |
The corresponding boundary conditions are: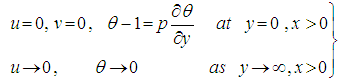 | (15) |
Here 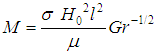 is the magnetic parameter,
is the magnetic parameter, 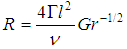 is the radiation parameter and the Prandtl number,
is the radiation parameter and the Prandtl number, 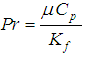 and
and 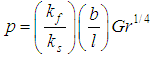 is a conjugate conduction parameter has an important effect on the flow field. The steam function,
is a conjugate conduction parameter has an important effect on the flow field. The steam function, 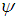 , similarity variables,
, similarity variables, 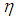 and temperature,
and temperature, 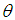 are considered in the following forms to solve the equations (13) and (14) and for the boundary conditions described in (15):
are considered in the following forms to solve the equations (13) and (14) and for the boundary conditions described in (15): 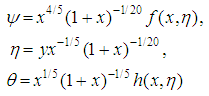 | (16) |
After simplifications, the non-linear partial differential equations are obtained as: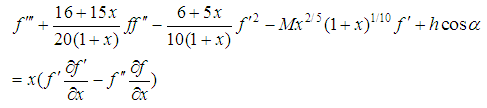 | (17) |
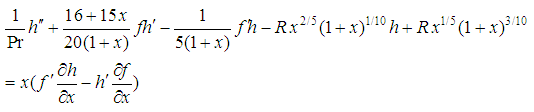 | (18) |
The boundary conditions (15) become as: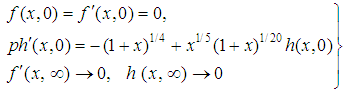 | (19) |
The set of equations (17) and (18) together with the boundary condition (19) are solved numerically by applying implicit finite difference method. The skin friction coefficient in terms of shear stress and the heat transfer rate in terms of Nusselt number are calculated due to their physical significance. These can be defined in the dimensionless form as: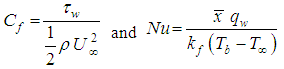 | (20) |
where 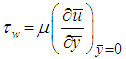 and
and 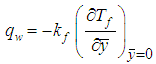 are the shearing stress and the heat flux, respectively. By using dimensionless variables and similarity transformations, the skin friction coefficient and the heat transfer rate can be found as:
are the shearing stress and the heat flux, respectively. By using dimensionless variables and similarity transformations, the skin friction coefficient and the heat transfer rate can be found as: 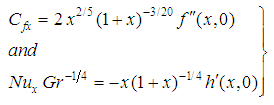 | (21) |
3. Results and Discussion
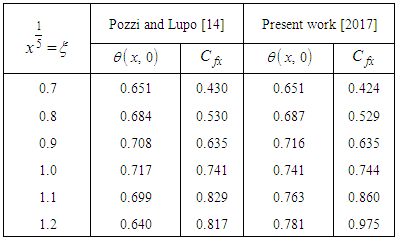
Equations (17) and (18) subject to the boundary condition (19) have been solved numerically. This numerical solutions are computed for Pr = 0.70 and a range of values of the magnetic parameter M (= 0.10, 0.50, 1.00), thermal radiation parameter R (= 0.00, 0.05, 0.10), inclination parameter α (= 0°, 30°, 45°) and conduction resistance parameter p (= 1.0, 2.0, 3.0). To assess the accuracy of the solutions, the present results for the surface temperature and skin friction while the plate is inclined at angle 0° to the vertical are compared with those calculated by Pozzi and Lupo [14]. The present results agree well with the solutions conducted by Pozzi and Lupo [14].Table 1. Comparison of the present numerical results of the surface temperature and local skin friction with Prandtl number Pr = 0.733, M = 0.00, R = 0.00, α = 0° and p = 1
 |
| |
|
Fig. 2 plots the numerical results of the velocity and temperature profiles for the different values of magnetic field parameters with R = 0.01, α = 30° and p = 1.0. It can be seen in Fig.2 (a) that the velocity profile decreases due to the applied magnetic field with Lorentz force, which retards the fluid motion. From Fig. 2 (b), it is clear that the temperature profiles increase with the increasing values of magnetic field parameter. This is because, interaction of magnetic field with flowing fluid particles produces heat in the fluid region and creates a hot fluid layer within the boundary layer.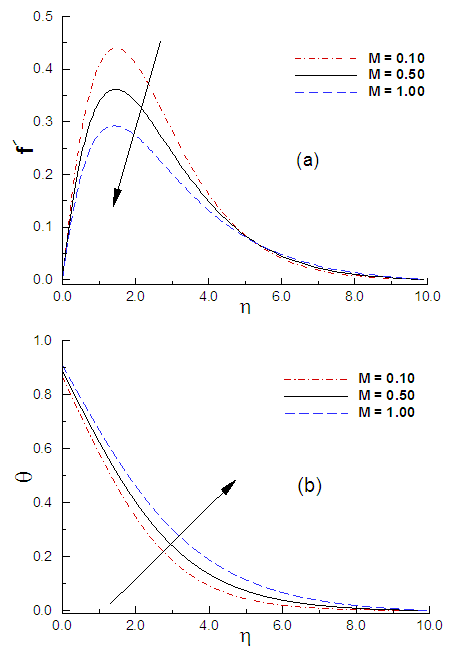 | Figure 2. (a) Variation of velocity and (b) variation of temperature against η for varying of M with R = 0.01, α = 30° and p = 1.0 |
The variation of the local skin friction coefficient and heat transfer rate with the same variation of the governing parameters at different locations of x is illustrated in Figs. 3(a) and 3(b), respectively. Comparing the profiles of Figs. 3(a) and 3(b), it is clear that both the skin friction and heat transfer factor are reduced with increasing of M, which are consistent with Fig. 2. The physics behind it’s that the applied magnetic force works against the fluid flow and also reduces the temperature difference between the plate and ambient fluid.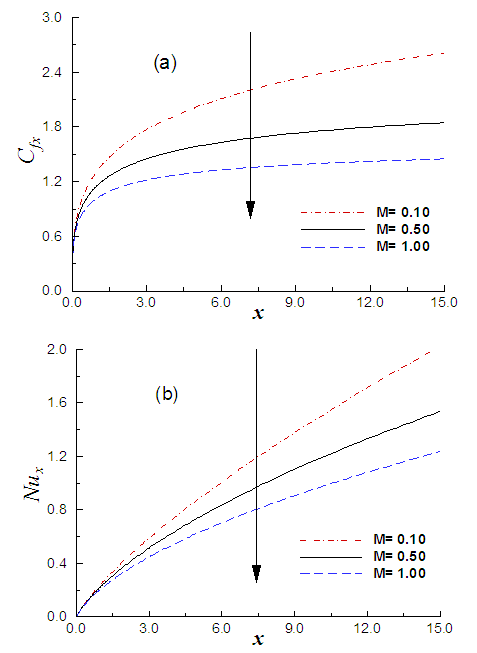 | Figure 3. (a) Variation of skin friction and (b) variation of heat transfer against x for varying of M with R = 0.01, α = 30° and p = 1.0 |
Fig.4 illustrates the variation of dimensionless velocity and temperature for selected values of the radiation parameter while the values of the other controlling parameters are M = 0.10, α = 30° and p = 1.0. From Fig. 4(b), it is seen that the fluid temperature increases with the increasing values of R due to the absorption of radiated heat from the heated inclined plate. Resulting temperature increases the buoyancy forces in the boundary layer which increase the fluid motion that is visible in Fig.4 (a). On the other hand, in Fig.5 (a), the local skin-friction increases for an increase in the radiation parameter when the value of magnetic parameter, angle of inclination parameter and conduction parameter are kept fixed. This is expected, because the considered radiation effect within the boundary layer increases the motion of the fluid which increases the surface frictions. As the temperature of the fluid increases for increasing R, consequently, the temperature difference between the plate and the ambient fluid reduces which turns to decrease the heat transfer rate in flow region that is presented in Fig. 5(b). 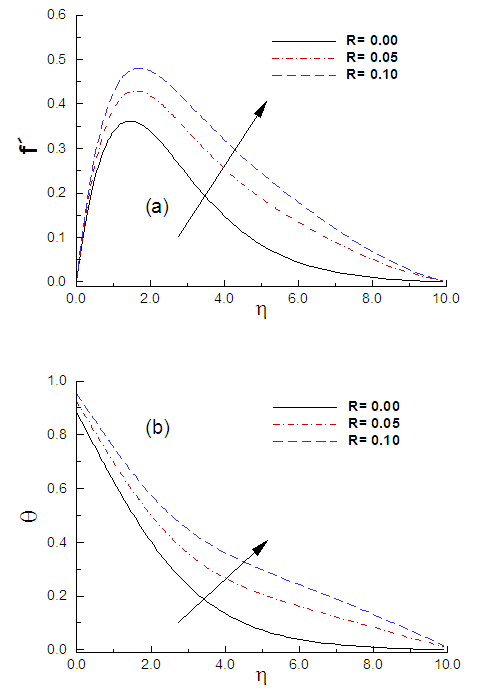 | Figure 4. (a) Variation of velocity and (b) variation of temperature against η for varying of R with M = 0.10, α = 30° and p = 1.0 |
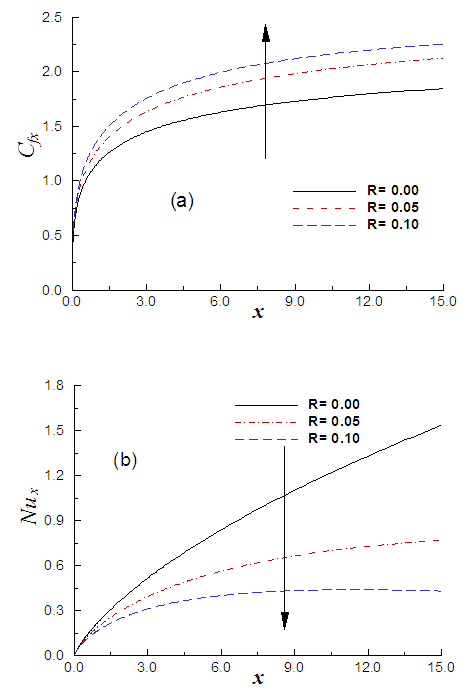 | Figure 5. (a) Variation of skin friction and (b) variation of heat transfer against x for varying of R with M = 0.10, α = 30° and p = 1.0 |
Fig. 6(a) and Fig. 6(b), respectively display the trend of the velocity and temperature profiles for the influence of inclination of the flat plate to the vertical. It can be observed in Fig.6 (a) that the velocity decreases with the increasing values of α and the opposite nature is found for the temperature distribution that is demonstrated in Fig.6 (b).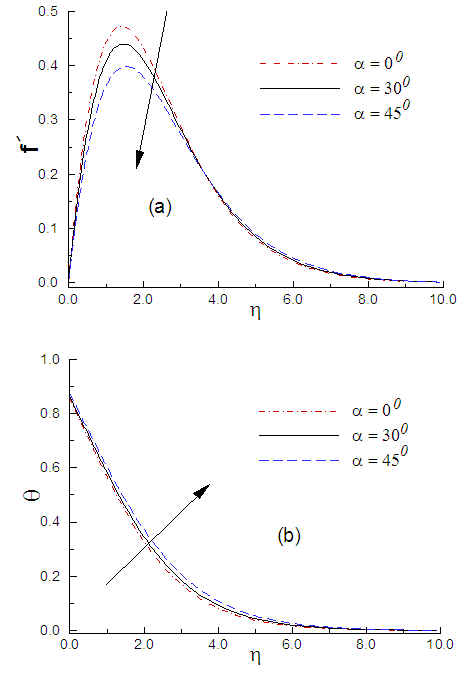 | Figure 6. (a) Variation of velocity and (b) variation of temperature against η for varying of α with M = 0.10, R = 0.01 and p = 1.0 |
The effects of angle of inclination parameter, α, on the local skin-friction coefficient and local Nusselt number are presented in Fig. 7(a) and Fig.7 (b), respectively. These figures confirm that the local skin friction coefficient and the local Nusselt number decreases with the increasing of inclination parameter. This behavior is much clear from the fact that the buoyancy force and temperature gradient decreases for increasing α, as a result, the heat transfer also decreases in the boundary layer.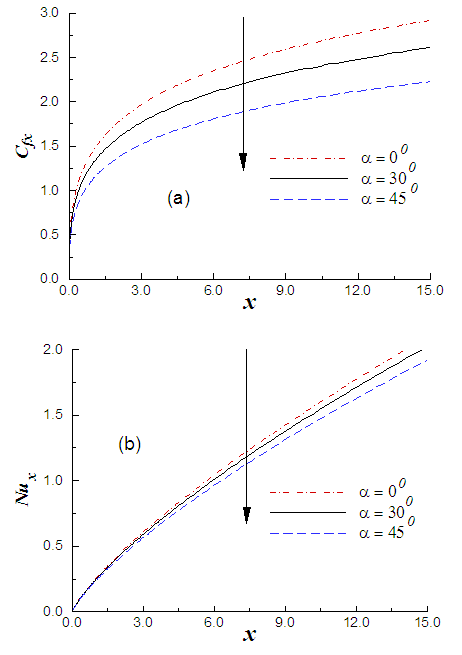 | Figure 7. (a) Variation of skin friction and (b) variation of heat transfer against x for varying of α with M = 0.10, R = 0.01 and p = 1.0 |
Figure 8, demonstrates the effect of the conjugate conduction parameter, p, on the velocity and temperature distributions within the boundary layer. The greater p produces the higher resistance force of heat flow within the plate which leads to decrease the energy transfer rate in fluid, accordingly, the velocity and temperature of the fluid decreases with increasing values of p. 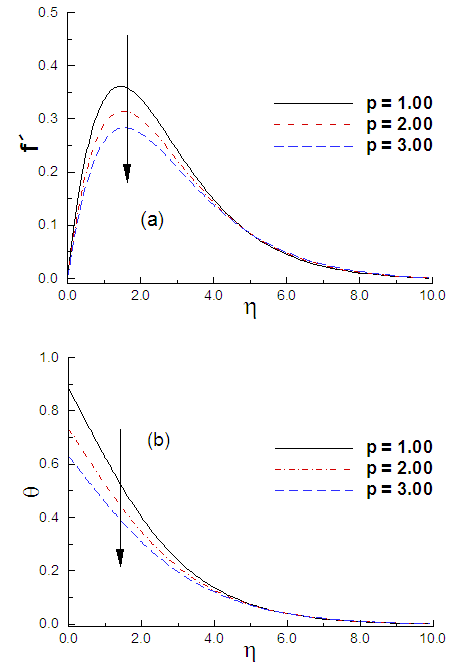 | Figure 8. (a) Variation of velocity and (b) variation of temperature against η for varying of p with M = 0.10, R = 0.01 and α = 30° |
The figure 9(a) indicates the skin friction factor which is decreased with an increasing value of p along the stream wise direction from the bottom of the inclined plate. It is to be expected because the greater p decreases the velocity boundary layer within the flow region. On the other hand, the lower heat flow from the heated plate to fluid due to higher p, decreases the heat transfer rate which is presented in figure 9(b).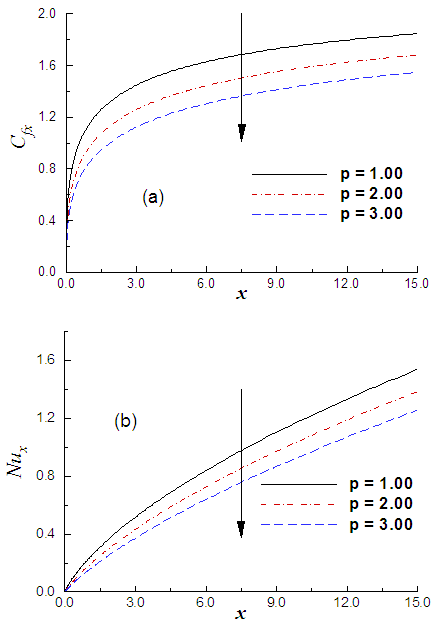 | Figure 9. (a) Variation of skin friction and (b) variation of heat transfer against x for varying of p with M = 0.10, R = 0.01 and α = 30° |
4. Conclusions
In this paper, the effect of magnetic field and radiative heat transfer on free convection flow for an inclined heated flat plate has been studied. It is found that the thermal radiation parameter has the effect to increase the fluid velocity and temperature as well as the skin friction coefficient but the opposite trend is found for heat transfer rate. Increasing magnetic field parameter and inclination parameter tends to decrease the fluid velocity and increase fluid temperature within the boundary layer, consequently, the skin friction factor in terms of shear stress and heat transfer rate in terms of Nusselt number are decreased. Both the velocity and temperature profiles decreased with an increase in conduction resistance parameter, p, and the local skin friction as well as heat transfer rate also decreased for greater p.
Nomenclature

References
| [1] | I. Pop, T.Y. Na Free convection from an arbitrarily inclined plate in a porous medium, Heat and Mass Transfer, Vol. 32, pp.55-59, 1996. |
| [2] | M. A. Hossain and H.S. Takhar, Thermal radiation effects on the natural convection flow over an isothermal horizontal plate, Heat and Mass Transfer, Vol. 35, pp. 321-326, 1999. |
| [3] | M. A. Hossain, M. A. Alim and D.A.S. Rees, The effect of radiation on free convection from a porous vertical plate, International Journal of Heat and Mass Transfer, Vol. 42, pp.181-191, 1999. |
| [4] | M. A. Abd El-Naby, Elsayed M. E. Elbarbaryand Nader Y. Abdelazem, Finite difference solution of radiation effect on MHD unsteady free convection flow over a vertical plate variable surface temperature, Journal of Applied Mathematics, Vol. 2, pp. 65-86, 2003. |
| [5] | Mohammad Mokaddes Ali, Rowsanara Akhter, N. H.M.A. Azim and Md. Abdul Maleque, Effects of radiation and viscous dissipation on conjugate free convection flow along a vertical flat plate, Journal of Science and Technology, Vol. 1, pp.11-21, 2011. |
| [6] | J. Chamkha Ali, Camille Issa, Khalil Khanafer, Natural convection from an inclined plate embedded in a variable porosity porous medium due to solar radiation, International Journal of Thermal Science, Vol. 41, pp.73-81, 2002. |
| [7] | Orhan Aydın, Ahmet Kaya, MHD mixed convective heat transfer flow about an inclined plate, Heat and Mass Transfer , Vol.46, pp.129-136, 2009. |
| [8] | S. Siddiqa, S. Asghar, M. A. Hossain, Natural convection flow over an inclined flat plate with internal heat generation and variable viscosity, Mathematical and computer Modeling, Vol. 52, pp.1739-1751, 2010. |
| [9] | Rowsanara Akhter, Mohammad Mokaddes Ali, Babul Hossain, M. Sharif Uddin, Conjugate Effect of Radiation and Thermal Conductivity Variation on MHD Free Convection Flow for a Vertical Plate, American Journal of Computational Mathematics, Vol. 3, pp. 252-259, 2013. |
| [10] | N. Sandeep and V. Sugunamma, Radiation and Inclined Magnetic Field Effects on Unsteady Hydromagnetic Free Convection Flow past an Impulsively Moving Vertical Plate in a Porous Medium, Journal of Applied Fluid Mechanics, Vol.7, pp. 275-286, 2014. |
| [11] | Jyotsna Rani Pattnaik, Gouranga Charan Dash, Suprava Singh, Radiation and mass transfer effects on MHD flow through porous medium past an exponentially accelerated inclined plate with variable temperature, Ain Shams Engineering Journal, doi.org/10.1016/j.asej.2015.08.014, October, 2015. |
| [12] | Zulkhibri Ismail, lyas Khan, Nadirah Mohd Nasir, Rahimah Jusoh wang, Mohd Zuki Salleh, and Sharidan Shafie, The effects of magnetohydrodynamic and radiation on flow of second grade fluid past an infinite inclined plate in porous medium, AIP Conference Proceedings 1643, 563, 2015. |
| [13] | T. Cebeci and P. Bradshow, Physical computational aspects of convective heat transfer, Springer, New York, ISBN: 3-540-96821-0, 1984. |
| [14] | M. Pozzi and M. Lupo, The coupling of conduction with laminar natural convection along a flat plate, International Journal of Heat and Mass Transfer, Vol. 31, pp. 1807-1814, 1988. |



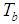 , where
, where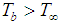 ,
, 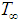 is the ambient temperature. A uniform magnetic field of strength is applied in the y-direction. The physical model and coordinate system is presented in Fig.1.
is the ambient temperature. A uniform magnetic field of strength is applied in the y-direction. The physical model and coordinate system is presented in Fig.1.
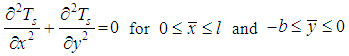
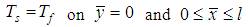
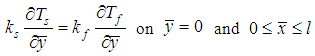
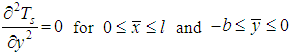
 and applying
and applying 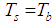 on
on 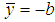 in equation (1) we obtain
in equation (1) we obtain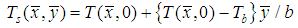
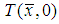 is the unknown temperature at the solid fluid interface which is calculated using the solution of the governing equations. Thus the condition (3) can be written as the following form
is the unknown temperature at the solid fluid interface which is calculated using the solution of the governing equations. Thus the condition (3) can be written as the following form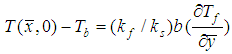
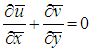
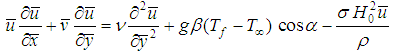
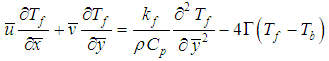
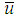 and
and 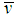 are the dimensional velocity components in the
are the dimensional velocity components in the 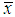 and
and 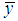 directions, respectively;
directions, respectively; 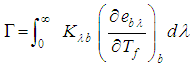 ,
, 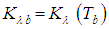 is the mean absorption coefficient,
is the mean absorption coefficient, 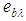 is Plank’s function and
is Plank’s function and 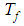 is the temperature of the fluid within the boundary layer,
is the temperature of the fluid within the boundary layer,  is the kinematic viscosity,
is the kinematic viscosity, 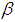 is the thermal expression co-efficient,
is the thermal expression co-efficient, 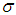 is the electrical conductivity, Cp is the specific heat due to constant pressure. The boundary conditions are given as follows:
is the electrical conductivity, Cp is the specific heat due to constant pressure. The boundary conditions are given as follows: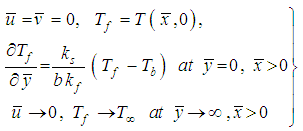
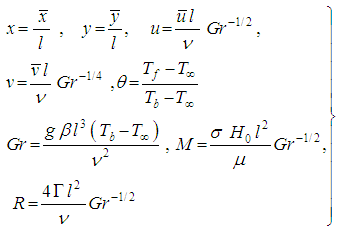
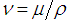 is the kinematic viscosity, Gr is the Grashof number and
is the kinematic viscosity, Gr is the Grashof number and 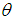 is the non-dimensional temperature. With the help of equation (11), the non-dimensional governing equations are:
is the non-dimensional temperature. With the help of equation (11), the non-dimensional governing equations are: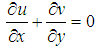
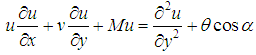
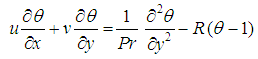
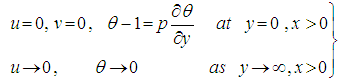
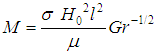 is the magnetic parameter,
is the magnetic parameter, 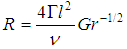 is the radiation parameter and the Prandtl number,
is the radiation parameter and the Prandtl number, 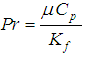 and
and 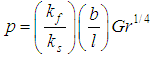 is a conjugate conduction parameter has an important effect on the flow field. The steam function,
is a conjugate conduction parameter has an important effect on the flow field. The steam function, 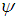 , similarity variables,
, similarity variables, 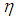 and temperature,
and temperature, 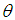 are considered in the following forms to solve the equations (13) and (14) and for the boundary conditions described in (15):
are considered in the following forms to solve the equations (13) and (14) and for the boundary conditions described in (15): 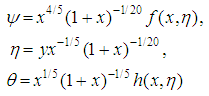
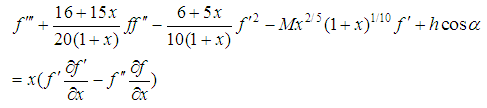
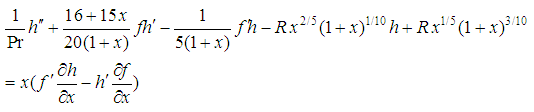
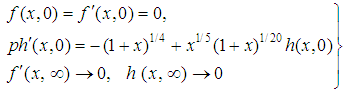
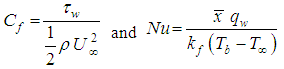
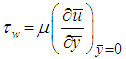 and
and 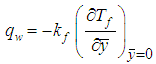 are the shearing stress and the heat flux, respectively. By using dimensionless variables and similarity transformations, the skin friction coefficient and the heat transfer rate can be found as:
are the shearing stress and the heat flux, respectively. By using dimensionless variables and similarity transformations, the skin friction coefficient and the heat transfer rate can be found as: 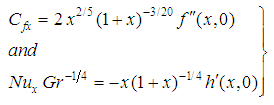









 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML