-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2017; 7(1): 1-11
doi:10.5923/j.ajfd.20170701.01

MHD Flow of an Oldroyd–B Fluid through Porous Medium in a Circular Channel under the Effect of Time Dependent Pressure Gradient
S. E. E. Hamza
Physics Department, Faculty of Science, Benha University, Benha, Egypt
Correspondence to: S. E. E. Hamza, Physics Department, Faculty of Science, Benha University, Benha, Egypt.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

In this paper the unsteady magnetohydrodynamic (MHD) flow of Oldroyd–B fluid through a tube filled with porous medium was investigated. A uniform circular magnetic field was applied perpendicular to the flow direction. The fluid was driven by an axial time dependent pressure gradient which increased or decreased or pulsated with time. The governing equations were accurately solved taking in consideration the modified Darcy's law to count the resistance presented by the porous medium. The obtained velocity profiles had Bessel and modified Bessel functions of zero order representations. The effects of the various parameters on the flow characteristics such as non–Newtonian, magnetic and permeability parameters had been studied and discussed graphically. Figures were provided to compare the velocity profile of Newtonian fluid and Maxwell fluid with Oldroyd fluid. It was found that the velocity distribution increased with the increase of permeability parameter of the porous medium, but it decreased with the increased magnetic and frequency parameters. The flow was parabolic for small frequencies but it had boundary layer characters at large frequencies. Solutions of Maxwell and Newtonian fluids were appeared as limited cases for the present analysis.
Keywords: MHD flow, Oldroyd–B fluid, Unsteady channel flow, Pulsating flow, Porous medium
Cite this paper: S. E. E. Hamza, MHD Flow of an Oldroyd–B Fluid through Porous Medium in a Circular Channel under the Effect of Time Dependent Pressure Gradient, American Journal of Fluid Dynamics, Vol. 7 No. 1, 2017, pp. 1-11. doi: 10.5923/j.ajfd.20170701.01.
Article Outline
1. Introduction
- MHD flow of non–Newtonian fluid through pipes represents significant role in different areas of science and technology such as petroleum industry, biomechanics, heat exchangers and so on. Due to the nonlinearity of the governing equations, exact solutions are difficult to be obtained and are few in number under certain conditions. As a consequence of different physical structures of non–Newtonian fluids, there is not a single constitutive model which can predict all its salient features. Generally, there are three non–Newtonian fluid models, namely empirical models, differential models and integral models. But the most famous amongst them are the last two models. In this work, we will study the second model and consider its subclass known as Oldroyd–B fluid. The simplest subclass of differential type models is the Maxwell fluid. This model can describe the fluid in terms of its relaxation parameter, while there are no any information about its retardation parameter. The Oldroyd–B model, on the other hand, has a measurable retardation time and can relate the viscoelastic manner of dilute polymeric solutions under general flow conditions. Fetecau [1] has provided analytical solutions for the flow of a non–Newtonian fluid in pipe like domain. Yin and Zhu [2] have studied the oscillating flow of viscoelastic fluid in a pipe with the fractional Maxwell model. Khan et al. [3] have investigated the hydromagnetic rotating flows of Oldroyd–B fluid in a porous medium. He obtained exact solutions by using the Laplace transform technique and discussed the effects of relaxation and retardation parameters on fluid motion. Khan and Zeeshan [4] studied the MHD flow of an Oldroyd–B fluid through a porous space induced by tooth pulses.It is well known that theory of time dependent pressure gradient flow through channels may help in understanding many technological problems such as pumping mechanisms used for transporting petrol through pipes. These mechanisms produce, in general, pressure gradient flow which is not constant but changes in some way about a non–zero mean. The unsteady flow of a fluid in cylindrical channels has applications in the chemical food and petroleum industries. Darke [5] has studied unsteady viscous incompressible flow through circular and elliptic tubes under the influence of periodic pressure. Batchelor [6] studied the starting flow in a circular pipe which is initially at rest and set in motion by pressure gradient suddenly imposed and maintained by external means. The laminar flow of an unsteady viscous liquid through a circular cylinder under the influence of exponentially decreasing pressure gradient was studied by Rao and Murthy [7]. Ramkissoon et al. [8] have studied unsteady viscoelastic pipe flow through circular pipe under the influence of periodic pressure gradient. A non–Newtonian fluid model that has attracted many researches is the Oldroyd–B fluid as this is found to be a better model for physiological fluids. So, several researchers have studied Oldroyd–B fluid flows under different conditions [9-13].Pulsating flow is composed of two superimposed components: steady component and oscillation component (time varying). Pulsating flow is appeared in natural systems e.g. respiratory system and circulatory system and in engineering systems e.g. pumps and pulse combustors. Using a finite difference method, Balmer and Fiorina [14] obtained a numerical solution for a power law fluid by considering the pressure pulse as a superposition of steady component and oscillation component. The computational study presented by Hung [15] is considered one of the excellent study in pulsatile nonlinear flow. Rahaman and Ramkissoon [16] studied the unsteady axial viscoelastic pipe flows under the influence of periodic pressure gradient. Bestman and Njoku [17] constructed a solution for hydrodynamic channel flow of viscous fluid induced by tooth pulses. Also, Ghosh and Debnath [18] considered the hydrodynamic channel flow of a two–phasic fluid particle system induced by tooth pulses and obtained a solution using the method of Laplace transforms. Datta and Dalal [19, 20] discussed the pulsatile flow and heat transfer of dusty fluid in a channel and in an annular pipe employing the method of perturbation.The study of flow through porous medium is of fundamental importance in geomechanics, biomechanics and industry e.g. flow of water through rocks, regulation of skin and filtration of fluids. Porous medium is a material formed of solid matrix with bores. This medium is characterized by its porosity which is a ratio between the void space and the total volume of the medium and by its permeability which is a measure of the flow conductivity in the porous medium. Earlier studies of flow in porous medium have taken in consideration the Darcy law which relates between the flow velocity and the pressure gradient across the porous medium.In recent years, the flow of fluids through porous medium has become an important topic because it is used in suction of crude oil through the pores of the rocks, here Darcy's law has a effective role. Elshehawey et al. [21] had studied the peristaltic transport in an asymmetric channel through a porous medium. Ghosh and Sana [22] discussed the unsteady flow of Oldroyd–B fluid induced by rectified sine pulses. Jyothi et al. [23] studied the pulsatile flow of Jeffrey fluid in a circular tube lined with a porous material from inside.During recent years, the study of viscoelastic fluids flow in the presence of magnetic field has applications in many areas including the medical therapy of biological fluids especially blood [24]. Hamza [25] studied Maxwell's fluid flow through circular pipe under the influence of periodic pressure gradient and in the presence of axial magnetic field. Misra et al. [26] had investigated a mathematical modeling of blood flow in porous vessel having double stenosis in the presence of external magnetic field. Eldabe et al. [27] studied the pulsatile flow of non–Newtonian fluid with heat and mass transfer through a porous medium in a channel under the effect of uniform magnetic field.The results of this paper may help in the field of medical research. The application of magnetic field could be useful in the treatment of some healthy problems such as cardiovascular diseases and blood flow in coronary arteries when fatty plaques of cholesterol and blood clots are formed in the lumen of the coronary artery. Also by using this appropriate magnetic field, it is possible to control blood pressure e.g. poor circulation. The pulsating flow passing through arteries attracted the attention of researchers for a long time due to its great importance in medical sciences. Under normal conditions, blood flow in the human circulatory system depends upon the pumping action of the heart and this produces a pressure gradient across the arterial network. Elshehawey et al. [28] studied MHD flow of blood under the effects of body acceleration considering the blood as an viscoelastic fluid. Chaturani and Palanisamy [29] studied pulsatile flow of blood through a rigid tube under the influence of body acceleration as a Newtonian fluid. Elsoud et al. [30] studied the interaction of peristaltic flow with pulsatile couple stress fluid. The mathematical model that considering a viscous incompressible couple stress fluid between infinite parallel walls on which a sinusoidal travelling wave is imposed. Elshehawey et al. [31] investigated the pulsating flow of blood through a porous medium under periodic body acceleration, but the arterial MHD pulsating flow of blood under periodic body acceleration has been studied by Das and Saha [32]. Assuming blood as a viscous fluid, the effect of uniform transverse magnetic field on pulsating motion of blood passing through an axial symmetric tube was analysed by Sanyal and Biswas [33].It is clear that, analysis of the flow properties of non–Newtonian fluids are very important in fluid dynamics field because of their technological application. In addition, the effects of magnetic field on non–Newtonian fluids also have great importance in engineering applications. Moreover, MHD flows in porous medium have applied in a wide fields e.g. development of energy generation systems, astrophysics and geophysical fluid dynamics. Therefore, the aim of this work is to obtain analytic solutions for MHD flow of an Oldroyd–B fluid passing through circular channel filled with porous medium. The fluid is moved by time dependent pressure gradient that increases or decreases or pulsates with time. A circular uniform magnetic field is applied perpendicular to the direction of the flow. Considering Darcy's law for Oldroyd–B fluid, the solutions of the governing equations have been obtained in an exact manner. With the help of these solutions, the effect of the non–dimensional parameters on the velocity field has been discussed for various particular values of the involved parameters. The obtained results show that, the flow is appreciably influenced by the non–Newtonian parameters of the fluid, the magnetic parameter, the permeability parameter of the porous medium and the frequency parameter.
2. Basic Equations
- In porous medium, the momentum and the continuity equations for unsteady MHD flow of incompressible fluid are:
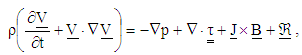 | (1) |
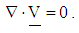 | (2) |
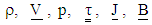 and
and 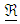 are density, velocity, pressure, extra stress tensor, current density, magnetic field and Darcy's resistance of the porous medium respectively. Notice that,
are density, velocity, pressure, extra stress tensor, current density, magnetic field and Darcy's resistance of the porous medium respectively. Notice that, 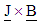 is the Lorentz force due to magnetic field and
is the Lorentz force due to magnetic field and 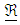 is the measure of the flow resistance offered by the solid matrix.This study is based on Oldroyd–B model of viscoelastic fluids. The properties of this fluids are specified by three constants: dynamic viscosity μ, relaxation time parameter
is the measure of the flow resistance offered by the solid matrix.This study is based on Oldroyd–B model of viscoelastic fluids. The properties of this fluids are specified by three constants: dynamic viscosity μ, relaxation time parameter 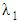 and retardation time parameter
and retardation time parameter 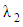 respectively. The extra stress tensor
respectively. The extra stress tensor 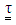 for Oldroyd–B fluid is satisfied by the following constitutive equation, Bird [34]:
for Oldroyd–B fluid is satisfied by the following constitutive equation, Bird [34]: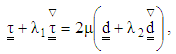 | (3) |
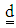 is the rate of deformation tensor and
is the rate of deformation tensor and 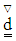 is the upper convected derivative of
is the upper convected derivative of 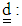
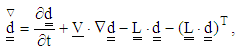 | (4) |
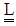 and
and 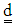 are defined as:
are defined as: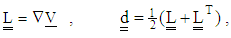 | (5) |
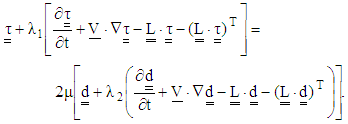 | (6) |
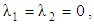 to Maxwell fluid when
to Maxwell fluid when 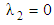 and to Oldroyd–B fluid when
and to Oldroyd–B fluid when 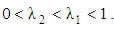 The Lorentz force due to magnetic field is:
The Lorentz force due to magnetic field is: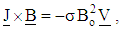 | (7) |
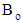 is the strength of the applied magnetic field.The Darcy's resistance for Oldroyd–B fluid satisfies the following expression [35]:
is the strength of the applied magnetic field.The Darcy's resistance for Oldroyd–B fluid satisfies the following expression [35]: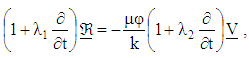 | (8) |
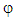 and k are the porosity and permeability constants of the medium, respectively.For the problem under consideration we assume that:
and k are the porosity and permeability constants of the medium, respectively.For the problem under consideration we assume that: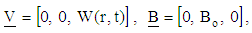 | (9a) |
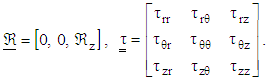 | (9b) |
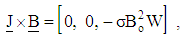 | (10) |
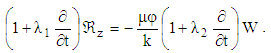 | (11) |
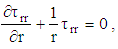 | (12) |
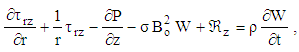 | (13) |
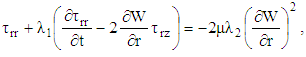 | (14) |
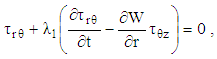 | (15) |
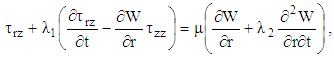 | (16) |
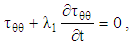 | (17) |
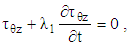 | (18) |
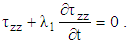 | (19) |
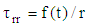 while Eqs. (15), (17), (18) and (19) yields
while Eqs. (15), (17), (18) and (19) yields 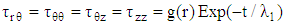 where
where 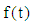 is an arbitrary function of time and
is an arbitrary function of time and 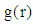 is an arbitrary function of r. The last components of the extra stress tensor,
is an arbitrary function of r. The last components of the extra stress tensor, 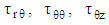 and
and 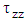 decays exponentially with time. Therefore, the remaining field equations can be expressed as:
decays exponentially with time. Therefore, the remaining field equations can be expressed as: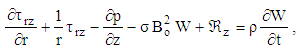 | (13) |
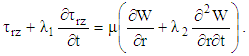 | (16) |
3. Formulation of the Problem
- In this work, we study the flow of an electrically conducting Oldroyd–B fluid through a circular cylinder of radius R filled with porous medium. We chose a cylindrical polar coordinate system (r, θ, z) in a way that z–axis is parallel to the flow direction and there is no flow assumed in the azimuthal direction. This flow is axially symmetric and fully developed in a porous medium. A circular magnetic field
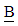 of strength
of strength 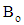 is applied on the azimuthal direction, Fig. 1, and the motion starts due to time dependent pressure gradient. In the analysis, we assumed that the induced magnetic field is negligible.
is applied on the azimuthal direction, Fig. 1, and the motion starts due to time dependent pressure gradient. In the analysis, we assumed that the induced magnetic field is negligible.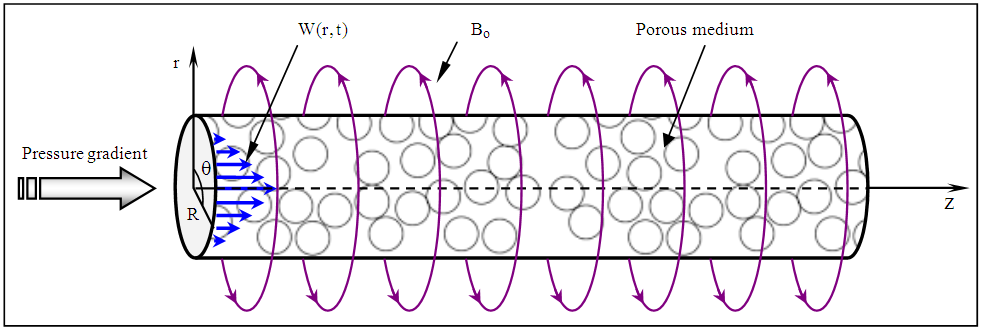 | Figure 1. Schematic diagram of rheological flow through a porous medium in a circular channel |
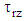 from these two equations shows that, velocity field
from these two equations shows that, velocity field 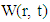 is governed by the equation:
is governed by the equation: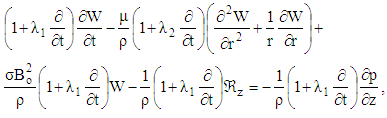 | (20) |
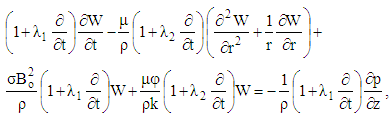 | (21) |
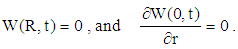 | (22) |
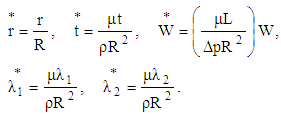 | (23) |
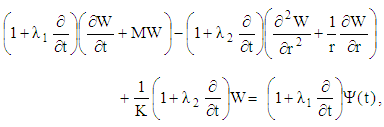 | (24) |
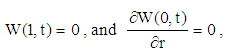 | (25) |
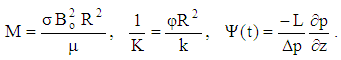 | (26) |
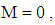 magnetic forces are absent. When M increases, the magnetic force becomes increasingly important. When the value
magnetic forces are absent. When M increases, the magnetic force becomes increasingly important. When the value 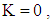 the cylinder is blocked (solid); and when
the cylinder is blocked (solid); and when 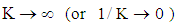 the cylinder becomes a hollow cylinder. Equation (24) subject to the boundary conditions, Eq. (25), is to be solved for different types of pressure gradients, i.e. different forms of the function
the cylinder becomes a hollow cylinder. Equation (24) subject to the boundary conditions, Eq. (25), is to be solved for different types of pressure gradients, i.e. different forms of the function 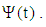
4. Solution of the Problem
4.1. Pressure Gradient Increasing Exponentially with Time
- Let
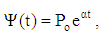 | (27) |
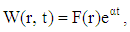 | (28) |
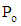 and
and 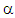 are known constants. Substituting Eqs. (27) and (28) into (24) and equating the harmonic terms, retaining coefficients of
are known constants. Substituting Eqs. (27) and (28) into (24) and equating the harmonic terms, retaining coefficients of 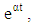 the corresponding equation becomes:
the corresponding equation becomes: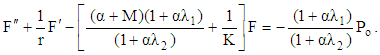 | (29) |
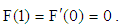 | (30) |
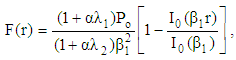 | (31) |
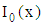 is the modified Bessel function of zero order, and
is the modified Bessel function of zero order, and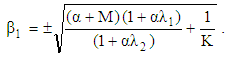 | (32) |
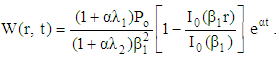 | (33) |
4.2. Pressure Gradient Decreasing Exponentially with Time
- The solution of this case is obtained by taking the function
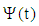 in the form:
in the form: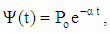 | (34) |
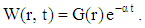 | (35) |
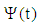 and
and 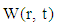 into (24) gives:
into (24) gives: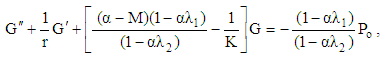 | (36) |
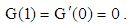 | (37) |
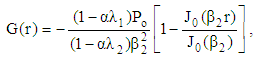 | (38) |
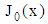 is the Bessel function of zero order, and
is the Bessel function of zero order, and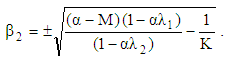 | (39) |
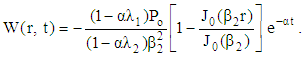 | (40) |
4.3. Pulsating Pressure Gradient
- In this case the flow is generates impulsively due to cosine pulses applied periodically on the positive z–direction. Equation (24) must be solved subject to boundary conditions (25) for pulsating pressure gradient. So, let the pressure gradient or the function
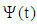 oscillate with frequency
oscillate with frequency 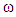 and amplitude
and amplitude 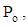 i.e.
i.e.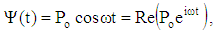 | (41) |
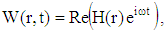 | (42) |
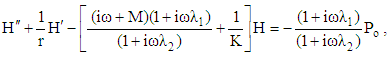 | (43) |
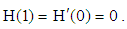 | (44) |
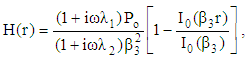 | (45) |
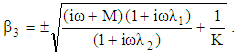 | (46) |
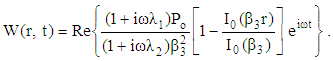 | (47) |
5. Results and Discussion
- In this work, analytic solutions for the velocity field corresponding to the unsteady MHD flow of Oldroyd–B fluids passing through circular channel filled with porous medium have been established. It is worth mentioning that, if
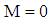 and
and 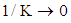 the solutions are reduced to those corresponding to Oldroyd–B fluid that flows in a hollow cylinder in the absence of magnetic field. The variation of velocity field with r is calculated from Eqs. (33), (40) and (47) for different values of the included physical parameters. These variations is shown in Figs. 2 to 10 at
the solutions are reduced to those corresponding to Oldroyd–B fluid that flows in a hollow cylinder in the absence of magnetic field. The variation of velocity field with r is calculated from Eqs. (33), (40) and (47) for different values of the included physical parameters. These variations is shown in Figs. 2 to 10 at 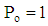 and for fixed
and for fixed 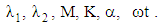 Initially, the effect of non–Newtonian parameters, and later on, the influence of magnetic and permeability parameters (M and K) on the velocity profile are examined graphically. The effect of non–Newtonian parameters
Initially, the effect of non–Newtonian parameters, and later on, the influence of magnetic and permeability parameters (M and K) on the velocity profile are examined graphically. The effect of non–Newtonian parameters 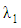 and
and 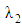 is shown in Figs. 2a, 2b, 5a, 5b and 8a for fixed
is shown in Figs. 2a, 2b, 5a, 5b and 8a for fixed 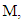
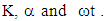 We observe that the velocity increases with increasing
We observe that the velocity increases with increasing 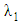 and decreases with increasing
and decreases with increasing 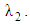 In this section we display the effect of magnetic parameter on axial velocity profiles. The influence of magnetic parameter M on velocity profile is presented in Figs. 3a, 6a and 8b for fixed
In this section we display the effect of magnetic parameter on axial velocity profiles. The influence of magnetic parameter M on velocity profile is presented in Figs. 3a, 6a and 8b for fixed 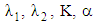 and
and 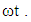 From these figures, it is noted that an increase in magnetic parameter M reduces the velocity profile monotonically due to the effect of the magnetic force against the direction of the flow.The influence of porous medium permeability K on the flow profile is illustrated in Figs. 3b, 6b and 9a for fixed values of
From these figures, it is noted that an increase in magnetic parameter M reduces the velocity profile monotonically due to the effect of the magnetic force against the direction of the flow.The influence of porous medium permeability K on the flow profile is illustrated in Figs. 3b, 6b and 9a for fixed values of 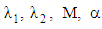 and
and 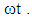 As expected from the governing equations, the increase in the permeability of the porous medium K yields an effect opposite to that of the magnetic parameter M.In case of pulsating pressure gradient, the variation of velocity field with r is calculated from Eq. (47) for different values of
As expected from the governing equations, the increase in the permeability of the porous medium K yields an effect opposite to that of the magnetic parameter M.In case of pulsating pressure gradient, the variation of velocity field with r is calculated from Eq. (47) for different values of 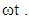 It is shown in Fig. 8 for fixed
It is shown in Fig. 8 for fixed 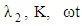 and in Fig. 9 for fixed
and in Fig. 9 for fixed 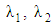 and M. We observe that, the velocity decreases with increasing
and M. We observe that, the velocity decreases with increasing 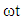 . The three–dimensional plot of velocity
. The three–dimensional plot of velocity 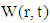 with r and
with r and 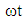 is shown in Fig. 4b for increasing pressure gradient, in Fig. 7b for decreasing pressure gradient and in 10a and 10b for pulsating pressure gradients.Finally, the present model gives a most general form of velocity expression from which the other models can be obtained by proper substitutions. It is of interest to note that the presented solution expressions, (33), (40) and (47), are more general and the results of several problems (e.g. upper convected Maxwell and Newtonian fluids) can be recovered as special cases, see Fig. 11 for upper convected Maxwell fluid; i.e.
is shown in Fig. 4b for increasing pressure gradient, in Fig. 7b for decreasing pressure gradient and in 10a and 10b for pulsating pressure gradients.Finally, the present model gives a most general form of velocity expression from which the other models can be obtained by proper substitutions. It is of interest to note that the presented solution expressions, (33), (40) and (47), are more general and the results of several problems (e.g. upper convected Maxwell and Newtonian fluids) can be recovered as special cases, see Fig. 11 for upper convected Maxwell fluid; i.e. 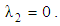
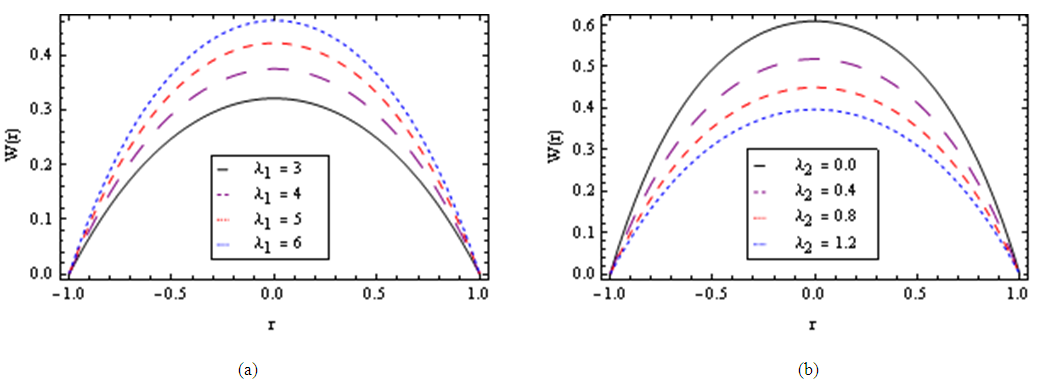 | Figure 2. The increasing pressure gradient velocity field for various values of 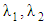 and for fixed and for fixed 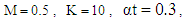 [ [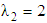 in (a) and in (a) and 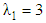 in (b)] in (b)] |
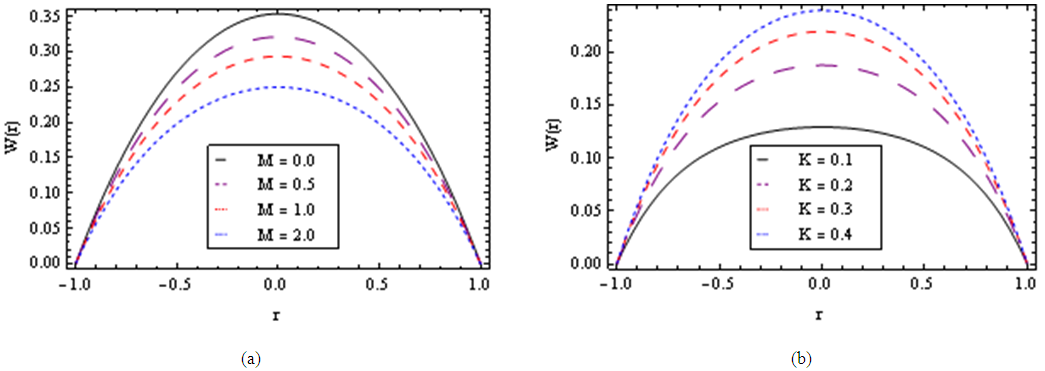 | Figure 3. The increasing pressure gradient velocity field for various values of M, K and for fixed 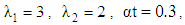 [ [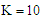 in (a) and in (a) and 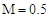 in (b)] in (b)] |
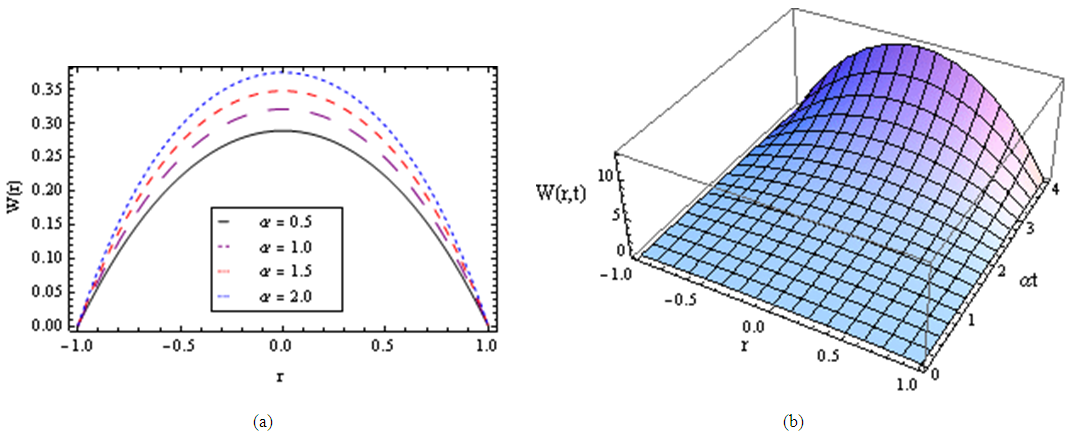 | Figure 4. The increasing pressure gradient velocity field for various values of α and for fixed  and and  |
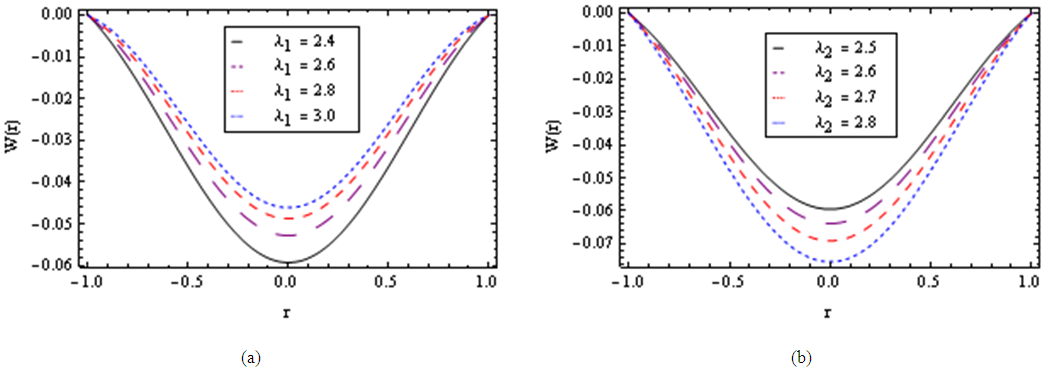 | Figure 5. The decreasing pressure gradient velocity field for various values of 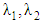 and for fixed and for fixed 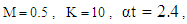 [ [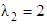 in (a) and in (a) and 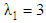 in (b)] in (b)] |
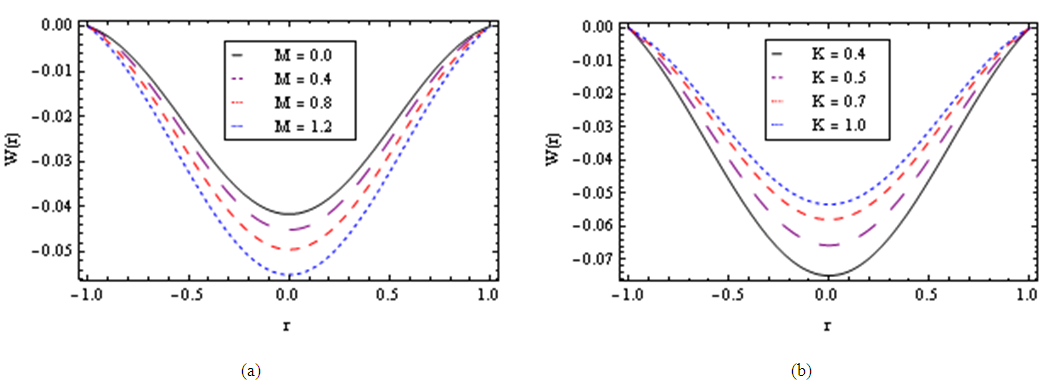 | Figure 6. The decreasing pressure gradient velocity field for various values of M, K and for fixed 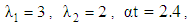 [ [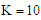 in (a) and in (a) and 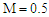 in (b)] in (b)] |
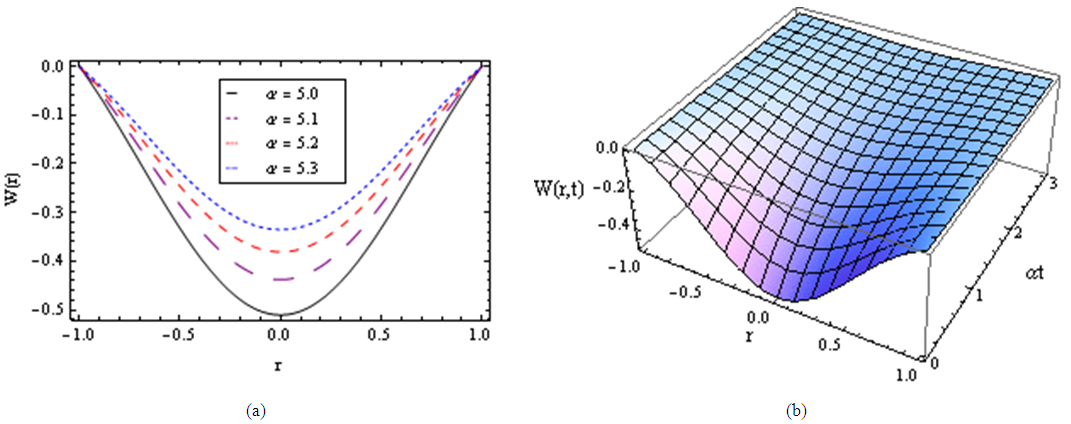 | Figure 7. The decreasing pressure gradient velocity field for various values of α and for fixed  and and  |
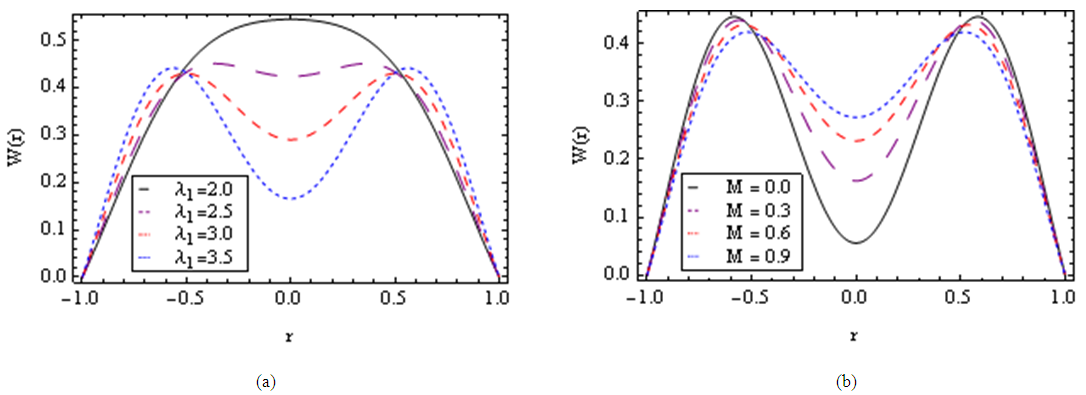 | Figure 8. Pulsating pressure gradient velocity field for various values of 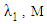 and for fixed and for fixed 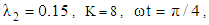 [ [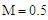 in (a) and in (a) and 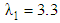 in (b)] in (b)] |
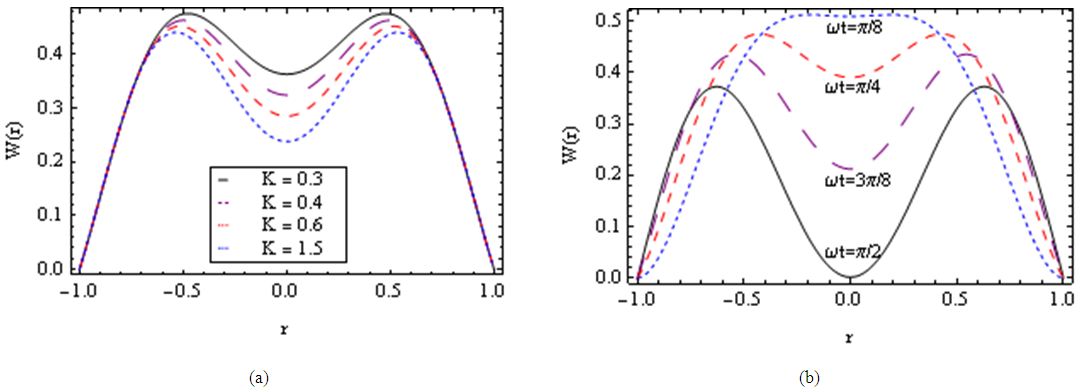 | Figure 9. Pulsating pressure gradient velocity field for various values of K, and for fixed 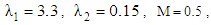 , [ , [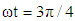 in (a) and in (a) and 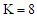 in (b)] in (b)] |
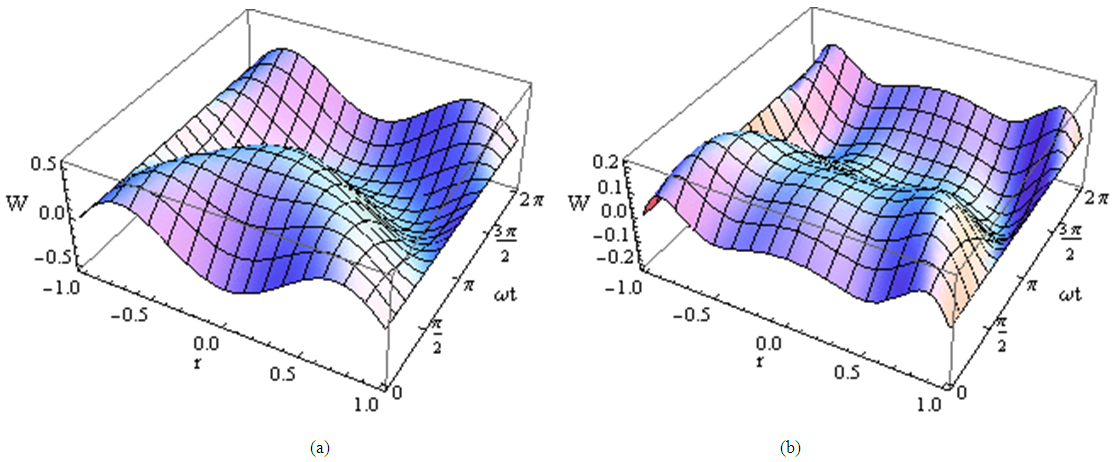 | Figure 10. Three dimension pulsating pressure gradient velocity field for fixed values of  [ [ in (a) and in (a) and  in (b)] in (b)] |
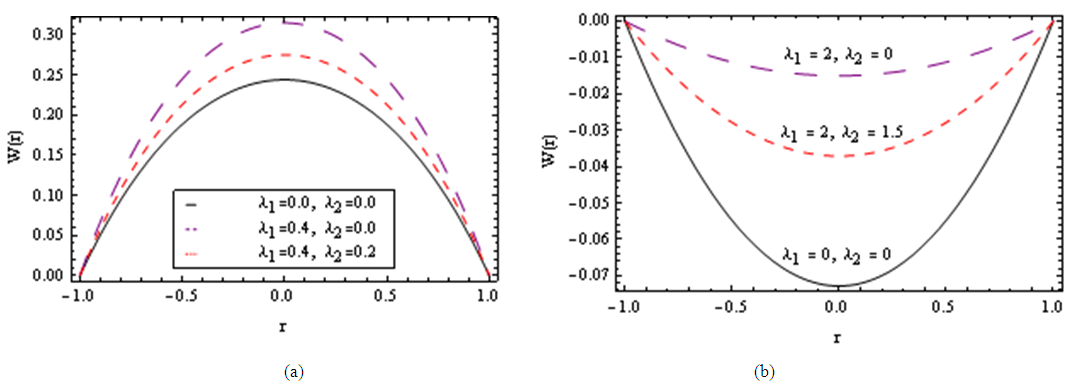 | Figure 11. Maxwell fluid Pulsating pressure gradient velocity field for fixed values of  [ [ in (a) and in (a) and  in (b)] in (b)] |
6. Concluding Remarks
- The main objective of this work is to examine basic MHD flow of an Oldroyd–B fluid through circular channel filled with porous medium in the presence of time dependent pressure gradients. We consider the unsteady flow of Oldroyd–B fluid in three cases: (i) when the pressure gradient change exponentially with time (increasing or decreasing) and (ii) when the pressure gradient is pulsating. The governing nonlinear partial differential equations are solved analytically. In the first problem we looked separately at the pressure gradient rising exponentially with time and falling exponentially wit time, i.e. the pressure gradient is proportional to
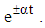 The effects of magnetic and permeability parameters (M and K) on the velocity field are studied. Therefore, we conclude the following remarks:§ The solution of the governing equations and hence the behaviour of the flow depend to a large extent on
The effects of magnetic and permeability parameters (M and K) on the velocity field are studied. Therefore, we conclude the following remarks:§ The solution of the governing equations and hence the behaviour of the flow depend to a large extent on 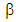 where
where 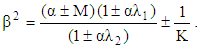 The positive sign for increasing pressure gradient and the negative sign for decreasing pressure gradient.§ The solutions depend on the parameter
The positive sign for increasing pressure gradient and the negative sign for decreasing pressure gradient.§ The solutions depend on the parameter 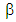 in the same form as the solution for the upper convected Maxwell fluid. However, in the present case the parameter
in the same form as the solution for the upper convected Maxwell fluid. However, in the present case the parameter  depend on
depend on 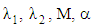 in addition to K.§ An increasing in the magnetic parameter M reduces the velocity profile due to the effect of magnetic force against the flow direction.§ An increasing in the permeability K yields an effect opposite to that of the magnetic parameter M.§ In the absence of the magnetic and permeability parameters (
in addition to K.§ An increasing in the magnetic parameter M reduces the velocity profile due to the effect of magnetic force against the flow direction.§ An increasing in the permeability K yields an effect opposite to that of the magnetic parameter M.§ In the absence of the magnetic and permeability parameters (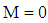 and
and 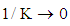 ), the obtained solutions reduce to those corresponding to the flow of Oldroyd–B fluids with
), the obtained solutions reduce to those corresponding to the flow of Oldroyd–B fluids with 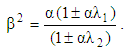 § For hollow cylinder
§ For hollow cylinder 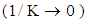 and if
and if 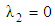 then
then 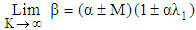 which coincides with Hamza [25] for MHD Maxwell fluid.§ The results of Rahaman [16] for upper convected Maxwell fluid in the absence of the applied magnetic field have been recovered by taking
which coincides with Hamza [25] for MHD Maxwell fluid.§ The results of Rahaman [16] for upper convected Maxwell fluid in the absence of the applied magnetic field have been recovered by taking 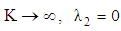 and
and 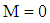 then
then 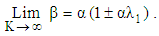 § As a result of the present study and with the help of Eqs. (33), (40) and (47), we can introduce the amplitude of the dimensionless velocity
§ As a result of the present study and with the help of Eqs. (33), (40) and (47), we can introduce the amplitude of the dimensionless velocity 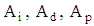 for increasing, decreasing and pulsating pressure gradients; respectively on the axis of the pipe
for increasing, decreasing and pulsating pressure gradients; respectively on the axis of the pipe 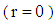 as:
as: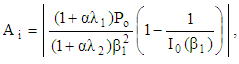 | (48) |
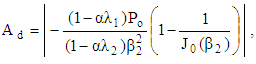 | (49) |
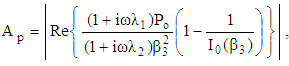 | (50) |
ACKNOWLEDGEMENTS
- I would like to thank Prof. Dr. A. Abu El Hassan Professor of theoretical physics, Faculty of Science, Benha University, for his helpful and valuable comments.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML