Kaveh Ostad-Ali-Askari 1, Mohammad Shayannejad 2
1PhD Student, Department of Water Engineering, Faculty of Civil Engineering, Najafabad Branch, Islamic Azad University, Najafabad, Iran
2Associate Professor, Water Engineering Department, Isfahan University of Technology, Isfahan Province, Iran
Correspondence to: Kaveh Ostad-Ali-Askari , PhD Student, Department of Water Engineering, Faculty of Civil Engineering, Najafabad Branch, Islamic Azad University, Najafabad, Iran.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Employment of delayed Rockfill dams without impermeable membrane is an appropriate tool for controlling flood. For this purpose first hydraulic currents should be discerned from the Rockfill dams so that we can obtain the stage discharge relation for them. Secondly the unsteady currents in the open channels should be fully analyzed. This can be performed through solving the Saint-Venant equations. Since solving such equations, especially for a network of open channels with various cross sections is very complex and time-consuming, appropriate software should be used. N this research the HEC-RAS has been employed. Results obtained for the discharge-gauge relation of Rockfill dam is used in this software. Data required for employing this software include: blueprint of the network of channels, mapping results of various network sections, roughness coefficient of various network, distances between the mapped sections, and hydrograph of a definite flood, location and specifications of Rockfill dam or dams. Output of this software includes: water level profile and the inflow hydrographs at various points of the network and hydrograph of the outflow flood the Rockfill dam.
Keywords:
Rockfill dam, Flood control, HES-RAS
Cite this paper: Kaveh Ostad-Ali-Askari , Mohammad Shayannejad , Usage of Rockfill Dams in the HEC-RAS Software for the Purpose of Controlling Floods, American Journal of Fluid Dynamics, Vol. 5 No. 1, 2015, pp. 23-29. doi: 10.5923/j.ajfd.20150501.03.
1. Introduction
The fundamental saint Saint-Venant equations, first proposed in 1871, present a complete from of the forces governing the current. Solution of these equations especially in a network of channels or open conduits especially with irregular sections is a very complex and time consuming task inevitable therefore, computerized models and programs should be used and employing several models are would be possible to draw the water level profile of each branch of the network of channels at any desired time. Also the hydrograph of the flow at any point of the network can be obtained. The flow hydrograph shows modifications of the discharge flow relative to time. Causes of such modifications can be various factors including changes of the inflow discharge to the network, enter of a flood in to the river, and/or fracture of the dam. One of the models available in this connection is the FLDWAV model which is the result of three decades attempt of experts at the National Oceanic and Atmospheric Administration of USA (Zhou et al., 2005). This model is a combination of the two DWOPRE and DAMBRK models the principal idea of which was proposed by Fread et al (Fread and Lewis 1988; Fread 1993). These two researchers wrote numerous papers in the field of introducing application and comparing results of the FLDWAV model with other models. The above said model simulates the outflow hydrograph generated due to fracture of the dam and wave movement in the downstream channels. Shamsai et al (Shamsai and Mousavi 2010) tested this model for the Aidoghmosh dam and results of this research showed an acceptable correspondence of the aforesaid model with the observations. Another model of the network flow analysis model in the open flows is the HEC-RAS model 3.01 version of this model (Yang et al., 2006). In this research, the aforesaid model is studied. The Rockfill dams used due to their being economical, and employed for flood control and can be employed as one of the boundary conditions in this model. To do so, based on hydraulic analysis of the flow obtain amongst them an appropriate relation between the flow discharge and the water height at up – and downstream. Rockfill dams bear large pores. Therefore in them, the flow will be fluctuating. Therefore the Darcy’s law does not apply in their case. Or, in the other words, the relation between velocity (V) and hydraulic gradient (i) is nonlinear. In case this relation is assumed to be in the power form, the relation between the Reynolds number and Darcy Weisbach’s friction factor will be in the nth power from. Various researchers have suggested different relations in this regard Samani et al (Samani et al., 2003; Samani et al., 2004). Fully analyzed the one-dimensional and two-dimensional hydraulic flows amongst the Rockfill dams, that in this research use will be made of their results.When rock is available, rockfill dam is an economical and fast tool for flood detention and control purposes. Rockfill dam can be designed satisfactorily when hydraulics of flow through rockfill dam is known. As this type of dam consists of coarse particles, the flow will deviate from Darcy’s law and mostly is turbulent. This means that the relationship between the flow velocity, V, and its hydraulic gradient, i, is a nonlinear one. Different researchers proposed the following nonlinear relationships: | (1) |
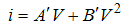 | (2) |
where 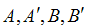 are coefficients dependent on the rock and fluid characteristics. Equation (1) was proposed by Prony in 1804 and Equation (2) by Forcheimer in 1901 (Li et al., 1998). Other researchers, to explain the hydraulics of flow through rocks, suggested relationships between Reynold’s number (Re) and Darcy-Weisbach coefficient (f) in the following forms:
are coefficients dependent on the rock and fluid characteristics. Equation (1) was proposed by Prony in 1804 and Equation (2) by Forcheimer in 1901 (Li et al., 1998). Other researchers, to explain the hydraulics of flow through rocks, suggested relationships between Reynold’s number (Re) and Darcy-Weisbach coefficient (f) in the following forms: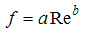 | (3) |
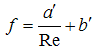 | (4) |
where 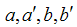 are also coefficients dependent on the rock and fluid characteristics. If the Reynold’s number is written in terms of v, the Darcy-Weisbach can be expressed in the form of Equations (1) and (2), respectively. The following shows some of the relationships proposed by different researchers.In 1952, Ergun proposed the following relationship (Ergun, 1952):
are also coefficients dependent on the rock and fluid characteristics. If the Reynold’s number is written in terms of v, the Darcy-Weisbach can be expressed in the form of Equations (1) and (2), respectively. The following shows some of the relationships proposed by different researchers.In 1952, Ergun proposed the following relationship (Ergun, 1952):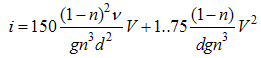 | (5) |
where n = rock porosity, 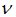 = kinematic viscosity, d = average size of rock material and g = acceleration due to gravity. Wilkins introduced the following relationship (Wilkins, 1956):
= kinematic viscosity, d = average size of rock material and g = acceleration due to gravity. Wilkins introduced the following relationship (Wilkins, 1956):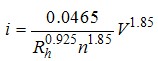 | (6) |
where 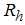 is the hydraulic radius of the rock material. He considered
is the hydraulic radius of the rock material. He considered  equal to d/10 for the range
equal to d/10 for the range 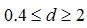 meters. Ward used the following (Ward, 1964):
meters. Ward used the following (Ward, 1964):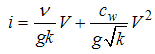 | (7) |
where 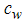 = a coefficient and k = intrinsic permeability. Leps introduced the following (Leps, 1973):
= a coefficient and k = intrinsic permeability. Leps introduced the following (Leps, 1973):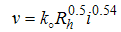 | (8) |
where 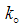 is a coefficient. McCorquodal used the following relationship (McCorquodal et al., 1978):
is a coefficient. McCorquodal used the following relationship (McCorquodal et al., 1978):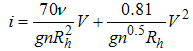 | (9) |
Stephensen proposed a relationship in a form of (Stephenson, 1979):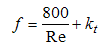 | (10) |
where 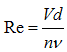 .
. 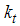 for a laminar flow through rock material is equal to zero and it takes different values when the rock shape changes. For turbulent flow (>10000), f is almost equal to
for a laminar flow through rock material is equal to zero and it takes different values when the rock shape changes. For turbulent flow (>10000), f is almost equal to 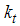 . Herrera and Felton introduced the following (Herrera and Felton, 1991).
. Herrera and Felton introduced the following (Herrera and Felton, 1991).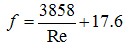 | (11) |
They defined Re as 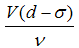 where
where 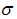 is the standard deviation of rock size distribution. Li and his colleagues used the following relationship (Li et al., 1998):
is the standard deviation of rock size distribution. Li and his colleagues used the following relationship (Li et al., 1998):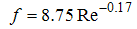 | (12) |
in which d considered equal to 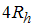 .
. 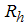 and Re are defined as:
and Re are defined as: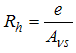 | (13) |
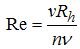 | (14) |
where e and 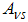 are the void ratio and particle surface area per unit volume, respectively. According to the above review of the different relationships it is concluded that the hydraulic gradient may be defined from Darcy-Weisbach equation considering f in a form similar to Equation (3).
are the void ratio and particle surface area per unit volume, respectively. According to the above review of the different relationships it is concluded that the hydraulic gradient may be defined from Darcy-Weisbach equation considering f in a form similar to Equation (3).
2. Materials and Methods
Phases are as follows:1. First specifications of a section of the river (including the blueprint, shape of sections at various points, figures relevant to the river floor, and Manning's roughness coefficient) are entered into the HEC-RAS software. 2. A specified flood at the beginning of the river is considered and its hydrograph as the upstream boundary condition is inserted into the HEC-RAS software.3. Location of the quarry-stone dam establishment is selected and its relevant relation as the downstream boundary condition is entered in to the software. This relation for the one-dimensional flow has been presented by Samani and Shayannejad (2003) as follows: 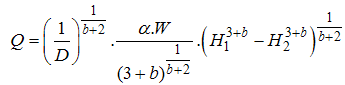 | (15) |
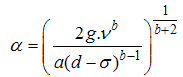 | (16) |
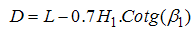 | (17) |
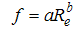 | (18) |
In the above relations: W = width of the flow section L = Lower width of the dam = Angle of the upstream wall of the dam with the horizon level.
= Angle of the upstream wall of the dam with the horizon level. 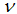 = Cinematic viscosity, g = Gravitation acceleration, d= Medium dimension of aggregates,
= Cinematic viscosity, g = Gravitation acceleration, d= Medium dimension of aggregates, 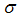 = the standard deviation of aggregate's size, f=Darcy-Weisbach friction factor, Re = Reynolds’s number Relation 1 is known as the stage-discharge relation for the Rockfill dam in the one-dimensional state. Samani and Shayannejad obtained the equation coefficients (4) as follows:
= the standard deviation of aggregate's size, f=Darcy-Weisbach friction factor, Re = Reynolds’s number Relation 1 is known as the stage-discharge relation for the Rockfill dam in the one-dimensional state. Samani and Shayannejad obtained the equation coefficients (4) as follows:
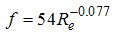 Following completing the above said stages, after running the HEC-RAS program, the flow hydrograph at any point of the river can be obtained.
Following completing the above said stages, after running the HEC-RAS program, the flow hydrograph at any point of the river can be obtained.
3. Model Development
To develop the model, either of Equations (17) or (18) can be combined with Darcy-Weisbach equation. When Equation (17) is used, 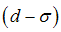 instead of d, and
instead of d, and 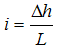 where
where 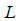 is the base length of the rockfill dam, Darcy-Weisbach equation becomes
is the base length of the rockfill dam, Darcy-Weisbach equation becomes | (19) |
If Re is defined as  Equation (19) becomes
Equation (19) becomes | (20) |
where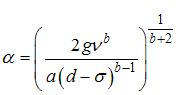 | (21) |
Equation (20) is similar to Darcy’s law except i exponent is not equal to unity. Combining Equation (20) with the continuity equation and defining i as 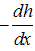 , yields
, yields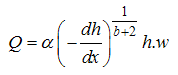 | (22) |
whereQ = flow rate,h = water level inside the rockfill dam,w = width of flow cross section,x = the longitudinal coordinate in flow direction.Integrating Equation (22) between the limits 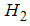 to
to 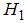 for h and zero to D for x, the following equation is resulted:
for h and zero to D for x, the following equation is resulted: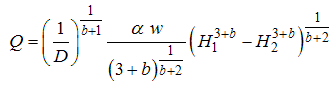 | (19) |
where D is defined according to Sharma (1979):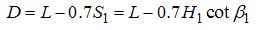 | (20) |
Samani and Shayannejad obtained the equation coefficients (3) as follows:
 Following completing the above said stages, after running the HEC-RAS program, the flow hydrograph at any point of the river can be obtained.
Following completing the above said stages, after running the HEC-RAS program, the flow hydrograph at any point of the river can be obtained.
4. Results
A quarry – stone dam is established at a distance of 2km from the inflow point of flood into the river. The river slope is 0.001, its Manning roughness coefficient is 0.03, floor width is 5m, and its side slope has been considered to be 1.5. Specifications of the quarry-stone dam is as follows: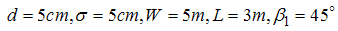 Considering the above data and equations 1 to 4, the stage – discharge slope of the quarry – stone dam will be drawn by the HRC-RAS software as presented in figure 1.
Considering the above data and equations 1 to 4, the stage – discharge slope of the quarry – stone dam will be drawn by the HRC-RAS software as presented in figure 1. 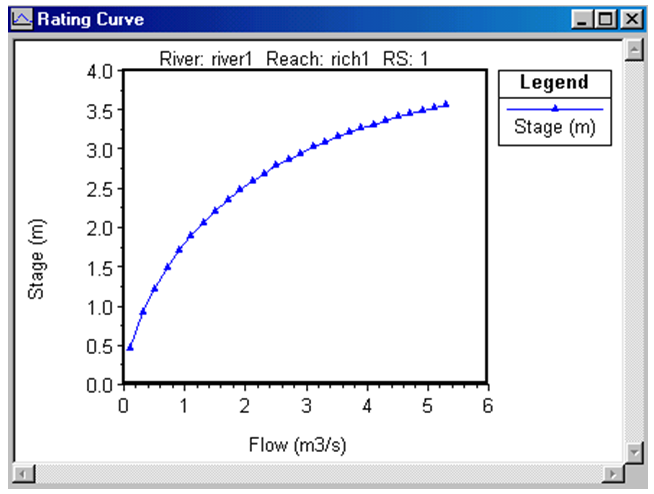 | Figure 1. Discharge–stage diagram of rockfill dam |
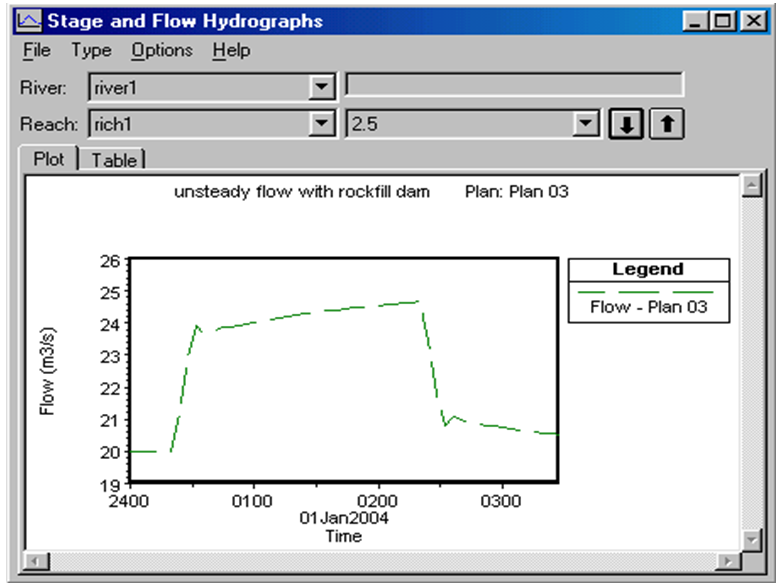
Hydrograph of the flood entered into the river has been depicted in figure 2. Regarding the above information, the HEC-RAS software can provide the flow hydrograph at various points including the outflow hydrograph from the quarry-stone dam and draw it. These hydrographs have been presented in figures 3 to 6. By comparison of figures 2 and 6, the delayed role of Rockfill dams in controlling the flood is specified.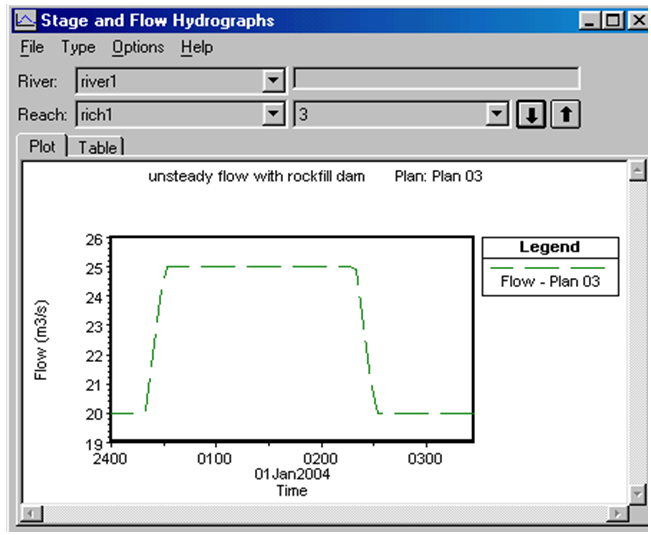 | Figure 2. Flood hydrograph |
 | Figure 3. Flow hydrograph in 600 meters of the top river |
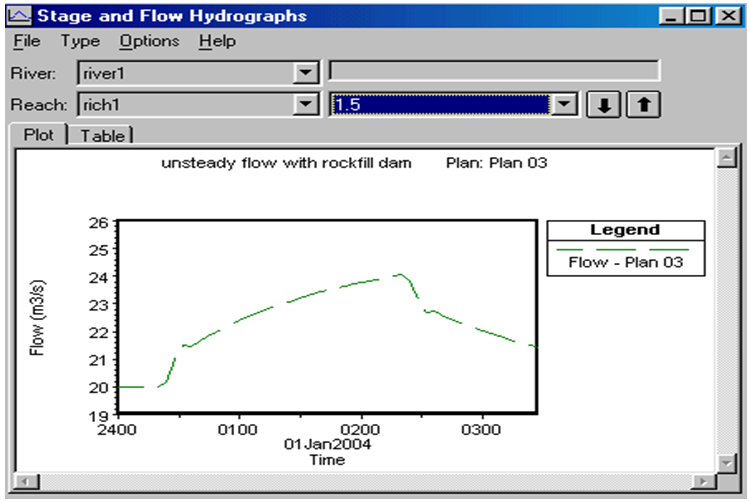 | Figure 4. Flow hydrograph in 1600 meters of the top river |
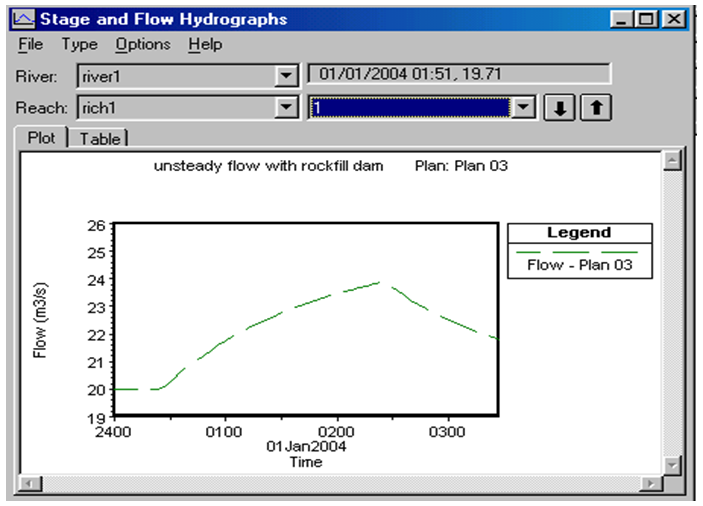 | Figure 5. Flow hydrograph through the rockfill dam (2 km from the beginning of the river) |
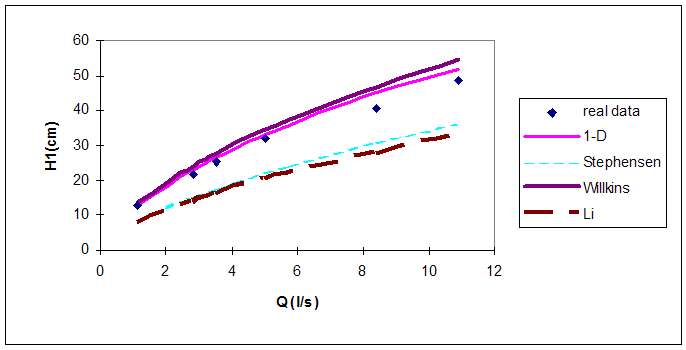 | Figure 6. Model and other reseacher’s results |
5. Discussion and Conclusions
Several elements require to the development of potential flooding from a dam failure. HEC-RAS is an unsteady flow routing model that is often used for the computation of downstream impacts resulting from hypothetical dam failures. Width and development time as breach parameters has estimated typically done external to the model. Gee D investigated incorporate several mechanisms for simulating breach widening, side slope collapse, and head cutting by HEC-RAS model (Gee, 2010). The flood routing in dam breaching parameters including peak outflow rate and breaching time and physical model is simulated with HEC-RAS (Peng et al, 2012).HEC-RAS is software that models water flowing by open channels systems and computing water surface. HEC-RAS finds peculiar commercial application in flood plain management and flood insurance studies to aeesee floodway violation. Other usage including bridge and drainer, dam breach design and analysis, bulwark studies, and channel modification studies.
References
| [1] | Fread, D. (1993). "NWS FLDWAV model: The replacement of DAMBRK for dam-break flood prediction." Dam Safety, vol. 93, pp.26-29. |
| [2] | Fread, D., Lewis J. (1988). “FLDWAV: A generalized flood routing model. Proceedings of National conference on Hydraulic Engineering, ASCE. |
| [3] | Gee, D. (2010) Dam Breach Modeling with HEC-RAS Using Embankment Erosion Process Models. World Environmental and Water Resources Congress 2010: pp. 1347-1356.doi: 10.1061/41114(371)144. |
| [4] | Peng, M ., Zhang LM. (2012). Analysis of human risks due to dam break floods—part 2: application to Tangjiashan landslide dam failure. Nat Hazards. 64:1899–1923. DOI 10.1007/s11069-012-0336-9. |
| [5] | Samani, H., Samani J., Shayannejad M. (2003). "Reservoir routing using steady and unstesdy flow through rockfill dams." J of Hydraulic Engineering Div ASCE, vol. 129, No. 6, pp. 448-454, DOI: 10.1061/(ASCE)0733-9429. |
| [6] | Samani, J., Samani, H., Shayannejad, M. (2004). "Reservoir routing with outflow through rockfill dams." J of Hydraulic Research, Vol. 42, No, 4, pp. 435-439, DOI: 10.1080/00221686.2004.9641211. |
| [7] | Shamsai, A. Mousavi, S. (2010). "Evaluation and assessment of dam-break parameters of embankment dams case study: Aidoghmosh dam" Journal of Civil Engineering Islamic Azad University, Vol. 2, No. 1, pp. 65-73. |
| [8] | Yang, J., Townsend R., D., Daneshfar B. (2006). "Applying the HEC-RAS model and GIS techniques in river network floodplain delineation." Canadian Journal of Civil Engineering, Vol. 33, No. 1, pp. 19-28, DOI: 10.1139/l05-102. |
| [9] | Zhou, R. D., Eng ,P., Donnelly, C., R. (2005). Comparison of HEC-RAS with FLDWAV and DAMBRK models for dam break analysis. CDA 2005 Annual Conference. |



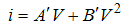
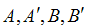 are coefficients dependent on the rock and fluid characteristics. Equation (1) was proposed by Prony in 1804 and Equation (2) by Forcheimer in 1901 (Li et al., 1998). Other researchers, to explain the hydraulics of flow through rocks, suggested relationships between Reynold’s number (Re) and Darcy-Weisbach coefficient (f) in the following forms:
are coefficients dependent on the rock and fluid characteristics. Equation (1) was proposed by Prony in 1804 and Equation (2) by Forcheimer in 1901 (Li et al., 1998). Other researchers, to explain the hydraulics of flow through rocks, suggested relationships between Reynold’s number (Re) and Darcy-Weisbach coefficient (f) in the following forms: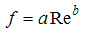
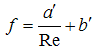
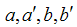 are also coefficients dependent on the rock and fluid characteristics. If the Reynold’s number is written in terms of v, the Darcy-Weisbach can be expressed in the form of Equations (1) and (2), respectively. The following shows some of the relationships proposed by different researchers.In 1952, Ergun proposed the following relationship (Ergun, 1952):
are also coefficients dependent on the rock and fluid characteristics. If the Reynold’s number is written in terms of v, the Darcy-Weisbach can be expressed in the form of Equations (1) and (2), respectively. The following shows some of the relationships proposed by different researchers.In 1952, Ergun proposed the following relationship (Ergun, 1952):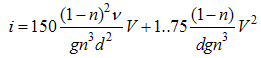
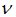 = kinematic viscosity, d = average size of rock material and g = acceleration due to gravity. Wilkins introduced the following relationship (Wilkins, 1956):
= kinematic viscosity, d = average size of rock material and g = acceleration due to gravity. Wilkins introduced the following relationship (Wilkins, 1956):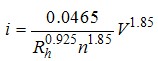
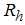 is the hydraulic radius of the rock material. He considered
is the hydraulic radius of the rock material. He considered  equal to d/10 for the range
equal to d/10 for the range 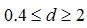 meters. Ward used the following (Ward, 1964):
meters. Ward used the following (Ward, 1964):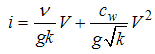
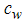 = a coefficient and k = intrinsic permeability. Leps introduced the following (Leps, 1973):
= a coefficient and k = intrinsic permeability. Leps introduced the following (Leps, 1973):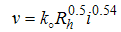
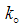 is a coefficient. McCorquodal used the following relationship (McCorquodal et al., 1978):
is a coefficient. McCorquodal used the following relationship (McCorquodal et al., 1978):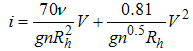
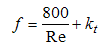
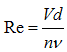 .
. 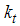 for a laminar flow through rock material is equal to zero and it takes different values when the rock shape changes. For turbulent flow (>10000), f is almost equal to
for a laminar flow through rock material is equal to zero and it takes different values when the rock shape changes. For turbulent flow (>10000), f is almost equal to 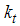 . Herrera and Felton introduced the following (Herrera and Felton, 1991).
. Herrera and Felton introduced the following (Herrera and Felton, 1991).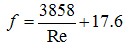
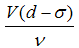 where
where 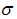 is the standard deviation of rock size distribution. Li and his colleagues used the following relationship (Li et al., 1998):
is the standard deviation of rock size distribution. Li and his colleagues used the following relationship (Li et al., 1998):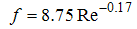
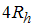 .
. 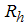 and Re are defined as:
and Re are defined as: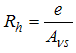
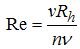
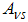 are the void ratio and particle surface area per unit volume, respectively. According to the above review of the different relationships it is concluded that the hydraulic gradient may be defined from Darcy-Weisbach equation considering f in a form similar to Equation (3).
are the void ratio and particle surface area per unit volume, respectively. According to the above review of the different relationships it is concluded that the hydraulic gradient may be defined from Darcy-Weisbach equation considering f in a form similar to Equation (3).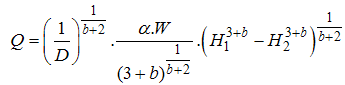
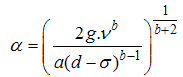
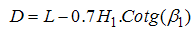
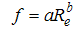
 = Angle of the upstream wall of the dam with the horizon level.
= Angle of the upstream wall of the dam with the horizon level. 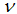 = Cinematic viscosity, g = Gravitation acceleration, d= Medium dimension of aggregates,
= Cinematic viscosity, g = Gravitation acceleration, d= Medium dimension of aggregates, 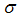 = the standard deviation of aggregate's size, f=Darcy-Weisbach friction factor, Re = Reynolds’s number Relation 1 is known as the stage-discharge relation for the Rockfill dam in the one-dimensional state. Samani and Shayannejad obtained the equation coefficients (4) as follows:
= the standard deviation of aggregate's size, f=Darcy-Weisbach friction factor, Re = Reynolds’s number Relation 1 is known as the stage-discharge relation for the Rockfill dam in the one-dimensional state. Samani and Shayannejad obtained the equation coefficients (4) as follows:
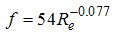 Following completing the above said stages, after running the HEC-RAS program, the flow hydrograph at any point of the river can be obtained.
Following completing the above said stages, after running the HEC-RAS program, the flow hydrograph at any point of the river can be obtained. 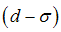 instead of d, and
instead of d, and 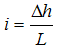 where
where 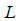 is the base length of the rockfill dam, Darcy-Weisbach equation becomes
is the base length of the rockfill dam, Darcy-Weisbach equation becomes
 Equation (19) becomes
Equation (19) becomes
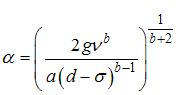
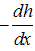 , yields
, yields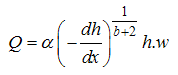
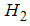 to
to 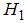 for h and zero to D for x, the following equation is resulted:
for h and zero to D for x, the following equation is resulted: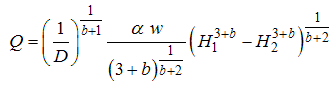
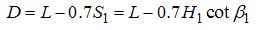

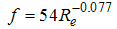 Following completing the above said stages, after running the HEC-RAS program, the flow hydrograph at any point of the river can be obtained.
Following completing the above said stages, after running the HEC-RAS program, the flow hydrograph at any point of the river can be obtained. 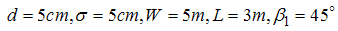 Considering the above data and equations 1 to 4, the stage – discharge slope of the quarry – stone dam will be drawn by the HRC-RAS software as presented in figure 1.
Considering the above data and equations 1 to 4, the stage – discharge slope of the quarry – stone dam will be drawn by the HRC-RAS software as presented in figure 1. 





 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML