Oyelami F. H. 1, Saka-Balogun O. Y. 1, Abdulwaheed J. 2
1Department of Mathematical and physical sciences, Afe Babalola University, Ado Ekiti, Nigeria
2Department of Mathematics, University of Ilorin, Ilorin, Nigeria
Correspondence to: Oyelami F. H. , Department of Mathematical and physical sciences, Afe Babalola University, Ado Ekiti, Nigeria.
| Email: |  |
Copyright © 2015 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The effects of variable thermo physical parameters on the natural convective heat and mass transfer of a viscous incompressible, gray absorbing-emitting fluid flowing past an impulsively started moving vertical plate under the action of transversely applied magnetic field in the presence of chemical reaction was considered. The governing boundary-layer equations are formulated with appropriate boundary conditions. The Roseland diffusion approximation is used to analyze the radiative heat flux and it is appropriate for non-Scattering media. The governing boundary layer equations were simplified and non-dimensionalized. The dimensionless equations were discretized and then solved using the Crank-Nicolson’s method. The effects of variable thermo physical parameters which are: Magnetic field, dissipation function, Prandtl number, radiation-conduction parameter, thermal Grashof number, species Grashof number, Schmidt number, Reynolds number, chemical reaction parameter and Darcy number are considered on the dimensionless velocity, temperature and concentration profile. It was discovered that Velocity profile decreases with increase in Magnetic field, conduction radiation parameter, Schmidt number, prandtl number, Eckert number and chemical reaction parameter while it decreases with increase in Grashof number. Temperature profile increases with increase in Magnetic field, Schmidt number, Eckert number and chemical reaction parameter while it decreases with increase in conduction radiation parameter, prandtl number, Eckert number, Grashof number and Darcy number. Concentration profile increases with increase in Magnetic field and Conduction Radiation parameter while it decreases with increase in Schmidt number, Grashof number and chemical reaction parameter.
Keywords:
Natural convection, MHD, Thermal conduction, Viscous dissipation, Chemical reaction
Cite this paper: Oyelami F. H. , Saka-Balogun O. Y. , Abdulwaheed J. , Magnetohydrodynamic Unsteady Natural-Convection Flow of a Newtonian Fluid in the Presence of Consistent Chemical Reaction, American Journal of Fluid Dynamics, Vol. 5 No. 1, 2015, pp. 1-16. doi: 10.5923/j.ajfd.20150501.01.
1. Introduction
The study of heat and mass transfer with a chemical reaction is very important to engineers and scientists because of its great importance in many branches of science and engineering.An unsteady two-dimensional laminar natural convection flow of a viscous, incompressible, electrically conducting, natural-convective heat and mass transfer considering the effects of variable thermo physical parameters in the presence of chemical reaction is considered. Series of temperature process in the industrial design and combustion and fire science involve thermal radiation heat transfer in combination with conduction convection and mass transfer. For example, radiative convective heat transfer flows arise in industrial furnace systems, astrophysical flows, forest fire dynamics, fire spread in buildings and so on. Considerable research has therefore appeared studying radiative convective flows in a variety of geometrical configurations with numerical and mathematical models, [1] reported on the effects of thermal radiation in the convection boundary layer-regime of an enclosure. [2] used a radiative flux diffusion approximation to model the interaction of convective and radiative heat transfer in two dimensional complex enclosures. [3] studied numerically the combined influence of radiative flux, gravity field and heat absorption on convection heat transfer in a two-phase flow.Considerable research work has been published on an impulsively started vertical plate with different boundary conditions. [4] presented analytic solution on the viscous flow past an impulsively started semi-infinite horizontal plate. [5] first presented an exact solution to the Navier-Stokes equation of the flow of a viscous incompressible fluid past an impulsively started infinite horizontal plate moving in its own plane. It is often called Rayleigh's problem in the literature. [6] solved the problem of [4] by finite difference method of a mixed explicit-implicit type which is convergent and stable. [7] obtained the exact solution of the Stokes problem for the case of an infinite vertical plate. For the first time, [8] studied the natural convection on flow past an impulsively started vertical plate with variable surface heat flux.Distribution of temperature in the fabric layers were known to be greatly affected by moisture content and thermal radiation flux. Generally, for low velocity hydromechanics of porous media, a Darcian model is used which relates the bulk matrix impedance in the regime to the pressure drop. This approach is generally accurate for situations where Reynolds number is less than approximately 10. Beyond this value, inertial effects become significant and must be incorporated in mathematical models. [9] studied the influence of solar radiation on free convection in an isotropic, homogeneous porous medium using a computational method. [10] employed a regular two-parameter perturbation analysis in studying radiative flux effects on free convection in a non-Darcian porous medium. They studied four different flow regimes i.e that adjacent to the isothermal surface, flow with a uniform heat flux, plane plume flow and also the flow generated from a horizontal line energy source on a vertical adiabatic surface. Radiation was found to significantly affect all flow cases. [11] used the implicit difference scheme and the Cogley-Vincenti-Giles non-gray model to simulate the radiation-convection gas flow in a non-Darcy porous medium with viscous heating effects. In all the investigations mentioned above, effects of variable thermo physical parameters in the presence of chemical reaction on an impulsively-started transient radiation-convection heat and mass transfer has not been given great attention. Effects of viscous dissipation are important in geophysical flow and also in certain industrial operations and are usually characterized by the Eckert number. A number of authors have considered viscous heating effects on Newtonian flows. [12] reported on the influence of viscous heating dissipation effects in natural convective flows, showing that the heat transfer rates are reduced by an increase in the dissipation parameter. Also, effects of magnetic field on viscous incompressible fluid of electrically conducting is of importance in many applications such as extrusion of plastics in the manufacture of Rayon and Nylon, purification of crude oil, textile industries and so on. [13] analyzed the problem of free convection effects on stokes problem for a vertical plate under the action of transversely applied magnetic field. [14] obtained an exact solution for unsteady MHD free convection flow on an impulsively started vertical plate with constant heat flux. Other studies discussing the effects of radiation on convection flows in porous media have been communicated by [15] who considered transient flow.The transformed problem is shown to be dictated by the following thermo physical parameters: dimensionless time, thermal Grashof number, species Grashof number, Darcy number, Reynolds number, Magnetic field, Eckert number, Prandtl number, chemical reaction parameter Darcy and Schmidt number. The influence of these parameters on the velocity profile, temperature function and concentration profiles are discussed graphically.
2. Formulation of Mathematical Problem
An unsteady two-dimensional laminar natural convection flow of a viscous, incompressible, electrically conducting, radiating fluid past an impulsively started semi-infinite vertical plate in the presence of chemical reaction is considered.We assume that the fluid is grey, absorbing-emitting but non-scattering. The 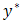 -axis is taken perpendicular to the plate at the leading edge while the
-axis is taken perpendicular to the plate at the leading edge while the 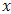 -axis is chosen along the plate in the vertical upward direction.The origin of
-axis is chosen along the plate in the vertical upward direction.The origin of 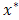 -axis is taken to be at the leading edge of the plate. The gravitational acceleration g is acting downward. At time
-axis is taken to be at the leading edge of the plate. The gravitational acceleration g is acting downward. At time 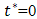 , it is assumed that the plate and the fluid are at the same ambient temperature
, it is assumed that the plate and the fluid are at the same ambient temperature 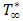 and the species concentration
and the species concentration 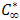 . When
. When 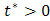 , the temperature of the plate and the species concentration is maintained to be
, the temperature of the plate and the species concentration is maintained to be 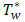 (greater than
(greater than 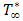 ) and
) and 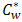 (greater than
(greater than 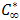 ) respectively.Effect of viscous dissipation is considered in the binary mixture and assumed to be very small compared with other chemical species, which are present. A uniformly transverse magnetic field is applied in the direction of flow. It is further assumed that the interaction of the induced magnetic with the flow is considered to be negligible compared to the interaction of the applied magnetic field with the flow. The fluid properties are assumed to be constant except for the body forces terms in the momentum equation which are approximated by Boussinesq relations.Thermal radiation is assumed to be present in the form of a unidirectional flux in the
) respectively.Effect of viscous dissipation is considered in the binary mixture and assumed to be very small compared with other chemical species, which are present. A uniformly transverse magnetic field is applied in the direction of flow. It is further assumed that the interaction of the induced magnetic with the flow is considered to be negligible compared to the interaction of the applied magnetic field with the flow. The fluid properties are assumed to be constant except for the body forces terms in the momentum equation which are approximated by Boussinesq relations.Thermal radiation is assumed to be present in the form of a unidirectional flux in the 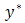 direction i.e
direction i.e 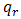 (transverse to the vertical surface).The Roseland diffusion flux is used and defined following [16] as follows:
(transverse to the vertical surface).The Roseland diffusion flux is used and defined following [16] as follows: 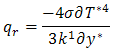 Where
Where 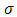 is the Stefan-Boltzmann constant and
is the Stefan-Boltzmann constant and 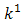 is the mean absorption coefficient. It should be noted that by using the Rosseland approximation, the present analysis is limited to optically thick fluid.Under the Boussinesq approximation, the flow model is governed by these set of equations:
is the mean absorption coefficient. It should be noted that by using the Rosseland approximation, the present analysis is limited to optically thick fluid.Under the Boussinesq approximation, the flow model is governed by these set of equations: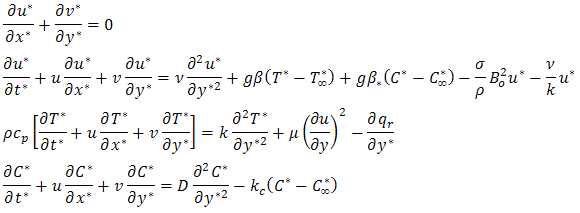 With the following boundary conditions
With the following boundary conditions 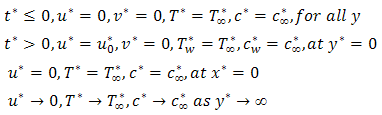 Where
Where 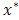 and
and 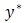 are coordinates,
are coordinates, 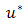 and
and 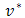 are velocity components in the
are velocity components in the 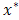 and
and 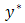 directions,
directions, 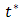 is the dimensionless time,
is the dimensionless time, 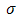 is the Stefan-Boltzmann constant,
is the Stefan-Boltzmann constant, 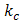 is the rate of chemical reaction, g is the gravitational acceleration,
is the rate of chemical reaction, g is the gravitational acceleration, 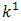 is the mean absorption coefficient of thermal expansion,
is the mean absorption coefficient of thermal expansion, 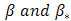 represent the thermal and mass transfer coefficient of expansion,
represent the thermal and mass transfer coefficient of expansion, 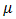 is the coefficient of dynamic viscosity of the grey fluid,
is the coefficient of dynamic viscosity of the grey fluid, 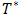 is the temperature of the fluid in the boundary layer,
is the temperature of the fluid in the boundary layer, 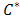 is the species concentration, k is the permeability (hydraulic conductivity of the porous medium with dimensions), D is the species diffusivity,
is the species concentration, k is the permeability (hydraulic conductivity of the porous medium with dimensions), D is the species diffusivity, 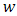 denotes condition at the wall, (vertical surface) and
denotes condition at the wall, (vertical surface) and 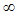 denotes condition in the free stream(outside the boundary layer).Following Raptis and Perdikis [22], we express the quartic temperature function in a linear function of temperature if the temperature differences within the flow are sufficiently small. The Taylor series for
denotes condition in the free stream(outside the boundary layer).Following Raptis and Perdikis [22], we express the quartic temperature function in a linear function of temperature if the temperature differences within the flow are sufficiently small. The Taylor series for 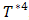 , discarding higher order terms can be shown as:
, discarding higher order terms can be shown as: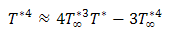 Substituting the above equation into the energy equation, we arrive at this equation:
Substituting the above equation into the energy equation, we arrive at this equation: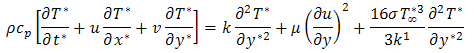 The four equations with their boundary conditions constitutes a two-point boundary value problem which is fairly challenging to solve. We therefore non-dimensionalise the model to facilitate a numerical solution by the Crank Nicolson's method. On introducing the following non dimensional quantities:
The four equations with their boundary conditions constitutes a two-point boundary value problem which is fairly challenging to solve. We therefore non-dimensionalise the model to facilitate a numerical solution by the Crank Nicolson's method. On introducing the following non dimensional quantities: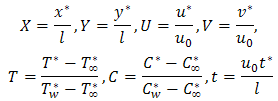 Where
Where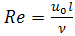 is the Reynolds number,
is the Reynolds number, 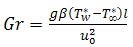 is the Grashof number,
is the Grashof number, 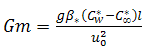 is the modified Grashof number,
is the modified Grashof number, 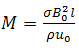 is the magnetic field,
is the magnetic field, 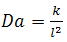 is the Darcy number,
is the Darcy number, 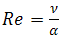 is the Prandtl number,
is the Prandtl number, 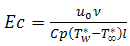 is the Eckert number,
is the Eckert number, 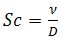 is the Schmidt number and
is the Schmidt number and 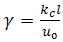 is the chemical reaction parameter.Substituting the above non-dimensional quantities and parameters into the equations yield the following dimensionless equations:
is the chemical reaction parameter.Substituting the above non-dimensional quantities and parameters into the equations yield the following dimensionless equations: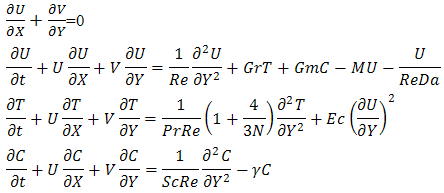 We define the dimensionless initial and boundary condition in the form:
We define the dimensionless initial and boundary condition in the form: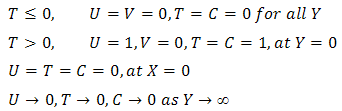
3. Numerical Solution and Discussion of Result
To be able to solve the set of unsteady non-linear partial differential equations together with the boundary conditions, we employ an implicit finite difference scheme by Crank-Nicolson which is known to converge faster due to its unconditional stability. The corresponding finite difference equations are given below: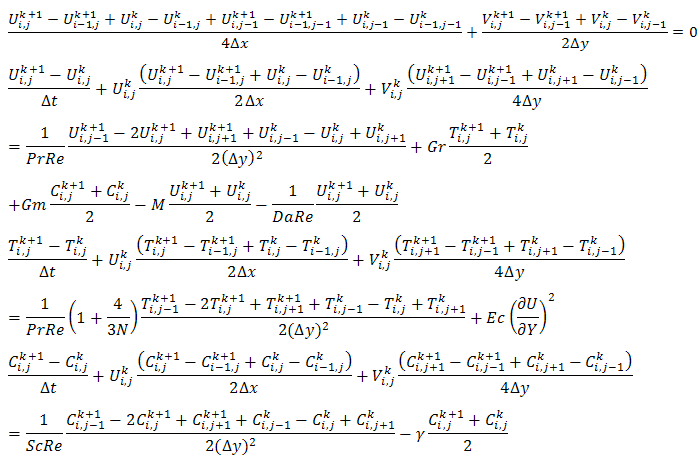 In the discretization of the equations, we define the co-ordinate of the mesh points of the solution by
In the discretization of the equations, we define the co-ordinate of the mesh points of the solution by 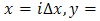
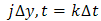 where i,j,k are positive integers and the value of U at the mesh point is given as
where i,j,k are positive integers and the value of U at the mesh point is given as 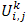 .The region of integration is considered to be a rectangle with sides X (MAX)=1 and Y (MAX)=1 whereby regarding Y(MAX) as Y=
.The region of integration is considered to be a rectangle with sides X (MAX)=1 and Y (MAX)=1 whereby regarding Y(MAX) as Y=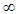 which lie very well outside the momentum, thermal and concentration boundary layers. The subscript I, j, k relates to grid points along x, y, t directions respectively. We therefore divide X and Y into M and N grid spacing respectively. The mesh sizes are
which lie very well outside the momentum, thermal and concentration boundary layers. The subscript I, j, k relates to grid points along x, y, t directions respectively. We therefore divide X and Y into M and N grid spacing respectively. The mesh sizes are 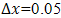 ,
, 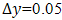 and
and 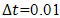 .The coefficients
.The coefficients 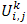 and
and 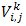 appearing in the difference equation are treated as constants in any one time step. The values of C, T, U and V are known at all grid point at t=0 from the initial conditions. The values of C, T, U and V at time level (k+1) are calculated using the known values at previous time level k.In view of this, the finite difference equation forms a tridiagonal system of equations at every internal nodal point on a particular i level which is solved with the aid of Matlab package using Thomas Algorithm as discussed in [17].We therefore calculate the values of C and T at every nodal point for a particular i at (k+1)th time level and the results were used in U at (k+1)th time level. The values of V are also calculated at every nodal point explicitly using equation (79) on a particular i level at (k+1)th time level. Following this step, we were able to determine the values of C, T, U, and V at all grid point at time level (k+1)th in the region. The process is repeated several times for various i we reach the required time. The local truncation error is
appearing in the difference equation are treated as constants in any one time step. The values of C, T, U and V are known at all grid point at t=0 from the initial conditions. The values of C, T, U and V at time level (k+1) are calculated using the known values at previous time level k.In view of this, the finite difference equation forms a tridiagonal system of equations at every internal nodal point on a particular i level which is solved with the aid of Matlab package using Thomas Algorithm as discussed in [17].We therefore calculate the values of C and T at every nodal point for a particular i at (k+1)th time level and the results were used in U at (k+1)th time level. The values of V are also calculated at every nodal point explicitly using equation (79) on a particular i level at (k+1)th time level. Following this step, we were able to determine the values of C, T, U, and V at all grid point at time level (k+1)th in the region. The process is repeated several times for various i we reach the required time. The local truncation error is 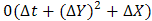 and it tends to zero as
and it tends to zero as 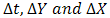 tends to zero, which indicates that the system is compatible. The compatibility and stability of Crank Nicolson scheme which is unconditionally stable ensures the convergence of the system.To be able to report on the analysis of the fluid flow, the numerical computations are carried out for various values Prandtl number (Pr), Darcy number (Da), Reynolds number (Re), Schmidt number (Sc), Magnetic field (M), conduction-radiation (n), Grashof number (Gr), modified Grashof number (Gm), Eckert number (Ec) and the chemical reaction parameter
tends to zero, which indicates that the system is compatible. The compatibility and stability of Crank Nicolson scheme which is unconditionally stable ensures the convergence of the system.To be able to report on the analysis of the fluid flow, the numerical computations are carried out for various values Prandtl number (Pr), Darcy number (Da), Reynolds number (Re), Schmidt number (Sc), Magnetic field (M), conduction-radiation (n), Grashof number (Gr), modified Grashof number (Gm), Eckert number (Ec) and the chemical reaction parameter 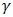 . We present the contribution of each parameter by varying parameter and keeping the others fixed. The fixed values are:Pr=0.1, Sc=0.5, N=3.0, M=10, Ec=0.001, Gr=10, Gm=10, Da=0.1, Re=1, gamma=1, t=1.0 Figure 1, 2 and 3 shows the effects of magnetic field M on the dimensionless velocity, temperature and concentration profiles respectively. Increase in the magnetic field causes reduction in the velocity profile. The application of magnetic field on electrically conducting fluid results to a resistive type of force called Lorentz force which has tendency to slow down the motion of a fluid and increase its temperature.
. We present the contribution of each parameter by varying parameter and keeping the others fixed. The fixed values are:Pr=0.1, Sc=0.5, N=3.0, M=10, Ec=0.001, Gr=10, Gm=10, Da=0.1, Re=1, gamma=1, t=1.0 Figure 1, 2 and 3 shows the effects of magnetic field M on the dimensionless velocity, temperature and concentration profiles respectively. Increase in the magnetic field causes reduction in the velocity profile. The application of magnetic field on electrically conducting fluid results to a resistive type of force called Lorentz force which has tendency to slow down the motion of a fluid and increase its temperature.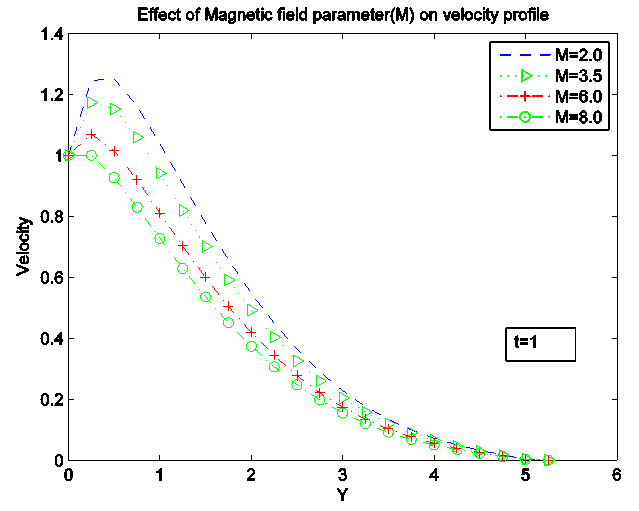 | Figure 1. Effect of Magnetic field (M) on velocity profile |
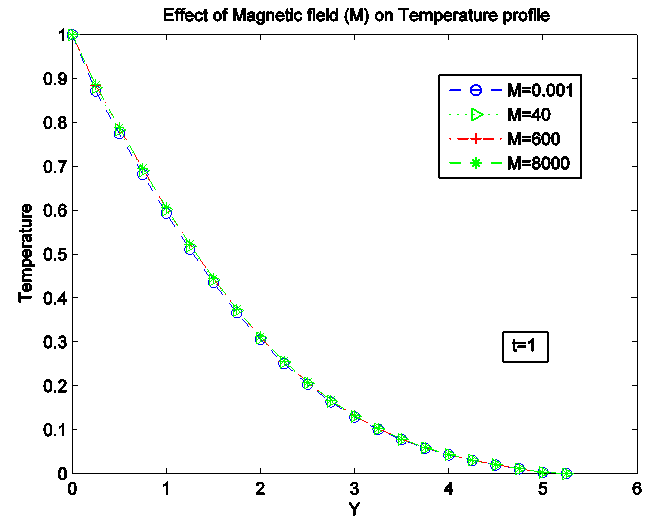 | Figure 2. Effect of Magnetic Field (M) on Temperature Profile |
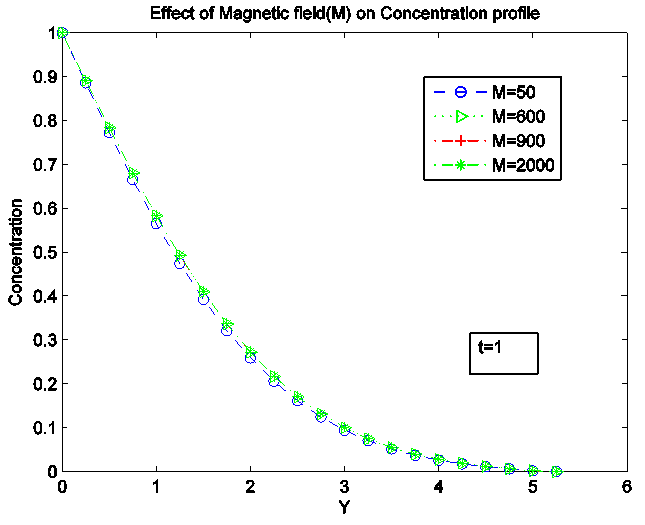 | Figure 3. Effect of Magnetic Field (M) on Concentration Profile |
Temperature increases with the increasing value of magnetic field parameter M for both the temperature and species concentration but the increase is so small that it can hardly been seen from the graphs.Figure 4, 5 and 6 shows the effect of Conduction-radiation on the velocity, temperature and concentration profile respectively. An increase in N corresponds to an increase in the relative contribution of conduction heat transfer to thermal radiation heat transfer. As N tends to infinity, conduction heat transfer dominates and the contribution of thermal radiative flux disappears. Small value of N corresponds to stronger thermal radiation flux and the maximum temperatures are observed for N=0.1. As N increases, considerable reduction is seen in the temperature values from the highest value N=4.0 at the wall across the boundary layer to the free stream at which temperature values are negligible for any value of N. All profiles decay to zero in the free stream.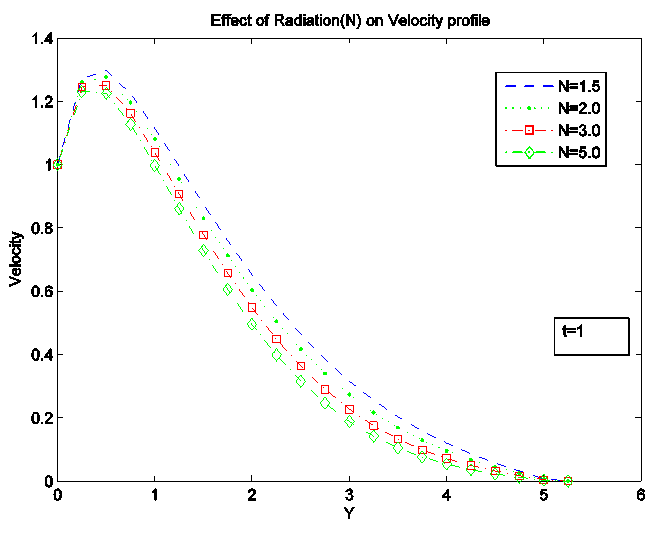 | Figure 4. Effect of Conduction-Radiation parameter (N) on velocity Profile |
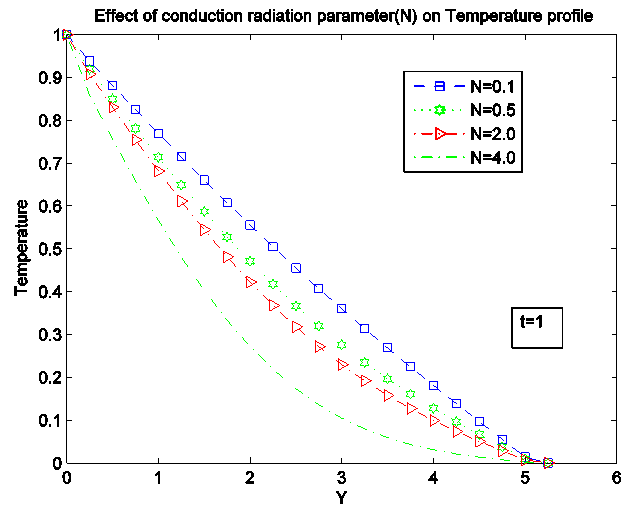 | Figure 5. Effect of Conduction-Radiation parameter (N) on Temperature Profile |
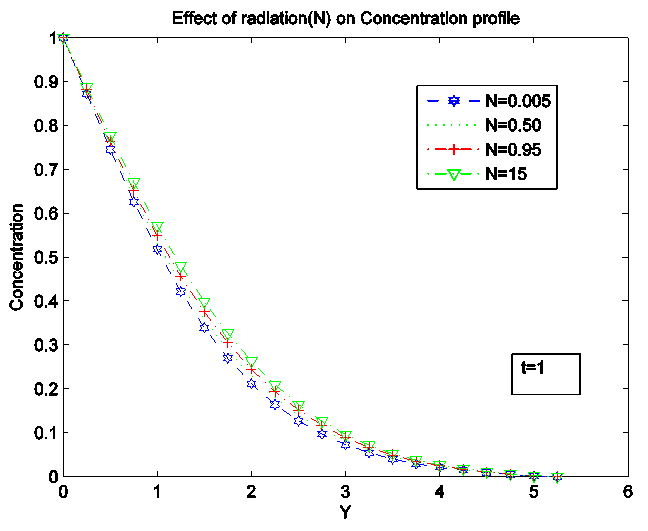 | Figure 6. Effect of Conduction-Radiation parameter (N) on Concentration Profile |
For the concentration profile, increase in Conduction-radiation parameter increases the profile.Figure 7, 8 and 9 presented the influence of Schmidt number (Sc) on the velocity, temperature and concentration profiles. We discovered that the velocity and concentration decreases with increase in Sc. Temperature profile increases greatly with an increase in Sc. The dimensionless concentration profile in turns decay from a maximum concentration of 1 at y=0 to zero at  . With higher values of Sc, fluid experiences lower diffusion properties and the concentration boundary layer becomes thinner than the velocity boundary layer thickness. A rise in Sc causes a decrease in Temperature.
. With higher values of Sc, fluid experiences lower diffusion properties and the concentration boundary layer becomes thinner than the velocity boundary layer thickness. A rise in Sc causes a decrease in Temperature. 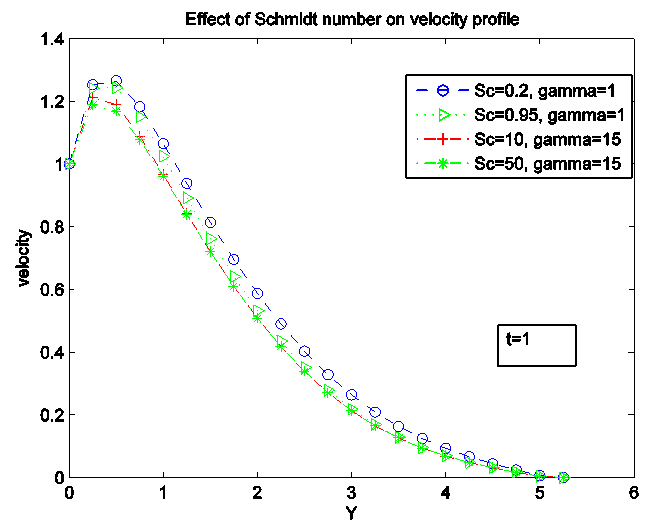 | Figure 7. Effect of Schmidt number (Sc) on velocity Profile |
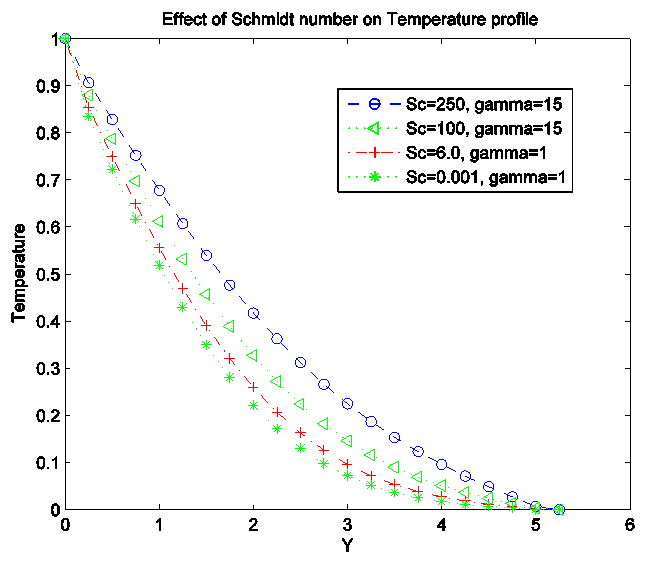 | Figure 8. Effect of Schmidt number (Sc) on Temperature Profile |
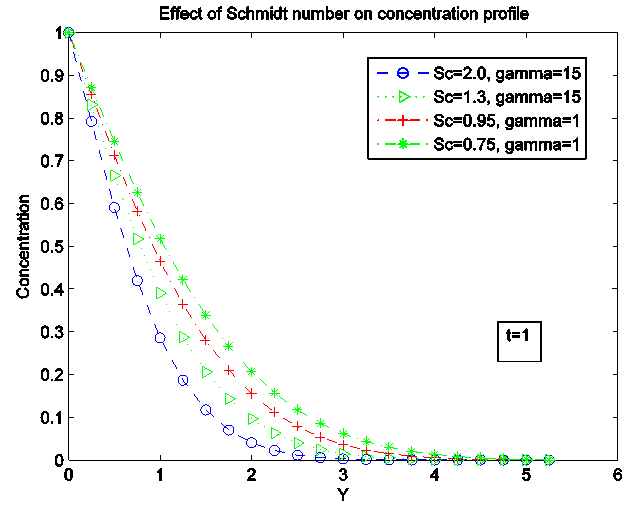 | Figure 9. Effect of Schmidt number (Sc) on Concentration Profile |
Figure 10 and 11 gives the effect of Prandtl number (Pr) for velocity and temperature profile.Prandtl number characterizes the ratio of thickness of the viscous and thermal boundary layers, therefore, from the graph, increase in Prandtl number causes the velocity and temperature profile to decrease.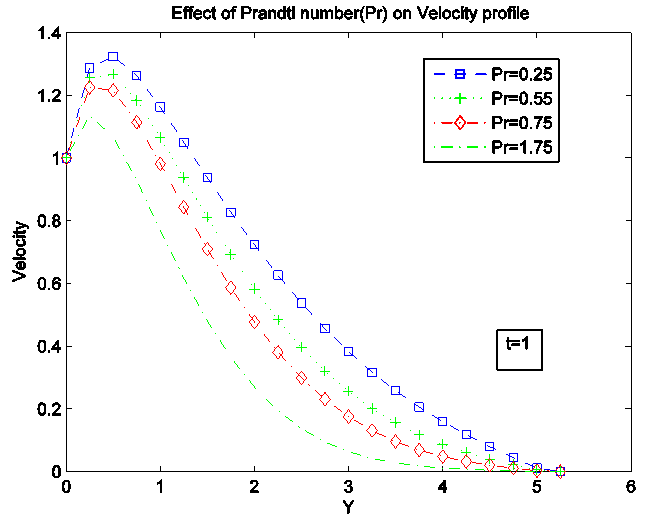 | Figure 10. Effect of Prandtl number (Pr) on velocity Profile |
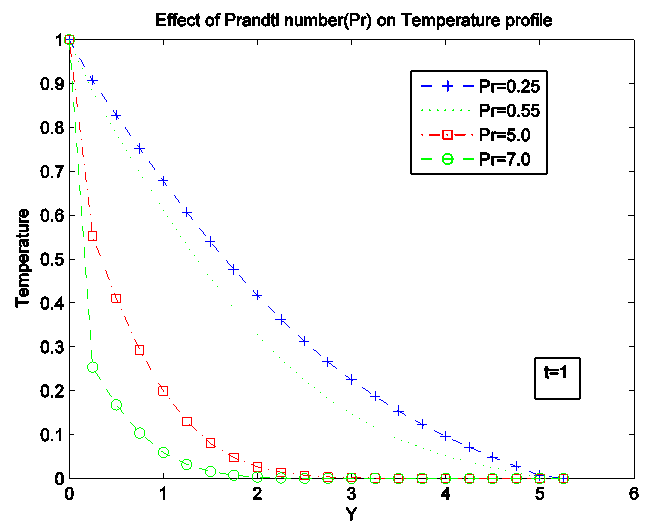 | Figure 11. Effect of Prandtl number (Pr) on Temperature Profile |
Figure 12, 13 and 14 present the influence of Grashof number on velocity, temperature and concentration profile. Increase in Gr leads to increase in velocity profile; decrease in temperature and concentration profiles respectively since increasing buoyancy body force has an inhibiting effect on the value of contaminant concentration within the boundary layer regime normal to the barrier. 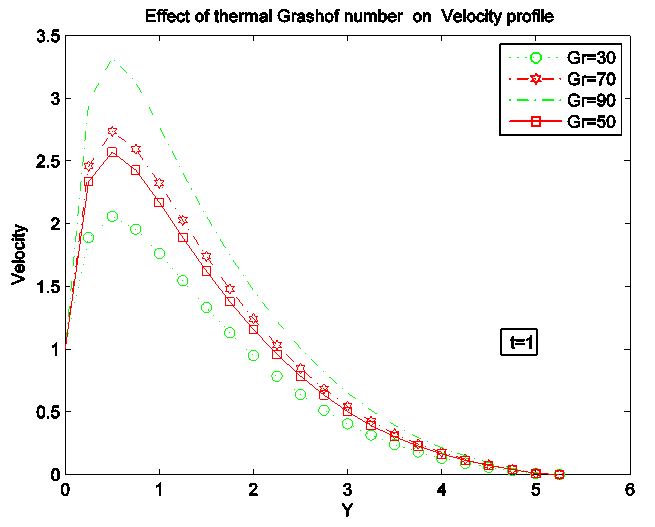 | Figure 12. Effect of Grashof number (Gr) on velocity Profile |
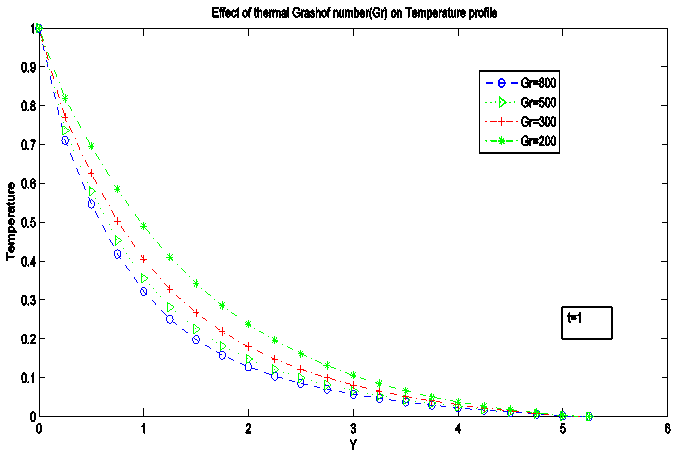 | Figure 13. Effect of Grashof number (Gr) on Temperature Profile |
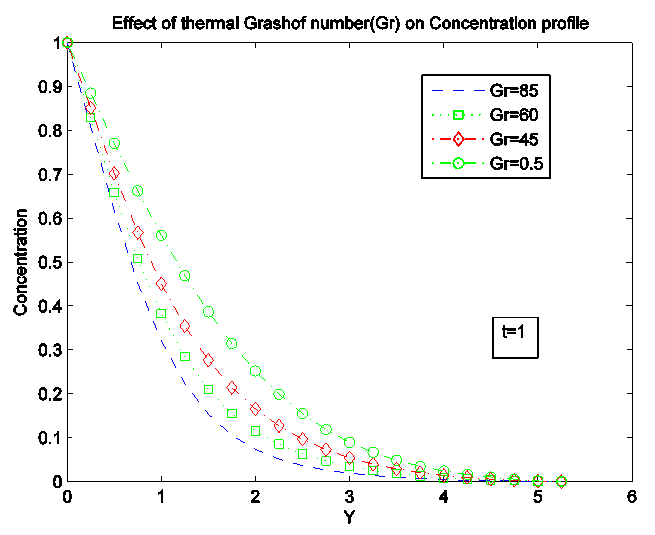 | Figure 14. Effect of Grashof number (Gr) on Concentration Profile |
Figure 15 and 16 show the effect of Eckert number on velocity and temperature profile.As shown on the graph, considering the values used, increase in Eckert number causes the velocity and temperature profile to reduce without any change in the momentum and boundary layer thickness.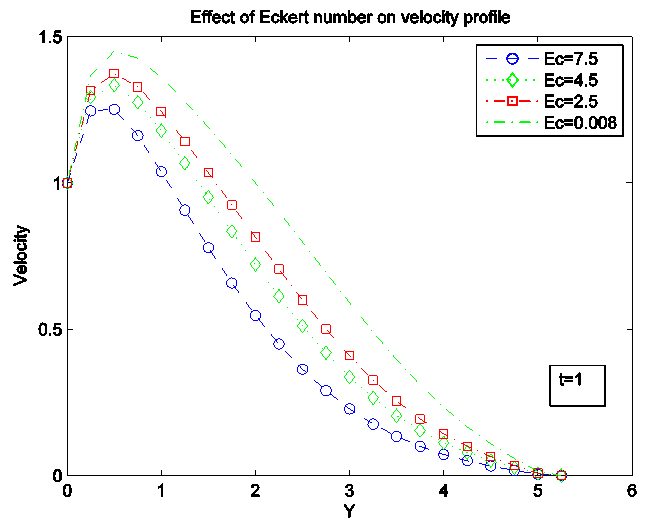 | Figure 15. Effect of Eckert number (Ec) on velocity Profile |
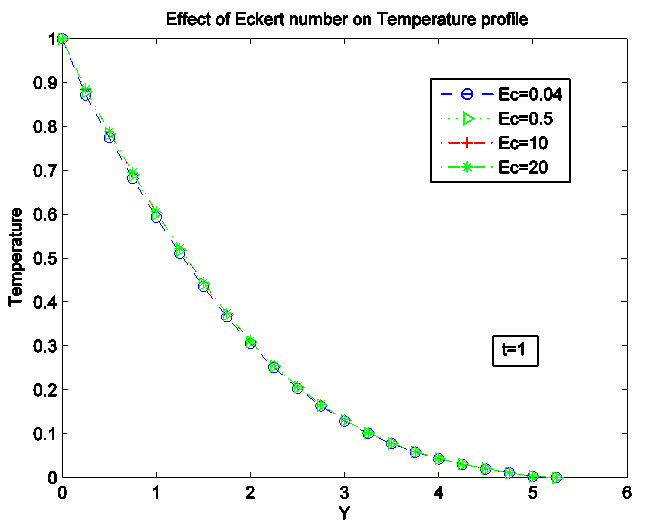 | Figure 16. Effect of Eckert number (Ec) on Temperature Profile |
Figure 17 shows the influence of Darcy (Da) number on Temperature profile. Increase in Darcy number results to a rise in temperature profile. The effect of this rise implies that conduction heat transfer becomes less prominent than convection heat transfer and this contributes to the marginal decrease in temperature across the boundary layer from the wall to the free stream.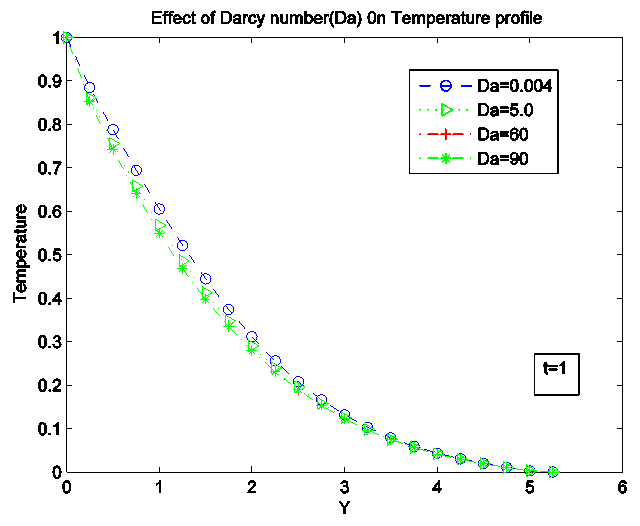 | Figure 17. Effect of Darcy number (Da) on Temperature Profile |
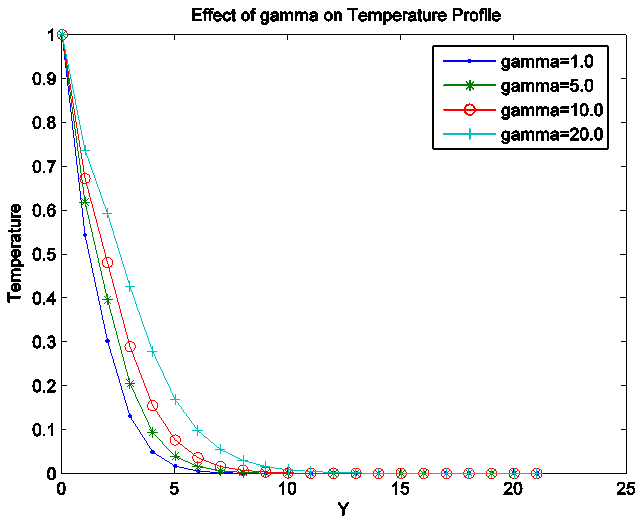
Figure 18, 19 and 20 display the velocity, temperature and concentration profile for various values of chemical reaction parameter (gamma). Increase in the chemical reaction parameter reduces the concentration profile which in turns causes the concentration buoyancy effects to decrease as gamma decreases. Increasing chemical reaction parameter causes increase in temperature profile and the velocity profile.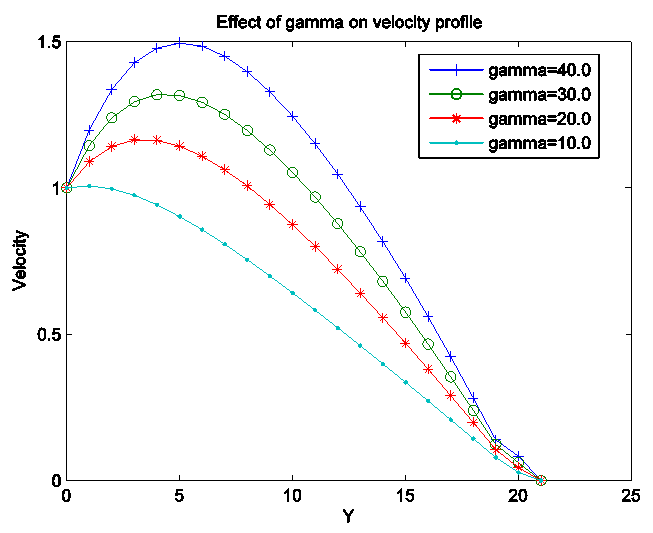 | Figure 18. Effect of chemical reaction parameter (gamma 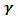 ) on velocity profile ) on velocity profile |
 | Figure 19. Effect of chemical reaction parameter (gamma 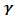 ) on Temperature profile ) on Temperature profile |
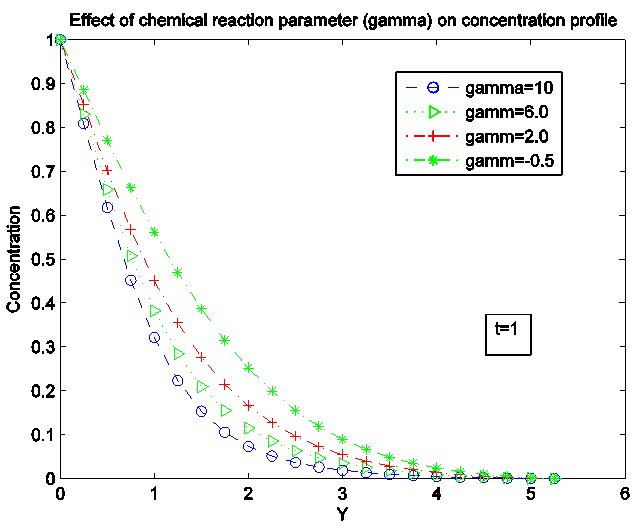 | Figure 20. Effect of chemical reaction parameter (gamma 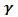 ) on Concentration profile ) on Concentration profile |
4. Conclusions
We investigate the effects of variable thermo physical parameters on the natural convective heat and mass transfer of a viscous incompressible, gray absorbing-emitting fluid flowing past an impulsively started moving vertical plate under the action of transversely applied magnetic field in the presence of chemical reaction. The governing boundary-layer equations are formulated with appropriate boundary conditions. The usual Roseland diffusion approximation was used to analyze the radiative heat flux and it is appropriate for non-Scattering media. The governing boundary layer equations were simplified and non-dimensionalized. The dimensionless equations were discretized and then solved using the Crank-Nicolsons method. The effects of variable thermo physical parameters which are: Magnetic field (M), Prandtlnumber(Pr), radiation-conduction parameter(N), thermal Grashof number(Gr), Schmidt number(Sc), chemical reaction parameter(gamma), Eckert number(Ec), Darcy number(Da) are considered on the dimensionless velocity, temperature and species profile. Computations on the variation of local skin friction, Nusselt number and Sherwood number are also recorded. From the graphs plotted, we discover that: Velocity profile decreases with increase in Magnetic field, conduction radiation parameter, Schmidt number, prandtl number, Eckert number and chemical reaction parameter while it decreases with increase in Grashof number.Temperature profile increases with increase in Magnetic field, Schmidt number, Eckert number and chemical reaction parameter while it decreases with increase in conduction radiation parameter, prandtl number, Eckert number, Grashof number and Darcy number.Concentration profile increases with increase in Magnetic field and Conduction Radiation parameter while it decreases with increase in Schmidt number, Grashof number and chemical reaction parameter.
References
| [1] | J.C. Bratis, J.R. Novotny, Radiation-convection interaction in the boundary layer regime of an enclosure, International journal of heat and mass transfer. 17 (1994) 365-379. |
| [2] | C. Chang, K.T. Kang, Radiation-natural convection interaction in two dimensional complex enclosure, ASME, Journal of heat transfer, 105 (1983) 89-95. |
| [3] | A.J. Chamkha, Effect of heat absorption and thermal radiation on heat transfer in a fluid-particle flow past a surface in the presence of a gravity field, Int. journal of thermal sciences, 39 (2000) 605-615. |
| [4] | K. Stewartson, On the impulsive motion of a flat plate in a viscous fluid, quarterly Journal of mechanics and applied mathematics iv 2 (1951) 182-198. |
| [5] | G.G. Stokes, On the effect of internal friction of fluids on the motion of pendulums, camb. phil. Trans. 2 (1951) 8-106. |
| [6] | M.G. Hall, The boundary layer over an impulsively started flat plate, proc. Ray, soc, A, 310, 1502 (1969) 401-414. |
| [7] | V.M. Soundalgekar, P. Ganesan, Finite difference analysis of transient free convection with mass transfer on an isothermal vertical plate, Int. journal of Engineering science, 19 (1981) 757-770. |
| [8] | R. Muthueumaraswamy, Natural convection of flow past an impulsively started vertical plate with variable surface heat flux, far east Journal of Applied mathematics, 14 1 (2004) 99-109. |
| [9] | A.J. Chamkha, Solar radiation assisted natural convection in a uniform porous medium supported by a vertical flat plate, ASME, Journal of Heat transfer, 119 (1997) 89-96. |
| [10] | A.A. Mohammadein, M.A. Mansour, Radiative effects on natural convection flows in a porous media, Transport porous media, 32(3) (1998) 263-283. |
| [11] | H.S. Tarkar, M. Kumari, Computational analysis of coupled radiation-convection dissipative non-grey gas flow in a non-Darcy porous medium using the keller-Box implicit scheme, Int. journal of Energy Research, 22 (1998) 141-159. |
| [12] | R.L. Mahajan, B.B. Gebhart, Viscous dissipation effects in bouyancy-induced flows, Int. journal of heat and mass transfer, 7 (1989) 1380-1382. |
| [13] | V.M. Soundalgekar, Free convection effects on the stokes problem of infinite vertical plate, ASME, Journal of heat transfer, 99c (1977) 499-50. |
| [14] | N.C. Sacheti, P. Chandran, An exact solution for unsteady MHD free convection flow with constant heat flux, Int.commun.heat and mass transfer, (1986) 1465-1478. |
| [15] | A. Rapits, C. Perdikis, Unsteady flow through a highly porous medium in the presence of radiation, Transport porous media, J.57(2) (2004) 171-179. |
| [16] | M.F. Modest, Radiation heat transfer, MacGraw-Hill, New York, 1993. |
| [17] | B. Carnahan, H.A. Luther, J.O. Willkes, Applied Numerical method, John Wiley and Sons, New York, USA, 1969. |
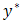 -axis is taken perpendicular to the plate at the leading edge while the
-axis is taken perpendicular to the plate at the leading edge while the 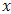 -axis is chosen along the plate in the vertical upward direction.The origin of
-axis is chosen along the plate in the vertical upward direction.The origin of 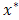 -axis is taken to be at the leading edge of the plate. The gravitational acceleration g is acting downward. At time
-axis is taken to be at the leading edge of the plate. The gravitational acceleration g is acting downward. At time 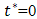 , it is assumed that the plate and the fluid are at the same ambient temperature
, it is assumed that the plate and the fluid are at the same ambient temperature 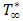 and the species concentration
and the species concentration 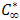 . When
. When 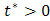 , the temperature of the plate and the species concentration is maintained to be
, the temperature of the plate and the species concentration is maintained to be 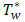 (greater than
(greater than 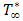 ) and
) and 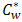 (greater than
(greater than 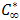 ) respectively.Effect of viscous dissipation is considered in the binary mixture and assumed to be very small compared with other chemical species, which are present. A uniformly transverse magnetic field is applied in the direction of flow. It is further assumed that the interaction of the induced magnetic with the flow is considered to be negligible compared to the interaction of the applied magnetic field with the flow. The fluid properties are assumed to be constant except for the body forces terms in the momentum equation which are approximated by Boussinesq relations.Thermal radiation is assumed to be present in the form of a unidirectional flux in the
) respectively.Effect of viscous dissipation is considered in the binary mixture and assumed to be very small compared with other chemical species, which are present. A uniformly transverse magnetic field is applied in the direction of flow. It is further assumed that the interaction of the induced magnetic with the flow is considered to be negligible compared to the interaction of the applied magnetic field with the flow. The fluid properties are assumed to be constant except for the body forces terms in the momentum equation which are approximated by Boussinesq relations.Thermal radiation is assumed to be present in the form of a unidirectional flux in the 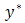 direction i.e
direction i.e 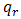 (transverse to the vertical surface).The Roseland diffusion flux is used and defined following [16] as follows:
(transverse to the vertical surface).The Roseland diffusion flux is used and defined following [16] as follows: 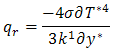 Where
Where 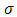 is the Stefan-Boltzmann constant and
is the Stefan-Boltzmann constant and 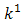 is the mean absorption coefficient. It should be noted that by using the Rosseland approximation, the present analysis is limited to optically thick fluid.Under the Boussinesq approximation, the flow model is governed by these set of equations:
is the mean absorption coefficient. It should be noted that by using the Rosseland approximation, the present analysis is limited to optically thick fluid.Under the Boussinesq approximation, the flow model is governed by these set of equations: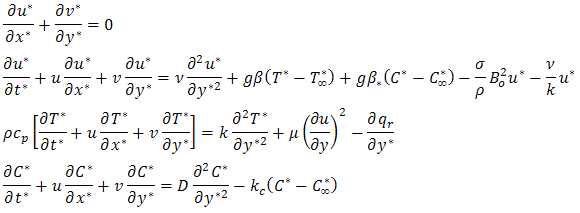 With the following boundary conditions
With the following boundary conditions 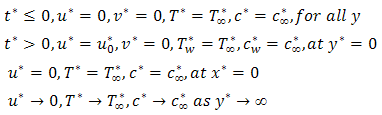 Where
Where  and
and  are coordinates,
are coordinates, 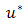 and
and 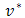 are velocity components in the
are velocity components in the 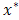 and
and 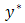 directions,
directions, 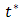 is the dimensionless time,
is the dimensionless time, 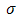 is the Stefan-Boltzmann constant,
is the Stefan-Boltzmann constant, 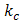 is the rate of chemical reaction, g is the gravitational acceleration,
is the rate of chemical reaction, g is the gravitational acceleration, 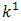 is the mean absorption coefficient of thermal expansion,
is the mean absorption coefficient of thermal expansion, 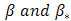 represent the thermal and mass transfer coefficient of expansion,
represent the thermal and mass transfer coefficient of expansion, 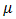 is the coefficient of dynamic viscosity of the grey fluid,
is the coefficient of dynamic viscosity of the grey fluid, 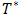 is the temperature of the fluid in the boundary layer,
is the temperature of the fluid in the boundary layer, 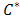 is the species concentration, k is the permeability (hydraulic conductivity of the porous medium with dimensions), D is the species diffusivity,
is the species concentration, k is the permeability (hydraulic conductivity of the porous medium with dimensions), D is the species diffusivity, 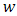 denotes condition at the wall, (vertical surface) and
denotes condition at the wall, (vertical surface) and 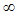 denotes condition in the free stream(outside the boundary layer).Following Raptis and Perdikis [22], we express the quartic temperature function in a linear function of temperature if the temperature differences within the flow are sufficiently small. The Taylor series for
denotes condition in the free stream(outside the boundary layer).Following Raptis and Perdikis [22], we express the quartic temperature function in a linear function of temperature if the temperature differences within the flow are sufficiently small. The Taylor series for 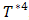 , discarding higher order terms can be shown as:
, discarding higher order terms can be shown as: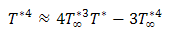 Substituting the above equation into the energy equation, we arrive at this equation:
Substituting the above equation into the energy equation, we arrive at this equation: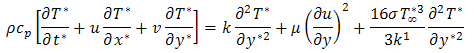 The four equations with their boundary conditions constitutes a two-point boundary value problem which is fairly challenging to solve. We therefore non-dimensionalise the model to facilitate a numerical solution by the Crank Nicolson's method. On introducing the following non dimensional quantities:
The four equations with their boundary conditions constitutes a two-point boundary value problem which is fairly challenging to solve. We therefore non-dimensionalise the model to facilitate a numerical solution by the Crank Nicolson's method. On introducing the following non dimensional quantities: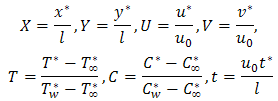 Where
Where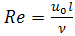 is the Reynolds number,
is the Reynolds number, 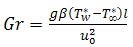 is the Grashof number,
is the Grashof number, 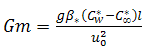 is the modified Grashof number,
is the modified Grashof number, 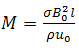 is the magnetic field,
is the magnetic field, 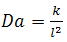 is the Darcy number,
is the Darcy number, 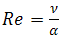 is the Prandtl number,
is the Prandtl number, 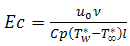 is the Eckert number,
is the Eckert number, 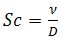 is the Schmidt number and
is the Schmidt number and 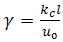 is the chemical reaction parameter.Substituting the above non-dimensional quantities and parameters into the equations yield the following dimensionless equations:
is the chemical reaction parameter.Substituting the above non-dimensional quantities and parameters into the equations yield the following dimensionless equations: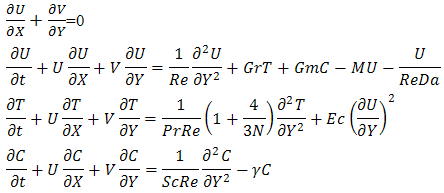 We define the dimensionless initial and boundary condition in the form:
We define the dimensionless initial and boundary condition in the form: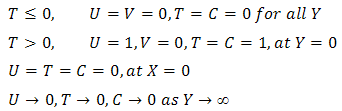
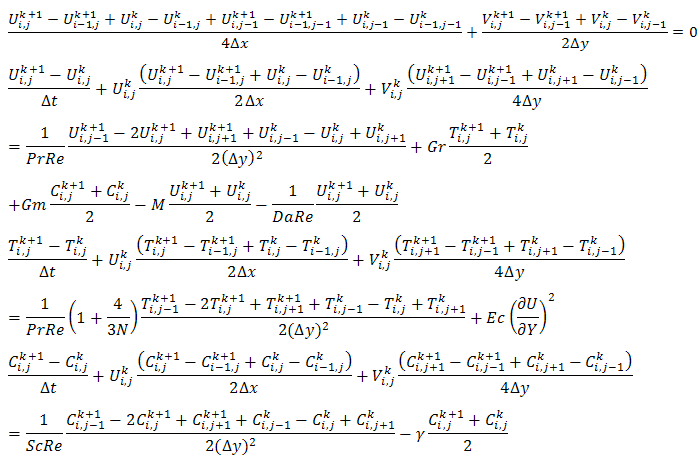 In the discretization of the equations, we define the co-ordinate of the mesh points of the solution by
In the discretization of the equations, we define the co-ordinate of the mesh points of the solution by 
 where i,j,k are positive integers and the value of U at the mesh point is given as
where i,j,k are positive integers and the value of U at the mesh point is given as 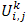 .The region of integration is considered to be a rectangle with sides X (MAX)=1 and Y (MAX)=1 whereby regarding Y(MAX) as Y=
.The region of integration is considered to be a rectangle with sides X (MAX)=1 and Y (MAX)=1 whereby regarding Y(MAX) as Y=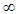 which lie very well outside the momentum, thermal and concentration boundary layers. The subscript I, j, k relates to grid points along x, y, t directions respectively. We therefore divide X and Y into M and N grid spacing respectively. The mesh sizes are
which lie very well outside the momentum, thermal and concentration boundary layers. The subscript I, j, k relates to grid points along x, y, t directions respectively. We therefore divide X and Y into M and N grid spacing respectively. The mesh sizes are 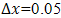 ,
, 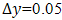 and
and 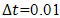 .The coefficients
.The coefficients 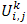 and
and 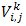 appearing in the difference equation are treated as constants in any one time step. The values of C, T, U and V are known at all grid point at t=0 from the initial conditions. The values of C, T, U and V at time level (k+1) are calculated using the known values at previous time level k.In view of this, the finite difference equation forms a tridiagonal system of equations at every internal nodal point on a particular i level which is solved with the aid of Matlab package using Thomas Algorithm as discussed in [17].We therefore calculate the values of C and T at every nodal point for a particular i at (k+1)th time level and the results were used in U at (k+1)th time level. The values of V are also calculated at every nodal point explicitly using equation (79) on a particular i level at (k+1)th time level. Following this step, we were able to determine the values of C, T, U, and V at all grid point at time level (k+1)th in the region. The process is repeated several times for various i we reach the required time. The local truncation error is
appearing in the difference equation are treated as constants in any one time step. The values of C, T, U and V are known at all grid point at t=0 from the initial conditions. The values of C, T, U and V at time level (k+1) are calculated using the known values at previous time level k.In view of this, the finite difference equation forms a tridiagonal system of equations at every internal nodal point on a particular i level which is solved with the aid of Matlab package using Thomas Algorithm as discussed in [17].We therefore calculate the values of C and T at every nodal point for a particular i at (k+1)th time level and the results were used in U at (k+1)th time level. The values of V are also calculated at every nodal point explicitly using equation (79) on a particular i level at (k+1)th time level. Following this step, we were able to determine the values of C, T, U, and V at all grid point at time level (k+1)th in the region. The process is repeated several times for various i we reach the required time. The local truncation error is 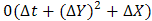 and it tends to zero as
and it tends to zero as 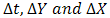 tends to zero, which indicates that the system is compatible. The compatibility and stability of Crank Nicolson scheme which is unconditionally stable ensures the convergence of the system.To be able to report on the analysis of the fluid flow, the numerical computations are carried out for various values Prandtl number (Pr), Darcy number (Da), Reynolds number (Re), Schmidt number (Sc), Magnetic field (M), conduction-radiation (n), Grashof number (Gr), modified Grashof number (Gm), Eckert number (Ec) and the chemical reaction parameter
tends to zero, which indicates that the system is compatible. The compatibility and stability of Crank Nicolson scheme which is unconditionally stable ensures the convergence of the system.To be able to report on the analysis of the fluid flow, the numerical computations are carried out for various values Prandtl number (Pr), Darcy number (Da), Reynolds number (Re), Schmidt number (Sc), Magnetic field (M), conduction-radiation (n), Grashof number (Gr), modified Grashof number (Gm), Eckert number (Ec) and the chemical reaction parameter 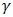 . We present the contribution of each parameter by varying parameter and keeping the others fixed. The fixed values are:Pr=0.1, Sc=0.5, N=3.0, M=10, Ec=0.001, Gr=10, Gm=10, Da=0.1, Re=1, gamma=1, t=1.0 Figure 1, 2 and 3 shows the effects of magnetic field M on the dimensionless velocity, temperature and concentration profiles respectively. Increase in the magnetic field causes reduction in the velocity profile. The application of magnetic field on electrically conducting fluid results to a resistive type of force called Lorentz force which has tendency to slow down the motion of a fluid and increase its temperature.
. We present the contribution of each parameter by varying parameter and keeping the others fixed. The fixed values are:Pr=0.1, Sc=0.5, N=3.0, M=10, Ec=0.001, Gr=10, Gm=10, Da=0.1, Re=1, gamma=1, t=1.0 Figure 1, 2 and 3 shows the effects of magnetic field M on the dimensionless velocity, temperature and concentration profiles respectively. Increase in the magnetic field causes reduction in the velocity profile. The application of magnetic field on electrically conducting fluid results to a resistive type of force called Lorentz force which has tendency to slow down the motion of a fluid and increase its temperature.





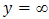 . With higher values of Sc, fluid experiences lower diffusion properties and the concentration boundary layer becomes thinner than the velocity boundary layer thickness. A rise in Sc causes a decrease in Temperature.
. With higher values of Sc, fluid experiences lower diffusion properties and the concentration boundary layer becomes thinner than the velocity boundary layer thickness. A rise in Sc causes a decrease in Temperature. 











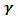 ) on velocity profile
) on velocity profile
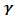 ) on Temperature profile
) on Temperature profile
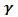 ) on Concentration profile
) on Concentration profile Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML