-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2014; 4(4): 181-193
doi:10.5923/j.ajfd.20140404.02
Modeling and Simulation of Compressible Three-Phase Flows in an Oil Reservoir: Case Study of Tsimiroro Madagascar
Malik El’Houyoun Ahamadi1, Hery Tiana Rakotondramiarana1, Rakotonindrainy2
1Institut pour la Maîtrise de l’Energie (IME), University of Antananarivo, Antananarivo, Madagascar
2Ecole Supérieure Polytechnique d'Antananarivo (ESPA), University of Antananarivo, Antananarivo, Madagascar
Correspondence to: Hery Tiana Rakotondramiarana, Institut pour la Maîtrise de l’Energie (IME), University of Antananarivo, Antananarivo, Madagascar.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Oil extraction represents an important investment and the control of a rational exploitation of a field means mastering various scientific techniques including the understanding of the dynamics of fluids in place. This paper presents a theoretical investigation of the dynamic behavior of an oil reservoir during its exploitation. More exactly, the mining process consists in introducing a miscible gas into the oil phase of the field by means of four injection wells which are placed on four corners of the reservoir while the production well is situated in the middle of this one. So, a mathematical model of multiphase multi-component flows in porous media was presented and the cell-centered finite volume method was used as discretization scheme of the considered model equations. For the simulation on Matlab, the case of the oil-field of Tsimiroro Madagascar was studied. It ensues from the analysis of the contour representation of respective saturations of oil, gas and water phases that the conservation law of pore volume is well respected. Besides, the more one moves away from the injection wells towards the production well; the lower is the pressure value. However, an increase of this model variable value was noticed during production period. Furthermore, a significant accumulated flow of oil was observed at the level of the production well, whereas the aqueous and gaseous phases are there present in weak accumulated flow. The considered model so allows the prediction of the dynamic behavior of the studied reservoir and highlights the achievement of the exploitation process aim.
Keywords: Multi-phase flows, Multi-component systems, Porous media, Black-oil, Finite volume method, Dynamic behavior
Cite this paper: Malik El’Houyoun Ahamadi, Hery Tiana Rakotondramiarana, Rakotonindrainy, Modeling and Simulation of Compressible Three-Phase Flows in an Oil Reservoir: Case Study of Tsimiroro Madagascar, American Journal of Fluid Dynamics, Vol. 4 No. 4, 2014, pp. 181-193. doi: 10.5923/j.ajfd.20140404.02.
Article Outline
1. Introduction
- The discovery of the Malagasy oil-fields is an asset in the economic development of the country. Indeed, due to the depletion of the currently exploited fields and the rarefaction of new field discovery, the Malagasy fields are going to open new economic opportunities for this fourth globally largest island. However, the control of a rational exploitation of a field means mastering various scientific techniques including the understanding of the dynamics of fluids in place. This goes to the sense where during the exploitation, fluids can enter and replace the fluids already in position, phases can appear or disappear, etc. However, the physical phenomena involved in an oil reservoir are complex. The understanding of these phenomena requires then the combination of physics, mathematics and computing [1, 2]. The “black-oil” model has been developed and used in several works for studying the dynamic behavior of fluids within oil reservoirs. Dehkordi and Manzari [3] used a multiscale finite volume method to multi-resolution coarse grid solvers for modeling a single phase incompressible flows. Mourzenko et al. [4] modeled a single phase and slightly compressible flow through a fracture porous media. The authors used a tetrahedral finite volume discretization for the rock matrix and triangular surface elements for fractures. Amir et al. [5] worked in modeling the flow of a single phase fluid in a porous medium with fractures using domain decomposition methods.Douglas [6] surveyed a two-phase incompressible flow in porous media by using finite difference method. Douglas and Roberts [7] studied a single phase miscible displacement of one compressible fluid by another in a porous medium by using finite element method. Coutinho et al. [8] studied a black-oil model in an immiscible two-phase case such that gravity effects were not taken into account. Bell et al. [9] used a Godunov scheme of the first order and the second order for discretizing a two-phase black-oil model in one dimension. Miguel de la Cruz and Monsivais [10] studied a two phase flow model in porous media but the considered fluid was immiscible and incompressible; while using finite volume method for the discretization of equations. Using finite difference methods, Trangenstein and Bell [11] developed two-phase flow model incorporating compressibility and general mass transfer between phases. Chou and Li [12] developed a two-component model for the single-phase, miscible displacement of one compressible fluid by another in a reservoir. Krogstad et al. [13] presented a three-phase black oil model. The multiscale mixed finite-element is used for the discretization of the equations. However, the model presented is related to immiscible flow and gravity is not taken into account. Geiger et al. [14] consider a three-phase black-oil model using a finite element/ finite volume scheme. In their study, they neglected the gravity forces and capillary forces. Abreu [15] presented a three-phase oil-water-gas model. However, this model does not take into account the compressibility of the flows and miscibility of component in phase. Lee et al. [16] has carried out the modeling of a three phase compressible flow in porous media. The authors used a multiscale finite volume scheme for the discretization of the equations of the model. However, the developed model was related to immiscible components. Hajibeygi and Jenny [17] applied a multiscale finite volume framework to model a mutilphase flow in porous media. Two models are considered in their works: the first model considers an incompressible flow and the second model considers a compressible multiphase flow. Nevertheless, in this work the miscibility is not taken into account. Lunati and Jenny [18] presented a model for compressible multiphase flow, wherein the multiscale finite volume method has been applied for the discretization of equations. However, their model is not related to a multicomponent system and the effect of gravity is not taken into account. Liu [19] considered two dimensional compressible miscible displacement flows in porous media. A finite difference scheme on grids with local refinement in time is constructed. The construction was done by use of a modified upwind approximation and a linear interpolation at the slave nodes.Accordingly in the literature, there are rare works that study the three-phase compressible multicomponent flows using a finite volume scheme and take into account gravity and the miscibility of the lighter component in the oil phase.The objective of the present investigation is to work out a numerical tool, capable of meeting the needs for understanding the dynamics of multiphase flows taking place within an oil reservoir. More precisely, while using the black-oil model, the compressibility, the miscibility of the lighter component in the oil phase, and the gravity were taken into account. The spatial discretization of flows was done by use of the cell-centered finite volume method. Implicit Euler scheme was used for the temporal discretization of equations. The studied model was coded on Matlab and the oil-field of Tsimiroro Madagascar was chosen for simulations. Having the aforementioned numerical tool, it would be interesting to see the evolution of the model variables such as the pressure, the saturations of the present various phases in the reservoir and the accumulated flows of phases in the production well.
2. Methods
2.1. Simplifying Hypotheses
- The “black-oil” model is considered as constituted by three fluid phases (oil, gas, and water) in each of them can be present the following three components: a lighter component (gas) which can be at the same time in the oil phase and in the gas phase, a heavier component which can only be in the oil phase, and a component water which can only be in the water phase [20]. The capillary pressures are assumed to be negligible [21, 13]. Accordingly, all the present phases in the reservoir have the same pressure. Moreover, the studied medium is considered as isotropic so that the components of the permeability tensor have the same values in all directions [10].
2.2. Mathematical Modeling
- As there is a mass transfer between the oil and gas phases, mass conservation is not satisfied for these two phases. However, the total mass of each component is conserved. Besides, as the water phase is completely separated from the other phases and the component water is only present in the water phase, the mass conservation is well respected for this phase. Hence, the equations of the black-oil model can be formulated as follows [20].Mass conservation related to the component water can be written as:
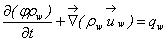 | (1) |
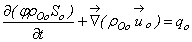 | (2) |
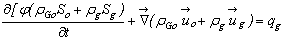 | (3) |
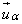 (α = w, o, g) is governed by the generalized Darcy’s law and can be calculated by the following relationship:
(α = w, o, g) is governed by the generalized Darcy’s law and can be calculated by the following relationship: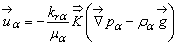 | (4) |
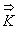 denotes the tensor of the absolute permeabilities of the porous media, whereas g→ denotes the gravity acceleration vector.The system of equations (1) to (3) is completed by the following closing relationships:- Conservation of pore volume (the sum of the saturations in a pore is equal to unity)
denotes the tensor of the absolute permeabilities of the porous media, whereas g→ denotes the gravity acceleration vector.The system of equations (1) to (3) is completed by the following closing relationships:- Conservation of pore volume (the sum of the saturations in a pore is equal to unity)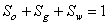 | (5) |
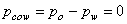 | (6) |
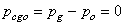 | (7) |
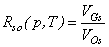 | (8) |
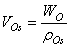 | (9) |
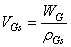 | (10) |
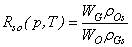 | (11) |
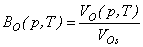 | (12) |
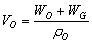 | (13) |
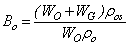 | (14) |
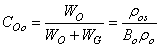 | (15) |
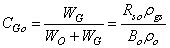 | (16) |
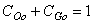 | (17) |
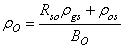 | (18) |
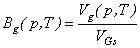 | (19) |
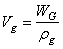 | (20) |
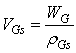 | (21) |
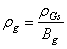 | (22) |
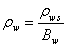 | (23) |
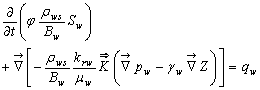 | (24) |
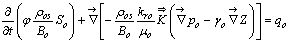 | (25) |
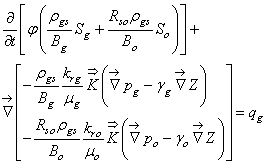 | (26) |
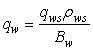 | (27) |
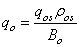 | (28) |
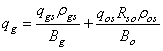 | (29) |
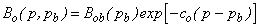 | (30) |
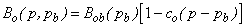 | (31) |
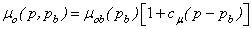 | (32) |
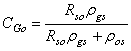 | (33) |
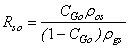 | (34) |
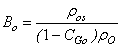 | (35) |
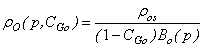 | (36) |
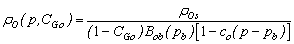 | (37) |
2.3. Thermodynamic Equilibrium
- To study the thermodynamic equilibrium, the model proposed by Masson [22] is used. By Gibbs’ law, two-phase oil (o) - gas (g) equilibrium of a mixture of both lighter and heavier components, depends only on the pressure p when the temperature is assumed to be constant, which is the case in this work. This equilibrium is characterized by state laws of densities
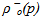 and
and 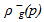 and of viscosities
and of viscosities 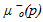 and
and 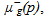 and the mass fraction of the lighter component
and the mass fraction of the lighter component 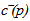 in the oil phase (o). In the following section, barred symbol mean that the considered parameter is related to equilibrium state while unbarred one mean that there is no precision about the equilibrium state.The thermodynamic of the black-oil system is given by the laws of
in the oil phase (o). In the following section, barred symbol mean that the considered parameter is related to equilibrium state while unbarred one mean that there is no precision about the equilibrium state.The thermodynamic of the black-oil system is given by the laws of 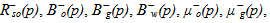 and
and 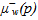 whose signs and variations are:
whose signs and variations are: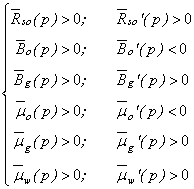 | (38) |
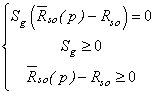 | (39) |
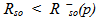 the reservoir is in the oil-water two-phase state; in this case, oil phase is qualified as under saturated. On the other hand, if
the reservoir is in the oil-water two-phase state; in this case, oil phase is qualified as under saturated. On the other hand, if 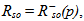 the reservoir is in the saturated state; this means that the three phases oil-gas-water coexist in the reservoir. The oil-gas two-phase state is observed when
the reservoir is in the saturated state; this means that the three phases oil-gas-water coexist in the reservoir. The oil-gas two-phase state is observed when 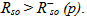 The bubble pressure pb is defined, similarly as done by Masson [22], by introducing the inverse function of
The bubble pressure pb is defined, similarly as done by Masson [22], by introducing the inverse function of 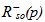 that is here denoted by
that is here denoted by 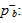
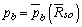 | (40) |
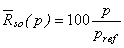 | (41) |
2.4. Numerical Procedures
2.4.1. Temporal and Spatial Discretization Methods
- Temporal discretization is defined by the sequence tn, n being a positive integer such that t0=0 and ∆tn+1=tn+1-tn > 0; the superscript n implicitly means that the variable is considered at time tn. An implicit Euler scheme is used for the time discretization.A cell-centered finite volume scheme was used for spatial discretization. Indeed, the developed model is constituted by conservation equations. Since the finite volume schemes are conservative, they are better suited for solving the considered system of equations [23-24].
2.4.2. Boundary Conditions
- All the borders of the reservoir are considered impervious. No flow either goes out or enters anywhere but places where wells are positioned. As depicted in Figure 1, four injection wells are placed in the four corners of the reservoir while a production well is placed in its center. A condition of pressure in each cell containing a well with perforation is imposed. While the injection of gas in the reservoir and in each cell containing an injection wells being the simulation object, gas saturation is considered equal to one.
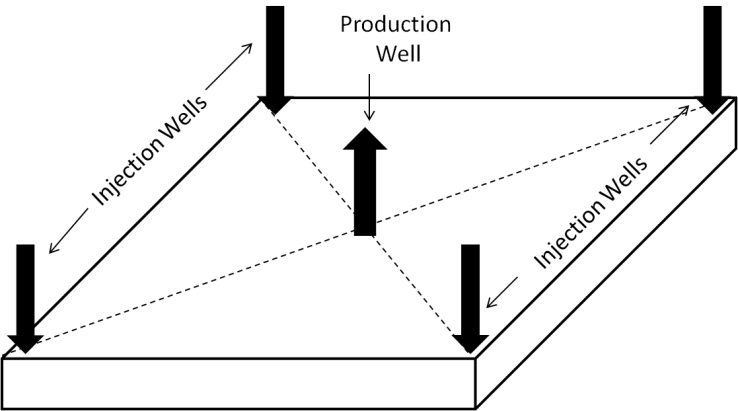 | Figure 1. Sketch of the reservoir with the four injection wells at the corners and the production well in the center |
2.4.3. System of Discretized Equations
- By applying the aforementioned discretization methods to the considered model, the following system of discretized equations is obtained:
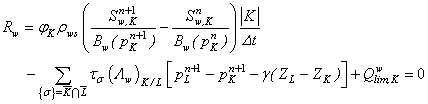 | (42) |
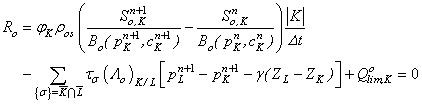 | (43) |
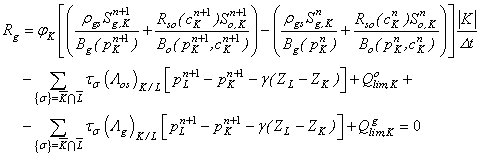 | (44) |
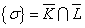 is a singleton set whose element is the common edge σ between cells K and L (see Figure 2) and is equal to empty set otherwise.- |K| is the volume of the cell K and Λα the mobility of the phase α (α = w, o, g) defined by:
is a singleton set whose element is the common edge σ between cells K and L (see Figure 2) and is equal to empty set otherwise.- |K| is the volume of the cell K and Λα the mobility of the phase α (α = w, o, g) defined by: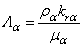 | (45) |
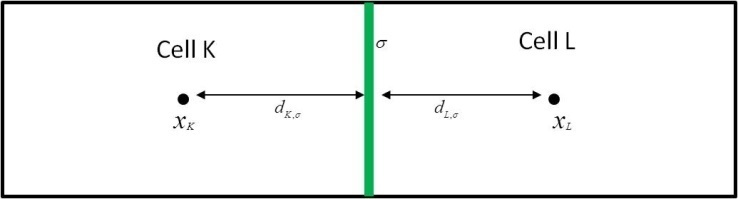 | Figure 2. Sketch of two neighboring cells K and L separated by a common edge σ |
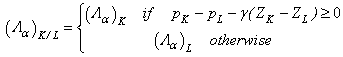 | (46) |
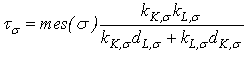 | (47) |
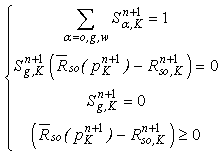 | (48) |
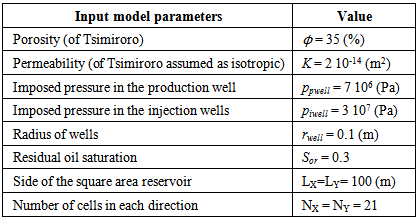
2.5. Data of Tsimiroro oil-field and Model Input Parameter Values for Simulations
- It is worth noting that Tsimiroro is located approximately 125km from the west coast of Madagascar and the Best Estimate Original Oil in Place resulted in a Contingent Resource volume of 1.1 Billion barrels.A log-log analysis of Tsimiroro wells was done to know the types of geological formations constituting the reservoir. Thus were obtained the reservoir petrophysical parameters including the porosity ϕ and permeability K of the site.In addition to these petrophysical data, other model input parameter values that were used for simulations are also presented in Table 1.
|
3. Results and Discussion
- Results presented in the following figures are obtained by two-dimensionally (X,Y) simulating a three-phase oil-water-gas three components model whose lighter component may be simultaneously in the oil phase as well as in the gas phase. They show the evolution of the pressure, saturation and cumulative flow rate generated during the oil extraction.Figures 3 and 4 show the pressure distribution in the reservoir per day and for five days of production. Observing isobars formed by these contours, it can clearly be understood how the pressure of the injection wells changes as when one approaches the producing well (in the middle). More precisely, this pressure is changing in two ways: it changes over both time and space. A spatial decay of pressure is observed while a temporal pressure increase occurs. The pressure imposed on the injection wells is higher than the pressure within the reservoir; the aforementioned spatial pressure decay that is observed following the fluid displacement front towards the center may be due to a pressure drop in the gas flow through the porous medium. Moreover, the energy transferred by the gas to fluids that are in place (oil and water) justifies the temporal pressure increase. However, the pressure is still quite enough to push the oil to the production well and ease its drawing out. Indeed, the purpose of the gas injection in the reservoir is not only to increase the pressure, but also to make the oil less viscous to facilitate mobility for its extraction.
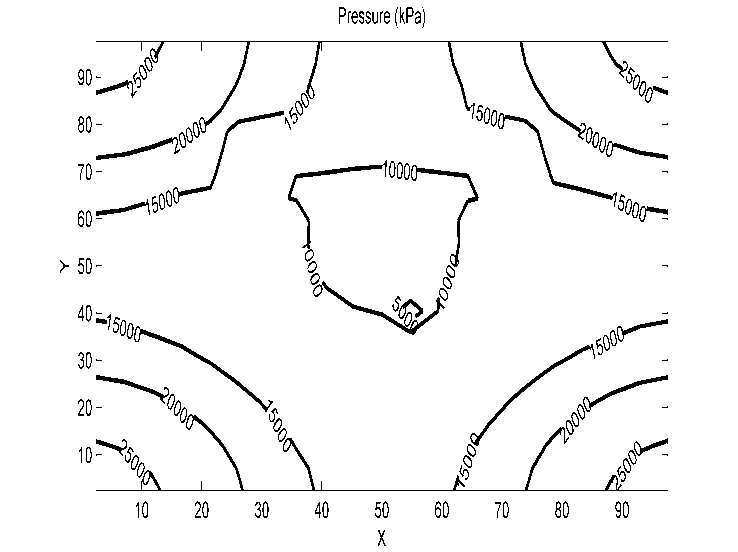 | Figure 3. Pressure for a production day |
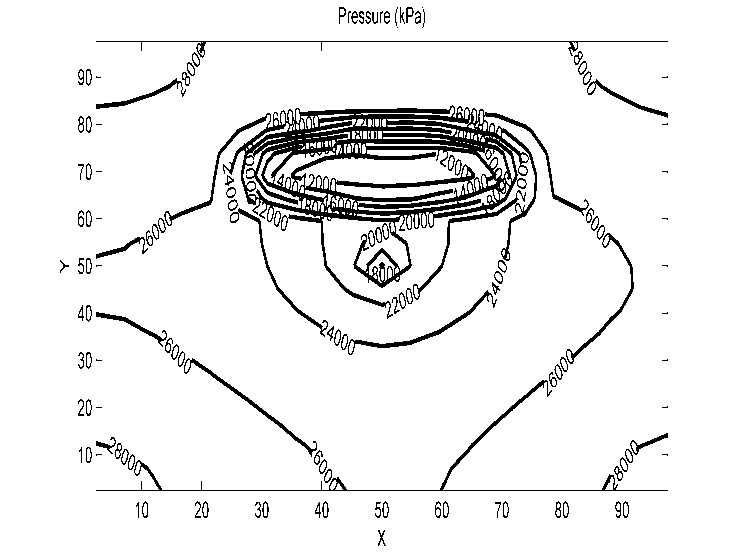 | Figure 4. Pressure for 5 days of production |
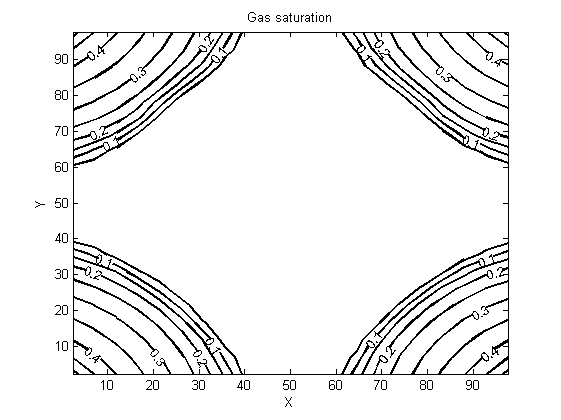 | Figure 5. Gas saturation for a production day |
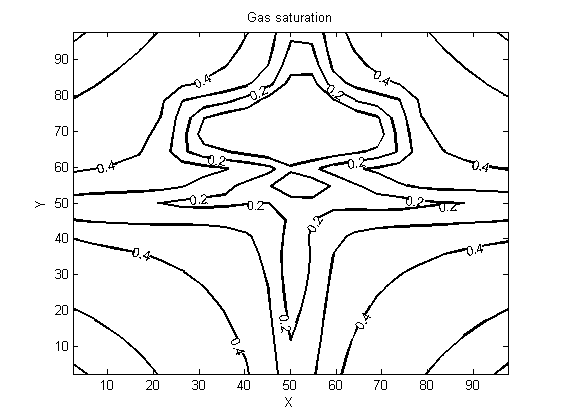 | Figure 6. Gas saturation for 5 days of production |
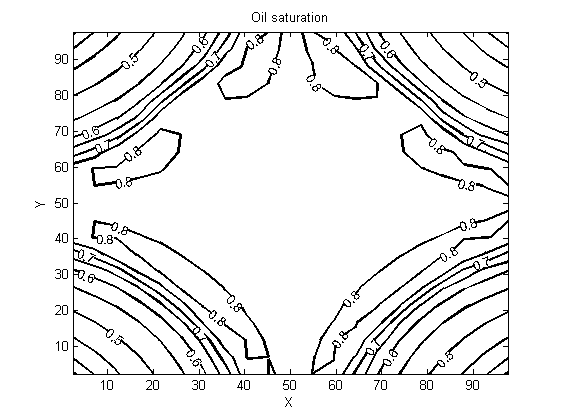 | Figure 7. Oil saturation for a production day |
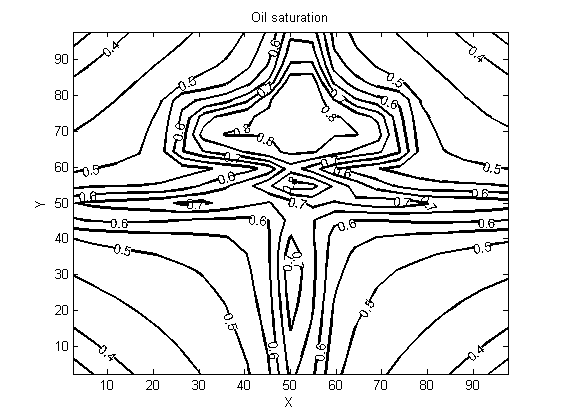 | Figure 8. Oil saturation for five days of production |
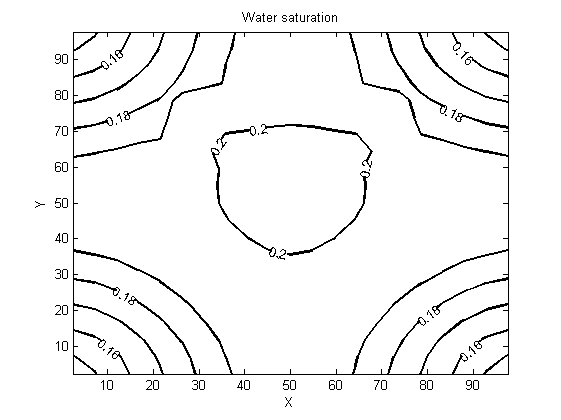 | Figure 9. Water saturation for a production day |
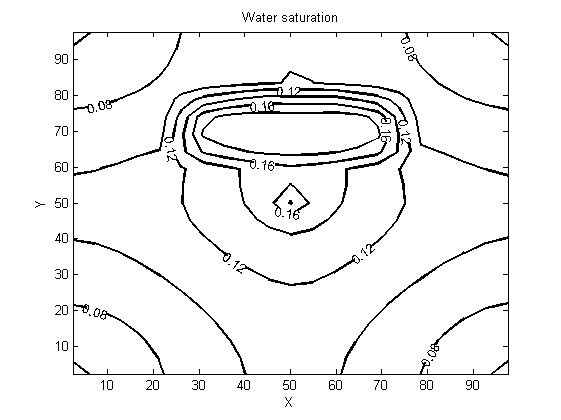 | Figure 10. Water saturation for five days of production |
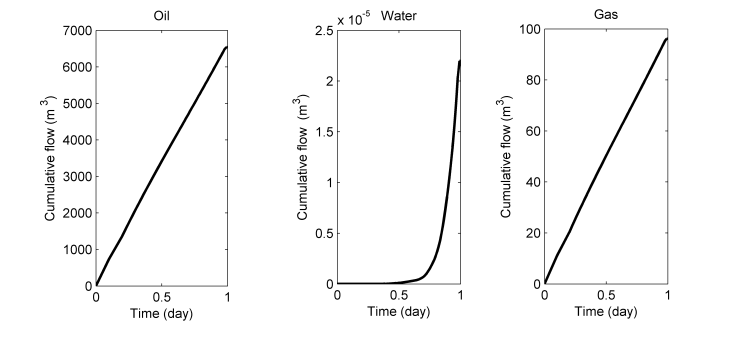 | Figure 11. Cumulative flow in the production well for a production day |
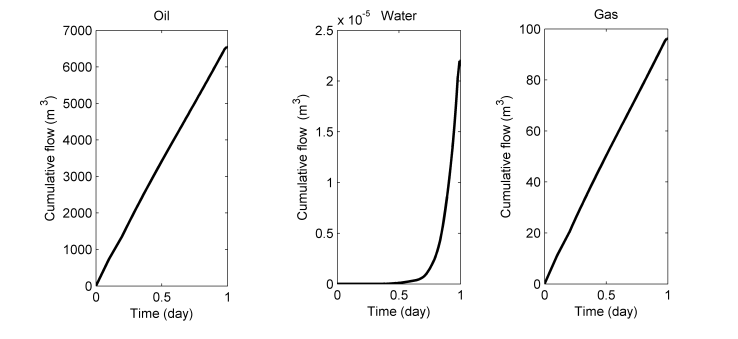 | Figure 12. Cumulative flow in the production well for 5 days of production |
4. Conclusions
- In the present work was studied a three-phase compressible multicomponent flow while using the black-oil model. More precisely, three components were considered: a lighter component (gas) which can be at the same time in the oil phase and in the gas phase, a heavier component which can only be in the oil phase, and a component water which can only be in the water phase. The present study differs from other works [13-16] that have studied the compressible three-phase flows by the fact that it has taken into account both gravity and the miscibility of a lighter component in the oil phase, while using a finite volume scheme. The considered model is complex as it comprises a nonlinear system of partial differential equations. A cell-centered finite volume discretization of the model has permitted to develop a Matlab code which has served to make numerical experiences on the extraction process of the oil field of Tsimiroro Madagascar.It follows from simulation results that the code is able to predict the daily production operations (indicated by the cumulative flow), using gas as injected fluid. In addition, the mobility of the oil depends heavily on the gas saturation. When there is more gas somewhere in the reservoir, there is less oil. Besides, the conservation law of the pore volume is well respected. As extension work, it would be interesting to consider the fact that the heavier component (oil) can evaporate into the gas-phase while using finite volume method. Another possibility of future work is also the thermal transfer study in which steam is injected into the reservoir. Indeed, such process is currently used by the company exploiting the Tsimiroro oil-field.
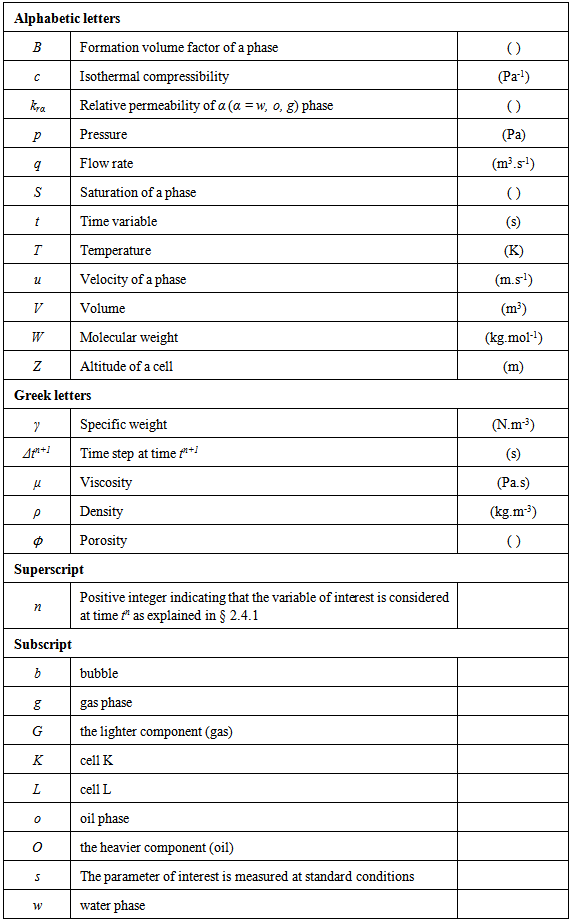
Nomenclature
Appendix
Management of appearance and disappearance of phase combined with Newton-Raphson method
- While interested readers being referred to [25-28] for more details, the principle of the Newton-Raphson method applied to the considered model is the following:A vector R whose elements are the residuals in each cell is defined as:
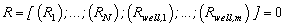 | (A1) |
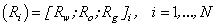 | (A2) |
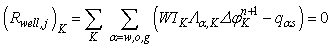 | (A3) |
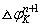 is the potential in the well of the cell K at time tn+1.The Newton-Raphson algorithm requires the definition of the Jacobian matrix J such that:
is the potential in the well of the cell K at time tn+1.The Newton-Raphson algorithm requires the definition of the Jacobian matrix J such that: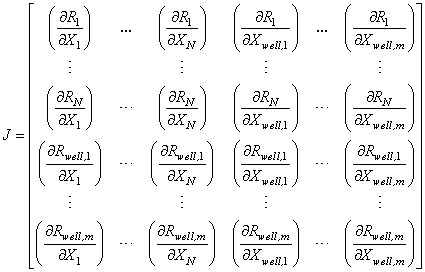 | (A4) |
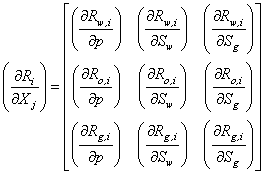 | (A5) |
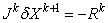 | (A6) |
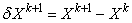 | (A7) |
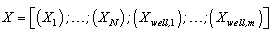 | (A8) |
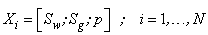 | (A9) |
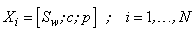 | (A10) |
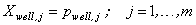 | (A11) |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML