Amos S. Idowu1, Abdulwaheed Jimoh1, Funmilayo H. Oyelami2, Moses S. Dada1
1Department of Mathematics, University of Ilorin, Ilorin, Nigeria
2Department of Mathematics, Afe Babalola University, Ado-Ekiti, Nigeria
Correspondence to: Amos S. Idowu, Department of Mathematics, University of Ilorin, Ilorin, Nigeria.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Abstract
An investigation was carried out on the numerical solution for thermal radiation effect on inclined magnetic field of magneto hydrodynamic (MHD) free convective heat transfer dissipative fluid flow past a moving vertical porous plate with variable suction. The dimensionless governing equations are formulated in (y*, t*) co-ordinates sysytem with appropriate boundary condition s and the radiative heat flux takes the Rosseland approximation. The equations are solved by using an implicit finite difference method of Crank-Nicolson type. The effects of various parameters on the velocity and temperature fields as well as the Coefficient of skin-friction and Nusselt number were presented graphically and in tabulated forms. It was observed that, when the radiation parameter increases, the velocity and temperature increases in the boundary layer. The effect of increasing values of Hartman number (M) which resulted in decrease in velocity distribution, while, increase in temperature across the boundary layer because of the application of transfer magnetic field which resulted in a restrictive type of force (Lorenz force) similar to drag force which tends to resist the fluid and this reducing its velocity. This model finds applications in geophiscs, metallurgic and also in the design of high temperature industrial processing systems.
Keywords:
Inclined magnetic, Unsteady, Porous medium, MHD, Radiation, Heat transfer and suction
Cite this paper: Amos S. Idowu, Abdulwaheed Jimoh, Funmilayo H. Oyelami, Moses S. Dada, Numerical Solution for Thermal Radiation Effect on Inclined Magnetic Field of Mhd Free Convective Heat Transfer Dissipative Fluid Flow Past a Moving Vertical Porous Plate with Variable Suction, American Journal of Fluid Dynamics, Vol. 4 No. 3, 2014, pp. 91-101. doi: 10.5923/j.ajfd.20140403.02.
1. Introduction
The problem of fluid flow in an electromagnetic field has been studied for its importance in geophysics, metallurgy and aerodynamic extrusion of plastic sheets and other engineering process such as in petroleum engineering, chemical engineering, composite or ceramic engineering and heat exchangers. Also, the effect of thermal radiation is significant in some industrial application such as glass production and furnace design and in space technology application such as comical flight aerodynamics rocket, populsion system, plasma physics which operate at high temperature. Vajravelu and Hadjinicolaou (1993) studied the heat transfer characteristics in the laminar boundary layer of a viscous fluid over a stretching sheet with viscous dissipation or frictional heating and internal heat generation. Muthucumaraswamy and Ganesan (2001) investigated the effect of the chemical reaction and injection on flow characteristics in an unsteady upward motion of an isothermal plate. Chamkha, Takhar and Soundalgekar (2001), also, observed the radiation effect on free convection flow past a semi-infinite vertical plate with mass transfer. Muthucumaraswamy and Senthih (2004) considered heat and mass transfer effect on moving vertical plate in the presence of thermal radiation. Kim and Fedorov (2004) studied transient mixed radiative convection flow of a micro polar fluid past a moving semi-infinite vertical porous plate. Hossain et al. (2004) investigated the problem of natural convection flown along a vertical wavy surface with uniform surface temperature in the presence of heat generation/ absorption. Hady, Mohammed and Mahdy (2006), gave attention to MHD Free convection flow along a vertical wavy surface with heat generation or absorption effect. Gnaneshwara and Bhaskar (2009) investigated the radiation and mass transfer effects on an unsteady MHD free convection flow past a heated vertical porous plate with viscous dissipation. Alam, Rahman and Sattar (2009), tried transient magnetohydrodynamic free convective heat and mass transfer flow with thermophoresis past a radiative inclined permeable plate in the presence of variable chemical reaction and temperature dependent viscosity. Ahmed, Sarma and Baruna (2012), studied the Magnetic field effect on free convective oscillatory flow between two vertical parallel plates with periodic plate temperature and dissipative heat. Rushi, Kumar and Sivaraj, (2012), MHD Visco elastic fluid non-darcy flow along a moving vertical cone. Idowu, Dada and Jimoh (2013) investigated the heat and mass transfer of magnetohydrodynamic (MHD) and dissipative fluid flow pass a moving vertical porous plate with variable suction.The study of heat generation or absorption effects in moving fluids is important in view of several physical problems such as fluids undergoing exothermic or endothermic or transfer chemical reaction. In this direction Alam et al. (2006) studied the problem of free convection heat and mass transfer flow past an inclined semi-infinite heated surface of an electrically conducting and steady viscous incompressible fluid in the presence of a magnetic field and heat generation. Md Abdus and Mohammed (2006) considered the thermal radiation interaction with unsteady MHD flow past a vertical porous plate immersed in a porous medium. The importance of radiation in the fluid led Muthucumaraswamy and Chandrakala (2006) to study radiative heat and mass transfer effect on moving isothermal vertical plate in the presence of chemical reaction. In many Chemical Engineering processes, the chemical reaction do occur between a mass and fluid in which plate is moving. These processes take place in numerous industrial applications such as polymer production, manufacturing of ceramics or glassware and food processing. In the light of the fact that, the combination of heat and mass transfer problems with chemical reaction are of importance in many processes, and have, therefore, received a considerable amount of attention in recent years. In processes such as drying, evaporation at the surface of a water body, energy transfer in a wet cooling tower and the flow in a desert cooler, heat and mass transfer occur simultaneously. Possible applications of this type of flow can be found in many industries. For example, in the power industry, among the methods of generating electricity is one in which electrical energy is extracted directly from moving conducting fluid. Naving Kumar and Sandeep Gupta (2008) investigated the effect of variable permeability on unsteady two-dimensional free convective flow through a porous medium bounded by a vertical porous surface. Sandeep and Sugunamma (2013) investigated the effect of inclined magnetic field on unsteady free convective flow of dissipative fluid past a vertical plate. Sharma, Navin and Pooja (2011) have studied the influence of chemical reaction on unsteady MHD free convective flow and mass transfer through viscous incompressible fluid past a heated vertical plate immersed in porous medium in the presence of heat source. Mohammed (2009) studied double-diffusive convection-radiation interaction on unsteady MHD flow over a vertical moving porous plate with heat generation and Soret effects.Based on these investigations and works that have been reported in the field of study, in particular, the study of heat and mass transfer, heat radiation is of considerable importance in chemical and hydrometallurgical industries. Mass transfer process and evaporation of water from a pound to the atmosphere the diffusion of chemical impurities in lakes, rivers and ocean from natural or artificial sources. Magneto hydrodynamic mixed convection heat transfer flow in porous plate and non-porous media is of considerable interest in the technical field due to its frequent occurrence in industrial technology and geothermal application, high temperature plasma application to nuclear fusion energy conversion, liquid metal fluid and MHD power generation systems combined heat and mass transfer in natural convective flows on moving vertical porous plate. Das, Sarkar and Jana (2012), investigated MHD Natural Convection Vertical parallel Plates with Oscillatory Wall Temperature. Srinvasa Rao, An and Babu. (2010), studied the finite element analysis of radiation and mass transfer flow past semi-infinite moving vertical plate with viscous dissipation.Motivated by the above mentioned investigations and applications, we analyzed the unsteady MHD free convective, thermal radiation, inclined magnetic and dissipative fluid flow over a moving vertical porous plate with variable suction using the numerical approach of implicit finite difference method of Crank-Nicolson.
2. Mathematical Analysis
Consider unsteady two-dimensional unsteady flow of an incompressible, electrically conducting viscous Boussinesq fluid in a cartesian 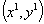 coordinate system with a transversely applied magnetic field, the flow is assumed to be in the x-direction, which is taking along semi-infinite inclined plate and y-axis normal to it. A magnetic field normal of uniform strength
coordinate system with a transversely applied magnetic field, the flow is assumed to be in the x-direction, which is taking along semi-infinite inclined plate and y-axis normal to it. A magnetic field normal of uniform strength 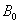 is introduced normal to the direction of the flow. In the analysis we assume, that the magnetic Reynold number is much lesser than unity so that the induced magnetic field is negleted in comparison to the applied magnetic field. It is also assumed that all fluid properties are constant except that of the influence of the density variation and temperature in the body force term. The surface is maintained at a constant temperature
is introduced normal to the direction of the flow. In the analysis we assume, that the magnetic Reynold number is much lesser than unity so that the induced magnetic field is negleted in comparison to the applied magnetic field. It is also assumed that all fluid properties are constant except that of the influence of the density variation and temperature in the body force term. The surface is maintained at a constant temperature 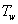 which is higher than the constant temperature
which is higher than the constant temperature 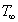 of the surrounding fluid. Since the plate is considered semi-infinite in the x-direction, all physical variables are functions of y and t only. Then, under the Boussinesq’s and boundary layer approximation s, also with the spirit of Gebhart (1962), Singh and Sacheti (1988) and Gebhart and Mollendorf (1969) proposed the governing equations:Continuity equation
of the surrounding fluid. Since the plate is considered semi-infinite in the x-direction, all physical variables are functions of y and t only. Then, under the Boussinesq’s and boundary layer approximation s, also with the spirit of Gebhart (1962), Singh and Sacheti (1988) and Gebhart and Mollendorf (1969) proposed the governing equations:Continuity equation 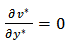 | (1) |
Linear momentum equation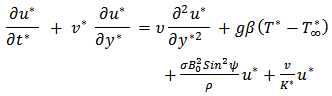 | (2) |
Energy equation is given as 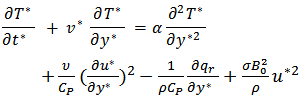 | (3) |
The boundary conditions for the velocity, temperature and concentration fields are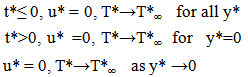 | (4) |
Where y is dimensions coordinates, u* is velocitie component,, t* is dimensionless time, T* is the dimensional temperature, g- the acceleration due to gravity, β - the volumetric coefficient of thermal expansion, β * is the volumetric coefficient of thermal expansion with concentration, ρ - the density of the fluid, Cp is the specific heat at constant pressure, ψ is the inclined angle, K* is the permeability of the porous medium, qr is the radiation heat flux, B0- magnetic induction, ν- the kinematic viscosity and subscript 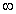 denotes conditions in the free stream. For optically thick fluid we have Modest (1993) as follows the radiative heat flux term by using the Rosseland approximation is given by
denotes conditions in the free stream. For optically thick fluid we have Modest (1993) as follows the radiative heat flux term by using the Rosseland approximation is given by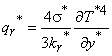 | (5) |
Where σ* is the Stefan-Boltzmann constant and k*r- the mean absorption co-efficent. It should be noted that by using the Rosseland approximation the present analysis is limited to optically thick fluids. If temperature differences within the flow are sufficient small, then Equation (5) can be literalized by expanding T*4 into the Taylor series about T*∞, which after neglecting higher order terms takes the form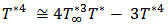 | (6) |
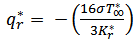 | (7) |
Substituting equation (6) and (7), into equation (3), gives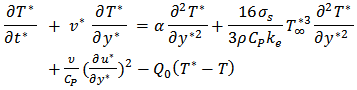 | (8) |
Introducing these non-dimensional quantities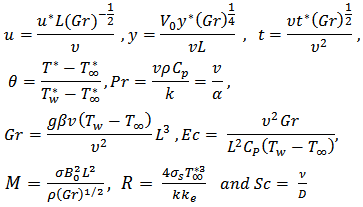 | (9) |
into the equations (2) and (8) with equation (1) identically satisfied the following set of differential equations: 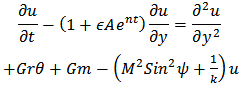 | (10) |
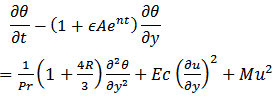 | (11) |
From (7) –(11) we have that Tw* is wall dimensional temperature, T*∞- the free stream temperature far away from the plate, Re is the Reynolds number, R is the radiation parameter, Pr is Prandtl number, U is velocity, n is the frequency, M is the Hartmann number, K is the permeability parameter, Gr is thermal Grashoff number, Ec is Eckert number, A is a real positive constant of suction velocity parameter, ε, and ε A<1 are small less than unity, i.e εA<<1, V0 is a scale of suction velocity normal to the plate -the constant.The boundary conditions (4) are given by the following dimensionless form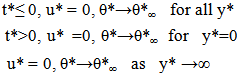 | (12) |
The dimensionless local value of skin friction 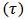 and Nusselt number (Nu) can be characterized in order by
and Nusselt number (Nu) can be characterized in order by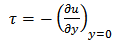 | (13) |
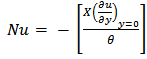 | (14) |
The average of skin friction 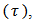 average of Nusselt number (Nu) in dimensionless form can be written as
average of Nusselt number (Nu) in dimensionless form can be written as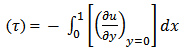 | (15) |
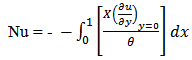 | (16) |
3. Method of Solution
In order to solve the non-linear coupled equation s (10), (11) and (16) under the initial and boundary condition (12), an implicit finite difference scheme of crank-Nicolson type has been employed. The finite difference equations corresponding to equations (10) and (11) are discretized using the Crank-Nicolson Method as follows: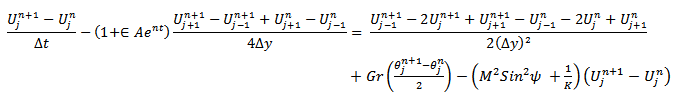 | (17) |
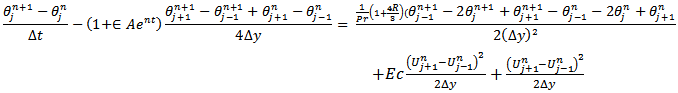 | (18) |
With the following boundary conditions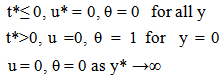 | (19) |
The subscript j and n denote the grid points along y- and t-directions respectively. The value of u and  are known at all grid points at t=0 from the initial conditions. The computations of the values of u and
are known at all grid points at t=0 from the initial conditions. The computations of the values of u and  at the (n+1)th time using the values at previous time (n)th are carried out in this form:At all grid points, the values of
at the (n+1)th time using the values at previous time (n)th are carried out in this form:At all grid points, the values of 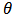 and u at t=0 from the initial conditions are known. Therefore, the values of
and u at t=0 from the initial conditions are known. Therefore, the values of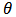 at the next time step are calculated using the values already known from the previous values. In this case, the finite difference Equations form a tri-diagonal system of equations where the values of
at the next time step are calculated using the values already known from the previous values. In this case, the finite difference Equations form a tri-diagonal system of equations where the values of 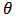 at every nodal point at next time step are determined using the known values at the previous time. We therefore employ Thomas algorithm to solve the tri-diagonal system of equations. In this way, we were able to get the values of
at every nodal point at next time step are determined using the known values at the previous time. We therefore employ Thomas algorithm to solve the tri-diagonal system of equations. In this way, we were able to get the values of 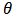 at every nodal point. The values of u are also computed at that particular time. Several values of u and
at every nodal point. The values of u are also computed at that particular time. Several values of u and 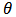 were obtained for the required time using this process. The mesh size are ∆Y =0.16 and
were obtained for the required time using this process. The mesh size are ∆Y =0.16 and 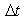 =0.01.
=0.01.
4. Results and Discussions
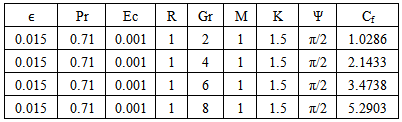
Numerical evaluation for the solutions of this problem is performed and the results are illustrated graphically in Fig.1-13, to the interesting features of significant parameters on velocity, temperature local skin friction and local Nusselt number. Throughout the computations we employ A=0.5, t=1.0, n=0.1 and ϵ=0.001, while R, kr2, Sc, Gr, Gc, M, Pr, η, and K were varied in order to account for their effects. Fig.12. shows the effect of radiation R on velocity. It was observed that as the value of R increases, the velocity increases with an increasing in the flow boundary layer thickness. Thus, thermal radiation enhances the flow. The effect of radiation parameter R on the temperature profiles are presented in Fig. 6 it shows that, as the value of R increases the temperature profiles increases, with an increasing in the thermal boundary layer thickness.The velocity profiles for different values of Grashof number Gr were described in the fig.1 and fig.7. It is observed that an increasing in Gr leads to a rise in the values of velocity and temperature. Here the Grashof number represents the effect of the free convection currents. Physically, Gr>0 means heating of fluid of cooling of the boundary surface, Gr<0 means cooling of the fluid of heating of the boundary surface and Gr=0 corresponds to the absence of free convection current. In addition, the curves show that the peak value of velocity increases rapidly near the wall of the porous plate as Grashof number increases, and then decays to the relevant free stream velocity.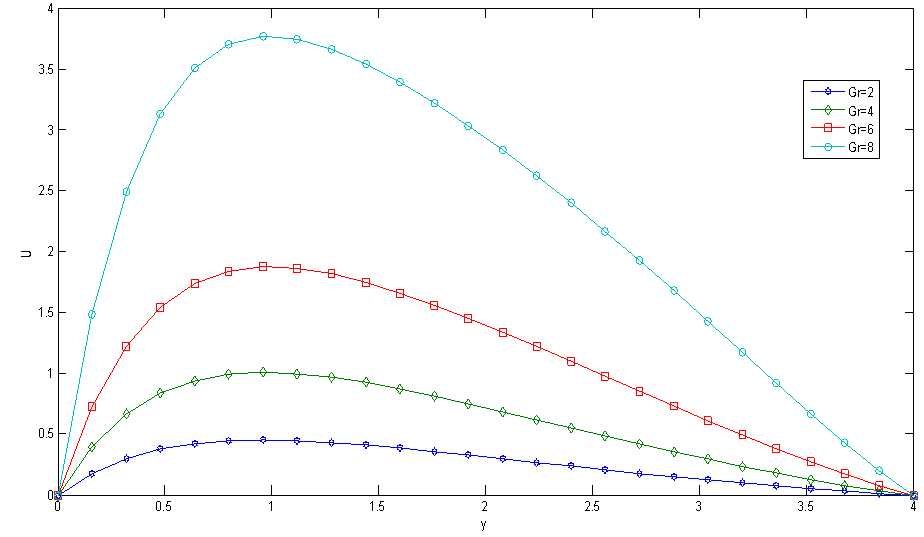 | Figure 1. Effect of Gr on Velocity |
 | Figure 2. Effect of K on Velocity |
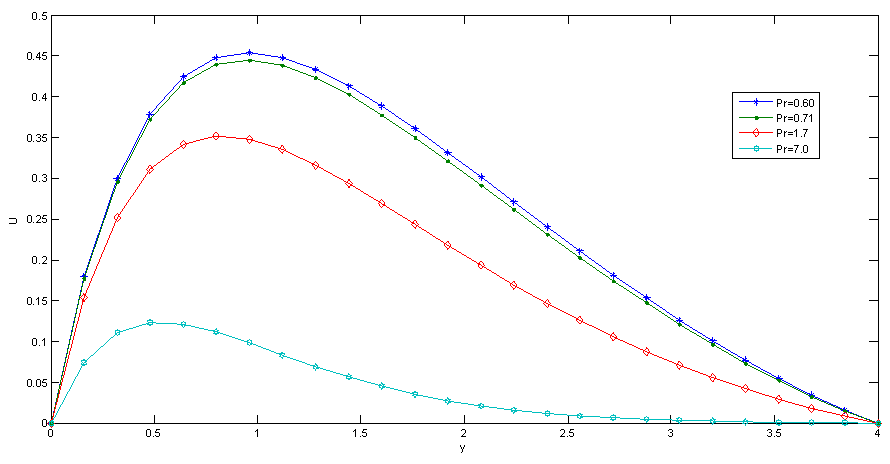 | Figure 3. Effect of Pr on Velocity |
 | Figure 4. Effect of Ψ on Velocity |
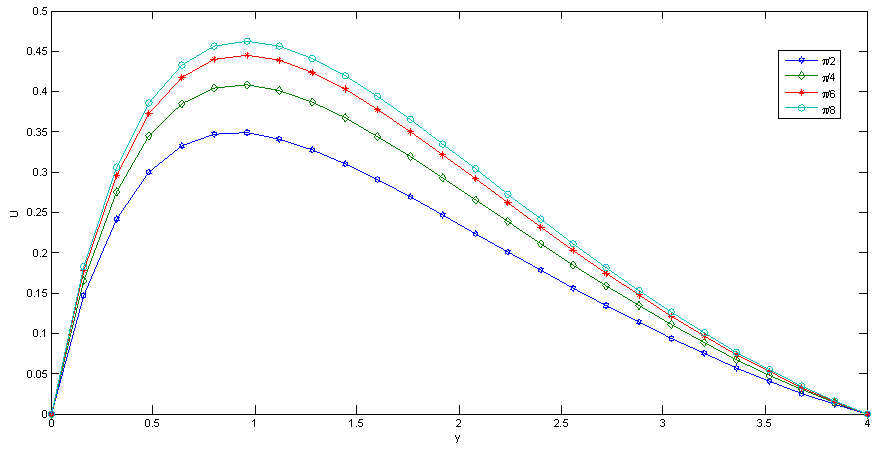
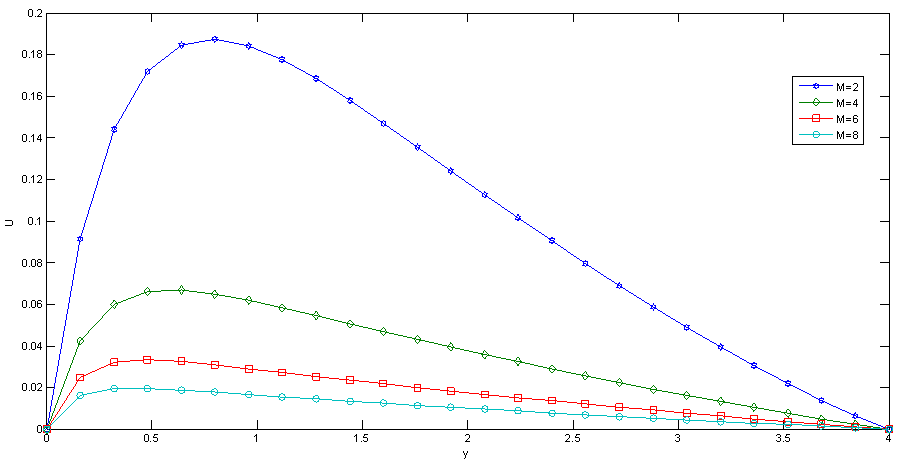 | Figure 5. Effect of M on Velocity |
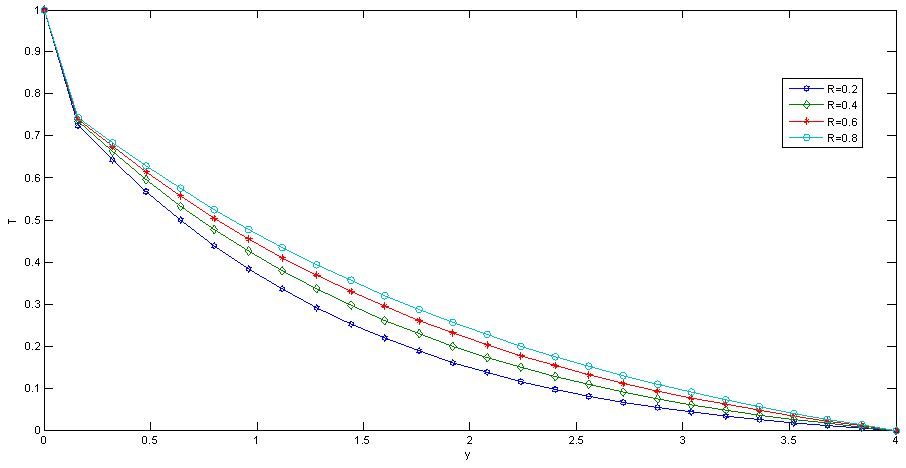 | Figure 6. Effect of R on Temperature |
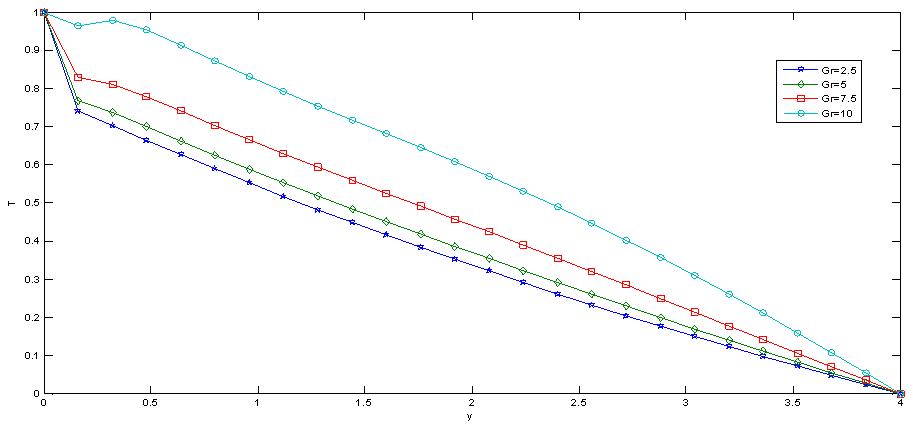 | Figure 7. Effect of Gr on Temperature |
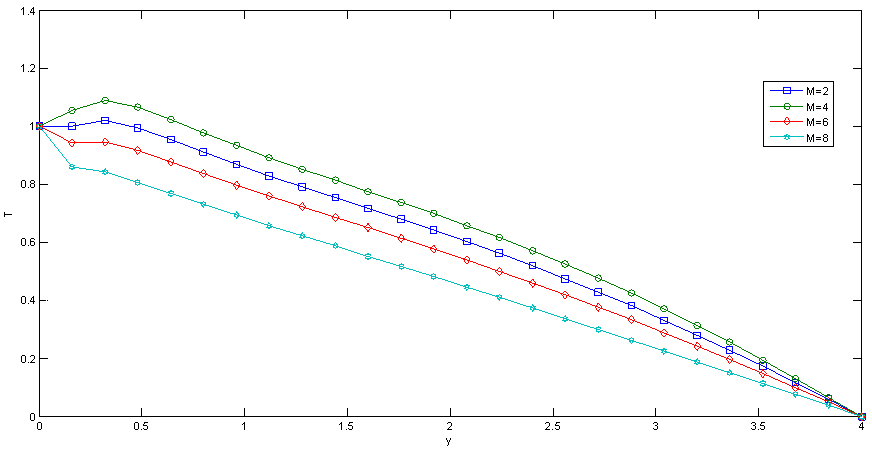 | Figure 8. Effect of M on Temperature |
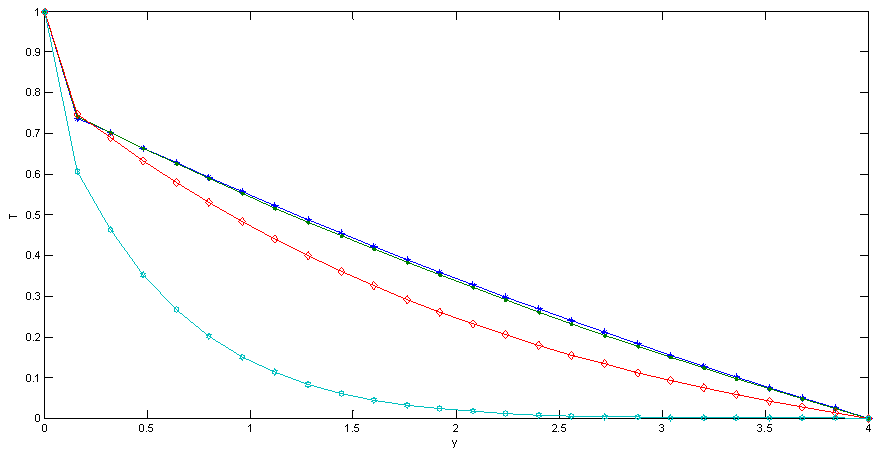 | Figure 9. Effect of Pr on Temperature |
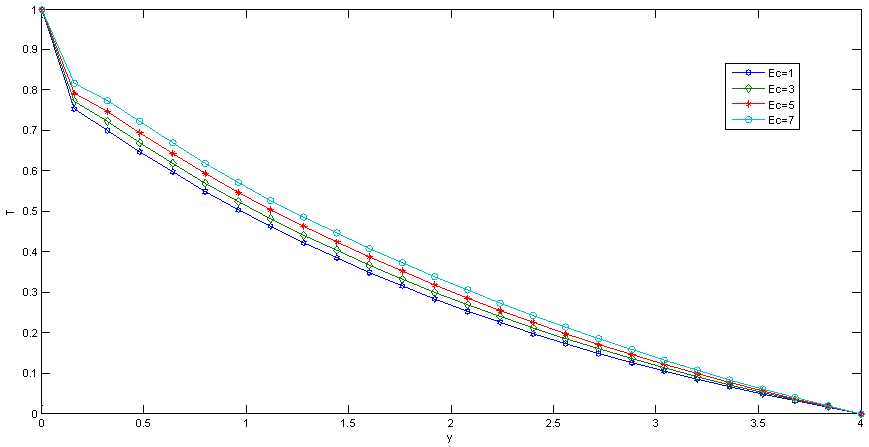 | Figure 10. Effect of Ec on Temperature |
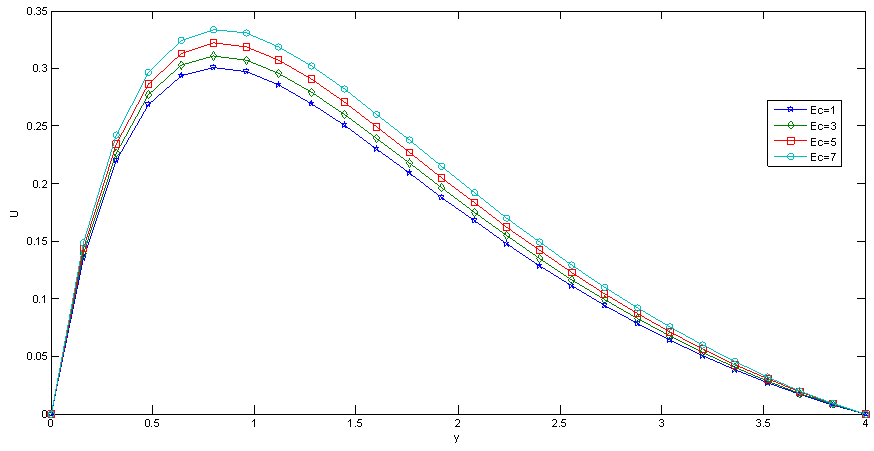 | Figure 11. Effect of Ec on Velocity |
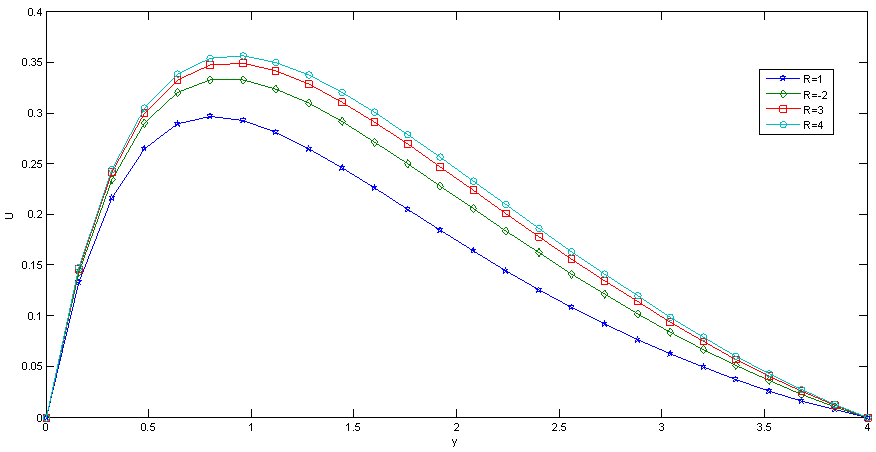 | Figure 12. Effect of R on Velocity |
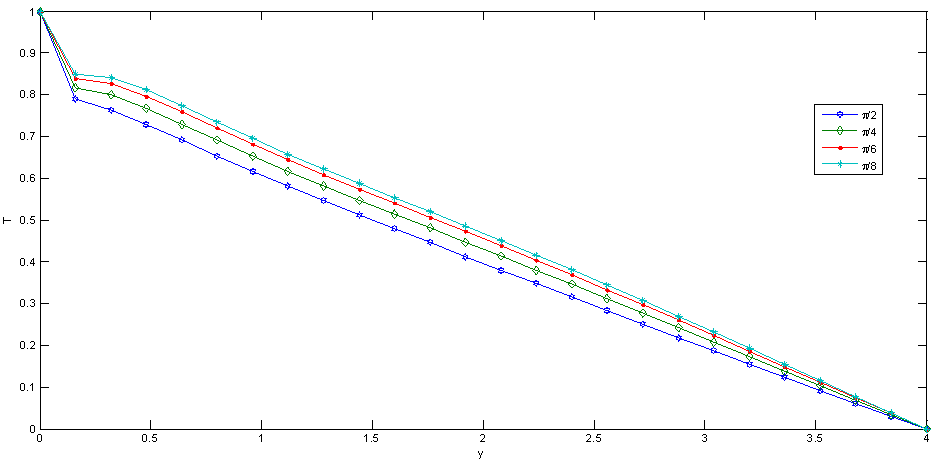 | Figure 13. Effect of Ψ on Temperature |
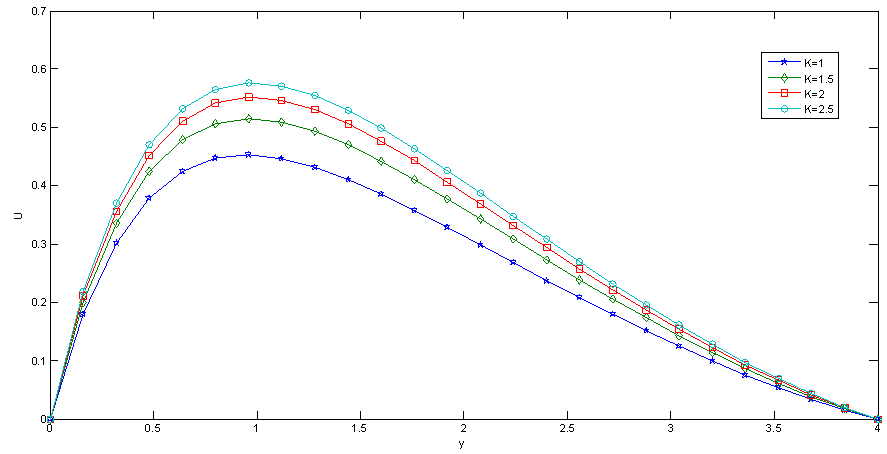
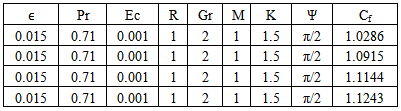
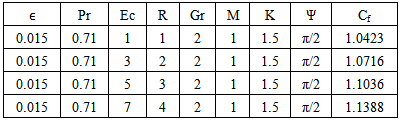
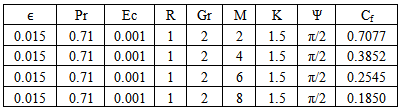
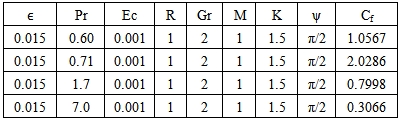
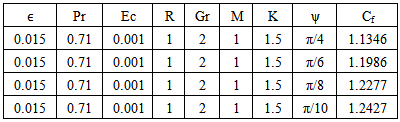
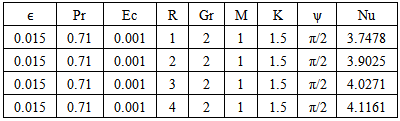
Fig.5 and Fig 8. shows that the effect of increasing values of Hartman number M parameter which results in decreasing velocity distribution, while increase in temperature across the boundary layer because of the application of transfer magnetic field it will result in a restrictive type of force(Lorenz force) similar to drag force which tends to resist the fluid and this reducing its velocity.The velocity profiles across the boundary layer for different values of Prandtl number Pr were plotted in Fig.3 and Fig 9. The results shows that the effect of increasing values of Pr results in decreasing the velocity and temperature, while it peak up again at the value of 1.7 and 7.It was observed from Fig.4. that an increase in inclined angle ψ results in decreasing the thermal boundary layer thickness and more uniform temperature distribution across the boundary layer. Fig.13. show that the effect of inclined angle on the velocity profile. It shows that an increase in the inclined angle parameter increase the velocity profile.It was observed from fig.2. the velocity profiles for different values of the permeability K. Clearly, as K increases the value of velocity tends to increase. These results could be very useful in deciding the applicability of enhanced oil recovery in reservoir engineering.Fig.10. and Fig.11. shows the effects of Eckert number on velocity and temperature respectively, as Eckert number increases the velocity distribution across the boundary layer increases while, temperature distribution across the boundary layer decreases.Table-(1)-(7) for velocity: The effects of the radiation parameter and inclined angle on the skin- friction coefficient. It is observed from this table that as radiation parameter, Grashof number, Eckert number, Porosity Permeability or inclined angle Parameter increases, the skin-friction coefficients increases. Also an increase in the Prandlt number Parameter and Magnetic field Parameter effect brings about a decrease in the skin-friction coefficient.Table 1. Effect of R on Velocity n=0.1, t=1 and A=1
 |
| |
|
Table 2. Effect of Ec on Velocity n=0.1, t=1 and A=1
 |
| |
|
Table 3. Effect of Gr on Velocity n=0.1, t=1 and A=1
 |
| |
|
Table 4. Effect of M on Velocity n=0.1, t=1 and A=1
 |
| |
|
Table 5. Effect of Pr on Velocity n=0.1, t=1 and A=1
 |
| |
|
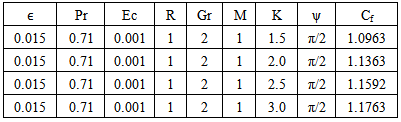
Table 6. Effect of K on Velocity n=0.1, t=1 and A=1
 |
| |
|
Table 7. Effect of ψ on Velocity n=0.1, t=1 and A=1
 |
| |
|
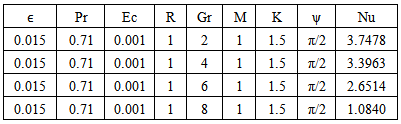
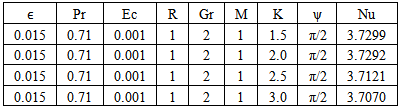
Table-(8)-(14) for temperature: As the Prandtl number, radiation and the magnetic field Parameters effect increases, the Nusselt number increases. An increase in inclined angle, Grashof number for heat transfer, Permeability parameter, and Eckert number resulted in the decrease in the Nusselt number.Table 8. Effect of Gr on Temperature n=0.1, t=1 and A=1
 |
| |
|
Table 9. Effect of K on Temperature n=0.1, t=1 and A=1
 |
| |
|
Table 10. Effect of ψ on Temperature n=0.1, t=1 and A=1
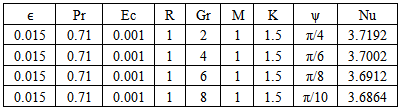 |
| |
|
Table 11. Effect of Pr on Temperature n=0.1, t=1 and A=1
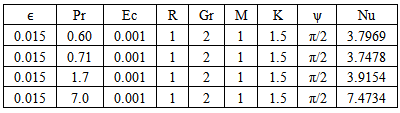 |
| |
|
Table 12. Effect of M on Temperature n=0.1, t=1 and A=1
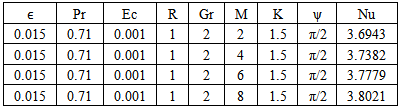 |
| |
|
Table 13. Effect of Ec on Temperature n=0.1, t=1 and A=1
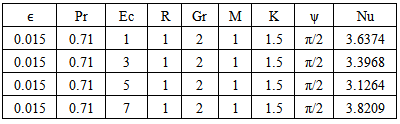 |
| |
|
Table 14. Effect of R on Temperature n=0.1, t=1 and A=1
 |
| |
|
5. Conclusions
A numerical study has been carried out to study the numerical solution for thermal radiation effect on inclined magnetic field of magnetohydrodynamic (MHD) free convective heat transfer dissipative fluid flow past a moving vertical porous plate with variable suction. The fluid is gray absorbing-emitting but non-scattering medium and the radiative heat flux in the energy equation. A family of governing partial differential equations was solved by an implicit finite difference scheme of Crank-Nicolson type, which is stable and convergent. The result were obtained for different values of radiation parameter R, thermal Grashof number Gr, inclined angle ψ, Eckert number Ec. Conclusion of this study were as follows.A rise in the velocity leads to a fall in size of the temperature at the Grashof number Gr.As velocity and temperature increases the Porosity Parameter K also amplify.The velocity increases with an increase in the Prandtl number Pr.A rise in the inclined angle parameter ψ leads to an accelerated increase in velocity as well as the reduction in temperature.The size of fluid velocity and temperature reduces with the increase Eckert number Ec.The level of fluid temperature falls while velocity amplifies with the rise of Magnetic Parameter M.The velocity as well as temperature increases with an increase in radiation.It shows obviously that the thermal radiation has a positive significant effect on both the velocity and temperature of the fluid through the medium which it flows.
References
| [1] | Ahmed, N. sarma, K. and Baruna, D.P. (2012): Magnetic field effect on free convective oscillatory flow between two vertical parallel plates with periodic plate temperature and dissipative heat. Applied Mathematical Sciences, 6(39), 1913-1924. |
| [2] | A. S. Idowu, M.S. Dada and .A. Jimoh (2013): Heat and mass transfer of magnetohydrodynamic (MHD) and dissipative fluid flow pass a moving vertical porous plate with variable suction. Mathematical Theory and Modeling. ISSN: 2224-5804 (Paper), ISSN: 2225-0522(online),3(3). |
| [3] | Alam M.S, Rahman M.M and sattar M.A, (2009): Transient magnetohydrodynamic free convective heat and mass transfer flow with thermophoresis past a radiate inclined permeable plate in the presence of variable chemical reaction and temperature dependent viscosity, Nonlinear Analysis: Modelling and control (14): 3-20. |
| [4] | A.J Chamkha, Takhar H.S. and soundalgekar V.M. (2001): Radiation effect on free convection flow past a semi-infinite vertical plate with mass transfer, Chem. Engr. J., .84:335-342 |
| [5] | B. Rushi Kumar and R. Sivaraj, (2012): MHD Viscoelastic fluid non-darcy flow along a moving vertical cone. Int. J. of Appl. Math. and Mech.8(11):69-81,2012. |
| [6] | Carnahan B., Luther H.A., and Willkes J.O (1969). Applied Numerical Method. John Wiley and Sons, New York, USA. |
| [7] | F.M. Hady, R.A. Mohammed, A. Mahdy, (2006): MHD Free convection flow along a vertical wavy surface wiyh heat generation or absorption effect Int. Comm Heat Mass Transfer 33: 1253-1263. |
| [8] | Gnaneshwara Reddy M and Bhaskar Reddy N (2009): Radiation and mass transfer effect on an unsteady MHD free convection flow past a heated vertical porous plate with viscous dissipation, Int. J. of Appl. Math and Mech, 6 (6): 96-110. |
| [9] | Kim Y.J. and Fedorov A.G. (2003): Transient Mixed Radiation Convection Flow of a Micro polar Fluid past a Moving, Semi-infinite vertical porous plate. Internation Journal of Heat and Mass Transfer. 46:1751-1758. |
| [10] | K. Vajravelu, A. Hdjinicolaou, (1993): Heat transfer in a viscous fluid over a streching sheet with viscous dissipation and internal heat generation, Int. Comm. Heat Mass Transfer 20, 417-430. |
| [11] | M. A. Hossain, M. M. Molla, L.S. Yaa, (2004), Natural convection flow along a vertical wavy surface temperature in the presence of heat generation /absorption, Int. J. Thermal Science 43: 157-163. |
| [12] | M.S. Alam, M.M. Rahman, M.A. Sattar. (2006): MHD Free convective heat and mass transfer flow past an inclined semi-infinite heated surface of an electrically conducting and steady viscous incompressible fluid in the presence of a magnetic field and generation Thamasat. Int. J. Sci. Tech. 11(4): 1-8. |
| [13] | Md Abdus Samad and Mohammed Mansur Rahman. (2006): Thermal radiation interraction with unsteady MHD flow past a vertical porous plate immersed in a porous medium. |
| [14] | Muthucumaraswamy R and Chandrakala P (2006): Radiative heat and mass transfer effect on moving isothermal vertical plate in the presence of chemical reaction, International Journal of Applied Mechanics and Engineering, 11:639-646. |
| [15] | Muthucumaraswamy R and Senthih Kumar G (2004): Heat and mass transfer effects on moving vertical plate in the presence of thermal radiation, Theoretical Applied Mechanics, 31:35-46. |
| [16] | N. Sandeep, V. Sugunamma (2013): Effect of inclined magnetic field on unsteady free convective flow of dissipative fluid past a vertical plate.1(1):6-23 ISSN: 2336-0062. |
| [17] | Naving Kumar and Sandeep Gupta (2008): Effect of variable permeability on unsteady two-dimensional free convective flow through a porous bounded by a vertical porous surface, Asian J, Exp. Sci.. 22 (3): 275-284. |
| [18] | P.R. Sharma, Navin Kumar and Pooja Sharma (2011): Influence of Chemical Reaction and Radiation on Unsteady MHD Free Convective Flow and Mass Transfer through Viscous Incompressible Fluid Past a Heated Vertical Plate Immersed in Porous Medium in the Presence of Heat Source. |
| [19] | R. Muthucumaraswamy, P. Ganesan, (2001), Effect of the chemical reaction and injection on flow characteristics in an unsteady motion of an isothermal plate, J. Appl. Mech. Tech. Phys. 42,65-667. |
| [20] | R.A Mohamed (2009): Double-Diffusive Convection- Radiation Interaction on Unsteady MHD Flow over a Vertical Moving Porous Plate with Heat Generation and Soret Effects, Applied Mathematics Science, (3) (13):629-651. |
| [21] | S. Das, B.C. Sarkar and R.N. Jana (2012): MHD Natural Convection Vertical parallel Plates with Oscillatory Wall Temperature. J. Comp. and Math. Sci 3(4):426-438. |
| [22] | Sugunamma and Sandeep (2011): Unsteady hydromagnetic free convective flow of a flux. Int. J. of mathematics and computer reseach. 1(1):37-50. |
| [23] | V. Srinivasa Rao and L. Anand Babu (2010): Finite element analysis of radiation and mass transfer flow past semi-infinite moving vertical plate with viscous dissipation. ARPN Journal of Engineering and Applied Sciences. (5) 11. |

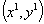 coordinate system with a transversely applied magnetic field, the flow is assumed to be in the x-direction, which is taking along semi-infinite inclined plate and y-axis normal to it. A magnetic field normal of uniform strength
coordinate system with a transversely applied magnetic field, the flow is assumed to be in the x-direction, which is taking along semi-infinite inclined plate and y-axis normal to it. A magnetic field normal of uniform strength 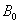 is introduced normal to the direction of the flow. In the analysis we assume, that the magnetic Reynold number is much lesser than unity so that the induced magnetic field is negleted in comparison to the applied magnetic field. It is also assumed that all fluid properties are constant except that of the influence of the density variation and temperature in the body force term. The surface is maintained at a constant temperature
is introduced normal to the direction of the flow. In the analysis we assume, that the magnetic Reynold number is much lesser than unity so that the induced magnetic field is negleted in comparison to the applied magnetic field. It is also assumed that all fluid properties are constant except that of the influence of the density variation and temperature in the body force term. The surface is maintained at a constant temperature 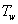 which is higher than the constant temperature
which is higher than the constant temperature 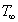 of the surrounding fluid. Since the plate is considered semi-infinite in the x-direction, all physical variables are functions of y and t only. Then, under the Boussinesq’s and boundary layer approximation s, also with the spirit of Gebhart (1962), Singh and Sacheti (1988) and Gebhart and Mollendorf (1969) proposed the governing equations:Continuity equation
of the surrounding fluid. Since the plate is considered semi-infinite in the x-direction, all physical variables are functions of y and t only. Then, under the Boussinesq’s and boundary layer approximation s, also with the spirit of Gebhart (1962), Singh and Sacheti (1988) and Gebhart and Mollendorf (1969) proposed the governing equations:Continuity equation 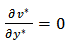
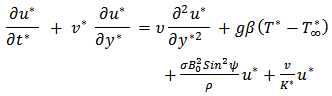
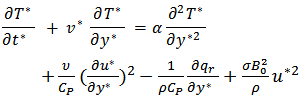
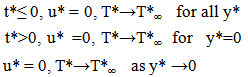
 denotes conditions in the free stream. For optically thick fluid we have Modest (1993) as follows the radiative heat flux term by using the Rosseland approximation is given by
denotes conditions in the free stream. For optically thick fluid we have Modest (1993) as follows the radiative heat flux term by using the Rosseland approximation is given by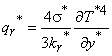
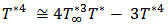
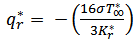
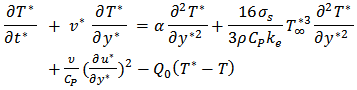
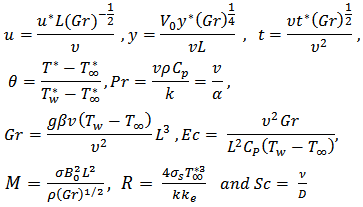
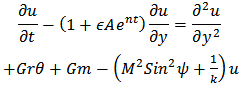
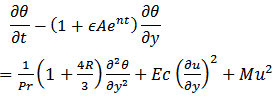
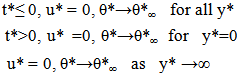
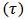 and Nusselt number (Nu) can be characterized in order by
and Nusselt number (Nu) can be characterized in order by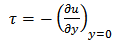
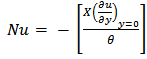
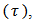 average of Nusselt number (Nu) in dimensionless form can be written as
average of Nusselt number (Nu) in dimensionless form can be written as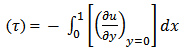
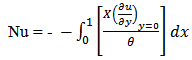
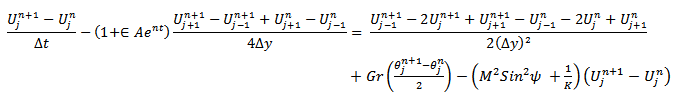
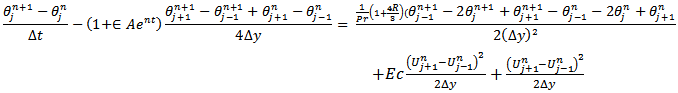
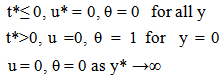
 are known at all grid points at t=0 from the initial conditions. The computations of the values of u and
are known at all grid points at t=0 from the initial conditions. The computations of the values of u and 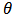 at the (n+1)th time using the values at previous time (n)th are carried out in this form:At all grid points, the values of
at the (n+1)th time using the values at previous time (n)th are carried out in this form:At all grid points, the values of 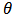 and u at t=0 from the initial conditions are known. Therefore, the values of
and u at t=0 from the initial conditions are known. Therefore, the values of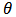 at the next time step are calculated using the values already known from the previous values. In this case, the finite difference Equations form a tri-diagonal system of equations where the values of
at the next time step are calculated using the values already known from the previous values. In this case, the finite difference Equations form a tri-diagonal system of equations where the values of 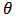 at every nodal point at next time step are determined using the known values at the previous time. We therefore employ Thomas algorithm to solve the tri-diagonal system of equations. In this way, we were able to get the values of
at every nodal point at next time step are determined using the known values at the previous time. We therefore employ Thomas algorithm to solve the tri-diagonal system of equations. In this way, we were able to get the values of 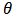 at every nodal point. The values of u are also computed at that particular time. Several values of u and
at every nodal point. The values of u are also computed at that particular time. Several values of u and 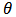 were obtained for the required time using this process. The mesh size are ∆Y =0.16 and
were obtained for the required time using this process. The mesh size are ∆Y =0.16 and 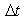 =0.01.
=0.01.












 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML












