-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2014; 4(2): 69-78
doi:10.5923/j.ajfd.20140402.03
LES Modelling of Nitric Oxide (NO) Formation in a Propane-Air Turbulent Reacting Flame
Sreebash C. Paul1, Manosh C. Paul2, Suvash C. Saha3
1Department of Arts and Sciences, Ahsanullah University of Science and Technology, Dhaka 1208, Bangladesh
2Systems, Power & Energy Research Division, School of Engineering, University of Glasgow, Glasgow G12 8QQ, UK
3School of Chemistry, Physics and Mechanical Engineering, Queensland University of Technology, 2 George St., GPO Box 2434, Brisbane QLD 4001, Australia
Correspondence to: Suvash C. Saha, School of Chemistry, Physics and Mechanical Engineering, Queensland University of Technology, 2 George St., GPO Box 2434, Brisbane QLD 4001, Australia.
| Email: |  |
Copyright © 2014 Scientific & Academic Publishing. All Rights Reserved.
Large Eddy Simulation (LES) technique is applied to investigate the nitric oxide (NO) formation in the propane-air flame inside a cylindrical combustor. In LES a spatial filtering is applied to the governing equations to separate the flow field into large scale eddies and small scale eddies. The large scale eddies which carry most of the turbulent energy are resolved explicitly while the unresolved small scale eddies are modelled. A Smagorinsky model with model constant Cs = 0.1 as well as a dynamic model has been employed for modelling of the sub-grid scale eddies, while the nonpremixed combustion process is modelled through the conserved scalar approach with laminar flamelet model. In NO formation model, the extended Zeldovich (thermal) reaction mechanism is taken into account through a transport equation for NO mass fraction. The computational results are compared with those of the experimental results investigated by Nishida and Mukohara [1] in co-flowing turbulent flame.
Keywords: Large Eddy Simulation, Turbulent Flow, Combustion, Laminar Flamelet, NO formation, Sub-Grid Scale
Cite this paper: Sreebash C. Paul, Manosh C. Paul, Suvash C. Saha, LES Modelling of Nitric Oxide (NO) Formation in a Propane-Air Turbulent Reacting Flame, American Journal of Fluid Dynamics, Vol. 4 No. 2, 2014, pp. 69-78. doi: 10.5923/j.ajfd.20140402.03.
Article Outline
1. Introduction
- In every circumstances where combustion occurs, the formation of Nitrogen Oxides (NOx) are unavoidable. From a home open fire to a coal fired power plant, NOx is formed as an undesired product and a contributor to air pollution and health problems. Due to the increasing concerns over the environmental pollution, the understanding of the NOx formation mechanism during the combustion process and of the development of their reduction technologies is essential for the efficient design of combustion devices. But, one of the great challenges in predicting the formation of the NOx in a combustion process is the chemical time-scale, which is slow.NOx is used to refer to the nitric oxide NO and the nitrogen oxide NO2. Typically 95% of the total NOx emissions is nitric oxide, NO, which is the primary form in combustion products. The nitric oxide NO is subsequently oxidized to NO2 in the atmosphere.There are four different routes or mechanisms in the formation of NOx, which were identified by Bowman [2]. These are the thermal NO route, the prompt NO route, the N2O (nitrous oxide) route, and the fuel-bound nitrogen route.But, it is known that in nonpremixed combustion of hydrocarbon fuels, the first two mechanisms dominate the process of nitric oxide, NO, formation. The thermal NO also well-known as the Zeldovich NO proposed by Zeldovich [3], which dominantly depends on its local temperature and reactants (O2 and N2). The prompt or Fenimore NO mechanism proposed by Fenimore [4], is formed through hydro-carbon radical reaction with molecular nitrogen under fuel-rich condition. In most flames, especially those from nitrogen-containing fuels, the prompt mechanism is responsible for only a small fraction of the total NOx.Meunier et al. [5] investigated the NOx emissions from turbulent propane diffusion flames experimentally as well as numerically. In numerical investigation both the thermal and prompt NO reaction mechanism were used to predict NO formation. The equations were closed by k-ϵ turbulence model where as the combustion was modelled using the stretched laminar flamelet model and the probability density function (PDF) method.Formation characteristics of the nitric oxide in a three-stage air/LPG flame has been investigated both experimentally and numerically by Kim et al. [6] including both the thermal and the prompt NO formation mechanism through a conservation equation of NO mass fraction. The computed results were compared with the experimental measurements.For the hydrogen jet diffusion flame, a prediction method for NO applicable to LES was presented by Taniguchi et al. [7]. To model NO production, they considered the extended Zeldovich mechanism with the quasi-steady state approximation of the nitric atom through the balance equation of NO mass fraction. In LES, they neglected the SGS contribution to the NO production. Modeling of radiation and NO formation in turbulent nonpremixed flames using a flamelet/progress variable formulation has been investigated by Ihme and Pitsch [8]. In NO production model, a transport equation for the NO mass fraction was considered, and they obtained the chemical source term from the flamelet library. The NO model formulation was analyzed separately for the thermal, nitrous oxide, and prompt NO reaction mechanisms.Chun et al. [9] performed a numerical study on extinction and NOx formation in nonpremixed flames with syngas fuel. Numerical simulations were done in a quasi-one dimensional counterflow configuration using the OPPDIF code adopting GRI-Mech 3.0 for the chemical reaction mechanism. They have considered a reaction path diagram to analyze NOx formation pathways along with the thermal NOx formation mechanism. They found that the NO production through the thermal mechanism was weakened more than that through the non-thermal mechanism, and most of the NOx production started from the N2 → NNH pathway. In this paper LES technique has been applied to investigate the NO formation in the non-premixed propane-air turbulent combustion process within a cylindrical combustor. A schematic of computational domain is shown in Fig. 1. Gaseous propane (C3H8) is injected through a circular nozzle of an internal diameter of 2mm at the centre of the combustor inlet while the preheated air of temperature 773K with an averaged velocity of 0.96ms−1 is supplied through the circular inlet of 115mm internal diameter into the 350mm long combustion chamber. The overall equivalence ratio is 0.6 so that burning occurs in a fuel-rich nonpremixed combustion mode, which produces various forms of hydrocarbons in the combustion products. The average fuel velocity measured by [1] at the inlet is 30ms−1. A Smagorinsky model with Cs = 0.1 as well as its dynamic calibration has been employed to model the sub-grid scale stresses, while the non-premixed combustion process is modelled through the conserved scalar approach with laminar flamelet model. The NO production mechanism is modelled through a balance equation for NO mass fraction. The extended Zeldovich (thermal) reaction mechanism is taken into account to model the NO production.
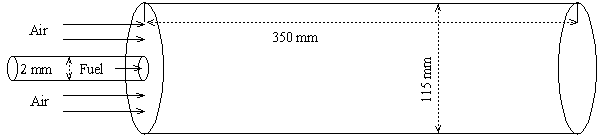 | Figure 1. A schematic of the cylindrical combustor with short computational domain |
2. Nitric Oxide (NO) Prediction Model
- In a non-premixed combustion process a high temperature is occurred at the stoichiometric interface where the thermal reaction mechanism of NO dominates its formation. So, the maximum flame temperature is the most important parameter that determines the potential for NO formation. The high NO levels that occur in practical systems can only be reduced by reducing the thermal NO formation. In the present NO formation model, the extended Zeldovich (thermal) reaction mechanism proposed by Zeldovich [3], is taken into account through the solution of a transport equation for NO mass fraction (see equation (8)). The extended Zeldovich reaction mechanism has the following three reactions;
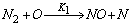 | (1) |
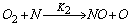 | (2) |
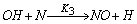 | (3) |
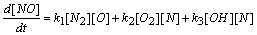 | (4) |
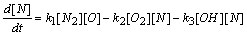 | (5) |
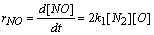 | (6) |
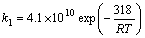 | (7) |
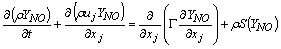 | (8) |
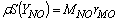 | (9) |
3. Mathematical Formulation for LES
- In LES, a spatial filtering operation is applied to the governing equations of motions to separate the large scale (resolved scale) flow field from the small scale (sub-grid scale), Leonard [12]. Employing the density weighted Favre-filtered function, Favre [13] to the continuity equation, Navier- Stokes equations, the mixture fraction (conserved scalar) equation, and the conservation equation for NO mass fraction equation gives:
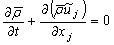 | (10) |
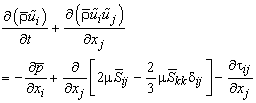 | (11) |
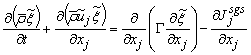 | (12) |
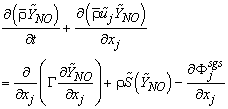 | (13) |
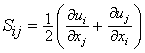 is the strain rate, δij is the kronecker delta, ξ is the conserved scalar or mixture fraction and
is the strain rate, δij is the kronecker delta, ξ is the conserved scalar or mixture fraction and 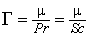 is the diffusion coefficient.The instantaneous source term,
is the diffusion coefficient.The instantaneous source term, 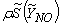 , in conservation equation (13) for NO mass fraction is written as,
, in conservation equation (13) for NO mass fraction is written as,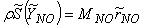 | (14) |
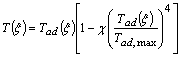 | (15) |
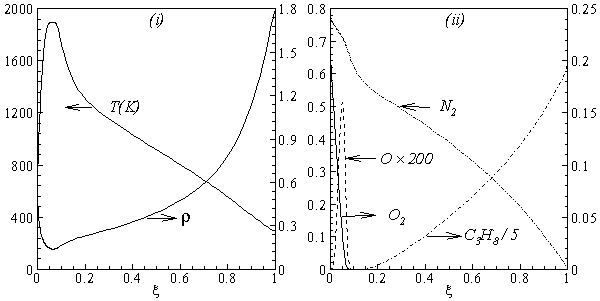 | Figure 2. Laminar flamelet calculation for strain rate of 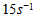 : dependance of (i) temparature and density; and (ii) mole fractions of C3H8, N2, O and O2, on the mixture fraction, ξ : dependance of (i) temparature and density; and (ii) mole fractions of C3H8, N2, O and O2, on the mixture fraction, ξ |
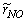 , for NO formation may therefore be determined by
, for NO formation may therefore be determined by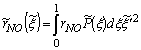 | (16) |
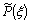 is the β-pdf (probability density function) constructed from predicted values of the conserved scalar,
is the β-pdf (probability density function) constructed from predicted values of the conserved scalar, 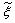 , and the sub-grid scalar variance,
, and the sub-grid scalar variance, 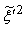 . Due to high peak appeared in NO production rate, it is convenient to use a piece-wise polynomial fitting approach (for details see, Paul [16]) for the best data fitting of the rNO. Thus, a piece-wise polynomial fitting approach is used to integrate the β-pdf.
. Due to high peak appeared in NO production rate, it is convenient to use a piece-wise polynomial fitting approach (for details see, Paul [16]) for the best data fitting of the rNO. Thus, a piece-wise polynomial fitting approach is used to integrate the β-pdf.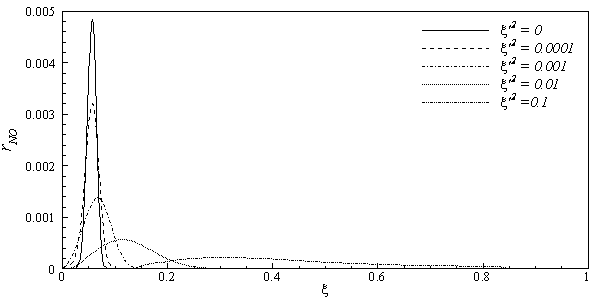 | Figure 3. Dependence of the instantaneous NO production rate on the mixture fraction and mixture fraction variances |
 | (17) |
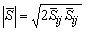 is the magnitude of the large scale strain rate tensor,
is the magnitude of the large scale strain rate tensor, 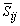 . Two computations have been performed, one with Cs = 0.1 (Case1) and another one with its dynamically calibrated values (Case2), proposed by Germano et al. [18].For the subgrid scale scalar fluxes,
. Two computations have been performed, one with Cs = 0.1 (Case1) and another one with its dynamically calibrated values (Case2), proposed by Germano et al. [18].For the subgrid scale scalar fluxes, 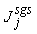 , a gradient model, proposed by Schmidt and Schumann [19], of the form
, a gradient model, proposed by Schmidt and Schumann [19], of the form | (18) |
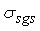 is a constant sub-grid scale Prandtl/Schmidt number which is assigned a value of 0.7.In the NO model, we have used the same gradient model of Schmidt and Schumann [19] for modelling the subgrid scale NO mass fraction fluxes,
is a constant sub-grid scale Prandtl/Schmidt number which is assigned a value of 0.7.In the NO model, we have used the same gradient model of Schmidt and Schumann [19] for modelling the subgrid scale NO mass fraction fluxes, 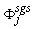 .The conserved scalar modelling approach with the laminar flamelet model, Peters [20], is applied to model the combustion. In this approach, it is assumed that the chemical reaction rates are fast compared to the rate at which the reactants mix. The mixing process is described by a conserved scalar which is also known as the mixture fraction. It is then considered that the instantaneous species concentrations are a unique function of this mixture fraction. Since this functional dependence is highly nonlinear, the mean or filtered values are obtained via the probability density function of the mixture fraction, Bilger [21]. The filtered density (
.The conserved scalar modelling approach with the laminar flamelet model, Peters [20], is applied to model the combustion. In this approach, it is assumed that the chemical reaction rates are fast compared to the rate at which the reactants mix. The mixing process is described by a conserved scalar which is also known as the mixture fraction. It is then considered that the instantaneous species concentrations are a unique function of this mixture fraction. Since this functional dependence is highly nonlinear, the mean or filtered values are obtained via the probability density function of the mixture fraction, Bilger [21]. The filtered density (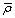 ) and density weighted thermochemical variables (
) and density weighted thermochemical variables (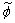 ) are obtained by integrating over a β - probability density function, once the density weighted mixture fraction,
) are obtained by integrating over a β - probability density function, once the density weighted mixture fraction, 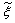 , and its sub-grid scale variance are known. Further details of this model are found in Paul [16], Paul et al. [22] and di Mare et al. [23].
, and its sub-grid scale variance are known. Further details of this model are found in Paul [16], Paul et al. [22] and di Mare et al. [23].4. Numerical Procedure
- For the present simulation, a curvilinear body fitted coordinate system is employed. Inside the combustion chamber the grid consisting of a total of about 1.5 million nodes with a non-uniform mesh distributed along the three co-ordinate directions. As the fuel is injected through a circular nozzle at centre of the combustor inlet at a speed relatively higher than that of the air supplied through the cylinder, a steep gradient appears in this area. To resolve this steep gradient adequately a very fine mesh is required at the centre of the combustor. The mesh lines are contracted at the centre and the inlet of the combustor, and they are expanded smoothly in all the three directions outwards from the centerline and inlet. The numerical solution procedure is based on the finite volume approach where the governing equations are integrated over the mesh control volume. The finite volume based in-house developed code LES-BOFFIN (Boundary Fitted Flow Integrator) has been used to solve the governing equations. The code is second order accurate in both space and time. The BOFFIN code has been applied extensively in the LES of reacting and non-reacting turbulent flows; for examples, see LES of a turbulent non-premixed propane-ar reacting flame, Paul et al. [22], of a gas turbine combustor, di Mare et al. [23] and of a turbulent nonpremixed flame, Branley and Jones [24]. Details of the numerical method used in the BOFFIN are not presented here for brevity.In the simulation fully-developed turbulent pipe flow profiles were applied as the instantaneous inflow boundary conditions at the fuel nozzle, while a uniform velocity profile is applied for the air flow. The mixture fraction at the inlet is defined as
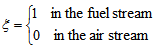 | (19) |
5. Results and Discussion
- We present the computational results in this section. The average time step, dt, used in the computation is at the order of 10−6. The results presented here in the form of time mean which are defined as
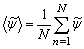 | (20) |
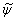 is the time dependent results of a total of N = 3 x 105 time steps.The results are obtained for two cases, Smagorinsky constant, Cs, of 0.1 (Case 1) and dynamically calibrated Cs (Case 2). The solid lines indicate Case 1 and the dashed lines represent Case 2.
is the time dependent results of a total of N = 3 x 105 time steps.The results are obtained for two cases, Smagorinsky constant, Cs, of 0.1 (Case 1) and dynamically calibrated Cs (Case 2). The solid lines indicate Case 1 and the dashed lines represent Case 2.5.1. Temperature and Species Mole Fractions
- The results of temperature and species mole fractions, which are required as an input to the NO formation model, are presented here.Computationally predicted mean temperature,
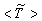 , results along axial and radial direction at different cross sectional positions are compared against the experimental measurement done by Nishida and Mukohara [1] in Fig. 4. In Fig. 4(a), at the inlet the predicted mean axial temperature on the centerline is same as the injected fuel temperature. The flame temperature then starts increasing and achieves a maximum value of 1696K (Case1) and 1730K (Case2) at the outlet. The corresponding peak temperature in the experimental investigation was recorded as 1765K, so the computation slightly under predict the temperature at the outlet. But the peak level of the mean temperature is better predicted in Case2. Moreover, the experimental results show a concave like shape around y = 0.2m, which is not evident in the predictions where a slight over-prediction is evident in both the cases.In Fig. 4(b-d), the radial distribution of the mean temperature shows that the peak value of the computed temperature is slightly under-predicted and moves towards the wall near the inlet (frames b, c), and the temperature at the centre shows slight over-prediction in both the Cases. But a slight under-prediction of the temperature occurs at the centre in the downstream (frames d), but a better prediction is found in Case 2. Comparing the computed temperature distributions with the experiment, it is found that the trend of increasing and decaying of the temperature in the radial direction is matched reasonably well with the experimental data. However, both quantitatively and qualitatively a very good agreement is achieved with experiment.
, results along axial and radial direction at different cross sectional positions are compared against the experimental measurement done by Nishida and Mukohara [1] in Fig. 4. In Fig. 4(a), at the inlet the predicted mean axial temperature on the centerline is same as the injected fuel temperature. The flame temperature then starts increasing and achieves a maximum value of 1696K (Case1) and 1730K (Case2) at the outlet. The corresponding peak temperature in the experimental investigation was recorded as 1765K, so the computation slightly under predict the temperature at the outlet. But the peak level of the mean temperature is better predicted in Case2. Moreover, the experimental results show a concave like shape around y = 0.2m, which is not evident in the predictions where a slight over-prediction is evident in both the cases.In Fig. 4(b-d), the radial distribution of the mean temperature shows that the peak value of the computed temperature is slightly under-predicted and moves towards the wall near the inlet (frames b, c), and the temperature at the centre shows slight over-prediction in both the Cases. But a slight under-prediction of the temperature occurs at the centre in the downstream (frames d), but a better prediction is found in Case 2. Comparing the computed temperature distributions with the experiment, it is found that the trend of increasing and decaying of the temperature in the radial direction is matched reasonably well with the experimental data. However, both quantitatively and qualitatively a very good agreement is achieved with experiment.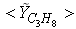 has an excellent agreement with the experimental result. The mole fraction of the reactant
has an excellent agreement with the experimental result. The mole fraction of the reactant  in Fig. 5(b) is predicted well. While the
in Fig. 5(b) is predicted well. While the 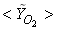 in Fig. 5(c) is under-predicted at the downstream but predicted well against the experiment at the upstream. From the radial profiles for reactants
in Fig. 5(c) is under-predicted at the downstream but predicted well against the experiment at the upstream. From the radial profiles for reactants 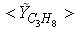 ,
, 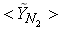 and
and 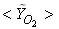 in both locations at y = 0.1m (Fig. 6) and y = 0.3m (Fig. 7), we have a good agreement with the experiment. However, there are slightly over- and under- prediction at some positions but the trend is matched well with experimental measurements.
in both locations at y = 0.1m (Fig. 6) and y = 0.3m (Fig. 7), we have a good agreement with the experiment. However, there are slightly over- and under- prediction at some positions but the trend is matched well with experimental measurements. 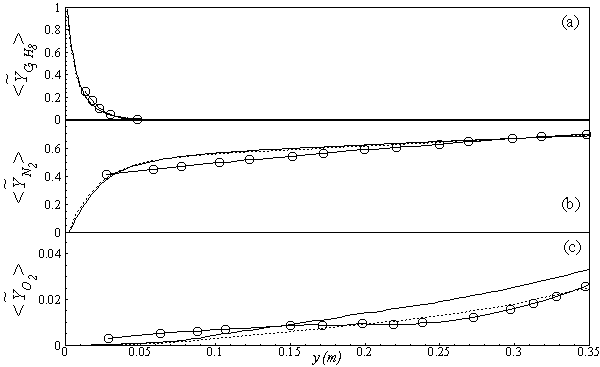 | Figure 5. Mean mole fractions: (a) 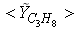 , (b) , (b) 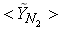 and (c) and (c) 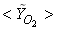 along the axial direction; Solid line, Case1; Dashed line, Case2; Solid line with circle, experiment along the axial direction; Solid line, Case1; Dashed line, Case2; Solid line with circle, experiment |
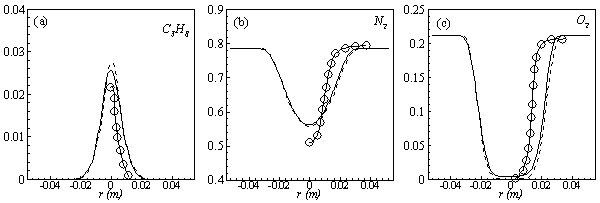 | Figure 6. Mean mole fractions: (a) 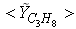 , (b) , (b) 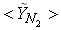 and (c) and (c) 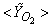 along the radial direction at y = 0.1m; Solid line, Case1; Dashed line, Case2; Solid line with circle, experiment along the radial direction at y = 0.1m; Solid line, Case1; Dashed line, Case2; Solid line with circle, experiment |
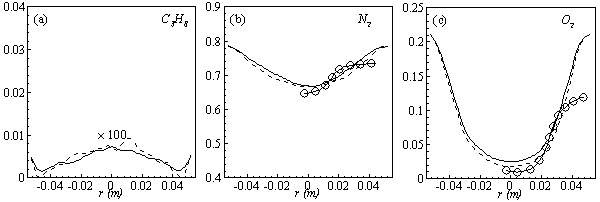 | Figure 7. Mean mole fractions: (a) 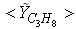 , (b) , (b) 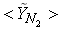 and (c) and (c) 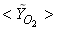 along the radial direction at y = 0.3m; Solid line, Case1; Dashed line, Case2; Solid line with circle, experiment along the radial direction at y = 0.3m; Solid line, Case1; Dashed line, Case2; Solid line with circle, experiment |
5.2. Production Rate and Mass Fraction of NO
- In Fig. 8 the time averaged results of the (a) temperature,
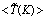 , (b) NO production rate,
, (b) NO production rate, 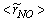 , and (c) mass fraction of NO,
, and (c) mass fraction of NO, 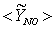 , on the horizontal midplane of the combustor are plotted. The solid lines shown on the contour plots represent the locus of the stoichiometric mixture fraction. These contour plots, obtained in Case1, clearly show that the production of NO is highly dependent on both the flame temperature (frame (a)) and the concentration of N2 (Fig. 5(b)). The mass fraction of NO reaches the maximum level at the stoichiometric zone.
, on the horizontal midplane of the combustor are plotted. The solid lines shown on the contour plots represent the locus of the stoichiometric mixture fraction. These contour plots, obtained in Case1, clearly show that the production of NO is highly dependent on both the flame temperature (frame (a)) and the concentration of N2 (Fig. 5(b)). The mass fraction of NO reaches the maximum level at the stoichiometric zone. 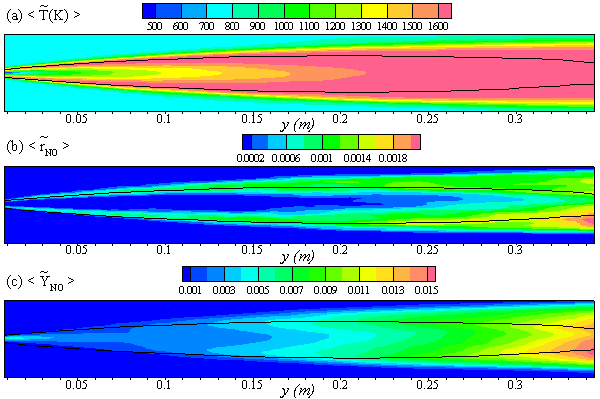 | Figure 8. The mean values of the (a) temperature, 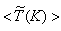 , (b) NO production rate, , (b) NO production rate, 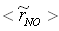 , and (c) NO mass fraction, , and (c) NO mass fraction, 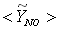 on the horizontal mid-plane of the combustor, for Case 1 on the horizontal mid-plane of the combustor, for Case 1 |
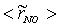 , are depicted in Fig. 9. Axial profile on the centerline of the combustor, plotted in Fig. 9(a), shows that the rate is zero upto the axial distance y = 0.1, where the fuel stream dominates, afterwards the rate increases and gets its maximum at the outlet of the combustor. From the radial profile of the NO production rate, plotted in Fig. 9(b-d), it can be seen that the peak values are predicted in between the centerline and the combustor wall where the temperature (see Fig. 5(b-d)) as well as the concentration of N2 (Fig. 6(b), 7(b)) has also its maximum, which can clearly be seen from the mean plot of the NO production rate presented in Fig. 8.Predicted axial profile of the NO mass fraction (Fig. 10(a)) increases gradually as the flame temperature increases and achieves a peak level at the outlet of the combustor the maximum temperature (Fig. 4(a)) is recorded. This is simply because the present NO formation model includes the Zeldovich or thermal reaction mechanism in which the NO production rate is highly dependent on the temperature and reactants (N2 and O2). The radial profiles (Figs. 10(b-d)) of the NO mass fraction show that the NO production level decreases along the radial direction because of the temperature near the combustor wall which is very low although the N2 level is predicted high in this region.
, are depicted in Fig. 9. Axial profile on the centerline of the combustor, plotted in Fig. 9(a), shows that the rate is zero upto the axial distance y = 0.1, where the fuel stream dominates, afterwards the rate increases and gets its maximum at the outlet of the combustor. From the radial profile of the NO production rate, plotted in Fig. 9(b-d), it can be seen that the peak values are predicted in between the centerline and the combustor wall where the temperature (see Fig. 5(b-d)) as well as the concentration of N2 (Fig. 6(b), 7(b)) has also its maximum, which can clearly be seen from the mean plot of the NO production rate presented in Fig. 8.Predicted axial profile of the NO mass fraction (Fig. 10(a)) increases gradually as the flame temperature increases and achieves a peak level at the outlet of the combustor the maximum temperature (Fig. 4(a)) is recorded. This is simply because the present NO formation model includes the Zeldovich or thermal reaction mechanism in which the NO production rate is highly dependent on the temperature and reactants (N2 and O2). The radial profiles (Figs. 10(b-d)) of the NO mass fraction show that the NO production level decreases along the radial direction because of the temperature near the combustor wall which is very low although the N2 level is predicted high in this region. 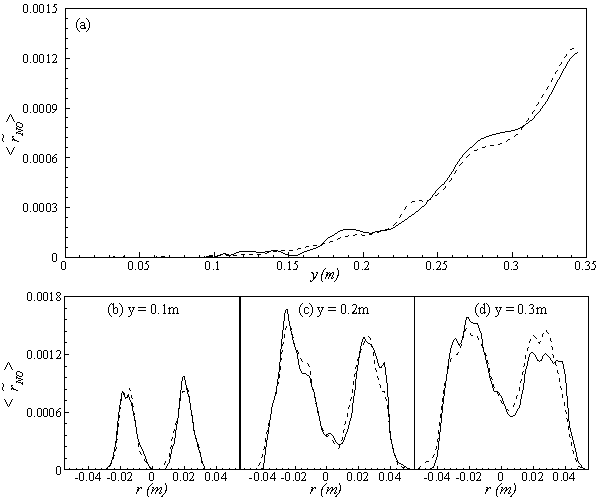 | Figure 9. Mean values of NO production rate, 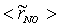 , along the (a) axial direction and radial direction at the different cross-section positions: (b) y = 0:1m, (c) y = 0:2m, (d) y = 0:3m of the combustor , along the (a) axial direction and radial direction at the different cross-section positions: (b) y = 0:1m, (c) y = 0:2m, (d) y = 0:3m of the combustor |
6. Conclusions
- Large Eddy Simulation technique has been applied to investigate the NO production in the non-premixed propane/air turbulent combustion process within a cylindrical combustor. In LES a constant valued Smagorinsky model as well as a dynamic model is taken into account for modelling the sub-grid scale stresses. The non-premixed combustion process is modelled through the conserved scalar approach with the laminar flamelet model, while the NO production mechanism is modelled through a balance equation for NO mass fraction. The extended Zeldovich (thermal) reaction mechanism is taken into account to model the NO production.The computational results of temperature and selected species mole fractions have been compared with the experimental data obtained by Nishida and Mukohara [1] in the turbulent co-flowing propane and preheated air combustion, where a good agreement is achieved. It was not possible to compare the computational results of the NO mass fraction with experimental data, as Nishida and Mukohara [1] did not perform any measurements on the NO mass fraction. However, the present results of NO clearly agree well with the principle and reaction mechanism of the extended Zeldovich (thermal) used for the modeling of NO. The NO mass fraction is predicted high in the high temperature zone.The results are almost uninfluenced by the choice of sub-grid scale models although slightly lower prediction of NO mass fraction is found with dynamic Cs in the upstream. However, dynamic Cs produces a higher levels of the sub-grid scale quantities in the upstream region.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML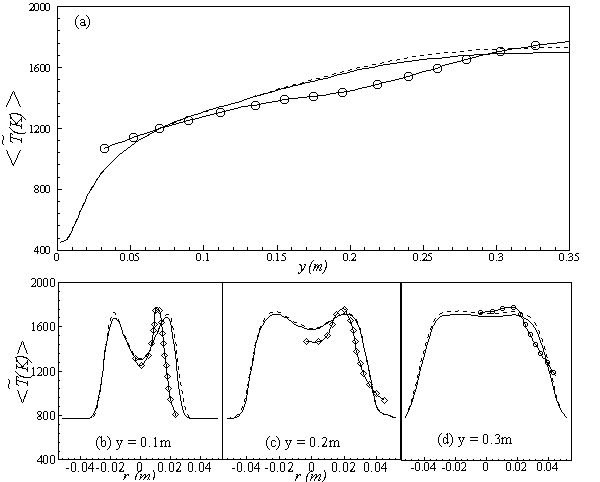
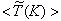 , with those of the experimental data along the (a) axial direction, and the radial direction at different cross-sectional positions: (b) y = 0:1m, (c) y = 0:2m and (d) y = 0.3m; Solid line, Case1; Dashed line, Case2; Solid line with circle, experimental
, with those of the experimental data along the (a) axial direction, and the radial direction at different cross-sectional positions: (b) y = 0:1m, (c) y = 0:2m and (d) y = 0.3m; Solid line, Case1; Dashed line, Case2; Solid line with circle, experimental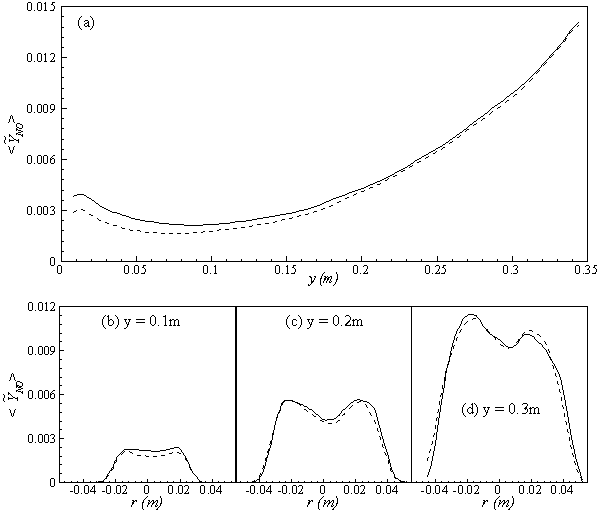
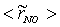 , along the (a) axial direction and radial direction at the different cross-section positions: (b) y = 0:1m, (c) y = 0:2m, (d) y = 0:3m of the combustor
, along the (a) axial direction and radial direction at the different cross-section positions: (b) y = 0:1m, (c) y = 0:2m, (d) y = 0:3m of the combustor