-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2013; 3(5): 135-142
doi:10.5923/j.ajfd.20130305.01
Derivation of the Similarity Equation of the 2-D Unsteady Boundary Layer Equations and the Corresponding Similarity Conditions
Md. Abdus Sattar
Britannia University, Comilla, Bangladesh
Correspondence to: Md. Abdus Sattar, Britannia University, Comilla, Bangladesh.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
A local similarity equation for the hydrodynamic 2-D unsteady boundary layer equations has been derived based on a time dependent length scale initially introduced by the author in solving several unsteady one-dimensional boundary layer problems. Similarity conditions for the potential flow velocity distribution are also derived. This derivation shows that local similarity solutions exist only when the potential velocity is inversely proportional to a power of the length scale mentioned above and is directly proportional to a power of the length measured along the boundary. For a particular case of a flat plate the de rived similarity equation exactly corresponds to the one obtained by Ma and Hui[1]. Numerical solutions to the above similarity equation are also obtained and displayed graphically. The obtained results are found to agree well with published results.
Keywords: Similarity equation, Boundary layer equations, Potential flow velocity
Cite this paper: Md. Abdus Sattar, Derivation of the Similarity Equation of the 2-D Unsteady Boundary Layer Equations and the Corresponding Similarity Conditions, American Journal of Fluid Dynamics, Vol. 3 No. 5, 2013, pp. 135-142. doi: 10.5923/j.ajfd.20130305.01.
Article Outline
1. Introduction
- Similar solutions to a boundary layer flow are important with respect to the mathematical character of the solutions. In particular the phenomenon of similarity constitutes a considerable mathematical simplification of the problem of solving a system of partial differential equations that arise in boundary layer flows. A goal of this simplification however looks for the type of potential flows for which similar solutions exist.When the question of similarity solutions of the 2-D steady boundary layer equations arise, there appears two classes of solutions which are characterized completely by the potential flow velocity one of which is
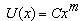 where
where 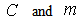 are constants. Falkner and Skan[2] derived this potential flow velocity as a condition for the similarity solutions to exist. Two special cases of the Falkner and Skan similarity solutions are (i)
are constants. Falkner and Skan[2] derived this potential flow velocity as a condition for the similarity solutions to exist. Two special cases of the Falkner and Skan similarity solutions are (i) 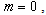 that leads to the famous Blasius[3] solution and (ii)
that leads to the famous Blasius[3] solution and (ii) 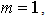 that leads to the Hiemenz[4] stagnation point flow. The other case of the potential flow velocity is
that leads to the Hiemenz[4] stagnation point flow. The other case of the potential flow velocity is 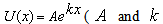 are constants) which may be considered as a limiting case of the first case when
are constants) which may be considered as a limiting case of the first case when 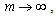 and which is less explored.The similarity solutions to the unsteady 2-D boundary layer equations compared to the steady case mentioned above is much complex due to the fact that the three variables
and which is less explored.The similarity solutions to the unsteady 2-D boundary layer equations compared to the steady case mentioned above is much complex due to the fact that the three variables 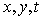 need to be reduced to a single variable, say,
need to be reduced to a single variable, say, 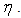 Perhaps Rayleigh[5] was the pioneer in this respect. However H. Schuh[6] and Th. Geis[7] have indicated the class of similarity solutions for which a reduction to a single variable is possible such as
Perhaps Rayleigh[5] was the pioneer in this respect. However H. Schuh[6] and Th. Geis[7] have indicated the class of similarity solutions for which a reduction to a single variable is possible such as 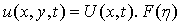 with
with 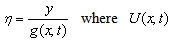 is the potential flow velocity and
is the potential flow velocity and 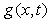 is the scale factor of the ordinate. Potential flow velocity in such cases were taken to be of the form
is the scale factor of the ordinate. Potential flow velocity in such cases were taken to be of the form 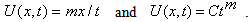 Similarity solutions for the potential flow velocity of the form
Similarity solutions for the potential flow velocity of the form 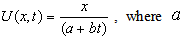 and b are constants, were analyzed by Yang[8]. In recent time Ma and Hui[1] discussed briefly the three types of similarity solutions of the 2-D unsteady boundary layer equations starting with that of Rayleigh and analyzed those solutions using classical Lie Algebra. Their solutions were, however, limited to the case of taking density
and b are constants, were analyzed by Yang[8]. In recent time Ma and Hui[1] discussed briefly the three types of similarity solutions of the 2-D unsteady boundary layer equations starting with that of Rayleigh and analyzed those solutions using classical Lie Algebra. Their solutions were, however, limited to the case of taking density 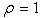 and kinematic viscosity
and kinematic viscosity 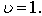 Semi-similar solutions of the unsteady boundary layer flows including separation was developed by Williams and Johnson[9] using a simplified scheme. Burde[10] constructed several new explicit solutions of unsteady boundary layer flows some of which appear to be undetected by other similarity reduction method. Following Ma and Hui, Ludlow et al.[11] made a rigorous approach by using one parameter Lie Group to obtain some new similarity solutions of the same boundary layer equations.An approximate integral method analogous to the Karman-Pohlhausen procedure was introduced by Bianchini et al.[12] to calculate the characteristics of the unsteady 2-D boundary layer flows, but taking the potential flow velocity simply as a function of time
Semi-similar solutions of the unsteady boundary layer flows including separation was developed by Williams and Johnson[9] using a simplified scheme. Burde[10] constructed several new explicit solutions of unsteady boundary layer flows some of which appear to be undetected by other similarity reduction method. Following Ma and Hui, Ludlow et al.[11] made a rigorous approach by using one parameter Lie Group to obtain some new similarity solutions of the same boundary layer equations.An approximate integral method analogous to the Karman-Pohlhausen procedure was introduced by Bianchini et al.[12] to calculate the characteristics of the unsteady 2-D boundary layer flows, but taking the potential flow velocity simply as a function of time 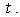 Later, this method was modified by Sattar[13] taking the potential flow velocity as a function of
Later, this method was modified by Sattar[13] taking the potential flow velocity as a function of 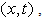 where a time dependent length scale
where a time dependent length scale 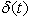 was introduced. The first introduction of this length scale to obtain local similarity solution in time of a one-dimensional unsteady heat and mass transfer flow was, to the best of the knowledge of the author, made by Sattar and Hossain[14]. With the aid of this similarity concept, many papers were published by the author and his co-workers some of which are Sattar[15,16], Alam and Sattar[17], Sattar and Maleque[18] and Rahman and Sattar[19]. Seddeek & Aboeldahab[20] and recently Chamkha et al.[21] applied the same time-dependent similarity parameter technique for the solutions of unsteady one-dimensional MHD free convection boundary layer problems.The objective in this article is to find a similarity reduction of the 2-D unsteady hydrodynamic boundary layer partial differential equations to a single ordinary differential equation, namely a local similarity equation, with a goal to derive the similarity conditions for the potential flow velocity distribution. Unlike the methods adopted so far in solving 2-D unsteady boundary layer equations, a further goal of the article is to extend the idea of introducing the time dependent length scale
was introduced. The first introduction of this length scale to obtain local similarity solution in time of a one-dimensional unsteady heat and mass transfer flow was, to the best of the knowledge of the author, made by Sattar and Hossain[14]. With the aid of this similarity concept, many papers were published by the author and his co-workers some of which are Sattar[15,16], Alam and Sattar[17], Sattar and Maleque[18] and Rahman and Sattar[19]. Seddeek & Aboeldahab[20] and recently Chamkha et al.[21] applied the same time-dependent similarity parameter technique for the solutions of unsteady one-dimensional MHD free convection boundary layer problems.The objective in this article is to find a similarity reduction of the 2-D unsteady hydrodynamic boundary layer partial differential equations to a single ordinary differential equation, namely a local similarity equation, with a goal to derive the similarity conditions for the potential flow velocity distribution. Unlike the methods adopted so far in solving 2-D unsteady boundary layer equations, a further goal of the article is to extend the idea of introducing the time dependent length scale 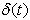 to obtain the local similarity equation.
to obtain the local similarity equation.2. Mathematical Formulation
- Let us consider the unsteady two-dimensional hydrodynamic boundary layer equations which are
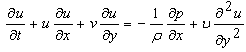 | (1) |
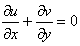 | (2) |
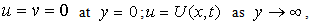 | (3) |
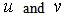 are the velocity components along
are the velocity components along 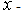 axis which is the direction of the flow along the boundary and
axis which is the direction of the flow along the boundary and 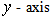 perpendicular to the boundary respectively,
perpendicular to the boundary respectively, 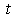 is the time,
is the time, 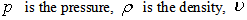 is the kinematic coefficient of viscosity and
is the kinematic coefficient of viscosity and 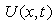 is the potential flow velocity.In order to address the question of similarity of the equations (1) and (2), dimensionless quantities need to be introduced. Thus all lengths are referred to a time dependent length scale
is the potential flow velocity.In order to address the question of similarity of the equations (1) and (2), dimensionless quantities need to be introduced. Thus all lengths are referred to a time dependent length scale 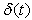 in line with the work of Sattar & Hossain [14]. Since the
in line with the work of Sattar & Hossain [14]. Since the 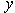 -coordinate is mainly related to the boundary layer growth, it is referred to a dimensionless scale factor
-coordinate is mainly related to the boundary layer growth, it is referred to a dimensionless scale factor 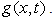 Therefore, the following dimensionless lengths are introduced:
Therefore, the following dimensionless lengths are introduced: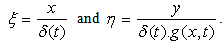 | (4) |
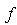 is defined as
is defined as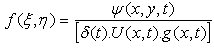 | (5) |
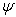 is the stream function of the boundary layer flow that satisfies the continuity equation (2).Consequently the velocity components
is the stream function of the boundary layer flow that satisfies the continuity equation (2).Consequently the velocity components 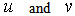 become
become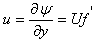 | (6) |
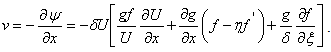 | (7) |
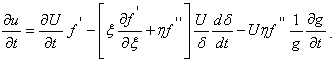 | (8) |
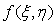 is now obtained as
is now obtained as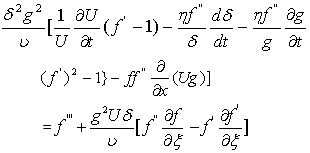 | (9) |
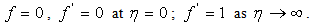 | (10) |
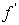 denotes differentiation with respect to
denotes differentiation with respect to 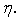 It is, however, seen directly from equation (9) that the velocity profiles
It is, however, seen directly from equation (9) that the velocity profiles 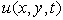 are similar when the stream function
are similar when the stream function 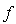 depends only on the variable
depends only on the variable 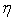 defined in (4) with the dependence of
defined in (4) with the dependence of 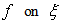 being cancelled. This would thus reduce the partial differential equations (1) and (2) to an ordinary differential equation for
being cancelled. This would thus reduce the partial differential equations (1) and (2) to an ordinary differential equation for 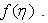 This reduction would thus lead to the derivation of the expression for the potential flow velocity
This reduction would thus lead to the derivation of the expression for the potential flow velocity 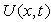 for which local similar solutions are to exist. Thus under the above assumption equation (9) reduces to
for which local similar solutions are to exist. Thus under the above assumption equation (9) reduces to 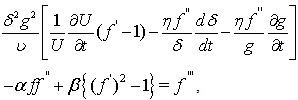 | (11) |
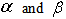 are the contractions for the functions
are the contractions for the functions 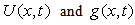 defined as
defined as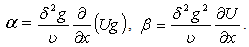 | (12) |
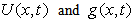 are separable and thus
are separable and thus 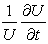 and
and 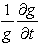 become exactly functions of
become exactly functions of 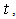 and hence both can be considered to be proportional to
and hence both can be considered to be proportional to 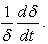 The above assumptions and the proportionality to
The above assumptions and the proportionality to 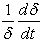 have been made to render the equation (11) to a similarity form.It is thus assumed that
have been made to render the equation (11) to a similarity form.It is thus assumed that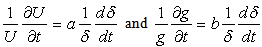 | (13) |
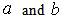 are the proportionality constants.Hence equation (11) becomes
are the proportionality constants.Hence equation (11) becomes 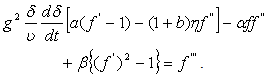 | (14) |
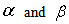 must be independent of
must be independent of 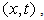 that is, they must be constants. This condition of consistency, combined with equation (12) will furnish two equations from which the potential flow velocity
that is, they must be constants. This condition of consistency, combined with equation (12) will furnish two equations from which the potential flow velocity 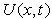 and the scale factor
and the scale factor 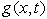 for the ordinate can be derived and hence the length scale
for the ordinate can be derived and hence the length scale 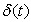 can be evaluated. Now for the purposes mentioned above, the procedure due to Falkner and Skan[2] is adopted here and thus the following expression is obtained
can be evaluated. Now for the purposes mentioned above, the procedure due to Falkner and Skan[2] is adopted here and thus the following expression is obtained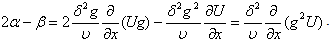 If now
If now 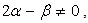 integrating the above expression with respect to
integrating the above expression with respect to 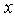 one obtains
one obtains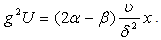 | (15) |
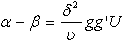
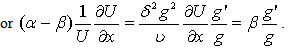 | (16) |
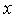 it is obtained that
it is obtained that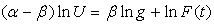 where
where 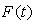 is an integrating constant but a function of time
is an integrating constant but a function of time 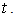 Thus follows
Thus follows 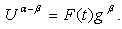 | (17) |
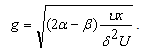 | (18) |
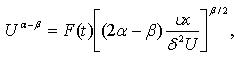 which finally yields
which finally yields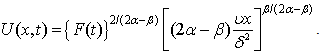 | (19) |
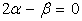 has, however, been excluded. Since the above results are independent of any common factor of
has, however, been excluded. Since the above results are independent of any common factor of 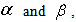 as long as
as long as 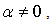 it is possible to put
it is possible to put 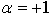 without loss of generality. It is, thus convenient to introduce a new constant
without loss of generality. It is, thus convenient to introduce a new constant 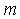 to replace
to replace 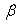 by taking
by taking 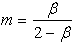 so
so 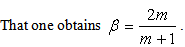 | (20) |
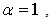 the velocity distribution of the potential flow and the scale factor for the ordinate become respectively
the velocity distribution of the potential flow and the scale factor for the ordinate become respectively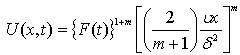 | (21) |
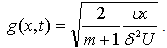 | (22) |
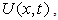 two choices of the function
two choices of the function 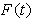 are made:
are made: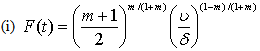 | (23) |
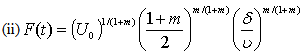 | (24) |
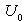 is a reference velocity.With the use of (23), from (21) the potential flow velocity turn out to be
is a reference velocity.With the use of (23), from (21) the potential flow velocity turn out to be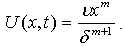 | (25) |
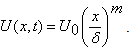 | (26) |
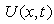 is inversely proportional to a power of
is inversely proportional to a power of 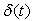 and directly proportional to a power of
and directly proportional to a power of 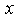 measured along the wall from the stagnation point. The above two forms of
measured along the wall from the stagnation point. The above two forms of 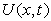 so obtained refers to the wedge flow where
so obtained refers to the wedge flow where 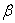 is the wedge angle. At this stage, the similarity of the equation (14) still remains unresolved because of the term
is the wedge angle. At this stage, the similarity of the equation (14) still remains unresolved because of the term 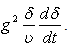 The above term is now explored by introducing
The above term is now explored by introducing 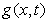 from (22) and
from (22) and 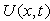 from (25). It thus appears that
from (25). It thus appears that 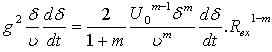 | (27) |
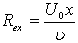 is the local Reynolds number.Now the similarity (local) of the equation (14) requires that the term
is the local Reynolds number.Now the similarity (local) of the equation (14) requires that the term  in (27) must be a constant. Hence let
in (27) must be a constant. Hence let 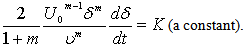 | (28) |
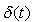 which is obtained by integrating equation (28) as
which is obtained by integrating equation (28) as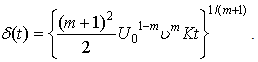 | (29) |
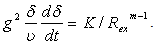 | (30) |
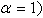
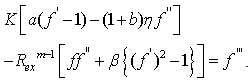 Without loss of generality it is further assumed that
Without loss of generality it is further assumed that 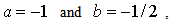 so that the above equation becomes
so that the above equation becomes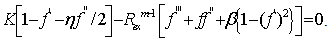 | (31) |
3. Steady Case
- When the flow is steady,
 is no longer a function of time rather can be considered as a characteristic length such as
is no longer a function of time rather can be considered as a characteristic length such as 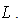 Thus from (28), we can take
Thus from (28), we can take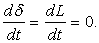 Thus the parameter
Thus the parameter 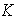 in (28) in this case becomes identically zero. Hence putting
in (28) in this case becomes identically zero. Hence putting 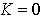 equation (31) reduces to
equation (31) reduces to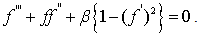 | (32) |
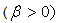 and decelerated
and decelerated 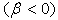 flows. On the other hand many fold solutions of the equation (32) was obtained by Stewartson[23].
flows. On the other hand many fold solutions of the equation (32) was obtained by Stewartson[23]. 4. Reduction of Eq. (31) to the Case of a Flat Plate
- In order to justify the general form of the equation (31) and the derivation of the potential flow velocity represented in (25), let us consider the unsteady 2-D boundary layer flow along a flat plate where
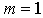 so that the potential flow velocity becomes
so that the potential flow velocity becomes 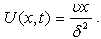 | (33) |
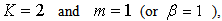 the similarity equation (31) turns out to be
the similarity equation (31) turns out to be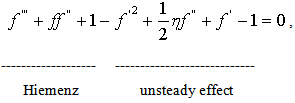 | (34) |
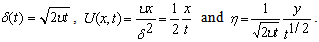 | (35) |
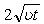 for the ordinate similar to one seen in (35) was initially used by Stokes[24] for an unsteady parallel flow but
for the ordinate similar to one seen in (35) was initially used by Stokes[24] for an unsteady parallel flow but 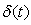 form of the length scale was initially developed by Sattar and Hossain[14] in case of a solution of an unsteady one-dimensional boundary layer problem. The characteristic length scale
form of the length scale was initially developed by Sattar and Hossain[14] in case of a solution of an unsteady one-dimensional boundary layer problem. The characteristic length scale 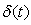 defined particularly in (35) physically relates to the boundary layer thickness which can be viewed in Schlichting[25].
defined particularly in (35) physically relates to the boundary layer thickness which can be viewed in Schlichting[25].5. Results and Discussion
- Explicit solutions to steady or unsteady boundary layer equations are important both from theoretical and practical points of view. Such solutions are, however, related to the reduction of the boundary layer equations to a similarity form and to the conditions for the existence of the relevant similarity solutions. In case of the steady boundary layer equations it was earlier established that the similar solutions would exist if the velocity distribution of the potential flow is proportional to a power of the length of arc, measured along the wall from the stagnation point (Schlichting[25]). In this work the author has thus explored the possibility of obtaining a very simple but general form of a local similarity equation of the 2-D unsteady Prandtl boundary layer equations vis-à-vis the condition for the existence of similar solutions of this equation. This principle has thus led to the derivation of the equation (31) and the condition (25) or (26) for the potential flow velocity distribution. The validity of the equation (31) can however be ascertained by the equation (34) which is a special case of equation (31) and which was earlier established by Ma and Hui[1].Although the prime goal of the work was to obtain similarity conditions for the existence of unsteady solutions, the equation (31) has been solved numerically in a comprehensive manner by using the efficient computer algebra software Maple-13 (Aziz[26]). The results of this numerical computation are displayed in Figures 1 and 2 in the form of velocity profiles to show the solution trends.
 | Figure 1. Velocity profiles for different values of the unsteadiness parameter 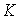 |
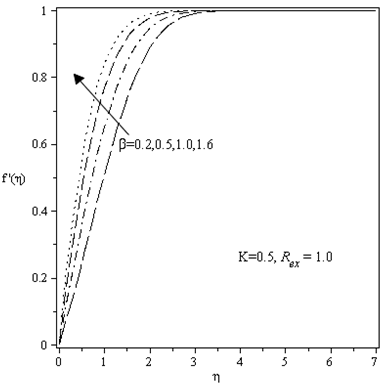 | Figure 2. Velocity profiles for different values of 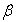 |
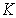 are shown for fixed values of
are shown for fixed values of 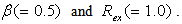 It appears from this figure that strong unsteadiness(larger values of
It appears from this figure that strong unsteadiness(larger values of  ) trigger separation which indicates that back flow occurs close to the surface of the wall. This is due to the fact that strong unsteadiness intensifies the kinematic viscosity of the fluid which causes the decrease of its ambient value and thus results in back flow.n Figure 2, velocity profiles for different values of
) trigger separation which indicates that back flow occurs close to the surface of the wall. This is due to the fact that strong unsteadiness intensifies the kinematic viscosity of the fluid which causes the decrease of its ambient value and thus results in back flow.n Figure 2, velocity profiles for different values of 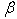 at
at  are displayed. Velocity is found to increase with the increase with the increase of
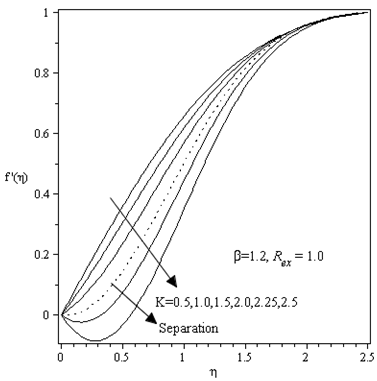
are displayed. Velocity is found to increase with the increase with the increase of 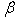 which confirms that the velocity profiles for unsteady case follow the same trend of those for the steady case(Schlichting and Garsten[27].As a comparison of the results displayed in Figures 1 and 2, Figures 3 and 4 respectively are reproduced from Sattar[28] who obtained local similarity solutions of the 2-D unsteady hydrodynamic boundary layer equations of a flow past a wedge. It appears that presents results agree well with those of Sattar.
which confirms that the velocity profiles for unsteady case follow the same trend of those for the steady case(Schlichting and Garsten[27].As a comparison of the results displayed in Figures 1 and 2, Figures 3 and 4 respectively are reproduced from Sattar[28] who obtained local similarity solutions of the 2-D unsteady hydrodynamic boundary layer equations of a flow past a wedge. It appears that presents results agree well with those of Sattar.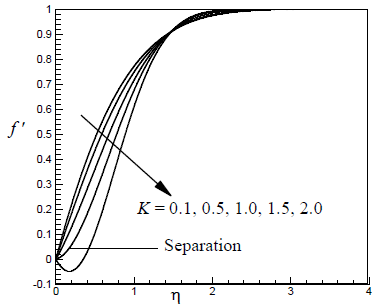 | Figure 3. Velocity profile for different values of K and for β =1.0, Rex = 2.0 |
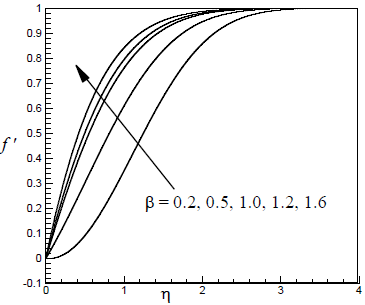 | Figure 4. Velocity profile for different values of β and for K =0.3, Rex = 2.0 |
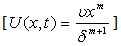 has been derived which to the best of my knowledge is a new finding. However, for a steady case such a condition is
has been derived which to the best of my knowledge is a new finding. However, for a steady case such a condition is 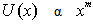 (Schlichting[25]) which corresponds to the condition (25) or (26). Taking
(Schlichting[25]) which corresponds to the condition (25) or (26). Taking 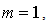 the potential flow velocity becomes
the potential flow velocity becomes 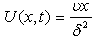 which is related to flat plate boundary layer (see section 4). Sattar and Ferdows[29] made a similar approach for the similarity solutions of an unsteady free-forced convective 2-D boundary layer flow along a flat plate. Inspired by the work of the author[28], by taking the general form of the of the potential flow velocity, Rahman et al.[30,31,32] obtained solutions to the unsteady 2-D boundary layer problems with heat and mass transfer under various flow conditions. Using the same general form of the potential flow, very recently Muhaiman et al.[33] obtained the effects of thermophoresis particle deposition and chemical reaction on an unsteady MHD two dimensional boundary layer problem. It is thus apparent from the above works[28,29,30, 31,32,33] that the use of the above potential flow velocity distributions to obtain exact similarity solutions of various unsteady 2-D boundary layer boundary layer problems can make fruitful contributions in computational fluid dynamics research.
which is related to flat plate boundary layer (see section 4). Sattar and Ferdows[29] made a similar approach for the similarity solutions of an unsteady free-forced convective 2-D boundary layer flow along a flat plate. Inspired by the work of the author[28], by taking the general form of the of the potential flow velocity, Rahman et al.[30,31,32] obtained solutions to the unsteady 2-D boundary layer problems with heat and mass transfer under various flow conditions. Using the same general form of the potential flow, very recently Muhaiman et al.[33] obtained the effects of thermophoresis particle deposition and chemical reaction on an unsteady MHD two dimensional boundary layer problem. It is thus apparent from the above works[28,29,30, 31,32,33] that the use of the above potential flow velocity distributions to obtain exact similarity solutions of various unsteady 2-D boundary layer boundary layer problems can make fruitful contributions in computational fluid dynamics research.6. Concluding Remarks
- In this work a comprehensive account of the similarity derivation of the two-dimensional unsteady Prandtl boundary layer equations has been presented. A new class of similarity transformation based on a time dependent length scale has been introduced to obtain a local similarity equation which can be considered to be of general form in contrast to other forms obtained in previous studies. The main findings of the study are now summarized below:(a) Local similarity solutions of the 2-D unsteady boundary layer equations will exist when the potential flow velocity is proportional to a power of the length scale
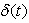 and directly proportional to a power of the length measured along the boundary in the flow direction from the stagnation point.(b) The derived similarity equations con be considered as general because both steady and unsteady solutions can be obtained separately.(c) The similarity equation for the steady case is a recovery of the Falkner and Skan equation.(d) For a particular case of a flat plate present derivations exactly agree with those of Ma and Hui[1}.(e) Strong unsteadiness(higher values of
and directly proportional to a power of the length measured along the boundary in the flow direction from the stagnation point.(b) The derived similarity equations con be considered as general because both steady and unsteady solutions can be obtained separately.(c) The similarity equation for the steady case is a recovery of the Falkner and Skan equation.(d) For a particular case of a flat plate present derivations exactly agree with those of Ma and Hui[1}.(e) Strong unsteadiness(higher values of 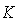 ) trigger separation resulting to the back flow.(f) As in the case of steady flow increase in
) trigger separation resulting to the back flow.(f) As in the case of steady flow increase in 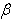 leads to the increase in the velocity distribution(h) From the point of fluid dynamics research, particularly in case of unsteady boundary layer problems it can be concluded that the researchers can rely on the general form of the local similarity equation (31) and the corresponding condition for the potential flow velocity derived in (25) or (26).
leads to the increase in the velocity distribution(h) From the point of fluid dynamics research, particularly in case of unsteady boundary layer problems it can be concluded that the researchers can rely on the general form of the local similarity equation (31) and the corresponding condition for the potential flow velocity derived in (25) or (26).  Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML