M. V. Kravtsov1, A. M. Kravtsov2
1The Institute of Improvement of Professional Skill and Retraining of the Staff on New Directions of Development of Engineering, Technology and Economy, Belarusian National Technical University, Minsk, Republic of Belarus
2Department of hydraulics and hydraulic machines, Belarusian State Agrarian Technical University, Minsk, Republic of Belarus
Correspondence to: A. M. Kravtsov, Department of hydraulics and hydraulic machines, Belarusian State Agrarian Technical University, Minsk, Republic of Belarus.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The present article deals with the search of the common law of uniform fall of a solid sphere due to gravity in an infinite volume of a viscous incompressible fluid. As a result of researches there was a suggestion of the formula for the calculation of velocity of free fall of single spheres in an infinite viscous medium in a wide range of Reynolds numbers. The experimental justification of the suggested formula in the range of Reynolds number from 0,000423 up to 251000 was received. Interesting results of observations of behaviour of fallen spheres at various motion modes are presented as well.
Keywords:
Free Fall of a Single Sphere in a Fluid, Fall Velocity, Resistance Coefficient, Estimate Range, Behaviour of a Fallen Sphere
Cite this paper: M. V. Kravtsov, A. M. Kravtsov, Laws of Free Fallen Single Spheres in Fluids, American Journal of Fluid Dynamics, Vol. 3 No. 4, 2013, pp. 96-100. doi: 10.5923/j.ajfd.20130304.02.
1. Introduction
One of the most important problem of hydrodynamics, which has been tried to be solved within more than three centuries, is the problem of hydraulic resistances during free fall of a single sphere in a viscous medium. The basis for the problem solution was set by theoretical and experimental investigations of Galileo and Newton. At the beginning of the XVIIth century Galileo discovered the free – fall law of bodies in a non – resisting (non-viscous) medium. And thereafter the thoughts of scientists turned to the solution of the problem concerning the free motion of single bodies in a resisting liquid viscous medium.The first fundamental data regarding the laws of the motion of a single sphere in fluids were obtained by Newton at the beginning of the ХVIIIth century. As a result of the researches of various cases of motion, Newton came to the conclusion that in a general case the magnitude of force of hydraulic resistance during the free fall of a sphere in an infinite volume of a viscous fluid is composed of three parts. The first component determines the resistance part proportional to the velocity in the first grade, the second component – to the sesquialteral grade of velocity, the third component – to the velocity squared. At the same time Newton suggested that in any case in the general resistance of a medium the part proportional to the velocity squared was prevailing. The conclusions of Newton laid foundation of the creation of the so called “quadric” formulae not only for the calculation of the velocity magnitude of a free fallen single sphere in a fluid, but also for the calculation of circular cylindrical pipes during the constraint uniform motion of fluids. Some of them are used for practical calculations even now. However at the beginning of the ХIХth century it became clear for many scientists that the quadric formula of Newton could have a highly limited area of application, because in the total resistance of a medium, as experience and theoretical solutions have shown, the major part is played by the parts of resistances proportional to the sesquialteral and first grades of velocity. The search of a more general law of resistances have been initiated and in some cases there were suggested double formulae, the first component in which expresses the resistance share proportional to the velocity in the first grade, the second component expresses the resistance share proportional to the velocity squared. From the end of the ХIХth and till the end of the ХХth centuries triple formulae, based on the Newton researches, were suggested for practical calculations. The ternary formula in a general version is presented as follows: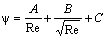 | (1) |
where A, B and C – constant coefficients; Re – Reynolds criterion.However the application of ternary formulae did not solve the problem as well, because the calculations according to them did not cover the whole range of investigated values.The majority of researches dealt with the study of the motion of a sphere in fluids, because its symmetric form made the solution easier. In this case the midsection area S = π d 2/4 (where d — sphere diameter). If it is a case of the motion of a body with a form different from the sphere form, then the midsection area S is determined by means of equivalent diameter of a sphere.At present the values of resistance coefficient ψ are considered to be connected with the value of Reynolds number Re, i.e. it is believed that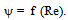 | (2) |
The discovery of the relation (2) went along the way of accumulation of experimental data and selection of formulae for the resistance coefficient ψ, and along the way of theoretical researches as well. The experimental researches were the most intensive within the thirties of the previous century. At the mid seventies they were practically ended. It was evidently connected with the fact that the empirical relation (2) was believed to be known. Really, the empirical relation (2) was studied experimentally in the case of a free fall of solid spheres in fluids[1, 2] in the range of Reynolds numbers from 0,1 up to 70000. At the same time the analysis of experimental data shows[3, 4], that within Reynolds numbers more 10000-20000 there is no determinacy within the relation (2) for the case of spheres fall in fluids. Empirical relations of various authors differ a lot. From our point of view the reason lies in the fact, that during the tests the conditions, providing free uniform fall of spheres, were not fulfilled (the initial accelerated motion section was not excluded, the motion constraint by closely set vessel walls took place etc.). Moreover, at big Reynolds numbers the attention was paid not to the uniform fall of spheres, but to the flow of stationary spheres by a uniform water stream. Taking into account the principle of relativity the results of the research of direct and reversed tasks are comparable. However here it is difficult to meet the set of similarity conditions as well (the flow constraint by the walls, suspension influence, limitations in the sphere behaviour etc.). Also during the processing and analysis of experimental data the behaviour of free fallen spheres was not considered. For example, at significant Reynolds numbers and small difference of a sphere and medium densities the “wandering” of spheres happens, i.e. their declination from the vertical path of motion during the fall process. Such declination often has a random-accidental character and is difficult to be considered when processing the experimental data.There are not many theoretically based particular formulae for the calculation of resistance coefficients. The main ones of them are presented graphically in Figure 1[4]. Each formula was true in the narrow range of calculated parameters only.First of all we should mention the formula, obtained in the middle of the ХIХth century as a result of a particular solution of differential equations of a viscous incompressible fluid by Stokes[5]. This formula is as follows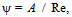 | (3) |
where А — a constant coefficient.It should be noted that Stokes formula (3) can be applied only at very small Reynolds numbers (Re<1). Additions for the relation (3) at large Re are the following empirical formulae:● Allen formula (2 < Re < 5∙102)[6]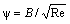 | (4) |
● Newton formula (5∙102 < Re < 2∙105)[7]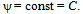 | (5) |
In formulae (4) and (5) B and C – constant coefficients.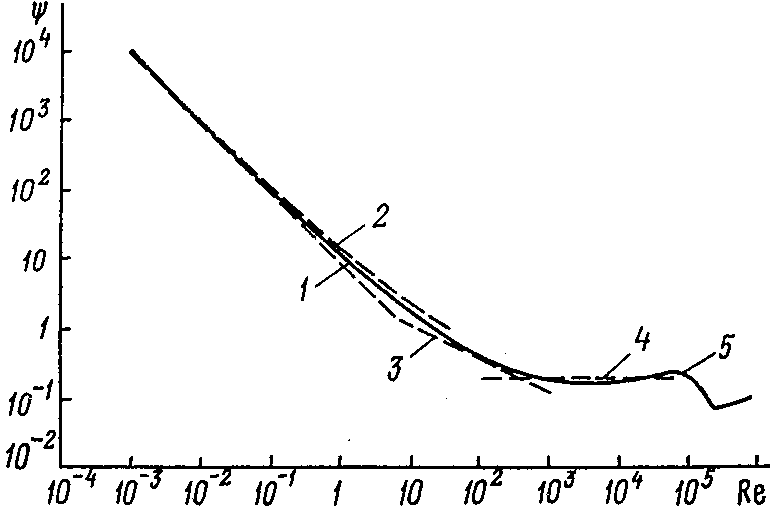 | Figure 1. Relation diagram ψ = f (Re): 1 – calculation according to Stokes formula; 2 – according to the Oseen formula; 3 – according to Allan formula; 4 – according to Newton formula; 5 – experimental curve |
Experimental data of various authors at large Reynolds numbers are presented in Figure 2[3]. Having such a spread of experimental curves one can judge only by a common tendency of relation ψ = f (Re). The spread of curves, to our opinion, is connected with various unrecorded conditions during experiments (trials were carried out mainly in aerohydrodynamical pipes with the influence on results by the walls constraint, changes in the behaviour of spheres, fixed fast, influence of the suspensions and nonuniformity of the flow etc.). | Figure 2. Experimental relation diagram ψ = f (Re) at large Reynolds numbers[3] |
2. Research Methodology, Equipment, Data Used
The present article deals with the search of a general law of a uniform fall of a solid sphere due to gravity in an infinite volume of a viscous incompressible fluid. In this case the total force of resistance F is counterbalanced by the effective weight of the sphere in a fluid Gef, i.e.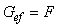 | (6) |
where 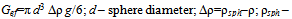 sphere density; ρ – fluid density; g – free fall acceleration.According to the current hydrodynamic theory the total force of resistance F is composed of separate summands, connected with the deformation of fluid particles, fluid pressure on the sphere surface etc. The prevaling component of the resistance forces is a part from the pressure (the inertia). Thus, various kinds of resistances are presented relatively as shares from the pressure[8]
sphere density; ρ – fluid density; g – free fall acceleration.According to the current hydrodynamic theory the total force of resistance F is composed of separate summands, connected with the deformation of fluid particles, fluid pressure on the sphere surface etc. The prevaling component of the resistance forces is a part from the pressure (the inertia). Thus, various kinds of resistances are presented relatively as shares from the pressure[8]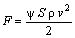 | (7) |
where ψ=ψ1+ψ2+...ψn – resistance coefficient, made up of particular coefficients from various kinds of resistances; S – sphere midsection area; v – body fall velocity.Previously efforts of many scientists were aimed at discovering the general relation of ψ from number Re=vdρ/µ (where µ – dynamical viscosity coefficient). This laborious way did not lead to any desirable results. The reason probably is that this relation turns out to be very complicated. Alongside with this, at the same time not a Reynolds number may be used, but other dimensionless criterion of Archimedes Аr = 3 ψ Re2/4=d3 Δρ ρ g/μ2.In order to find calculated relations for the case of free fallen spheres were taken experimental researches[4]. The installation used for trials, is presented in Figure 3.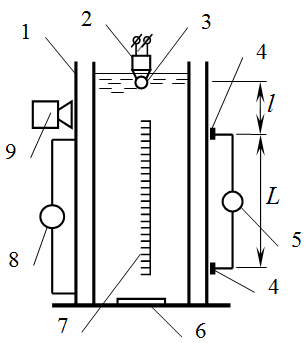 | Figure 3. Experimental installation: 1 – cylindrical vessel with double walls for thermostating; 2 – electromagnet with conic core; 3 – steel sphere; 4 – photocells; 5 – electronic stopwatch; 6 – target; 7 – ruler; 8 – thermostat; 9 – camera |
In trials there was a study of a free fall of spheres of steel, with the diameter from 3 up to 76,2 mm and glass with the diameter from 0,9 up to 5,5 mm in fluids (water, glycerine and hydroglyceric solution) when the influence of the vessel walls is absent. Reynolds numbers comprised from 0,0534 up to 250000. Steel spheres were thrown from the point of the conic core of electromagnet 2. With the help of photocells 4 and electric stopwatch 5 the time of a sphere fall on the calculated section was fixed. The dimensions of the vessel 1 (cross section and height) changed depending on the kind of a viscous medium used, which underwent a thorough thermostating by thermostat 8.
3. Results and Comparison
As a result of the analysis of the data of experimental researches, the relation between ψ and Ar as follows: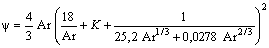 | (8) |
where 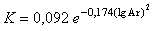 .From (8) we get
.From (8) we get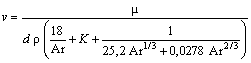 | (9) |
The comparison of calculated data according to formulae (8) and (9) and experimental values ψ, Ar, v and d is presented in Figures 4 and 5.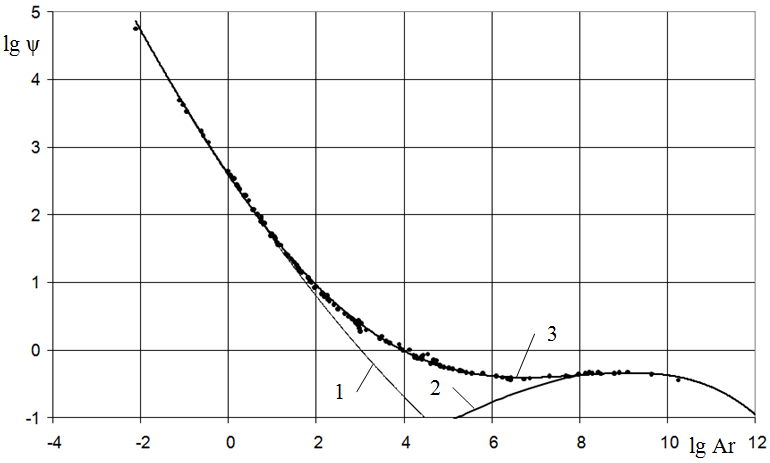 | Figure 4. Relation ψ = f(Ar) at the free fall of single spheres in fluids (points – experimental data, lines – calculation): 1 – according to formula (10); 2 – according to formula (12); 3 – according to formula (8) |
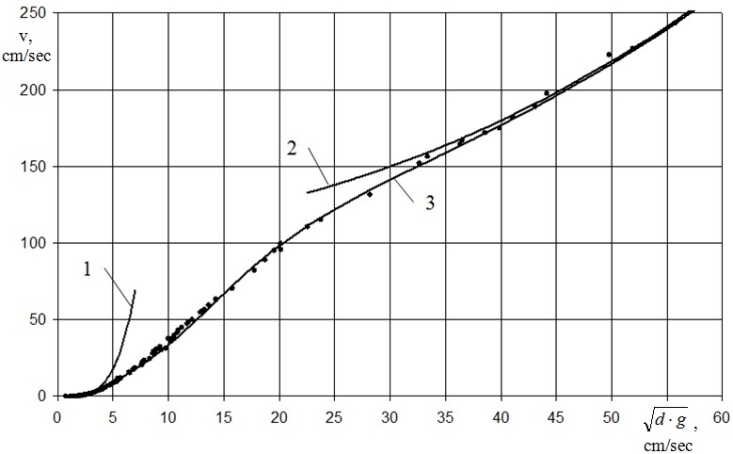 | Figure 5. Relation of v = f (d) at the free fall of single spheres in fluids (points – experimental data, lines – calculation): 1 – according to formula (11); 2 – according to formula (13); 3 – according to formula (9) |
Comparisons of calculated data according to formulae (8) and (9) were carried out alongside with the set of experimental data, obtained until 1990 by M.V. Kravtsov[4]. It is known that it is accepted to classify and publish these data as a relation of resistance coefficient ψ from Reynolds number Re. It is commonly known that, having a set of values of ψ and Re, it is easy to reproduce the corresponding set of values Ar. When comparing the calculations of velocities according to formula (9) it should be known except parameters, determining the properties of a fluid and sphere, the set of experimental values v and corresponding to them values of diameters of spheres d. In this case it is calculated in this way: for given μ, ρ, ∆ρ, g and pair of values ψ and Re of experimental relation ψ = f(Re), determining d = µ Re/(v ρ), d = 3 ψ ρ/(4 Δρ g). From the obtained formulae d and v are derived.Relations ψ = f(Ar) and v = f(Ar), determined according to formulae (8) and (9), have asymptotes (Fig. 4 and 5, lines 1 and 2). Thus, for example at the slow motion of a sphere (Ar ≤ 1,0) in formulae (8) and (9) it can use only the first member in brackets. Then, considering the relation for the determination of Ar, | (10) |
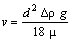 | (11) |
Formulae (10) and (11) present the famous Stokes law. Alongside with that they are asymptotes from the left to the graphic relations ψ = f(Ar) and v = f(d) (Fig. 4 and 5, line 1).When Ar tends to significantly big values, graphic relations (8) and (9) look like that: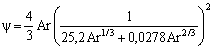 | (12) |
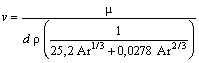 | (13) |
Formulae (12) and (13) are asymptotes from the right to the graphic relations ψ = f(Ar) and v = (d) (Fig. 4 and 5, line 2).When the sphere moves very slowly, when current laws are asymptotes from the left in the form of formulae (10) and (11), there is “irrotational”, so called “creeping” flow – around of a sphere. In this case tensions induced by the sphere motion, generate the particle acceleration of the fluid within a large distance from the body and deformation resistance. If a sphere moves fast, when current laws are asymptotes from the right in the form of formulae (12) and (13), creation of whirls and their breaking from the surface of the sphere afterbody happen, and tensions in the fluid generate accelerations near the body surface and determine the friction resistance.The connecting share of resistances and the velocity between these two cases is determined by a medial member K in formulae (8) and (9). The analysis of the relation K=f(Ar) in Figure 6 may give a lot of additional information for the valuation of physical substance of hydraulic resistances when spheres move. Also here we can note that after simple transformations the curve K=f(Ar) reduces to the curve of Gauss as follows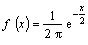 | (14) |
Moreover, the important issue concerning the limits of Stokes formula (10) application has not been cleared up so far. Various Reynolds numbers are named (Re = 0,1…1,0). When analyzing the ration of members of formula (8) К and Ar/18 the limit of application of Stokes (10) formula has been determined, which is Ar = 10 (Re = 0,556).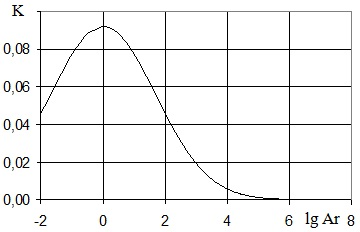 | Figure 6. Calculated relation for a medial member K = f(Ar) in formulae (8) and (9) |
On the basis of the analysis, observations results and parameters of the fall the following conclusions have been drawn:● at the sphere fall in the air (the fluid is not available), the spheres have fallen strictly vertically and arrived to the centre of a target;● within the limits of Stokes law at small Reynolds numbers and further up to numbers Re 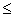 1000 the declination from the vertical when the spheres fall, were not significant or not available at all – spheres have fallen into the centre of the target;● within limits Re = 1000-12000 spheres when fallen declined from the vertical and have fallen onto the target in various sectors within a radius of approx. 4 cm, alongside with that, in spite of a thorough thermostating and strict observation of constancy of reset conditions there was no stability in the behaviour of spheres and repeatability of the magnitudes of motion parameters fixed during trials;● at Re
1000 the declination from the vertical when the spheres fall, were not significant or not available at all – spheres have fallen into the centre of the target;● within limits Re = 1000-12000 spheres when fallen declined from the vertical and have fallen onto the target in various sectors within a radius of approx. 4 cm, alongside with that, in spite of a thorough thermostating and strict observation of constancy of reset conditions there was no stability in the behaviour of spheres and repeatability of the magnitudes of motion parameters fixed during trials;● at Re 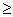 12000 spheres when fallen have declined significantly from the vertical and many of them have fallen in the centre of the target.
12000 spheres when fallen have declined significantly from the vertical and many of them have fallen in the centre of the target.
4. Conclusions
On the basis of a general law of resistances the given article suggests the formula (9) for the calculations of velocities of a free fall of single spheres in infinite volumes of fluids. According to the results of the processing of experimental measurements of a free fall of single spheres of steel and glass on conditions of absence of the influence of the vessel walls in viscous mediums of water, glycerine and hydroglyceric solutions, the experimental basis of the suggested formula at Reynolds numbers from 0,000423 up to 251000 has been obtained (Fig. 4 and 5).The results of researches contribute to the development of the theory of hydraulic resistances and can be used in the technique of viscometry and when solving the tasks, connected with the calculations of various kinds of motion when realizing various hydraulic processes.
References
| [1] | Tanaka, Z. New approximate equation of drag coefficient for spherical particles / Z. Tanaka[et al.] // J. Chem.Eng.of Japan. – 1970. – Vol. 3, № 2. |
| [2] | Lapple, C.E. Calculation of particle Trajectories / C.E. Lapple[et al.] // Ind. Eng. Chem. – 1940. – Vol. 32, № 5. |
| [3] | Achenbach, E. Experiments on the flow past spheres at very high Reynolds numbers / E. Achenbach // Journal of Fluid Mechanics. – 1972. – № 3. – P. 565 – 575. |
| [4] | Kravtsov, M.V. Hydraulics of granular materials / M.V. Kravtsov. – Minsk: Science and technique, 1980. – 126 p. |
| [5] | Stokes, G.G. On the effect of the Internal Friction of Fluids on the Motion Pendulum Trans. Camb. Phil. Soc., 8, 9, 1851. |
| [6] | Allen, H.C. The Motion of a sphere in a viscous Fluid. “Philosophical Magazine”, L., 1900. |
| [7] | Newton, I. Mathematical principalities of a natural philosophy. Collection of works of A.N. Krylov, vol. 7. M. – L., Publishing house SA USSR, 1936. |
| [8] | Prandtle, L. Hydro – and aeromechanics. vol.2 / L. Prandtle, O. Titiens. M.:, ONTI-NKTP USSR, 1935. – 283 p. |

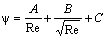
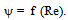
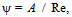
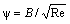
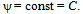

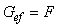
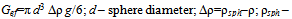 sphere density; ρ – fluid density; g – free fall acceleration.According to the current hydrodynamic theory the total force of resistance F is composed of separate summands, connected with the deformation of fluid particles, fluid pressure on the sphere surface etc. The prevaling component of the resistance forces is a part from the pressure (the inertia). Thus, various kinds of resistances are presented relatively as shares from the pressure[8]
sphere density; ρ – fluid density; g – free fall acceleration.According to the current hydrodynamic theory the total force of resistance F is composed of separate summands, connected with the deformation of fluid particles, fluid pressure on the sphere surface etc. The prevaling component of the resistance forces is a part from the pressure (the inertia). Thus, various kinds of resistances are presented relatively as shares from the pressure[8]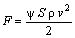
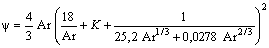
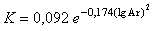 .From (8) we get
.From (8) we get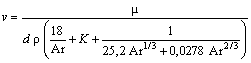

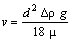
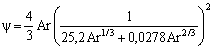
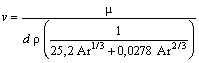
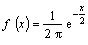

 1000 the declination from the vertical when the spheres fall, were not significant or not available at all – spheres have fallen into the centre of the target;● within limits Re = 1000-12000 spheres when fallen declined from the vertical and have fallen onto the target in various sectors within a radius of approx. 4 cm, alongside with that, in spite of a thorough thermostating and strict observation of constancy of reset conditions there was no stability in the behaviour of spheres and repeatability of the magnitudes of motion parameters fixed during trials;● at Re
1000 the declination from the vertical when the spheres fall, were not significant or not available at all – spheres have fallen into the centre of the target;● within limits Re = 1000-12000 spheres when fallen declined from the vertical and have fallen onto the target in various sectors within a radius of approx. 4 cm, alongside with that, in spite of a thorough thermostating and strict observation of constancy of reset conditions there was no stability in the behaviour of spheres and repeatability of the magnitudes of motion parameters fixed during trials;● at Re 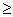 12000 spheres when fallen have declined significantly from the vertical and many of them have fallen in the centre of the target.
12000 spheres when fallen have declined significantly from the vertical and many of them have fallen in the centre of the target. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML


