V. Singh1, Shweta Agarwal2
1Dept. of Applied Science, Moradabad Institute of Technology, Moradabad-244001, Uttar Pradesh, India
2Dept. of Mathematics, Hindu College, Moradabad-244001, Uttar Pradesh, India
Correspondence to: Shweta Agarwal, Dept. of Mathematics, Hindu College, Moradabad-244001, Uttar Pradesh, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In this paper we investigate effects of variable viscosity and variable thermal conductivity on the steady flow and heat transfer of Maxwell fluid over an exponentially stretching sheet. Momentum equation and energy equation are solved numerically using an implicit finite-difference scheme known as Keller-box method. The numerical solutions for the wall skin friction coefficients, heat transfer coefficient and the velocity and temperature profiles are computationally analyzed and discussed through graphs and tables. Here Prandtl number also treated as variable because it depends on variable viscosity and variable thermal conductivity. It is found that skin friction coefficient and heat transfer coefficient are lower for the Maxwell fluid of constant viscosity and thermal conductivity.
Keywords:
Maxwell Fluid, Exponentially Stretching Sheet, Variable Prandtl Number, Variable Viscosity, Variable Thermal Conductivity
Cite this paper: V. Singh, Shweta Agarwal, Flow and Heat Transfer of Maxwell Fluid with Variable Viscosity and Thermal Conductivity over an Exponentially Stretching Sheet, American Journal of Fluid Dynamics, Vol. 3 No. 4, 2013, pp. 87-95. doi: 10.5923/j.ajfd.20130304.01.
1. Introduction
The flow and heat transfer analysis in the boundary on a continuously moving or stretching surface has wide important applications in many polymer industries and several manufacturing processes such as glass-fiber and paper production, drawing of plastic films, wire drawing, manufacturing of polymeric sheets and polymer extraction of plastic sheets. During the manufacture of these sheets, the melt substance passing through a slit and is subsequently stretched to achieve the desired thickness[see Fig.1]. The mechanicals properties of the final product is regulated by the extensibility of the sheet, rate of cooling (depending on physical property of the cooling medium e.g. thermal conductivity) and rheological properties (like viscosity which determines drag required to pull the sheet) of the fluid. Since the pioneering study by Crane[7] who presented an exact analytical solution for the study of two-dimensional stretching of a surface with a velocity proportional to the distance from the origin , many authors[3,10,11,20] have considered various aspects of this problem and obtain similarity solutions. Some authors[6,13,22] have studied the boundary layer flow of heat transfer by taking non-linear stretching sheet. Elbashbeshy[8], Magyari and Keller[15] and Sanjayanand and Khan[19] have studied the flow, heat transfer and mass transfer of a viscoelastic fluid over an exponentially stretching sheet. Singh and Agarwal[21] extended the work of Khan and Sanjayanand[12]. They have analyzed the influence of magnetic field on flow field and heat transfer for a second grade fluid over an exponentially stretching sheet with radiation and elastic deformation through graphs and tables. Eldabe and Mohamed[9] have investigated the heat and mass transfer occurring in the magnetohydrodynamic flow of the non-Newtonian fluid (Walter’s liquid B) through porous medium on a linearly accelerating surface with temperature dependent heat source subject to suction or blowing. They presented a series solution to the energy equation and concentration equation in terms of Kummer’s function. Able and Mahesha[1] have studied the influence of variable thermal conductivity with temperature dependent heat source/sink, in the presence of thermal radiation. Vajravelu and Rollins[23] have investigated the flow and heat transfer in electrically conducting fluid over a stretching surface. Prasad et al.[16] have studied the effect of thermal radiation on MHD viscoelastic fluid flow and heat transfer of Walter’s liquid-B past a stretching sheet with variable fluid viscosity and variable thermal conductivity.Aliakbar[2] investigated the MHD flow and heat transfer of a UCM, fluid above a semi-infinite stretching sheet with viscous dissipation and Radiative heat transfer. For finding an analytic solution they have used homotopy analysis method. Prasad et al.[17] have theoretically studied the effects of the temperature-dependent viscosity and thermal conductivity on the MHD boundary layer flow and heat transfer of a UCM fluid over a linear stretching sheet.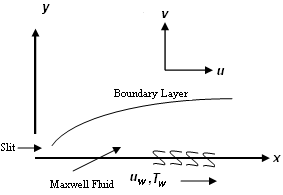 | Figure 1. Physical model and co-ordinate system |
Rahman and Salahuddin[18] have investigated the MHD heat and mass transfer flow over a radiative isothermal inclined heated surface with variable viscosity and electric conductivity. In this research we have attempted to solve the problem that involves the flow and heat in the presence of suction/blowing with variable viscosity and variable thermal conductivity (Prandtl number is also variable inside the boundary layer), to the best of our knowledge which has never been explored before.
2. Mathematical Formulation
Let us consider a steady 2-D boundary layer flow of a viscous incompressible upper convected Maxwell fluid over an exponentially stretching sheet. The sketch of the physical configuration and co-ordinate system are shown in Fig. 1.The boundary layer equations of the fluid flow and energy in the presence of variable fluid properties (fluid viscosity and thermal conductivity) can be written as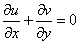 | (1) |
 | (2) |
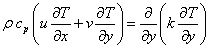 | (3) |
where u and v are the components of velocity in x and y axis respectively, cp is the specific heat at constant pressure and ρ is the fluid density (assumed constant).Let us consider the temperature dependent thermal conductivity k(T) vary as the linear function of temperature[5] and temperature dependent coefficient of viscosity μ(T) vary as inverse function of temperature[14] such as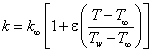 | (4) |
where ε is the small parameter, k∞ is the conductivity of the fluid far away from the sheet, Tw is the wall temperature, T∞ is the temperature far away from the sheet and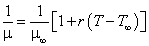 | (5a) |
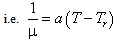 | (5b) |
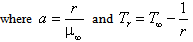 | (5c) |
Here a and Tr are the constants and their values depend on reference state, and r is the thermal property of the fluid. Generally for the liquids a > 0 and for gases a < 0.The boundary conditions for the velocity components and temperature are given by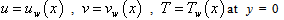 | (6a) |
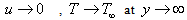 | (6b) |
The stretching velocity uw, variable mass transfer velocity vw and the exponential temperature distribution are defined as[4]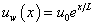 | (7a) |
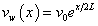 | (7b) |
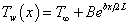 | (7c) |
where u0 is reference velocity , L is the reference length, v0 is constant with v0 < 0 for suction and v0 > 0 for injection and B is a constant depending on the thermal property of the liquid. The above exponential boundary condition is valid only when x <<L, which occurs very near to the slit.Equations (2) and (3) can be changed into ODE by introducing the following non dimensional variables.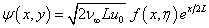 | (8a) |
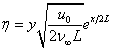 | (8b) |
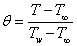 | (8c) |
where ψ (x, y) is the stream function f is the dimensionless stream function and θ is the non-dimensional temperature.Since 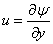 , and
, and 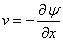 , the equation of continuity (1) is automatically satisfied.With the help of equations (4), (5) and (8), Equation (2) gets reduced to,
, the equation of continuity (1) is automatically satisfied.With the help of equations (4), (5) and (8), Equation (2) gets reduced to,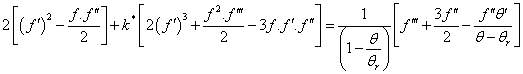 | (9) |
where 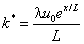 is the Maxwell parameter or viscoelastic parameter and
is the Maxwell parameter or viscoelastic parameter and 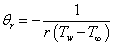 is the fluid viscosity parameter (depends on viscosity/temperature characteristics of the fluid under consideration and the temperature difference). We get the relation between constant viscosity and variable viscosity is
is the fluid viscosity parameter (depends on viscosity/temperature characteristics of the fluid under consideration and the temperature difference). We get the relation between constant viscosity and variable viscosity is 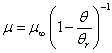 .Since the Prandtl number depends on variable viscosity and variable thermal conductivity therefore Prandtl number also varies as[18]
.Since the Prandtl number depends on variable viscosity and variable thermal conductivity therefore Prandtl number also varies as[18]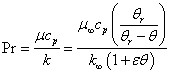
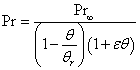 | (10a) |
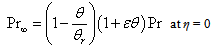 | (10b) |
where 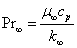 is the Prandtl number related to constant viscosity. From equation (10a) it is clear that for large θr (θr → ∞) and small ε (ε → 0), Pr → Pr∞. To reduce the energy equation (3) in ODE, use equations (4), (5), (6) and (8c) in equation (3) we get
is the Prandtl number related to constant viscosity. From equation (10a) it is clear that for large θr (θr → ∞) and small ε (ε → 0), Pr → Pr∞. To reduce the energy equation (3) in ODE, use equations (4), (5), (6) and (8c) in equation (3) we get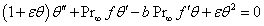 | (11) |
This is the energy equation for the constant Prandtl number, and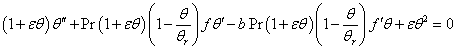 | (12) |
is the energy equation for variable Prandtl number. It is clear from equation (12) large θr (θr → ∞) and small ε (ε → 0), (θ/θr) → 0. The equation (12) reduces into Equation (11). The corresponding boundary conditions for the flow and temperature distribution are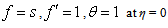 | (13a) |
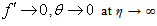 | (13b) |
where 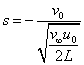 is the mass transfer parameter.s > 0 {v0 < 0} corresponds suction and s < 0 {v0 > 0} corresponds to the injection.
is the mass transfer parameter.s > 0 {v0 < 0} corresponds suction and s < 0 {v0 > 0} corresponds to the injection.
3. Numerical Method
The system of transformed governing equations (9) and (12) subject to the boundary conditions (13) is solved numerically using an implicit finite-difference scheme which is known as Keller box method. This method has second-order accuracy and unconditionally stable. In this method, the transformed differential equations were first rewritten as a system of first order equations and using central differences these equations are converted into a set of finite difference equations. The resulting non-linear system of equation is solved by using the Newton Quasi-linearization method. Finally the difference equations are solved using a block matrix algorithm.
4. Result and Discussions
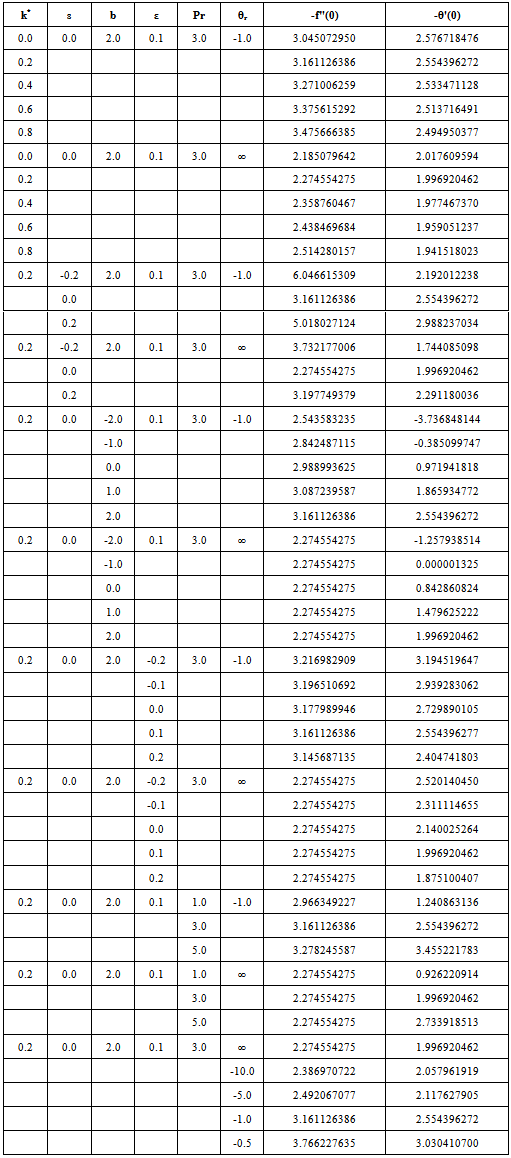
In order to get a physical insight into the problem, extensive computations have been performed for the effects of the controlling thermofluid parameters on the dimensionless velocity and temperature and also on the skin-friction and Nusselt number. These computational results are shown in Figs. 2-10. The graphs are drawn in the presence (θr ≠ 0) /absence (θr→∞) of fluid viscosity parameter cases. The skin friction coefficient (-f"(0)) and wall temperature gradient ( -θ'(0)) are presented in table 1.The effects of Maxwell parameter k* on velocity components u-v (u along x axis called horizontal velocity and v along y axis called vertical velocity) are shown in Figs. 2(a) and 2(b). It is noted that k* = 0 is for Newtonian fluid. It is evident from these figures that increase in the Maxwell parameter or elasticity parameter k* is reduced the velocity profiles on both directions. This is due to the fact that with an increase in the Maxwell parameter k* decreases the velocity boundary layer thickness which results in the decrease in the velocity profile for both cases (θr=-1 and θr→∞). Figs. 3(a) and 3(b) shows the effects of suction/injection parameters s on velocity components in x and y directions respectively. It is clear from Fig 3(a) that as compared to an impermeable sheet (s=0), injection (s<0) has the effect to reduce the boundary layer thickness and thus the horizontal velocity, whereas suction (s>0) tends to thicken the boundary layer and the velocity increase accordingly in x direction while the trend reverse in y direction which shown in Fig. 3(b). This result is consistent with the physical situation.Figs. 4(a) and 4(b) exhibit the velocity distribution in x and y directions for different values of variable fluid viscosity parameter θr. From these graphs we observe that the velocity profile decreases with increases in the variable fluid viscosity parameter θr as compared to constant fluid viscosity parameter (θr→∞). This is due to the fact that increase of the viscosity/temperature parameter θr makes decreases of the boundary layer thickness which results in decrease of the velocity along both directions.Table 1. Values of skin friction coefficient (-f"(0)) and wall temperature gradient (-θ'(0)) for different values of pertinent parameters
 |
| |
|
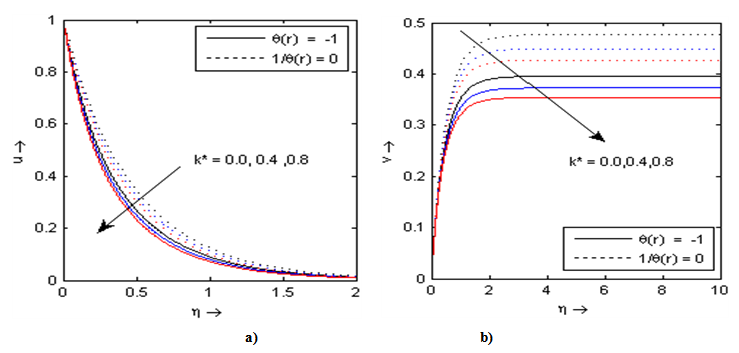 | Figure 2. Velocity profiles for different values of Maxwell parameter k* with s = 0, b = 2, ε = 0.1, Pr = 3 |
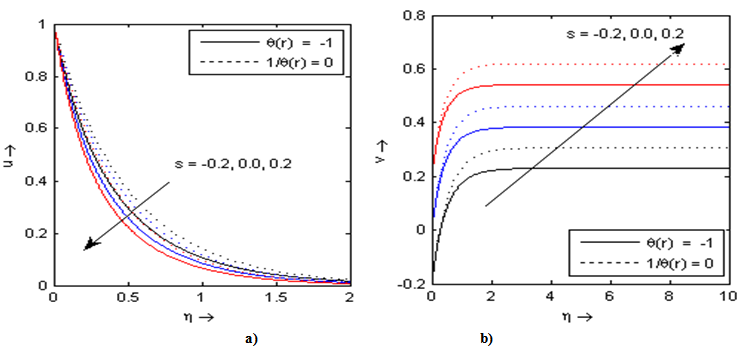 | Figure 3. Velocity profiles for different values of suction/injection parameter s with k* = 0.2, b = 2, ε = 0.1, Pr = 3 |
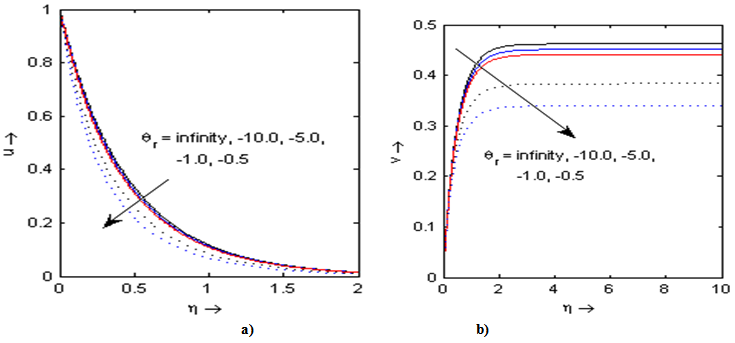 | Figure 4. Velocity profiles for different values of variable fluid viscosity parameter θr with k* = 0.2, s=0, b = 2, ε = 0.1, Pr = 3 |
Fig. 5 illustrates the effect of Maxwell parameter k* on temperature profile θ(η) in both cases (θr=-1 and θr→∞). It is observe that temperature profile θ(η) increases with increasing values of Maxwell parameter k* because the thermal boundary layer becomes broadened as we increase Maxwell parameter k*.Fig. 6 depicts the effects of suction/injection parameter s on the temperature distribution. The thermal boundary layer becomes thicker for suction and thinner for blowing as compared to an impermeable sheet for both cases (θr=-1 and θr→∞). We may notice that the effect of suction/injection parameter is reversed with increase in the fluid viscosity parameter θr. The graph for the temperature profile θ(η) with η for different values of variable thermal conductivity parameter ε in the presence (θr=-1)/ absence (θr→∞) of fluid viscosity parameter cases is shown in Fig. 7. It is noticed from this figure that an increase in the value of thermal conductivity parameter ε also increases temperature profile θ(η). This is due to the fact that the assumption of temperature-dependent thermal conductivity (linear form) implies a reduction in the magnitude of the transverse velocity by a quantity 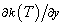 as can be seen from the heat transfer equation. We may further notice that the effect of variable thermal conductivity is to reduce the temperature with increase in the fluid viscosity parameter θr.
as can be seen from the heat transfer equation. We may further notice that the effect of variable thermal conductivity is to reduce the temperature with increase in the fluid viscosity parameter θr.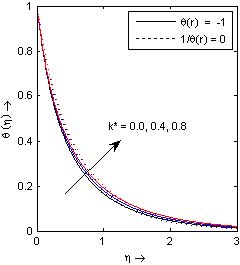 | Figure 5. Temperature profile for different values of Maxwell parameter k* with s = 0, b = 2, ε = 0.1, Pr = 3 |
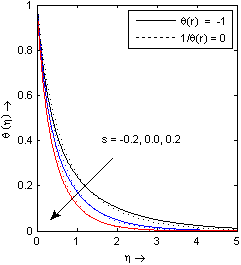 | Figure 6. Temperature profile for different values of suction / injection parameter s with k* = 0.2, b = 2, ε = 0.1, Pr = 3 |
The effects of power indices b on temperature profiles θ(η) with η may be analyzed from the Fig. 8 in both cases (θr=-1 and θr→∞). This graph depict that an increase in the value of power indices b results in decrease the temperature profile θ(η). The variation of temperature profile θ(η) with η for various values of Prandtl number Pr presence (θr=-1)/ absence (θr→∞) of fluid viscosity parameter cases are displayed in Fig. 9. This figure demonstrate that the increase of Prandtl number Pr ( increase if Prandtl number Pr means decrease of thermal conductivity k∞) results in decrease of temperature distribution which tend to zero as the space variable η increase from the wall and hence thermal boundary layer thickness decreases as Prandtl number Pr increases. This behaviour is observed in both the cases (θr=-1 and θr→∞). Near the boundary the thermal boundary layer thickness is higher at θr=-1 (as compare to θr→∞) and away from boundary, thermal boundary layer thickness is higher at θr→∞ (as compare to θr=-1).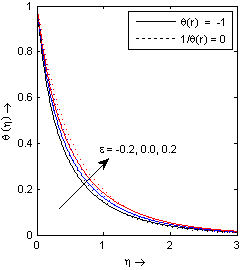 | Figure 7. Temperature profile for different values of power index b with k* = 0.2, s=0, ε = 0.1, Pr = 3 |
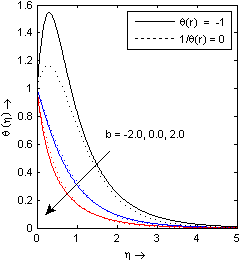 | Figure 8. Temperature profile for different values of power index b with k* = 0.2, s=0, ε = 0.1, Pr = 3 |
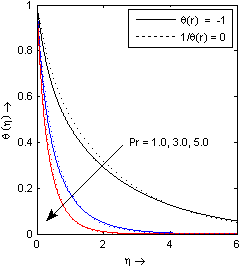 | Figure 9. Temperature profile for different values of Prandtl number Pr with k* = 0.2, s=0, b=2, ε = 0.1 |
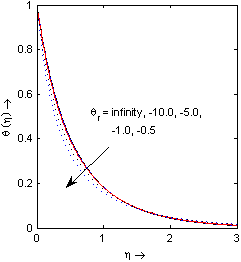 | Figure 10. Temperature profile for different values of variable fluid viscosity parameter θr with k* = 0.2, s=0, b = 2, ε = 0.1, Pr = 3 |
Fig. 10 elucidate the effects of the variable fluid viscosity parameter θr on temperature profile θ(η). It is interesting to find from Fig.10 that when we increases the value of fluid viscosity parameter θr, temperature θ(η) becomes decreases because temperature dependent coefficient of viscosity µ(T) vary as inverse function of temperature.
5. Conclusions
The following conclusions have been made from the above work1. The effect of Maxwell parameter is to decrease velocity distribution and to increase temperature distribution in the boundary layer.2. It is observed that the velocity profiles decreases with the increase of the value of fluid viscosity parameter θr. Thus viscoelastic fluid must be chosen since it is having low viscous dissipation for effective cooling of the stretching sheet.3. The velocity and temperature profiles in the case of constant viscosity are higher than the corresponding case of variable viscosity.4. The variable thermal conductivity also has an impact in enhancing the temperature profile, hence fluid with less thermal conductivity may be opted for effective cooling.5. The effect of Prandtl number is to decrease the thermal boundary layer thickness.6. The temperature profile is lower for injection parameter and higher for suction parameter.
ACKNOWLEDGEMENTS
The authors would like to thank the Council of Scientific and Industrial Research, New Delhi, for providing financial support through Grant No. 08/043(0005)/2008-EMR-1.
References
| [1] | Abel.M.S, Mahesha.N, Heat transfer in MHD viscoelastic fluid flow over a stretching sheet with variable thermal conductivity, non-uniform heat source and radiation, Appl. Math. Modeling 32(2008) 1965-1983. |
| [2] | Aliakbar. V, Alizadeh-Pahlavan. A, Sadeghy. k, The influence of thermal radiation on MHD flow of Maxwellian fluids above stretching sheets, Comm. Non-Linear Sci. and Numerical simulation 14(2009) 779-794. |
| [3] | Andersson H.I, MHD flow of a viscoelastic fluid past a stretching surface, Acta Mech. 95 (1992) 227-230. |
| [4] | Bhattacharyya Krishnendu, Boundary layer flow and heat transfer over an exponentially shrinking sheet, Chin. Phys. Lett. 28(7)-(2011), 074701(1-4) |
| [5] | Chaim. TC, Heat transfer with variable thermal conductivity in a stagnation-point flow towards a stretching sheet, Int. Commun. Heat Mass Transfer 1996;23:239-48. |
| [6] | Cortell.R, Effects of viscous dissipation and radiation on the thermal boundary layer over a nonlinearly stretching sheet, Phys Lett A 2008; 372:631-6. |
| [7] | Crane.L.J, Flow past a stretching sheet, ZAMP 21 (1970) 645-647. |
| [8] | Elbashbeshy.E.M.A, Heat transfer over an exponentially stretching continuous surface with suction, Arch. Mech. 53 (6) (2001) 643-651. |
| [9] | Eldabe Nabil.T.M, Mohamed Mona.A.A, Heat and mass transfer in hydromagnetic flow of the non-Newtonian fluid with heat source over an accelerating surface through a porous medium, Chaos, Solutions and Fractals 13 (2002) 907-917. |
| [10] | Grubka.L.J, Bobba. K.M, Heat transfer characteristics of a continuous stretching surface with variable temperature, ASME J. Heat Transfer 107 (1985) 248-250. |
| [11] | Gupta.P.S, Gupta.A.S, Heat and Mass Transfer on a stretching sheet with suction or blowing, Canda. J. Chem. Engng. 55 (1977) 744-746. |
| [12] | Khan.S.K, Sanjayanand.E, Viscoelastic boundary layer flow and heat transfer over an exponentially stretching sheet, Int. J. Heat Mass Transfer 48 (2005) 1534-1542. |
| [13] | Kumaran.V, Ramanaiah.G, A note on the flow over a stretching sheet, Acta Mech. 116 (1996) 229-233. |
| [14] | Lai. FC, Kulacki. FA, The effect of variable viscosity on convective heat transfer along a vertical surface in a saturated porous medium, Int. J. Heat Mass Transfer 1990;33-1028-31. |
| [15] | Magyari. E, Keller .B, Heat and mass transfer in the boundary layers on an exponentially stretching continuous surface, J.Phys. D Appl. Phys.32 (1999) 577-585. |
| [16] | Prasad. K.V, Pal. Dulal, Umesh. V, Prasanna Rao. N.S, The effect of variable viscosity on MHD viscoelastic fluid flow and heat transfer over a stretching sheet, Commun Nonlinear Sci. Numer. Simulat. 15(2010) 331-344. |
| [17] | Prasad. K.V, Sujatha. A, Vajravelu. K, Pop. I, MHD flow and heat transfer of a UCM fluid over a stretching surface with variable thermophysical properties, Meccanica DOI 10.1007/s11012-011-9526-x |
| [18] | Rahman. M.M, Salahuddin. K.M, Study of hydromagnetic heat and mass transfer flow over an inclined heated surface with variable viscosity and electric conductivity, Commun Nonlinear Sci. Numer. Simulat. 15(2010) 2073-2085. |
| [19] | Sanjayanand.E, Khan.S.K, On heat and mass transfer in a viscoelastic boundary layer flow over an exponentially stretching sheet, Int. J. Therm. Sci. 45 (2006) 819-828. |
| [20] | Sarpakaya.T, Flow of non-Newtonian fluids in a magnetic field, AIChE J.7 (1961) 324-328. |
| [21] | Singh. V, Agarwal. S, Heat transfer in a second grade fluid over an exponentially stretching sheet through porous medium with thermal radiation and elastic deformation under the effect of magnetic field, Int. l J. Applied Mathematics and Mechanics 8(4): 41 - 63, 2012. |
| [22] | Vajravelu, K, Viscous flow over a nonlinearly stretching sheet. Appl. Math. Comput. 124, 281–288 (2001). |
| [23] | Vajravelu.K, Rollins.D, Heat transfer in electrically conducting fluid over a stretching surface. Int. J. Non-linear Mech. 27 (2) (1992) 265-277. |

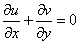

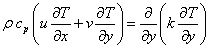
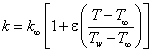
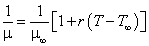
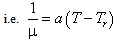
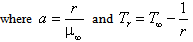
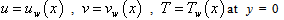
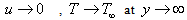
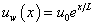
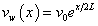
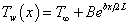
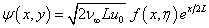
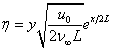
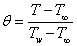
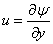 , and
, and 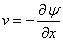 , the equation of continuity (1) is automatically satisfied.With the help of equations (4), (5) and (8), Equation (2) gets reduced to,
, the equation of continuity (1) is automatically satisfied.With the help of equations (4), (5) and (8), Equation (2) gets reduced to,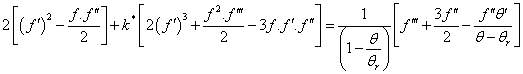
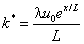 is the Maxwell parameter or viscoelastic parameter and
is the Maxwell parameter or viscoelastic parameter and 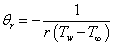 is the fluid viscosity parameter (depends on viscosity/temperature characteristics of the fluid under consideration and the temperature difference). We get the relation between constant viscosity and variable viscosity is
is the fluid viscosity parameter (depends on viscosity/temperature characteristics of the fluid under consideration and the temperature difference). We get the relation between constant viscosity and variable viscosity is 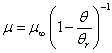 .Since the Prandtl number depends on variable viscosity and variable thermal conductivity therefore Prandtl number also varies as[18]
.Since the Prandtl number depends on variable viscosity and variable thermal conductivity therefore Prandtl number also varies as[18]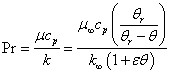
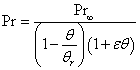
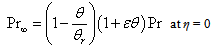
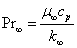 is the Prandtl number related to constant viscosity. From equation (10a) it is clear that for large θr (θr → ∞) and small ε (ε → 0), Pr → Pr∞. To reduce the energy equation (3) in ODE, use equations (4), (5), (6) and (8c) in equation (3) we get
is the Prandtl number related to constant viscosity. From equation (10a) it is clear that for large θr (θr → ∞) and small ε (ε → 0), Pr → Pr∞. To reduce the energy equation (3) in ODE, use equations (4), (5), (6) and (8c) in equation (3) we get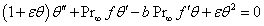
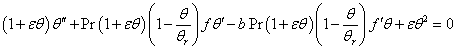
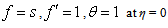
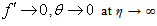
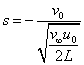 is the mass transfer parameter.s > 0 {v0 < 0} corresponds suction and s < 0 {v0 > 0} corresponds to the injection.
is the mass transfer parameter.s > 0 {v0 < 0} corresponds suction and s < 0 {v0 > 0} corresponds to the injection.


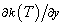 as can be seen from the heat transfer equation. We may further notice that the effect of variable thermal conductivity is to reduce the temperature with increase in the fluid viscosity parameter θr.
as can be seen from the heat transfer equation. We may further notice that the effect of variable thermal conductivity is to reduce the temperature with increase in the fluid viscosity parameter θr.





 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML