-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2013; 3(3): 75-79
doi:10.5923/j.ajfd.20130303.04
A Stochastic Analysis of Liquid Mixing in Bubble Column
Rajeev Parmar, Subrata Kumar Majumder
Department of Chemical Engineering, Indian Institute of Technology Guwahati, Guwahati, Assam, 781039, India
Correspondence to: Subrata Kumar Majumder, Department of Chemical Engineering, Indian Institute of Technology Guwahati, Guwahati, Assam, 781039, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In the present study, the mixing of liquid phase in bubble column is analysed by an entropy theory. The Kolmogorov entropy factor depending on the operating parameter is estimated to evaluate the concentration profile of the solute dispersed in the dynamic two-phase system. The intensity of mixing is enunciated by the Kolmogorov entropy parameter and correlated with the degree of mixing in the bubble column. Correlations have also been developed to predict the parameters by dimensional analysis. The analysis may be helpful for further understanding of the two-phase mixing in the multiphase system.
Keywords: Mixing, Bubble Column, Entropy, Two-Phase Flow
Cite this paper: Rajeev Parmar, Subrata Kumar Majumder, A Stochastic Analysis of Liquid Mixing in Bubble Column, American Journal of Fluid Dynamics, Vol. 3 No. 3, 2013, pp. 75-79. doi: 10.5923/j.ajfd.20130303.04.
Article Outline
1. Introduction
- Bubble columns are extensively used as gas-liquid contactors in the chemical, petrochemical and biochemical industries. Effective phase mixing leading to improve heat and mass transfer characteristics and other various advantages of bubble column reactors render it an attractive choice of reactors for different chemical and bio-chemical processes. The design and scale-up of these reactors has been primarily based on empiricism. This can be attributed to the complexity and scale dependency of the hydrodynamics and transport parameters in these systems. Considerable effort has been directed in recent years to obtain fundamental models for the description of hydrodynamics in bubble columns. The bubble column has been modified in different way according to the industrial need and applications[1]. Bubble column with various type of gas-liquid distributer utilises the kinetic energy of the high velocity liquid for the entrainment and dispersion of gas phase. They provide several advantages during operation and maintenance such as high heat and mass transfer rates, compactness and low operating and maintenance costs[1]. The advantages claimed for bubble columns compared to other multiphase contactors are: i) absence of moving parts and hence low maintenance cost, ii) higher effective interfacial area and volumetric mass transfer coefficients, (ii) less floor space requirement and iv) large liquid residence times especially suited for slow reactions, (v) high heat and mass transfer rate. A distinct advantage of bubble columns is that the mixing is effected by the action of rising bubbles, a process significantly more energy-efficient than mechanical stirring. But the operation and performance of bubble column reactor significantly depend on the fluid dynamic characteristic of bubble column. Ejector induced downflow bubble column has certain advantages such as uniform bubble size, finer bubbles, less power consumption, high gas utilization, easy maintenance[2-4]. For the analysis of performance of bubble column based on mixing characteristics, the axial dispersion model (ADM) is commonly used. The liquid is assumed to be in plug flow with axial dispersion superimposed on it. This model lumps the different mechanisms of liquid mixing into a single axial dispersion coefficient. The ADM lacks a proper physical basis for bubble columns but its popularity is reached due to a single unknown parameter. There are many correlations available in literature developed by different authors[5-7] to predict the axial dispersion coefficient. As per Deckwer (1992)[1], there is a wide scatter in the data and correlation predictions of the liquid mixing that are represented by simplified way. Other different phenomenological based models developed by Kastanec et al.(1973)[8], Nauman and Buffham (1983)[9], Deckwer and Schumpe (1993)[10], Krishna et al. (2000)[11] and Majumder (2008)[12] are also available for describing liquid backmixing in a way that can associate it with the fundamental mechanisms. Such models have a strong physical basis for understanding the liquid mixing behavior without relying on the complete solution of the fundamental hydrodynamic equations[13]. From the literature it is seen that mixing characteristics have been extensively studied in bubble column reactor and reported in the scientific literature[1, 4, 5, 14 – 21]. Many of the studies covered in the literature use conventional liquid-phase mixing models to interpret the obtained experimental data and to quantify the effect of the different operating and/or design parameters. The axial dispersion model (ADM) has been traditionally used to describe and quantify the extent of liquid backmixing in different reactor systems[22]. In the present study the mixing characteristics in bubble column has been analysed by a different a unified approach. In this case the time dependent tracer distribution which is an estimation of intensity of mixing in bubble column reactor has been analysed by Kolmogorov information entropy theory.
2. Theoretical Background
- The flow behaviour through a system is conveniently achieved by determining the age distribution of the elements of the fluid in the exit stream or the residence time distribution (RTD) within the system. The RTD for flowing fluid is normally obtained by the so called “Stimulus response” technique. This technique involves the injection of a solute as a tracer at the inlet streams and the corresponding response of tracer concentration within the system. The variation of solute concentration is characterized by molecular diffusion and convective diffusion in a system. The variation of concentration with a time step of ∆t results the information about the solute dispersion intensity and the local concentration at a certain time. In general for P dimension case, the experimentally obtained time signal of concentration C(t), in a time step ∆t, the (m+1) values of concentration results as C(i, ∆t) for i = 0, 1, 2, 3, 4 m. Thus a vector information distribution for the tracer particle can be expressed as[23]:
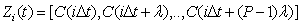 | (1) |
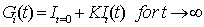 | (2) |
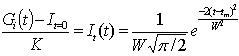 | (3) |
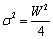 | (4) |
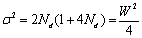 | (5) |
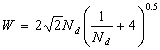 | (6) |
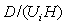 ). Higher the dispersion number more the mixing of phases in the system. The dispersion number can be expressed in terms of parameter W as:
). Higher the dispersion number more the mixing of phases in the system. The dispersion number can be expressed in terms of parameter W as: 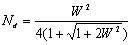 | (7) |
3. Results and Discussion
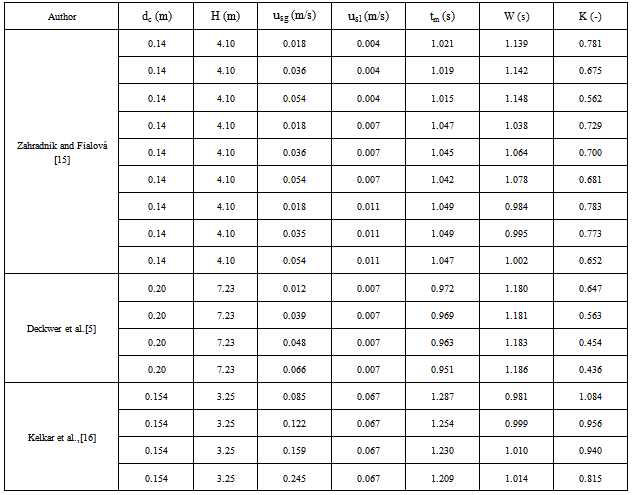
- The degree of dispersion examined by the parameter which is known as Kolmogorov entropy (K) and the information characteristic factor (W) of spreading of solute distribution which quantifies the intensity of the mixing of phases in the system. As the parameter increases the mixing intensity increases. In the following section, the Kolmogorov entropy (K) and the effective characteristic factor (W) of spreading of solute distribution in bubble column reactor are enunciated based on the published data[5, 15, 16]. In the following section effect of operating variables on mixing characteristic factors are enunciated.
3.1. Rate of Generation of Information
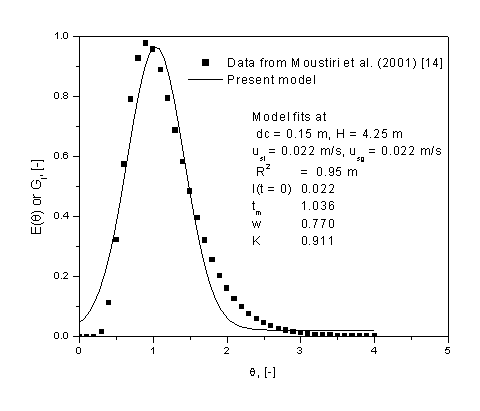 | Figure 1. The rate of generation of information with respect to time |
3.2. Effect of Phase Velocity on Mixing Characteristic Factors (W)
- From the experimental data on mixing in bubble column published by Deckwer et al. (1974)[5], Zaharandnik and Fialova (1996)[15], Kelkar et al. (1983)[16]. The variation of mixing characteristic factor with gas phase velocities is shown in Figure 2. It is observed that the mixing characteristic factor (W) increases with increase in gas velocity. At constant liquid velocity increasing gas velocity indicates a higher dispersion or higher mixing in the column.
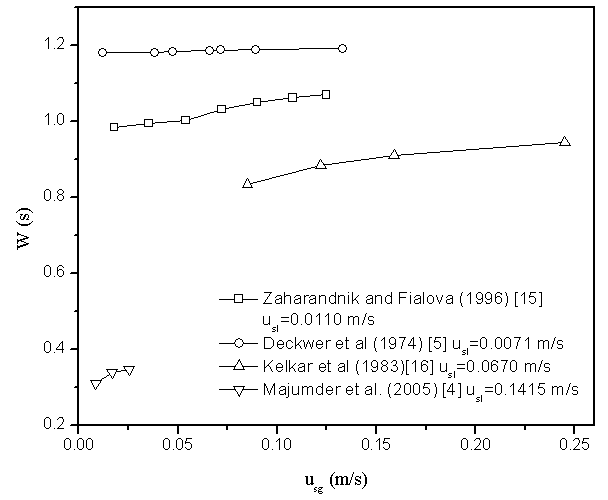 | Figure 2. Variation of mixing characteristic factor with phase velocities |
3.3. Effect of Phase Velocity on Entropy (K)
- From the data analysis by the entropy theory it is seen that the Kolmogorov entropy (K) decreases with increases in gas velocity as shown in Figure 3. The entropy increases with increase in liquid velocity but decreases with increase in gas velocity. The increase in entropy with liquid velocity indicates more dispersion of solute in the column but as the gas velocity increases with constant liquid velocity, the uniform distribution of the solute may be hindered by the internal circulation of the liquid due to pressure difference in the column. The overall effects of the entropy may lead to the increase in mixing characteristics (W) to represent the concentration profile of the tracer particle inside the column.
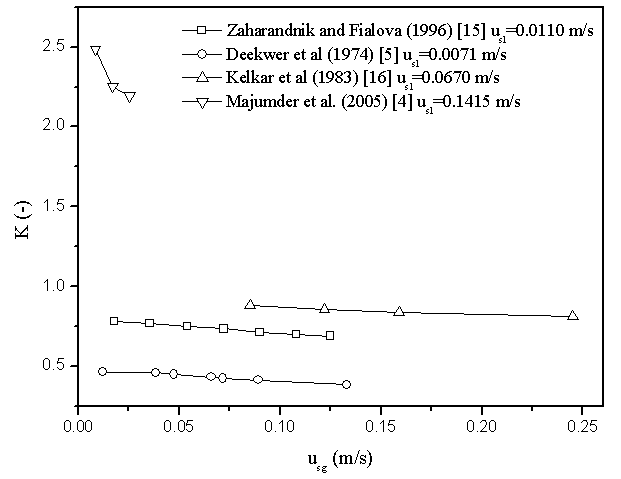 | Figure 3. Variation of entropy with phase velocities |
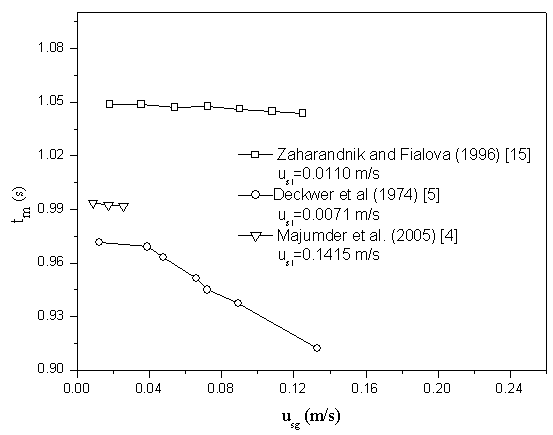
3.4. Effect of Phase Velocity on Mean Residence Time (MRT)
- The mean residence time of the tracer particles inside the column depends on the liquid and the gas velocities. Geometric configurations have also effects on the mean residence time of the particle. As the liquid or gas velocity increases the mean residence time of the tracer particles decreases. The mean residence time can be calculated from the relation, αgH/usg. As the gas velocity increases the gas holdup increases in the column which results in overall decrease of mean residence time of the liquid in the column. The same effect of liquid velocity on the gas holdup may lead to the decrease of mean residence time of the liquid in the column. The parameter tc represents the mean residence time in the present analysis. The variation of the mean residence time with gas velocity at different liquid velocity is shown in Figure 4. Some typical data’s of different mixing characteristics vary with different operating variables are obtained by present analysis from different authors are shown in Table 1. From the table it is seen that parameters are affected not only by dynamic variables but also with the geometric variables like height and diameters of the bubble column.
3.5. Correlations for Model Parameters
- The present model is fitted with the experimental data of different authors, to find the different parameters. It is seen that the parameters are affected by the different operating variables as shown in Table 1. Based on the different operating variables, correlations are developed to predict the parameters by multiple regression analysis with the help of Microsoft excel data analysis tool.
 | Figure 4. Variation of mean residence time of tracer with phase velocity |
|
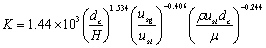 | (8) |
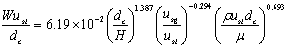 | (9) |
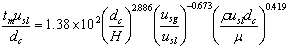 | (10) |
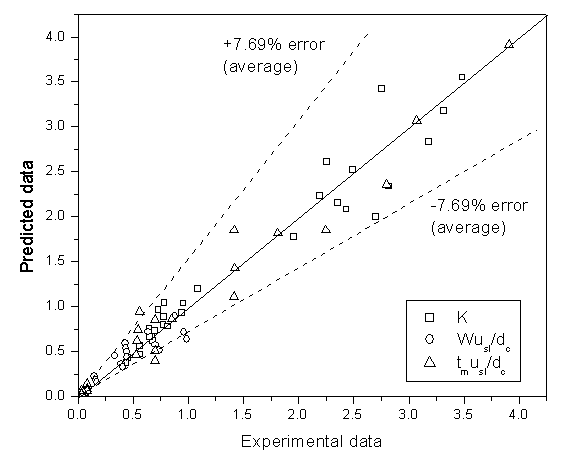 | Figure 5. Experimental versus predicted values of different parameters |
4. Conclusions
- The mixing characteristics in a bubble column have been analysed in the present study by an entropy theory. The entropy theory describes the intensity of dispersion in the bubble column under different operating variables. Different authors described the dispersion in multiphase system with axial dispersion model. But in this present study, an alternative way has been enunciated to describe the mixing characteristics in the bubble column reactor. The degree of dispersion and the information characteristic factor of spreading of solute distribution quantify the intensity of the mixing of phases in the system. The overall affects of the entropy plays an important role in mixing characteristics to represent the concentration profile of the tracer particle. The flow behavior through a system can be analysed with the developed correlations which are achieved by determining the age distribution of the elements of the fluid in the exit stream. The correlations developed to predict the parameters are found to be well fitted with the experimental data. The analysis may be useful for further understanding to analyse the mixing characteristics in multiphase system.
NOTATIONS

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML