Kapil Kumar1, V. Singh2, Seema Sharma1
1Department of Mathematics & Statistics, Gurukula Kangri Vishwavidyalaya, Haridwar, 249404, India
2Department of Applied Sciences, Moradabad Institute of Technology, Moradabad, 244001, India
Correspondence to: Kapil Kumar, Department of Mathematics & Statistics, Gurukula Kangri Vishwavidyalaya, Haridwar, 249404, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The effect of suspended particles, variable gravity and magnetic field on the thermal stability of an Oldroydian viscoelastic fluid through Brinkman porous medium is considered. Following the linearized stability theory and normal mode method, the dispersion relation is obtained. It has been found that for stationary convection, Oldroydian viscoelastic fluid behaves like an ordinary Newtonian fluid and medium permeability, medium porosity and suspended particles have destabilizing effects on the system whereas the magnetic field and Darcy-Brinkman number have stabilizing effects on the system. The sufficient conditions for the non-existence of overstability are obtained and it has also been found that the modes may be oscillatory and non-oscillatory. It is also noted that the principle of exchange of stabilities is valid under certain conditions.
Keywords:
Stability, Suspended Particles, Magnetic Field, Brinkman Porous Medium
Cite this paper: Kapil Kumar, V. Singh, Seema Sharma, Stability of an Oldroydian Viscoelastic Fluid Permeated with Suspended Particles through a Brinkman Porous Medium with Variable Gravity Field in Hydromagnetics, American Journal of Fluid Dynamics, Vol. 3 No. 3, 2013, pp. 58-66. doi: 10.5923/j.ajfd.20130303.02.
1. Introduction
The theoretical and experimental results of the onset of convection in a horizontal layer of Newtonian fluid heated from below under varying assumptions of hydrodynamics and hydromagnetics has been discussed in detail by Chandrasekhar[1]. The flow through porous medium is important in filtering equipment, chemical reactors, oil and gas extraction, recovery of crude oil from earth’s interior, movement of ground water, etc. The physical properties of comets, meteorites and interplanetary dust strongly suggest the importance of porosity in astrophysical situations (McDonnel[2]). A porous medium is defined as a material volume consisting of solid matrix with an interconnected void. It is mainly characterized by its porosity which is defined as the ratio of the void space to the total volume of the medium. A comprehensive and detailed study of convection through porous medium has been given by Nield and Bejan[3]. At low velocities a saturated porous medium with high porosity is well described by the Darcy-Brinkman approximation and require that classical frictional term be added in the classical Darcy equation. The dynamic viscosity 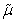 associated with the Brinkman[4] term is known as effective viscosity. Tissues can be treated as a porous medium as it is composed of dispersed cells separated by connective voids which allow for flow of nutrients, minerals, etc. There are several evidences, both theoretical and experimental, which suggest that the Darcy’s equation gives inadequate results of the hydrodynamic conditions, particularly near the boundaries of a porous medium. The Darcy-Brinkman equation, which takes into account the boundary effects, has been employed in recent years in biomedical hydrodynamic studies[5], modeling a thin fibrous surface layer coating blood vessels (endothelial surface layer) as it is a highly permeable porous medium[6,7]. It is, therefore, of interest to study the characteristics of the Darcy-Brinkman equation which have relevance importance in several biological, geological, chemical reactors and medical science applications, thus forming a motivation for the present study.In geophysical context, the fluid is often not pure but may instead be permeated with dust particles. The effects of suspended particles on the stability of superposed fluids have industrial and scientific importance in geophysics, chemical engineering and astrophysics. Scanlon and Segel[8] have considered the effect of suspended particles on the onset of Bénard convection and found that the critical Rayleigh number was reduced solely because the heat capacity of the pure fluid was supplemented by that of the particles. So the effect of suspended particles was thus found to increase the instability of the layer. An experimental demonstration by Toms and Strawbridge[9] reveals that a dilute solution of methyl methacrylate in n-butyl acetate behaves in accordance with the theoretical model of Oldroyd fluid[10]. The present analysis would be relevant to the stability of some polymer solutions like a dilute solution of methyl methacrylate in n-butyl acetate and also find its importance in several geographical situations and in chemical technology. Bhatia and Steiner[11] have studied the problem of thermal instability of a Maxwellian visco-elastic fluid in the presence of a magnetic field and found that the magnetic field has a stabilizing influence on the overstable mode of convection in a visco-elastic fluid layer. The problem of thermal instability of a fluid layer under variable gravity field has been considered by Pradhan and Samal[12]. Since the earth’s gravity field varies with its distance from its surface so it is of utmost important to take into account the effect of variable gravity field having its importance in several convective flows, atmospheric science, astrophysics, geophysics and also in material processing technology.Sharma[13] studied the stability of a layer of an electrically conducting Oldroyd fluid in the presence of a magnetic field and found that the magnetic field has a stabilizing influence while the effect of suspended particles on the onset of Bénard convection in hydromagnetics have been studied by Sharma et al.[14]. Sharma and Sharma[15] have investigated the effect of suspended particles on thermal instability in Maxwellian and Oldroydian viscoelastic fluids in a porous medium and found that for stationary convection both the Maxwellian and Oldroydian fluids behave like Newtonian fluid and the medium permeability and suspended particles have destabilizing effects on the system. Sharma and Sunil[16] considered the thermal instability of an Oldroydian viscoelastic fluid with suspended particles in hydromagnetics in porous medium and concluded that, for stationary convection, magnetic field has a stabilizing effect whereas medium permeability and suspended particles have destabilizing effects on the system. The problem of the onset of electroconvective instability of an Oldroydian viscoelastic liquid layer through Brinkman porous medium under the simultaneous action of an electric field and a vertical temperature gradient has been investigated by El-Sayed[17]. The purpose of the present note treated here is to examine theoretically the problem of the onset of stability of an Oldroydian viscoelastic fluid permeated with suspended particles through a Brinkman porous medium under the simultaneous action of varying gravity field and vertical magnetic field.
associated with the Brinkman[4] term is known as effective viscosity. Tissues can be treated as a porous medium as it is composed of dispersed cells separated by connective voids which allow for flow of nutrients, minerals, etc. There are several evidences, both theoretical and experimental, which suggest that the Darcy’s equation gives inadequate results of the hydrodynamic conditions, particularly near the boundaries of a porous medium. The Darcy-Brinkman equation, which takes into account the boundary effects, has been employed in recent years in biomedical hydrodynamic studies[5], modeling a thin fibrous surface layer coating blood vessels (endothelial surface layer) as it is a highly permeable porous medium[6,7]. It is, therefore, of interest to study the characteristics of the Darcy-Brinkman equation which have relevance importance in several biological, geological, chemical reactors and medical science applications, thus forming a motivation for the present study.In geophysical context, the fluid is often not pure but may instead be permeated with dust particles. The effects of suspended particles on the stability of superposed fluids have industrial and scientific importance in geophysics, chemical engineering and astrophysics. Scanlon and Segel[8] have considered the effect of suspended particles on the onset of Bénard convection and found that the critical Rayleigh number was reduced solely because the heat capacity of the pure fluid was supplemented by that of the particles. So the effect of suspended particles was thus found to increase the instability of the layer. An experimental demonstration by Toms and Strawbridge[9] reveals that a dilute solution of methyl methacrylate in n-butyl acetate behaves in accordance with the theoretical model of Oldroyd fluid[10]. The present analysis would be relevant to the stability of some polymer solutions like a dilute solution of methyl methacrylate in n-butyl acetate and also find its importance in several geographical situations and in chemical technology. Bhatia and Steiner[11] have studied the problem of thermal instability of a Maxwellian visco-elastic fluid in the presence of a magnetic field and found that the magnetic field has a stabilizing influence on the overstable mode of convection in a visco-elastic fluid layer. The problem of thermal instability of a fluid layer under variable gravity field has been considered by Pradhan and Samal[12]. Since the earth’s gravity field varies with its distance from its surface so it is of utmost important to take into account the effect of variable gravity field having its importance in several convective flows, atmospheric science, astrophysics, geophysics and also in material processing technology.Sharma[13] studied the stability of a layer of an electrically conducting Oldroyd fluid in the presence of a magnetic field and found that the magnetic field has a stabilizing influence while the effect of suspended particles on the onset of Bénard convection in hydromagnetics have been studied by Sharma et al.[14]. Sharma and Sharma[15] have investigated the effect of suspended particles on thermal instability in Maxwellian and Oldroydian viscoelastic fluids in a porous medium and found that for stationary convection both the Maxwellian and Oldroydian fluids behave like Newtonian fluid and the medium permeability and suspended particles have destabilizing effects on the system. Sharma and Sunil[16] considered the thermal instability of an Oldroydian viscoelastic fluid with suspended particles in hydromagnetics in porous medium and concluded that, for stationary convection, magnetic field has a stabilizing effect whereas medium permeability and suspended particles have destabilizing effects on the system. The problem of the onset of electroconvective instability of an Oldroydian viscoelastic liquid layer through Brinkman porous medium under the simultaneous action of an electric field and a vertical temperature gradient has been investigated by El-Sayed[17]. The purpose of the present note treated here is to examine theoretically the problem of the onset of stability of an Oldroydian viscoelastic fluid permeated with suspended particles through a Brinkman porous medium under the simultaneous action of varying gravity field and vertical magnetic field.
2. Formulation of the Problem and Perturbation Equations
Let 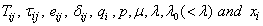 denote, respectively, the total stress tensor, shear stress tensor, rate of strain tensor, Kronecker delta, velocity vector, pressure, viscosity, stress relaxation time, strain retardation time and position vector. Then the Jeffrey (Oldroydian) constitutive relations for performing linear stability of Rayleigh–Bénard convection in clear viscoelastic fluids are
denote, respectively, the total stress tensor, shear stress tensor, rate of strain tensor, Kronecker delta, velocity vector, pressure, viscosity, stress relaxation time, strain retardation time and position vector. Then the Jeffrey (Oldroydian) constitutive relations for performing linear stability of Rayleigh–Bénard convection in clear viscoelastic fluids are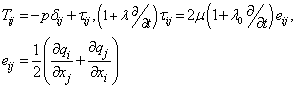 | (1) |
Relations of the type (1) were proposed and studied by Oldroyd[10]. He also showed that many rheological equations of general validity reduce to (1) when linearized. 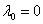 yields the Maxwellian fluid, whereas
yields the Maxwellian fluid, whereas 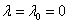 gives the Newtonian viscous fluid. Here we consider an infinite horizontal layer of an Oldroydian viscoelastic fluid permeated with suspended particles and bounded by the planes z=0 and z=d in a porous medium of porosity
gives the Newtonian viscous fluid. Here we consider an infinite horizontal layer of an Oldroydian viscoelastic fluid permeated with suspended particles and bounded by the planes z=0 and z=d in a porous medium of porosity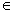 and medium permeability
and medium permeability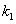 . The fluid layer is acted on by a uniform vertical magnetic field H (0, 0, H) and a variable gravity force
. The fluid layer is acted on by a uniform vertical magnetic field H (0, 0, H) and a variable gravity force 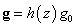 , where
, where 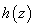 can be positive or negative according as the gravity increase or decreases upward from its value
can be positive or negative according as the gravity increase or decreases upward from its value 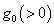 . The layer is heated from below so that a uniform temperature gradient
. The layer is heated from below so that a uniform temperature gradient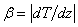 is maintained. The governing equations of motion and continuity for the Oldroydian viscoelastic fluid based on the Darcy-Brinkman approximation are
is maintained. The governing equations of motion and continuity for the Oldroydian viscoelastic fluid based on the Darcy-Brinkman approximation are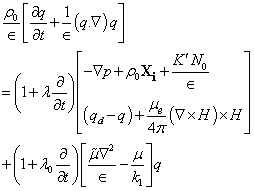 | (2) |
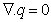 | (3) |
Where 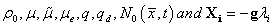 denote, respectively, the density of fluid, viscosity, effective viscosity, magnetic permeability, velocity of pure fluid, velocity of suspended particles, number density of the suspended particles and the gravitational acceleration.
denote, respectively, the density of fluid, viscosity, effective viscosity, magnetic permeability, velocity of pure fluid, velocity of suspended particles, number density of the suspended particles and the gravitational acceleration. 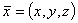 and
and 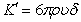 where
where 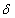 being particle radius, is the Stokes’ drag coefficient.The presence of suspended particles adds an extra force term, in equation of motion, proportional to velocity difference between particles and fluid. Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite in sign, in the equations of motion for the particles. Inter-particle reactions are ignored as the distances between the particles are assumed to be quite large compared with their diameters. The effects of pressure, magnetic field and gravity on the particles are very small and hence ignored.If mN is the mass of particles per unit volume, then the equations of motion and continuity for the particles are:
being particle radius, is the Stokes’ drag coefficient.The presence of suspended particles adds an extra force term, in equation of motion, proportional to velocity difference between particles and fluid. Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite in sign, in the equations of motion for the particles. Inter-particle reactions are ignored as the distances between the particles are assumed to be quite large compared with their diameters. The effects of pressure, magnetic field and gravity on the particles are very small and hence ignored.If mN is the mass of particles per unit volume, then the equations of motion and continuity for the particles are: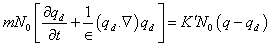 | (4) |
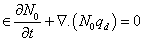 | (5) |
The energy equation is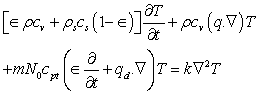 | (6) |
Where 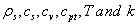 denote, respectively, the density of solid material, heat capacity of solid material, the specific heat at constant volume, heat capacity of suspended particles, the temperature and the thermal conductivity.The Maxwell’s equation yields
denote, respectively, the density of solid material, heat capacity of solid material, the specific heat at constant volume, heat capacity of suspended particles, the temperature and the thermal conductivity.The Maxwell’s equation yields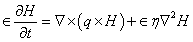 | (7) |
and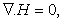 | (8) |
Where 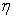 denote the electrical resistivity.The equation of state is
denote the electrical resistivity.The equation of state is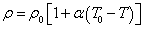 | (9) |
The steady state solution corresponding to the system of equations (2)-(9) are: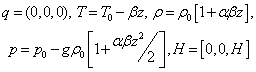 | (10) |
Let the initial state solution described by equation (10) be slightly perturbed. We assume that q (u,v,w), qd (l,r,s), N, θ, 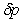 ,
,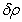 and
and 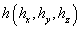 denote, respectively, the perturbation in fluid velocity q(0,0,0), perturbation in particle velocity qd (0,0,0), perturbation in particle number density
denote, respectively, the perturbation in fluid velocity q(0,0,0), perturbation in particle velocity qd (0,0,0), perturbation in particle number density 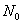 , temperature T, pressure p, density
, temperature T, pressure p, density 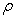 and magnetic field H. The change in density
and magnetic field H. The change in density 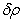 caused by perturbation θ in temperature, is given by
caused by perturbation θ in temperature, is given by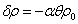 | (11) |
The governing perturbation equations (usingOberbeck-Boussinesq approximation) due to linearization procedure are: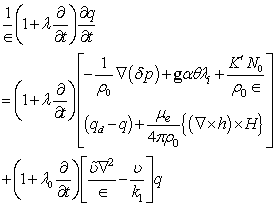 | (12) |
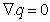 | (13) |
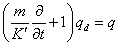 | (14) |
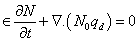 | (15) |
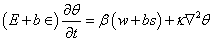 | (16) |
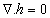 | (17) |
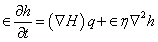 | (18) |
where 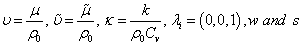 denote, respectively, the kinematic viscosity, the effective kinematic viscosity, the co-efficient of thermometric conductivity, unit vertical vector, vertical fluid velocity and suspended particles velocity and
denote, respectively, the kinematic viscosity, the effective kinematic viscosity, the co-efficient of thermometric conductivity, unit vertical vector, vertical fluid velocity and suspended particles velocity and 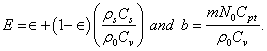 Eliminating
Eliminating 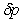 between the three component equations of (12) and using equations (13) and (14), we obtain:
between the three component equations of (12) and using equations (13) and (14), we obtain: 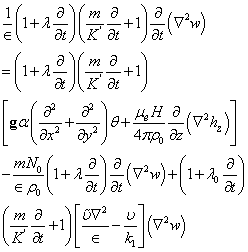 | (19) |
and 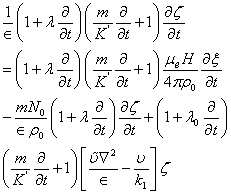 | (20) |
Where 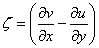 and
and 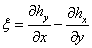 stand for the z-component of vorticity and z-component of current density, respectively.From equation (16), we obtain:
stand for the z-component of vorticity and z-component of current density, respectively.From equation (16), we obtain: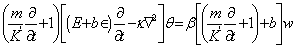 | (21) |
The x and y component equations of (18) along with (17) yields: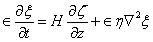 | (22) |
and the z- component equation of (18) is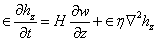 | (23) |
Where 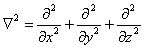 is the three dimensional Laplacian operator.
is the three dimensional Laplacian operator.
3. Dispersion Relation and Discussion
Decomposing the disturbances into normal modes by seeking solutions whose dependence on x, y and t is given by: 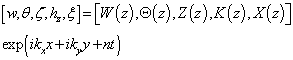 | (24) |
Where 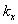 ,
, 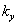 are the wave numbers along x and y directions, respectively and
are the wave numbers along x and y directions, respectively and 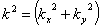 is the resultant wave number and n is the frequency of the harmonic disturbance, which is, in general, a complex constant.Using expression (24) and making the substitutions of the non-dimensional quantities of the form
is the resultant wave number and n is the frequency of the harmonic disturbance, which is, in general, a complex constant.Using expression (24) and making the substitutions of the non-dimensional quantities of the form 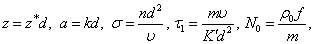
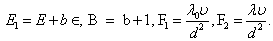
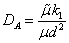 , is the Darcy-Brinkman number,
, is the Darcy-Brinkman number, 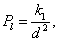 is the dimensionless medium permeability,
is the dimensionless medium permeability, 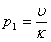 , is the thermal Prandtl number and
, is the thermal Prandtl number and 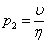 , is the magnetic Prandtl number.We obtain the non-dimensional form of Equations (19)-(23) (after dropping the asterisk for convenience) as:
, is the magnetic Prandtl number.We obtain the non-dimensional form of Equations (19)-(23) (after dropping the asterisk for convenience) as: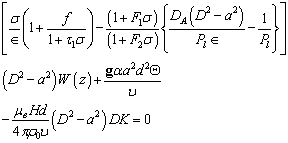 | (25) |
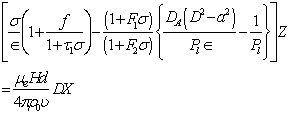 | (26) |
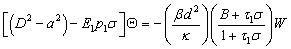 | (27) |
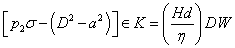 | (28) |
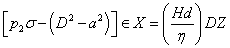 | (29) |
Eliminating 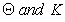 from equations (25), (27) and (28), we obtain:
from equations (25), (27) and (28), we obtain: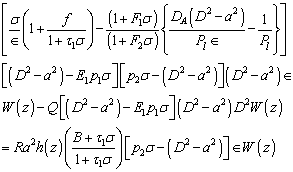 | (30) |
Where 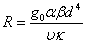 , is the thermal Rayleigh number and
, is the thermal Rayleigh number and 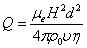 , is the Chandrasekhar number.
, is the Chandrasekhar number.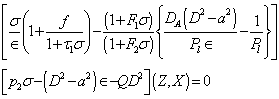 | (31) |
It is apparent from equation (31) that for the problem under consideration 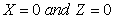 | (32) |
that is the z- components of vorticity and current density vanish identically for the problem on hand.The boundary conditions appropriate to two free and perfectly conducting boundaries are defined as: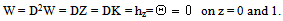 | (33) |
Equation (30) together with the boundary conditions (32) and (33) constitute an eigen-value problem for the problem on hand. It is evident that when 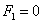 , the system reduces to that for a Maxwell fluid whereas for
, the system reduces to that for a Maxwell fluid whereas for 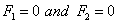 , the system reduces to that for an ordinary viscous fluid.
, the system reduces to that for an ordinary viscous fluid.
4. Solution of the Eigen-value Problem
The boundary conditions (32) and (33) suggest that a proper solution for W belonging to the lowest mode is defined by 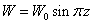 | (34) |
where W0 is a constant. Substituting solution (34) in equation (30) and letting 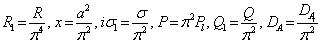 , we get the eigenvalue relationship of the form:
, we get the eigenvalue relationship of the form: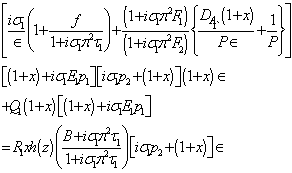 | (35) |
Equation (35) is required dispersion relation accounting the effects of magnetic field, suspended particles and medium permeability on thermal instability of an Oldroyd visco-elastic fluid through a Brinkman porous medium.
5. The Stationary Convection
When instability sets in as stationary convection, the marginal state will be characterized by putting 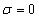 in equation (35) and get the eigenvalue relationship for a stationary instability of the form:
in equation (35) and get the eigenvalue relationship for a stationary instability of the form: 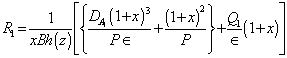 | (36) |
Thus it is clear from equation (36) that for stationary convection Oldroydian visco-elastic fluid behaves like an ordinary Newtonian fluid since the stress relaxation parameter 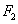 and strain retardation parameter
and strain retardation parameter 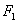 vanishes with
vanishes with 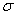 .Minimizing equation (36) with respect to
.Minimizing equation (36) with respect to 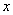 , yields the third order equation in
, yields the third order equation in 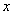 as
as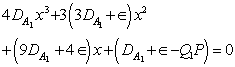 | (37) |
Substituting the value of critical wave number 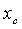 thus obtained from equation (37), in equation (36), gives the value of critical Rayleigh number for stationary instability.In order to investigate the effects of suspended particles, magnetic field, medium permeability, Darcy-Brinkman number and medium porosity, we examine the behaviour of
thus obtained from equation (37), in equation (36), gives the value of critical Rayleigh number for stationary instability.In order to investigate the effects of suspended particles, magnetic field, medium permeability, Darcy-Brinkman number and medium porosity, we examine the behaviour of 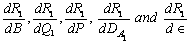 analytically. Equation (36) yields
analytically. Equation (36) yields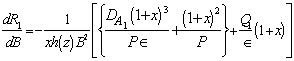 | (38) |
which is negative implying thereby that the suspended particles have a destabilizing effect on the viscoelastic Oldroydian fluid for the case of stationary convection when the gravity field increases upward from its value g0 i.e. 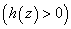 . This destabilizing effect of suspended particles agrees with previous published work by Scanlon and Segel[8], Sharma and Sharma[15] and Sharma and Sunil[16].From equation (36), we get
. This destabilizing effect of suspended particles agrees with previous published work by Scanlon and Segel[8], Sharma and Sharma[15] and Sharma and Sunil[16].From equation (36), we get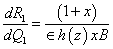 | (39) |
which shows that magnetic field always has a stabilizing effect on the viscoelastic Oldroydian fluid for the case of stationary convection when the gravity field increases upward from its value g0 i.e. 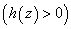 . This stabilizing effect of magnetic field is an agreement of the previous results by Sharma[13] and Sharma and Sunil[16].From equation (36), we get
. This stabilizing effect of magnetic field is an agreement of the previous results by Sharma[13] and Sharma and Sunil[16].From equation (36), we get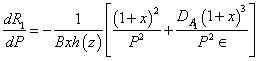 | (40) |
which is always negative implying thereby that the medium permeability has a destabilizing effect on the viscoelastic Oldroydian fluid for the case of stationary convection as the gravity field increases upward from its value g0 i.e. 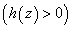 . This destabilizing result agrees with the earlier work reported by Sharma and Sharma[15] and Sharma and Sunil[16].From equation (36), we get
. This destabilizing result agrees with the earlier work reported by Sharma and Sharma[15] and Sharma and Sunil[16].From equation (36), we get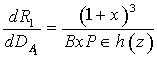 | (41) |
which is always positive. Therefore, the modified Darcy-Brinkman number has a stabilizing effect on the system for the case of stationary convection as the gravity field increases upward from its value g0 i.e. 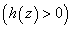 . From equation (36), we get
. From equation (36), we get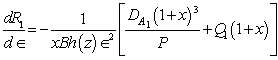 | (42) |
which is negative implying thereby that the effect of medium porosity is to destabilize the system for the case of stationary convection as the gravity increases upward from its value g0 i.e. 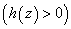 . This destabilizing effect of porosity agrees with the result of El-Sayed[17].
. This destabilizing effect of porosity agrees with the result of El-Sayed[17].
6. Results and Discussion
The dispersion relation (36) is analyzed numerically. The region of stationary instability for different values of suspended particles, magnetic field, medium permeability, Darcy-Brinkman number and medium porosity is shown in figures 1, 2, 3, 4, and 5, respectively. It is clear from figure1 that the critical Rayleigh number decreases with an increase in the value of suspended particles. Figure 2 illustrates that critical Rayleigh number increases with an increase in magnetic field. Figure 3 shows a decrease in critical Rayleigh number with permeability. Figure 4 illustrates that an increase in the value of Darcy-Brinkman number increases the critical Rayleigh number, thereby depicting the stabilizing effect of Darcy-Brinkman number for the problem on hand. From figure 5, we find that an increase in the medium porosity decreases the critical Rayleigh number, and hence decreases the region of stability.  | Figure 1. Variation of Rayleigh number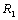 with wave number x, for with wave number x, for 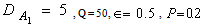 and B=5,10,15,20,25 and B=5,10,15,20,25 |
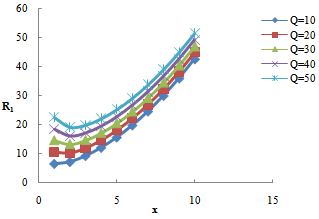 | Figure 2. Variation of Rayleigh number with wave number x, for with wave number x, for 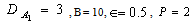 and Q=10,20,30,40,50 and Q=10,20,30,40,50 |
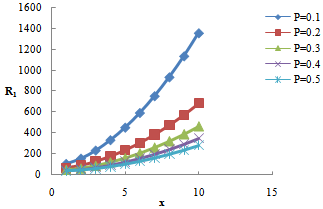 | Figure 3. Variation of Rayleigh number 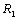 with wave number x, for with wave number x, for 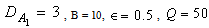 and P=0.1, 0.2, 0.3, 0.4, 0.5 and P=0.1, 0.2, 0.3, 0.4, 0.5 |
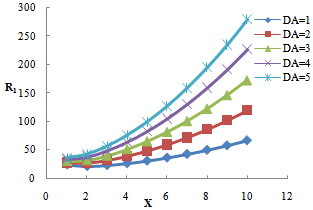 | Figure 4. Variation of Rayleigh number 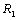 with wave number x, for P=0.5, B = 10, with wave number x, for P=0.5, B = 10, 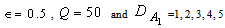 |
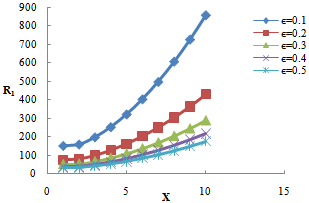 | Figure 5. Variation of Rayleigh number 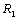 with wave number x, for with wave number x, for 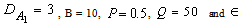 =0.1, 0.2, 0.3, 0.4, 0.5 =0.1, 0.2, 0.3, 0.4, 0.5 |
7. Overstability Case
Here we examine the possibility of whether the instability may occur as overstability. Since for overstability we wish to determine the critical Rayleigh number for the onset of instability via a state of pure oscillations, it suffices to find the conditions for which equation (35) will admit solutions with real. Equating the real and imaginary parts of equation (35), we get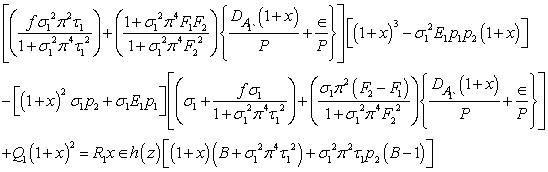 | (43) |
and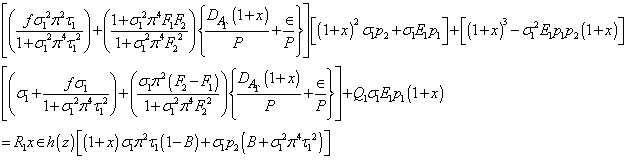 | (44) |
Eliminating R1 between equations (43) and (44) and assuming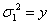 , we get a fourth order polynomial in y of the form:
, we get a fourth order polynomial in y of the form: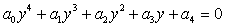 | (45) |
Where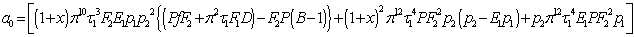 | (46) |
and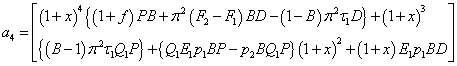 | (47) |
where 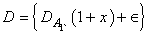 The values of the coefficients
The values of the coefficients 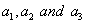 involving large number of terms are not included to save spaces. Since
involving large number of terms are not included to save spaces. Since 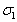 is real for overstability to occur therefore all the roots of y should be positive.From equation (45), the product of root
is real for overstability to occur therefore all the roots of y should be positive.From equation (45), the product of root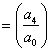 is positive.
is positive.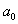 is negative if
is negative if 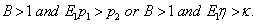 | (48) |
and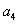 is positive if
is positive if 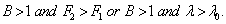 | (49) |
The inequalities defined by (48) and (49) are the sufficient conditions for the non-existence of overstability.
8. Principal of Exchange of Stabilities and Oscillatory Modes
Here we determine the condition, if any, under which principle of exchange of stabilities is satisfied and the possibility of oscillatory modes for the Oldroydian viscoelastic fluid under the influences of variable gravity, suspended particle and magnetic field through Brinkman porous medium. For this, we multiply equation (25) by W* (the complex conjugate of W), integrating over the range of z and making use of equations (27) and (28) with the help of boundary conditions (32) and (33), we obtain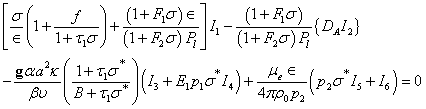 | (50) |
Where 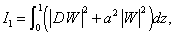
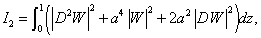
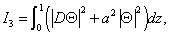
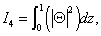
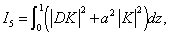
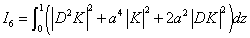 All the above integrals I1-I6 are positive definite. Putting
All the above integrals I1-I6 are positive definite. Putting 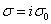 , where
, where 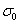 is real, into equation (50), and equating imaginary part, we obtain
is real, into equation (50), and equating imaginary part, we obtain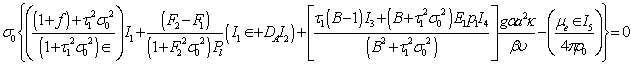 | (51) |
Equation (51) implies that 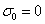 or
or 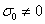 which mean that modes may be non oscillatory or oscillatory. The oscillatory modes introduced due to presence of magnetic field, suspended particles, visco-elasticity, medium permeability and Darcy-Brinkman parameter.In the absence of magnetic field, equation (51) reduces to
which mean that modes may be non oscillatory or oscillatory. The oscillatory modes introduced due to presence of magnetic field, suspended particles, visco-elasticity, medium permeability and Darcy-Brinkman parameter.In the absence of magnetic field, equation (51) reduces to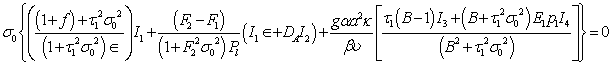 | (52) |
It is evident from equation (52) that if 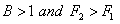 then the term inside the bracket is positive which implies that
then the term inside the bracket is positive which implies that 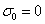 , thus the modes are non-oscillatory and the principle of exchange of stabilities is satisfied.
, thus the modes are non-oscillatory and the principle of exchange of stabilities is satisfied.
9. Conclusions
The problem of thermal instability of an Oldroydian viscoelastic fluid permeated with suspended particles in the presence of variable gravity and vertical magnetic field through a Brinkman porous medium is considered in the present paper. For stationary convection, Oldroydian fluid behaves like an ordinary Newtonian fluid. The effect of suspended particles, medium porosity and medium permeability are found to hasten the onset of thermal instability whereas magnetic field and Darcy-Brinkman number have a stabilizing effect on the system, as such their effect is to postpone the onset of thermal instability when the gravity field increases upward from its value g0 i.e. 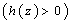 . We thus find that, in case of Brinkman porous medium, the Darcy-Brinkman number has a stabilizing effect for the problem under consideration whereas both medium porosity and medium permeability have destabilizing effects on the system for the case of stationary convection. The oscillatory modes are introduced due to presence of magnetic field, suspended particles, visco-elasticity, medium permeability and Darcy-Brinkman parameter. The principle of exchange of stabilities is found to hold under certain conditions. The sufficient conditions for the non-existence of overstability are also obtained. The present analysis would be relevant to the stability of some polymer solutions and Oldroydian viscoelastic fluids and finds its importance in several scientific and engineering fields like ground water hydrology, petroleum engineering and in geophysics.
. We thus find that, in case of Brinkman porous medium, the Darcy-Brinkman number has a stabilizing effect for the problem under consideration whereas both medium porosity and medium permeability have destabilizing effects on the system for the case of stationary convection. The oscillatory modes are introduced due to presence of magnetic field, suspended particles, visco-elasticity, medium permeability and Darcy-Brinkman parameter. The principle of exchange of stabilities is found to hold under certain conditions. The sufficient conditions for the non-existence of overstability are also obtained. The present analysis would be relevant to the stability of some polymer solutions and Oldroydian viscoelastic fluids and finds its importance in several scientific and engineering fields like ground water hydrology, petroleum engineering and in geophysics.
ACKNOWLEDGEMENTS
The authors wish to thank the reviewer for useful comments which have lead to the improvement of the paper in the present form.
References
| [1] | Chandrasekhar, S.C.: Hydrodynamic and Hydromagnetic Stability, Dover Publication, New York, 1981. |
| [2] | McDonnel J.A.M.: Cosmic Dust, John Wiley & Sons, Toronto, Canada, 1978. |
| [3] | Nield, D.A. and Bejan, A.: Convection in porous media. Springer, New-York, 2006. |
| [4] | Brinkman, H.C.: A calculation of the viscous force exerted by a flowing fluid on a dense swarm of particles, Appl. Sci. Res., A 1, pp. 81–86, 1947. |
| [5] | Khaled, A.R.A. and Vafai, K. : The role of porous media in modeling flow and heat transfer in biological tissues. Int. J. Heat Mass Transfer, Vol. 46, pp.4989-5003, 2003. |
| [6] | Pries, A.R., Secomb, T.W., Jacobs, H., Sperandio, M., Osterloh, K. and Gaehtgens, P.: Microvascular blood flow resistance: role of endothelial surface layer. Am. J. Physiol, Vol. 273, H2272-H2279, 1997. |
| [7] | Pries, A.R., Secomb, T.W., and Gaehtgens, P.: The endothelial surface layer. Pflugers Arch.- Eur. J. Physiol, Vol. 440, pp. 653-666, 2000. |
| [8] | Scanlon, J.W. and Segel, L.A.: Effect of suspended particles on onset of Bénard convection, Physics Fluids, 16, pp. 1573-1578, 1973. |
| [9] | Toms B.A. and Strawbridge D.J.: Elastic and viscous properties of dilute solutions of polymethyl methacrylate in organic liquids, Trans. Faraday Soc., Vol. 49, pp. 1225-1232, 1953. |
| [10] | Oldroyd J.G. : Non-Newtonian effects in steady motion of some idealized elastic-viscous liquids, Proc. Royal Soc. London, A 245, pp. 278-297, 1958. |
| [11] | Bhatia, P.K. and Steiner, J.M.: Thermal instability of fluid layer in Hydromagnetics, J. Math. Anal. Appl.,41, pp. 271-289, 1973. |
| [12] | Pradhan, G.K. and Samal, P.C.: Thermal instability of a fluid layer under variable body forces, J. Math. Anal. Appl., 122, pp. 487-498, 1987. |
| [13] | Sharma R.C.: Thermal instability in a viscoelastic fluid in hydromagnetics, Acta Phys. Hung., Vol. 38, pp. 293-298, 1975. |
| [14] | Sharma R.C., Prakash K. and Dube S.N.: Effect of suspended particles on the onset of Bénard convection in hydromagnetics, Acta Phys. Hung., Vol. 40, pp. 3-10, 1976. |
| [15] | Sharma R.C. and Sharma N.D.: Thermal instability in Maxwellian and Oldroydian viscoelastic fluids with suspended particles in porous medium, Czechoslovak J. Phys., Vol. 42, no. 5, pp. 513-523, 1992. |
| [16] | Sharma R.C. and Sunil.: Thermal instability of Oldroydian viscoelastic fluid with suspended particles in hydromagnetics in porous medium, Polymer Plastics Technology and Engineering, Vol. 33, Issue 3, pp. 323-339, 1994. |
| [17] | El-Sayed M. F. : Onset of electroconvective instability of Oldroydian viscoelastic liquid layer in Brinkman porous medium, Arch. Appl. Mech. Vol. 78, pp. 211–224, 2008. |

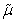 associated with the Brinkman[4] term is known as effective viscosity. Tissues can be treated as a porous medium as it is composed of dispersed cells separated by connective voids which allow for flow of nutrients, minerals, etc. There are several evidences, both theoretical and experimental, which suggest that the Darcy’s equation gives inadequate results of the hydrodynamic conditions, particularly near the boundaries of a porous medium. The Darcy-Brinkman equation, which takes into account the boundary effects, has been employed in recent years in biomedical hydrodynamic studies[5], modeling a thin fibrous surface layer coating blood vessels (endothelial surface layer) as it is a highly permeable porous medium[6,7]. It is, therefore, of interest to study the characteristics of the Darcy-Brinkman equation which have relevance importance in several biological, geological, chemical reactors and medical science applications, thus forming a motivation for the present study.In geophysical context, the fluid is often not pure but may instead be permeated with dust particles. The effects of suspended particles on the stability of superposed fluids have industrial and scientific importance in geophysics, chemical engineering and astrophysics. Scanlon and Segel[8] have considered the effect of suspended particles on the onset of Bénard convection and found that the critical Rayleigh number was reduced solely because the heat capacity of the pure fluid was supplemented by that of the particles. So the effect of suspended particles was thus found to increase the instability of the layer. An experimental demonstration by Toms and Strawbridge[9] reveals that a dilute solution of methyl methacrylate in n-butyl acetate behaves in accordance with the theoretical model of Oldroyd fluid[10]. The present analysis would be relevant to the stability of some polymer solutions like a dilute solution of methyl methacrylate in n-butyl acetate and also find its importance in several geographical situations and in chemical technology. Bhatia and Steiner[11] have studied the problem of thermal instability of a Maxwellian visco-elastic fluid in the presence of a magnetic field and found that the magnetic field has a stabilizing influence on the overstable mode of convection in a visco-elastic fluid layer. The problem of thermal instability of a fluid layer under variable gravity field has been considered by Pradhan and Samal[12]. Since the earth’s gravity field varies with its distance from its surface so it is of utmost important to take into account the effect of variable gravity field having its importance in several convective flows, atmospheric science, astrophysics, geophysics and also in material processing technology.Sharma[13] studied the stability of a layer of an electrically conducting Oldroyd fluid in the presence of a magnetic field and found that the magnetic field has a stabilizing influence while the effect of suspended particles on the onset of Bénard convection in hydromagnetics have been studied by Sharma et al.[14]. Sharma and Sharma[15] have investigated the effect of suspended particles on thermal instability in Maxwellian and Oldroydian viscoelastic fluids in a porous medium and found that for stationary convection both the Maxwellian and Oldroydian fluids behave like Newtonian fluid and the medium permeability and suspended particles have destabilizing effects on the system. Sharma and Sunil[16] considered the thermal instability of an Oldroydian viscoelastic fluid with suspended particles in hydromagnetics in porous medium and concluded that, for stationary convection, magnetic field has a stabilizing effect whereas medium permeability and suspended particles have destabilizing effects on the system. The problem of the onset of electroconvective instability of an Oldroydian viscoelastic liquid layer through Brinkman porous medium under the simultaneous action of an electric field and a vertical temperature gradient has been investigated by El-Sayed[17]. The purpose of the present note treated here is to examine theoretically the problem of the onset of stability of an Oldroydian viscoelastic fluid permeated with suspended particles through a Brinkman porous medium under the simultaneous action of varying gravity field and vertical magnetic field.
associated with the Brinkman[4] term is known as effective viscosity. Tissues can be treated as a porous medium as it is composed of dispersed cells separated by connective voids which allow for flow of nutrients, minerals, etc. There are several evidences, both theoretical and experimental, which suggest that the Darcy’s equation gives inadequate results of the hydrodynamic conditions, particularly near the boundaries of a porous medium. The Darcy-Brinkman equation, which takes into account the boundary effects, has been employed in recent years in biomedical hydrodynamic studies[5], modeling a thin fibrous surface layer coating blood vessels (endothelial surface layer) as it is a highly permeable porous medium[6,7]. It is, therefore, of interest to study the characteristics of the Darcy-Brinkman equation which have relevance importance in several biological, geological, chemical reactors and medical science applications, thus forming a motivation for the present study.In geophysical context, the fluid is often not pure but may instead be permeated with dust particles. The effects of suspended particles on the stability of superposed fluids have industrial and scientific importance in geophysics, chemical engineering and astrophysics. Scanlon and Segel[8] have considered the effect of suspended particles on the onset of Bénard convection and found that the critical Rayleigh number was reduced solely because the heat capacity of the pure fluid was supplemented by that of the particles. So the effect of suspended particles was thus found to increase the instability of the layer. An experimental demonstration by Toms and Strawbridge[9] reveals that a dilute solution of methyl methacrylate in n-butyl acetate behaves in accordance with the theoretical model of Oldroyd fluid[10]. The present analysis would be relevant to the stability of some polymer solutions like a dilute solution of methyl methacrylate in n-butyl acetate and also find its importance in several geographical situations and in chemical technology. Bhatia and Steiner[11] have studied the problem of thermal instability of a Maxwellian visco-elastic fluid in the presence of a magnetic field and found that the magnetic field has a stabilizing influence on the overstable mode of convection in a visco-elastic fluid layer. The problem of thermal instability of a fluid layer under variable gravity field has been considered by Pradhan and Samal[12]. Since the earth’s gravity field varies with its distance from its surface so it is of utmost important to take into account the effect of variable gravity field having its importance in several convective flows, atmospheric science, astrophysics, geophysics and also in material processing technology.Sharma[13] studied the stability of a layer of an electrically conducting Oldroyd fluid in the presence of a magnetic field and found that the magnetic field has a stabilizing influence while the effect of suspended particles on the onset of Bénard convection in hydromagnetics have been studied by Sharma et al.[14]. Sharma and Sharma[15] have investigated the effect of suspended particles on thermal instability in Maxwellian and Oldroydian viscoelastic fluids in a porous medium and found that for stationary convection both the Maxwellian and Oldroydian fluids behave like Newtonian fluid and the medium permeability and suspended particles have destabilizing effects on the system. Sharma and Sunil[16] considered the thermal instability of an Oldroydian viscoelastic fluid with suspended particles in hydromagnetics in porous medium and concluded that, for stationary convection, magnetic field has a stabilizing effect whereas medium permeability and suspended particles have destabilizing effects on the system. The problem of the onset of electroconvective instability of an Oldroydian viscoelastic liquid layer through Brinkman porous medium under the simultaneous action of an electric field and a vertical temperature gradient has been investigated by El-Sayed[17]. The purpose of the present note treated here is to examine theoretically the problem of the onset of stability of an Oldroydian viscoelastic fluid permeated with suspended particles through a Brinkman porous medium under the simultaneous action of varying gravity field and vertical magnetic field.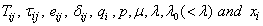 denote, respectively, the total stress tensor, shear stress tensor, rate of strain tensor, Kronecker delta, velocity vector, pressure, viscosity, stress relaxation time, strain retardation time and position vector. Then the Jeffrey (Oldroydian) constitutive relations for performing linear stability of Rayleigh–Bénard convection in clear viscoelastic fluids are
denote, respectively, the total stress tensor, shear stress tensor, rate of strain tensor, Kronecker delta, velocity vector, pressure, viscosity, stress relaxation time, strain retardation time and position vector. Then the Jeffrey (Oldroydian) constitutive relations for performing linear stability of Rayleigh–Bénard convection in clear viscoelastic fluids are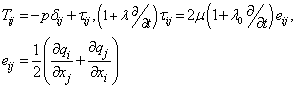
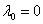 yields the Maxwellian fluid, whereas
yields the Maxwellian fluid, whereas 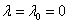 gives the Newtonian viscous fluid. Here we consider an infinite horizontal layer of an Oldroydian viscoelastic fluid permeated with suspended particles and bounded by the planes z=0 and z=d in a porous medium of porosity
gives the Newtonian viscous fluid. Here we consider an infinite horizontal layer of an Oldroydian viscoelastic fluid permeated with suspended particles and bounded by the planes z=0 and z=d in a porous medium of porosity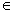 and medium permeability
and medium permeability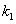 . The fluid layer is acted on by a uniform vertical magnetic field H (0, 0, H) and a variable gravity force
. The fluid layer is acted on by a uniform vertical magnetic field H (0, 0, H) and a variable gravity force 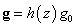 , where
, where 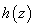 can be positive or negative according as the gravity increase or decreases upward from its value
can be positive or negative according as the gravity increase or decreases upward from its value 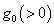 . The layer is heated from below so that a uniform temperature gradient
. The layer is heated from below so that a uniform temperature gradient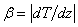 is maintained. The governing equations of motion and continuity for the Oldroydian viscoelastic fluid based on the Darcy-Brinkman approximation are
is maintained. The governing equations of motion and continuity for the Oldroydian viscoelastic fluid based on the Darcy-Brinkman approximation are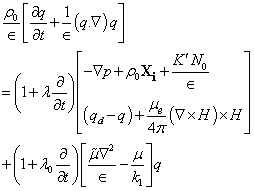
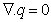
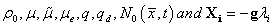 denote, respectively, the density of fluid, viscosity, effective viscosity, magnetic permeability, velocity of pure fluid, velocity of suspended particles, number density of the suspended particles and the gravitational acceleration.
denote, respectively, the density of fluid, viscosity, effective viscosity, magnetic permeability, velocity of pure fluid, velocity of suspended particles, number density of the suspended particles and the gravitational acceleration. 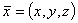 and
and 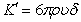 where
where 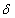 being particle radius, is the Stokes’ drag coefficient.The presence of suspended particles adds an extra force term, in equation of motion, proportional to velocity difference between particles and fluid. Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite in sign, in the equations of motion for the particles. Inter-particle reactions are ignored as the distances between the particles are assumed to be quite large compared with their diameters. The effects of pressure, magnetic field and gravity on the particles are very small and hence ignored.If mN is the mass of particles per unit volume, then the equations of motion and continuity for the particles are:
being particle radius, is the Stokes’ drag coefficient.The presence of suspended particles adds an extra force term, in equation of motion, proportional to velocity difference between particles and fluid. Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite in sign, in the equations of motion for the particles. Inter-particle reactions are ignored as the distances between the particles are assumed to be quite large compared with their diameters. The effects of pressure, magnetic field and gravity on the particles are very small and hence ignored.If mN is the mass of particles per unit volume, then the equations of motion and continuity for the particles are: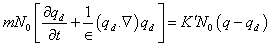
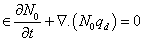
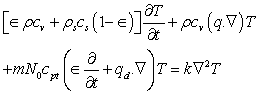
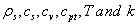 denote, respectively, the density of solid material, heat capacity of solid material, the specific heat at constant volume, heat capacity of suspended particles, the temperature and the thermal conductivity.The Maxwell’s equation yields
denote, respectively, the density of solid material, heat capacity of solid material, the specific heat at constant volume, heat capacity of suspended particles, the temperature and the thermal conductivity.The Maxwell’s equation yields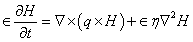
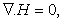
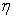 denote the electrical resistivity.The equation of state is
denote the electrical resistivity.The equation of state is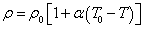
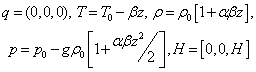
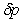 ,
,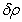 and
and 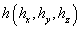 denote, respectively, the perturbation in fluid velocity q(0,0,0), perturbation in particle velocity qd (0,0,0), perturbation in particle number density
denote, respectively, the perturbation in fluid velocity q(0,0,0), perturbation in particle velocity qd (0,0,0), perturbation in particle number density 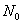 , temperature T, pressure p, density
, temperature T, pressure p, density 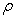 and magnetic field H. The change in density
and magnetic field H. The change in density 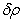 caused by perturbation θ in temperature, is given by
caused by perturbation θ in temperature, is given by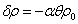
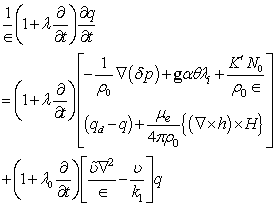
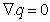
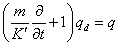
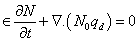
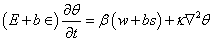
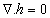
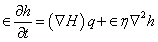
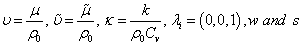 denote, respectively, the kinematic viscosity, the effective kinematic viscosity, the co-efficient of thermometric conductivity, unit vertical vector, vertical fluid velocity and suspended particles velocity and
denote, respectively, the kinematic viscosity, the effective kinematic viscosity, the co-efficient of thermometric conductivity, unit vertical vector, vertical fluid velocity and suspended particles velocity and 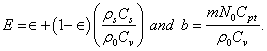 Eliminating
Eliminating 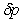 between the three component equations of (12) and using equations (13) and (14), we obtain:
between the three component equations of (12) and using equations (13) and (14), we obtain: 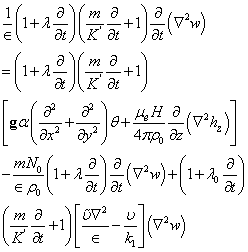
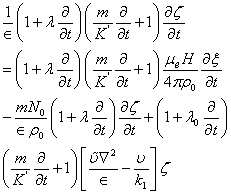
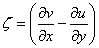 and
and 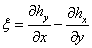 stand for the z-component of vorticity and z-component of current density, respectively.From equation (16), we obtain:
stand for the z-component of vorticity and z-component of current density, respectively.From equation (16), we obtain: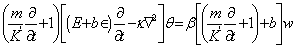
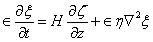
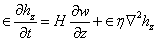
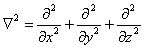 is the three dimensional Laplacian operator.
is the three dimensional Laplacian operator.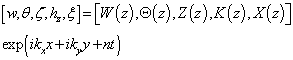
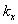 ,
, 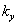 are the wave numbers along x and y directions, respectively and
are the wave numbers along x and y directions, respectively and 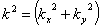 is the resultant wave number and n is the frequency of the harmonic disturbance, which is, in general, a complex constant.Using expression (24) and making the substitutions of the non-dimensional quantities of the form
is the resultant wave number and n is the frequency of the harmonic disturbance, which is, in general, a complex constant.Using expression (24) and making the substitutions of the non-dimensional quantities of the form 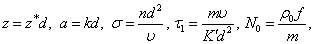
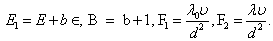
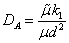 , is the Darcy-Brinkman number,
, is the Darcy-Brinkman number, 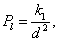 is the dimensionless medium permeability,
is the dimensionless medium permeability, 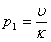 , is the thermal Prandtl number and
, is the thermal Prandtl number and 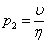 , is the magnetic Prandtl number.We obtain the non-dimensional form of Equations (19)-(23) (after dropping the asterisk for convenience) as:
, is the magnetic Prandtl number.We obtain the non-dimensional form of Equations (19)-(23) (after dropping the asterisk for convenience) as: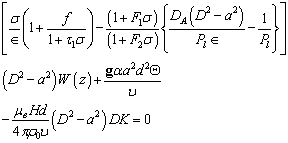
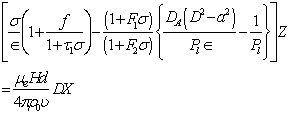
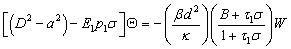
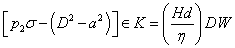
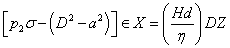
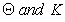 from equations (25), (27) and (28), we obtain:
from equations (25), (27) and (28), we obtain: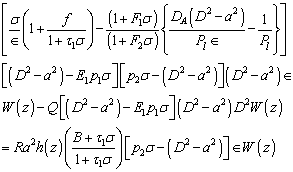
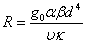 , is the thermal Rayleigh number and
, is the thermal Rayleigh number and 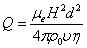 , is the Chandrasekhar number.
, is the Chandrasekhar number.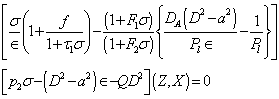
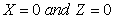
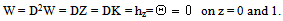
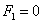 , the system reduces to that for a Maxwell fluid whereas for
, the system reduces to that for a Maxwell fluid whereas for 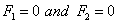 , the system reduces to that for an ordinary viscous fluid.
, the system reduces to that for an ordinary viscous fluid.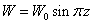
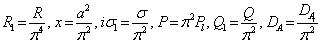 , we get the eigenvalue relationship of the form:
, we get the eigenvalue relationship of the form: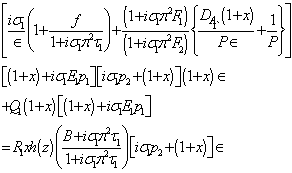
 in equation (35) and get the eigenvalue relationship for a stationary instability of the form:
in equation (35) and get the eigenvalue relationship for a stationary instability of the form: 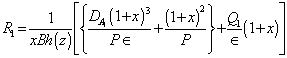
 and strain retardation parameter
and strain retardation parameter 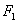 vanishes with
vanishes with 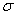 .Minimizing equation (36) with respect to
.Minimizing equation (36) with respect to 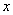 , yields the third order equation in
, yields the third order equation in 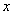 as
as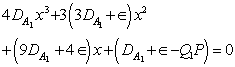
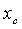 thus obtained from equation (37), in equation (36), gives the value of critical Rayleigh number for stationary instability.In order to investigate the effects of suspended particles, magnetic field, medium permeability, Darcy-Brinkman number and medium porosity, we examine the behaviour of
thus obtained from equation (37), in equation (36), gives the value of critical Rayleigh number for stationary instability.In order to investigate the effects of suspended particles, magnetic field, medium permeability, Darcy-Brinkman number and medium porosity, we examine the behaviour of 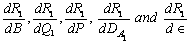 analytically. Equation (36) yields
analytically. Equation (36) yields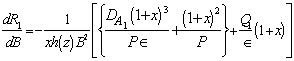
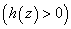 . This destabilizing effect of suspended particles agrees with previous published work by Scanlon and Segel[8], Sharma and Sharma[15] and Sharma and Sunil[16].From equation (36), we get
. This destabilizing effect of suspended particles agrees with previous published work by Scanlon and Segel[8], Sharma and Sharma[15] and Sharma and Sunil[16].From equation (36), we get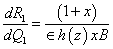
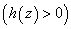 . This stabilizing effect of magnetic field is an agreement of the previous results by Sharma[13] and Sharma and Sunil[16].From equation (36), we get
. This stabilizing effect of magnetic field is an agreement of the previous results by Sharma[13] and Sharma and Sunil[16].From equation (36), we get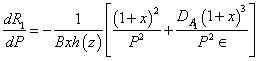
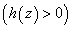 . This destabilizing result agrees with the earlier work reported by Sharma and Sharma[15] and Sharma and Sunil[16].From equation (36), we get
. This destabilizing result agrees with the earlier work reported by Sharma and Sharma[15] and Sharma and Sunil[16].From equation (36), we get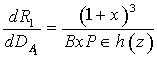
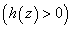 . From equation (36), we get
. From equation (36), we get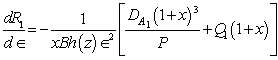
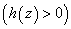 . This destabilizing effect of porosity agrees with the result of El-Sayed[17].
. This destabilizing effect of porosity agrees with the result of El-Sayed[17].
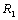 with wave number x, for
with wave number x, for 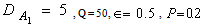 and B=5,10,15,20,25
and B=5,10,15,20,25
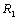 with wave number x, for
with wave number x, for 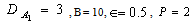 and Q=10,20,30,40,50
and Q=10,20,30,40,50
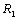 with wave number x, for
with wave number x, for 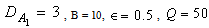 and P=0.1, 0.2, 0.3, 0.4, 0.5
and P=0.1, 0.2, 0.3, 0.4, 0.5
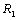 with wave number x, for P=0.5, B = 10,
with wave number x, for P=0.5, B = 10, 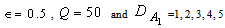

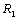 with wave number x, for
with wave number x, for 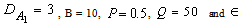 =0.1, 0.2, 0.3, 0.4, 0.5
=0.1, 0.2, 0.3, 0.4, 0.5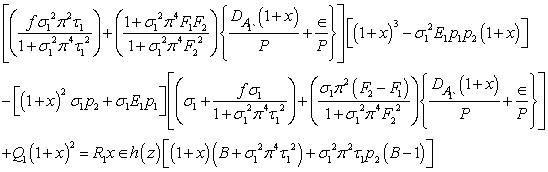
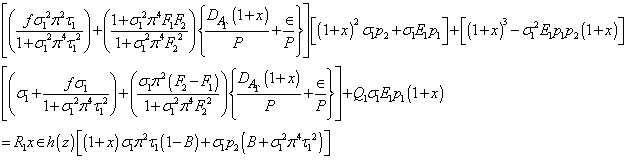
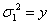 , we get a fourth order polynomial in y of the form:
, we get a fourth order polynomial in y of the form: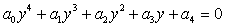
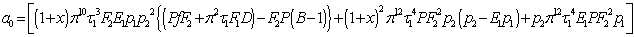
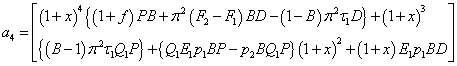
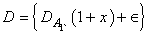 The values of the coefficients
The values of the coefficients 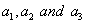 involving large number of terms are not included to save spaces. Since
involving large number of terms are not included to save spaces. Since 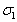 is real for overstability to occur therefore all the roots of y should be positive.From equation (45), the product of root
is real for overstability to occur therefore all the roots of y should be positive.From equation (45), the product of root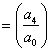 is positive.
is positive.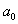 is negative if
is negative if 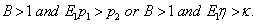
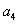 is positive if
is positive if 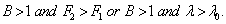
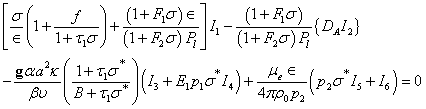
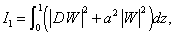
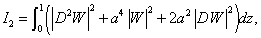
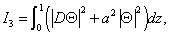
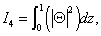
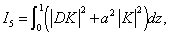
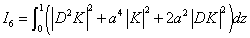 All the above integrals I1-I6 are positive definite. Putting
All the above integrals I1-I6 are positive definite. Putting 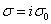 , where
, where 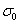 is real, into equation (50), and equating imaginary part, we obtain
is real, into equation (50), and equating imaginary part, we obtain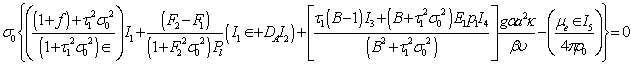
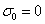 or
or 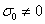 which mean that modes may be non oscillatory or oscillatory. The oscillatory modes introduced due to presence of magnetic field, suspended particles, visco-elasticity, medium permeability and Darcy-Brinkman parameter.In the absence of magnetic field, equation (51) reduces to
which mean that modes may be non oscillatory or oscillatory. The oscillatory modes introduced due to presence of magnetic field, suspended particles, visco-elasticity, medium permeability and Darcy-Brinkman parameter.In the absence of magnetic field, equation (51) reduces to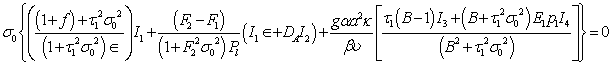
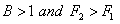 then the term inside the bracket is positive which implies that
then the term inside the bracket is positive which implies that 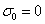 , thus the modes are non-oscillatory and the principle of exchange of stabilities is satisfied.
, thus the modes are non-oscillatory and the principle of exchange of stabilities is satisfied.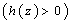 . We thus find that, in case of Brinkman porous medium, the Darcy-Brinkman number has a stabilizing effect for the problem under consideration whereas both medium porosity and medium permeability have destabilizing effects on the system for the case of stationary convection. The oscillatory modes are introduced due to presence of magnetic field, suspended particles, visco-elasticity, medium permeability and Darcy-Brinkman parameter. The principle of exchange of stabilities is found to hold under certain conditions. The sufficient conditions for the non-existence of overstability are also obtained. The present analysis would be relevant to the stability of some polymer solutions and Oldroydian viscoelastic fluids and finds its importance in several scientific and engineering fields like ground water hydrology, petroleum engineering and in geophysics.
. We thus find that, in case of Brinkman porous medium, the Darcy-Brinkman number has a stabilizing effect for the problem under consideration whereas both medium porosity and medium permeability have destabilizing effects on the system for the case of stationary convection. The oscillatory modes are introduced due to presence of magnetic field, suspended particles, visco-elasticity, medium permeability and Darcy-Brinkman parameter. The principle of exchange of stabilities is found to hold under certain conditions. The sufficient conditions for the non-existence of overstability are also obtained. The present analysis would be relevant to the stability of some polymer solutions and Oldroydian viscoelastic fluids and finds its importance in several scientific and engineering fields like ground water hydrology, petroleum engineering and in geophysics. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML