Samba Dia, Cheikh Mbow
Université Cheikh Anta Diop de Dakar, Physical Department, Dakar, B.P. 5005 Dakar-Fann, Senegal
Correspondence to: Samba Dia, Université Cheikh Anta Diop de Dakar, Physical Department, Dakar, B.P. 5005 Dakar-Fann, Senegal.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Using a paraboloidal coordinates system and a vorticity- stream function formulation, the authors study numerically the two-dimensional unsteady natural convection of a Newtonian fluid confined between two paraboloids of revolution with vertical axes. The upwardly open paraboloid is half heated and half insulated. The upper surface downwardly open is completely cooled. Two different cases, based on the position of the hot and the insulated region are considered. A finite volume method is used to approximate the dimensionless equations of vorticity, heat and stream function. A fully implicit scheme is adopted for time discretization and algebraic systems obtained are solved by a successive under relaxation method. The authors analyzed the effects of the Rayleigh number and the active zone location on the convective flow motion and heat transfer. For different Rayleigh numbers, and depending on the position of the active and inert zone, flows observed are very different.
Keywords:
Convection, Finite Volume, Rayleigh Number, Active zone
Cite this paper: Samba Dia, Cheikh Mbow, Effects of the Heater Location on the Unsteady Two Dimensional Natural Convection in Enclosures Bounded by Two Paraboloids of Revolution, American Journal of Fluid Dynamics, Vol. 3 No. 3, 2013, pp. 49-57. doi: 10.5923/j.ajfd.20130303.01.
1. Introduction
During the last four decades considerable efforts have been devoted both experimentally and numerically to the study of Natural convection generated by buoyancy forces in finite geometries. The interest in such problems stems from their importance in such area as in geophysical applications, in solar energy collectors, in thermal storage systems , in electronic components cooling, in nuclear reactor designs and in many other situations. Even after 40 years of research most of the investigations found in the literature are related to regular shapes as square rectangular, cylindrical, annulus. Due to the complexity of natural convection in non rectangular and non cylindrical types of enclosures particularly curved boundary enclosures, very few studies have been found. A few investigations concerning heat and fluid flow in systems partially heated from below have been also reported. These and other published investigations that are considered to be of relevance to the present work are briefly reviewed in the next section. With respect to the wall curved considerable attention has been given to the effect of convective transfer due to the curved wall. An numerical investigation of convective motion inside enclosures of different hemispherical concave and convex shape have been done by Lewandowsky et al[1]. By studying the unsteady laminar natural convection inside a vertical axisymetric ellipsoid filled with air, Najoua et al[2] showed that the instatneous average Nusselt number decreases in a monotonous way with time when the flow is unicellular and increases or decreases abruptly with each appearance or disappearance of cells. Das and Morsi[3][4] investigated numerically the steady two dimensional natural convection inside a dome shaped enclosures. In this study, dome of circular, elliptical, parabolic and hyperbolic shapes have been considered. The results showed that the shape of the dome has major effects on the convective flow and heat transfer characteristics. The interaction of natural convection and surface radiation in parabolic enclosures with flat bottom, is numerically investigated in[5][6]. Concerning natural convection in an enclosure with localized heating, Valencia and Frederick[7] have numerically studied the natural convection of air in square cavities with half-active and half-insulated vertical walls for Rayleigh numbers between 103 and 107. Aydin and Yang[8] investigated natural convection in enclosures with localized heating from below and symmetrical cooling from sides. The effects of the heat source length were investigated as well as the heat source thickness. Basak et al[9] studied the effects of thermal boundary conditions on natural convection.In the present study, the two-dimensional unsteady natural convection of a Newtonian fluid confined between two paraboloids of revolution with half-heated and half-insulated bottom surface is investigated. The analysis are focused on the effects of the position of the hot and insulate region on the convection.To our knowledge, this study is the first attempt at studying the effects of the location of thermal boundary conditions on such a geometry.
2. Formulation and Method of Resolution
Let’s consider an incompressible Newtonian fluid enclosed in a space delimited by two paraboloids of revolution with vertical axes. The paraboloid upwardly open is partially heated 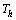 and partially insulated, while the downwardly open is maintained at a temperature below
and partially insulated, while the downwardly open is maintained at a temperature below 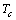 . Only half the surface of the paraboloid is heated at a temperature
. Only half the surface of the paraboloid is heated at a temperature 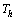 . The two cases considered are shown in Figure 1.The two paraboloids being heated differently a transient natural convection develops inside the enclosed space. To formulate and solve this problem, it is assumed that:● The phenomena are symmetrical with respect to the revolution axis and are two dimensional● All fluid properties are taken to be constant, with the exception of the density in the momentum equation. In this equation variations of density obey to the Boussinesq linear law.● The fluid is non absorbing and the radiative effects are regarded as negligible.● In the heat equation the viscous dissipation function as well as the pression effects are neglected.Taking into account the geometry of the studied system, it seems more adequate to use a paraboloidal[10] coordinates system
. The two cases considered are shown in Figure 1.The two paraboloids being heated differently a transient natural convection develops inside the enclosed space. To formulate and solve this problem, it is assumed that:● The phenomena are symmetrical with respect to the revolution axis and are two dimensional● All fluid properties are taken to be constant, with the exception of the density in the momentum equation. In this equation variations of density obey to the Boussinesq linear law.● The fluid is non absorbing and the radiative effects are regarded as negligible.● In the heat equation the viscous dissipation function as well as the pression effects are neglected.Taking into account the geometry of the studied system, it seems more adequate to use a paraboloidal[10] coordinates system 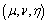 in which boundary conditions of the domain are given by constant coordinates lines. Paraboloidal coordinates are related to the Cartesian coordinate by the formulas:
in which boundary conditions of the domain are given by constant coordinates lines. Paraboloidal coordinates are related to the Cartesian coordinate by the formulas: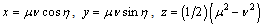 , The revolution symmetrical axis is given by
, The revolution symmetrical axis is given by 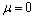 and
and  . The upper and the lower paraboloids are respectively materialized by lines of coordinates
. The upper and the lower paraboloids are respectively materialized by lines of coordinates  and
and  .From the above assumption and the coordinate transformation, the governing equation in dimensionless stream function-vorticity form are:Stream function equation:
.From the above assumption and the coordinate transformation, the governing equation in dimensionless stream function-vorticity form are:Stream function equation: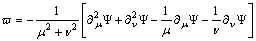 | (1) |
Momentum equation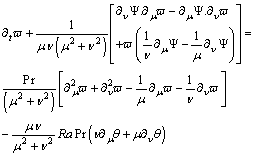 | (2) |
 | Figure 1. Geometry and thermal boundary conditions of the problem |
Heat equation: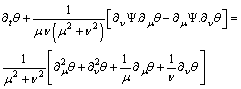 | (3) |
With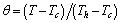 .The velocities are:
.The velocities are: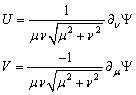 | (4) |
The time ( ), velocity(
), velocity(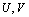 ), stream function (
), stream function (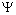 ), vorticity(
), vorticity(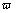 ) of reference are respectively defines as:
) of reference are respectively defines as: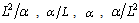 ,where
,where 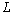 is the length of reference
is the length of reference 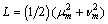 The associated dimensionless initial and boundary conditions for the problem considered are:At
The associated dimensionless initial and boundary conditions for the problem considered are:At 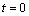 :Vorticity, temperature, stream function, velocities, and their respective derivatives are null throughout the system.At
:Vorticity, temperature, stream function, velocities, and their respective derivatives are null throughout the system.At 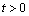 :On the lower paraboloid (
:On the lower paraboloid (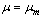 ):
):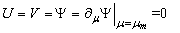 | (5) |
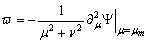 | (6) |
for the active zone: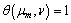 | (7) |
for the inert zone: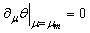 | (8) |
On the upper paraboloid ( )
)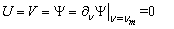 | (9) |
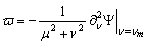 | (10) |
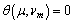 | (11) |
On the symmetry axis (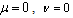 ):
):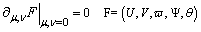 | (12) |
The Nusselt number ( ) and the friction coefficient (
) and the friction coefficient (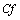 ) relative to the lower paraboloid are defined by:
) relative to the lower paraboloid are defined by: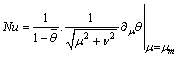 | (13) |
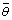 is the dimensionless average temperature
is the dimensionless average temperature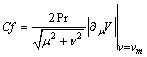 | (14) |
Their average values are respectively: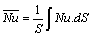 | (15) |
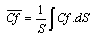 | (16) |
3. Numerical Technique
The different equations subject to the boundary conditions are integrated numerically using the control volume method[11] ,[12]. An a fully implicit procedure is retain for treating the temporary derivatives. The resulting algebraic equations were solved by successive under relaxation iterating scheme. The iteration process is terminated if the following criterion is satisfied: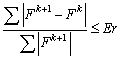 | (17) |
with 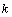 the incrementing index of the iterative process and
the incrementing index of the iterative process and  the precision of the iterative process.The solution domain, consists of grid points at which equations are applied. The grid size selected is equal to
the precision of the iterative process.The solution domain, consists of grid points at which equations are applied. The grid size selected is equal to 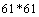 and a uniform grid has been used for all the computations. The Figure 2 shows the influence of the grid system according to the instantaneous average Nusselt number for the case I, the largest gap in relation to the chosen mesh occurs between
and a uniform grid has been used for all the computations. The Figure 2 shows the influence of the grid system according to the instantaneous average Nusselt number for the case I, the largest gap in relation to the chosen mesh occurs between 
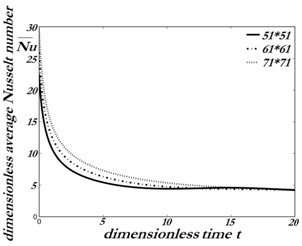 | Figure 2. Grid independence test for the case I |
All the results are obtained with  and a time step
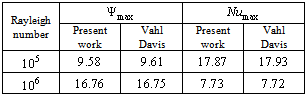
and a time step 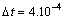 is retained to carry out all numerical tests. Refining this time step results in minor changes of the transient patterns. Due to lack of suitable results in the literature pertaining to the present configuration, the numerical algorithm used in this study was tested with the classical problem of natural convection in a square cavity by De Vahl Davis[13].
is retained to carry out all numerical tests. Refining this time step results in minor changes of the transient patterns. Due to lack of suitable results in the literature pertaining to the present configuration, the numerical algorithm used in this study was tested with the classical problem of natural convection in a square cavity by De Vahl Davis[13].Table 1. Validation of the Numerical Method
 |
| |
|
4. Results and Discussion
The flow field, the temperature field and heat transfers in a cavity whose bottom wall is partially heated and partially insulated are examined. Depending on the position of the active area, two different cases will be considered. The range of  for this study is varying between
for this study is varying between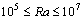 . For
. For 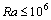 the precision
the precision of the iterative process is equal to
of the iterative process is equal to 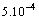 and for
and for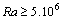 ,
, 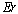 is equal to
is equal to 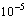 Owing to the symmetrical boundary conditions, the flows in the left and right of the symmetry axis are identical except for the sense of rotation. Figure 3 and Figure 4 represent the time evolution of isotherms and streamlines for the case I at different values of
Owing to the symmetrical boundary conditions, the flows in the left and right of the symmetry axis are identical except for the sense of rotation. Figure 3 and Figure 4 represent the time evolution of isotherms and streamlines for the case I at different values of . In the first moments, for the relatively weak values of the Rayleigh number (
. In the first moments, for the relatively weak values of the Rayleigh number (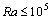 ) in the two studied cases, the isotherms are lines that are parallel to the heated inferior wall. The flow consists of a single clockwise rotating cell (dotted lines) of weak intensity. We have then here a pseudo-conductive regime. The latter, despite the continuous distortion of the isotherms due to the increasing of convection effects when Ra augments up to
) in the two studied cases, the isotherms are lines that are parallel to the heated inferior wall. The flow consists of a single clockwise rotating cell (dotted lines) of weak intensity. We have then here a pseudo-conductive regime. The latter, despite the continuous distortion of the isotherms due to the increasing of convection effects when Ra augments up to 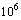 always remain the dominant mode of heat transfer within the enclosure. For the largest values of the Rayleigh number namely
always remain the dominant mode of heat transfer within the enclosure. For the largest values of the Rayleigh number namely 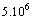 and
and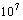 , convection becomes the dominant mode of transfer. For case I, there is a quick formation of another cell (solid line) turning in the trigonometric sense. As we progress in time the intensity of the clockwise rotating cell decreases in favor of the trigonometric one. For
, convection becomes the dominant mode of transfer. For case I, there is a quick formation of another cell (solid line) turning in the trigonometric sense. As we progress in time the intensity of the clockwise rotating cell decreases in favor of the trigonometric one. For 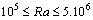 the circulation of the fluid within the enclosure is essentially due to the stable trigonometric cell.
the circulation of the fluid within the enclosure is essentially due to the stable trigonometric cell.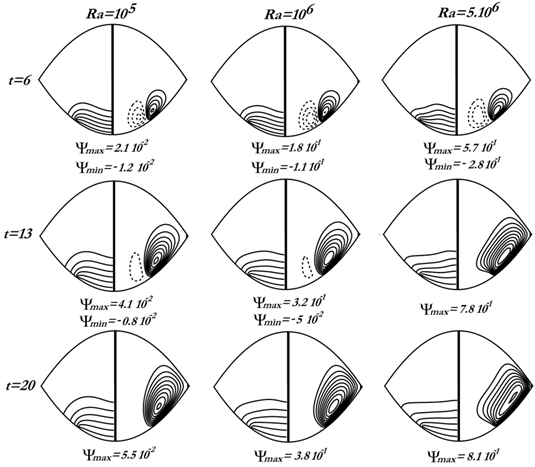 | Figure 3. Isotherms and streamlines at  for the case I for the case I |
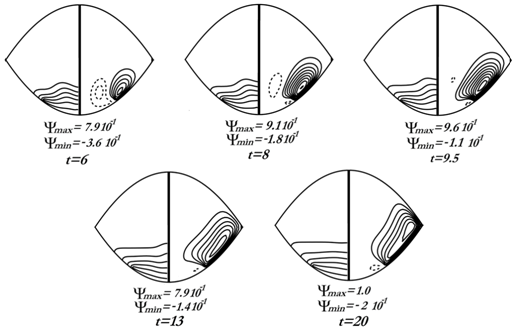 | Figure 4. Isotherms and streamlines at 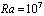 for the case I for the case I |
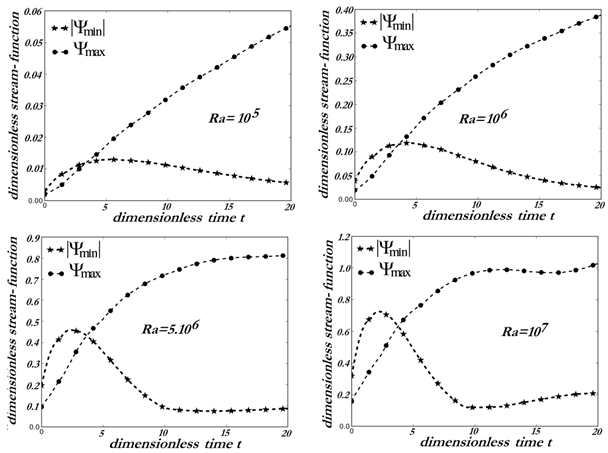 | Figure 5. Variations of the maximum and the minimum of the stream function against dimensionless time for different values of 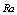 |
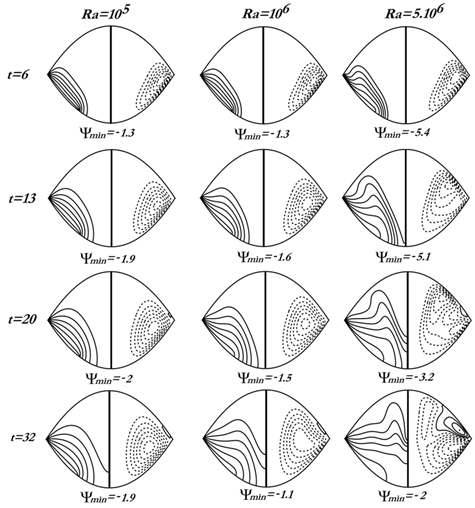 | Figure 6. Isotherms and streamlines at  for the case II for the case II |
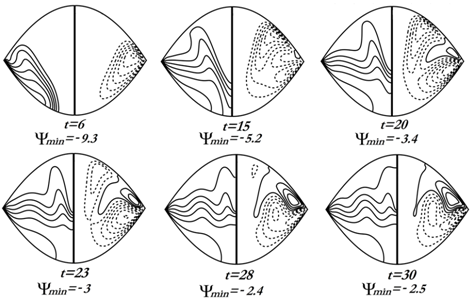 | Figure 7. Isotherms and streamlines at  for the case II for the case II |
To find out the reason for the observed streamline patterns, we analyze the Figure 5, where a comparison between  and
and  is made for different Rayleigh numbers. For all the values taken by the latter, one can see at the first moments (
is made for different Rayleigh numbers. For all the values taken by the latter, one can see at the first moments (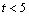 ) an increase phase of
) an increase phase of 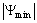 that corresponds to the apparition and development of the clockwise cell followed by a decrease of
that corresponds to the apparition and development of the clockwise cell followed by a decrease of 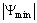 leading to a progressive vanishing of the clockwise cell. But for
leading to a progressive vanishing of the clockwise cell. But for 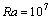 after having reached its weakest value (
after having reached its weakest value (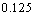 at
at 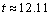 ),
),  starts again increasing. During this interval of time, when
starts again increasing. During this interval of time, when 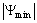 increases anew, one can see a concavity change in the shape of
increases anew, one can see a concavity change in the shape of 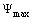 . This behavior which is specific to is indicative of the reformation process of the horary cell. The behavior of the system at
. This behavior which is specific to is indicative of the reformation process of the horary cell. The behavior of the system at  differs from the previous
differs from the previous 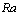 only through the resurgence of the horary cell at large time (
only through the resurgence of the horary cell at large time ( ). It should be noticed that the time when
). It should be noticed that the time when 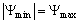 is independent of the Rayleigh number. In the case I, although the convection is established at
is independent of the Rayleigh number. In the case I, although the convection is established at 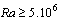 , the heat transfers remain confined in the area located under the equatorial plan. We have a boundary layer flow.When the thermal boundary conditions are reversed on the inferior wall (case II), the apparition of the trigonometric cell is more lately achieved (beyond
, the heat transfers remain confined in the area located under the equatorial plan. We have a boundary layer flow.When the thermal boundary conditions are reversed on the inferior wall (case II), the apparition of the trigonometric cell is more lately achieved (beyond 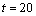 for
for 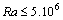 and at
and at 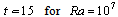 ). Thus, for weak Rayleigh numbers (
). Thus, for weak Rayleigh numbers (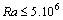 ), the flow is mainly due to the clockwise cell, the intensity of the trigonometric cell being too weak. Contrary to case I, in case II the clockwise cell is no longer unstable and the front of heat invades the enclosure more and more. When the convective effects become dominant (
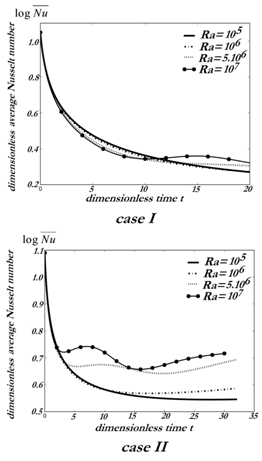
), the flow is mainly due to the clockwise cell, the intensity of the trigonometric cell being too weak. Contrary to case I, in case II the clockwise cell is no longer unstable and the front of heat invades the enclosure more and more. When the convective effects become dominant (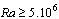 ), the growth of the trigonometric cell favors the division of the horary cell into two parts. The most intense part is contiguous to the heated inferior wall. At large time, the circulation inside the enclosure is due to the competition between the two types of cells, the dynamic field is multi-cellular.In this section, it has been carried out an analysis of the average values such as
), the growth of the trigonometric cell favors the division of the horary cell into two parts. The most intense part is contiguous to the heated inferior wall. At large time, the circulation inside the enclosure is due to the competition between the two types of cells, the dynamic field is multi-cellular.In this section, it has been carried out an analysis of the average values such as If the cases I and case II differ only through the relative position of the active and inert zones, for a same quantity of energy brought to the system, the average values of case II are by far superior, due to the confinement of the main transfers for the case I in a zone close to the lower wall. In Figure 8, the evolution of
If the cases I and case II differ only through the relative position of the active and inert zones, for a same quantity of energy brought to the system, the average values of case II are by far superior, due to the confinement of the main transfers for the case I in a zone close to the lower wall. In Figure 8, the evolution of 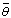 with time has been shown for different Rayleigh numbers. For case II, if
with time has been shown for different Rayleigh numbers. For case II, if 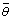 increases with time and Rayleigh numbers, the situation is not the same for case I. Though
increases with time and Rayleigh numbers, the situation is not the same for case I. Though 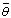 always augments with time, we notice at
always augments with time, we notice at 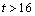 for
for 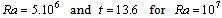 , that the average temperature becomes smaller than those of the previous Rayleigh.
, that the average temperature becomes smaller than those of the previous Rayleigh. 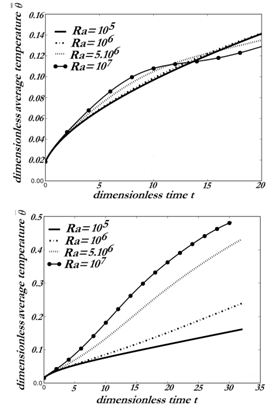 | Figure 8. Variations of against the dimensionless time |
 | Figure 9. Variations of  against the dimensionless time against the dimensionless time |
 | Figure 10. Variations of  against the dimensionless time against the dimensionless time |
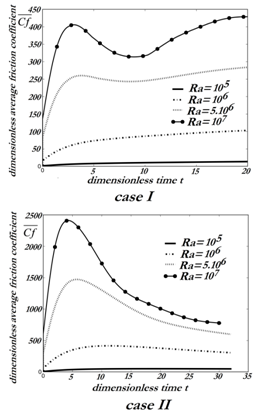
Figure 9 and Figure 10 show the variations of  and
and  against dimensionless time. Except for the weak values of the Rayleigh number (
against dimensionless time. Except for the weak values of the Rayleigh number (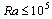 ) in the two cases,
) in the two cases, 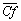 increases at the first moment corresponding to the start-up phase of the fluid motion and then decreases. The rate of decrease of the friction coefficient which is indicative of the slowing down of the flow in the neighborhood of the lower wall. In case II, the intensity of the horary cell initially localized in the neighborhood of the wall diminishes as time goes on in aid of the trigonometric cell. Thus, the competition between the two cells (the horary and the trigonometric) has the propensity to stabilize the values of the
increases at the first moment corresponding to the start-up phase of the fluid motion and then decreases. The rate of decrease of the friction coefficient which is indicative of the slowing down of the flow in the neighborhood of the lower wall. In case II, the intensity of the horary cell initially localized in the neighborhood of the wall diminishes as time goes on in aid of the trigonometric cell. Thus, the competition between the two cells (the horary and the trigonometric) has the propensity to stabilize the values of the 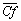 in the course of time. On the contrary, for
in the course of time. On the contrary, for 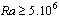 ,
, 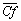 starts anew to increase above
starts anew to increase above 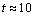 . This situation is accounted for by the intensity of the trigonometric cell, but also by the resurgence of the horary cell localized in the neighborhood of the heated zone. As on Figure 10, for a Rayleigh number equal to
. This situation is accounted for by the intensity of the trigonometric cell, but also by the resurgence of the horary cell localized in the neighborhood of the heated zone. As on Figure 10, for a Rayleigh number equal to 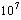 , one can notice that the resurgence of that horary cell creates a change of concavity on the curve (presence of an inflexion point at (
, one can notice that the resurgence of that horary cell creates a change of concavity on the curve (presence of an inflexion point at (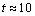 ). Whereas for case II, the inflexion point observed at
). Whereas for case II, the inflexion point observed at  always for the same Rayleigh number, is related to the trigonometric cell formation.
always for the same Rayleigh number, is related to the trigonometric cell formation.
5. Conclusions
The outcomes related to the natural convection of a Newtonian fluid between two paraboloid of revolution whose bottom wall is half-heated and half insulated, are presented in this study. Depending on the position of the active and inert zones, two cases have been considered. Apart from the fact that in both cases the regime is pseudo-conductive for 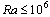 and then convective beyond, it has been noticed that for the same amount of energy supplied to the system, transfers are much more intense in the case II. In the case I the heat and fluid flow are confined in a area close to the heated wall, we have a boundary layer flow . For case I the dynamic field consists of a single trigonometric cell at large time, except at
and then convective beyond, it has been noticed that for the same amount of energy supplied to the system, transfers are much more intense in the case II. In the case I the heat and fluid flow are confined in a area close to the heated wall, we have a boundary layer flow . For case I the dynamic field consists of a single trigonometric cell at large time, except at 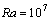 , a case for which an horary cell reforms. Whereas for case II, though the flow remains unicellular for weak Rayleigh numbers (
, a case for which an horary cell reforms. Whereas for case II, though the flow remains unicellular for weak Rayleigh numbers ( ), its rotating direction is this time clockwise, the flow becomes multi-cellular only at
), its rotating direction is this time clockwise, the flow becomes multi-cellular only at  . The reformation of the horary cell in case I has as a result a concavity change in the curves indicative of the temporal fluctuations of
. The reformation of the horary cell in case I has as a result a concavity change in the curves indicative of the temporal fluctuations of 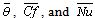 . For case II, the only observable concavity change takes place for
. For case II, the only observable concavity change takes place for  (at
(at 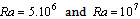 ) and as opposed to case I, it is linked to the formation of the trigonometric cell.
) and as opposed to case I, it is linked to the formation of the trigonometric cell.
Nomenclature
Latin letters: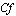 : friction coefficient.
: friction coefficient.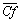 : average friction coefficient.
: average friction coefficient. : gravity acceleration.
: gravity acceleration.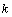 : incrementing index of the iterative process.
: incrementing index of the iterative process.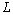 : length of reference.
: length of reference. : Nusselt number.
: Nusselt number. : average Nusselt number.
: average Nusselt number.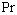 : Prandtl number,
: Prandtl number, 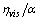 .
.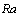 : Rayleigh number,
: Rayleigh number,  .
. : dimensionless
: dimensionless 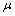 component of the velocity.
component of the velocity.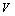 : dimensionless
: dimensionless 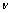 component of the velocity.
component of the velocity.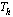 : Temperature of the heated portion of the bottom surface.
: Temperature of the heated portion of the bottom surface.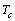 : Temperature of the upper surface.Greek Symbols:
: Temperature of the upper surface.Greek Symbols: : thermal diffusivity.
: thermal diffusivity.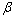 : thermal expansion coefficient.
: thermal expansion coefficient. : kinematical viscosity.
: kinematical viscosity.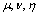 : paraboloidal coordinates.
: paraboloidal coordinates.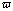 : dimensionless vorticity.
: dimensionless vorticity.  : dimensionless temperature.
: dimensionless temperature. : average dimensionless temperature.
: average dimensionless temperature.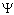 : dimensionless stream function. Subscript
: dimensionless stream function. Subscript : maximum value.
: maximum value. : minimum value.
: minimum value.
References
| [1] | W.M. Lewandowski, J.M. Khubeiz, P. Kubski, H. Bieszk, T. Wilczewski, and S. Szymaski, 1998, Natural convection heat transfer from complex surface., International Journal of Heat and Mass Transfer, 41(12), 1857-1868. |
| [2] | S. Najoua, C. Mbow, J.H. Lee, W.H. Park, and M. Daguenet, 1997, Étude numérique du modèle de Boussinesq de convection naturelle laminaire transitoire dans un ellipsoide de révolution de grand axe vertical rempli d'air., Revue Générale de Thermique, 36(3), 224-233. |
| [3] | S. Das and Y. Morsi, 2002, Natural convection inside dome shaped enclosures., International Journal of Numerical Methods for Heat & Fluid Flow, 12 (2), 126-141. |
| [4] | Y. Morsi and S. Das, 2003, Natural convection inside dome shaped enclosures., Heat Transfer Engineering, 24(2), 30-41. |
| [5] | G. Diaz, and R. Winston, 2008, Effect of surface radiation on natural convection in parabolic enclosures., Numerical Heat Transfer, Part A: Applications, 53(9), 891-906. |
| [6] | A.W. Mustafa, 2011, Natural convection in parabolic enclosure heated from below., Modern Applied Science, 5(3), 213-220. |
| [7] | A. Valencia and R. L. Frederick, 1989, Heat transfer in square cavities with partially active vertical walls., International Journal of Heat and Mass Transfer, 32 (8), 1567 - 1574. |
| [8] | O. Aydin and W. J. Yang, 2000, Natural convection in enclosures with localized heating from below and symmetrical cooling from sides., International Journal of Numerical Methods for Heat & Fluid Flow, 10 (5), 518 - 529. |
| [9] | T. Basak, S. Roy, and A.R. Balakrishnan, 2006, Effects of thermal boundary conditions on natural convection flows within a square cavity., International Journal of Heat and Mass Transfer, 49 (23-24), 4525 - 4535. |
| [10] | Moon, P.H. and Spencer, D.E., 1961, Field theory for engineers, Van Nostrand. |
| [11] | Patankar, S.V., 1980, Numerical heat transfer and fluid flow, Hemisphere Pub. Corp,. |
| [12] | Ferziger, J.H. and Perïc, M., 2002, Computational Methods for Fluid Dynamics, Springer-Verlag GmbH. |
| [13] | G. De Vahl Davis, 1983, Natural convection of air in a square cavity: A bench mark numerical solution., International Journal for Numerical Methods in Fluids, 3(3), 249-264. |

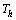 and partially insulated, while the downwardly open is maintained at a temperature below
and partially insulated, while the downwardly open is maintained at a temperature below 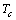 . Only half the surface of the paraboloid is heated at a temperature
. Only half the surface of the paraboloid is heated at a temperature 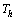 . The two cases considered are shown in Figure 1.The two paraboloids being heated differently a transient natural convection develops inside the enclosed space. To formulate and solve this problem, it is assumed that:● The phenomena are symmetrical with respect to the revolution axis and are two dimensional● All fluid properties are taken to be constant, with the exception of the density in the momentum equation. In this equation variations of density obey to the Boussinesq linear law.● The fluid is non absorbing and the radiative effects are regarded as negligible.● In the heat equation the viscous dissipation function as well as the pression effects are neglected.Taking into account the geometry of the studied system, it seems more adequate to use a paraboloidal[10] coordinates system
. The two cases considered are shown in Figure 1.The two paraboloids being heated differently a transient natural convection develops inside the enclosed space. To formulate and solve this problem, it is assumed that:● The phenomena are symmetrical with respect to the revolution axis and are two dimensional● All fluid properties are taken to be constant, with the exception of the density in the momentum equation. In this equation variations of density obey to the Boussinesq linear law.● The fluid is non absorbing and the radiative effects are regarded as negligible.● In the heat equation the viscous dissipation function as well as the pression effects are neglected.Taking into account the geometry of the studied system, it seems more adequate to use a paraboloidal[10] coordinates system 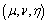 in which boundary conditions of the domain are given by constant coordinates lines. Paraboloidal coordinates are related to the Cartesian coordinate by the formulas:
in which boundary conditions of the domain are given by constant coordinates lines. Paraboloidal coordinates are related to the Cartesian coordinate by the formulas: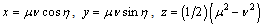 , The revolution symmetrical axis is given by
, The revolution symmetrical axis is given by 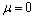 and
and  . The upper and the lower paraboloids are respectively materialized by lines of coordinates
. The upper and the lower paraboloids are respectively materialized by lines of coordinates  and
and  .From the above assumption and the coordinate transformation, the governing equation in dimensionless stream function-vorticity form are:Stream function equation:
.From the above assumption and the coordinate transformation, the governing equation in dimensionless stream function-vorticity form are:Stream function equation: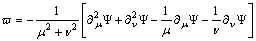
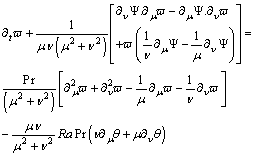

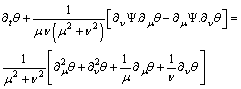
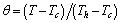 .The velocities are:
.The velocities are: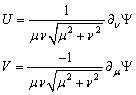
 ), velocity(
), velocity(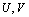 ), stream function (
), stream function (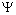 ), vorticity(
), vorticity(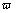 ) of reference are respectively defines as:
) of reference are respectively defines as: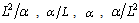 ,where
,where 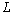 is the length of reference
is the length of reference 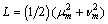 The associated dimensionless initial and boundary conditions for the problem considered are:At
The associated dimensionless initial and boundary conditions for the problem considered are:At 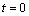 :Vorticity, temperature, stream function, velocities, and their respective derivatives are null throughout the system.At
:Vorticity, temperature, stream function, velocities, and their respective derivatives are null throughout the system.At 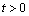 :On the lower paraboloid (
:On the lower paraboloid (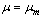 ):
):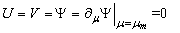
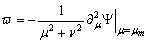
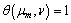
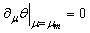
 )
)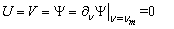
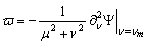
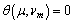
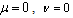 ):
):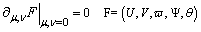
 ) and the friction coefficient (
) and the friction coefficient (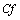 ) relative to the lower paraboloid are defined by:
) relative to the lower paraboloid are defined by: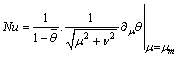
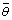 is the dimensionless average temperature
is the dimensionless average temperature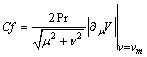
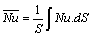
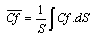
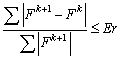
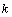 the incrementing index of the iterative process and
the incrementing index of the iterative process and  the precision of the iterative process.The solution domain, consists of grid points at which equations are applied. The grid size selected is equal to
the precision of the iterative process.The solution domain, consists of grid points at which equations are applied. The grid size selected is equal to 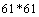 and a uniform grid has been used for all the computations. The Figure 2 shows the influence of the grid system according to the instantaneous average Nusselt number for the case I, the largest gap in relation to the chosen mesh occurs between
and a uniform grid has been used for all the computations. The Figure 2 shows the influence of the grid system according to the instantaneous average Nusselt number for the case I, the largest gap in relation to the chosen mesh occurs between 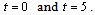

 and a time step
and a time step 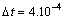 is retained to carry out all numerical tests. Refining this time step results in minor changes of the transient patterns. Due to lack of suitable results in the literature pertaining to the present configuration, the numerical algorithm used in this study was tested with the classical problem of natural convection in a square cavity by De Vahl Davis[13].
is retained to carry out all numerical tests. Refining this time step results in minor changes of the transient patterns. Due to lack of suitable results in the literature pertaining to the present configuration, the numerical algorithm used in this study was tested with the classical problem of natural convection in a square cavity by De Vahl Davis[13]. for this study is varying between
for this study is varying between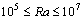 . For
. For 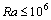 the precision
the precision of the iterative process is equal to
of the iterative process is equal to 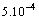 and for
and for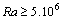 ,
, 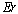 is equal to
is equal to 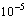 Owing to the symmetrical boundary conditions, the flows in the left and right of the symmetry axis are identical except for the sense of rotation. Figure 3 and Figure 4 represent the time evolution of isotherms and streamlines for the case I at different values of
Owing to the symmetrical boundary conditions, the flows in the left and right of the symmetry axis are identical except for the sense of rotation. Figure 3 and Figure 4 represent the time evolution of isotherms and streamlines for the case I at different values of . In the first moments, for the relatively weak values of the Rayleigh number (
. In the first moments, for the relatively weak values of the Rayleigh number (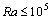 ) in the two studied cases, the isotherms are lines that are parallel to the heated inferior wall. The flow consists of a single clockwise rotating cell (dotted lines) of weak intensity. We have then here a pseudo-conductive regime. The latter, despite the continuous distortion of the isotherms due to the increasing of convection effects when Ra augments up to
) in the two studied cases, the isotherms are lines that are parallel to the heated inferior wall. The flow consists of a single clockwise rotating cell (dotted lines) of weak intensity. We have then here a pseudo-conductive regime. The latter, despite the continuous distortion of the isotherms due to the increasing of convection effects when Ra augments up to 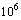 always remain the dominant mode of heat transfer within the enclosure. For the largest values of the Rayleigh number namely
always remain the dominant mode of heat transfer within the enclosure. For the largest values of the Rayleigh number namely 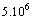 and
and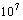 , convection becomes the dominant mode of transfer. For case I, there is a quick formation of another cell (solid line) turning in the trigonometric sense. As we progress in time the intensity of the clockwise rotating cell decreases in favor of the trigonometric one. For
, convection becomes the dominant mode of transfer. For case I, there is a quick formation of another cell (solid line) turning in the trigonometric sense. As we progress in time the intensity of the clockwise rotating cell decreases in favor of the trigonometric one. For 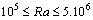 the circulation of the fluid within the enclosure is essentially due to the stable trigonometric cell.
the circulation of the fluid within the enclosure is essentially due to the stable trigonometric cell.
 for the case I
for the case I
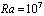 for the case I
for the case I
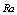

 for the case II
for the case II
 for the case II
for the case II and
and  is made for different Rayleigh numbers. For all the values taken by the latter, one can see at the first moments (
is made for different Rayleigh numbers. For all the values taken by the latter, one can see at the first moments (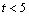 ) an increase phase of
) an increase phase of 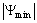 that corresponds to the apparition and development of the clockwise cell followed by a decrease of
that corresponds to the apparition and development of the clockwise cell followed by a decrease of 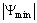 leading to a progressive vanishing of the clockwise cell. But for
leading to a progressive vanishing of the clockwise cell. But for 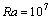 after having reached its weakest value (
after having reached its weakest value (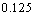 at
at 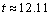 ),
),  starts again increasing. During this interval of time, when
starts again increasing. During this interval of time, when 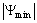 increases anew, one can see a concavity change in the shape of
increases anew, one can see a concavity change in the shape of 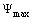 . This behavior which is specific to is indicative of the reformation process of the horary cell. The behavior of the system at
. This behavior which is specific to is indicative of the reformation process of the horary cell. The behavior of the system at  differs from the previous
differs from the previous 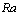 only through the resurgence of the horary cell at large time (
only through the resurgence of the horary cell at large time ( ). It should be noticed that the time when
). It should be noticed that the time when 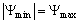 is independent of the Rayleigh number. In the case I, although the convection is established at
is independent of the Rayleigh number. In the case I, although the convection is established at 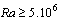 , the heat transfers remain confined in the area located under the equatorial plan. We have a boundary layer flow.When the thermal boundary conditions are reversed on the inferior wall (case II), the apparition of the trigonometric cell is more lately achieved (beyond
, the heat transfers remain confined in the area located under the equatorial plan. We have a boundary layer flow.When the thermal boundary conditions are reversed on the inferior wall (case II), the apparition of the trigonometric cell is more lately achieved (beyond 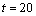 for
for 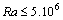 and at
and at 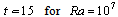 ). Thus, for weak Rayleigh numbers (
). Thus, for weak Rayleigh numbers (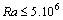 ), the flow is mainly due to the clockwise cell, the intensity of the trigonometric cell being too weak. Contrary to case I, in case II the clockwise cell is no longer unstable and the front of heat invades the enclosure more and more. When the convective effects become dominant (
), the flow is mainly due to the clockwise cell, the intensity of the trigonometric cell being too weak. Contrary to case I, in case II the clockwise cell is no longer unstable and the front of heat invades the enclosure more and more. When the convective effects become dominant (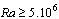 ), the growth of the trigonometric cell favors the division of the horary cell into two parts. The most intense part is contiguous to the heated inferior wall. At large time, the circulation inside the enclosure is due to the competition between the two types of cells, the dynamic field is multi-cellular.In this section, it has been carried out an analysis of the average values such as
), the growth of the trigonometric cell favors the division of the horary cell into two parts. The most intense part is contiguous to the heated inferior wall. At large time, the circulation inside the enclosure is due to the competition between the two types of cells, the dynamic field is multi-cellular.In this section, it has been carried out an analysis of the average values such as If the cases I and case II differ only through the relative position of the active and inert zones, for a same quantity of energy brought to the system, the average values of case II are by far superior, due to the confinement of the main transfers for the case I in a zone close to the lower wall. In Figure 8, the evolution of
If the cases I and case II differ only through the relative position of the active and inert zones, for a same quantity of energy brought to the system, the average values of case II are by far superior, due to the confinement of the main transfers for the case I in a zone close to the lower wall. In Figure 8, the evolution of 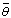 with time has been shown for different Rayleigh numbers. For case II, if
with time has been shown for different Rayleigh numbers. For case II, if 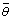 increases with time and Rayleigh numbers, the situation is not the same for case I. Though
increases with time and Rayleigh numbers, the situation is not the same for case I. Though 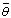 always augments with time, we notice at
always augments with time, we notice at 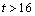 for
for 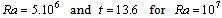 , that the average temperature becomes smaller than those of the previous Rayleigh.
, that the average temperature becomes smaller than those of the previous Rayleigh. 

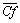 against the dimensionless time
against the dimensionless time
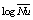 against the dimensionless time
against the dimensionless time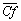 and
and 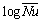 against dimensionless time. Except for the weak values of the Rayleigh number (
against dimensionless time. Except for the weak values of the Rayleigh number (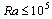 ) in the two cases,
) in the two cases, 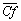 increases at the first moment corresponding to the start-up phase of the fluid motion and then decreases. The rate of decrease of the friction coefficient which is indicative of the slowing down of the flow in the neighborhood of the lower wall. In case II, the intensity of the horary cell initially localized in the neighborhood of the wall diminishes as time goes on in aid of the trigonometric cell. Thus, the competition between the two cells (the horary and the trigonometric) has the propensity to stabilize the values of the
increases at the first moment corresponding to the start-up phase of the fluid motion and then decreases. The rate of decrease of the friction coefficient which is indicative of the slowing down of the flow in the neighborhood of the lower wall. In case II, the intensity of the horary cell initially localized in the neighborhood of the wall diminishes as time goes on in aid of the trigonometric cell. Thus, the competition between the two cells (the horary and the trigonometric) has the propensity to stabilize the values of the 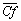 in the course of time. On the contrary, for
in the course of time. On the contrary, for 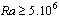 ,
, 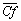 starts anew to increase above
starts anew to increase above 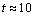 . This situation is accounted for by the intensity of the trigonometric cell, but also by the resurgence of the horary cell localized in the neighborhood of the heated zone. As on Figure 10, for a Rayleigh number equal to
. This situation is accounted for by the intensity of the trigonometric cell, but also by the resurgence of the horary cell localized in the neighborhood of the heated zone. As on Figure 10, for a Rayleigh number equal to 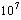 , one can notice that the resurgence of that horary cell creates a change of concavity on the curve (presence of an inflexion point at (
, one can notice that the resurgence of that horary cell creates a change of concavity on the curve (presence of an inflexion point at (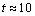 ). Whereas for case II, the inflexion point observed at
). Whereas for case II, the inflexion point observed at  always for the same Rayleigh number, is related to the trigonometric cell formation.
always for the same Rayleigh number, is related to the trigonometric cell formation.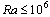 and then convective beyond, it has been noticed that for the same amount of energy supplied to the system, transfers are much more intense in the case II. In the case I the heat and fluid flow are confined in a area close to the heated wall, we have a boundary layer flow . For case I the dynamic field consists of a single trigonometric cell at large time, except at
and then convective beyond, it has been noticed that for the same amount of energy supplied to the system, transfers are much more intense in the case II. In the case I the heat and fluid flow are confined in a area close to the heated wall, we have a boundary layer flow . For case I the dynamic field consists of a single trigonometric cell at large time, except at 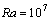 , a case for which an horary cell reforms. Whereas for case II, though the flow remains unicellular for weak Rayleigh numbers (
, a case for which an horary cell reforms. Whereas for case II, though the flow remains unicellular for weak Rayleigh numbers ( ), its rotating direction is this time clockwise, the flow becomes multi-cellular only at
), its rotating direction is this time clockwise, the flow becomes multi-cellular only at  . The reformation of the horary cell in case I has as a result a concavity change in the curves indicative of the temporal fluctuations of
. The reformation of the horary cell in case I has as a result a concavity change in the curves indicative of the temporal fluctuations of 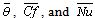 . For case II, the only observable concavity change takes place for
. For case II, the only observable concavity change takes place for  (at
(at 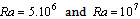 ) and as opposed to case I, it is linked to the formation of the trigonometric cell.
) and as opposed to case I, it is linked to the formation of the trigonometric cell.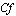 : friction coefficient.
: friction coefficient.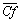 : average friction coefficient.
: average friction coefficient. : gravity acceleration.
: gravity acceleration.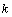 : incrementing index of the iterative process.
: incrementing index of the iterative process.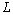 : length of reference.
: length of reference. : Nusselt number.
: Nusselt number. : average Nusselt number.
: average Nusselt number.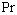 : Prandtl number,
: Prandtl number, 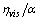 .
.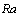 : Rayleigh number,
: Rayleigh number,  .
. : dimensionless
: dimensionless 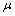 component of the velocity.
component of the velocity.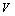 : dimensionless
: dimensionless 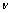 component of the velocity.
component of the velocity.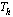 : Temperature of the heated portion of the bottom surface.
: Temperature of the heated portion of the bottom surface.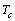 : Temperature of the upper surface.Greek Symbols:
: Temperature of the upper surface.Greek Symbols: : thermal diffusivity.
: thermal diffusivity.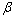 : thermal expansion coefficient.
: thermal expansion coefficient. : kinematical viscosity.
: kinematical viscosity. : paraboloidal coordinates.
: paraboloidal coordinates.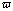 : dimensionless vorticity.
: dimensionless vorticity.  : dimensionless temperature.
: dimensionless temperature. : average dimensionless temperature.
: average dimensionless temperature.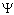 : dimensionless stream function. Subscript
: dimensionless stream function. Subscript : maximum value.
: maximum value. : minimum value.
: minimum value. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML