Kapil Kumar1, V. Singh2, Seema Sharma
1,3Department of Mathematics, Gurukula Kangri Vishwavidyalaya, Haridwar, 249404, India
2Department of Applied Sciences, Moradabad Institute of Technology, Moradabad, 244001, India
Correspondence to: Kapil Kumar, ,3Department of Mathematics, Gurukula Kangri Vishwavidyalaya, Haridwar, 249404, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The objective of the present paper is to study the stability of a rotating Walters’ B' elastico-viscous fluid layer heated from below through a Brinkman porous medium in the presence of magnetic field, variable gravity and suspended particles for the case of free boundaries. After linearizing the governing hydrodynamic equations and applying normal mode analysis method, dispersion relation is obtained and solved numerically. For the case of stationary convection, Walters’ B' elastico-viscous fluid behaves like an ordinary Newtonian fluid. The suspended particles have a destabilizing effect on the system whereas rotation has a stabilizing effect on the system. The magnetic field, medium permeability and Darcy number have both stabilizing and destabilizing effects on the system under certain conditions. The effects of suspended particles, rotation, magnetic field, medium permeability and Darcy-Brinkman number on critical Rayleigh number have also been plotted graphically to depict the stability characteristics. It is also observed that suspended particles, rotation, magnetic field and medium permeability introduce oscillatory modes in the system which is non-existent in their absence. Comparisons with the previous published work are also presented.
Keywords:
Thermal Convection, Suspended Particles, Magnetic Field, Permeability, Rotation, Brinkman Porous Medium
Cite this paper: Kapil Kumar, V. Singh, Seema Sharma, Magneto-hydrodynamic Thermal Instability of Walters’ B' Fluid under the Effects of Rotation, Variable Gravity Field and Suspended Particles in a Brinkman Porous Medium, American Journal of Fluid Dynamics, Vol. 3 No. 2, 2013, pp. 31-39. doi: 10.5923/j.ajfd.20130302.03.
1. Introduction
When a horizontal layer of a viscous fluid is heated from below in a gravitational field, the system becomes unstable and convection sets in form of a regular cellular pattern when the Rayleigh number R exceeds a certain critical value Rc. A detailed account of the onset of thermal instability (Bénard convection) of a Newtonian fluid in a fluid layer under varying assumptions of hydrodynamics has been given by Chandrasekhar[1] in his celebrated monograph. Rayleigh[2] was the first to study the problem theoretically. Scanlon & Segel[3] have investigated the effect of suspended particles on the onset of Bénard convection and found that the critical Rayleigh number is reduced because the heat capacity of the pure gas was supplemented by the particles. Thus the effect of the suspended particles is to destabilize the layer. Thermal instability in a horizontal layer of an electrically conducting fluid heated from below and permeated by a uniform vertical magnetic field has been studied by Thompson[4] and experimentally by Nakagawa[5]. Bhatia & Steiner[6] have studied the problem of thermal instability of a Maxwellian visco-elastic fluid in the presence of a magnetic field and found that the magnetic field has a stabilizing influence on the overstable mode of convection in a visco-elastic fluid layer. In stellar atmospheres and interiors, the magnetic field may be variable and may alter the nature of the instability. Coriolis forces also play an important role on the stability of a system. Numerous studies have been undertaken in the past to understand the convective instability of Newtonian fluids. The interest for investigations of non-Newtonian fluids (e.g. polymer suspensions, ketchup, paint, shampoo, blood, protein solutions, soap solution, liquid crystals, starch suspensions) is motivated by a wide range of engineering applications which include geophysical fluid dynamics, chemical technology and petroleum industry. There are many elastico-viscous fluids that cannot be characterized either by Oldroyd’s constitutive relations or Maxwell’s constitutive relations. One such class of viscoelastic fluid is Walters’ (model B') fluid. Walters’[7] reported that the mixture of polymethyl methacrylate and pyridine at 25℃containing 30.5g of polymer with density 0.98g per litre behaves very closely as the Walters’ (model B') fluid. With the growing importance of Walters’ (model B’) fluids in the manufacture of parts of space crafts, cushions, ropes, tyres, foams, seats, engineering equipments, the investigations on such fluids are desirable. Thermal instability of a Walters’ B' elastic-viscous fluid in the presence of a variable gravity field and rotation in a porous medium has been investigated by Sharma & Rana[8]. Rana & Kumar[9] have studied the effect of rotation and suspended particles on the stability of an incompressible Walters’ (model B') fluid heated from below under a variable gravity field in a porous medium while the problem of thermal convection in Walter’ (model B’) rotating fluid permeated with suspended particles and variable gravity field in porous medium in hydromagnetics have been studied by Sharma and Rana [10]. Recently, Rana[11] investigated the effect of suspended particles on thermal instability of Walters’ (model B') fluid in a Brinkman porous medium.Flow through porous medium has gained considerable interest and has been recognized as a problem of fundamental importance for many decades owing to its importance in several branches of engineering and science like ground water hydrology, petroleum engineering, soil science, chemical engineering, geophysics, astrophysics etc. The physical properties of comets and meteorites suggest the importance of porosity in astrophysical context. The investigation in porous medium has been started by Darcy model and gradually was extended to Darcy-Brinkman model. It is found, both theoretically and experimentally, that Darcy’s equation provides inadequate results of the hydrodynamic conditions, particularly near the boundaries of a porous medium. To be mathematically compatible with the Navier-Stokes equations, Brinkman proposed the inclusion of the term 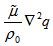 in addition to
in addition to 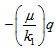 in the equations of motion. Nield and Bejan[12] have studied the problem of convection in a porous medium. Lapwood[13] and Wooding[14] have investigated the stability of convective flow in a porous medium taking into account the Darcy’s resistance. Durlofsky & Brady[15], using a Green’s function, showed that the Brinkman model is valid for particles whose porosity
in the equations of motion. Nield and Bejan[12] have studied the problem of convection in a porous medium. Lapwood[13] and Wooding[14] have investigated the stability of convective flow in a porous medium taking into account the Darcy’s resistance. Durlofsky & Brady[15], using a Green’s function, showed that the Brinkman model is valid for particles whose porosity 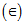 > 0.95.Since the earth’s gravity field varies with the vertical distance from its surface, so it is necessary to take into account the gravity as a variable quantity with height from the earth’s centre. This variation of gravity plays an important role for large scale flows in ocean, atmosphere and mantle but for laboratory purposes, we usually neglect these variations. Thermal instability of a fluid layer under varying gravity field heated from above and below has been investigated by Pradhan and Samal[16]. We have performed a linear stability analysis as a first step towards investigating this problem. Keeping in mind the importance and various applications of non-Newtonian fluids, our main objective, in the present paper, is to study the effects of rotation, magnetic field and suspended particles on thermal instability of a Walters’ (model B') fluid in a Brinkman porous medium in the presence of a variable gravity field. The interest for studying this problem is to control the magneto-hydrodynamic thermal instability under the influences of variable gravity, rotation, suspended particles in a Brinkman porous medium.
> 0.95.Since the earth’s gravity field varies with the vertical distance from its surface, so it is necessary to take into account the gravity as a variable quantity with height from the earth’s centre. This variation of gravity plays an important role for large scale flows in ocean, atmosphere and mantle but for laboratory purposes, we usually neglect these variations. Thermal instability of a fluid layer under varying gravity field heated from above and below has been investigated by Pradhan and Samal[16]. We have performed a linear stability analysis as a first step towards investigating this problem. Keeping in mind the importance and various applications of non-Newtonian fluids, our main objective, in the present paper, is to study the effects of rotation, magnetic field and suspended particles on thermal instability of a Walters’ (model B') fluid in a Brinkman porous medium in the presence of a variable gravity field. The interest for studying this problem is to control the magneto-hydrodynamic thermal instability under the influences of variable gravity, rotation, suspended particles in a Brinkman porous medium.
2. Mathematical Formulation and Linear Stability Analysis
We consider a horizontal layer of an incompressible Walters’ B' visco-elastic fluid between two plates at a distance d apart in the presence of a porous medium of porosityand permeability k. The fluid layer is acted upon by a uniform rotation Ω (0, 0, Ω), vertical magnetic field H (0, 0, H) and variable gravity field 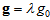 , where
, where 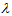 can be positive or negative according as the gravity increases or decreases upward from its value
can be positive or negative according as the gravity increases or decreases upward from its value 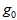 (>0). An adverse temperature gradient
(>0). An adverse temperature gradient 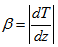 is maintained by underside heating. The pressure p, density
is maintained by underside heating. The pressure p, density 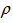 , viscosity
, viscosity 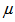 and visco-elasticity
and visco-elasticity 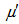 depend upon the vertical co-ordinate z- only. The basic equations of hydromagnetic in unsteady state relevant to the problem are defined as:
depend upon the vertical co-ordinate z- only. The basic equations of hydromagnetic in unsteady state relevant to the problem are defined as: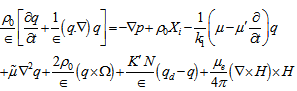 | (1) |
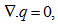 | (2) |
Where in the above equations 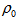 is the fluid density, is porosity,
is the fluid density, is porosity, 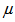 denotes viscosity,
denotes viscosity, 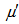 denotes visco-elasticity,
denotes visco-elasticity, 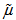 is the effective viscosity of the porous medium,
is the effective viscosity of the porous medium, 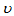 is the kinematic viscosity,
is the kinematic viscosity, 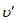 is the kinematic visco-elasticity, p is the pressure,
is the kinematic visco-elasticity, p is the pressure, 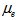 is magnetic permeability,
is magnetic permeability, 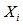 is the external force due to gravity variations,
is the external force due to gravity variations, 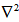 is the three dimensional Laplacian operator,
is the three dimensional Laplacian operator, 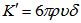 where
where 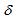 being particle radius, is the Stokes’ drag coefficient,
being particle radius, is the Stokes’ drag coefficient, 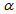 is the co-efficient of volume expansion and q is the velocity of pure fluid. The last term on the right side of equation (1) incorporates the effect of the magnetic field on the fluid motion and also known as Lorentz force. Here
is the co-efficient of volume expansion and q is the velocity of pure fluid. The last term on the right side of equation (1) incorporates the effect of the magnetic field on the fluid motion and also known as Lorentz force. Here 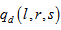 and
and 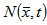 denote the velocity and number density of the particles respectively. The presence of suspended particles adds an extra force term, in equation of motion, proportional to velocity difference between particles and fluid. Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite in sign, in the equations of motion for the particles. The distances between the particles are assumed to be quite large compared with their diameters thereby neglecting the effect of inter-particle reactions. The effects of pressure, magnetic field and gravity on the particles are very small and hence ignored.If mN is the mass of particles per unit volume, then the equations of motion and continuity for the particles are:
denote the velocity and number density of the particles respectively. The presence of suspended particles adds an extra force term, in equation of motion, proportional to velocity difference between particles and fluid. Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite in sign, in the equations of motion for the particles. The distances between the particles are assumed to be quite large compared with their diameters thereby neglecting the effect of inter-particle reactions. The effects of pressure, magnetic field and gravity on the particles are very small and hence ignored.If mN is the mass of particles per unit volume, then the equations of motion and continuity for the particles are: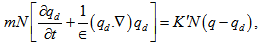 | (3) |
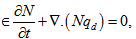 | (4) |
Assuming that the suspended particles and the fluid particles are in thermal equilibrium then the equation of heat conduction gives: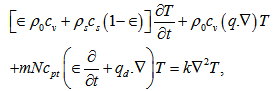 | (5) |
In the above equation 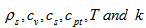 denote, respectively, the density of solid material, specific heat at constant volume, heat capacity of solid material, heat capacity of particles, the temperature and the effective thermal conductivity of the pure fluid.The Maxwell’s electromagnetic equation yields
denote, respectively, the density of solid material, specific heat at constant volume, heat capacity of solid material, heat capacity of particles, the temperature and the effective thermal conductivity of the pure fluid.The Maxwell’s electromagnetic equation yields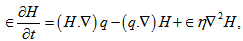 | (6) |
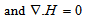 | (7) |
Where 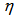 denote the resistivity. The equation of state of the system is
denote the resistivity. The equation of state of the system is 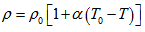 | (8) |
3. Perturbation Equations
Let the perturbations in fluid velocity q(0,0,0), particle velocity qd (0,0,0), temperature T, pressure p, density 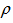 and magnetic field H be denoted by q (u,v,w), qd (l,r,s),
and magnetic field H be denoted by q (u,v,w), qd (l,r,s), 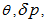
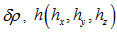 , respectively.After linearizing the system of equations (1) - (8), we have the perturbation equations:
, respectively.After linearizing the system of equations (1) - (8), we have the perturbation equations: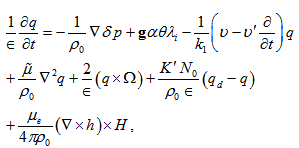 | (9) |
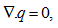 | (10) |
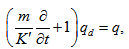 | (11) |
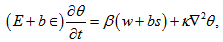 | (12) |
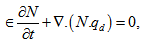 | (13) |
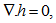 | (14) |
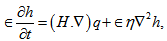 | (15) |
where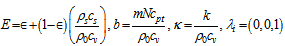 and w, s be the vertical fluid and particles velocity, respectively.In the Cartesian form, equations (9)-(15) can be expressed as
and w, s be the vertical fluid and particles velocity, respectively.In the Cartesian form, equations (9)-(15) can be expressed as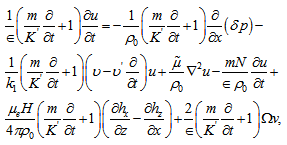 | (16) |
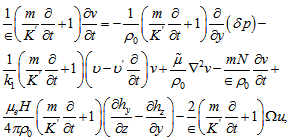 | (17) |
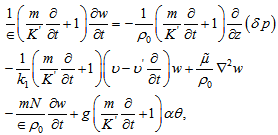 | (18) |
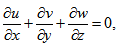 | (19) |
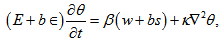 | (20) |
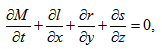 | (21) |
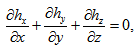 | (22) |
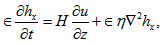 | (23) |
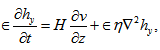 | (24) |
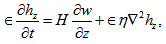 | (25) |
Operating equations (16) and (17) by 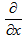 and
and 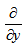 respectively, adding them and using eq. (19), we get:
respectively, adding them and using eq. (19), we get: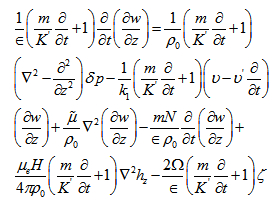 | (26) |
Where 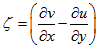 denotes the z-component of the vorticity. Operating equations (18) and (26) by
denotes the z-component of the vorticity. Operating equations (18) and (26) by 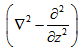 and
and 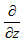 respectively and adding them to eliminate
respectively and adding them to eliminate 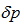 , we get:
, we get: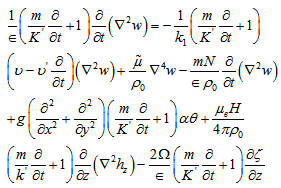 | (27) |
where 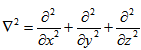 .Now, operating equation (16) and (17) by
.Now, operating equation (16) and (17) by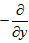 and
and 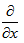 respectively and adding them, we get:
respectively and adding them, we get: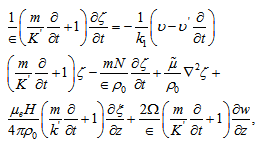 | (28) |
Where 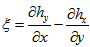 is the z-component of current density.From equation (20), we get
is the z-component of current density.From equation (20), we get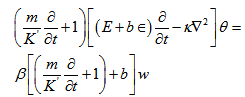 | (29) |
Now, operating equations (23) and (24) by 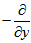 and
and 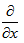 respectively, adding them and using equations (19) & (22), we get
respectively, adding them and using equations (19) & (22), we get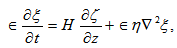 | (30) |
From equation (25), we get,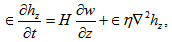 | (31) |
Equations (27)-(31) are the basic equations governing the motion of a Walters’ B’ visco-elastic fluid under the influences of rotation, magnetic field, suspended particles and Brinkman porous medium.
4. Normal Mode Method and Dispersion Relation
By supposing that the perturbations in various physical quantities have a solution with a dependence on x, y and t of the form: 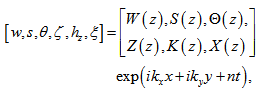 | (32) |
Where 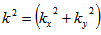 , is the resultant wave number of the disturbance and n is the frequency of the harmonic disturbance, which is, in general, a complex constant.
, is the resultant wave number of the disturbance and n is the frequency of the harmonic disturbance, which is, in general, a complex constant.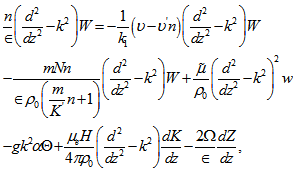 | (33) |
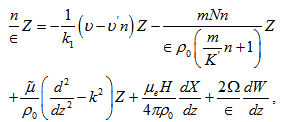 | (34) |
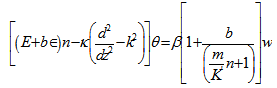 | (35) |
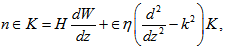 | (36) |
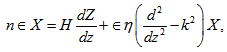 | (37) |
Equations (33) – (37) in non-dimensional form becomes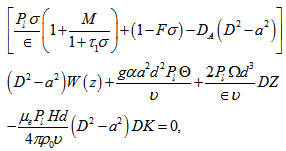 | (38) |
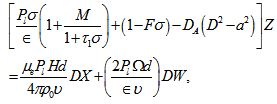 | (39) |
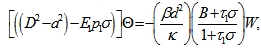 | (40) |
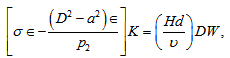 | (41) |
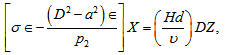 | (42) |
where we have used the following non-dimensional quantities with the scaling: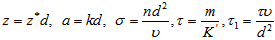 ,
,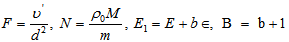
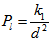 , is the dimensionless medium permeability,
, is the dimensionless medium permeability, 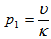 , is the thermal Prandtl number,
, is the thermal Prandtl number, 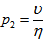 , is the magnetic Prandtl number and
, is the magnetic Prandtl number and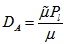 is the Darcy-Brinkman number modified by the viscosity ratio.Eliminating K, Θ, X and Z between equations (38) – (42), we obtain:
is the Darcy-Brinkman number modified by the viscosity ratio.Eliminating K, Θ, X and Z between equations (38) – (42), we obtain: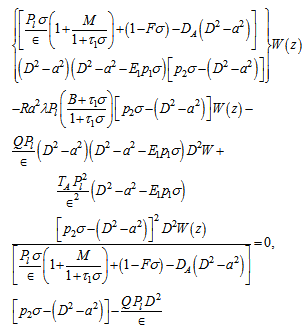 | (43) |
Where 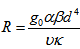 , is the thermal Rayleigh number,
, is the thermal Rayleigh number, 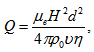 is the Chandrasekhar number and
is the Chandrasekhar number and 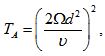 is the Taylor number.For the case of two free boundaries, the boundary conditions appropriate to the problem are defined as:
is the Taylor number.For the case of two free boundaries, the boundary conditions appropriate to the problem are defined as: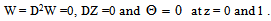 | (44) |
and the components of h are continuous.Since the components of the magnetic field are continuous and the tangential components are zero outside the fluid, we have 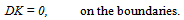 | (45) |
The boundary conditions (44) and (45) imply that all even order derivatives of W must vanish at the boundaries. So a suitable solution of W characterizing the lowest mode is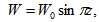 | (46) |
where W0 is a constant. Using solution (46) in equation (43), we obtain the dispersion relation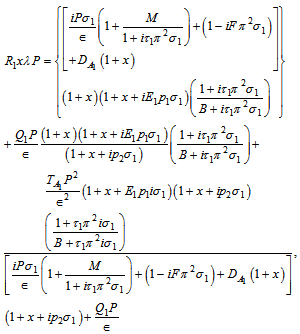 | (47) |
where 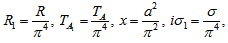
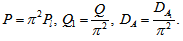 Equation (47) is required dispersion relation accounting the effects of rotation, medium permeability, variable gravity and magnetic field on thermal instability of Walters’ (Model B') elastico-viscous fluid permeated with suspended particles in a Brinkman porous medium.
Equation (47) is required dispersion relation accounting the effects of rotation, medium permeability, variable gravity and magnetic field on thermal instability of Walters’ (Model B') elastico-viscous fluid permeated with suspended particles in a Brinkman porous medium.
5. The Stationary Convection
When instability sets in as stationary convection, the marginal state will be characterized by 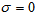 . So, we put
. So, we put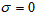 in equation (47) and get:
in equation (47) and get: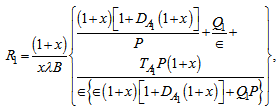 | (48) |
which expresses the modified Rayleigh number R1 as a function of the dimensionless wave number x and the parameters 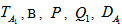 . Hence, it is clear that for stationary convection Walters’ (Model B') elastico-viscous fluid behave like an ordinary Newtonian fluid since elastico-viscous parameter F vanishes with
. Hence, it is clear that for stationary convection Walters’ (Model B') elastico-viscous fluid behave like an ordinary Newtonian fluid since elastico-viscous parameter F vanishes with 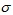 .In the absence of rotation, magnetic field and variable gravity field
.In the absence of rotation, magnetic field and variable gravity field 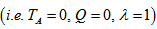 , expression (48) reduces to:
, expression (48) reduces to: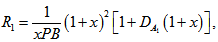 | (49) |
which is identical with the expression derived by Rana[10].To study the effects of suspended particles, rotation, magnetic field, medium permeability and Darcy number, we examine the behaviour of 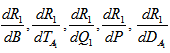 analytically.Equation (48) yields
analytically.Equation (48) yields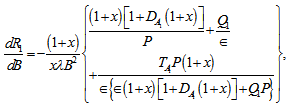 | (50) |
which is negative implying thereby that the effect of suspended particles is to destabilize the system. This result is a good agreement of the earlier work of Scanlon & Segel[3].From equation (48), we get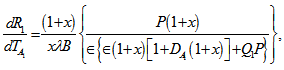 | (51) |
which shows that rotation has stabilizing effect on the system. This stabilizing effect is an agreement of the earlier work of Sharma & Rana[8].From equation (48), we get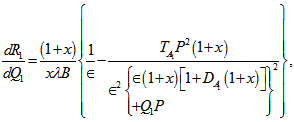 | (52) |
which shows that magnetic field stabilizes the system if 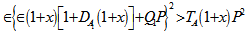 and destabilizes the system if
and destabilizes the system if 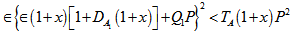 Equation (48) yields
Equation (48) yields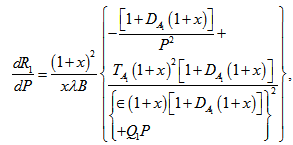 | (53) |
From equation (53), we observe that medium permeability has destabilizing effect when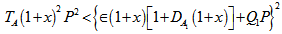 and medium permeability has a stabilizing effect when
and medium permeability has a stabilizing effect when 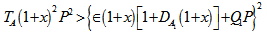 Equation (48) yields
Equation (48) yields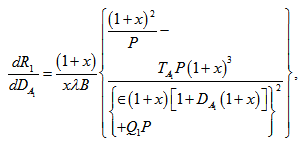 | (54) |
From equation (54), we observe that Darcy-Brinkman number has destabilizing effect when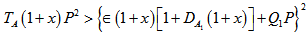 and has a stabilizing effect when
and has a stabilizing effect when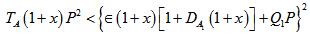
6. Results and Discussion
The dispersion relation (48) is analyzed numerically. Graphs have been plotted for various values of the parameters to determine the region of stability.Figure 1 shows the decrease in critical Rayleigh number 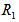 with the increase in suspended particles B. This shows that the effect of suspended particles is to destabilize the system.Figure 2 shows that the critical Rayleigh number
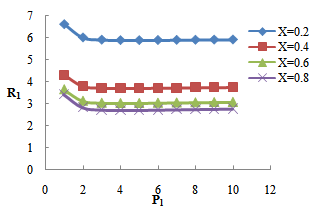
with the increase in suspended particles B. This shows that the effect of suspended particles is to destabilize the system.Figure 2 shows that the critical Rayleigh number 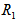 increases with the increase in rotation TA, thereby depicting the stabilizing effects of rotation TA.Figure 3, 4 and 5 shows that the magnetic field, medium permeability and Darcy number have a destabilizing effect for Q=1 to Q=2, P=1 to P=5, DA=1 to DA=3 and stabilizing effect for Q=2.5 to Q=5.5, P=6 to P=10, DA=4 to DA=10 respectively. Therefore, magnetic field, medium permeability and Darcy-Brinkman number have both destabilizing and stabilizing influences on the system.
increases with the increase in rotation TA, thereby depicting the stabilizing effects of rotation TA.Figure 3, 4 and 5 shows that the magnetic field, medium permeability and Darcy number have a destabilizing effect for Q=1 to Q=2, P=1 to P=5, DA=1 to DA=3 and stabilizing effect for Q=2.5 to Q=5.5, P=6 to P=10, DA=4 to DA=10 respectively. Therefore, magnetic field, medium permeability and Darcy-Brinkman number have both destabilizing and stabilizing influences on the system. | Figure 1. Variation of Rayleigh number 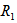 with suspended particles B for fixed values of with suspended particles B for fixed values of 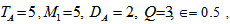 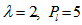 and and 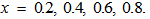 |
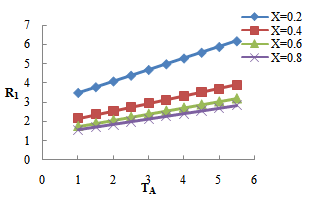 | Figure 2. Variation of Rayleigh number 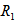 with rotation with rotation 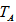 for fixed values of for fixed values of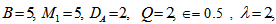 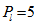 and and 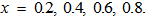 |
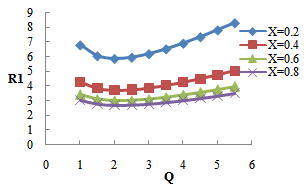 | Figure 3. Variation of Rayleigh number 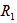 with magnetic field with magnetic field 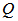 for fixed values of for fixed values of 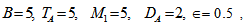 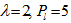 and and 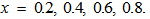 |
 | Figure 4. Variation of Rayleigh number 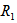 with medium permeability for fixed values of with medium permeability for fixed values of 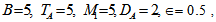 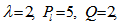 and and 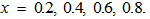 |
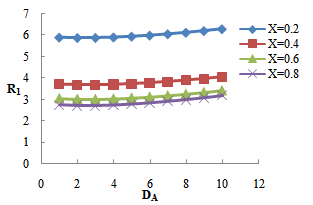 | Figure 5. Variation of Rayleigh number 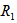 with Darcy –Brinkman number with Darcy –Brinkman number 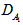 for fixed values of for fixed values of 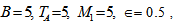 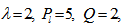 and and 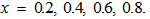 |
7. Stability of the system and Oscillatory modes
Here we examine the possibility of oscillatory modes, if any, in Walters’ (Model B') elastico-viscous fluid due to the presence of suspended particles, rotation, magnetic field and variable gravity field in a Brinkman porous medium. Multiply equation (38) by W* (the complex conjugate of W), integrating over the range of z and making use of equations (39)-(42) with the help of boundary conditions (44) and (45), we obtain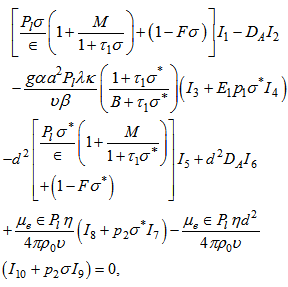 | (55) |
where The integral part I1-I10 are all positive definite. Putting 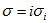 in equation (55), where
in equation (55), where 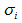 is real and equating the imaginary parts, we obtain
is real and equating the imaginary parts, we obtain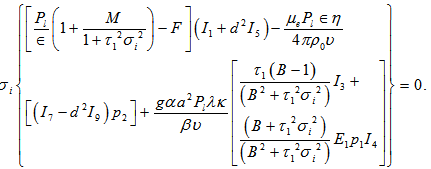 | (56) |
Equation (56) implies that 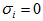 or
or 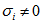 which mean that modes may be non oscillatory or oscillatory. The oscillatory modes introduced due to presence of rotation, magnetic field, suspended particles, visco-elasticity and medium permeability.
which mean that modes may be non oscillatory or oscillatory. The oscillatory modes introduced due to presence of rotation, magnetic field, suspended particles, visco-elasticity and medium permeability.
8. Conclusions
The problem of thermal convection in Walters’ (Model B') visco-elastic fluid permitted with suspended particles in the presence of rotation, variable gravity and magnetic field has been investigated in a Brinkman porous medium. The main conclusions of the paper are as follows:(a). For the case of stationary convection, Walters’ (B') elastico-viscous fluid behaves like an ordinary Newtonian fluid.(b).The expressions for 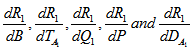 are examined analytically and it has been found that the effect of suspended particles is to destabilize the system as gravity increases upward from its value
are examined analytically and it has been found that the effect of suspended particles is to destabilize the system as gravity increases upward from its value 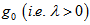 whereas the effect of rotation is to stabilize the system.(c). The magnetic field has both stabilizing and destabilizing effects on the system under the conditions
whereas the effect of rotation is to stabilize the system.(c). The magnetic field has both stabilizing and destabilizing effects on the system under the conditions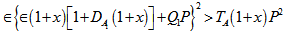 and
and 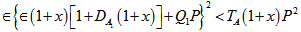 respectively.(d). The medium permeability has both stabilizing and destabilizing effects on the system under the conditions
respectively.(d). The medium permeability has both stabilizing and destabilizing effects on the system under the conditions 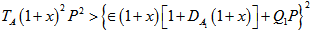 and
and 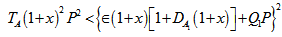 respectively.(e). The Darcy-Brinkman number has both stabilizing and destabilizing effects on the system under the conditions
respectively.(e). The Darcy-Brinkman number has both stabilizing and destabilizing effects on the system under the conditions 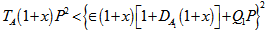 and
and 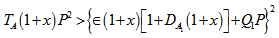 respectively.(f). The effects of suspended particles, rotation, magnetic field and medium permeability and Darcy-Brinkman number on thermal instability of Walters’ (model B’) fluids in a Brinkman porous medium have also been shown graphically in fig. 1, 2, 3, 4, and 5.
respectively.(f). The effects of suspended particles, rotation, magnetic field and medium permeability and Darcy-Brinkman number on thermal instability of Walters’ (model B’) fluids in a Brinkman porous medium have also been shown graphically in fig. 1, 2, 3, 4, and 5.
References
| [1] | Chandrasekhar, S.C.: Hydrodynamic and Hydromagnetic Stability, Dover Publication, New York, 1981. |
| [2] | Rayleigh, L.: On Convection Currents in a Horizontal Layer of Fluid, When the Higher Temperature is on the Underside, Phil. Mag., 32, pp. 529-546, 1916. |
| [3] | Scanlon, J.W. and Segel, L.A.: Effect of suspended particles on onset of Bénard convection, Physics Fluids, 16, pp. 1573-1578, 1973. |
| [4] | Thompson,W.B.: Thermal convection in a magnetic field, Philosophical Magazine Series 7, 42, 1417-1432, 1951. |
| [5] | Nakagawa, S.K.: An experiment on the inhibition of thermal convection by magnetic field, Nature, 175, pp. 417-419, 1955. |
| [6] | Bhatia, P.K. and Steiner, J.M.: Thermal instability of fluid layer in Hydromagnetics, J. Math. Anal. Appl.,41, pp. 271-289, 1973. |
| [7] | Walters, K.: Non-Newtonian effects in some elastico-viscous liquids whose behavior at some rates of shear is characterized by a general linear equation of state, Quart. J. Mech. Appl. Math., 15, 1, pp. 63-76, 1962. |
| [8] | Sharma, V. and Rana, G.C.: Thermal instability of a Walters’ (model B’) elastico-viscous fluid in the presence of variable gravity field and rotation in porous medium, J. Non-Equilib. Thermodyn., 26, pp 31-40, 2001. |
| [9] | Rana, G.C. and Kumar, S.: Effect of rotation and suspended particles on the stability of an incompressible Walters’ (model B') fluid heated from below under a variable gravity field in a porous medium, Engg. Trans., 60, pp. 55-68, 2012. |
| [10] | Sharma, V. and Rana, G.C.: Thermal Convection in Walter’ (Model B’) Rotating Fluid permeated with suspended particles and variable gravity field in porous medium in Hydromagnetics, Int. J. Appl. Eng. Res. Vol. 2, Issue 2, pp. 390-405, 2011. |
| [11] | Rana, G.C.: Effect of suspended particles on thermal instability of Walters’ (model B') fluid in a Brinkman porous medium, Int. J. Math. Arch., 3, pp. 399-406, 2012. |
| [12] | Nield, D.A. and Bejan, A.: Convection in porous media. Springer, New-York, 2006. |
| [13] | Lapwood, E.R.: Convection of a fluid in a porous medium, Proc. Camb. Phil. Soc., 44, pp. 508-519, 1948. |
| [14] | Wooding, R.A.: Rayleigh instability of a thermal boundary layer in flow through a porous medium, J. Fluid Mech., 9, pp. 183-192, 1960. |
| [15] | Durlofsky, L. and Brady, J.F.: Analysis of the Brinkman equation as a model for flow in porous media, Phys. Fluids, 30, pp. 3329–3341, 1987. |
| [16] | Pradhan, G.K. and Samal, P.C.: Thermal instability of a fluid layer under variable body forces, J. Math. Anal. Appl., 122, pp. 487-498, 1987. |

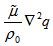 in addition to
in addition to 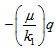 in the equations of motion. Nield and Bejan[12] have studied the problem of convection in a porous medium. Lapwood[13] and Wooding[14] have investigated the stability of convective flow in a porous medium taking into account the Darcy’s resistance. Durlofsky & Brady[15], using a Green’s function, showed that the Brinkman model is valid for particles whose porosity
in the equations of motion. Nield and Bejan[12] have studied the problem of convection in a porous medium. Lapwood[13] and Wooding[14] have investigated the stability of convective flow in a porous medium taking into account the Darcy’s resistance. Durlofsky & Brady[15], using a Green’s function, showed that the Brinkman model is valid for particles whose porosity 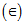 > 0.95.Since the earth’s gravity field varies with the vertical distance from its surface, so it is necessary to take into account the gravity as a variable quantity with height from the earth’s centre. This variation of gravity plays an important role for large scale flows in ocean, atmosphere and mantle but for laboratory purposes, we usually neglect these variations. Thermal instability of a fluid layer under varying gravity field heated from above and below has been investigated by Pradhan and Samal[16]. We have performed a linear stability analysis as a first step towards investigating this problem. Keeping in mind the importance and various applications of non-Newtonian fluids, our main objective, in the present paper, is to study the effects of rotation, magnetic field and suspended particles on thermal instability of a Walters’ (model B') fluid in a Brinkman porous medium in the presence of a variable gravity field. The interest for studying this problem is to control the magneto-hydrodynamic thermal instability under the influences of variable gravity, rotation, suspended particles in a Brinkman porous medium.
> 0.95.Since the earth’s gravity field varies with the vertical distance from its surface, so it is necessary to take into account the gravity as a variable quantity with height from the earth’s centre. This variation of gravity plays an important role for large scale flows in ocean, atmosphere and mantle but for laboratory purposes, we usually neglect these variations. Thermal instability of a fluid layer under varying gravity field heated from above and below has been investigated by Pradhan and Samal[16]. We have performed a linear stability analysis as a first step towards investigating this problem. Keeping in mind the importance and various applications of non-Newtonian fluids, our main objective, in the present paper, is to study the effects of rotation, magnetic field and suspended particles on thermal instability of a Walters’ (model B') fluid in a Brinkman porous medium in the presence of a variable gravity field. The interest for studying this problem is to control the magneto-hydrodynamic thermal instability under the influences of variable gravity, rotation, suspended particles in a Brinkman porous medium.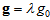 , where
, where 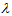 can be positive or negative according as the gravity increases or decreases upward from its value
can be positive or negative according as the gravity increases or decreases upward from its value 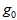 (>0). An adverse temperature gradient
(>0). An adverse temperature gradient 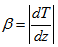 is maintained by underside heating. The pressure p, density
is maintained by underside heating. The pressure p, density 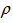 , viscosity
, viscosity 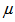 and visco-elasticity
and visco-elasticity 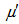 depend upon the vertical co-ordinate z- only. The basic equations of hydromagnetic in unsteady state relevant to the problem are defined as:
depend upon the vertical co-ordinate z- only. The basic equations of hydromagnetic in unsteady state relevant to the problem are defined as: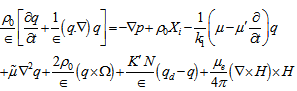
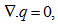
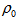 is the fluid density, is porosity,
is the fluid density, is porosity, 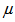 denotes viscosity,
denotes viscosity, 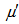 denotes visco-elasticity,
denotes visco-elasticity, 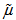 is the effective viscosity of the porous medium,
is the effective viscosity of the porous medium, 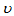 is the kinematic viscosity,
is the kinematic viscosity, 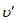 is the kinematic visco-elasticity, p is the pressure,
is the kinematic visco-elasticity, p is the pressure, 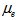 is magnetic permeability,
is magnetic permeability, 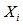 is the external force due to gravity variations,
is the external force due to gravity variations, 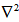 is the three dimensional Laplacian operator,
is the three dimensional Laplacian operator, 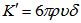 where
where 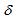 being particle radius, is the Stokes’ drag coefficient,
being particle radius, is the Stokes’ drag coefficient, 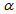 is the co-efficient of volume expansion and q is the velocity of pure fluid. The last term on the right side of equation (1) incorporates the effect of the magnetic field on the fluid motion and also known as Lorentz force. Here
is the co-efficient of volume expansion and q is the velocity of pure fluid. The last term on the right side of equation (1) incorporates the effect of the magnetic field on the fluid motion and also known as Lorentz force. Here 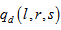 and
and 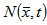 denote the velocity and number density of the particles respectively. The presence of suspended particles adds an extra force term, in equation of motion, proportional to velocity difference between particles and fluid. Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite in sign, in the equations of motion for the particles. The distances between the particles are assumed to be quite large compared with their diameters thereby neglecting the effect of inter-particle reactions. The effects of pressure, magnetic field and gravity on the particles are very small and hence ignored.If mN is the mass of particles per unit volume, then the equations of motion and continuity for the particles are:
denote the velocity and number density of the particles respectively. The presence of suspended particles adds an extra force term, in equation of motion, proportional to velocity difference between particles and fluid. Since the force exerted by the fluid on the particles is equal and opposite to that exerted by the particles on the fluid, there must be an extra force term, equal in magnitude but opposite in sign, in the equations of motion for the particles. The distances between the particles are assumed to be quite large compared with their diameters thereby neglecting the effect of inter-particle reactions. The effects of pressure, magnetic field and gravity on the particles are very small and hence ignored.If mN is the mass of particles per unit volume, then the equations of motion and continuity for the particles are: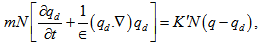
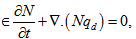
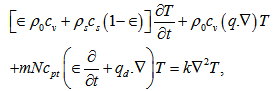
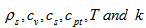 denote, respectively, the density of solid material, specific heat at constant volume, heat capacity of solid material, heat capacity of particles, the temperature and the effective thermal conductivity of the pure fluid.The Maxwell’s electromagnetic equation yields
denote, respectively, the density of solid material, specific heat at constant volume, heat capacity of solid material, heat capacity of particles, the temperature and the effective thermal conductivity of the pure fluid.The Maxwell’s electromagnetic equation yields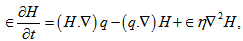
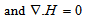
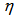 denote the resistivity. The equation of state of the system is
denote the resistivity. The equation of state of the system is 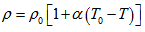
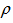 and magnetic field H be denoted by q (u,v,w), qd (l,r,s),
and magnetic field H be denoted by q (u,v,w), qd (l,r,s), 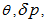
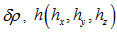 , respectively.After linearizing the system of equations (1) - (8), we have the perturbation equations:
, respectively.After linearizing the system of equations (1) - (8), we have the perturbation equations: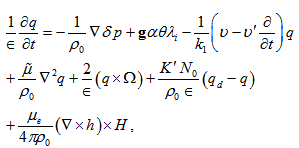
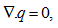
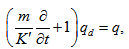
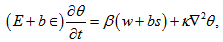
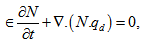
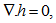
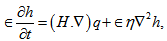
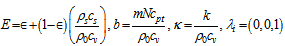 and w, s be the vertical fluid and particles velocity, respectively.In the Cartesian form, equations (9)-(15) can be expressed as
and w, s be the vertical fluid and particles velocity, respectively.In the Cartesian form, equations (9)-(15) can be expressed as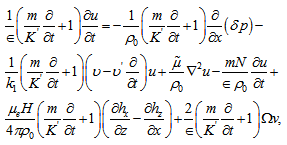
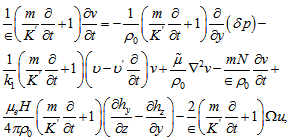
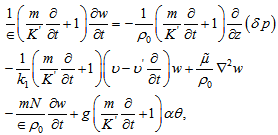
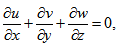
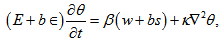
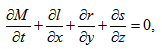
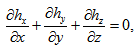
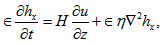
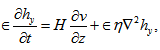
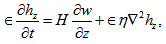
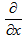 and
and 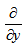 respectively, adding them and using eq. (19), we get:
respectively, adding them and using eq. (19), we get: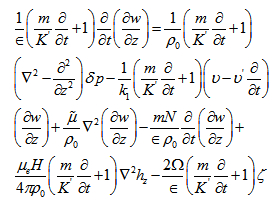
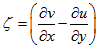 denotes the z-component of the vorticity. Operating equations (18) and (26) by
denotes the z-component of the vorticity. Operating equations (18) and (26) by 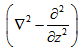 and
and 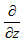 respectively and adding them to eliminate
respectively and adding them to eliminate 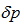 , we get:
, we get: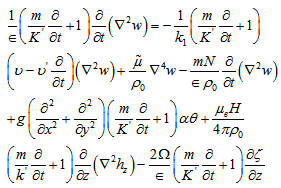
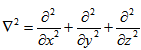 .Now, operating equation (16) and (17) by
.Now, operating equation (16) and (17) by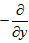 and
and 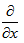 respectively and adding them, we get:
respectively and adding them, we get: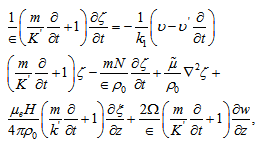
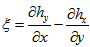 is the z-component of current density.From equation (20), we get
is the z-component of current density.From equation (20), we get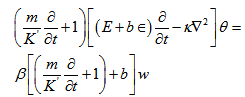
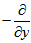 and
and 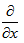 respectively, adding them and using equations (19) & (22), we get
respectively, adding them and using equations (19) & (22), we get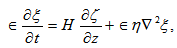
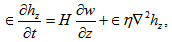
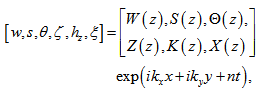
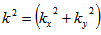 , is the resultant wave number of the disturbance and n is the frequency of the harmonic disturbance, which is, in general, a complex constant.
, is the resultant wave number of the disturbance and n is the frequency of the harmonic disturbance, which is, in general, a complex constant.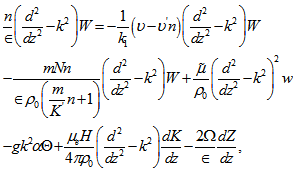
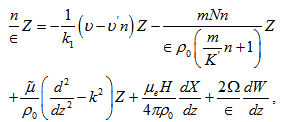
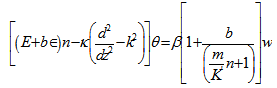
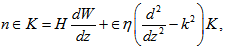
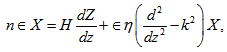
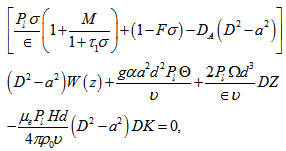
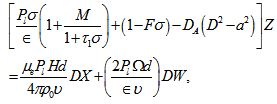
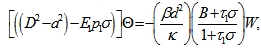
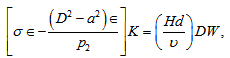
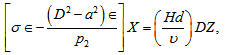
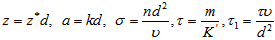 ,
,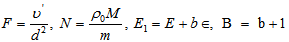
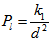 , is the dimensionless medium permeability,
, is the dimensionless medium permeability, 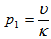 , is the thermal Prandtl number,
, is the thermal Prandtl number, 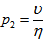 , is the magnetic Prandtl number and
, is the magnetic Prandtl number and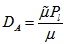 is the Darcy-Brinkman number modified by the viscosity ratio.Eliminating K, Θ, X and Z between equations (38) – (42), we obtain:
is the Darcy-Brinkman number modified by the viscosity ratio.Eliminating K, Θ, X and Z between equations (38) – (42), we obtain: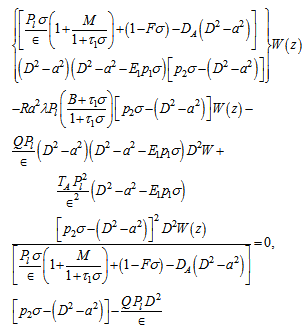
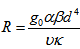 , is the thermal Rayleigh number,
, is the thermal Rayleigh number, 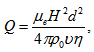 is the Chandrasekhar number and
is the Chandrasekhar number and 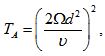 is the Taylor number.For the case of two free boundaries, the boundary conditions appropriate to the problem are defined as:
is the Taylor number.For the case of two free boundaries, the boundary conditions appropriate to the problem are defined as: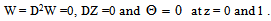
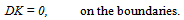
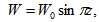
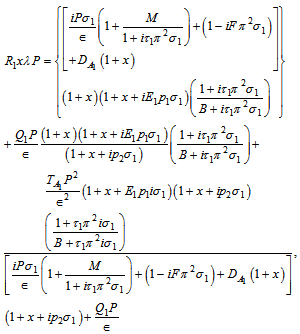
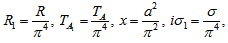
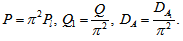 Equation (47) is required dispersion relation accounting the effects of rotation, medium permeability, variable gravity and magnetic field on thermal instability of Walters’ (Model B') elastico-viscous fluid permeated with suspended particles in a Brinkman porous medium.
Equation (47) is required dispersion relation accounting the effects of rotation, medium permeability, variable gravity and magnetic field on thermal instability of Walters’ (Model B') elastico-viscous fluid permeated with suspended particles in a Brinkman porous medium.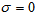 . So, we put
. So, we put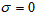 in equation (47) and get:
in equation (47) and get: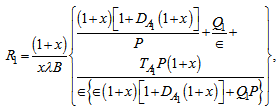
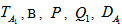 . Hence, it is clear that for stationary convection Walters’ (Model B') elastico-viscous fluid behave like an ordinary Newtonian fluid since elastico-viscous parameter F vanishes with
. Hence, it is clear that for stationary convection Walters’ (Model B') elastico-viscous fluid behave like an ordinary Newtonian fluid since elastico-viscous parameter F vanishes with 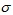 .In the absence of rotation, magnetic field and variable gravity field
.In the absence of rotation, magnetic field and variable gravity field 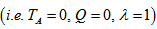 , expression (48) reduces to:
, expression (48) reduces to: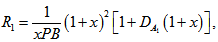
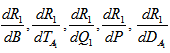 analytically.Equation (48) yields
analytically.Equation (48) yields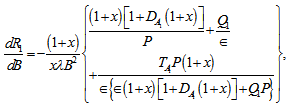
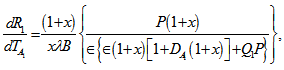
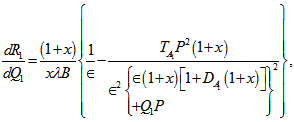
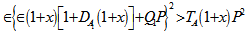 and destabilizes the system if
and destabilizes the system if 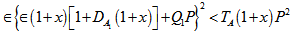 Equation (48) yields
Equation (48) yields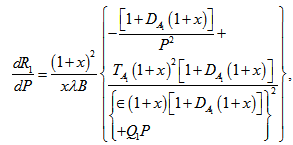
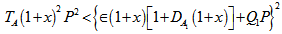 and medium permeability has a stabilizing effect when
and medium permeability has a stabilizing effect when 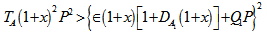 Equation (48) yields
Equation (48) yields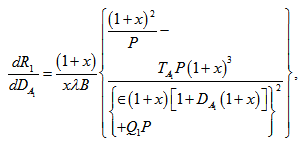
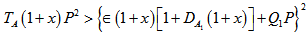 and has a stabilizing effect when
and has a stabilizing effect when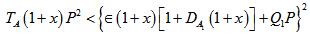
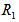 with the increase in suspended particles B. This shows that the effect of suspended particles is to destabilize the system.Figure 2 shows that the critical Rayleigh number
with the increase in suspended particles B. This shows that the effect of suspended particles is to destabilize the system.Figure 2 shows that the critical Rayleigh number 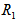 increases with the increase in rotation TA, thereby depicting the stabilizing effects of rotation TA.Figure 3, 4 and 5 shows that the magnetic field, medium permeability and Darcy number have a destabilizing effect for Q=1 to Q=2, P=1 to P=5, DA=1 to DA=3 and stabilizing effect for Q=2.5 to Q=5.5, P=6 to P=10, DA=4 to DA=10 respectively. Therefore, magnetic field, medium permeability and Darcy-Brinkman number have both destabilizing and stabilizing influences on the system.
increases with the increase in rotation TA, thereby depicting the stabilizing effects of rotation TA.Figure 3, 4 and 5 shows that the magnetic field, medium permeability and Darcy number have a destabilizing effect for Q=1 to Q=2, P=1 to P=5, DA=1 to DA=3 and stabilizing effect for Q=2.5 to Q=5.5, P=6 to P=10, DA=4 to DA=10 respectively. Therefore, magnetic field, medium permeability and Darcy-Brinkman number have both destabilizing and stabilizing influences on the system.
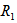 with suspended particles B for fixed values of
with suspended particles B for fixed values of 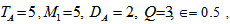
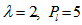 and
and 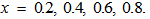

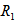 with rotation
with rotation 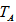 for fixed values of
for fixed values of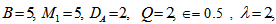
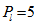 and
and 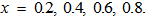

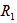 with magnetic field
with magnetic field 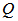 for fixed values of
for fixed values of 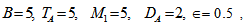
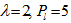 and
and 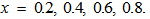

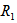 with medium permeability for fixed values of
with medium permeability for fixed values of 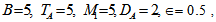
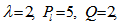 and
and 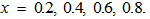

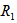 with Darcy –Brinkman number
with Darcy –Brinkman number 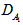 for fixed values of
for fixed values of 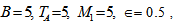
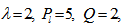 and
and 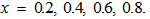
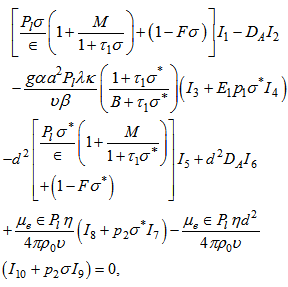
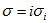 in equation (55), where
in equation (55), where 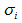 is real and equating the imaginary parts, we obtain
is real and equating the imaginary parts, we obtain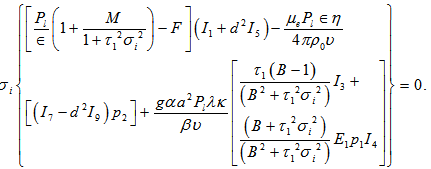
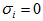 or
or 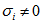 which mean that modes may be non oscillatory or oscillatory. The oscillatory modes introduced due to presence of rotation, magnetic field, suspended particles, visco-elasticity and medium permeability.
which mean that modes may be non oscillatory or oscillatory. The oscillatory modes introduced due to presence of rotation, magnetic field, suspended particles, visco-elasticity and medium permeability. are examined analytically and it has been found that the effect of suspended particles is to destabilize the system as gravity increases upward from its value
are examined analytically and it has been found that the effect of suspended particles is to destabilize the system as gravity increases upward from its value 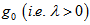 whereas the effect of rotation is to stabilize the system.(c). The magnetic field has both stabilizing and destabilizing effects on the system under the conditions
whereas the effect of rotation is to stabilize the system.(c). The magnetic field has both stabilizing and destabilizing effects on the system under the conditions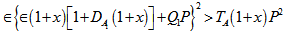 and
and 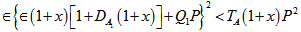 respectively.(d). The medium permeability has both stabilizing and destabilizing effects on the system under the conditions
respectively.(d). The medium permeability has both stabilizing and destabilizing effects on the system under the conditions 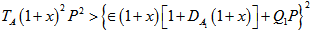 and
and 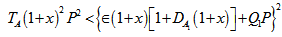 respectively.(e). The Darcy-Brinkman number has both stabilizing and destabilizing effects on the system under the conditions
respectively.(e). The Darcy-Brinkman number has both stabilizing and destabilizing effects on the system under the conditions 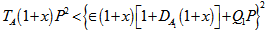 and
and 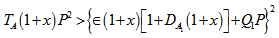 respectively.(f). The effects of suspended particles, rotation, magnetic field and medium permeability and Darcy-Brinkman number on thermal instability of Walters’ (model B’) fluids in a Brinkman porous medium have also been shown graphically in fig. 1, 2, 3, 4, and 5.
respectively.(f). The effects of suspended particles, rotation, magnetic field and medium permeability and Darcy-Brinkman number on thermal instability of Walters’ (model B’) fluids in a Brinkman porous medium have also been shown graphically in fig. 1, 2, 3, 4, and 5. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML