-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2013; 3(2): 20-30
doi:10.5923/j.ajfd.20130302.02
Non-Newtonian Natural Convection Flow along an Isothermal Horizontal Circular Cylinder Using Modified Power-law Model
Sidhartha Bhowmick1, Md. Mamun Molla2, Suvash C. Saha3
1Department of Mathematics, Jagannath University, Dhaka, Bangladesh
2Department of Electrical Engineering and Computer Science, North South University, Dhaka, 1229, Bangladesh
3Institute of Future Environments, School of Chemistry, Physics and Mechanical Engineering, Queensland University of Technology, GPO Box 2434, Brisbane, QLD 4001, Australia
Correspondence to: Suvash C. Saha, Institute of Future Environments, School of Chemistry, Physics and Mechanical Engineering, Queensland University of Technology, GPO Box 2434, Brisbane, QLD 4001, Australia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Laminar two-dimensional natural convection boundary-layer flow of non-Newtonian fluids along an isothermal horizontal circular cylinder has been studied using a modified power-law viscosity model. In this model, there are no unrealistic limits of zero or infinite viscosity. Therefore, the boundary-layer equations can be solved numerically by using marching order implicit finite difference method with double sweep technique. Numerical results are presented for the case of shear-thinning as well as shear thickening fluids in terms of the fluid velocity and temperature distributions, shear stresses and rate of heat transfer in terms of the local skin-friction and local Nusselt number respectively.
Keywords: Non-Newtonian, Power-law, Shear-thinning, Shear-thickening, Finite Difference
Cite this paper: Sidhartha Bhowmick, Md. Mamun Molla, Suvash C. Saha, Non-Newtonian Natural Convection Flow along an Isothermal Horizontal Circular Cylinder Using Modified Power-law Model, American Journal of Fluid Dynamics, Vol. 3 No. 2, 2013, pp. 20-30. doi: 10.5923/j.ajfd.20130302.02.
Article Outline
1. Introduction
- Natural convection laminar flow of non-Newtonian power-law fluids from an isothermal horizontal circular cylinder plays an important role in numerous engineering applications those are related with pseudo-plastic fluids. The pseudo-plastic fluid is characterized by a constant viscosity at very low shear rates, a viscosity, which decreases with shear rate, at intermediate shear rates and an apparently constant viscosity at very high shear rates. The interest in heat transfer problems involving power-law non-Newtonian fluids has grown in the past half century. An excellent research on non-Newtonian fluids was performed by Boger[1]. Acrivos[2] was the first who considered boundary-layer flows for such non-Newtonian fluids. Since then, a large number of papers have been published, due to their wide relevance in pseudo-plastic fluids like chemicals, foods, polymers, molten plastics and petroleum production and various natural phenomena.It should be noted that a complete survey of these literatures was impractical; however, selected papers are listed here to provide starting points for a broader literature search [3-15]. In the boundary-layer study, the previous researchers used the traditional power-law viscosity correlation that viscosity becomes infinite for small shear rates or vanishes for the limits of large shear rates, which are giving the unrealistic physical results. Because an infinite viscosity corresponds to solids and no frictionless fluid has ever been found, a partial set of measured viscosity shear relations are not sufficient for a boundary-layer study.The recently proposed modified power-law correlation is sketched for various values of power index n, which has been shown in Fig. 2. The present model is formulated based on the available experimental data for the non-Newtonian fluids (see Boger[1]). It is clear that the new correlation does not contain the physically unrealistic limits of zero and infinite viscosity displayed by traditional power-law correlations[2]. The modified power-law, in fact, fits measured viscosity data well. The constants in the proposed model can be fixed with available measurements and are described in detail in Yao and Molla[16]. The boundary-layer formulation on a flat plate is described and numerically solved for non-Newtonian fluid in Yao and Molla[16, 17] and the associated heat transfer for two different heating conditions is reported in Molla and Yao[18, 19] for shear-thinning fluid. In this investigation, the behavior of both shear-thinning and shear-thickening fluids on the natural convection laminar flow from a uniformly heated horizontal circular cylinder are studied by choosing the power-law index as n (=0.6, 0.8, 1.0, 1.2, 1.4) to fully demonstrate the performance of various non-Newtonian fluids.
2. Formulation of the Problem
- A steady two-dimensional laminar natural convection boundary-layer of a non-Newtonian fluid over an isothermal horizontal circular cylinder of radius ‘a’ with uniform surface temperature and a distributed heat source of the form
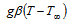 has been considered. The viscosity depends on shear rate and is correlated by a modified power-law. We consider shear-thinning and shear-thickening situations of non-Newtonian fluids. It is assumed that the surface temperature of the cylinder is
has been considered. The viscosity depends on shear rate and is correlated by a modified power-law. We consider shear-thinning and shear-thickening situations of non-Newtonian fluids. It is assumed that the surface temperature of the cylinder is 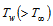 , where,
, where, 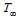 is the ambient temperature of the fluid and T is the temperature of the fluid. The configuration considered is as shown in Fig. 1.Under the above assumptions, the boundary-layer equations governing the flow and heat transfer are
is the ambient temperature of the fluid and T is the temperature of the fluid. The configuration considered is as shown in Fig. 1.Under the above assumptions, the boundary-layer equations governing the flow and heat transfer are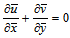 | (1) |
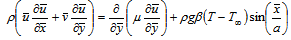 | (2) |
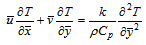 | (3) |
 and
and  are velocity components along the
are velocity components along the 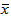 and
and 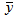 axes,
axes, 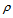 is the fluid density,
is the fluid density, 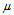 is the dynamic viscosity of the fluid in the boundary-layer region, g is the acceleration due to gravity,
is the dynamic viscosity of the fluid in the boundary-layer region, g is the acceleration due to gravity, 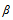 is the coefficient of thermal expansion, k is the thermal conductivity and Cp is the specific heat at constant pressure. The kinematic viscosity
is the coefficient of thermal expansion, k is the thermal conductivity and Cp is the specific heat at constant pressure. The kinematic viscosity 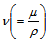 is correlated by a modified power-law, which is
is correlated by a modified power-law, which is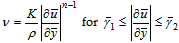 | (4) |
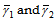 are threshold shear rates, which are given according to the model of Boger[1], K is the dimensional constant, for which dimension depends on the power-law index n. The values of these constants can be determined by matching with measurements. Outside of the preceding range, viscosity is assumed to be constant; its value can be fixed with data given in Fig. 2.The boundary conditions for the present problems are
are threshold shear rates, which are given according to the model of Boger[1], K is the dimensional constant, for which dimension depends on the power-law index n. The values of these constants can be determined by matching with measurements. Outside of the preceding range, viscosity is assumed to be constant; its value can be fixed with data given in Fig. 2.The boundary conditions for the present problems are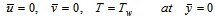 | (5a) |
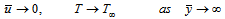 | (5b) |
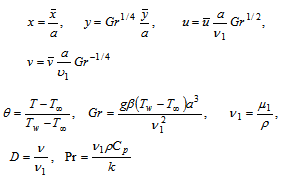 | (6) |
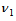 is the reference viscosity at
is the reference viscosity at 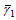 ,
, 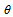 is the non-dimensional temperature of the fluid, Gr is the Grashof number and Pr is the Prandtl number. Using equation (6) in equations (1-4) we get the following non-dimensional equations:
is the non-dimensional temperature of the fluid, Gr is the Grashof number and Pr is the Prandtl number. Using equation (6) in equations (1-4) we get the following non-dimensional equations: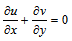 | (7) |
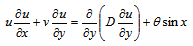 | (8) |
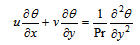 | (9) |
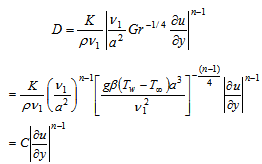 | (10) |
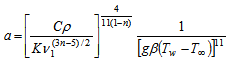 | (11) |
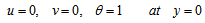 | (12a) |
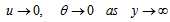 | (12b) |
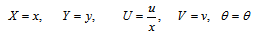 | (13) |
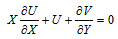 | (14) |
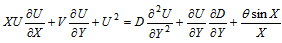 | (15) |
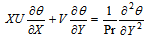 | (16) |
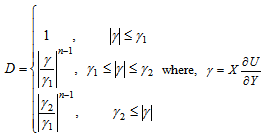 | (17) |
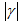 lies between the threshold shear rates
lies between the threshold shear rates 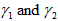 , then the non-Newtonian viscosity, D, varies with the power-law of γ. On the other hand, if the shear rate
, then the non-Newtonian viscosity, D, varies with the power-law of γ. On the other hand, if the shear rate 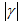 does not lie within this range, then the non-Newtonian viscosities are different constants, as shown in Fig. 2. This is a property of many measured viscosities.Equation (14-16) can be solved by marching downstream with the leading edge condition satisfying the following differential equations, which are the limits of equations (14-16) as X→0.
does not lie within this range, then the non-Newtonian viscosities are different constants, as shown in Fig. 2. This is a property of many measured viscosities.Equation (14-16) can be solved by marching downstream with the leading edge condition satisfying the following differential equations, which are the limits of equations (14-16) as X→0.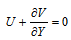 | (18) |
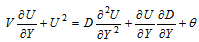 | (19) |
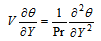 | (20) |
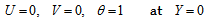 | (21a) |
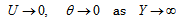 | (22b) |
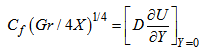 | (23) |
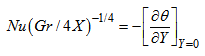 | (24) |
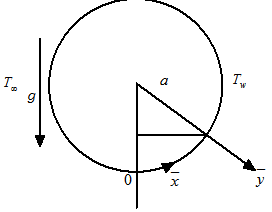 | Figure 1. The flow model and coordinate system |
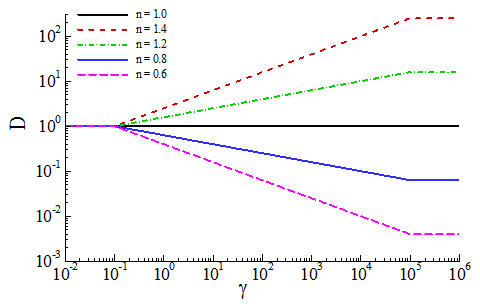 | Figure 2. Modified power-law correlation for the power-law index n (=0.6, 0.8, 1.0, 1.2, 1.4) while 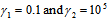 |
3. Results and Discussion
- The numerical results are presented for the non-Newtonian power-law of shear-thinning fluids ( n = 0.6 and 0.8) and the shear-thickening fluids (n = 1.2 and 1.4) as well as the Newtonian case (n = 1) while the Prandtl number, Pr = 10 and 50. Based on the experimental data of Boger[1] the thresholds shears
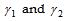 have been chosen as 0.1 and 105, respectively. The obtained results include the viscosity, velocity and temperature distribution, velocity gradient and the wall shear stress in terms of the local skin-friction coefficient,
have been chosen as 0.1 and 105, respectively. The obtained results include the viscosity, velocity and temperature distribution, velocity gradient and the wall shear stress in terms of the local skin-friction coefficient, 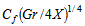 and the rate of heat transfer as a form of the local Nusselt number,
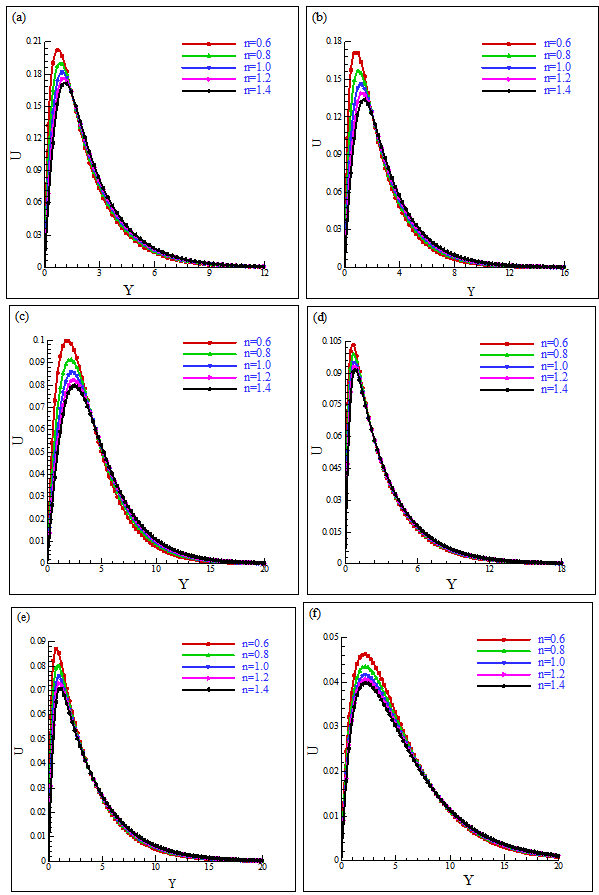
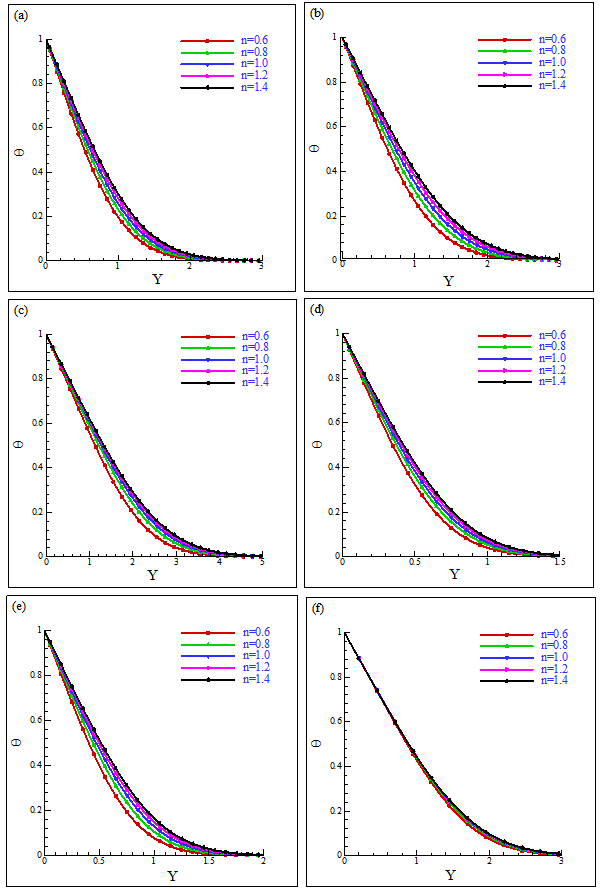
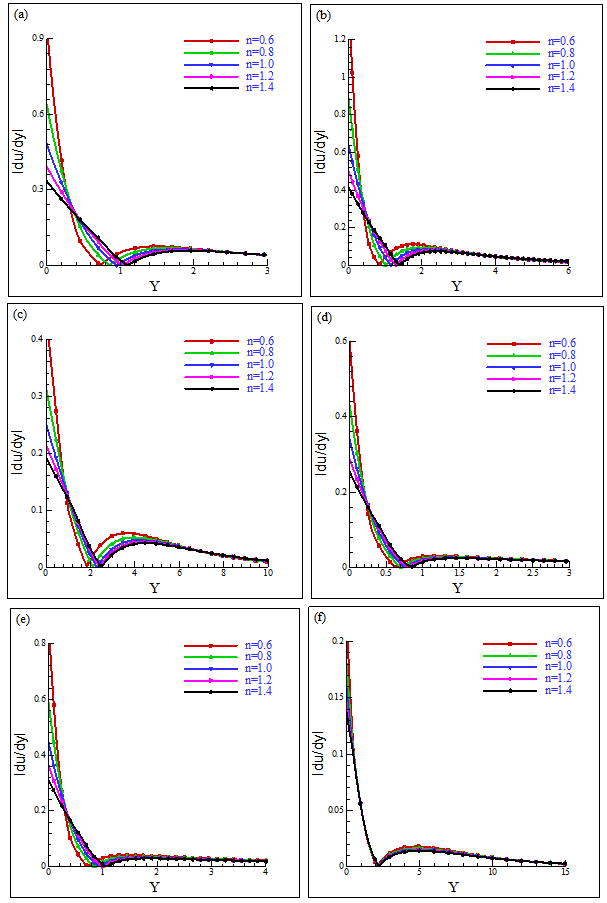
and the rate of heat transfer as a form of the local Nusselt number, 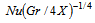 for the wide range of the power-law index n (=0.6, 0.8, 1.0, 1.2, 1.4).Figs. 3a and 3b show the viscosity distribution, D as a function of Y at selected X (=1, 2, 3) locations for Pr =10 and 50, respectively and n = 0.6. From Fig.3a, it is found for Pr =10 that there is one region of variable viscosity at X =1 and 3, but there are two such regions at X =2; the primary region lies from Y ≈0.0 to 1.1 and the secondary variable viscosity region lies between Y ≈1.37 to 2.19. On the other hand, only one variable viscosity region was found in the case of Pr =50 in Fig. 3b. Again, Figs. 4(a)-(f) show the viscosity distribution, D as a function of Y at X = 1, 2, 3 respectively with n = 0.6, 0.8, 1.0, 1.2, 1.4 for Pr = 10 and 50. It is clearly seen in Fig. 4c that there are two viscosity distribution regions for n=0.6 at X =2 of Pr =10; all other viscosity distributions are in one region.The velocity distribution as a function of Y at the selected locations (X =1, 2, 3) for the different power-law indices (n = 0.6, 0.8, 1.0, 1.2, 1.4) are presented in Figs. 5(a-c) for Pr =10 and 5(d-f) for Pr =50, respectively. Fig. 5 shows that for shear-thinning fluids (n=0.6 and 0.8), the velocity increases due to the decrease of viscosities at the downstream region; consequently, the boundary–layer is thinned. On the other hand, for shear-thickening fluids (n = 1.2 and 1.4), the velocity decreases slowly and the boundary-layer is thickened as the fluid becomes more viscous. We may conclude that for Pr =50, the fluid velocity is smaller than that for Pr =10 and the boundary-layer thickness is larger for Pr =50 than that for Pr =10.The corresponding temperature distribution are plotted for Pr =10 and 50 in Figs. 6(a-c) and 6(d-f), respectively. For both of these Prandtl numbers, at the downstream region, in the case of shear-thinning fluids, the variation of temperature in the boundary-layer is smaller than that of the shear-thickening non-Newtonian fluids. As expected, the thermal boundary-layer is thinner for larger Prandtl numbers.Figures 7(a-c) and 7(d-f) show the corresponding velocity gradient for Pr =10 and 50, respectively. For the shear-thinning fluids (n=0.6 and 0.8), the boundary-layer thickness decreases more at the downstream region than for the shear-thickening fluids (n = 1.2 and 1.4). The boundary-layer thickness for Pr =50 is almost half of the boundary-layer for Pr =10.
for the wide range of the power-law index n (=0.6, 0.8, 1.0, 1.2, 1.4).Figs. 3a and 3b show the viscosity distribution, D as a function of Y at selected X (=1, 2, 3) locations for Pr =10 and 50, respectively and n = 0.6. From Fig.3a, it is found for Pr =10 that there is one region of variable viscosity at X =1 and 3, but there are two such regions at X =2; the primary region lies from Y ≈0.0 to 1.1 and the secondary variable viscosity region lies between Y ≈1.37 to 2.19. On the other hand, only one variable viscosity region was found in the case of Pr =50 in Fig. 3b. Again, Figs. 4(a)-(f) show the viscosity distribution, D as a function of Y at X = 1, 2, 3 respectively with n = 0.6, 0.8, 1.0, 1.2, 1.4 for Pr = 10 and 50. It is clearly seen in Fig. 4c that there are two viscosity distribution regions for n=0.6 at X =2 of Pr =10; all other viscosity distributions are in one region.The velocity distribution as a function of Y at the selected locations (X =1, 2, 3) for the different power-law indices (n = 0.6, 0.8, 1.0, 1.2, 1.4) are presented in Figs. 5(a-c) for Pr =10 and 5(d-f) for Pr =50, respectively. Fig. 5 shows that for shear-thinning fluids (n=0.6 and 0.8), the velocity increases due to the decrease of viscosities at the downstream region; consequently, the boundary–layer is thinned. On the other hand, for shear-thickening fluids (n = 1.2 and 1.4), the velocity decreases slowly and the boundary-layer is thickened as the fluid becomes more viscous. We may conclude that for Pr =50, the fluid velocity is smaller than that for Pr =10 and the boundary-layer thickness is larger for Pr =50 than that for Pr =10.The corresponding temperature distribution are plotted for Pr =10 and 50 in Figs. 6(a-c) and 6(d-f), respectively. For both of these Prandtl numbers, at the downstream region, in the case of shear-thinning fluids, the variation of temperature in the boundary-layer is smaller than that of the shear-thickening non-Newtonian fluids. As expected, the thermal boundary-layer is thinner for larger Prandtl numbers.Figures 7(a-c) and 7(d-f) show the corresponding velocity gradient for Pr =10 and 50, respectively. For the shear-thinning fluids (n=0.6 and 0.8), the boundary-layer thickness decreases more at the downstream region than for the shear-thickening fluids (n = 1.2 and 1.4). The boundary-layer thickness for Pr =50 is almost half of the boundary-layer for Pr =10.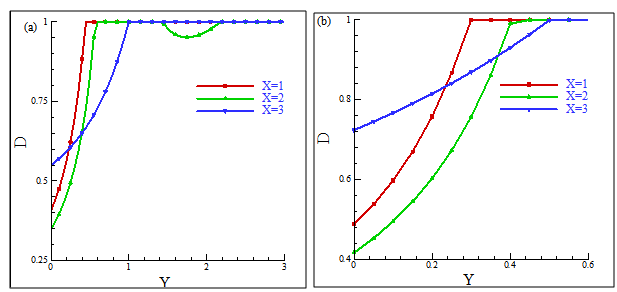 | Figure 3. Viscosity distribution for different values of X at n = 0.6 for (a) Pr = 10, (b) Pr = 50 |
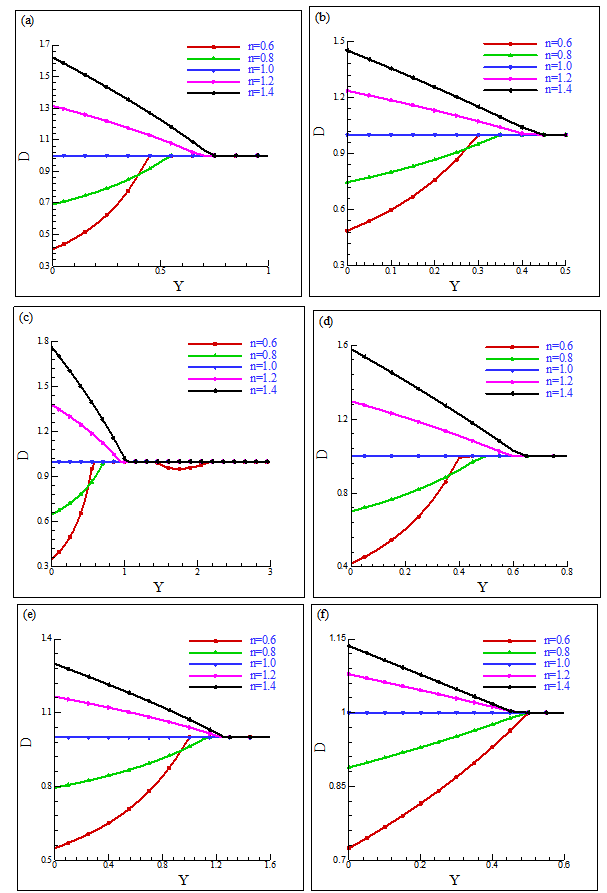 | Figure 4. Viscosity distribution for different n at (a) X = 1, Pr = 10, (b) X = 1, Pr = 50, (c) X = 2, Pr = 10, (d) X = 2, Pr = 50, (e) X = 3, Pr = 10, (f) X = 3, Pr = 50 |
 | Figure 5. Velocity distribution for different n at (a) X = 1, (b) X = 2, (c) X = 3; Pr = 10 and (d) X = 1, (e) X = 2, (f) X = 3; Pr = 50 |
 | Figure 6. Temperature distribution for different n at (a) X = 1, (b) X = 2, (c) X = 3; Pr = 10 and (d) X = 1, (e) X = 2, (f) X = 3; Pr = 50 |
 | Figure 7. Velocity gradient for different n at (a) X = 1, (b) X = 2, (c) X = 3; Pr = 10 and (d) X = 1, (e) X = 2, (f) X = 3; Pr = 50 |
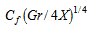 are shown in Fig. 8a for Pr =10 and in Fig. 8b for Pr =50. The results from these figures clearly show that at the leading edge of non-Newtonian fluids, whose effects start from
are shown in Fig. 8a for Pr =10 and in Fig. 8b for Pr =50. The results from these figures clearly show that at the leading edge of non-Newtonian fluids, whose effects start from 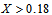 for Pr =10 and
for Pr =10 and 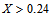 for Pr =50, the wall shear stress decreases for the shear-thinning fluids (n=0.6 and 0.8) and increases for the shear-thickening fluids (n=1.2 and 1.4). At the downstream region, there is a similarity solution at
for Pr =50, the wall shear stress decreases for the shear-thinning fluids (n=0.6 and 0.8) and increases for the shear-thickening fluids (n=1.2 and 1.4). At the downstream region, there is a similarity solution at 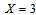 and at
and at 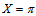 , the boundary-layer of shear-thinning fluids is greater than that of shear-thickening fluids. As expected, the boundary-layer is thinner for larger Prandtl number. Figs. 9(a) and 9(b) represent the local-rate of heat transfer in terms of the local Nusselt number
, the boundary-layer of shear-thinning fluids is greater than that of shear-thickening fluids. As expected, the boundary-layer is thinner for larger Prandtl number. Figs. 9(a) and 9(b) represent the local-rate of heat transfer in terms of the local Nusselt number 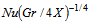 for Pr =10 and Pr =50, respectively. The local Nusselt number increases for n < 1 and decreases for n > 1 at the leading edge of non-Newtonian fluids, whose effects start from
for Pr =10 and Pr =50, respectively. The local Nusselt number increases for n < 1 and decreases for n > 1 at the leading edge of non-Newtonian fluids, whose effects start from 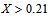 for Pr =10 and
for Pr =10 and 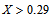 for Pr =50. At the downstream region, heat transfer is similar at
for Pr =50. At the downstream region, heat transfer is similar at 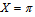 .
.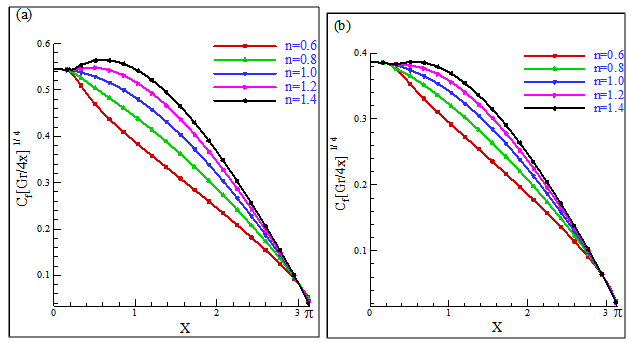 | Figure 8. Wall shear stress for different values of n: (a) Pr =10, (b) Pr = 50 |
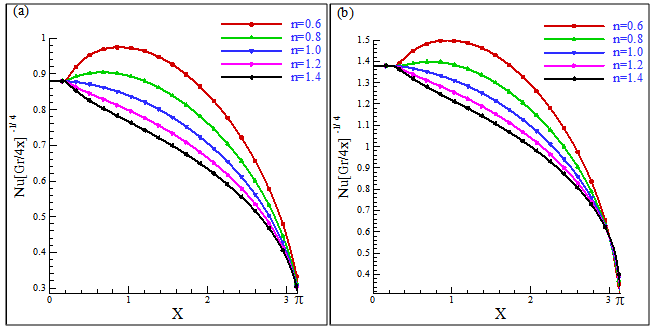 | Figure 9. Local Nusselt number for different values of n: (a) Pr =10, (b) Pr = 50 |
4. Conclusions
- This study deals with the laminar two-dimensional natural convection boundary-layer flow of non-Newtonian fluids along an isothermal horizontal circular cylinder using a modified power-law viscosity model. The proposed modified power-law correlation agrees well with the actual measurements for non-Newtonian fluids; consequently, it is a physically realistic model. The problem associated with the non-removal singularity introduced by the traditional power-law correlations do not exists for the modified power-law correlation proposed in this paper. Therefore, we may conclude from the above numerical simulations that the proposed modified power-law correlations can be used to investigate other heat transfer related problems for shear-thinning or shear-thickening non-Newtonian fluids in boundary-layers. It is revealed that the effect of non-Newtonian fluids eventually becomes dominant when shear rate increases within the threshold shear limits. We may summarise our results from above simulations as follows: ●It is seen from the numerical simulations that the velocity increases due to the decrease of viscosities at the downstream region for shear-thinning fluids. However, the velocity decreases slowly as the fluid becomes more viscous for the case of shear-thickening fluids.●At the downstream region of the boundary layer, the variation of the temperature inside the boundary-layer is smaller for the case of shear-thinning fluids than that of the shear-thickening non-Newtonian fluids for all Prandtl numbers considered here.●The boundary-layer thickness decreases more at the downstream region for the shear-thinning fluids than that for the shear-thickening fluids. It is revealed that the boundary-layer thickness for Pr =50 is almost half of the boundary-layer for Pr =10.●It is observed that the local Nusselt number increases when n < 1 and decreases when n > 1at the leading edge of non-Newtonian fluids for both Prandtl number considered here.
Nomenclature

 Greek symbols
Greek symbols
ACKNOWLEDGEMENTS
- The second author wishes to thank Professor L. S. Yao, Arizona State University, USA, for the idea of the modified power-law viscosity model.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML