-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2013; 3(2): 9-19
doi:10.5923/j.ajfd.20130302.01
On Simulation of Backward Facing Step Flow Using Immersed Boundary Method
C. A. Saleel, A. Shaija, S. Jayaraj
Department of Mechanical Engineering, National Institute of Technology, Calicut, 673 601 India
Correspondence to: C. A. Saleel, Department of Mechanical Engineering, National Institute of Technology, Calicut, 673 601 India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Treatment of complex geometries with fluid-solid interaction has been one of the challenging issues in CFD because most engineering problems have complex geometries with fluid-solid interaction for the purpose. The unstructured grid method and the immersed boundary method (IBM) are two different approaches that have been developed so far. This paper details the numerical investigation of 2D laminar flow over a backward facing step in hydro-dynamically developing regions (entrance region) as well in the hydro-dynamically developed regions using IBM. Although this flow represents one of the simplest expansion flows, the physics involved are rather complex. For a flow in to an expansion in the form of a step, the boundary layer separates at the step corner, forming a new free shear layer. The present numerical method is based on a finite volume approach on a staggered grid together with a fractional step approach. The momentum forcing and mass source terms are applied on the step to satisfy the no-slip boundary condition and also to satisfy the continuity for the mesh containing the same. The numerically obtained velocity profiles, and stream line plots in the channel with backward facing step shows excellent agreement with the published results in various literatures.
Keywords: Immersed Boundary Method, Backward Facing Step Flow, Forcing Functions etc
Cite this paper: C. A. Saleel, A. Shaija, S. Jayaraj, On Simulation of Backward Facing Step Flow Using Immersed Boundary Method, American Journal of Fluid Dynamics, Vol. 3 No. 2, 2013, pp. 9-19. doi: 10.5923/j.ajfd.20130302.01.
Article Outline
1. Introduction
- Computer simulations are becoming a primary drive for the design and analysis of complex systems. The advancement of computing urges engineers to include high fidelity computational fluid dynamics (CFD) in the design and testing tools of new technological products and processes. Computational simulations are now recognized to be a part of the computer-aided engineering (CAE) spectrum of tools used extensively today in all industries, and its approach to modeling fluid flow phenomena allows equipment designers and technical analysts to have the power of a virtual wind tunnel on their desktop computer. Computational simulation software has evolved far beyond what Navier, Stokes or Da Vinci could ever have imagined. It has become an indispensable part of the aerodynamic and hydrodynamic design process for planes, trains, automobiles, rockets, ships, submarines, micro-electromechanical systems (MEMS), Lab-on-Chip (LOC) devices and so on; and indeed any moving craft or manufacturing process that mankind has devised so far. The advantage of numerical simulation with respect to experimentation is well-known. Despite with these developments some primary issues of fluid dynamic simulations are like accuracy, computational efficiency and ability to handle complex geometries are predominant. A brief and concise literature survey on immersed boundary method, backward-facing step flows and the channel flows with obstructions are presented here. The governing equations and their numerical solution methods, including the boundary conditions employed are briefed in the next Section. The results and discussion are provided separately after that.
1.1. Immersed Boundary Method (IBM)
- Fluids flows in complex geometries are very common in engineering problems, and the major difficulty arise in how to represent the body, its moving walls and its interaction with the fluid. The most usual approach is using Neumann and Dirichlet boundary conditions to represent the body geometry. Therefore, if the geometry is complex ones have a hard and, probably, a difficult work. This difficulty grows up if the body has a poignant and deformable geometry. In short, treating the coupling of the structure deformations and the fluid flow poses a number of challenging problems for numerical simulations. Both the unstructured grid method and IBM are used for simulating flow with complex geometries. In most industrial applications, geometrical complexity is combined with moving boundaries and high Reynolds numbers which considerably increase the computational difficulties since they require, respectively, regeneration or deformation of the grid and turbulence modeling. As a result, engineering flow simulations have large computational overhead and low accuracy owing to a large number of operations per node and high storage requirements in combination with low-order dissipative spatial discretization. Given the finite memory and speed of computers, these simulations are very expensive and time consuming, with discretizations that are generally limited to a particular maximum number of nodes.In addition to the above mentioned two methods, some authors have proposed different methods to treat this kind of problem. For example Harlow and Welch[1] proposed the marker and cell (MAC) approach. In this method the fluid region on one side of the boundary is identified by markers, while on the other side of the boundary, which can be fluid or solid, is identified by another marker. It requires huge storage space and CPU time.In view of these difficulties it is clear that an alternative numerical procedure that can cope with the flow complexity but at the same time retain the accuracy and high efficiency of the simulations performed on fixed regular grids would represent a significant advance in the study of industrial flows. One possibility for the solution of this problem is the immersed boundary method (IBM).The term “immersed boundary method” was first appeared in literature in reference to a method developed by Peskin[2] in the year 1972. A force term added to the Navier-Stokes equation is in charge to promote the interaction between fluid-solid interactions. Varieties of ideas have been proposed to calculate this force term leads to different immersed boundary techniques. Originally this method was used to simulate cardiac mechanics and associated blood flow. The distinguished feature of this method was that, the entire simulation was carried out on a Cartesian grid, which did not conform to the geometry of the heart. Hence, a novel procedure was simulated for imposing the effect of the immersed boundary (IB) on the flow. That is, imposing the boundary conditions is not straight forward in IBM. Since Peskin introduced this method, numerous modifications and refinements have been proposed and a number of variants of this approach now exist. The main advantages of the Immersed Boundary Method include computer memory and CPU time savings. Also easy grid generation is possible with IBM compared to the unstructured grid method. Even moving boundary problems can be handled using IBM without regenerating grids in time, unlike the structured grid method. It is to be noted that generating body conformal structured or unstructured grid is usually very cumbersome. Imposition of boundary conditions on the IB is the key factor in developing an IB algorithm and distinguishes one IB method from another. In the former approach, which is termed as “continuous forcing approach”, the forcing function is incorporated into the continuous equations before discretization, where as in the latter approach, which can be termed the “discrete forcing approach”, the forcing function is introduced after the equations are discretized. An attractive feature of the continuous forcing approach is that it is formulated independent of the underlying spatial discretization. On the other hand, the discrete forcing approach very much depends on the discretization method. However, this allows direct control over the numerical accuracy, stability, and discrete conservation properties of the solver. The merits of continuous forcing approach are its attractiveness for problems with elastic boundaries, closeness to the physics of the problem; hence relatively easy to conjure up the realistic flow problems especially high feasibility for successful simulation of biological and multiphase flows. The demerits of the aforementioned method include development of “stiff” numerical systems due to the presence of rigid Immersed Boundary in flow problems. Here satisfactory results have only been attained for low Reynolds number flows with moderate unsteadiness. Smoothing of the forcing function prohibits the sharp representation of the IB, which is not acceptable at high Reynolds numbers. The method also necessitates the computation in substantial amount of grid points located inside the body which simply results in unnecessary extra computation time.The merits of discrete forcing approach include (i) Suitability for flows around rigid bodies, (ii) Handling of higher Reynolds number flows,(iii) Absence of stiffness or user defined parameters that can impact the stability of the method, (iv) The ability to represent sharp IB by imposing the boundary conditions directly on the numerical scheme and (v) Computation of flow variables inside a rigid body becomes unnecessary. Where as its demerits are need for a pressure boundary condition on the IB and moving boundaries are harder to deal with than in continuous forcing IBMs. A review about Immersed Boundary Methods (IBM) encompassing all variants is cited by Mittal and Iaccarino[3]. Feedback forcing method is applied to represent a solid body by Goldstein et al.[4] which induced spurious oscillations and restricted the computational time step associated with numerical stability.Yusof[5] proposed a different approach to evaluate the momentum forcing function in a spectral method, and his method does not require a smaller computational time step, which is an important benefit of this method over preceding methods. The Discrete Immersed Boundary Finite Volume Method[6] used to simulate the present problem (i.e., to simulate the channel flows with obstructions) is based on a finite volume approach on a staggered mesh together with a fractional step method. The obstruction is treated as an Immersed Boundary. Both momentum forcing and mass source are applied on the body surface or inside the body to suit the no-slip boundary condition on the immersed boundary and also to satisfy the continuity for the cell containing the immersed boundary. In the IBM, the choice of an accurate interpolation scheme satisfying the no-slip condition on the IB is important.The main advantages of the Immersed Boundary Method (IBM) include memory and CPU time savings. Also easy grid generation is possible with IBM compared to the unstructured grid method. Even moving boundary problems can be handled using IBM without regenerating grids in time, unlike the structured grid method.
1.2. Backward Facing Step Flows
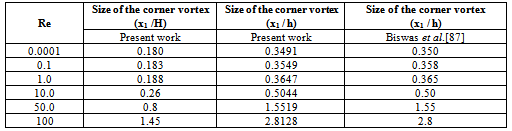
- The study of backward-facing step flows constitutes an important branch of fundamental fluid mechanics. Flow geometry of the same is very significant for investigating separated flows. This flow is of particular interest because it facilitates the study of the reattachment process by minimizing the effect of the separation process, while for other separating and reattaching flow geometries there may be a stronger interaction between the two. The principal flow features of the backward facing step flow are illustrated in Figure 1[7].
 | Figure 1. Detailed flow features of the backward facing step flow |
2. Computational Methodology
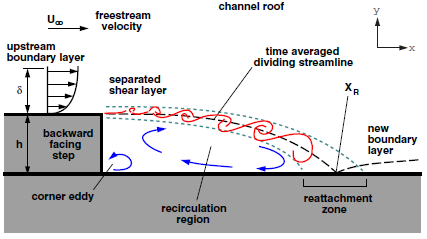
- To explain the concept of immersed boundary method, consider the simulation of flow past a solid body shown in Figure 2.
 | Figure 2. Schematic showing a generic body past which flow is to be simulated |
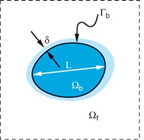
 | Figure 3. Schematic of body immersed in a Cartesian grid on which the governing equations are discretized |
2.1. Governing Equations
- The general governing equations for unsteady, incompressible, viscous flow between parallel plates are written as
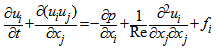 | (1) |
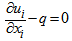 | (2) |
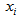 are the Cartesian coordinates,
are the Cartesian coordinates, 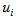 are the corresponding velocity components, p is the pressure,
are the corresponding velocity components, p is the pressure, 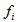 are the momentum forcing components defined at the cell faces on the immersed boundary or inside the body, and q is the mass source/sink defined at the cell center on the immersed boundary or inside the body. All the variables are non-dimensionalized by the bulk average velocity of the inlet flow, Ub and the length scales are non-dimensionalised by the channel height at the downstream, H. The only dimensionless number appearing in the governing equations is the Reynolds number. For the flow problem considered, the following definition is used for the Reynolds number, Re.
are the momentum forcing components defined at the cell faces on the immersed boundary or inside the body, and q is the mass source/sink defined at the cell center on the immersed boundary or inside the body. All the variables are non-dimensionalized by the bulk average velocity of the inlet flow, Ub and the length scales are non-dimensionalised by the channel height at the downstream, H. The only dimensionless number appearing in the governing equations is the Reynolds number. For the flow problem considered, the following definition is used for the Reynolds number, Re.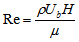 | (3) |
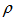 and
and 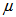 are the density and the dynamic viscosity, respectively
are the density and the dynamic viscosity, respectively 2.2. Geometry of Flow Domain and Boundary Conditions
- Figure 4 depicts the two-dimensional channel with a backward facing step provided near the channel entrance. The finite distance in between the channel, which is small compared to its length and width makes the flow through this channel predominantly two dimensional. In addition, an incompressible Newtonian fluid with constant fluid properties is assumed as well. Buoyant forces involved are negligible compared with viscous and pressure forces.
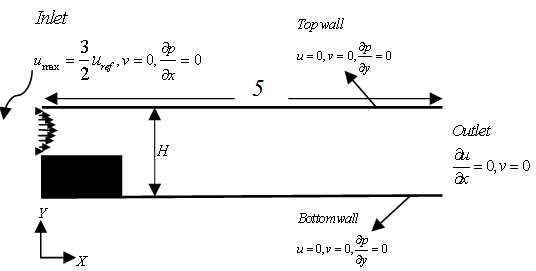 | Figure 4. Sketch of the flow configuration and definition of length scales |
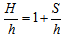 | (4) |
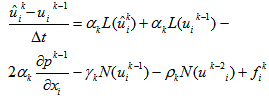 | (5) |
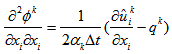 | (6) |
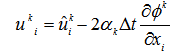 | (7) |
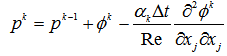 | (8) |
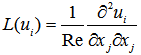 | (9) |
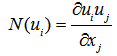 | (10) |
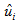 is the intermediate velocity,
is the intermediate velocity, 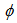 is the pseudo-pressure,
is the pseudo-pressure, 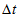 is the computational time step,
is the computational time step, 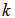 the sub-step index, and
the sub-step index, and 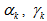 and
and 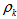 are the coefficients of RK3 (Third order Runge-Kutta) whose values are
are the coefficients of RK3 (Third order Runge-Kutta) whose values are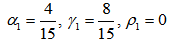 | (11) |
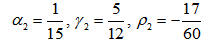 | (12) |
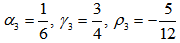 | (13) |
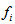 should be appended with the Navier-Stokes equations to treat the immersed boundary (IB) as a kind of forcing so that it mimic the effect of IB. Here it is extracted from the literature presented Yusof[5]. This forcing function is incorporated to satisfy the no-slip condition on the immersed boundary (IB) and is applied only on the immersed boundary or inside the body. In the absence of IB,
should be appended with the Navier-Stokes equations to treat the immersed boundary (IB) as a kind of forcing so that it mimic the effect of IB. Here it is extracted from the literature presented Yusof[5]. This forcing function is incorporated to satisfy the no-slip condition on the immersed boundary (IB) and is applied only on the immersed boundary or inside the body. In the absence of IB, 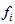 should be made equal to zero. The location of points, where the forcing function has to be introduced, is determined in a similar fashion as that of the velocity components defined on a staggered grid. When the forcing point coincides with the immersed boundary, momentum forcing is applied at that point so that the velocity is zero (see
should be made equal to zero. The location of points, where the forcing function has to be introduced, is determined in a similar fashion as that of the velocity components defined on a staggered grid. When the forcing point coincides with the immersed boundary, momentum forcing is applied at that point so that the velocity is zero (see 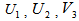 and
and 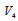 in Figure 5). On the other hand, when the forcing point exists inside the body, momentum forcing is applied in such a way that the velocity (
in Figure 5). On the other hand, when the forcing point exists inside the body, momentum forcing is applied in such a way that the velocity (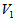 or
or 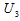 ) is the opposite of that (
) is the opposite of that (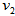 or
or 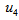 ) outside the body for both the wall-normal and tangential velocity components (respectively), as shown in Figure 5. However, because
) outside the body for both the wall-normal and tangential velocity components (respectively), as shown in Figure 5. However, because  (no-slip) conditions and
(no-slip) conditions and 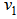 and
and 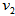 come into the cell (as shown in Figure 6), the cell containing the immersed boundary does not satisfy the mass conservation. Hence, a mass source/sink term
come into the cell (as shown in Figure 6), the cell containing the immersed boundary does not satisfy the mass conservation. Hence, a mass source/sink term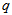 is introduced for the cell containing the immersed boundary to satisfy the mass conservation. The mass source/sink term is applied to the cell center on the immersed boundary or inside the body.
is introduced for the cell containing the immersed boundary to satisfy the mass conservation. The mass source/sink term is applied to the cell center on the immersed boundary or inside the body. | Figure 5. Velocity vectors near the wall on a staggered mesh with wall-normal velocity and tangential velocity for a very simple situation (The shaded area denotes the IB) |
2.3. Momentum Forcing and Interpolation for the Velocity
- To obtain
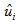 , from Eq. (5), the momentum forcing
, from Eq. (5), the momentum forcing 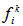 must be determined in advance such that
must be determined in advance such that 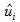 satisfies the no-slip condition on the immersed boundary. When Eq. (1) is provisionally discretized explicitly in time (RK3 for the convection terms and forward Euler method for the diffusion terms) to derive the momentum forcing value, we have
satisfies the no-slip condition on the immersed boundary. When Eq. (1) is provisionally discretized explicitly in time (RK3 for the convection terms and forward Euler method for the diffusion terms) to derive the momentum forcing value, we have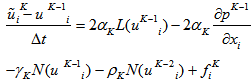 | (14) |
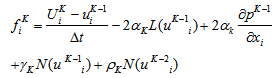 | (15) |
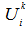 is the velocity to be obtained at a forcing point by applying momentum forcing. In the following,
is the velocity to be obtained at a forcing point by applying momentum forcing. In the following, 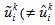 in Eq. (5)) indicates the velocity at a grid point nearby the forcing point updated from Eq. (14) with
in Eq. (5)) indicates the velocity at a grid point nearby the forcing point updated from Eq. (14) with 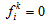 to determine
to determine 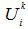 using the linear interpolation.In case of the no-slip wall,
using the linear interpolation.In case of the no-slip wall, 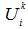 is zero whenever the forcing point coincides with the immersed boundary. However, in general the forcing point exists not on the immersed boundary but inside the body, and thus an interpolation procedure for the velocity
is zero whenever the forcing point coincides with the immersed boundary. However, in general the forcing point exists not on the immersed boundary but inside the body, and thus an interpolation procedure for the velocity 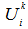 is required. In the present study, second-order linear interpolations are used, and Figure 6 shows the schematic diagrams for the calculation of interpolation velocity when the backward facing step is considered as the IB.
is required. In the present study, second-order linear interpolations are used, and Figure 6 shows the schematic diagrams for the calculation of interpolation velocity when the backward facing step is considered as the IB.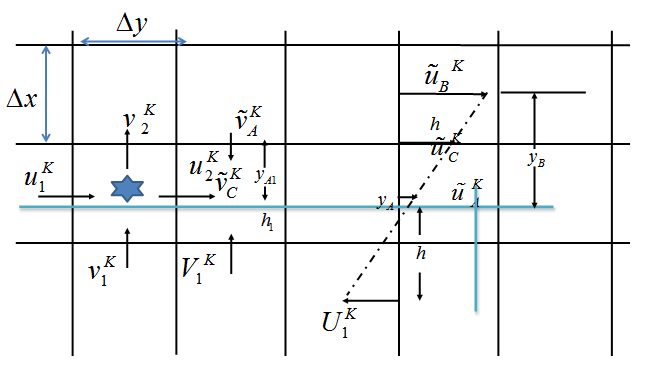 | Figure 6. Stencil for the linear interpolation scheme in the vicinity of backward facing step (IB) which shows instantaneous velocity, interpolation velocity, forcing points, etc |
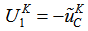 | (16) |
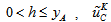 is obtained from a linear interpolation between
is obtained from a linear interpolation between 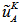 and the no-slip condition at the IB, whereas for
and the no-slip condition at the IB, whereas for 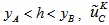 is obtained from
is obtained from 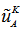 and
and 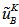 . That is
. That is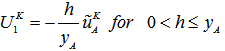 | (17) |
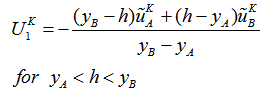 | (18) |
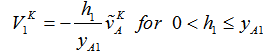 | (19) |
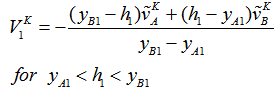 | (20) |
2.4. Mass Source and Continuity Equation
- The procedure of obtaining the mass source
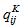 in Eq. (6) is explained in this section. Consider the star marked two-dimensional cell shown in Fig. 6, where is the velocity components inside the body and, and are those outside the body. For the rectangular cell containing only fluid, the continuity reads
in Eq. (6) is explained in this section. Consider the star marked two-dimensional cell shown in Fig. 6, where is the velocity components inside the body and, and are those outside the body. For the rectangular cell containing only fluid, the continuity reads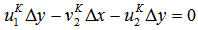 | (21) |
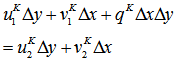 | (22) |
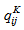 is obtained as
is obtained as 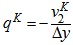 . In general,
. In general, 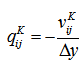 | (23) |
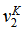 is unknown until equations (6) and (7) are solved and thus we use
is unknown until equations (6) and (7) are solved and thus we use 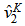 instead of
instead of 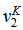 and is updated as and when
and is updated as and when 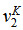 is being found out. Therefore, in general the mass source
is being found out. Therefore, in general the mass source 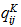 is defined as
is defined as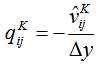 | (24) |
2.5. Solution Procedure
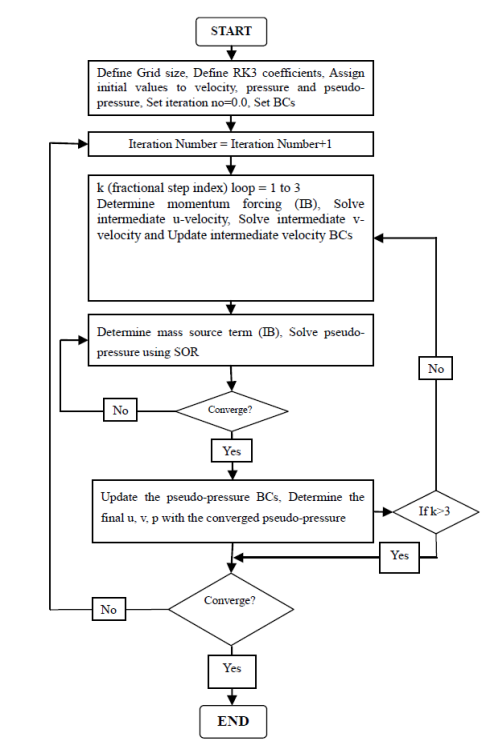 | Figure 7. Flow chart for the Immersed Boundary Method |
3. Results and Discussions
- In order to ensure whether the predicted results are grid independent or not, extensive grid refinement studies were carried out. Finally, in backward facing step flow problem, the non -dimensional stream wise velocity at the centre of the channel outlet for Re=1.0 is tabulated (Table 1). It is seen that for the computational stencil of 252x102, percentage change of stream wise velocity with respect to previous stencil (202x82) is negligible. Hence the same grid size was selected for the code execution for all numerical examples presented here.
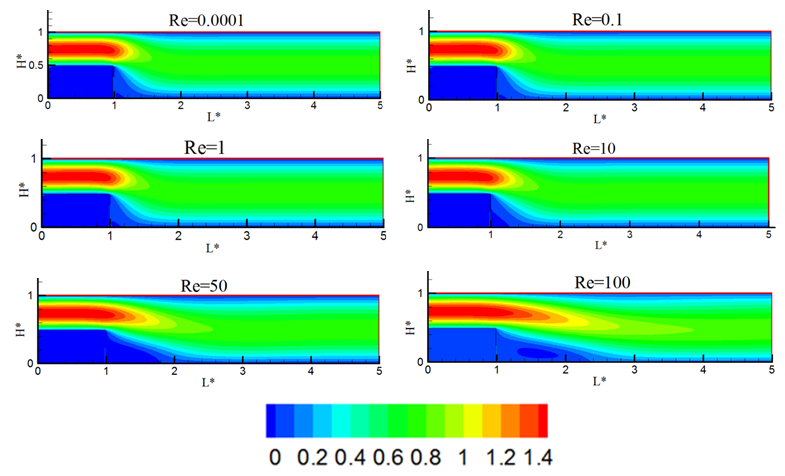 | Figure 8. Stream wise velocity contours for backward facing step flow for different Reynolds numbers |
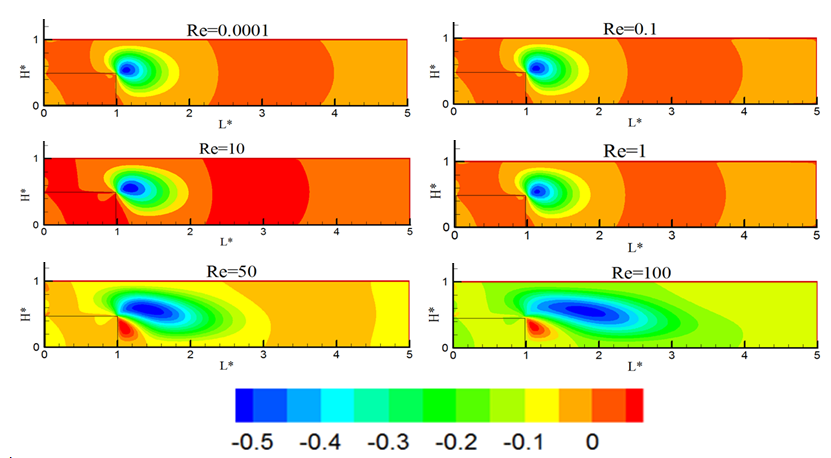 | Figure 9. Transverse velocity contours for backward facing step flow for different Reynolds numbers |
|
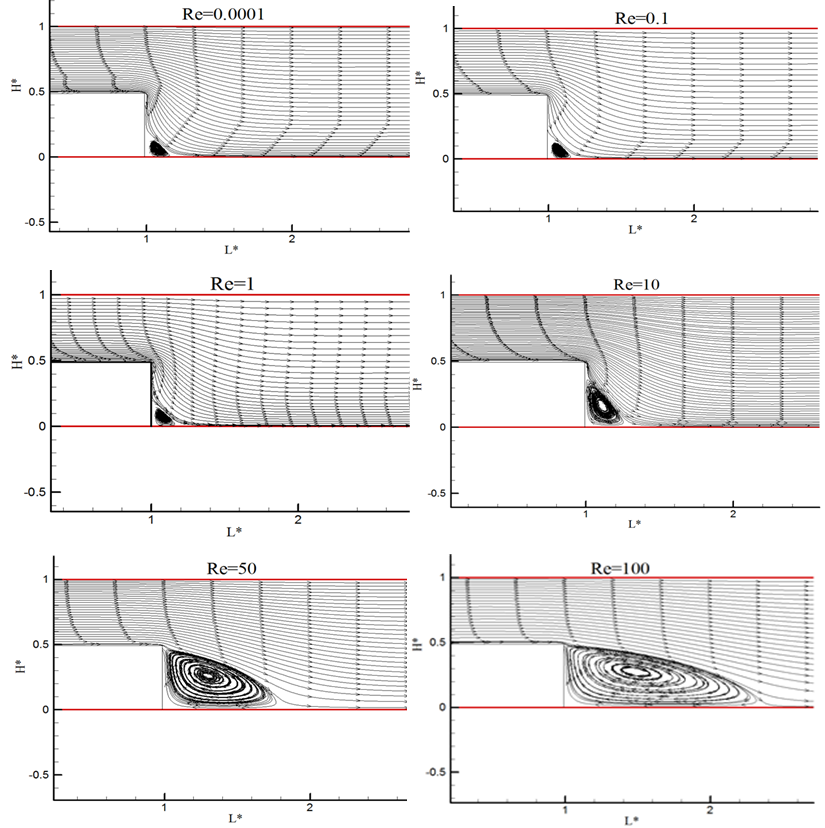 | Figure 10. Streamlines in the vicinity of backward facing step for different Reynolds numbers |
4. Conclusions
- Immersed-boundary method is adopted to validate a relevant fluid mechanics bench mark problem, the backward facing step flow problem. The present method is based on a finite volume approach on a staggered mesh together with a fractional-step method. The momentum forcing and the mass source/sink are applied on the body surface or inside the body to satisfy the no-slip boundary condition on the immersed boundary and the continuity for the cell containing the immersed boundary, respectively. A linear interpolation scheme is used to satisfy the no-slip velocity on the immersed boundary, which is numerically stable regardless of the relative position between the grid and the immersed boundary. The present algorithm is ideally suited to low Reynolds number flows also. Predictions from the numerical model have been compared against experimental data of different Reynolds numbers of flow past backward-facing step geometries. In addition, computed reattachment and separation lengths have been compared against alternative numerical predictions in the published literatures. Also, the immersed boundary method with both the momentum forcing and mass source/sink is found to gives realistic velocity profiles and recirculation eddies for the backward facing step flow problem demonstrating the accuracy of the method. By conducting this numerical study, we can conclude that immersed boundary method is a robust way of determining flow field and can rival experimental and laboratory study. Generally for backward facing step flow, the velocities are very small in the recirculation zone compared to the velocity of the mean flow. Hence the separation surface is submitted to a strong shear. In order to characterize the topology of the separated zone, measurements of the reattachment length in the stream wise direction may be captured. The range of Reynolds numbers, where the analysis is made possible only in three dimensional way, may be identified by rigorous numerical experimentation. The discrepancy in the primary recirculation length between the experimental results and the numerical predictions in both 2D and 3D analysis may analysed critically. According to Armaly et alI[8], during experimentation a secondary recirculation zone was observed at the channel upper wall when the Reynolds number is greater than 400. It may also be ensured numerically that the discrepancy between the experimental measurements and the numerical prediction is due to the secondary recirculation zone that perturbed the two-dimensional character of the flow. Further numerical experimentation of poignant bodies may l\also be carried out.
ACKNOWLEDGEMENTS
- This work was supported by the National Institute of Technology, Calicut, India.
References
| [1] | F. H. Harlow, and J.E. Welch, 1965, Numerical calculation of time-dependent viscous of incompressible flow of fluid with free surface, Physics Fluids, vol. 8, pp. 2182-2189. |
| [2] | C.S. Peskin, 1972, Flow patterns around heart valves: a numerical method, Journal of Computational Physics, vol. 10, pp 252-271. |
| [3] | R. Mittal, and G. Iaccarino, 2005, Immersed Boundary Methods, Annual Review of Fluid Mechanics, vol. 37, pp. 239-261. |
| [4] | D. Goldstein, R. Handler, and R Sirovich, 1993, Modeling a no-slip flow boundary with an external force field, Journal of Computational Physics, vol.105, p.354. |
| [5] | M. J. Yusof, 1997, Combined Immersed-Boundary/B-Spline Methods for Simulations of Flow in Complex Geometries, Annual Research Briefs (Center for Turbulence Research, NASA Ames and Stanford University), p. 317. |
| [6] | J. Kim, D. Kim, and H. Choi, 2001, An Immersed-Boundary Finite-Volume Method for Simulations of Flow in Complex Geometries, Journal of Computational Physics, vol. 171, pp. 132–150. |
| [7] | J. Kostas, J, Soria, and M.S. Chong, 2001, A study of backward facing step flow at two Reynolds numbers, 14th Australian Fluid Mechanics Conference, Adelaide University, Adelaide, Australia, pp. 10-14. |
| [8] | B. F. Armaly, F. Durst, J. C. F. Peireira, and B. Schonung, 1983, Experimental and theoretical investigation of backward-facing step flow, Journal of Fluid Mechanics, vol. 127, pp. 473–496. |
| [9] | J. Kim, and P. Moin, 1985, Application of a fractional-step method to incompressible Navier-Stokes equations,” Journal of Computational Physics, vol. 59, pp. 308–323. |
| [10] | D.K. Gartling, 1990, A test problem for outflow boundary conditions—flow over a backward-facing step, International Journal of Numerical Methods in Fluids, vol. 11, pp. 953–967. |
| [11] | T. Lee, and D. Mateescu, 1998, Experimental and numerical investigation of 2D backward-facing step flow, Journal of Fluids Structures, vol. 12, pp. 703–716. |
| [12] | L. Kaiktsis, G. E. Karniadakis, and S.A. Orszag, 1991, Onset of three dimensionality, equilibria, and early transition in flow over a backward-facing step, Journal of Fluid Mechanics, vol. 231, pp. 501–528. |
| [13] | F. Durst, J. C. F. Peireira, and C. Tropea, 1993, The plane symmetric sudden-expansion flow at low Reynolds numbers,” Journal of Fluid Mechanics, vol. 248, pp. 567–581. |
| [14] | L. Kaiktsis, G. E. Karniadakis, & S. A. Orszag, 1996, Unsteadiness and convective instabilities in a two-dimensional flow over a backward-facing step, Journal of Fluid Mechanics, vol. 321, pp. 157–187. |
| [15] | A. F. Heenan, and J. F. Morrison, 1998, Passive control of back step flow, Exp. Therm. Fluid Sci., vol. 16, pp. 122–132. |
| [16] | E. Erturk, T. C. Corke, & C. Gokcol, 2005, Numerical Solutions of 2-D Steady Incompressible Driven Cavity Flow at High Reynolds Numbers, International Journal for Numerical Methods in Fluids, vol. 48, pp 747-774. |
| [17] | Ferziger, J.H., and Peric, M., Computational Methods in Fluid Dynamics, Springer-Verlag, New York, 1996. |
| [18] | G. Biswas, M. Breuer, and F. Durst, 2004, Backward-facing step flows for various expansion ratios at low and moderate ReynoldsnNumbers, J. Fluid Engg., vol. 126, pp. 362–374. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML