-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2012; 2(6): 122-136
doi: 10.5923/j.ajfd.20120206.05
On Alternative Model of Sound Scattering in Turbulent Moving Media
Andrew G. Semenov
Acad. N. N. Andreev’s Acoustics Institute RAS, 4 Shvernik Street, Moscow, 117036, Russia
Correspondence to: Andrew G. Semenov, Acad. N. N. Andreev’s Acoustics Institute RAS, 4 Shvernik Street, Moscow, 117036, Russia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Model of sound scattering in turbulent medium comprising chaotically distributed in space moving in manifold directions spherically symmetric structures - localized flows, say, vortices of various linear dimensions from smallest “Kolmogorov’s” to outer turbulent scales is proposed. Scattering crossections and distance attenuation parameters related to structures motion in the presence and absence of vorticity inside them for sound waves are calculated on etalon problem solutions basis. Resulting frequency dependencies and scattering laws in model medium differ substantially not only from Rayleigh law but from several other well known predicted patterns of sound scattering in turbulent medium as well. Attenuation value is expected to depend on vortices Mach number to scattering wave parameter ratio. Model parameter control is available by means of dimensions, velocities and concentration of basic localized flow changes corresponding to turbulence scale, intensity and degree of development changes. Comparison of expected attenuation parameters with experimental data and estimates based on classical isotropic turbulence models is presented. PACS numbers: 43.20.Fn, 43.28.Gq, 43.28.Py
Keywords: Turbulent Moving Media, Microinhomogeneneous Media, Sound Scattering, Orderly or Chaotically Moving Particle, Strong and Weak Turbulent Flow, Attenuation Law, Ideal ,Viscose Flow, Reynolds Number
Cite this paper: Andrew G. Semenov, "On Alternative Model of Sound Scattering in Turbulent Moving Media", American Journal of Fluid Dynamics, Vol. 2 No. 6, 2012, pp. 122-136. doi: 10.5923/j.ajfd.20120206.05.
Article Outline
1. Introduction
- This paper is devoted to the problem of sound scattering by small chaotically situated spherically symmetric gas dynamic structures intended to model turbulent velocity fluctuations. If these structures were at rest then scattered field frequency spectrum will be the same as for each structure, while total scattered power will be the power scattered by any isolated structure multiplied by their number due to their chaotic space distribution[16]. A lot of experimental and theoretical works are devoted to chaotic motion media and to sound scattering[1-36]. For instance, in[14] Brown motion basic properties investigated in the beginning of previous century by A. Einstein and M. Smolukhovtsky are discussed as specific example of suspended particles chaotic motion. Brown motion laws are based on the following principle – particle displacements in any direction are equally probable, while inertial forces could be neglected with respect to friction forces influence governing particle motion. In[31] laws of Brown particles sound scattering are investigated in relation to low frequency sound scattered in their suspensions (solutions). However in this paper we shall be interested in opposite microinhomogeneous media example – the media where in particles (microstructures) motion viscose forces could be neglected with respect to corresponding inertial forces [35-36]. This is the case of developed (full-blown) turbulence and sound scattering there. Multiple works were devoted to this problem study[1, 3-6 and 8-22]. All of them are based on turbulent flows gas dynamic structure analysis as well as on definite microinhomogeneous media structure models. Possible turbulent media models could be separated in two classes – wave and corpuscular models. First type models are more widely spread. Most part of turbulent flows structure heuristic theories are based on wave model fundaments[1, 4, 6, 14-22 and 35-36]. Corpuscular models[2, 6 and 8-13] allow solving a sequence of application problems of flow and heat exchange description in wall layer turbulence[12], contributing as well to turbulent theory development[8]. One of the initial turbulence models developed by L. Prandtl was corpuscular[2]. Recent years give rise to specific part of turbulence theory related to study of “large” vortices role in mass and heat exchange processes. It is based on “coherent” turbulence model generated in turbulent jets, in wakes behind streamlined bodies, in preseparation regions of wall turbulent boundary layers and in nature (tornados, hurricanes) as well. Basis of turbulence model in[12] is a statement that vortices - structures of scale larger than molecules take major part in turbulent flow formation. In turbulent flow to be generated their behavior and sizes distribution obey specific laws allowing stochastic consideration. Traditional method of turbulence theory composition[8, 35-36] is based on Reynolds equation system. Basic equations and generalized kinetic theory relationships are formulated there to close up Reynolds equations system. It is shown that state of media in locally kinetic gas theory dynamics is defined by distribution functions sequence - not isolate distribution function. Each molecule group dynamic state function is derived from related Reynolds equations system. So, that after pooled data definition dynamic state of system is expressed by simple summation. We shall use same principle in total sound scattering definition.Experiments on light scattering in turbulent and laminar flows[9-11] are most conclusive proof of turbulent media structure corpuscularity. It is well known that for turbulent fluctuations of definite substantion closed description in local point of flow two independent functions are customary used. Distribution function of substantion quantity fluctuations (say, velocity, temperature or touch concentration) acts as process amplitude characteristic. Fluctuations spectrum represents distribution of fluctuation energy over frequency range, characterizing process scale properties. Definite body of mathematics is developing or already developed for both characteristics[2-7, 12 and 13]. But such turbulent fluctuation description method suffers from few disadvantages. One of them lie in the fact that fluctuation spectrum is a process mathematization (harmonic analysis) product not describing fluctuation physical structure univocally[9-11]. Technical applications and a sequence of theoretical models require namely physically existing fluctuation scale knowledge. Moreover, it is difficult to acquire such important turbulence feature as intermittency with aid of distribution function. In experiments touch concentration changes being used to fluctuation optical perceptibility improvement were frequently of purely turbulent nature not complicated by additional factors such as molecular diffusion. That is why splinter process to be observed was close to splinter process predicted in[13], where logarithmically normal fractions dimensions distribution law was derived. In experiments existing scales of turbulent inhomogeneities (vortices) acquire mathematical definition together with such characteristics as “mole dimension” and few other widely used in physical phenomena corpuscular models (say, in combustion theory) called forth by turbulent mixing. As a whole these data are to be considered as turbulence corpuscular properties reflection and opposite to the spectrum governed by its wave properties. We shall try to develop similar approach to one of basic turbulent media physical properties – to sound scattering by full-blown turbulence description. Namely, not ignoring “wave model” progress and results, we shall try to develop turbulent medium scattering sound corpuscular model, based on the fact that this microinhomogeneous medium consists of multiple spherically symmetric chaotically moving gas dynamic structures – localized flows, say, vortices. In addition to variation of velocities and dimensions specifics of such structures, to be compared with results of[23-27], lies in the fact that media flow will be observed not only outside but inside such structures (inhomogeneity) as well. Each structure inside will consist not of rigid matter as in[23-25, 27], but of environment medium substance, say, of fluid (gas) as in[26]. In our model substance exchange between inner and outer structure regions will be allowed in principle. As before in[28-32], we shall consider the case of microinhomogeneous media – as media comprising great many microstructures (fluctuations or vortice) situated at distances smaller then incident sound wavelength. However, minimum distance between them should still substantially exceed structure linear dimension. If such identical structures were distributed uniformly over the entire volume, say in the form of regular lattice, then no scattering would be observed at all[16]. So that immediate case of scattering to be studied is chaotic structures distribution with their concentration being constant on the average only. Basis of low frequency sound scattering in such media lies in scattering law of single inhomogeneity (structure) of dimension
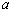 small with respect to sound wavelength
small with respect to sound wavelength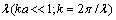 . For structures (particles) at rest classical Rayleigh law is valid[3, 16]:
. For structures (particles) at rest classical Rayleigh law is valid[3, 16]: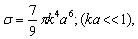 | (1) |
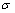 is proportional to structure crossection
is proportional to structure crossection 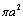 multiplied by highly small quantity
multiplied by highly small quantity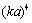 . Inhomogeneity concentration n and unit scattering crossection
. Inhomogeneity concentration n and unit scattering crossection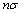 , determining media unite volume scattering capability, provide microinhomogeneous media wave attenuation property. Then sound intensity
, determining media unite volume scattering capability, provide microinhomogeneous media wave attenuation property. Then sound intensity 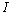 will decrease exponentially (
will decrease exponentially (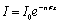 ) with distance
) with distance 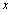 due to scattering on inhomogeneities. Logarithmic intensity attenuation γ, measured in dB per unit distance of sound wave travel takes the form
due to scattering on inhomogeneities. Logarithmic intensity attenuation γ, measured in dB per unit distance of sound wave travel takes the form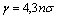 . Formulating inhomogeneity volume and total inhomogeneity material unit content in medium τ through inhomogenety average radius and concentration (
. Formulating inhomogeneity volume and total inhomogeneity material unit content in medium τ through inhomogenety average radius and concentration (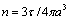 ), we obtain γ in the form
), we obtain γ in the form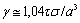 . In general, inhomogeneity scattering crossection
. In general, inhomogeneity scattering crossection 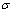 [28-32], say, for moving inhomogeneity, could be expressed as a product of its crossection and some dimensionless function
[28-32], say, for moving inhomogeneity, could be expressed as a product of its crossection and some dimensionless function 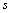 :
: 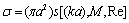 , where
, where 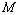 - Mach number,
- Mach number, 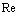 - Reynolds number. Then we can write
- Reynolds number. Then we can write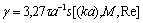 . In the presence of several (
. In the presence of several (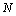 types) types of particles (inhomogeneities) mixture, characterized by concentration ni and unit scattering crossection
types) types of particles (inhomogeneities) mixture, characterized by concentration ni and unit scattering crossection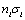 , wave intensity will decrease exponentially with distance
, wave intensity will decrease exponentially with distance 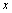 in accordance to law:
in accordance to law: 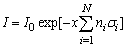 | (2) |
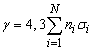 .For
.For 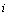 -th type of scatterer with radius ai and concentration ni, expressed through unit volume fraction τi (
-th type of scatterer with radius ai and concentration ni, expressed through unit volume fraction τi (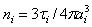 ), total attenuation γ looks like:
), total attenuation γ looks like: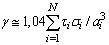 .Or taking into account expression for
.Or taking into account expression for 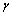 introduced above [32]
introduced above [32] 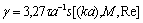 , for total attenuation factor (decrement) we obtain:
, for total attenuation factor (decrement) we obtain: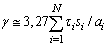 | (3) |
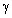 low frequency dependence (
low frequency dependence (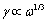 )[1] is not supported by experimental data. In the same time, development of adequate sound scattering theory for isotropic homogeneous turbulent media is possible on the basis of its behavior fundamental laws further study only.
)[1] is not supported by experimental data. In the same time, development of adequate sound scattering theory for isotropic homogeneous turbulent media is possible on the basis of its behavior fundamental laws further study only.2. Turbulence Corpuscular Model
- From theoretical point of view the case of homogeneous isotropic turbulence is the simplest. But practically this case occurs rarely in turbulent flows. These conditions are violated for instance due to flow boundaries or to anisotropy introduced by space dependent mean velocity of turbulent flow. From the other hand, there are reasons to believe that large Reynolds number small-scale flow fluctuations in limited space regions will be locally homogeneous and isotropic. This hope is based on qualitative picture of full-blown turbulence origin proposed in last century 20-th by Richardson and developed by A.N. Kolmogorov and A.M. Obukhov[1-3, 6, 13, 35 and 36]. L.G. Loitsiansky fairly called turbulent flow velocity fluctuations as various scale vortices driving turbulent flow[6]. It is important to note, that viscosity plays no perceptible role in flow formation, for each scale Reynolds numbers are too large, and nonlinear effects govern this process first of all. That is why energy is not lost in the process of transfer from larger flow scales down to smaller scales. It is defined by scale independent quantity
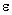 - energy per unit mass in that flow. Its value order was defined by dimensionality considerations as initial flow energy decrease[13, 18, 35 and 36]. The only value of dimension
- energy per unit mass in that flow. Its value order was defined by dimensionality considerations as initial flow energy decrease[13, 18, 35 and 36]. The only value of dimension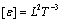 , to be constructed using
, to be constructed using 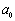 and
and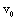 , is
, is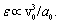 | (4) |
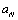 (
(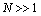 ), for which
), for which 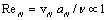 (or, more precisely,
(or, more precisely, 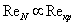 ). These scales flow is hydrodynamically stable and not splinting further in smaller scales. Energy
). These scales flow is hydrodynamically stable and not splinting further in smaller scales. Energy 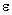 received by these scales in unit time is transferred directly to heat due to viscose forces. So that parameter
received by these scales in unit time is transferred directly to heat due to viscose forces. So that parameter  defines energy dissipation of flow unit mass per unit time as well. In outer
defines energy dissipation of flow unit mass per unit time as well. In outer  scale splinter to
scale splinter to 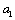 scale fluctuations – they are observed not only in direction of mean flow velocity
scale fluctuations – they are observed not only in direction of mean flow velocity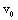 . In other words, motion in
. In other words, motion in 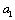 scale is more isotropic then outer (average) flow. Similarly in scale
scale is more isotropic then outer (average) flow. Similarly in scale 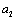 generated by
generated by 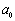 scale fluctuations isotropy will increase, while average flow influence – decrease and so on. As a result after few multiplication stages turbulent flow becomes isotropic. In other words, in full-blown turbulence most fluctuation scales, with exception of few largest, become statistically homogeneous and isotropic. Scale
scale fluctuations isotropy will increase, while average flow influence – decrease and so on. As a result after few multiplication stages turbulent flow becomes isotropic. In other words, in full-blown turbulence most fluctuation scales, with exception of few largest, become statistically homogeneous and isotropic. Scale 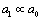 is called outer scale, while
is called outer scale, while 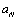 inner (Kolmogorov) scale[6, 13, 18 and 35, 36].
inner (Kolmogorov) scale[6, 13, 18 and 35, 36]. 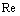 , the more its splinter stages with serially decreasing scales from
, the more its splinter stages with serially decreasing scales from  until
until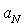 . That is why, for large initial Reynolds numbers, there exists representative scales “inertial” interval
. That is why, for large initial Reynolds numbers, there exists representative scales “inertial” interval 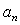 (
(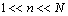 ), where
), where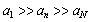 , or, simply speaking, turbulence inertial interval. Qualitative picture of turbulence corpuscular model is shown on Fig.1.All scales (dimensions) of vortices with sequentially decreasing scales
, or, simply speaking, turbulence inertial interval. Qualitative picture of turbulence corpuscular model is shown on Fig.1.All scales (dimensions) of vortices with sequentially decreasing scales 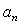 from
from 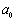 until inner Kolmogorov’s scale
until inner Kolmogorov’s scale 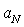 are presented in corpuscular turbulence structure. These fluctuations (vortices) being universal for any turbulent flow, they have forgotten about outer turbulent flow structure, while viscosity forces are still not important for their behavior. That is why this interval is characterized by two parameters - scale
are presented in corpuscular turbulence structure. These fluctuations (vortices) being universal for any turbulent flow, they have forgotten about outer turbulent flow structure, while viscosity forces are still not important for their behavior. That is why this interval is characterized by two parameters - scale 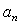 and energy flow velocity
and energy flow velocity 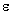 only. Few flow estimates to be used in the sections to follow could be derived easily on the basis of dimensionality considerations. Let us define first the order of fluctuation velocity
only. Few flow estimates to be used in the sections to follow could be derived easily on the basis of dimensionality considerations. Let us define first the order of fluctuation velocity 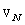 for scale
for scale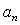 . It can depend on
. It can depend on 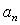 and
and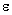 , while the only possible combination of velocity dimension to be arranged using them be
, while the only possible combination of velocity dimension to be arranged using them be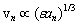 | (5) |
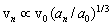 | (6) |
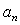 is
is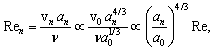 | (7) |
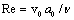 - Reynolds number of initial (outer) flow. If we suppose that our estimates are fair until inner turbulence scale
- Reynolds number of initial (outer) flow. If we suppose that our estimates are fair until inner turbulence scale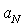 , for which
, for which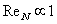 , then the order of value of
, then the order of value of 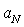 and corresponding fluctuation velocity
and corresponding fluctuation velocity 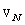 are
are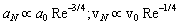 | (8) |
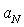 and
and 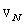 are decreasing with initial flow Reynolds number increase proportionate to
are decreasing with initial flow Reynolds number increase proportionate to 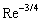 and to
and to 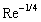 respectively. From the point of sound scattering discussed below its worth to note, that relationship between
respectively. From the point of sound scattering discussed below its worth to note, that relationship between 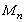 and
and 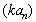 , defining scattering conditions for moving vortex[26-27 and 29] is reduced for large Reynolds numbers to relationship between sound frequency
, defining scattering conditions for moving vortex[26-27 and 29] is reduced for large Reynolds numbers to relationship between sound frequency 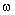 and ratio
and ratio 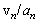 value, expressed in the form
value, expressed in the form 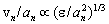 in accordance to (6).
in accordance to (6).3. Scattering Theory Contradictions
- As to most important experimental data, it is widely believed that sound audibility decreases drastically in the presence of wind. This effect is observed on not very large distances and usually could not be explained by sound ray distortion in gradient wind flow[1]. It is directly related to wind turbulence. Dahl and Dewick were the first to point this effect out in 1937 in relation to fading observation[1, 34]. Sukharevsky confirmed a little later in 1940 it in Caucasus measurements. Bad sound audibility in wind condition was underlined by Stewart in 1919[1].But most thorough experimental study was undertaken by Sieg in 1940[1, 33]. Не called attention to additional attenuation of sound in the presence of wind, attenuation substantially exceeding sound absorption related to air molecular properties (viscosity, heat conduction and air humidity - Knezer effect). Sieg basic results could be reduced to following. In the frequency range 250 - 4000 Hz in weak wind (1 - 2 m/s or in almost dead calm) perceptible intensity sound fluctuations (fading) are not observed, but intensity decreases with distance. But for all that even if molecular absorption will be subtracted, sound attenuation factor (decrement)
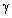 comprises still up to 1,5 - 2,2 dB at 100 m. In Siegs experiments frequency dependence of
comprises still up to 1,5 - 2,2 dB at 100 m. In Siegs experiments frequency dependence of 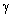 was not detected. However, as to Siegs critics opinion, his observations accuracy was not substantial, sound source directivity was not taken into account and conditions of various frequency sound attenuation observations were not identical enough. So that his results may represent
was not detected. However, as to Siegs critics opinion, his observations accuracy was not substantial, sound source directivity was not taken into account and conditions of various frequency sound attenuation observations were not identical enough. So that his results may represent 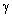 order of value estimate only, being approximately constant in the frequency range 250 - 4000 Hz. In strong gusty wind attenuation factor
order of value estimate only, being approximately constant in the frequency range 250 - 4000 Hz. In strong gusty wind attenuation factor 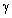 increases running up to 5 - 9 dB value at 100 meters (at gusty wind from 7 to 17 m/s). In these conditions frequency dependence of
increases running up to 5 - 9 dB value at 100 meters (at gusty wind from 7 to 17 m/s). In these conditions frequency dependence of 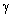 becomes observable, namely
becomes observable, namely 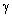 equals 5 dB for 250 Hz, 8 dB for 2000 Hz, 9 dB for 4000 Hz (at 100 meters). At the same conditions intensity fluctuations (fading) runs up to 25 dB. Effect explanation first attempts are related to first half of ХХ century. Turbulent flow influence on sound wave could be reduced to sound scattering resembling partly scattering of light traveling in turbid media: both cases comprises random fluctuations of propagation velocities. It is not out of place to note, that as it is shown in[28, 32], perfect analogy is not observed. Theoretical problem study in[1] proceeded from the version of moving media sound propagation wave equation – Obukhov equation approximately taking into account presence of vorticity in the medium. However, any conclusions related to specific role of vorticity in sound scattering was not done there. Farther, just like in[23-32] for Lighthill equation, to calculate scattering amplitude
equals 5 dB for 250 Hz, 8 dB for 2000 Hz, 9 dB for 4000 Hz (at 100 meters). At the same conditions intensity fluctuations (fading) runs up to 25 dB. Effect explanation first attempts are related to first half of ХХ century. Turbulent flow influence on sound wave could be reduced to sound scattering resembling partly scattering of light traveling in turbid media: both cases comprises random fluctuations of propagation velocities. It is not out of place to note, that as it is shown in[28, 32], perfect analogy is not observed. Theoretical problem study in[1] proceeded from the version of moving media sound propagation wave equation – Obukhov equation approximately taking into account presence of vorticity in the medium. However, any conclusions related to specific role of vorticity in sound scattering was not done there. Farther, just like in[23-32] for Lighthill equation, to calculate scattering amplitude 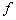 and attenuation factor
and attenuation factor 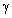 sound scattering problem was solved in[1]. Scattered wave amplitude
sound scattering problem was solved in[1]. Scattered wave amplitude 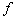 was shown to be
was shown to be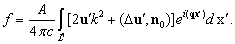 | (9) |
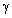 was expressed through scattering amplitude and after integration and averaging it was derived in[1]
was expressed through scattering amplitude and after integration and averaging it was derived in[1]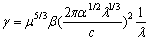 | (10) |
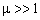 ,
, 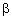 and
and 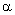 - numerical factors related to turbulent fluctuations spectrum with values to be specified empirically. Quantity
- numerical factors related to turbulent fluctuations spectrum with values to be specified empirically. Quantity 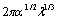 means fluctuation velocity with scale below sound wavelength
means fluctuation velocity with scale below sound wavelength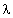 . Thus, turbulent flow sound attenuation factor
. Thus, turbulent flow sound attenuation factor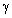 is proportional to scales below
is proportional to scales below 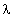 fluctuation velocity Mach number
fluctuation velocity Mach number 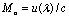 squared and inversely proportional to sound wavelength
squared and inversely proportional to sound wavelength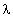 . As a whole,
. As a whole, 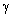 frequency dependence looks like
frequency dependence looks like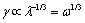 . Issuing from Obukhov 1941 preliminary estimate quantity
. Issuing from Obukhov 1941 preliminary estimate quantity 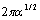 should be equal to 3 and at moderate wind
should be equal to 3 and at moderate wind 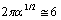 [1]. For wind turbulence could not be considered as completely isotropic,
[1]. For wind turbulence could not be considered as completely isotropic, 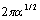 is wind velocity increasing function. On the basis of experimental data[1],
is wind velocity increasing function. On the basis of experimental data[1], 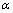 is considered to be linear in wind velocity. It explains attenuation factor
is considered to be linear in wind velocity. It explains attenuation factor 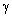 increase with wind velocity. Weak enough dependence of
increase with wind velocity. Weak enough dependence of 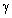 on wavelength
on wavelength 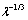 is consistent with Sieg experimental data[33]. Numerical factor
is consistent with Sieg experimental data[33]. Numerical factor 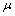 value was estimated on the basis of the same Sieg data for moderate wind. Factor
value was estimated on the basis of the same Sieg data for moderate wind. Factor 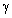 equals to 1, 5 dB at 100 meters, which in absolute units means
equals to 1, 5 dB at 100 meters, which in absolute units means 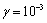 м-1. For sound frequency 500 Hz (
м-1. For sound frequency 500 Hz (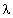 = 68 cm) it yields
= 68 cm) it yields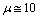 , which was considered as reasonable value in[1]. It is worth to note that introduction of empirical factor
, which was considered as reasonable value in[1]. It is worth to note that introduction of empirical factor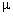 , specifying integration limits in (9) and in fact
, specifying integration limits in (9) and in fact 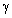 value, together with introduction of
value, together with introduction of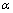 there look like wave theory compromise with its capability to explain data observed experimentally.In[4] by means of perturbation method solution of resembling but slightly simplified wave equation expression for differential sound scattering crossection for wave frequency
there look like wave theory compromise with its capability to explain data observed experimentally.In[4] by means of perturbation method solution of resembling but slightly simplified wave equation expression for differential sound scattering crossection for wave frequency 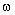 (
(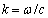 ), produced by turbulence volume
), produced by turbulence volume 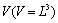 , in direction of observation angle
, in direction of observation angle  was derived. Author of[4] proceeded from doubtful enough analogy between scattering of sound and radio waves[28, 32].It follows from[4] that angle
was derived. Author of[4] proceeded from doubtful enough analogy between scattering of sound and radio waves[28, 32].It follows from[4] that angle 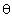 effective scattering crossection depends exclusively on turbulence components with wavenumbers
effective scattering crossection depends exclusively on turbulence components with wavenumbers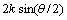 , corresponding to “diffraction lattices” satisfying Bragg conditions. This reason leads to results fair for fluctuation velocity and temperature statistically homogeneous and isotropic turbulent field expansion to locally isotropic field cases. Obtained results evidence that temperature and wind velocity fluctuations contribution to total atmosphere sound wave scattering is approximately equal. This statement looks slightly doubtful as well, for it is known that generally in compressible gas flow (atmospheric turbulence is an example of it) compressibility, density and temperature fluctuations have the same order with respect to Mach number (
, corresponding to “diffraction lattices” satisfying Bragg conditions. This reason leads to results fair for fluctuation velocity and temperature statistically homogeneous and isotropic turbulent field expansion to locally isotropic field cases. Obtained results evidence that temperature and wind velocity fluctuations contribution to total atmosphere sound wave scattering is approximately equal. This statement looks slightly doubtful as well, for it is known that generally in compressible gas flow (atmospheric turbulence is an example of it) compressibility, density and temperature fluctuations have the same order with respect to Mach number (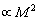 )[2-3 and 6]. So that in low velocity flows (
)[2-3 and 6]. So that in low velocity flows (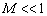 ) they could be safely neglected as compared to velocity fluctuations offering linear order dependence (
) they could be safely neglected as compared to velocity fluctuations offering linear order dependence (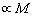 ) in Mach number[15]. Probably we are to believe, that atmospheric turbulence specific properties are somehow related to sunlight heat inflow and considering temperature fluctuations as a sort of “touch” for gas flow. Predicted scattering crossection frequency dependences agree with Rayleigh law (1). Scattering crossection velocity dependence
) in Mach number[15]. Probably we are to believe, that atmospheric turbulence specific properties are somehow related to sunlight heat inflow and considering temperature fluctuations as a sort of “touch” for gas flow. Predicted scattering crossection frequency dependences agree with Rayleigh law (1). Scattering crossection velocity dependence 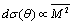 is close to expression (10)[1]. Scattering angle dependence experimental observations were provided by M.A. Kallistratova[17]. In author of[4] opinion, these data agree satisfactory with his predictions. By means of[4] results, it is possible to derive expressions for
is close to expression (10)[1]. Scattering angle dependence experimental observations were provided by M.A. Kallistratova[17]. In author of[4] opinion, these data agree satisfactory with his predictions. By means of[4] results, it is possible to derive expressions for 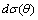 valid for several specific correlation functions version set apart from homogeneous turbulent velocity and temperature fluctuation fields correlation functions[4]. For instance in[4] expression for
valid for several specific correlation functions version set apart from homogeneous turbulent velocity and temperature fluctuation fields correlation functions[4]. For instance in[4] expression for 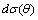 is derived for the case where fluctuation velocity and temperature correlation functions represent an exponents with definite characteristic scale
is derived for the case where fluctuation velocity and temperature correlation functions represent an exponents with definite characteristic scale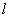 . It is worth to note, that
. It is worth to note, that 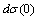 there depends exclusively on temperature fluctuations, so that no contribution to zero angle scattering is predicted for velocity fluctuations. This doubtful statement is directly related to small wavenumber values turbulent velocity fluctuations spectral density form chosen in[4]. It is fair for homogeneous turbulence only – which in author opinion is not the case for atmospheric turbulence.
there depends exclusively on temperature fluctuations, so that no contribution to zero angle scattering is predicted for velocity fluctuations. This doubtful statement is directly related to small wavenumber values turbulent velocity fluctuations spectral density form chosen in[4]. It is fair for homogeneous turbulence only – which in author opinion is not the case for atmospheric turbulence.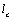 and time
and time 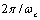 correlation radii are considered to be close. It is taken into account that for
correlation radii are considered to be close. It is taken into account that for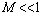 , density and compressibility flow fluctuations are of an order of
, density and compressibility flow fluctuations are of an order of 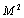 in Mach number, so that their average squared values could be neglected with respect to turbulent velocity fluctuation squared value. Fig.2 shows scattered by turbulence sound field intensity angular distribution[15]. Total sound field intensity to be observed at angle
in Mach number, so that their average squared values could be neglected with respect to turbulent velocity fluctuation squared value. Fig.2 shows scattered by turbulence sound field intensity angular distribution[15]. Total sound field intensity to be observed at angle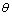 , was defined by expression
, was defined by expression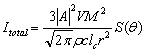 ,where values of function
,where values of function 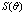 are shown on ordinate axis of Fig.2. It is denoted
are shown on ordinate axis of Fig.2. It is denoted 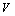 - turbulent flow region volume,
- turbulent flow region volume, 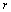 - observation point distance,
- observation point distance, 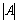 - incident sound wave amplitude,
- incident sound wave amplitude, 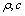 - media density and sound velocity. Fig.2 shows data for several relationships of incident sound wave frequency
- media density and sound velocity. Fig.2 shows data for several relationships of incident sound wave frequency 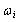 with correlation spectrum characteristic frequency corresponding to correlation time
with correlation spectrum characteristic frequency corresponding to correlation time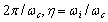 , and several parameter
, and several parameter 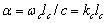 values. Results of this study evidence that turbulence velocity fluctuation scattering maximum is always predicted in forward direction at
values. Results of this study evidence that turbulence velocity fluctuation scattering maximum is always predicted in forward direction at 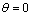 for any parameter relationship. It is in contradiction with conclusion of[4], provided for homogeneous turbulence. Scattered field frequency dependence in high frequency limit at
for any parameter relationship. It is in contradiction with conclusion of[4], provided for homogeneous turbulence. Scattered field frequency dependence in high frequency limit at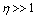 is the same as (1) -
is the same as (1) - 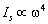 . And vice versa at
. And vice versa at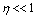 , in low frequency limit
, in low frequency limit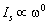 . It rather supports Zieg experimental data than expression (10), used in for their explanation[1]. As we have already noted – the reason is in turbulence correlation function form used there. The only thing looking a little surprising is perceptible intensity
. It rather supports Zieg experimental data than expression (10), used in for their explanation[1]. As we have already noted – the reason is in turbulence correlation function form used there. The only thing looking a little surprising is perceptible intensity 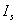 predicted in backward direction – at authors of[15] opinion (c.f. Fig.2) backward intensity (
predicted in backward direction – at authors of[15] opinion (c.f. Fig.2) backward intensity (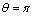 ) is comparable to forward intensity (
) is comparable to forward intensity (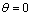 ). As we shall see below (28), backward scattering in unbounded media for various localized flows (say, free turbulence or a set of vortices) at small M values is impossible. It is predicted in the presence of boundaries due to wave reflections only, but it is not the case studied in[15]. The problem of sound attenuation in turbulent medium was not stated in[4, 15] and evaluation of factorwas not provided.Monograph[18] cites[4, 13], while turbulence sound scattering description is also based on two velocity fluctuations correlation function models (exponential and Gauss type). It is noted that not only inertial turbulent fluctuations interval is to be taken into account in scattering study. Importance of viscose interval described by Kolmogorov or Karman spectrum is underlined. Fig.3 shows structure of spectrum
). As we shall see below (28), backward scattering in unbounded media for various localized flows (say, free turbulence or a set of vortices) at small M values is impossible. It is predicted in the presence of boundaries due to wave reflections only, but it is not the case studied in[15]. The problem of sound attenuation in turbulent medium was not stated in[4, 15] and evaluation of factorwas not provided.Monograph[18] cites[4, 13], while turbulence sound scattering description is also based on two velocity fluctuations correlation function models (exponential and Gauss type). It is noted that not only inertial turbulent fluctuations interval is to be taken into account in scattering study. Importance of viscose interval described by Kolmogorov or Karman spectrum is underlined. Fig.3 shows structure of spectrum 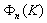 describing distribution of sound refraction index over inverse turbulent fluctuation scale
describing distribution of sound refraction index over inverse turbulent fluctuation scale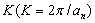 . Distribution
. Distribution 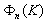 behavior in so called energetic or outer turbulent fluctuations range (general expression for it is not known) is depicted on Fig.3 by number 3. Well known dependence of
behavior in so called energetic or outer turbulent fluctuations range (general expression for it is not known) is depicted on Fig.3 by number 3. Well known dependence of 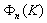 in turbulent fluctuations inertial range, where
in turbulent fluctuations inertial range, where 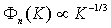 - by number 2. In turbulent fluctuations viscose range where viscose losses exceed turbulent fluctuation kinetic energy dependence of
- by number 2. In turbulent fluctuations viscose range where viscose losses exceed turbulent fluctuation kinetic energy dependence of 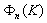 is depicted by number 1[22].
is depicted by number 1[22].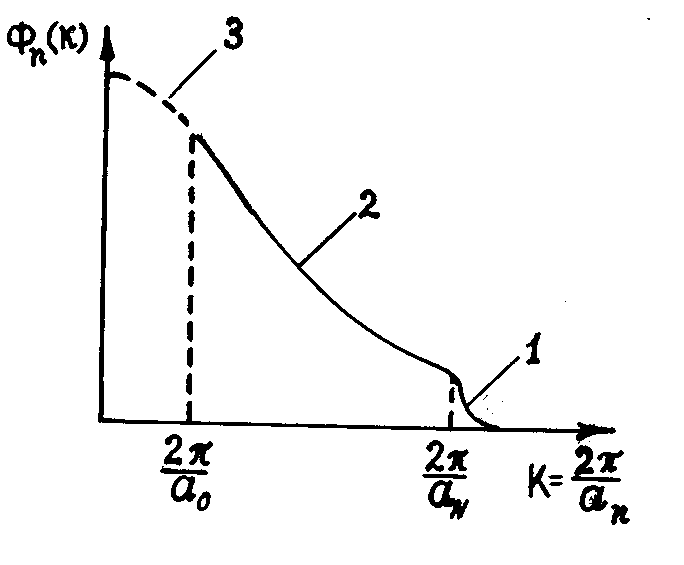 | Figure 3. Kolmogorov’s turbulence spectrum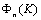 , describing fluctuation (vortices) intensity distribution over vortices inverse sizes space[18] , describing fluctuation (vortices) intensity distribution over vortices inverse sizes space[18] |
4. Moving Media Scattering
- Sound scattering crossections for various types of inhomogeneities[23-27] involved in chaotic motion were evaluated in[32] by means of averaging them with respect to sound wave incidence angle. Let us mention basic results of these works excluding corresponding solid bodies’ contributions and taking into account relationship introduced above
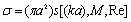 , for several scatterer types. For instance, in[23] we have found
, for several scatterer types. For instance, in[23] we have found 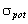 - partial contribution of potential flow around sphere moving in ideal fluid in total scattering crossection
- partial contribution of potential flow around sphere moving in ideal fluid in total scattering crossection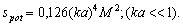 | (11) |
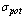 sense bears crossection derived in[25] for acoustically “transparent” body moving in ideal fluid
sense bears crossection derived in[25] for acoustically “transparent” body moving in ideal fluid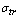 , body for which density and compressibility characteristics are the same as in ambient fluid (ρ =
, body for which density and compressibility characteristics are the same as in ambient fluid (ρ = 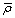 , с =
, с = 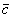 ). It is equal to
). It is equal to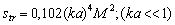 | (12) |
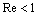 , sound scattering crossection value depends on M and
, sound scattering crossection value depends on M and 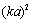 relationship[28-32], but for
relationship[28-32], but for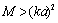 it is possible to derive
it is possible to derive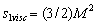 . This expression is independent on moving particle contribution being the same for
. This expression is independent on moving particle contribution being the same for 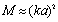 and
and 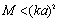 in the absence of solid particles, while explicit dependence of
in the absence of solid particles, while explicit dependence of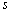 on
on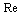 at
at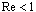 in viscose media is absent. However, we are interested in microinhomogeneous media cases where viscosity influence could be safely neglected with respect to definite structure inertia. That is why expression
in viscose media is absent. However, we are interested in microinhomogeneous media cases where viscosity influence could be safely neglected with respect to definite structure inertia. That is why expression 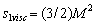 could be used for inner minimal (Kolmogorov) turbulence scale at
could be used for inner minimal (Kolmogorov) turbulence scale at 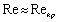 only[2-3, 6, 13 and 22]. With Reynolds number increase flow around spherical structures (inhomogeneities) achieve laminar wake regime[2-3, 5-6, 27 and 29-32].In large Reynolds number range specific for turbulent media motion at
only[2-3, 6, 13 and 22]. With Reynolds number increase flow around spherical structures (inhomogeneities) achieve laminar wake regime[2-3, 5-6, 27 and 29-32].In large Reynolds number range specific for turbulent media motion at 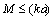 two main factors are responsible for scattering – the volume of individual moving inhomogeneity (structure) itself and laminar wake behind it. It is worth to note that to eliminate divergence in wake scattering evaluation[29] we recourse to integration region restriction by physical wake length. Divergence of zero angle scattering amplitude was eliminated there by formal introduction of finite wake length L. It was shown that resulting wake scattering amplitude exceeds basic potential flow around the sphere amplitude in
two main factors are responsible for scattering – the volume of individual moving inhomogeneity (structure) itself and laminar wake behind it. It is worth to note that to eliminate divergence in wake scattering evaluation[29] we recourse to integration region restriction by physical wake length. Divergence of zero angle scattering amplitude was eliminated there by formal introduction of finite wake length L. It was shown that resulting wake scattering amplitude exceeds basic potential flow around the sphere amplitude in 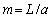 times[28-29]. So that at
times[28-29]. So that at 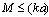 and
and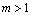 , expression for sound scattering crossection of solid particle moving in viscose media with laminar wake generation
, expression for sound scattering crossection of solid particle moving in viscose media with laminar wake generation 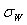 at
at 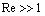 was
was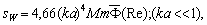 | (13) |
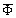 - the value of space averaged function
- the value of space averaged function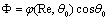 , while
, while 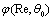 - factor depending on wave incidence angle
- factor depending on wave incidence angle 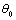 and flow Reynolds number Re. Its explicit expression is derived in[29]. In general case however
and flow Reynolds number Re. Its explicit expression is derived in[29]. In general case however 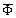 - is a factor dependent on and equals to unity in an order of magnitude. If solid particle is absent or replaced by vortex then crossection dependence
- is a factor dependent on and equals to unity in an order of magnitude. If solid particle is absent or replaced by vortex then crossection dependence 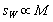 is transformed to
is transformed to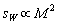 , because arbitrary flow (say, wake or vortex) scattering amplitude has the form
, because arbitrary flow (say, wake or vortex) scattering amplitude has the form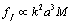 , while in the presence of solid particle it is
, while in the presence of solid particle it is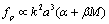 . Total expression for
. Total expression for 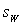 could be either the result of flow and particle contributions or - two types of flow contributions. Second case leads to
could be either the result of flow and particle contributions or - two types of flow contributions. Second case leads to 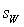 expression with
expression with 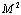 proportionality members only, being neglected in derivation of (13)[29], while
proportionality members only, being neglected in derivation of (13)[29], while 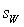 in that case takes the form
in that case takes the form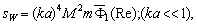 | (13a) |
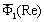 - the value of angle averaged function
- the value of angle averaged function 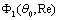 , factor depending on wave incidence angle
, factor depending on wave incidence angle 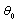 and flow Reynolds number Re. Factor
and flow Reynolds number Re. Factor 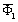 in (13а) bears a close analogy to factor
in (13а) bears a close analogy to factor 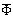 в (13). The only difference of
в (13). The only difference of 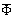 with respect to
with respect to 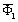 - the latter is not restricted to unity in an order of magnitude.At
- the latter is not restricted to unity in an order of magnitude.At 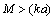 the monopole type of fluid flow outside wake is mainly responsible for sound scattering. Its contribution comprising three main components[27-30 and 32], exceeds particle and wake contributions. Corresponding angle averaged crossection expression
the monopole type of fluid flow outside wake is mainly responsible for sound scattering. Its contribution comprising three main components[27-30 and 32], exceeds particle and wake contributions. Corresponding angle averaged crossection expression 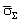 for chaotic flow motion could be reduced to the form
for chaotic flow motion could be reduced to the form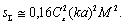 | (14) |
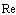 through
through 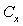 [2]. In[29] constant value equal to unity was taken for
[2]. In[29] constant value equal to unity was taken for 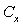 [3], but
[3], but 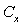 values can decrease down to 0.2 for larger
values can decrease down to 0.2 for larger 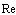 [2].All results cited above[26, 32] are valid for structures provided by solid chaotically moving particles or derived in conditions where motion inside inhomogeneity is somehow “frozen”, for instance (10). Expression (11) - (14) comprise weak enough components related to backward scattering generated by flows around moving inhomogeneity or reflected by its surface. For “full-blown” turbulence inhomogeneity structure changes and scattering crossection expressions should be further specified.The aim of the paper is development of alternative turbulent media sound scattering model based on spherically symmetric moving gas dynamic structure sound scattering problem solution, for instance, localized vortex problem and generalization of scattering attenuation laws on the basis mentioned.
[2].All results cited above[26, 32] are valid for structures provided by solid chaotically moving particles or derived in conditions where motion inside inhomogeneity is somehow “frozen”, for instance (10). Expression (11) - (14) comprise weak enough components related to backward scattering generated by flows around moving inhomogeneity or reflected by its surface. For “full-blown” turbulence inhomogeneity structure changes and scattering crossection expressions should be further specified.The aim of the paper is development of alternative turbulent media sound scattering model based on spherically symmetric moving gas dynamic structure sound scattering problem solution, for instance, localized vortex problem and generalization of scattering attenuation laws on the basis mentioned. 5. Localized Flow Scattering
- Let us single out stationary flow class to be used in turbulence scattering model development. Let us consider that spherical structure of radius а arbitrary related to sound wavelength is moving in the fluid. Sphere velocity V and ambient flow velocity
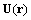 are constant and small with respect to sound velocity с. For generality sake, let us suppose that inner sphere substance acoustic properties are possible to coincide or differ from outer flow properties. For potential flow in ideal fluid velocity distribution described in moving frame of reference
are constant and small with respect to sound velocity с. For generality sake, let us suppose that inner sphere substance acoustic properties are possible to coincide or differ from outer flow properties. For potential flow in ideal fluid velocity distribution described in moving frame of reference 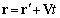 outside sphere is given by[3, 5-6]
outside sphere is given by[3, 5-6]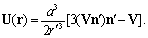 | (15) |
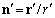 - unit vector,
- unit vector, 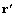 - radius vector in the frame of reference where moving sphere center is at rest. For viscose fluid moving at low Reynolds number, the flow is described by stationary Navier-Stokes linearized equation. After application of
- radius vector in the frame of reference where moving sphere center is at rest. For viscose fluid moving at low Reynolds number, the flow is described by stationary Navier-Stokes linearized equation. After application of 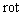 operation to both side of equation it is reduced to simple equation
operation to both side of equation it is reduced to simple equation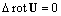 . Vortex flow around sphere moving with constant velocity
. Vortex flow around sphere moving with constant velocity 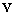 in viscose fluid is described with aid of vector potential А. On the basis of symmetry requirements it could be evaluated through scalar function
in viscose fluid is described with aid of vector potential А. On the basis of symmetry requirements it could be evaluated through scalar function  depending on scalar argument r by means of simple relationship
depending on scalar argument r by means of simple relationship 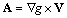 [3, 5-6]. Using this relation together with expression for flow velocity
[3, 5-6]. Using this relation together with expression for flow velocity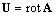 , equation could be rewritten in the form
, equation could be rewritten in the form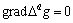 | (16) |
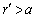 is included. Using sphere center velocity finiteness, we can solve equation (16) for
is included. Using sphere center velocity finiteness, we can solve equation (16) for 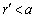 to have
to have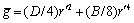 . Corresponding flow velocity distribution is[3]
. Corresponding flow velocity distribution is[3]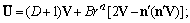 | (17) |
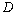 and
and 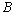 are to be found from boundary conditions at
are to be found from boundary conditions at 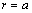 . Unlike solution (15) the flow defined by expression (17), is of vortex nature and its curl is nonzero. Simple enough calculations lead to the value of its vorticity
. Unlike solution (15) the flow defined by expression (17), is of vortex nature and its curl is nonzero. Simple enough calculations lead to the value of its vorticity 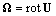 being equal to
being equal to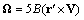 . It is worth to note, that expression (17) for viscose fluid vortex flow velocity is valid for ideal fluid as well. In fact, introducing (17) in equation
. It is worth to note, that expression (17) for viscose fluid vortex flow velocity is valid for ideal fluid as well. In fact, introducing (17) in equation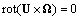 , being sequential to Euler equation (after application of
, being sequential to Euler equation (after application of 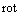 operation), we can see that it is satisfied identically. Solutions (15) and (17) in this case are to be sewed together on the basis of tangential and normal velocity identity at
operation), we can see that it is satisfied identically. Solutions (15) and (17) in this case are to be sewed together on the basis of tangential and normal velocity identity at 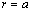 to found unknown factors
to found unknown factors 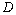 and В, being equal to
and В, being equal to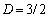 and
and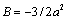 . For acoustical characteristics inside and outside sphere coincidence resulting flow defines Hill vortex[5]. Velocity distribution outside sphere is potential to be described by expression (15) with vorticity
. For acoustical characteristics inside and outside sphere coincidence resulting flow defines Hill vortex[5]. Velocity distribution outside sphere is potential to be described by expression (15) with vorticity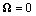 , while inside vortex nucleus the flow is vortex
, while inside vortex nucleus the flow is vortex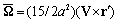 . In accordance to (17) velocity
. In accordance to (17) velocity 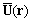 inside sphere is equal[5]
inside sphere is equal[5]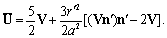 | (18) |
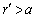 ) equation (16) generalized solution taking into account that
) equation (16) generalized solution taking into account that 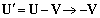 for
for 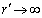 become
become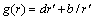 . In laboratory frame of reference it corresponds to flow velocity at
. In laboratory frame of reference it corresponds to flow velocity at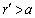 , equal to[4]
, equal to[4]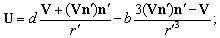 | (19) |
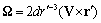 .It is worth to note that for
.It is worth to note that for 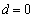 and
and 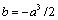 we formally obtain velocity distribution (15) with from (19). For solid sphere
we formally obtain velocity distribution (15) with from (19). For solid sphere 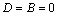 and velocity distribution (17), (19) is describing in fact potential flow generated by sphere moving in ideal fluid. If absolutely rigid sphere is moving in viscose fluid so that at sphere boundary
and velocity distribution (17), (19) is describing in fact potential flow generated by sphere moving in ideal fluid. If absolutely rigid sphere is moving in viscose fluid so that at sphere boundary 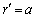 velocity
velocity  coincides with sphere center velocity V, Stokes flow with factors
coincides with sphere center velocity V, Stokes flow with factors 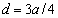 and
and 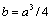 is obtained[3]. To obtain factors
is obtained[3]. To obtain factors 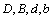 in general case of moving impedance sphere it is necessary that few conditions are to be fulfilled on sphere surface. First of all velocity normal components are to be equal and equals to
in general case of moving impedance sphere it is necessary that few conditions are to be fulfilled on sphere surface. First of all velocity normal components are to be equal and equals to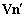 . In particular it leads to pair of equations
. In particular it leads to pair of equations 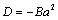 and
and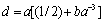 . Secondly, velocity tangential components are to be equal
. Secondly, velocity tangential components are to be equal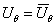 , leading to equation
, leading to equation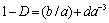 . And at last tangential stresses components are to be equal
. And at last tangential stresses components are to be equal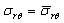 . Satisfying these conditions leads to results for
. Satisfying these conditions leads to results for  and
and 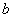 [3]
[3]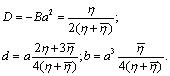 | (20) |
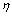 and
and 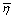 respectively. For rigid sphere
respectively. For rigid sphere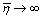 , while for homogeneous media inside and outside moving structure (say, vortex)
, while for homogeneous media inside and outside moving structure (say, vortex) 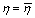 . In the last case it follows from (20) that factors are equal to
. In the last case it follows from (20) that factors are equal to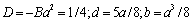 .Returning to localized flow sound scattering problem solution we note, that as in[23-32], sound propagation will be described in the frames of Lighthill equation becoming
.Returning to localized flow sound scattering problem solution we note, that as in[23-32], sound propagation will be described in the frames of Lighthill equation becoming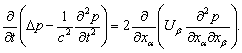 | (21) |
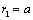 looks like
looks like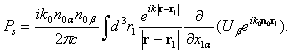 | (22) |
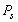 is expressed through scattering amplitude
is expressed through scattering amplitude 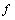 - the factor in outgoing spherical sound wave
- the factor in outgoing spherical sound wave 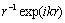 in expansion of (22), in following form
in expansion of (22), in following form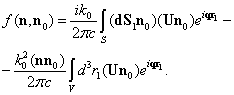 | (23) |
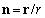 characterizes scattered wave propagation direction, while wave vector
characterizes scattered wave propagation direction, while wave vector 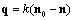 bears the sense of “impulse” delivered to fluid by wave. Its module equals to
bears the sense of “impulse” delivered to fluid by wave. Its module equals to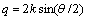 , where
, where 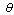 - scattering angle is defined by equation
- scattering angle is defined by equation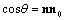 .As before[23-32], integration by parts in right hand side second summand of (23), is performed over entire region occupied by flow. It means that in rigid sphere motion integration is performed over region where
.As before[23-32], integration by parts in right hand side second summand of (23), is performed over entire region occupied by flow. It means that in rigid sphere motion integration is performed over region where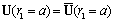
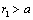 , while for liquid or gaseous drops or vortices it is performed not only for
, while for liquid or gaseous drops or vortices it is performed not only for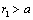 , but for
, but for 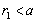 as well. First summand integration in (23) is performed over far enough surfaces and over both sides of spherical surface at
as well. First summand integration in (23) is performed over far enough surfaces and over both sides of spherical surface at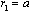 . Generally it can delimit flow regions with different velocities
. Generally it can delimit flow regions with different velocities 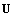 and
and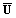 . Far enough surface integral is reduced to zero. It is obvious for potential flow (15), where velocity
. Far enough surface integral is reduced to zero. It is obvious for potential flow (15), where velocity 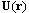 decreases with distance as
decreases with distance as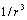 . For surface area is proportional to
. For surface area is proportional to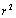 , integral is aimed to zero for
, integral is aimed to zero for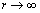 . For flows described by general expression (19) velocity
. For flows described by general expression (19) velocity 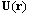 at
at 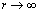 decreases slower - as
decreases slower - as 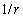 only and that is why integral may diverge. However, it is known[3, 6], that velocity distribution (19) is valid until distances of an order ~
only and that is why integral may diverge. However, it is known[3, 6], that velocity distribution (19) is valid until distances of an order ~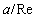 only, where
only, where 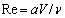 - flow Reynolds number. Analysis of more general equation
- flow Reynolds number. Analysis of more general equation 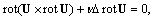 | (24) |
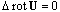 , shows that far from the body at
, shows that far from the body at 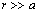 flow velocity decreases exponentially, proportionally to factor
flow velocity decreases exponentially, proportionally to factor 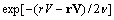 [3, 7]. That is why integral over far enough surfaces is reduced to zero in that case as well.Integral over spherical surface
[3, 7]. That is why integral over far enough surfaces is reduced to zero in that case as well.Integral over spherical surface 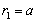 reduces to zero in the case where flow exists on both side of it only. It is observed when velocity on the surface
reduces to zero in the case where flow exists on both side of it only. It is observed when velocity on the surface 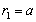 is continuous, i.e.
is continuous, i.e. 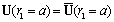 . For the case of rigid body motion the flow is observed on outer side of the body surface (
. For the case of rigid body motion the flow is observed on outer side of the body surface (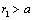 ) only, so that calculation show[23], that corresponding surface integral is non-zero. Resembling result is expected when tangential (or normal) velocity gap takes place on
) only, so that calculation show[23], that corresponding surface integral is non-zero. Resembling result is expected when tangential (or normal) velocity gap takes place on 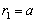 surface (say, due to mass exchange process). Integrals over inner and outer sides of sphere at
surface (say, due to mass exchange process). Integrals over inner and outer sides of sphere at 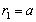 will not coincide and result will be non-zero as well.Now let us transform the only non-zero volume integral in the right hand side of (23) with aid of procedure used in[26]. It is based on identity known in theoretical hydrodynamics[5]
will not coincide and result will be non-zero as well.Now let us transform the only non-zero volume integral in the right hand side of (23) with aid of procedure used in[26]. It is based on identity known in theoretical hydrodynamics[5]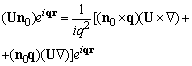 | (25) |
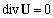 , we can rewrite expression (23) for f in the form
, we can rewrite expression (23) for f in the form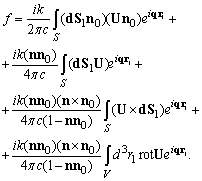 | (26) |
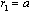 , for the case of rigid body motion only. In the cases of flow occupying entire space
, for the case of rigid body motion only. In the cases of flow occupying entire space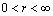 , integration is performed over both sides of surface
, integration is performed over both sides of surface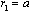 . However in the absence of velocity gap corresponding integrals cancel each other. Expression (26) is simplified and reduced to the form
. However in the absence of velocity gap corresponding integrals cancel each other. Expression (26) is simplified and reduced to the form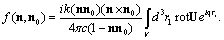 | (27) |
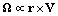 . With aid of it scattering amplitude
. With aid of it scattering amplitude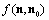 angular structure could be calculated. Integral (27) turn out to be proportional to
angular structure could be calculated. Integral (27) turn out to be proportional to 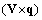 vector, while scattering amplitude is presented in the form
vector, while scattering amplitude is presented in the form | (28) |
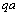 is denoted here as
is denoted here as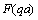 . It follows from expression (28) that scattering amplitudef turns to zero in backward scattering where equality
. It follows from expression (28) that scattering amplitudef turns to zero in backward scattering where equality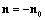 is valid and in the plane normal to wave incidence direction where
is valid and in the plane normal to wave incidence direction where or
or .It is worth to note that scattering amplitudef vanishing in backward scattering is continuous flows occupying entire space sound scattering general property. It is specific for not only localized flows under analysis. Being held for the case of sound scattering in unbounded turbulent media[19, 26 and 30] it obviated validity of doubts in results of[15] mentioned above in Sec.3.For evaluation of amplitude (28) angle dependence it is necessary to derive specific expression for
.It is worth to note that scattering amplitudef vanishing in backward scattering is continuous flows occupying entire space sound scattering general property. It is specific for not only localized flows under analysis. Being held for the case of sound scattering in unbounded turbulent media[19, 26 and 30] it obviated validity of doubts in results of[15] mentioned above in Sec.3.For evaluation of amplitude (28) angle dependence it is necessary to derive specific expression for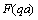 with its argument
with its argument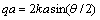 depending itself on scattering angle. We are to substitute in (27) expressions for vorticity outside and inside sphere derived above
depending itself on scattering angle. We are to substitute in (27) expressions for vorticity outside and inside sphere derived above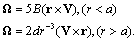 General expression for scattering amplitude for local flow (17), (19) acquires the form
General expression for scattering amplitude for local flow (17), (19) acquires the form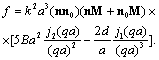 | (29) |
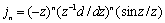 - is spherical Bessel function. Few already obtained useful results follows from (29). For instance for Hill vortex where
- is spherical Bessel function. Few already obtained useful results follows from (29). For instance for Hill vortex where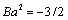 , and
, and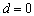 , scattering amplitude (29) acquires the form derived in[30] for the first time
, scattering amplitude (29) acquires the form derived in[30] for the first time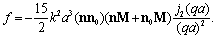 | (30) |
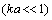 amplitudef is equal to
amplitudef is equal to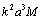 in an order of magnitude. Its behavior resembles scattering amplitude for potential flow near small rigid moving sphere in ideal fluid[23]. Turning to the low frequency limit in (30) we obtain Hill vortex scattering amplitude limiting value
in an order of magnitude. Its behavior resembles scattering amplitude for potential flow near small rigid moving sphere in ideal fluid[23]. Turning to the low frequency limit in (30) we obtain Hill vortex scattering amplitude limiting value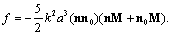 | (31) |
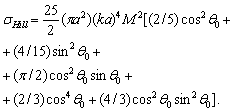 | (32) |
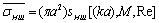 introduced above, we have
introduced above, we have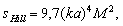 | (33) |
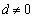 and vorticity
and vorticity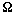 in outer sphere region is non-zero it follows from (29) that low frequency sound scattering amplitude turns out to be (
in outer sphere region is non-zero it follows from (29) that low frequency sound scattering amplitude turns out to be (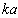 )-2 greater than in potential flow case. It is proportional toаМ and behaves as in the case of Stokes flow generated by sphere motion in viscose fluid[24]. If flow is restricted by particles surfaces or if flow velocity
)-2 greater than in potential flow case. It is proportional toаМ and behaves as in the case of Stokes flow generated by sphere motion in viscose fluid[24]. If flow is restricted by particles surfaces or if flow velocity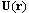 has the gap on the surface
has the gap on the surface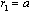 then surface integrals in general expression (26) are non-zero. As we have seen in that case scattering amplitude is non-zero even in the case of potential flow. To calculate integrals mentioned in general form let us introduce flow velocity on the surface
then surface integrals in general expression (26) are non-zero. As we have seen in that case scattering amplitude is non-zero even in the case of potential flow. To calculate integrals mentioned in general form let us introduce flow velocity on the surface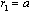 as a sum of components normal and tangential with respect to surface to have
as a sum of components normal and tangential with respect to surface to have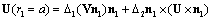 | (34) |
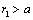 only or for flows occupying entire space
only or for flows occupying entire space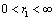 and even for flow with velocity gap on
and even for flow with velocity gap on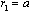 surface. With aid of (22) we can derive those factors
surface. With aid of (22) we can derive those factors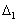 and
and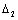 in equality (34) in first case take the values
in equality (34) in first case take the values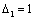 and
and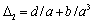 respectively. In second case velocity gap
respectively. In second case velocity gap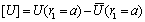 is presented in fact under integrals in three first summands of (26). For normal velocity component is to be continuous at
is presented in fact under integrals in three first summands of (26). For normal velocity component is to be continuous at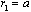 (gap is not allowed) then
(gap is not allowed) then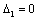 . In relation to tangential velocity component gap using (17) and (19) we find
. In relation to tangential velocity component gap using (17) and (19) we find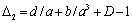 . In calculations of surface integrals in (26) with aid of (34) we perform integration over outer surface
. In calculations of surface integrals in (26) with aid of (34) we perform integration over outer surface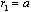 side i.e. we consider that
side i.e. we consider that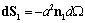 , where
, where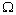 - space angle. Calculation of surface integrals leads to
- space angle. Calculation of surface integrals leads to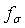 value
value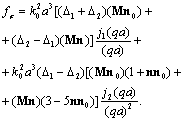 | (35) |
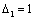 ,
,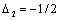 . It is result derived before in[23, 25]. We note that for small sphere in that case amplitude
. It is result derived before in[23, 25]. We note that for small sphere in that case amplitude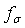 is
is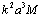 in an order of magnitude. In the absence of velocity gap at
in an order of magnitude. In the absence of velocity gap at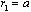 ,
,  and surface integrals in (35) are equal to zero. Scattering amplitude is defined by volume integral (27) exclusively. It is worth to note that unbounded space vortex flow scattering amplitude angular structure defined by (28), generally in the presence of other scatterers and velocity gap surfaces could lose correctness. As it follows from (35) backward scattering could be observed while scattering amplitudef could be non-zero in the plane normal to wave incidence direction (at
and surface integrals in (35) are equal to zero. Scattering amplitude is defined by volume integral (27) exclusively. It is worth to note that unbounded space vortex flow scattering amplitude angular structure defined by (28), generally in the presence of other scatterers and velocity gap surfaces could lose correctness. As it follows from (35) backward scattering could be observed while scattering amplitudef could be non-zero in the plane normal to wave incidence direction (at ). Moreover contributions of flows in the vicinity of vortex or inhomogeneities in scattered fields could be expected. That is why observation of weak backward scattering contribution in turbulent media sound scattering is related mainly to rescattering, wake flows and passive touch influence. From our point weak backward scattering observation evidences multiplicity of chaotically moving scattering inhomogeneities (flows) contributing to scattering thus supporting corpuscular model of turbulent media developed here instead of formerly used model of sound scattering by large scale continuous flow.
). Moreover contributions of flows in the vicinity of vortex or inhomogeneities in scattered fields could be expected. That is why observation of weak backward scattering contribution in turbulent media sound scattering is related mainly to rescattering, wake flows and passive touch influence. From our point weak backward scattering observation evidences multiplicity of chaotically moving scattering inhomogeneities (flows) contributing to scattering thus supporting corpuscular model of turbulent media developed here instead of formerly used model of sound scattering by large scale continuous flow.6. Models of Scattering Media
- Now we are to complete scattering medium model formulation. In the frame of model we suppose isotropic and homogeneous turbulence as a set of localized flows of various scales from outer to Kolmogorov’s. In basic flow disintegration on localized flows (vortices), say, of scale
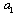 , chaotic fluctuations of not only the direction of average initial flow velocity
, chaotic fluctuations of not only the direction of average initial flow velocity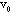 are observed. In other words, scale
are observed. In other words, scale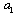 motion is more isotropic than average flow. In the same way in scale
motion is more isotropic than average flow. In the same way in scale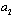 formation from scale
formation from scale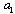 , fluctuations isotropy increases with a number of vortexes born, while basic flow influence decreases and so on. As a result after few “multiplication” stages turbulent flow becomes isotropic. In other words, in full-blown turbulence almost all vortex structure sets, except most large, are statistically homogeneous and isotropic. The larger basic flow Reynolds number
, fluctuations isotropy increases with a number of vortexes born, while basic flow influence decreases and so on. As a result after few “multiplication” stages turbulent flow becomes isotropic. In other words, in full-blown turbulence almost all vortex structure sets, except most large, are statistically homogeneous and isotropic. The larger basic flow Reynolds number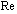 value, the more fragmentation number with scales decreasing from
value, the more fragmentation number with scales decreasing from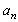 until
until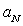 is observed. In inertial scale interval
is observed. In inertial scale interval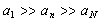 vortex structures are distinguished by dimensions and velocity directions only. They are universal for turbulent flows, because they have already “forgotten” basic flow structure, while viscose forces are still not important. In non-dissipative media where viscosity influences can be ignored basic these features of model are sufficient. However in realistic media scattering evaluation (in the presence of viscosity) numerical strength of most small inner “Kolmogorov” scale vortices will play substantial role. The only phenomenon side to pay attention for – is two turbulence models – “weak” and “strong”.
vortex structures are distinguished by dimensions and velocity directions only. They are universal for turbulent flows, because they have already “forgotten” basic flow structure, while viscose forces are still not important. In non-dissipative media where viscosity influences can be ignored basic these features of model are sufficient. However in realistic media scattering evaluation (in the presence of viscosity) numerical strength of most small inner “Kolmogorov” scale vortices will play substantial role. The only phenomenon side to pay attention for – is two turbulence models – “weak” and “strong”. 6.1. Weak Turbulence Model
- In first model to be fair probably for flows with small enough initial vorticity, say, in wind tunnels or various small scale flow models[2, 6] – we use moving with velocity
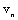 in arbitrary direction acoustically “transparent” sphere (12) of inertial range scale
in arbitrary direction acoustically “transparent” sphere (12) of inertial range scale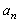 as basic structure (c.f. Fig.4). In turbulent flow region structures motion is completely chaotic and of zero vorticity while expression (3) for attenuation factor
as basic structure (c.f. Fig.4). In turbulent flow region structures motion is completely chaotic and of zero vorticity while expression (3) for attenuation factor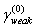 with aid of (5), (6) and (12) takes the form
with aid of (5), (6) and (12) takes the form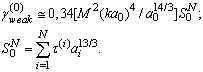 | (36) |
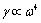 is expected here as in[4, 15 and 17-22]. In principle, i-th type basic structure volume content factor
is expected here as in[4, 15 and 17-22]. In principle, i-th type basic structure volume content factor 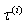 - is different for various structures. They can be assumed the same and equal to unity for all scales in simplest case of full-blown homogeneous isotropic turbulence however. Numbers Mandunder summation sign and scale
- is different for various structures. They can be assumed the same and equal to unity for all scales in simplest case of full-blown homogeneous isotropic turbulence however. Numbers Mandunder summation sign and scale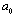 , are related to basic flow and supposed to be known.
, are related to basic flow and supposed to be known.6.2. Strong Turbulence Model
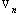 in arbitrary direction Hill vortex (33) of inertial range scale
in arbitrary direction Hill vortex (33) of inertial range scale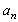 as basic structure. Its inner flow is shown qualitatively on Fig.5. As before for “weak” turbulence model – all scales of such elements from outer
as basic structure. Its inner flow is shown qualitatively on Fig.5. As before for “weak” turbulence model – all scales of such elements from outer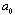 to inner (Kolmogorov’s)
to inner (Kolmogorov’s) 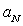 are present in model.Moving to the right “strong” turbulence model basic element (spherical Hill vortex) meridian plane hydrodynamic velocity field lines are shown on Fig.5. Characteristic parameters of substance inside vortex
are present in model.Moving to the right “strong” turbulence model basic element (spherical Hill vortex) meridian plane hydrodynamic velocity field lines are shown on Fig.5. Characteristic parameters of substance inside vortex 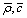 coincide with outside parameters. It ensures basic structure acoustic “transparency” and thus scattering is provided by fluid flow inside and outside structure only. Vortex lines are situated in the planes normal to structure symmetry axis. Flow velocity field lines are tightened around thick points on Fig.5[5]. In that case fluid flow in turbulent volume is partly vortex (inside vortexes) completely chaotically and expression (3) for attenuation factor
coincide with outside parameters. It ensures basic structure acoustic “transparency” and thus scattering is provided by fluid flow inside and outside structure only. Vortex lines are situated in the planes normal to structure symmetry axis. Flow velocity field lines are tightened around thick points on Fig.5[5]. In that case fluid flow in turbulent volume is partly vortex (inside vortexes) completely chaotically and expression (3) for attenuation factor 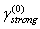 with aid of (5), (6) and (33) takes the form
with aid of (5), (6) and (33) takes the form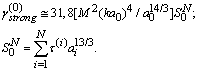 | (37) |
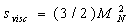 [24] in conditions where structure inertia is to be neglected. Kolmogorov’s vortexes volume fraction can be taken equal to unity for preliminary evaluation. Large Reynolds number flows sound scattering was studied in[27-30 and 32] and it was shown that scattered sound structure and spectrum are dependent on relationship of structure Mach number
[24] in conditions where structure inertia is to be neglected. Kolmogorov’s vortexes volume fraction can be taken equal to unity for preliminary evaluation. Large Reynolds number flows sound scattering was studied in[27-30 and 32] and it was shown that scattered sound structure and spectrum are dependent on relationship of structure Mach number 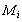 and wave dimension
and wave dimension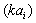 in inertial scale range. At least three cases are available. In first case at
in inertial scale range. At least three cases are available. In first case at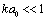 and
and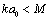 , low frequency sound wave is scattered in inertia structures scale range. Vortex flow outside wake is responsible mainly for sound scattering defined by first monopole summand of (19). Hill vortex (33) is used here as a basic structure with dimension
, low frequency sound wave is scattered in inertia structures scale range. Vortex flow outside wake is responsible mainly for sound scattering defined by first monopole summand of (19). Hill vortex (33) is used here as a basic structure with dimension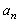 belonging to inertial scales interval and moving with velocity
belonging to inertial scales interval and moving with velocity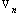 in arbitrary direction. Resulting flow is vortex (inside vortex volumes and partly outside wake) and completely chaotic. Expression (3) for attenuation factor
in arbitrary direction. Resulting flow is vortex (inside vortex volumes and partly outside wake) and completely chaotic. Expression (3) for attenuation factor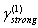 allowing for sound scattering by Kolmogorov’s scale turbulence with aid of (5), (6), (33) and (14) takes the form
allowing for sound scattering by Kolmogorov’s scale turbulence with aid of (5), (6), (33) and (14) takes the form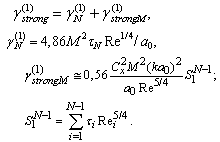 | (38) |
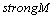 » in (38) indicates influence of monopole type flow outside wake.In second case at
» in (38) indicates influence of monopole type flow outside wake.In second case at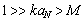 slightly higher frequency sound wave is scattered in inertial turbulence scale where inner structure volume and laminar wake beside it are responsible for scattering. Hill vortex (33) is used here as a basic structure with dimension
slightly higher frequency sound wave is scattered in inertial turbulence scale where inner structure volume and laminar wake beside it are responsible for scattering. Hill vortex (33) is used here as a basic structure with dimension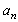 belonging to inertial scales interval and moving with velocity
belonging to inertial scales interval and moving with velocity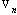 in arbitrary direction. Resulting flow is vortex (inside vortex volumes and partly inside wake) and completely chaotic. Expression (3) for attenuation factor
in arbitrary direction. Resulting flow is vortex (inside vortex volumes and partly inside wake) and completely chaotic. Expression (3) for attenuation factor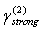 allowing for sound scattering by Kolmogorov’s scale turbulence with aid of (6), (8), (33) and (13a) takes the form
allowing for sound scattering by Kolmogorov’s scale turbulence with aid of (6), (8), (33) and (13a) takes the form 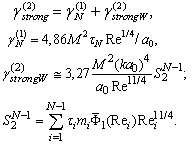 | (39) |
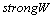 » in (39) indicates influence of moving vortex wake. In third case, for given sound frequency in turbulence inertial scale range first case of scattering is observed in definite range part, while second case of scattering is observed in reminder part. Hill vortex (33) is used here as a basic structure with dimension
» in (39) indicates influence of moving vortex wake. In third case, for given sound frequency in turbulence inertial scale range first case of scattering is observed in definite range part, while second case of scattering is observed in reminder part. Hill vortex (33) is used here as a basic structure with dimension belonging to inertial scales interval and moving with velocity
belonging to inertial scales interval and moving with velocity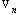 in arbitrary direction. Resulting flow is vortex (inside vortex volumes, inside wake and partly outside wake) and completely chaotic. Expression (3) for attenuation factor
in arbitrary direction. Resulting flow is vortex (inside vortex volumes, inside wake and partly outside wake) and completely chaotic. Expression (3) for attenuation factor 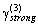 allowing for sound scattering by Kolmogorov’s scale turbulence with aid of (5), (6), (33), (13a) and (14) takes the form
allowing for sound scattering by Kolmogorov’s scale turbulence with aid of (5), (6), (33), (13a) and (14) takes the form 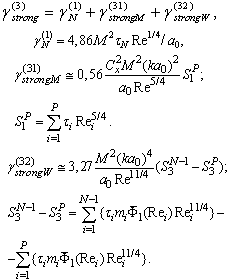 | (40) |
 corresponds to sum term number for which at definite
corresponds to sum term number for which at definite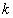 relationship
relationship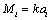 is attained. In other words, related to turbulence scale
is attained. In other words, related to turbulence scale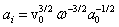 . It is worth to note passive touch (say, dust) role in sound scattering – it is more noticeable in particles scale range
. It is worth to note passive touch (say, dust) role in sound scattering – it is more noticeable in particles scale range . Finer scale touch particles have negligible influence on total scattering. Quite the contrary, when condition
. Finer scale touch particles have negligible influence on total scattering. Quite the contrary, when condition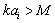 is valid total sound attenuation factor
is valid total sound attenuation factor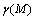 can change from the form (16а) -
can change from the form (16а) - 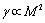 , at least partly to the form (13) -
, at least partly to the form (13) - 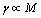 , providing more intensive sound wave scattering.
, providing more intensive sound wave scattering.7. Discussion
- Thus, in general, for touchless turbulence, attenuation factor spectrum in realistic viscose turbulent medium depends on frequency in the following manner. At lowest frequencies as well as for small M, key contribution to total attenuation provides scattering of sound by Kolmogorov’s turbulence scale
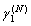 . It is independent of frequency and provides definite attenuation spectrum pedestal. Further on with frequency increase at
. It is independent of frequency and provides definite attenuation spectrum pedestal. Further on with frequency increase at 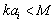 attenuation component
attenuation component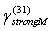 related to scattering on flow vorticity outside moving structure and structure wake come into force. This spectrum component increases with frequency squired until scales where
related to scattering on flow vorticity outside moving structure and structure wake come into force. This spectrum component increases with frequency squired until scales where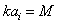 . And, at last, at
. And, at last, at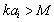 attenuation component
attenuation component 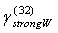 related to scattering inside moving structure wake and volume come into force. This spectrum component increases with frequency fourth grade until
related to scattering inside moving structure wake and volume come into force. This spectrum component increases with frequency fourth grade until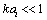 for scales up to
for scales up to  , if
, if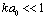 for sure. These laws are partly different from well-known propositions of wave turbulence scattering theory[1, 4, 15 and 17-19]. Moreover, mentioned component relationship (40) depends additionally on a set of internal problem factors, say, Mach number, Reynolds number and several numerical factors. It could be changed in changing conditions. That is why mentioned above Sieg experiment results[1, 33] for small M look understandable. They rather allow discussing turbulent flow structure in experiments. Preliminary quantitate estimates are performed on the basis of spectrum pedestal mentioned above
for sure. These laws are partly different from well-known propositions of wave turbulence scattering theory[1, 4, 15 and 17-19]. Moreover, mentioned component relationship (40) depends additionally on a set of internal problem factors, say, Mach number, Reynolds number and several numerical factors. It could be changed in changing conditions. That is why mentioned above Sieg experiment results[1, 33] for small M look understandable. They rather allow discussing turbulent flow structure in experiments. Preliminary quantitate estimates are performed on the basis of spectrum pedestal mentioned above 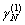 . In fact, in Sieg experiment frequency range 250 – 4000 Hz[1, 33-34], condition
. In fact, in Sieg experiment frequency range 250 – 4000 Hz[1, 33-34], condition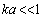 is to be met even for outer turbulence scale. So that
is to be met even for outer turbulence scale. So that 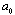 should be of an order of 10-2 m. At
should be of an order of 10-2 m. At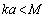 contributions of second (
contributions of second (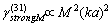 ) and third (
) and third (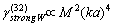 ) summands of (40) are to be neglected with respect to contribution of (
) summands of (40) are to be neglected with respect to contribution of (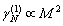 ). To evaluate boundary frequency value it is of use to note, that expression for
). To evaluate boundary frequency value it is of use to note, that expression for is derived with aid of (21), in condition where flow is described by equation (16). That is when it is possible to neglect partial time derivative in (16) in expression for total derivative[28, 32]. In other words when flow vorticity exceed characteristic incident sound frequency. Estimates on the basis of vorticity expression
is derived with aid of (21), in condition where flow is described by equation (16). That is when it is possible to neglect partial time derivative in (16) in expression for total derivative[28, 32]. In other words when flow vorticity exceed characteristic incident sound frequency. Estimates on the basis of vorticity expression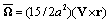 for outer atmosphere turbulence scale
for outer atmosphere turbulence scale and wind velocities in Sieg experiments lead to frequency boundary value of an order 150 – 250 Hz[33]. For wind velocity in interval 1 - 2 m/s, Reynolds number
and wind velocities in Sieg experiments lead to frequency boundary value of an order 150 – 250 Hz[33]. For wind velocity in interval 1 - 2 m/s, Reynolds number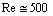 , Mach number squared
, Mach number squared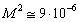 , give for
, give for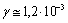 m-1. Resulting attenuation is close to value 1 – 1.5 dB at 100 m, as in Sieg data[1, 33-34], without frequency dependence of
m-1. Resulting attenuation is close to value 1 – 1.5 dB at 100 m, as in Sieg data[1, 33-34], without frequency dependence of . For wind velocity increase up to 10 m/s at frequency 250 Hz taking into account outer scale increase we obtain
. For wind velocity increase up to 10 m/s at frequency 250 Hz taking into account outer scale increase we obtain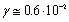 m-1, attenuation close to 7 dB at 100 meters. Further increase of
m-1, attenuation close to 7 dB at 100 meters. Further increase of with frequency and wind velocity observed in experiment coincides with law (40) accounting for spectra
with frequency and wind velocity observed in experiment coincides with law (40) accounting for spectra 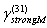 and
and 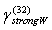 . It evidences qualitative coincidence of proposed model predictions with experiment. Typical attenuation factor
. It evidences qualitative coincidence of proposed model predictions with experiment. Typical attenuation factor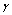 frequency (wave parameter) dependence derived in the frames of corpuscular turbulence scattering models for “weak” (curves 1, 3) and “strong” (curves 2, 3, 4, 5) turbulent media are shown on Fig.6. Dependence related to well-known turbulence wave model[4, 18] – curve 6 while crosses[1, 33] show Sieg experiment results.It is seen that available experimental data on sound attenuation in atmosphere are explained by proposed “strong” turbulence scattering corpuscular model (zero frequency power dependence,
frequency (wave parameter) dependence derived in the frames of corpuscular turbulence scattering models for “weak” (curves 1, 3) and “strong” (curves 2, 3, 4, 5) turbulent media are shown on Fig.6. Dependence related to well-known turbulence wave model[4, 18] – curve 6 while crosses[1, 33] show Sieg experiment results.It is seen that available experimental data on sound attenuation in atmosphere are explained by proposed “strong” turbulence scattering corpuscular model (zero frequency power dependence,  ), while known wave models in low frequency range (fourth frequency power dependence,
), while known wave models in low frequency range (fourth frequency power dependence, 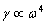 ) are at noticeable variance with experimental data.
) are at noticeable variance with experimental data.8. Conclusions
- As a general paper result we can conclude:It is recommended to use in turbulent media low frequency sound scattering and attenuation modeling “corpuscular” model of scattering developed in the paper. The model comprises media as a set of chaotically situated and moving localized flows of various scales. Both inner and outer flow parts are responsible for scattering.In the absence of boundaries scattering amplitude of arbitrary continuous flow (say, turbulent flow) for arbitrary relationship of characteristic scale to sound wavelength is defined by flow vorticity and turns to zero for backward scattering and for scattering in the plane normal to wave incidence direction. For further sound scattering and attenuation modeling applications we can recommend to take into account specific features of model:Turbulence non-dissipative attenuation factor frequency spectrum acquires ordinary Rayleigh law form
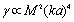 - the same form as in known turbulence sound scattering models. Spectrum increases with fourth frequency degree until
- the same form as in known turbulence sound scattering models. Spectrum increases with fourth frequency degree until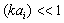 up to scale
up to scale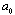 , if
, if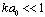 . Normalized factors for corpuscular models of “strong” and “weak” turbulent media differs in two orders due to contribution of inner flow in “strong” turbulence scattering model, but for low frequency sound scattering at low Mach number both models are to be provided with contribution of viscose flow corrections scattering.Corrections to attenuation factor spectrum related to viscosity influence depend on frequency in the following way. In low Mach number low sound frequency case defining contribution is provided by sound scattering on Kolmogorov’s scale turbulent fluctuations. It is perceptible in any frequency range providing a kind of pedestal for attenuation spectrum. Then with frequency increase at
. Normalized factors for corpuscular models of “strong” and “weak” turbulent media differs in two orders due to contribution of inner flow in “strong” turbulence scattering model, but for low frequency sound scattering at low Mach number both models are to be provided with contribution of viscose flow corrections scattering.Corrections to attenuation factor spectrum related to viscosity influence depend on frequency in the following way. In low Mach number low sound frequency case defining contribution is provided by sound scattering on Kolmogorov’s scale turbulent fluctuations. It is perceptible in any frequency range providing a kind of pedestal for attenuation spectrum. Then with frequency increase at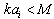 , spectrum component related to vorticity outside model structures and their wakes come into force. This spectrum component increases with frequency squared in scale range until scales
, spectrum component related to vorticity outside model structures and their wakes come into force. This spectrum component increases with frequency squared in scale range until scales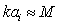 . And, at last, at
. And, at last, at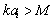 spectrum component related to vorticity inside model structures and inside their wakes come into force. This spectrum component increases with frequency fourth degree in scale range until
spectrum component related to vorticity inside model structures and inside their wakes come into force. This spectrum component increases with frequency fourth degree in scale range until up to scale
up to scale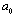 , if
, if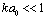 .Passive touch (say, dust) contribution to turbulence sound scattering – is most perceptible for particles scales in the range
.Passive touch (say, dust) contribution to turbulence sound scattering – is most perceptible for particles scales in the range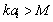 . Finer scale touch particles have negligible influence on total scattering. Quite the contrary, when condition
. Finer scale touch particles have negligible influence on total scattering. Quite the contrary, when condition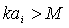 is valid total sound attenuation factor
is valid total sound attenuation factor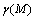 can change from the form
can change from the form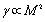 , at least partly to the form
, at least partly to the form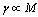 , providing more intensive sound wave scattering.
, providing more intensive sound wave scattering. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML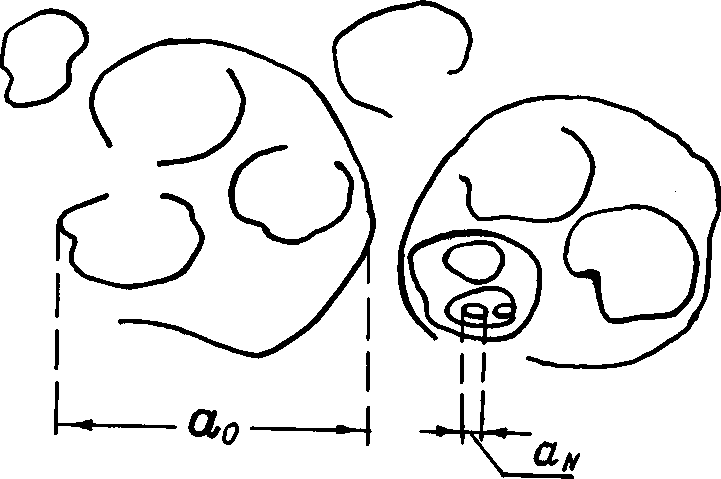
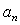 of contributing structures (fluctuations or vortices) from outer
of contributing structures (fluctuations or vortices) from outer 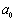 to inner (Kolmogorov’s) scale
to inner (Kolmogorov’s) scale 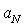 are presented[18]
are presented[18]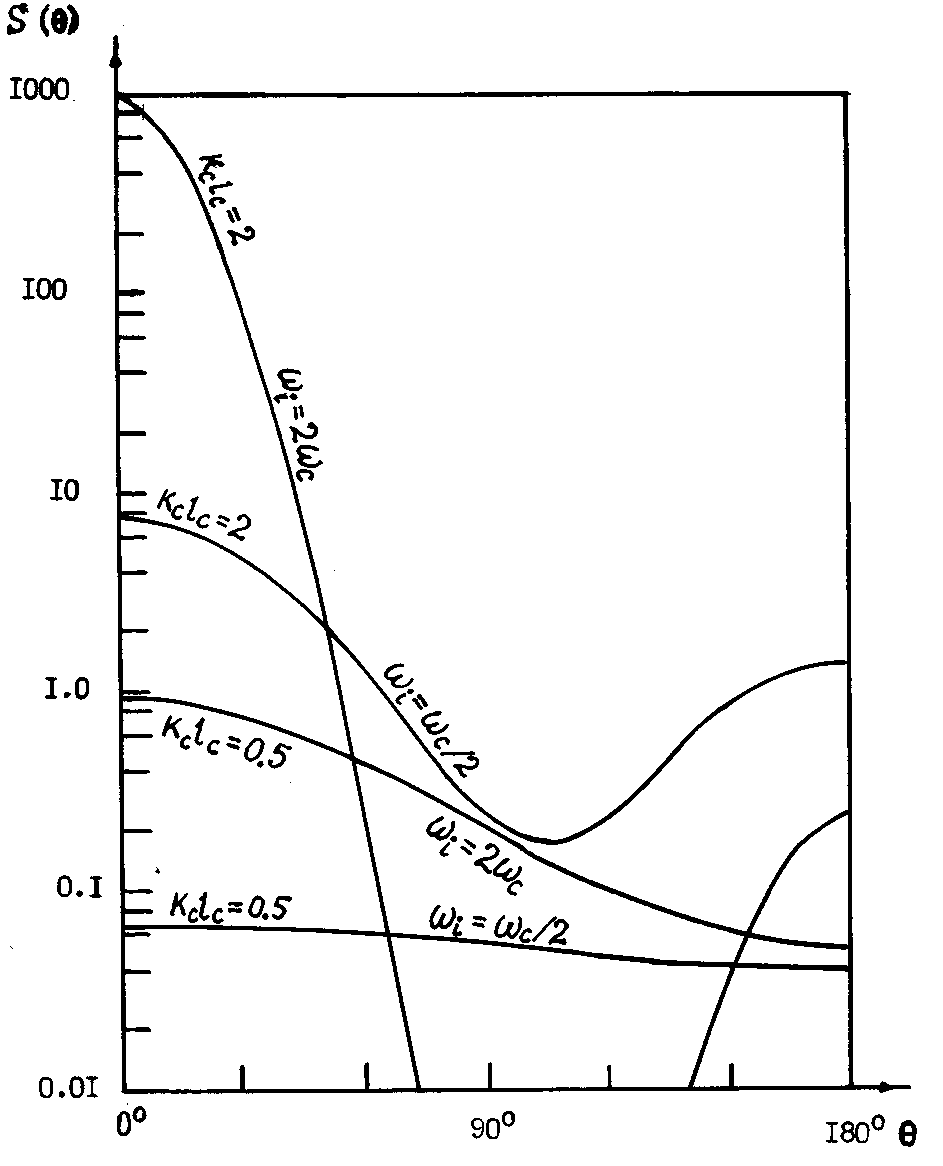
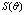 [15] of full-blown turbulence region for various incident wave frequency
[15] of full-blown turbulence region for various incident wave frequency 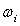 relationships with characteristic correlation function frequency
relationships with characteristic correlation function frequency 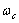 for various parameter
for various parameter 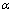 values
values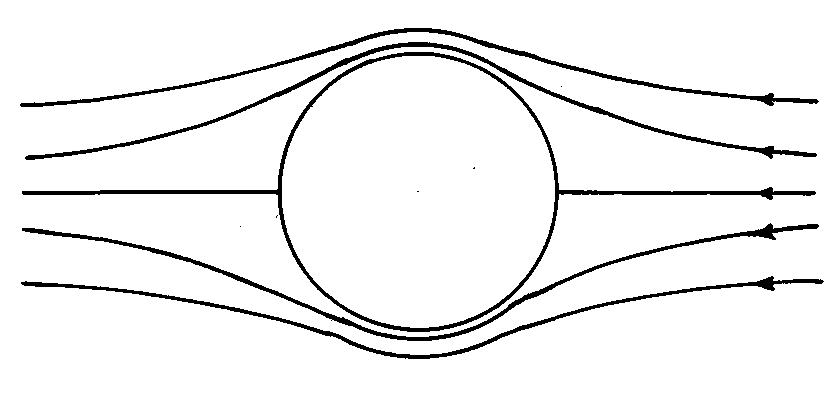
 as outside. All scales
as outside. All scales  of turbulence corpuscular structure chaotically moving elements from outer
of turbulence corpuscular structure chaotically moving elements from outer  to inner
to inner  are presented[5]
are presented[5]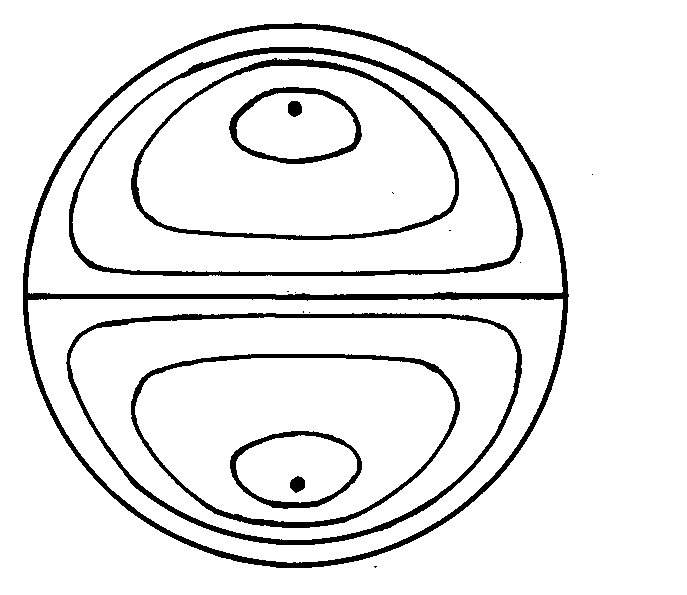
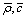 as outside. All scales
as outside. All scales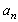 of chaotically moving elements - from outer scale
of chaotically moving elements - from outer scale 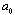 to inner scale
to inner scale 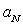 represent turbulence corpuscular structure
represent turbulence corpuscular structure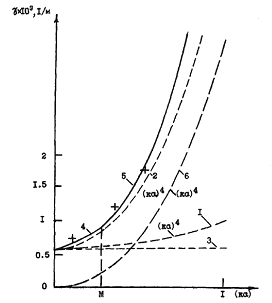
 (multiplied by 103) frequency (wave number parameter
(multiplied by 103) frequency (wave number parameter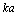 ) dependencies developed in the frames of atmospheric turbulence scattering corpuscular models for strong (curves 2, 4, 5) and weak (curve 1) turbulent wind flow regimes[30]
) dependencies developed in the frames of atmospheric turbulence scattering corpuscular models for strong (curves 2, 4, 5) and weak (curve 1) turbulent wind flow regimes[30]