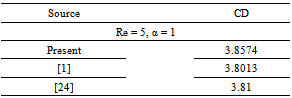Atta Sojoudi1, Suvash C. Saha2
1Mechanical engineering department of Sharif University of technology, Tehran, Iran
2School of Chemistry, Physics and Mechanical Engineering, Queensland University of Technology, GPO Box 2434, Brisbane QLD 4001, Australia
Correspondence to: Suvash C. Saha, School of Chemistry, Physics and Mechanical Engineering, Queensland University of Technology, GPO Box 2434, Brisbane QLD 4001, Australia.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
In present work, numerical solution is performed to study the confined flow of power-law non Newtonian fluids over a rotating cylinder. The main purpose is to evaluate drag and thermal coefficients as functions of the related governing dimensionless parameters, namely, power-law index (0.5 ≤ n ≤ 1.4), dimensionless rotational velocity (0 ≤ α ≤ 6) and the Reynolds number (100 ≤ Re ≤ 500). Over the range of Reynolds number, the flow is known to be steady. Results denoted that the increment of power law index and rotational velocity increases the drag coefficient due to momentum diffusivity improvement which is responsible for low rate of heat transfer, because the thicker the boundary layer, the lower the heat transfer is implemented.
Keywords:
Laminar Flow, Non-Newtonian Fluid, Rotating Cylinder, Numerical Solution
Cite this paper:
Atta Sojoudi, Suvash C. Saha, "Shear Thinning and Shear Thickening Non- Newtonian Confined Fluid Flow over Rotating Cylinder", American Journal of Fluid Dynamics, Vol. 2 No. 6, 2012, pp. 117-121. doi: 10.5923/j.ajfd.20120206.04.
1. Introduction
Most real fluids in industrial and academic applications aren't considered as Newtonian fluids, they denote non-Newtonian behavior, in which the shear stress is not linearly proportional to the velocity gradient. Typical examples can be polymer melts and solutions, foams, emulsions and suspensions, etc.[1]. Non-Newtonian fluids are divided into two categories: (1) shear-thinning fluids, and (2) shear-thickening fluids. Behavior and response to shear stress of shear-thinning and shear-thickening fluids are shown in Fig. 1. Newtonian fluids flow across cylinders is one of those typical problems have been investigated in many researches due to extensive applications[2–6]. Also imposing rotation to cylinders in order to control boundary layer on cylinder or other kinds of bluff bodies has been devoted much attention[7,8]. Non Newtonian fluids flow over rotating cylinders is included in many industrial applications such as coating operations, roller bearing applications, oil drilling operations, mixing vessels with novel impeller designs, etc. As Newtonian fluids flow over cylinder is not steady for every Re, non Newtonian fluids have also critical Re showing unsteadiness at about Re = 46–47 which is reported in[9,10]. Finally, again the flow reverts to a steady flow regime at Re = 100. Admittedly, extensive accurate results are now available on the momentum and heat transfer characteristics for a stationary cylinder in unconfined power-law fluids in the steady flow regime[11–15] for both shear-thinning and shear-thickening fluids. It has shown in the literature that for low Reynolds numbers, shear-thinning behavior increases drag above its Newtonian value and shear-thickening has repercussive effect. Patnana et al[10,11] studied the flow and heat transfer phenomena from a cylinder swamped in power law fluids in the laminar vortex shedding regime. Also researcher's results are available for elliptic cylinders[16,17] and square[18,19]submerged in confined and unconfined power-law fluids using steady state assumption. But Sahu[20] reported on the unsteady flow over a square cylinder in the laminar vortex shedding regime.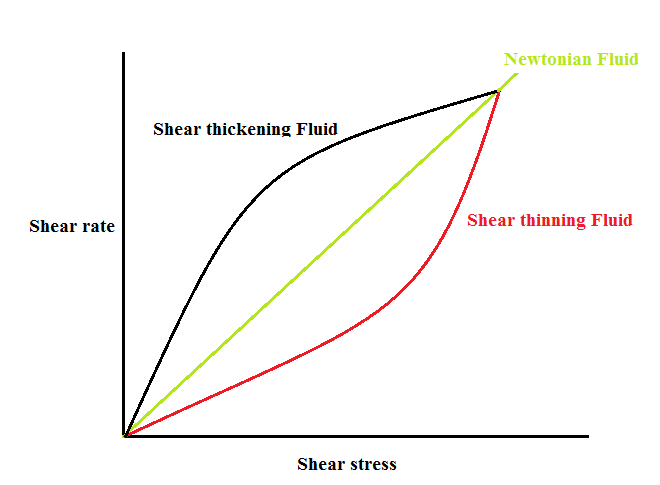 | Figure 1. Shear-thinning and shear-thickening fluids |
A comprehensive literature exists on the viscoelastic fluids flow over a stationary circular cylinder[21]; At low Re, viscoelasticity decreases the drag on a cylinder beneath its Newtonian value and it increments the drag at high Re.According to the authors knowledge, there have been only three reports on the flow of non-Newtonian fluids over a rotating cylinder. Christiansen[22,23] has reported experimental data on the local velocity field for a cylinder rotating in Newtonian and polymer solutions of varying levels of shear-thinning and viscoelasticity using laser-Doppler anemometry. Also, Panda and Chhabra[24] has studied the low Re non Newtonian shear thinning over rotating cylinder. They compared their results with[22,23] and showed only the behavior of shear thinning fluids for unconfined flow. But it is well known that the fluids flow should be implemented through a pipe or other confined channels. So investigation of non-Newotonian confined fluid flow over rotating Cylinder is still in rare and the present work will fill this gap. Also[24] has not reported any result for shear thickening fluids and as we know the industrial applications include the both kinds of non Newtonian fluids. It is thus safe to conclude that very little is known about the flow of high Re (in laminar range) non-Newtonian fluids past a rotating cylinder. This work is thus concerned with the flow of power-law fluids past a rotating cylinder over the range of conditions power-law index (0.5 ≤ n ≤ 1.4), dimensionless rotational velocity (0 ≤ α ≤ 6) and the Reynolds number (100 ≤ Re ≤ 500) over which the flow is expected to be steady and two-dimensional. After validation of results with[1] and[24], the both drag and thermal coefficients will be developed for the above range of variations.
2. Problem Statement and Governing Equations
We assume that the fluid is incompressible with uniform velocity U0 flowing over a cylinder of diameter D (infinite length in z-direction) rotating with an angular velocity of Ω in the counter-clockwise direction, as shown in Fig. 2. The cylinder is located at the center of a square of size H. The continuity and momentum equations written as follows[24]:• Continuity: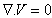 | (1) |
• Momentum: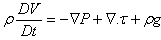 | (2) |
where ρ, V, P, τ and g, respectively, are the fluid density, velocity vector, isotropic pressure, extra stress tensor and gravity. The components of the extra stress tensor τij are emerged as: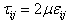 | (3) |
where the rate of deformation tensor and the scalar viscosity function are introduced by: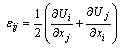 | (4) |
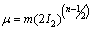 | (5) |
n is the power-law index. Admittedly, n = 1 denotes the Newtonian fluid, n < 1 denotes shear-thinning and n > 1 shows shear-thickening treatment. 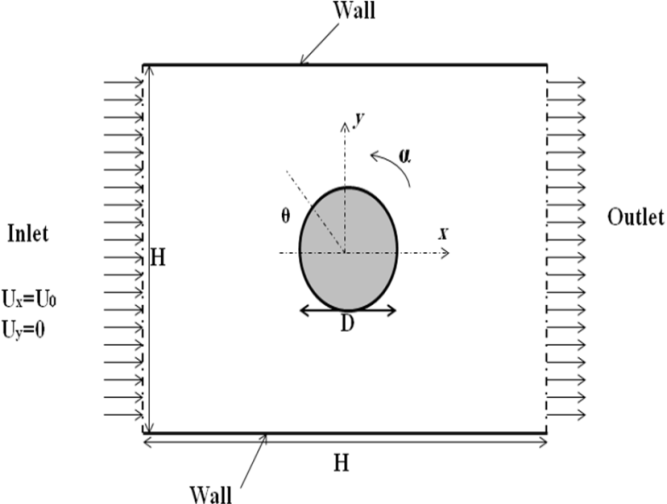 | Figure 2. Physical modelling |
Boundary conditions for this flow are written as follows:(1) inlet : It is the uniform flow in x-direction, i.eUx = U0, Uy = 0(2) No slip condition is assumed for top and bottom walls. These walls are insulated.Ux = 0; Uy = 0(3) Surface of the solid cylinder: The standard no-slip boundary condition is used, i.e.,Ux = −αsinθ and Uy = −αcosθthermal boundary condition used for the cylinder is constant temperature which is same for all simulations. (4) Outlet: Fully developed condition is imposed on the exit plane. This is similar to the homogeneous Neumann condition, that is,∂Ux/∂x = 0 and ∂Uy/∂x = 0The governing Eqs. (1) and (2) are solved numerically together with the mentioned boundary conditions. Then Ux, Uy and p are post processed to calculate the derived quantities such as stream function, drag and thermal coefficients as functions Reynolds number (Re), power-law index (n) and the non-dimensional rotational velocity of the cylinder (α). It is appropriate to introduce the definitions of some of these parameters as follows:• Reynolds number (Re)Re = (ρU02-nDn)/m• Rotational velocity (α)α = (DΩ/2U0)• Prandtl number (Pr)Pr = (UD/αt)Re(-2/n+1)• Thermal efficiency coefficient (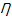 )
) = Nu/Pr1/3• Nusselt number (Nu)Nu = hD/K• Drag coefficient (CD)CD=(2FD/ρU02D)where FD is the drag force in the direction of flow exerted on the cylinder per unit length.
= Nu/Pr1/3• Nusselt number (Nu)Nu = hD/K• Drag coefficient (CD)CD=(2FD/ρU02D)where FD is the drag force in the direction of flow exerted on the cylinder per unit length.
3. Numerical Solution Method
3.1. Numerical Details
Governing equations have been solved using FLUENT (version 6.3.26). The cells (Fig. 3) were generated using the commercial grid tool GAMBIT (version 2.3.16). 2D laminar flow of incompressible non Newtonian fluid was used on the collocated grid arrangement. While the main purpose of this work is to solve the governing equations using steady state assumption, limited time-dependent simulations for extreme values of the governing parameters such as Re = 200, n = 3 and α = 6, etc were also conducted to make sure that the flow regime was steady in the study. Momentum equations were discritized using second order upwind scheme. The SIMPLE scheme was used for solving the pressure–velocity coupling equations. Relative convergence criteria of 10−5 for the residuals of the continuity and x and y-component of the momentum equations were set in this work.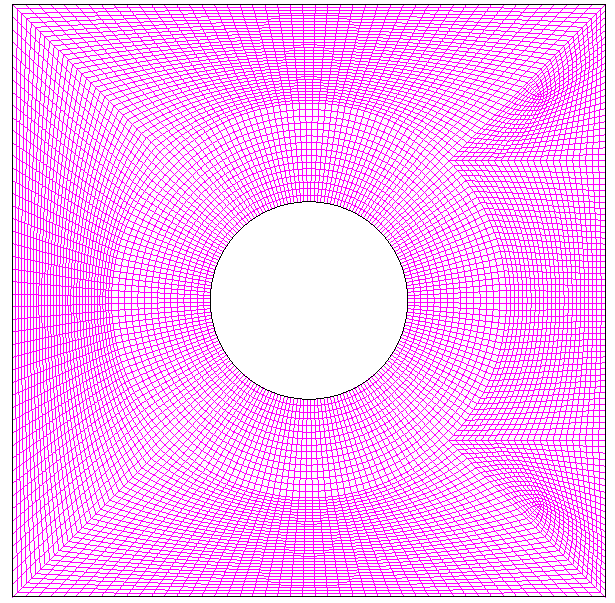 | Figure 3. schematic of generated cells |
3.2. Grid Independency
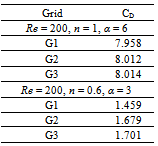
Three different sized cells are used to investigate the independency of the results to the mesh size. Coarse, medium and fine meshes which are related to 117600, 151100, 218100 number of cells, respectively, were put in use. Table 1 summarizes the relative quality and performance of the three grids for the resulting values of drag coefficient. As seen in table 1 results for G2 and G3 are close to each other resulting for a mesh independent values. Due to larger CPU time and computational cost of G3, grid G2 denotes a good compromise between the accuracy and computational efforts and hence all results reported herein are based on the use of grid G2. Table 1. Computed values of drag coefficient for different grids
 |
| |
|
4. Results and Discussion
The results are governed by 3 dimensionless parameters, namely, Re, n and α and the objective of the present study is to develop this functional relationship. Results from numerical solution are presented in parts containing the variation of the 3 dimensionless parameters. In each part, the effects on drag coefficient and heat transfer coefficient are studied.However, before demonstration of new results, it is useful to prove and ascertain the accuracy of the new results reported herein. Table 2 shows comparison among the results of present work and[1, 24]. A good agreement is verified through the simulation.Table 2. Verification of numerical result
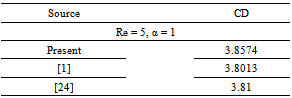 |
| |
|
4.1. Variation of Reynolds Number
In this part, Reynolds number increment was set from 100 to 500 while rotating velocity has been fixed in α = 2. As shown in Fig. 4, increasing Reynolds number increases the specified thermal coefficient. As the velocity of fluid increases, the thickness of the hydrodynamic boundary layer on the upper surface of cylinder increases as a result of high velocity gradient considering the cylinder rotational direction. So the net rate of heat transfer from the cylinder decreases. Although the boundary layer at the bottom surface of cylinder contains less velocity gradient, but increment of the difference among the fluid's velocity and the cylinder rotating velocity which causes an increase in the boundary layer thickness plays an important role in reducing the rate of thermal coefficient increment. It can be infrared from Fig. 4 that shear thickening of non-Newtonian fluids, make thicker boundary layer which reduces thermal treatment efficiently. As shown in Fig 5, the Hydrodynamic aspect of the results denotes that increasing Reynolds number increases the drag coefficient as a result of boundary layer thickness increment which is responsible for skin friction in the upper and lower sides of cylinder. 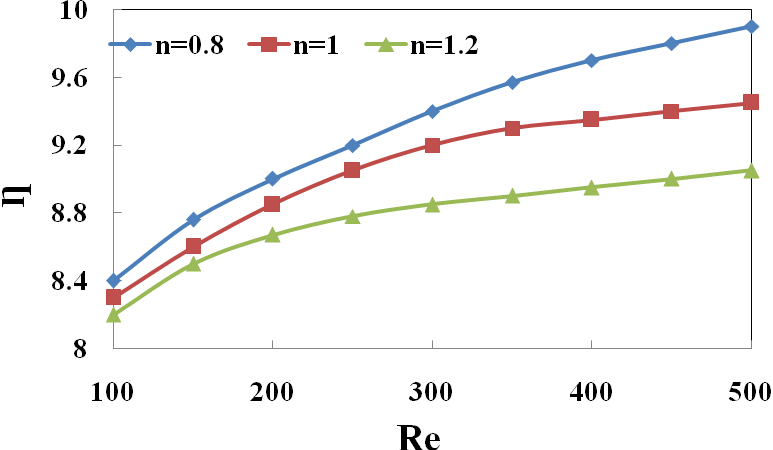 | Figure 4. Variation of thermal coefficient in different Reynolds number |
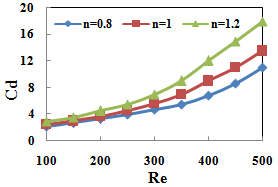 | Figure 5. Variation of drag coefficient in different Reynolds number |
4.2. Variation of Non-Newtonian Power
This section is devoted to non-Newtonian power index effects at various α. For the constant Re of 200, power index is varied from 0.5 to 1.4 for stationary cylinder and cylinder with α = 3 and 6. As shown in Fig 6, heat transfer decrease as non-Newtonian power increases. Velocity gradient increases faster for n > 1 in comparison with n < 1which causes a great decrease in heat transfer phenomenon. Even though rotational cylinder reduces the viscosity of fluid due to reduction of velocity gradient on cylinder surface. Fig.7 shows that increasing power index will arise the drag coefficient due to large skin friction at cylinder surface. It can be deduced that the industrial consumption of shear -thickening non Newtonian fluids at these conditions is not recommended, because the both increasing drag coefficient and descending thermal coefficient is encountered, which is not recommended. 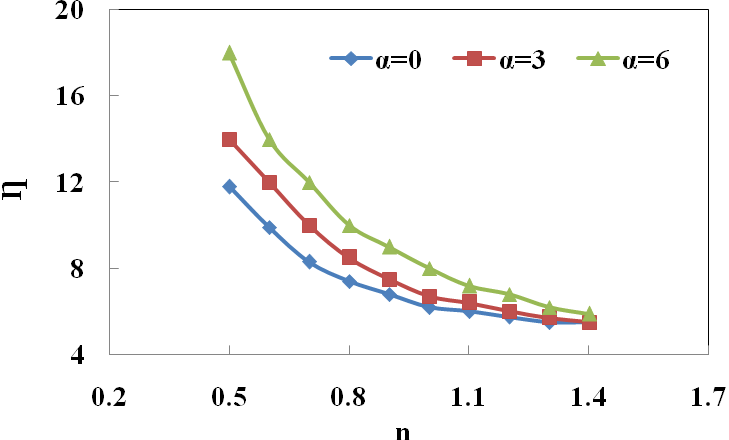 | Figure 6. Effect of power index on thermal coefficient at various rotational velocity for Re=200 |
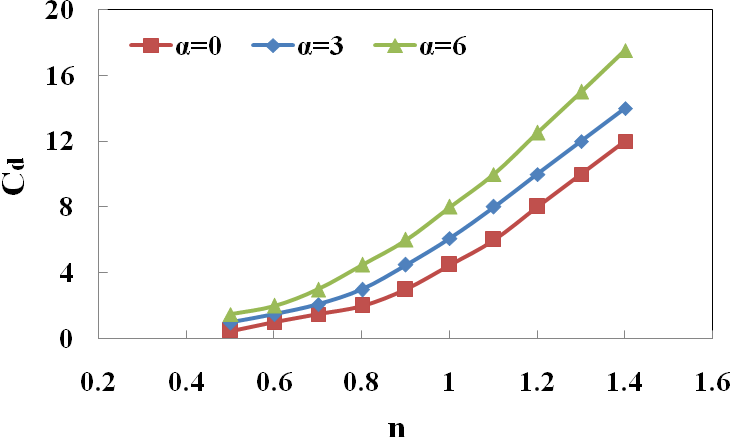 | Figure 7. Effect of power index on drag coefficient at various rotational velocities for Re=200 |
5. Conclusions
In the present study non-Newtonian laminar fluid flow over a rotating cylinder is investigated. Non-Newtonian power law model is used for simulation of the problem. Variation of different parameters such as non-Newtonian power, rotating velocity of the cylinder and Reynolds number of the inlet fluid are studied. Results indicated a great dependence of the thermal and hydrodynamic aspect of the problem on these parameters. Some of the results are pointed below:1) Increasing Reynolds number increases heat transfer amount and drag coefficient.2) Increasing non-Newtonian power, make the hydrodynamic boundary layer develop faster, resulting in a great reduction of heat transfer amount and therefore a great increase in drag coefficient.3) Increasing rotating velocity of the cylinder increases drag coefficient. Further studies are needed to develop the Re range and other effective parameters such as reducing the distance of rotating cylinder to the walls. This may influence on the thermal and drag coefficients.
References
| [1] | Chhabra, R. P., J. F. Richardson, and R. P. Chhabra. Non-Newtonian Flow and Applied Rheology: Engineering Applications. Amsterdam: Butterworth-Heinemann/Elsevier, 2008. |
| [2] | Zdravkovich, M. M. Flow around Circular Cylinders: A Comprehensive Guide through Flow Phenomena, Experiments, Applications, Mathematical Models, and Computer Simulations. Oxford: Oxford UP, 1997. |
| [3] | Zdravkovich, M. M. Flow around Circular Cylinders: A Comprehensive Guide through Flow Phenomena, Experiments, Applications, Mathematical Models, and Computer Simulations. Vol. 2,[Applications]. Oxford: Oxford UP, 2003. |
| [4] | Williamson, C H K. "Vortex Dynamics in the Cylinder Wake." Annual Review of Fluid Mechanics 28.1 (1996): 477-539. |
| [5] | Coutanceau, Madeleine, and Jean-René Defaye. "Circular Cylinder Wake Configurations: A Flow Visualization Survey." Applied Mechanics Reviews 44.6 (1991): 255. |
| [6] | Sumer, B. Mutlu., and Jørgen Fredsøe. Hydrodynamics around Cylindrical Structures. Singapore: World Scientific, 1997. |
| [7] | Paramane, Sachin B., and Atul Sharma. "Numerical Investigation of Heat and Fluid Flow across a Rotating Circular Cylinder Maintained at Constant Temperature in 2-D Laminar Flow Regime." International Journal of Heat and Mass Transfer 52.13-14 (2009): 3205-216. |
| [8] | D. Stojkovic, M. Breuer, F. Durst, Effect of high rotation rates on the laminar flow around a circular cylinder, Phys. Fluids 14 (2002) 3160–3178. |
| [9] | Badr, H. M., and S. C. R. Dennis. "Time-dependent Viscous Flow past an Impulsively Started Rotating and Translating Circular Cylinder." Journal of Fluid Mechanics 158.-1 (1985): 447. |
| [10] | Patnana, Vijaya K., Ram P. Bharti, and Raj P. Chhabra. "Two-dimensional Unsteady Flow of Power-law Fluids over a Cylinder." Chemical Engineering Science 64.12 (2009): 2978-999. |
| [11] | Patnana, Vijaya K., Ram P. Bharti, and Raj P. Chhabra. "Two-dimensional Unsteady Forced Convection Heat Transfer in Power-law Fluids from a Cylinder." International Journal of Heat and Mass Transfer 53.19-20 (2010): 4152-167. |
| [12] | R.I. Tanner, Stokes paradox for power-law flow around a cylinder, J. Non-Newt. Fluid Mech. 50 (1993) 217–224. |
| [13] | M.J. Whitney, G.J. Rodin, Force–velocity relationship for rigid bodies translating through unbounded shear-thinning power-law fluids, Int. J. Non-Linear Mech. 36 (2001) 947–953. |
| [14] | Chhabra, R. P., A. A. Soares, and J. M. Ferreira. "Steady Non-Newtonian Flow past a Circular Cylinder: A Numerical Study." Acta Mechanica 172.1-2 (2004): 1-16. |
| [15] | A.A. Soares, J.M. Ferreira, R.P. Chhabra, Flow and forced convection heat transfer in cross flow of non-Newtonian fluids over a circular cylinder, Ind. Eng. Chem. Res. 44 (2005) 5815–5827. |
| [16] | Sivakumar, P., R. Bharti, and R. Chhabra. "Steady Flow of Power-law Fluids across an Unconfined Elliptical Cylinder." Chemical Engineering Science 62.6 (2007): 1682-702. |
| [17] | Bharti, R., P. Sivakumar, and R. Chhabra. "Forced Convection Heat Transfer from an Elliptical Cylinder to Power-law Fluids." International Journal of Heat and Mass Transfer 51.7-8 (2008): 1838-853. |
| [18] | Dhiman, A., R. Chhabra, and V. Eswaran. "Flow and Heat Transfer across a Confined Square Cylinder in the Steady Flow Regime: Effect of Peclet Number." International Journal of Heat and Mass Transfer 48.21-22 (2005): 4598-614. |
| [19] | Dhiman, A., R. Chhabra, and V. Eswaran. "Steady Flow of Power-law Fluids Across a Square Cylinder." Chemical Engineering Research and Design 84.4 (2006): 300-10. |
| [20] | Sahu, Akhilesh K., R.P. Chhabra, and V. Eswaran. "Two-dimensional Laminar Flow of a Power-law Fluid across a Confined Square Cylinder." Journal of Non-Newtonian Fluid Mechanics 165.13-14 (2010): 752-63. |
| [21] | Townsend, P. "A Numerical Simulation of Newtonian and Visco-elastic Flow past Stationary and Rotating Cylinders." Journal of Non-Newtonian Fluid Mechanics 6.3-4 (1980): 219-43. |
| [22] | R.L. Christiansen, PhD Thesis, University of Wisconsin, Madison, WI, 1980. |
| [23] | R.L. Christiansen, A laser-doppler anemometry study of visco-elastic flow past a rotating cylinder, Ind. Eng. Chem. Fundam. 24 (1985) 403–408. |
| [24] | Panda, Saroj K., and R.P. Chhabra. "Laminar Flow of Power-law Fluids past a Rotating Cylinder." Journal of Non-Newtonian Fluid Mechanics 165.21-22 (2010): 1442-461. |


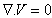
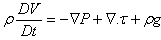
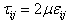
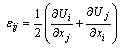
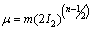

 )
) = Nu/Pr1/3• Nusselt number (Nu)Nu = hD/K• Drag coefficient (CD)CD=(2FD/ρU02D)where FD is the drag force in the direction of flow exerted on the cylinder per unit length.
= Nu/Pr1/3• Nusselt number (Nu)Nu = hD/K• Drag coefficient (CD)CD=(2FD/ρU02D)where FD is the drag force in the direction of flow exerted on the cylinder per unit length. 




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML