-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2012; 2(6): 89-94
doi: 10.5923/j.ajfd.20120206.01
Effectsof Order of Chemical Reaction on a Boundary Layer Flow with Heat and Mass Transfer Over a Linearly Stretching Sheet
M. Ferdows1, Qasem M. Al-Mdallal2
1Mathematics Department, Universityof Dhaka, Dhaka, 1000, Bangladesh
2Department of Mathematical Sciences, College of Science, United Arab Emirates University, P.O. Box 17551, Al-Ain, United Arab Emirates
Correspondence to: Qasem M. Al-Mdallal, Department of Mathematical Sciences, College of Science, United Arab Emirates University, P.O. Box 17551, Al-Ain, United Arab Emirates.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The heat and mass transfer characteristics over a linearly stretching sheet subjected to an order of chemical reaction are studied numerically.A similarity transformation is utilized to convert the governing nonlinear partial differential equations into ordinary differential equations. The numerical method of solution is based on the shooting method with six order Runge-Kutta iteration scheme. The numerical simulations are conducted at Schmidt number Sc varying from0.22to 0.78 and chemical reaction varying from 0.5 to 3. The effects of the governing parameters on the local skin friction and rateof mass transfer on the wall are accurately calculated.
Keywords: Boundary Layer, Partial Differential Equations, Similarity Transformation, Heat and Mass Transfer,Linearly Stretching Sheet
Cite this paper: M. Ferdows, Qasem M. Al-Mdallal, "Effectsof Order of Chemical Reaction on a Boundary Layer Flow with Heat and Mass Transfer Over a Linearly Stretching Sheet", American Journal of Fluid Dynamics, Vol. 2 No. 6, 2012, pp. 89-94. doi: 10.5923/j.ajfd.20120206.01.
Article Outline
1. Introduction
- The momentum, heat and mass transfer in laminar boundary layer flowovera linearly stretching sheet has important applications in polymer industry mass transfer over a stretching surface. In addition, the diffusing species can be generated or absorbed due to some kind of chemical reaction with the ambient fluid as was shown by[1-4]. This kind of generation or absorption of species can affect the flow properties and quality of the final product. Thus, the study of heat transfer and flow field is necessary for determining the quality of the final products of suchprocesses.Chambré and Young[5] studied a first-order chemical reaction in the neighborhoodof a horizontal plate. On the other hand, Crane[6] studied the flow over a linearly stretching sheet in an ambient fluid and gave a similarity solution in closed analytical form for the steady two-dimensional problem. Further, Anderson et al. [7] studied the diffusion of chemical reactive species with first-order and higher-order reactions over a linearly stretching sheet. Anjalidevi and Kandasamy[8] investigated the effects of chemical reaction; heat and mass transfer on a steady laminar flow along a semi-infinite horizontal plate. Additionally, Takharet al.[9] investigated the flow and mass diffusion of a chemical species with first-order and higher-order reactions over a continuously stretching sheet. Gupta and Gupta[10], Carragher and Crane[11], Dutta et al. [12],Magyari and Keller[13] andMahapatra and Gupta[14] studied the heat transfer in the steady two-dimensional stagnation point flow of a viscous, incompressible viscoelastic fluid over a horizontal stretching sheet considering the case of constant surface temperature. Recently, Afify[15] analyzed the MHD free convective flow and mass transfer over a stretching sheet with homogeneous chemical reaction of order n (where n was taken 1, 2 and 3).Samad and Mohebujjaman[16] exposed the effect of a chemical reaction on the flow over a linearly stretching vertical sheet in the presence of heat and mass transfer as well as a uniform magnetic field with heat generation/absorption. Recently, Hayat et al.[17] studied the effect on unsteady three dimensional flow of couple stress fluid overa stretching surface with chemical reaction based on using homotopy analysis method. Alam and Ahammad[18] investigated the effects of variable chemical reaction and variable electric conductivity on free convective flow with heat and mass transfer over an inclined permeable stretching sheet under the influence of Dufourand Soret effects with variable heat and mass fluxes. Kandasamy et al.[19]presented a study on free convective heat and mass transfer fluid flow considering thermophoresis and chemical reaction over a porous stretching surfacealong with several assumptions by using Group theory.Oluwole and Sibanda[20] has been focused to clarify the effects of first-order homogeneous chemical reaction on a two-dimensional boundary layer flow past a vertical stretching surface numerically. Effects of Chemical reaction flow through porous media over a stretching sheet was recently studied by Sing and Jai [21].Based on the above-mentioned investigations and applications, this paper is concerned with two-dimensional steady, incompressible, laminar boundary layer flow of a fluid over a linearly stretching sheet.In this paper we investigate numerically the effects of chemical reaction on the steady laminar two-dimensional boundary layer flow and heat and mass transfer over a stretching sheet. The method of solutionis based on the well-known similarity analysis together with shooting method.
2. Governing Equation of the Boundary Layer Flow
- Considertwo dimensional steady, incompressible, laminar boundary layer flow of a fluid over a linearly stretching sheet(i.e.stretched with a velocity proportional to x(
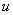 =
=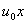 ) as shown in Figure1). We assume that the fluid far away from the sheet is at rest and at temperature T∞ and concentration C∞. Further,the stretched sheet is kept at fixed temperature
) as shown in Figure1). We assume that the fluid far away from the sheet is at rest and at temperature T∞ and concentration C∞. Further,the stretched sheet is kept at fixed temperature 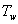 (
(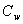 (
(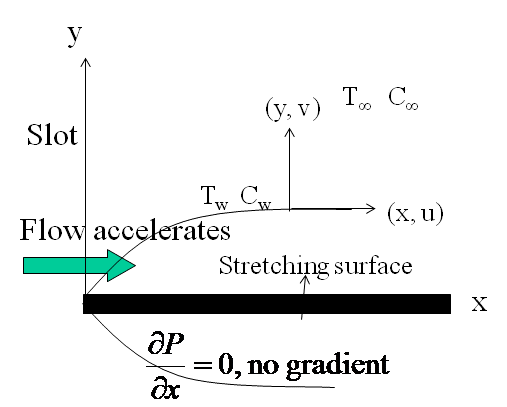 | Figure 1. Boundary layer on a stretching surface |
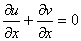 | (1) |
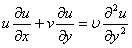 | (2) |
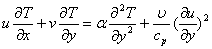 | (3) |
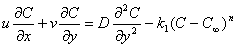 | (4) |
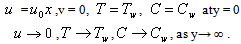 | (5) |
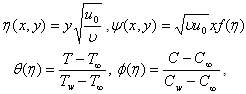 where
where 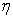 is the similarity variable,
is the similarity variable, 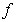 is the dimensionless stream function,
is the dimensionless stream function, 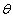 is the dimensionless temperature,
is the dimensionless temperature, 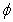 is thedimensionless concentration and
is thedimensionless concentration and 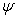 is the stream function defined as
is the stream function defined as 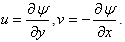 Consequently,equations (2)-(4) and the boundary conditions (5) can be written in the following form
Consequently,equations (2)-(4) and the boundary conditions (5) can be written in the following form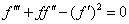 | (6) |
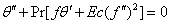 | (7) |
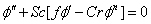 | (8) |
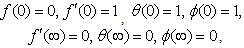 | (9) |
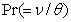 represents Prandtl number,
represents Prandtl number, 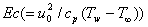 represents Eckert number,
represents Eckert number, 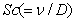 represents Schmidt number and
represents Schmidt number and 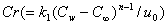 is the chemical reaction parameter.It should be noted that the physical quantities of interest in this problem are the local skin-friction coefficient,-
is the chemical reaction parameter.It should be noted that the physical quantities of interest in this problem are the local skin-friction coefficient,- 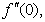 rate of heat transfers,
rate of heat transfers, 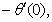 and rate of mass transfers,
and rate of mass transfers, 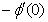 , which are defined as
, which are defined as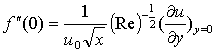 | (10) |
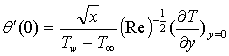 | (11) |
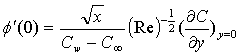 | (12) |
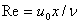 is the Reynolds number.
is the Reynolds number.3. Results and Discussion
- The ordinary differential equations (6)-(8) associated with the boundary conditions (9) are numerically solved by employing Nacktsheimswigertiteration technique togother with Range-Kutta shooting method. Since the computational domain in η direction is unbounded, a large enough artificial outer boundaryη∞(an approximation to η = ∞)must be chosen torepresent infinity for the numerical treatment. The numerical simulations suggest that choosinga step size of ∆η=0.05 was sufficient to provide accurate numerical results.Numerical simulations were carried out for 1. Pr = 0.71 corresponds physically to air is chosen. 2. The values of Schmidt number are chosen in such a way to correspond hydrogen (Sc=0.22), water vapour (Sc=0.62)and NH3 (Sc=0.78) at approximately250c and 1 atmosphere.3. Small value of Eckert number (Ec=0.01) which can be interpreted as the edition of heat hue to viscous dissipation.4. The values of chemical reaction Cr are chosen arbitrary.5.The rates of reaction for n=0, 1, 2; represent zeroth-order (n=0), first-order (n=1) and second -order (n=2) .Figures 2-4 show the results for the velocity, temperature and concentration profiles with variation of Schmidt number and order of reaction when Pr=0.71, Ec=0.01 and Cr=0.5. It is notedthat the velocity, temperature and concentration profiles areall decreasing as Schmidt number increase for fixed n. On the other hand, the flow profiles increases as order of reaction increases for fixed Sc. Additionally, the thermal boundary layer has larger effect in the region far away from the plate. It is also noted that the concentration (mass) fluids become more influenced by order of reaction and Schmidt number rather than thermal boundary layer fluid flow.
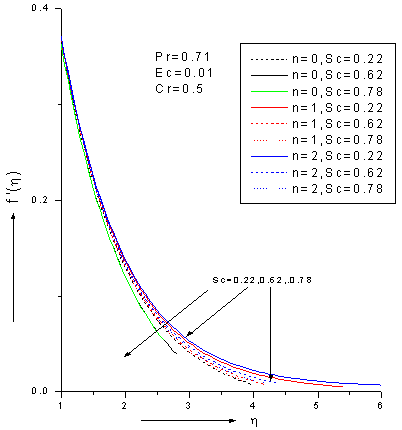 | Figure 2. Zeroth, 1stand 2nd order velo city profiles for different values of Schmidt number Sc with Pr=0.71, Ec=0.01 and Cr=0.5 |
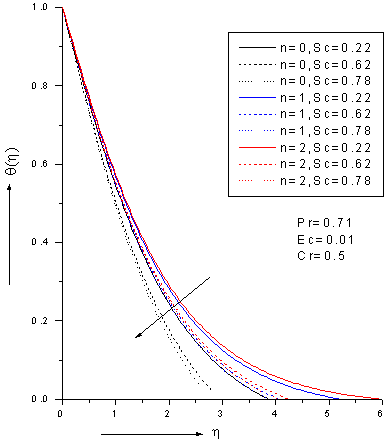 | Figure 3. Zeroth,1stand 2nd order temperature profiles for different values of Schmidt number Sc with Pr=0.71, Ec=0.01 and Cr=0.5 |
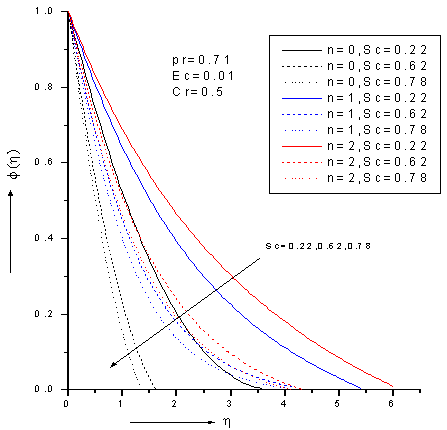 | Figure 4. Zeroth,1stand 2nd order concentration profiles for different values of Schmidt number Sc with Pr=0.71, Ec=0.01 and Cr=0.5 |
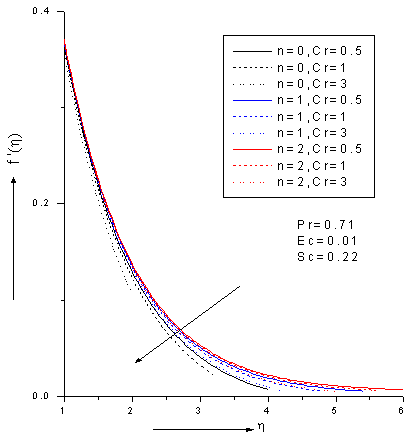 | Figure 5. Zeroth, 1stand 2nd order velocity profiles for various values chemical reaction parameter Cr with Pr=0.71, Ec=0.01 and Sc=0.22 |
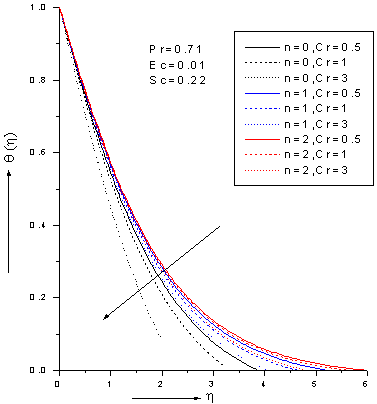 | Figure 6. Zeroth, 1st and 2nd order temperature profiles for various values chemical reaction parameter Cr with Pr=0.71, Ec=0.01 and Sc=0.22 |
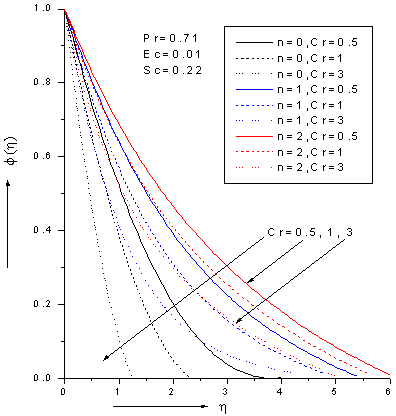 | Figure 7. Zeroth, 1stand 2nd order concentration profiles for various values chemical reaction parameter Cr with Pr=0.71, Ec=0.01 and Sc=0.22 |
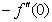 ), rate of heat transfer (
), rate of heat transfer (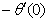 ) and rate of mass transfer (
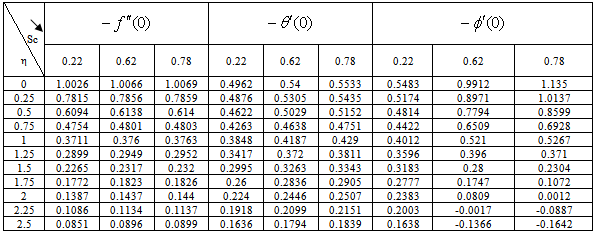
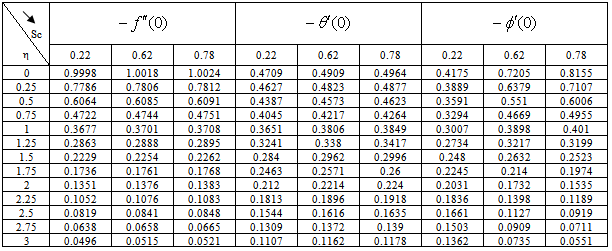
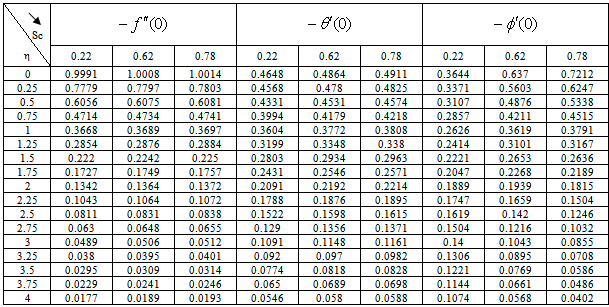
) and rate of mass transfer (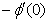 ) for 0.22 ≤Sc≤0.78,0≤n≤2. These tables indicate that
) for 0.22 ≤Sc≤0.78,0≤n≤2. These tables indicate that 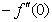 ,
,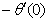 and
and 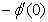 are continuously decreaseas η in crease for all values of n andSc. Moreover,the vales of
are continuously decreaseas η in crease for all values of n andSc. Moreover,the vales of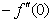 ,
, 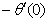 and
and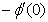 are greater in case of hydrogen (Sc=0.22) than that of water vapour (Sc = 0.62) or NH3 (Sc = 0.78).
are greater in case of hydrogen (Sc=0.22) than that of water vapour (Sc = 0.62) or NH3 (Sc = 0.78).
|
|
|
4. Conclusions
- In this paper,we consider two-dimensional laminar boundary layer flow bounded by stretching sheet in the present of chemical reaction. The transformed similar conservation ordinary differential equations are obtained and solved by Nacktsheimswigertiteration technique together with Range-Kutta shooting method. Numerical results are obtained for the dimensionless velocity, temperature and concentration profiles as well as missing slope for various values of problems parameters. It was found that the flow profiles increases with the increase of order of reaction and decreases with the increase of Schmidt number Sc and chemical reaction parameter Cr. Furthermore the missing slope is larger in the case of hydrogen (Sc = 0.22) than that of NH3 (Sc = 0.78).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML