1. Introduction

The theoretical and experimental results of the onset of thermal convection (Be'nard convection) in a fluid layer under varying assumptions of hydrodynamics has been treated in detail by Chandrasekhar[1] in his celebrated monograph. Veronis'[2] has investigated the problem of thermohaline convection in a layer of fluid heated from below and subjected to a stable salinity gradient. The buoyancy forces can arise not only from density differences due to variations in temperature but also from those due to variations in solute concentration. Double-diffusiveconvection problems arise in oceanography, limnology and engineering. Examples of particular interest are provided by ponds built to trap solar heat (Tabor and Matz[3]) and some Antarctic lakes (Shirtcliffe[4]).The physics is quite similar in the stellar case in that Helium acts like salt in raising the density and in diffusing more slowly than heat. The conditions under which convective motions are important in stellar atmospheres are usually far removed fromconsideration of single component fluid and rigid boundaries and therefore, it is desirable to consider a fluid acted on by solute gradient and free boundaries. The fluids have been considered to be Newtonian in all the above studies.

With the growing importance of non-Newtonian fluids in modern technology and industries, investigations on such fluids are desirable. Widely used theoretical models (models A and B, respectively) for certain classes of viscoelasticfluids have been proposed by Oldroyd[5]. Renardy[6] has studied the stability of the interface in a two-layer Couette flow of upper convected Maxwell liquids. The thermal instability of Maxwellian viscoelastic fluid in the presence of a uniform rotation has been considered by Bhatia and Steiner[7], where rotation is found to have a destabilizing effect. This is in contrast to the thermal instability of a Newtonian fluid where rotation has a stabilizing effect. The thermal instability of an Oldroydian viscoelastic fluid acted on by a uniform rotation has been studied by Sharma[8]. An experimental demonstration by Toms and Strawbridge[9] revealed that a dilute solution of methyl methacrylate in n-butyl acetate agrees with the theoretical model of Oldroyd[5]. There are many viscoelastic fluids that cannot be characterized by constitutive relations of the Maxwell/Oldroyd type. One such class of viscoelastic fluids is Walters B' viscoelastic fluid[10], having relevance and importance in geophysical fluid dynamics, chemical technology and petroleum industry. Walters[11] reported that the mixture of polymethyl methacrylate and pyridine at 250C containing 30.5g of polymer per litre with a density of 0.98 g/l behaves very nearly as the Walters B' elastico-viscous fluid. Kumar[12] has studied the effect of rotation on thermal instability in Walters B' elastico-viscous fluid. In another study, Kumar and Lal[13] have studied the effect of magnetic field and rotation on thermal convection in Walters B' elastico-viscous fluid. Sunil et al.[14] have studied the thermosolutal convection in Walters B' fluid in porous medium in presence of magnetic field.

Brakke[15] explained a double-diffusive instability that occurs when a solution of a slowly diffusing protein is layered over a denser solution of more rapidly diffusing sucrose. Nason et al.[16] found that this instability, which is deleterious to certain biochemical separations, can be suppressed by rotation in the ultracentrifuge. The effect of rotation on double-diffusive convection in compressible Walters B' fluid is important in certain chemical engineering and biochemical situations.

Keeping in mind the importance and applications in chemical engineering and biomechanics, the effect ofuniform rotation on thermosolutal convection in compressible Walters B' viscoelastic fluid has been considered in the present paper. The analysis of the present work begins with Section 2, which formulates the problem for Walters B’ viscoelastic compressible fluid in the presence of uniform rotation by using the Boussinesq approximation, linearized theory and the perturbation theory. In Section 3, a dispersion relation is obtained by using the normal mode technique. The effects of stable solute gradient and rotation for the case of stationary convection are discussed analytically and graphically in Section 4. In Section 5, the existence of oscillatory modes is discussed. Sufficient conditions for non-existence of overstability are obtained in Section 6. Section 7, the conclusion section, summarizes the results obtained in the preceding sections.

2. Formulation of the Problem and Perturbation Equations

Consider an infinite compressible layer of Walters B' viscoelastic fluid, confined between the planes z = 0 and z = d, acted on by a gravity force 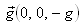and a uniform rotation 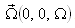. This layer is heated and soluted from below such that a steady adverse temperature gradient 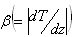and a solute concentration gradient 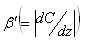are maintained. For thermosolutal convection problem, the Boussinesq approximation has been used, which is well justified in the case of incompressible fluids.

The equations governing the system become quite complicated when the fluids are compressible. To simplify them, Boussinesq try to justify the approximation for nearly incompressible fluids when the density variations arise principally from thermal effects by noting that atmospheric pressure fluctuations are much too small to produce the observed density changes. Spiegel and Veronis'[17] have simplified the set of equations governing the flow of compressible fluids under the following assumptions;

(1) The vertical dimension of the fluid is much less than any scale height, as defined by them, if only motions of infinitesimal amplitudes are considered and (2) The motion - induced fluctuations in density and pressure do not exceed in order of their total static variations.

Under the above approximations, Spiegel and Veronis'[17] have shown that the equations governing convection in a perfect gas are formally equivalent to those for an incompressible fluid if the static temperature gradient is replaced by its excess over the adiabatic and 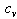is replaced by 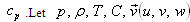denote respectively the fluid pressure, density, temperature, solute concentration and velocity. The equations expressing the conservation of momentum, mass, temperature, solute concentration and equation of state of compressible Walters B' viscoelastic fluids in presence of rotation are

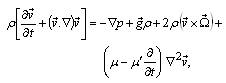(1)

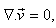(2)

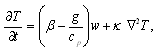(3)

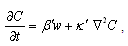(4)

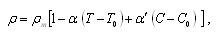(5)

where suffix zero refers to values at the reference level z = 0, α is the coefficient of thermal expansion and α′ is the analogous solvent expansion.

The basic motionless solution is

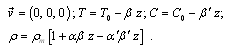(6)

The linearized perturbation equations are

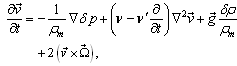(7)

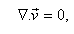(8)

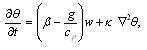(9)

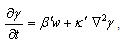(10)

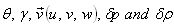where denote respectively the perturbations in temperature T, solute concentration C, fluid velocity, pressure p and density 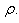Here 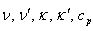stand for kinematic viscosity, kinematic viscoelasticity, thermal diffusivity, solute diffusivity and specific heat at constant pressure.

The change in density 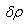caused by the perturbations and in temperature and solute concentration is given by

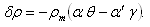(11)

Equations (7) – (10) yield

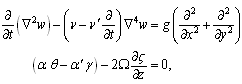(12)

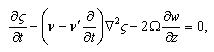(13)

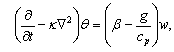(14)

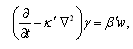(15)

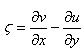where denotes the z-component of the vorticity and 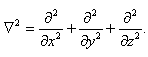We consider the case in which both the boundaries are free and here temperatures, solute concentrations at the boundaries are kept constant. Then the boundary conditions appropriate to the problem are

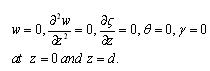(16)

3. The Dispersion Relation

Analyzing the disturbances into normal modes, we assume that perturbation quantities are of the form

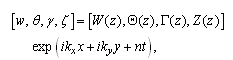(17)

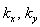where are the wave numbers along the x- and y- directions respectively. 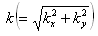is the resultant wave number and n is, in general, a complex constant.

Using (17), equations (12)–(15) in non–dimensional form become

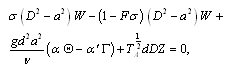(18)

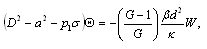(19)

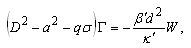(20)

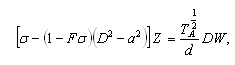(21)

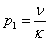where is the Prandtl number, 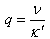is the Schmidt number, 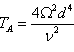is the

Taylor number, 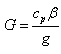is the dimensionless compressibility parameter, 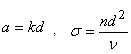and 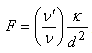. Eliminating between equations (18) to (21), we obtain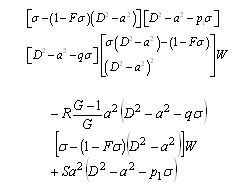

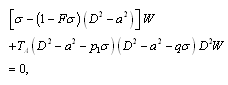(22)

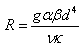where is the Rayleigh number, 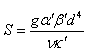is solute Rayleigh number.

The boundary conditions (16) transform to

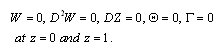(23)

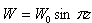Using the proper solution characterizing the lowest mode, equation (22) yields the dispersion relation as

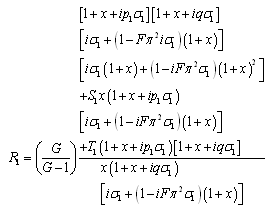(24)

where

.

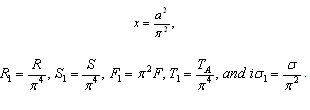4. The Stationary Convection

For the stationary convection 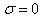, equation (24) reduces to

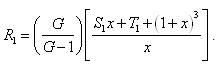(25)

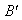Equation (25) implies that for stationary convection, compressible Walters viscoelastic fluid behaves like an ordinary compressible Newtonian fluid.

If the non-dimensional numbers 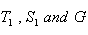accounting for the rotation, solute gradient and compressibility effects be kept as fixed in equation (25), then we find that

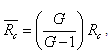(26)

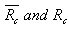where denote, respectively, the critical Rayleigh numbers in the presence and absence of compressibility. Since critical number is positive and finite, so G > 1 and we obtain a stabilizing effect of compressibility as its result is to postpone the onset of double-diffusive convection. The cases G < 1 and G =1 correspond to negative and infinite values of critical Rayleigh numbers in the presence of compressibility, that are not relevant in the present study.

To investigate the effect of stable solute gradient and rotation, we examine the behaviour of 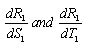analytically.

It is evident from equation (25) that

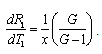(27)

and

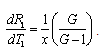(28)

The stable solute gradient and rotation, therefore, have stabilizing effects on the system for G >1.

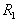We now give some realistic values to various parameters in equation (25) to demonstrate the above results through graphs. Figure 1 plots modified Rayleigh number against wave numbers x for fixed values of G = 10 and 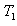= 50 and for 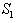= 10, 30 50, 80, 100. It is clear from Figure 1 that the stable solute gradient has stabilizing effect on the system. Figure 2 depicts 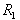against x for fixed values of G = 10, 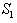= 100 and variable values of 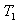= 10, 30, 50, 70, 90. It is evident from Figure 2 that Rayleigh number is increasing with the increase in the value of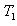, thus implying the stabilizing effect of rotation.

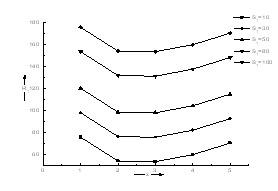Figure 1. Variation of Rayleigh number R1 against wave number x for G = 10 and T1 =50

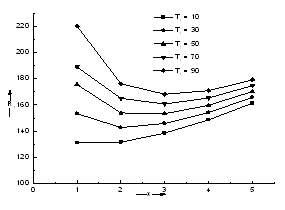Figure 2. Variation of Rayleigh number R1 against wave number x for G = 10 and S1 =100

5. Stability of the System and Oscillatory Modes

To examine the possibility of oscillatory modes if any due to the presence of kinematic viscoelasticity, stable solute gradient and rotation, we multiplying equation (18) by W*, the complex conjugate of W, integrating over the range of z and making use of equations (19)-(21), we get

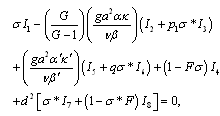(29)

where

,

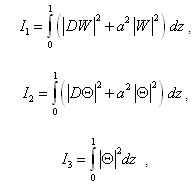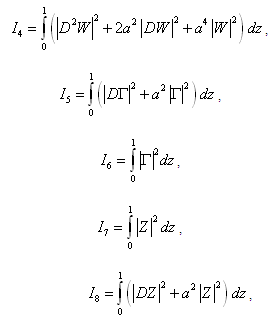(30)

is the complex conjugate of .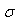

Putting 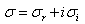and then equating real and imaginary parts of (29), we obtain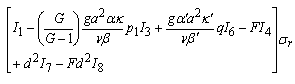

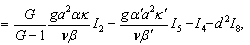(31)

and

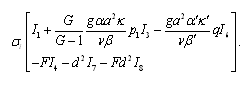(32)

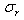Equation (31) yields that may be positive or negative, that is, there may be instability or stability in the presence of solute gradient. Equation (32) yields that 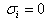or 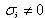which means that the modes may be non-oscillatory or oscillatory. The oscillatory modes are introduced due to the presence of rotation and solute gradient, which were non-existent in their absence.

6. The Case of Overstablity

Here we discuss the possibility of whether instability may occur as an overstability. Since we wish to determine the critical Rayleigh number for overstability, it suffices to find conditions for which equation (24) will admit of solution with 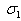real. Separating real and imaginary parts of equation, we have by eliminating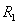

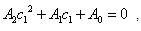where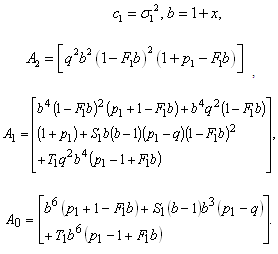

.

Thus 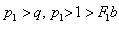are the sufficient conditions for non-existence of overstability, the violation of which does not necessarily imply occurrence of overstability.

7. Conclusions

The thermosolutal convection in a compressible Walters B’ viscoelastic fluid layer heated and soluted from below in the presence of uniform rotation is considered in the present paper. The investigation of thermosolutal convection is motivated by its interesting complexities as a double diffusion phenomena as well as its direct relevance to geophysics and astrophysics. The main conclusions from the analysis of this paper are as follows:

§ For the case of stationary convection, the compressible Walters B’ viscoelastic fluid behaves like an ordinary compressible Newtonian fluid.

§ It is observed for the case of stationary convection that the stable solute gradient and rotation have stabilizing effects on the system for G>1.

§ It is also observed graphically from Figures 1 and 2 that the stable solute gradient and rotation postpone the onset of convection.

§ It is observed that the presence of rotation and solute gradient introduce oscillatory modes in the system, which were non-existent in their absence.

§ The conditions 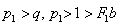are the sufficient conditions for the non-existence of overstability, the violation of which does not necessarily imply occurrence of overstability.

ACKNOWLEDGEMENTS

The author wish to express his sincere thanks to the learned referee whose critical and helpful comments have significantly improved the article in its present form.