-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
2012; 2(4): 55-60
doi: 10.5923/j.ajfd.20120204.04
Water Wave Scattering by a Dock in Presence of Bottom Undulation
U. Basu , S. De R. Maiti
Department of Applied Mathematics, University of Calcutta, 92, A.P.C Road, Kolkata-700009, India
Correspondence to: U. Basu , Department of Applied Mathematics, University of Calcutta, 92, A.P.C Road, Kolkata-700009, India.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The problem of water wave scattering by a semi-infinite floating dock on the free surface of an ocean with variable bottom topography is considered using linear theory. By employing a perturbation analysis and using Green's integral theorem, the analytical expression for the first order reflection coefficient is obtained in terms of a computable integral involving the bottom shape function. Also the zero order reflection coefficient is obtained by using residue calculus method. The first order reflection coefficient is computed numerically by considering some special types of bottom shape function and is depicted graphically against the wave number in a number of figures.
Keywords: Wave Scattering, Surface Discontinuity, Bottom Undulation, Shape Function, Perturbation Technique, Green's Integral Theorem, Reflection Coefficient
Article Outline
1. Introduction
- The problem of water wave scattering by obstacles situated at the bottom of water of finite depth having a free surface have been investigated within the framework of linearized theory during last few decades. The problem of propagation of long wave along free surface over a sudden change in depth was discussed by Lamb[1], Kreisel[2] who were the earliest contributors in this context. They employed the conformal transformation technique in the mathematical analysis. Davies[3] solved the problem of reflection of normally incident wave by a patch of sinusoidal undulation on the sea-bed in a finite region using Fourier transformation technique. Mei[4] considered the problem of wave scattering by periodic sandbars at the ocean bottom. Mandal and Basu[5] extended the problem for an obliquely incident surface wave-train in the presence of surface tension at the free surface and employed a perturbation analysis directly to the governing partial differential equation and boundary condition to obtain reflection and transmission coefficients up to the first order in terms of integrals involving bottom shape function describing the geometry of the bottom topography. Martha and Bora[6] investigated water wave scattering by small deformation of the ocean bottom in case of oblique incidence of incoming wave. They obtain reflection and transmission coefficients analytically using Green's integral theorem and the numerical results were depicted graphically. Mandal and Basu[7], Mandal and Maiti[8] studied water wave diffraction by a small elevation of the bottom of an ocean with an ice cover modelled as a thin elastic plate. Mohapatra and Bora[9] investigated the problem of oblique wave scattering over a bottom undulation in the case of ice covered two layered fluid. They obtained the reflection and transmission coefficient by using perturbation technique.Another class of water wave scattering problems involving a discontinuity in the surface boundary condition was considered in the literature where surface waves are propagating along an inertial surface e.g. broken ice floating mat etc. Weitz and Keller[10] considered a scattering problem involving a discontinuity in the surface boundary condition arising due to the presence of a broken ice on the half portion of the surface , the other half being free. They employed the Winner-Hopf technique in the mathematical analysis. Evans and Linton[11] considered a problem of water wave scattering by a discontinuity in the surface boundary condition and determined the explicit form of the reflection and transmission coefficient by employing residue calculus method of complex variable theory. Mandal and De[12] investigated a problem of water wave scattering by a small bottom undulation in presence of discontinuity in the upper surface boundary condition and obtained the first order correction of the reflection and transmission coefficients analytically in terms of the integral involving the bottom shape function using the perturbation technique.Problems concerning the scattering of water wave by a floating mat or a rigid dock on the free surface have a long history. Heins[13] considered interaction of water wave with a semi-infinite dock in water and used Wiener-Hopf technique for analytical solution of the mathematical problem. Friedrich and Lewy[14] solved the problem by using complex variable theory. Linton[15] solved the scattering of water wave by a dock of finite width in water of finite depth by using modified residue calculus technique. This problem has been formulated for the obliquely incident waves and the case of normal incidence is recovered by taking appropriate limit. Leppington[16] investigated the problem of water wave scattering due to a finite dock and obtained the amplitude of the reflected and transmitted wave train for short wave using integral equation technique. The dock problem was also re-investigated by Chackrabarti, Mandal and Gayen[17] by utilizing a Fourier type analysis, giving rise to the Carleman type singular integral equation over semi-infinite range.In the present paper, the problem of water wave scattering due to bottom undulation in the presence of a discontinuity in the upper boundary condition is considered. Here the free surface discontinuity arises due to the presence of a floating dock which is extended infinitely on other side of the ocean. The thickness of the dock is assumed to be very small compared to the water depth and the amplitude of the incoming wave. The reflection of incoming water wave occurs when a progressive wave train propagating from negative infinity is incident upon the dock in the presence of bottom undulation. Hence, it is interesting to study the reflection coefficients in the presence of a small undulation at the bottom. The solution is being obtained by employing a simplified perturbation technique directly to the governing partial differential equation and the boundary conditions. Use of the perturbation technique produces two boundary value problems up to the first order. The boundary value problem (BVP-1) for zero order potential function is concerned with the problem of scattering of normally incident wave by a rigid dock floating along the surface of water of uniform finite depth. Following Evans and Linton(1994), the BVP-1 is being solved by using residue calculus method and the zero order reflection coefficients are obtained. Now, without solving the second boundary value problem (BVP-2), the first order correction to the reflection coefficient is evaluated by appropriate use of Green's integral theorem. Analytical expression for the first order reflection coefficient is obtained in terms of the integral involving the shape function of the bottom undulation and the solution of the BVP-1. Considering two different types of bottom shape function the first order reflection coefficient is computed numerically. For the shape function in the form of a sinusoidal ripple of finite extent, a number of figures for the first order reflection coefficient are drawn against the wave number considering different values of the parameters. For an exponential decaying profile of bottom a few figures are also drawn.
2. Formulation of the Problem
- We consider the two dimensional motion in an ocean of variable bottom topography in the form of small undulation at the bottom. A rectangular cartesian coordinate system is chosen in which y-axis is taken vertically downwards into the fluid region and the undisturbed free surface corresponds to
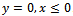 . A semi-infinite floating dock of negligible thickness occupies the region
. A semi-infinite floating dock of negligible thickness occupies the region 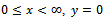 and other side
and other side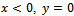 is the open free surface. This produces a discontinuity in the surface boundary condition in the sense that free surface boundary condition holds for
is the open free surface. This produces a discontinuity in the surface boundary condition in the sense that free surface boundary condition holds for 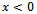 and there is another boundary condition for
and there is another boundary condition for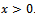 . Let a train of surface water wave be incident from negative infinity upon the semi-infinite dock. The water under the dock is undisturbed and since the plate extended infinitely along the positive x-axis, there is no transmission of the incident wave field. The fluid is assumed to be incompressible and inviscid. The flow is irrotational and the motion is simple harmonic in time t with angular frequency ω, it can be described by a velocity potential
. Let a train of surface water wave be incident from negative infinity upon the semi-infinite dock. The water under the dock is undisturbed and since the plate extended infinitely along the positive x-axis, there is no transmission of the incident wave field. The fluid is assumed to be incompressible and inviscid. The flow is irrotational and the motion is simple harmonic in time t with angular frequency ω, it can be described by a velocity potential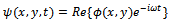 , where
, where 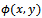 satisfies the two dimensional Laplace equation:
satisfies the two dimensional Laplace equation: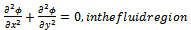 | (2.1) |
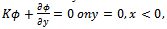 | (2.2) |
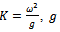 is the acceleration due to gravity. The surface boundary condition on the dock region is given by
is the acceleration due to gravity. The surface boundary condition on the dock region is given by 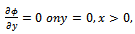 | (2.3) |
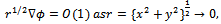 | (2.4) |
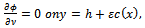 | (2.5) |
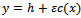 denotes the bottom of the sea of variable depth. ε is a small non-dimensional positive number signifying the smallness of the bottom undulation and
denotes the bottom of the sea of variable depth. ε is a small non-dimensional positive number signifying the smallness of the bottom undulation and 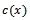 is a bounded, continuous function characterizing the shape of the bottom with the property that
is a bounded, continuous function characterizing the shape of the bottom with the property that 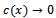 as
as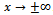 . This ensures that far away from the undulation the sea bottom is of uniform finite depth h below the mean free surface. The incident wave field from the direction of negativeinfinity is described by
. This ensures that far away from the undulation the sea bottom is of uniform finite depth h below the mean free surface. The incident wave field from the direction of negativeinfinity is described by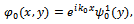 where
where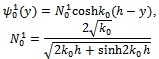 and
and 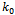 is unique the positive real root of the transcendental equation
is unique the positive real root of the transcendental equation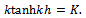 Finally, the far field behavior of the potential function is described by
Finally, the far field behavior of the potential function is described by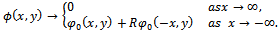 | (2.6) |
3. Method of Solution
- The boundary condition (2.5) can be written as,
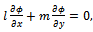 | (3.1) |
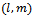 is the direction cosine of v to the curve
is the direction cosine of v to the curve 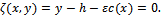 Using Taylor series expansion of
Using Taylor series expansion of 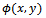 on
on 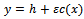 and the equation (2.1), we get the following form:
and the equation (2.1), we get the following form: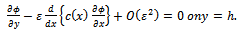 | (3.2) |
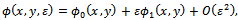 | (3.3) |
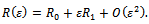 | (3.4) |
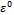 and
and 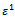 on both sides of the results, we find that, the zero and first order potentials
on both sides of the results, we find that, the zero and first order potentials 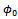 and
and 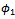 satisfies the following two different boundary value problems. They are named as BVP-1 and BVP-2 respectively.BVP-1:The function
satisfies the following two different boundary value problems. They are named as BVP-1 and BVP-2 respectively.BVP-1:The function 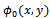 satisfies(i)
satisfies(i) 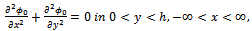 (ii)
(ii) 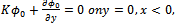 (iii)
(iii) 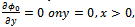 (iv)
(iv) 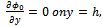 (v)
(v) 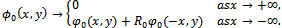 Where
Where 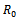 is the zero order reflection coefficient.BVP-2:The function
is the zero order reflection coefficient.BVP-2:The function 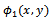 satisfies (i)
satisfies (i) 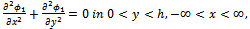 (ii)
(ii) 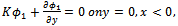 (iii)
(iii) 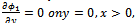 (iv)
(iv) 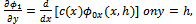 (v)
(v) 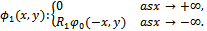 Where
Where 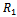 is the first order reflection coefficient.The BVP-1 involves wave scattering by a semi- infinite rigid dock floating on the free surface of an ocean of uniform finite depth and is of classical nature. This has been considered by Weitz and Keller [10] in connection with the reflection and transmission of water waves by floating ice. The BVP-2 is a radiation problem in presence of a free surface discontinuity with variable bottom depth. Here, Without solving the BVP-2, the analytical expression for the first order reflection coefficient is determined in terms of an integral involving the bottom shape function
is the first order reflection coefficient.The BVP-1 involves wave scattering by a semi- infinite rigid dock floating on the free surface of an ocean of uniform finite depth and is of classical nature. This has been considered by Weitz and Keller [10] in connection with the reflection and transmission of water waves by floating ice. The BVP-2 is a radiation problem in presence of a free surface discontinuity with variable bottom depth. Here, Without solving the BVP-2, the analytical expression for the first order reflection coefficient is determined in terms of an integral involving the bottom shape function 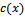 and the solution of the BVP-1, namely
and the solution of the BVP-1, namely 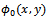 (Its first order partial derivative with respect to x).
(Its first order partial derivative with respect to x).4. The Zero Order Reflection Coefficient
- In this section, the zero order reflection coefficient is obtained by using residue calculus technique as used by Evans and Linton[11] for the problem of wave scattering by a upper surface discontinuity of somewhat different type in uniform finite depth water. The zero order potential function
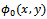 of the BVP-1 can be expanded in terms of orthogonal eigenfunctions for the free surface region
of the BVP-1 can be expanded in terms of orthogonal eigenfunctions for the free surface region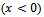 and the dock region
and the dock region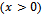 in the form given by
in the form given by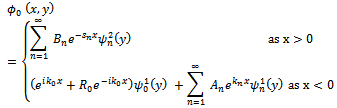 | (4.1) |
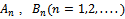 are unknown constants, ,
are unknown constants, , 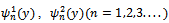 are the orthogonal depth eigenfunctions for the two regions (x<0 andx>0) given by
are the orthogonal depth eigenfunctions for the two regions (x<0 andx>0) given by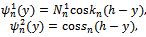 where
where 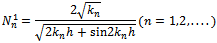 and
and  are given by the following two equations
are given by the following two equations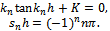 The matching conditions for
The matching conditions for 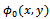 are the continuity of the velocity potential
are the continuity of the velocity potential 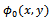 and the linear velocity at x=0:
and the linear velocity at x=0: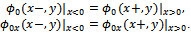 The orthogonality of the depth eigenfunctions of the two regions together with the above matching conditions at x=0 produces the following two systems of linear equations
The orthogonality of the depth eigenfunctions of the two regions together with the above matching conditions at x=0 produces the following two systems of linear equations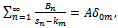 | (4.2) |
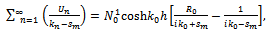 | (4.3) |
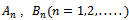 can be computed numerically from thesystem of linear equations (4.2) and (4.3) after truncation. The zero order reflection coefficient
can be computed numerically from thesystem of linear equations (4.2) and (4.3) after truncation. The zero order reflection coefficient 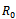 can be determined following the procedure used by Evans and Linton[11].We consider the integral
can be determined following the procedure used by Evans and Linton[11].We consider the integral 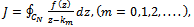 | (4.4) |
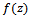 has simple poles at z=
has simple poles at z= 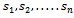 , simple zeroes at
, simple zeroes at 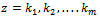 and
and 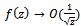 as
as 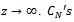 are the sequence of circles with radius
are the sequence of circles with radius 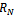 increases without bound as
increases without bound as 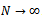 . These sequence of circles
. These sequence of circles 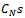 avoids the zeroes of the integrand and all the poles and zeroes of
avoids the zeroes of the integrand and all the poles and zeroes of 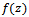 are inside of it and
are inside of it and 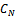 must not pass through (0,0) Further assuming that
must not pass through (0,0) Further assuming that 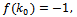 the function
the function 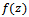 following the aforesaid properties can be taken as
following the aforesaid properties can be taken as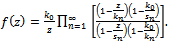 | (4.5) |
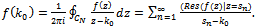 | (4.6) |
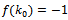 , with δ denoting the kronecker delta, we find
, with δ denoting the kronecker delta, we find 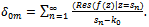 | (4.7) |
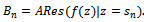 Again, we consider the integral
Again, we consider the integral 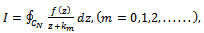 | (4.8) |
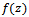 as mentioned above in(4.4). The matching conditions at x=0 can be combined to give
as mentioned above in(4.4). The matching conditions at x=0 can be combined to give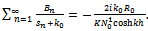 | (4.9) |
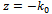
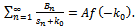 | (4.10) |
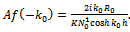 | (4.11) |
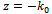 , using
, using 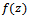 from (4.5), (4.10) gives
from (4.5), (4.10) gives 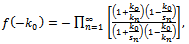 | (4.12) |
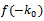 in(4.11), we obtain
in(4.11), we obtain 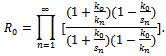 Thus
Thus 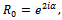 where
where 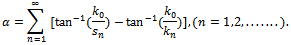 Thus |R0|=1, which is expected since all the incident waves are full reflected by the rigid dock floating on water of uniform finite depth.
Thus |R0|=1, which is expected since all the incident waves are full reflected by the rigid dock floating on water of uniform finite depth.5. The First Order Reflection Coefficient
- As mentioned earlier, without solving the BVP-2, the first order correction to the reflection coefficient
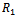 can be obtained by appropriate use of Green's integral theorem to the functions
can be obtained by appropriate use of Green's integral theorem to the functions 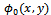 and
and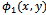 . We consider the region bounded by the lines
. We consider the region bounded by the lines 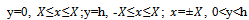 (where
(where  and employ Green's integral theorem in the form
and employ Green's integral theorem in the form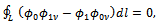 | (5.1) |
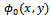 and
and 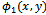 ensures that there is no contribution to the integral along the part
ensures that there is no contribution to the integral along the part 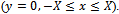 Furthermore the water under the dock region is undisturbed and there is no transmission of incoming wave. So there is no contribution to the integral along the part
Furthermore the water under the dock region is undisturbed and there is no transmission of incoming wave. So there is no contribution to the integral along the part 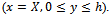 The only contribution to the integral (5.1) arises from the line
The only contribution to the integral (5.1) arises from the line 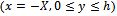 and the bottom. Finally making
and the bottom. Finally making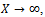 , we obtain
, we obtain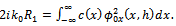 | (5.2) |
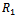 can be obtained explicitly once the shape function c(x) is known and the potential function
can be obtained explicitly once the shape function c(x) is known and the potential function 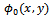 is obtained.
is obtained.6. Numerical Results and Discussions
- The first order correction to the reflection coefficient
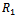 can be computed numerically from (5.2) once the shape function c(x) is known. In the present section, the values of
can be computed numerically from (5.2) once the shape function c(x) is known. In the present section, the values of  are computed for different values of the wave number Kh by considering two types of shape function c(x) characterizing the bottom undulations. It may be noted that for convenience both the bottom shape functions are chosen symmetric about the point of discontinuity of the surface boundary condition namely x=0 here. The expressions for
are computed for different values of the wave number Kh by considering two types of shape function c(x) characterizing the bottom undulations. It may be noted that for convenience both the bottom shape functions are chosen symmetric about the point of discontinuity of the surface boundary condition namely x=0 here. The expressions for  are given in the Appendix for such bottom profiles. For the numerical computation of
are given in the Appendix for such bottom profiles. For the numerical computation of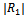 , the infinite series in the appendix are truncated upto desired accuracy. The convergence of the integral (5.2) for the chosen bottom shape functions is assured. Case-1:The first bottom shape function is chosen as
, the infinite series in the appendix are truncated upto desired accuracy. The convergence of the integral (5.2) for the chosen bottom shape functions is assured. Case-1:The first bottom shape function is chosen as 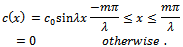 The above c(x) represents a bottom profile of m sinusoidal ripples with amplitude
The above c(x) represents a bottom profile of m sinusoidal ripples with amplitude 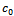 and wave number λ. The analytical expression for
and wave number λ. The analytical expression for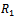 is given in the Appendix for the above bottom profile. For numerical computation the values of non dimensional ripple amplitude is taken as
is given in the Appendix for the above bottom profile. For numerical computation the values of non dimensional ripple amplitude is taken as 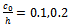 and ripple wave number
and ripple wave number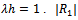 . is depicted graphically against the wave number Kh in figure-1. The graph of
. is depicted graphically against the wave number Kh in figure-1. The graph of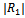 is observed to be oscillatory in nature against Kh and the oscillation peaks up to a highest value for a certain frequency. This observation can be explained as multiple interaction of the incident wave with different frequencies and the sinusoidally varying bottom topography. Occurrence of zeroes of
is observed to be oscillatory in nature against Kh and the oscillation peaks up to a highest value for a certain frequency. This observation can be explained as multiple interaction of the incident wave with different frequencies and the sinusoidally varying bottom topography. Occurrence of zeroes of 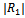 for certain Kh indicates that the sinusoidal bottom topography does not affect the reflected wave of the incident wave train up to first order. The peak values of
for certain Kh indicates that the sinusoidal bottom topography does not affect the reflected wave of the incident wave train up to first order. The peak values of 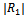 are found to be increasing with the values of
are found to be increasing with the values of 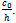 The heights of the oscillations of
The heights of the oscillations of 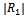 are gradually diminishing along with Kh. This can be explained as wave damping due to energy dissipation when wave propagates over uneven sea bottom and the presence of the upper surface discontinuity.The figure-2 is plotted by taking dimensionless ripple wave number
are gradually diminishing along with Kh. This can be explained as wave damping due to energy dissipation when wave propagates over uneven sea bottom and the presence of the upper surface discontinuity.The figure-2 is plotted by taking dimensionless ripple wave number 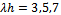 and fixed amplitude
and fixed amplitude 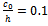 . In this case the oscillation also decreases and gradually vanishes with Kh. Also as the wave number λh of the sinusoidal bottom profile function increases, number of oscillations of
. In this case the oscillation also decreases and gradually vanishes with Kh. Also as the wave number λh of the sinusoidal bottom profile function increases, number of oscillations of 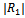 decreases with Kh. Also the highest peak values of
decreases with Kh. Also the highest peak values of 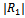 decrease with the increasing value of λh.
decrease with the increasing value of λh.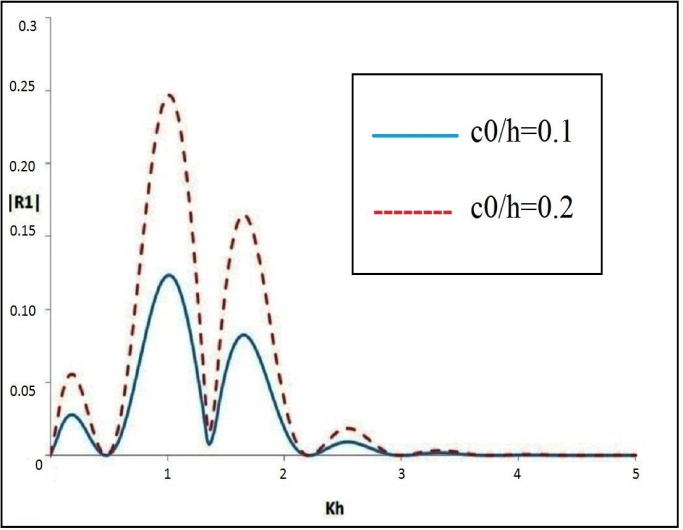 | Figure1.  for differentc 0/h for differentc 0/h |
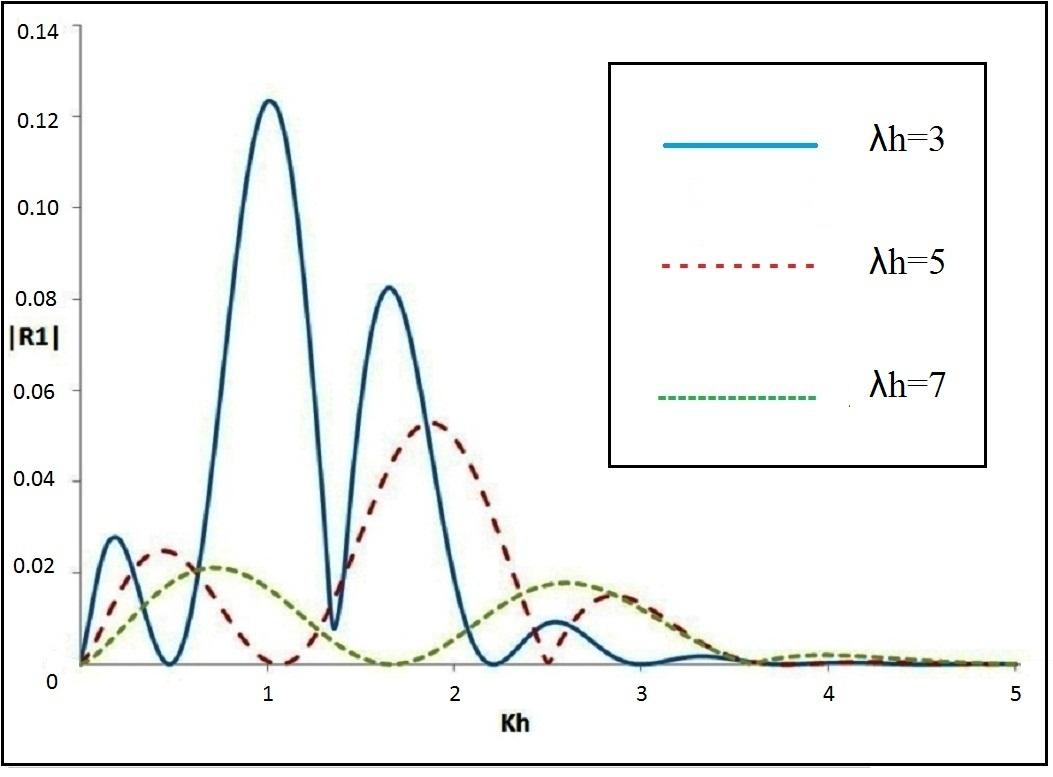 | Figure2.  for different λh for different λh |
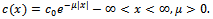 This above c(x)represents exponentially decaying bottom profile. The analytical expression of
This above c(x)represents exponentially decaying bottom profile. The analytical expression of 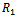 is given in the Appendix for this shape function.
is given in the Appendix for this shape function.  are depicted against Kh in figure-3 by taking
are depicted against Kh in figure-3 by taking 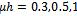 and
and 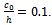 An important feature of this figure is that for each value of the parameter
An important feature of this figure is that for each value of the parameter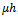 ,
, 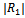 first increases with Kh and attains a maximum peak value and then gradually decreases with Kh. This may be attributed due to exponentially decaying bottom profile as the bottom undulation vanishes far away where the water is of uniform depth h. A noticeable feature of this figure is that this maximum peak value is found to be decreasing with the increasing value of
first increases with Kh and attains a maximum peak value and then gradually decreases with Kh. This may be attributed due to exponentially decaying bottom profile as the bottom undulation vanishes far away where the water is of uniform depth h. A noticeable feature of this figure is that this maximum peak value is found to be decreasing with the increasing value of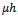 .
.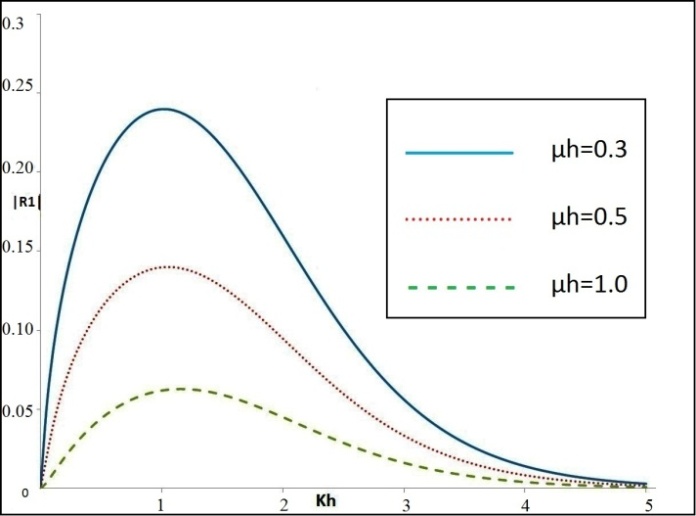 | Figure3. 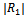 for different for different 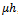 |
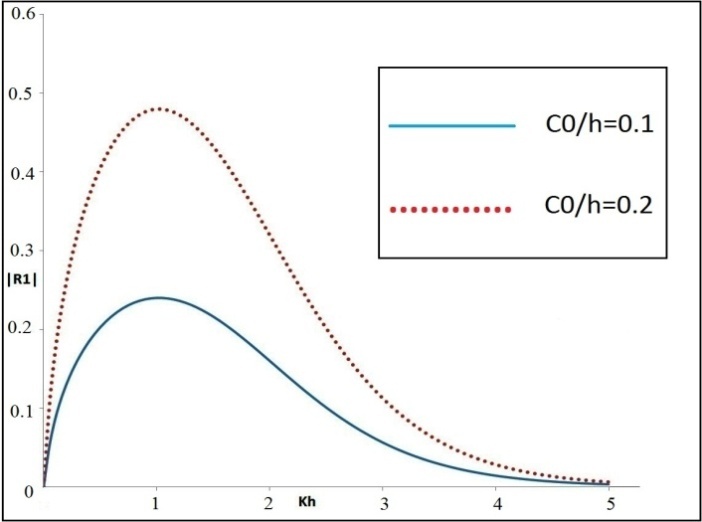 | Figure4. 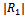 for different for different 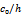 |
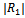 against Kh for different dimensionless ripple amplitude
against Kh for different dimensionless ripple amplitude 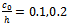 and fixed value of
and fixed value of 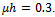 . As before,
. As before, 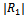 first increases with Kh and then rapidly decreases with Kh for
first increases with Kh and then rapidly decreases with Kh for  . Also the highest peak value of
. Also the highest peak value of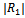 is found to be increasing with increasing value of the dimensionless ripple amplitude
is found to be increasing with increasing value of the dimensionless ripple amplitude 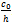 .
.7. Conclusions
- A few problems involving water wave scattering by surface discontinuity in presence variable bottomtopography has already been studied in the literature. The present study is concerned with water wave scattering by a semi-infinite floating dock in presence of a uneven bottom. Study of such type of problem is important for quite some time due to several valuable aspects in research areas in marine science and oceanography.A simplified perturbation analysis together withappropriate use of Green's integral theorem is employed to obtain first order correction to the reflection coefficient. Two different type of shape functions are chosen to describe the bottom topography in case of sinusoidal patch and exponentially decaying bottom undulation. The numerical results of the first-order correction of the reflection coefficient are being obtained by utilizing the expressions given in the appendix for both sinusoidal patches and exponentially decaying bottom undulation. These results are depicted graphically against the wave number of the incident wave in a number of figures. It may be noted that the discontinuity of the upper surface boundary condition may be at the another point and in that case same method can be applied.
ACKNOWLEDGEMENTS
- R. Maiti thanks CSIR, New Delhi (India) for providing support to prepare this paper.
Appendix
- For a sinusoidal bottom topography
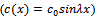 :
: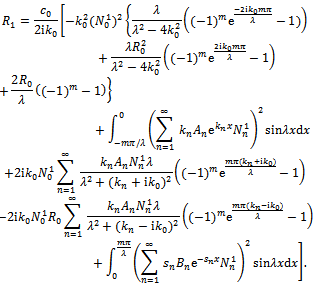 For an exponential bottom topography
For an exponential bottom topography 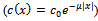 :
: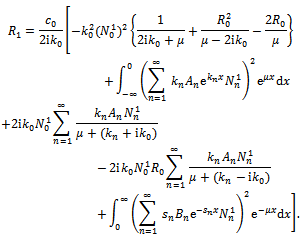
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML