M. A. Seddeek 1, M. A. Abdou 2, W. G. El-Sayed 2, F. M. El-Saedy 3
1Department of Mathematics, Deanship of Educational Services, Al-Qassim University, Saudi Arabia
2Department of Mathematics, Faculty of Science, Alexandria University, Egypt
3Department of Mathematics, Faculty of Science, Umm Al-Qura University, Makkah, Saudi Arabia
Correspondence to: M. A. Abdou , Department of Mathematics, Faculty of Science, Alexandria University, Egypt.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
This paper covered the study of the boundary value problem for isotropic homogeneous perforated infinite elastic media in presence of uniform flow of heat. For this, we considered the problem of a thin infinite plate of specific thickness with a curvilinear hole where the origin lie inside the hole is conformally mapped outside a unit circle by means of a specific rational mapping . The complex variable method has been applied and it transforms the problem to the integro-differential equation with Cauchy kernel that can be solved to find two complex potential functions which called Gaursat functions. Moreover, the three stress components  for the boundary value problem in the thermoelasticity plane are obtained. Many special cases of the conformal mapping and three applications for different cases are discussed and many main results derived from the work.
for the boundary value problem in the thermoelasticity plane are obtained. Many special cases of the conformal mapping and three applications for different cases are discussed and many main results derived from the work.
Keywords:
Boundary Value Problem of Infinite Plate Weakened by a Hole, Conformal Mapping, Integro-Differential Equation with Discontinuous Kernel, Complex Potential Functions
1. Introduction
Several authors wrote about the boundary value problems and their applications in many different sciences, see Gakhov[1], Ciarlet et al.[2], Zebib[3] and Saito and Yamamto[4]. From these problems, we established contact problems and mixed problems in the theory of elasticity , see Colton and Kress[5], and Abdou[6]. In Abdou[6,7], Abdou and Khamis[8] and Abdou and Khar-Eldin [9],Complex variable method is used to express the solutions of these problems in the form of power series by applied Laurant's theorem. On the other hand, some of authors applied the complex variable method to obtain the solutions in the form two complex potential functions which called Gaursat functions by using the properties of Cauchy integrals on the circle, or on any region mapped to outside a unit circle  by means of a general rational mapping
by means of a general rational mapping 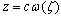 where,
where,  doesn't vanish or become infinite outside the unit circle. In thermoelastic problems for elastic media, the first and second boundary value problems are equivalent to finding two analytic functions
doesn't vanish or become infinite outside the unit circle. In thermoelastic problems for elastic media, the first and second boundary value problems are equivalent to finding two analytic functions 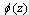 and
and  of one complex argument
of one complex argument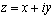 . These functions must satisfy the boundary conditions,
. These functions must satisfy the boundary conditions,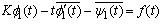 | (1.1) |
where  denotes the affix of a point on the boundary. In terms of
denotes the affix of a point on the boundary. In terms of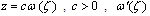 , does not vanish or become infinite for
, does not vanish or become infinite for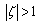 , the infinite region mapped to outside a unit circle
, the infinite region mapped to outside a unit circle .For the first fundamental boundary value problem or it called the stress boundary value problem we have
.For the first fundamental boundary value problem or it called the stress boundary value problem we have  and
and 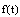 is a given function of stress. While for
is a given function of stress. While for  and
and 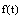 is a given function of displacement which called the thermal conductivity then eq.(1.1) called the second fundamental boundary value problems or the displacement boundary value problems. The books written by Noda et al.[10], Hetnarski and Ignaczak[11], Parkus[12] and Popov[13] contain many different methods to solve the problems in the theory of elasticity in one, two and three dimensions.The complex potential functions
is a given function of displacement which called the thermal conductivity then eq.(1.1) called the second fundamental boundary value problems or the displacement boundary value problems. The books written by Noda et al.[10], Hetnarski and Ignaczak[11], Parkus[12] and Popov[13] contain many different methods to solve the problems in the theory of elasticity in one, two and three dimensions.The complex potential functions 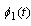 and
and 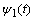 take the following form, see Parkus [12]
take the following form, see Parkus [12]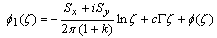 | (1.2) |
and,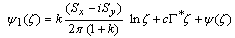 | (1.3) |
where, 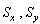 are the components of the resultant vector of all external forces acting on the boundary and
are the components of the resultant vector of all external forces acting on the boundary and 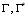 are complex constants. Generally the two complex functions
are complex constants. Generally the two complex functions  and
and  are single value analytic functions within the region outside the unit circle
are single value analytic functions within the region outside the unit circle  and
and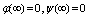 .In [14], Muskhelishvili used the rational mapping,
.In [14], Muskhelishvili used the rational mapping,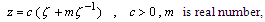 | (1.4) |
to solving the problem of infinite plate weakened by an elliptic hole.El-Sirafy and Abdou in [15], used the rational mapping,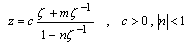 | (1.5) |
to solve the first and second fundamental problems for the infinite plate with general curvilinear hole  confrmally mapped on the domain outside a unit circle.The rational mapping,
confrmally mapped on the domain outside a unit circle.The rational mapping,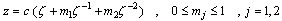 | (1.6) |
is used by Abdou and Khamis [8] to obtain the solution of the problem of an infinite plate with a curvilinear hole having three poles and they take the circle shape, ellipse shape and square shape as a special cases of the holes.Also, the conformal mapping function,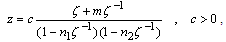 | (1.7) |
is studied completely by England [16].In this paper, we consider the boundary value problem for isotropic homogeneous perforated infinite elastic media in presence of uniform flow of heat. Then, we use the more general shape of conformal mapping to obtain the complex potential functions for the problem in the form integro- differential equation with singular kennel. Many special cases are obtained and several applications are discussed from the work.This study is useful for researchers who work on the studies of petroleum tubes industry or water or gas. It also benefits the physics scientists who work on the study of the ozone hole.
2. Formulation of the Problem
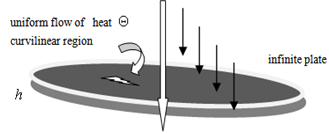
Consider a thin infinite plate of thickness 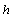 with a curvilinear hole
with a curvilinear hole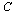 , where the origin lie inside the hole is conformally mapped on the domain outside a unit circle
, where the origin lie inside the hole is conformally mapped on the domain outside a unit circle 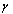 by means of a rational mapping,
by means of a rational mapping,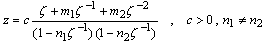 | (2.1) |
where 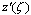 does not vanish or become infinite outside the unit circle
does not vanish or become infinite outside the unit circle 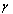 . If a temperature distribution
. If a temperature distribution 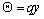 is following uniformly in the direction of the negative
is following uniformly in the direction of the negative 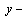 axis, where the increasing a temperature distribution
axis, where the increasing a temperature distribution 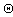 is assumed to be constant a cross the thickness of the plate, i.e.
is assumed to be constant a cross the thickness of the plate, i.e.  , and
, and 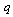 is the constant temperature gradient. The uniform flow of heat is distributed by the presence of an insulated curvilinear hole
is the constant temperature gradient. The uniform flow of heat is distributed by the presence of an insulated curvilinear hole .The heat equation satisfies the relation,
.The heat equation satisfies the relation, 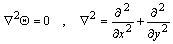 | (2.2) |
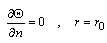 | (2.3) |
 | Figure (1). |
where  is the unit vector perpendicular to the surface.Neglecting the variation of the strain and the stress with respect to the thickness of the plate, the thermoelastic potential
is the unit vector perpendicular to the surface.Neglecting the variation of the strain and the stress with respect to the thickness of the plate, the thermoelastic potential 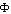 satisfies the formula, see Parkus [12]
satisfies the formula, see Parkus [12]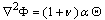 | (2.4) |
where  is a scalar which present the coefficient of the thermal expansion and
is a scalar which present the coefficient of the thermal expansion and  is Poisson’s ratio. Assume the force of the plate is free of applied loads.In this case, the formula (1.1) for the first and second boundary value problems respectively take the following form,
is Poisson’s ratio. Assume the force of the plate is free of applied loads.In this case, the formula (1.1) for the first and second boundary value problems respectively take the following form,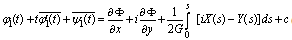 | (2.5) |
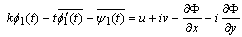 | (2.6) |
where the applied stresses 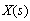 and
and 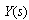 are prescribed on the boundary of the plane
are prescribed on the boundary of the plane  is the length measured from an arbitrary point,
is the length measured from an arbitrary point, 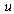 and
and 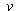 are the displacement components,
are the displacement components, 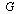 is the shear modulus. Also, here the applied stresses
is the shear modulus. Also, here the applied stresses 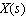 and
and 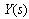 must satisfy the following, see Parkus [12]
must satisfy the following, see Parkus [12]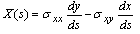 | (2.7) |
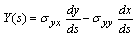 | (2.8) |
where 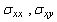 and
and 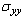 are the components of stresses which are given by the following relations,
are the components of stresses which are given by the following relations,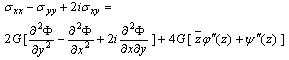 | (2.9) |
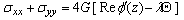 | (2.10) |
where 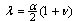 is the coefficient of heat transfer.The rational mapping
is the coefficient of heat transfer.The rational mapping 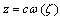 maps the boundary
maps the boundary 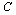 of the given region occupied by the middle plane of the plate in the
of the given region occupied by the middle plane of the plate in the 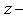 plane onto the unit circle
plane onto the unit circle  in the
in the  plane. Curvilinear coordinates
plane. Curvilinear coordinates  are thus introduce into the
are thus introduce into the 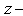 plane which are the maps of the polar conditions in the
plane which are the maps of the polar conditions in the  plane as given by
plane as given by 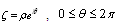 . By using the transformation
. By using the transformation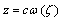 , Eq.(1.1) reduce to,
, Eq.(1.1) reduce to,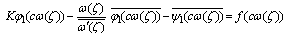 | (2.11) |
The last formula represent the first and second boundary value problems in 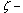 plane.
plane.
3. The Rational Mapping
The rational mapping (2.1) maps the curvilinear hole  in
in 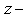 plane onto the domain of outside unit circle in
plane onto the domain of outside unit circle in 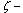 plane under the condition
plane under the condition 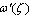 does not vanish or become infinite outside the unit circle
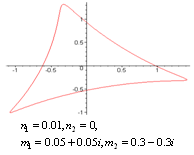
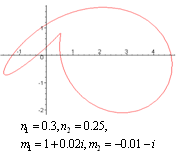
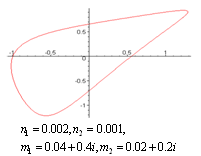
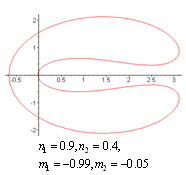
does not vanish or become infinite outside the unit circle . The following graphs give the different shapes of the rational mapping (2.1).
. The following graphs give the different shapes of the rational mapping (2.1). 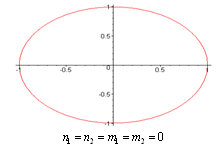 | Figure (2) |
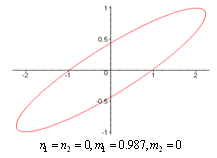 | Figure (3) |
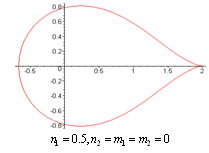 | Figure (4) |
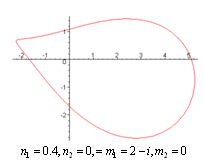 | Figure (5) |
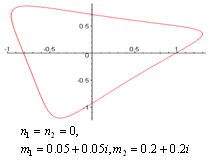 | Figure (6) |
 | Figure (7) |
 | Figure (8) |
 | Figure (9) |
 | Figure (10) |
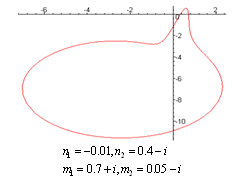 | Figure (11) |
4. Method of Solution
In this section, we use the complex variable method to obtain the two complex functions, Goursat functions,  and
and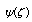 . Moreover, the three stress components
. Moreover, the three stress components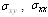 , and
, and 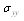 will be complete determined.
will be complete determined.
4.1. The Stress Components
The solution of Eq. (2.2) is given by, 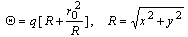 | (4.1) |
By substitute Eq.(4.1) in Eq.(2.4) and using the definition of  in polar coordinates the thermoelastic potential function take the form,
in polar coordinates the thermoelastic potential function take the form,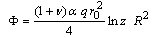 | (4.2) |
Also, the stresses components can be adapted in the form,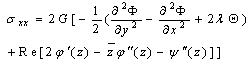 | , (4.3) |
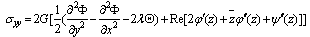 | (4.4) |
and,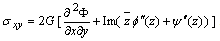 | (4.5) |
Eqs.(4.3), (4.4) and (4.5) after some derivatives and algebraic relations adapted as,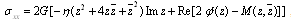 | (4.6) |
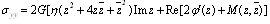 | (4.7) |
and,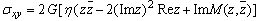 | , (4.8) |
where,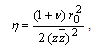 | (4.9) |
and,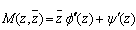 | (4.10) |
After determine the Goursat functions the components of stress are completely determined.
4.2. Goursat Functions
To obtain the two complex potential functions, Goursat functions by using the conformal mapping (2.1) in the boundary condition(1.1), we write the expression 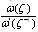 in the form,
in the form,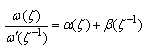 | (4.11) |
where,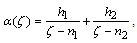 | (4.12) |
and,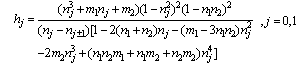 | (4.13) |
 is a regular function for
is a regular function for .
.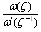 has a singularity at
has a singularity at 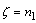 and
and .Using Eq.(1.2) and Eq.(1.3) in Eq.(2.11), we get
.Using Eq.(1.2) and Eq.(1.3) in Eq.(2.11), we get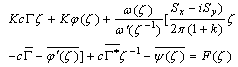 | (4.14) |
Using Eq.(4.12) in Eq.(4.14), we have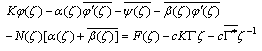 | (4.15) |
Taking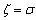 , we get
, we get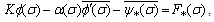 | (4.16) |
where,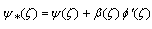 | (4.17) |
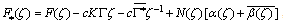 | (4.18) |
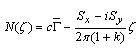 | (4.19) |
and,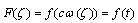 | (4.20) |
Assume the function  with its derivatives must satisfy
with its derivatives must satisfy  condition. Our aim is to determine the functions
condition. Our aim is to determine the functions 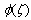 and
and 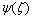 for the various boundary value problems. For this multiply both side of Eq.(4.16) by
for the various boundary value problems. For this multiply both side of Eq.(4.16) by 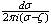 where
where 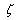 is any point the interior of
is any point the interior of  and integral over the circle, we obtain
and integral over the circle, we obtain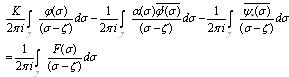 | (4.21) |
Using Eqs.(4.17),(4.18) and (4.19) in Eq.(4.21) then applying the properties of Cauchy integral to have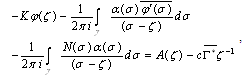 | (4.22) |
where,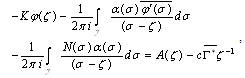 | (4.23) |
The formula (4.22) represents the integro-differential equation of second kind with Cauchy kernel. The references, Fedotov[17], Hanyga and Seredyńska[18], Bavula[19] and AL-Jawary and Wrobel[20], contain many different methods to solve this kind of the equations analytically and numerically in one, two and three dimensions.To obtain the integral terms of Eq. (4.22) we use Eq. (4.12) and then apply the residue theorem to have,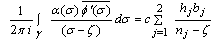 | (4.24) |
where 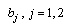 are complex constants.Also,
are complex constants.Also,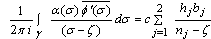 | (4.25) |
So, Eq.(4.22) reduce to,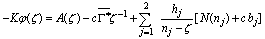 | (4.26) |
To determine the constants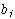 , differentiating Eq.(4.26) with respect to
, differentiating Eq.(4.26) with respect to 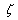 and substituting in Eq.(4.24), to get
and substituting in Eq.(4.24), to get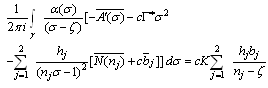 | (4.27) |
Substituting Eq.(4.12) in Eq.(4.27), then using the properties of Cauchy integral and applying the residue theorem at the singular points, we obtain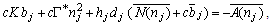 | (4.28) |
where,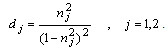 | (4.29) |
The last equation can be written in the form,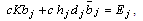 | (4.30) |
where,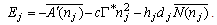 | (4.31) |
Taking the complex conjugate of Eq.(4.30) we get,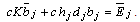 | (4.32) |
From Eq.(4.30) and Eq.(4.32) we have,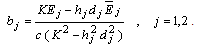 | (4.33) |
To obtain the complex functions 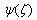 we have form Eq.(4.17) after substituting the expression of
we have form Eq.(4.17) after substituting the expression of  and
and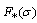 , and taking the complex conjugate of the resulting equation after using the expression of
, and taking the complex conjugate of the resulting equation after using the expression of 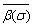 to yields,
to yields,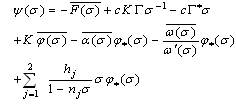 | (4.34) |
where,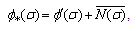 | (4.35) |
and,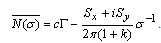 | (4.36) |
Multiplying both sides of Eq.(4.34) by  where
where  is any point in the interior of
is any point in the interior of 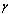 and integrating over the unit circle, then using the properties of Cauchy integral and calculate sum residue, we obtain
and integrating over the unit circle, then using the properties of Cauchy integral and calculate sum residue, we obtain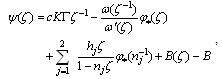 | (4.37) |
where,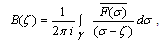 | (4.38) |
and,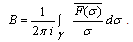 | (4.39) |
5. Some Applications
In this section, we assume different values of the given functions in the first or second fundamental boundary value problems. Then, we obtain the expression of Goursat functions. After that, the components of stresses can be calculated directly.
5.1. Application 1: Curvilinear Hole for an Infinite Plate Subjected to Uniform Tensile Stress and Flowing Heat
For we have,
we have,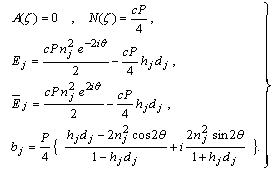 | .(5.1) |
Then Eq.(4.26) becomes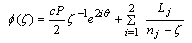 | (5.2) |
where,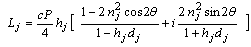 | . (5.3) |
Also,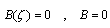 | (5.4) |
then,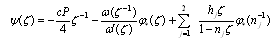 | (5.5) |
where,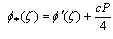 | (5.6) |
This application discusses the first fundamental boundary value problem of an infinite plate stretched at infinity by the application of a uniform tensile stress of intensity heat in the negative direction of 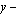 axis. This plate is weakened by a curvilinear hole C which is free from stress.For
axis. This plate is weakened by a curvilinear hole C which is free from stress.For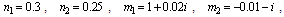
 , the stress components
, the stress components and
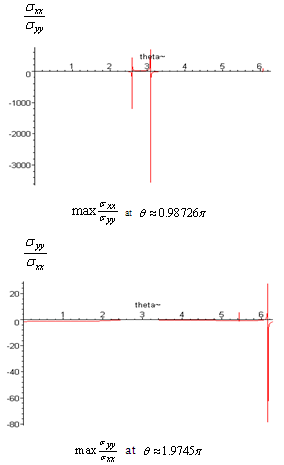
and 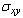 are obtained in large forms calculated by computer and illustrated in the following two cases :(i) When the study is in the normal plate, we have the following shapes for the stress components, see Fig.(12) and Fig.(13).(ii) In the thermoelasticity plate, we have the following shapes for the stress components by using the substitutions
are obtained in large forms calculated by computer and illustrated in the following two cases :(i) When the study is in the normal plate, we have the following shapes for the stress components, see Fig.(12) and Fig.(13).(ii) In the thermoelasticity plate, we have the following shapes for the stress components by using the substitutions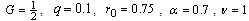 , see Fig.(14) and Fig.(15).
, see Fig.(14) and Fig.(15).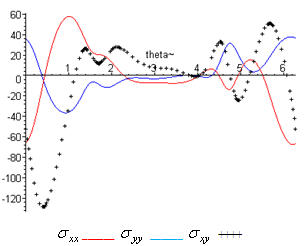 | Figure (12) |
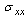 has positive values at
has positive values at 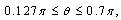
 has positive values at
has positive values at 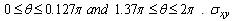 has positive values at
has positive values at 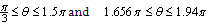 .
.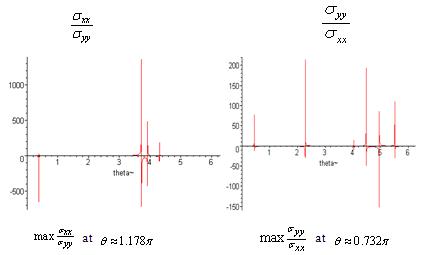 | Figure (13) |
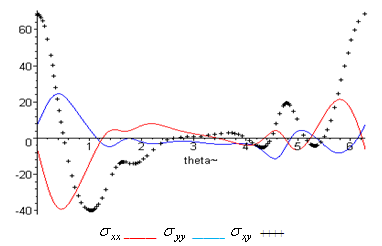 | Figure (14) |
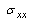 has positive values at
has positive values at 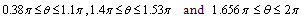 .
. 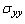 has positive values at
has positive values at 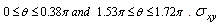 has positive values at
has positive values at 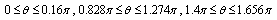 and
and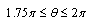 .
.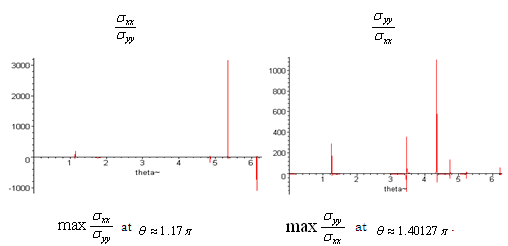 | Figure (15) |
5.2. Application 2: Curvilinear Hole Having two Poles and the Edge is Subject to a Uniform Pressur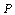
If 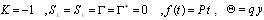 .Then,
.Then,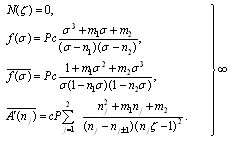 | (5.7) |
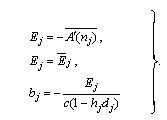 | (5.8) |
By using these values Eq.(4.26) becomes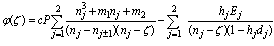 | (5.9) |
Also,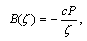 | (5.10) |
and,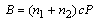 | (5.11) |
Hence Eq.(4.37) becomes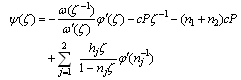 | (5.12) |
The previous discussing give the solutions of first fundamental boundary value problem when the edge of hole is subject to a uniform pressure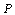 .For
.For 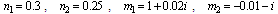
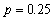 , the stress components
, the stress components 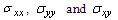 are obtained in large forms calculated by computer and illustrated in the following two cases :
are obtained in large forms calculated by computer and illustrated in the following two cases :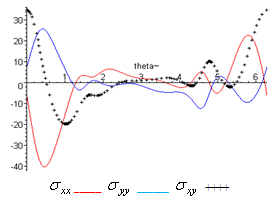 | Figure (16) |
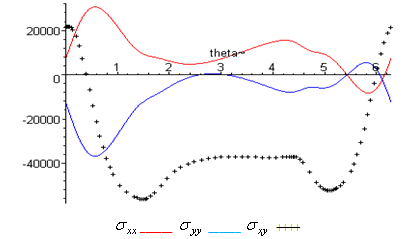
(i) When the study is in the normal plate, we have the following shapes for the stress components, see Fig.(16) and Fig.(17).(ii) In the thermoelasticity plate, we have the following shapes for the stress components by using the substitutions 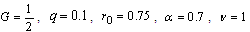 , see Fig.(18) and Fig.(19).
, see Fig.(18) and Fig.(19).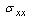 has positive values at
has positive values at 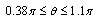
 .
. 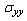 has positive values at
has positive values at 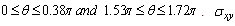 has positive values at
has positive values at 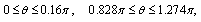
 and
and  .
.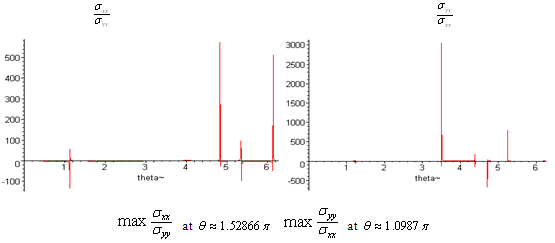 | Figure (17) |
 | Figure (18) |
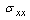 has positive values at
has positive values at has positive values at
has positive values at .
. has positive values at
has positive values at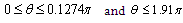 .
. | Figure (19) |
5.3. Application 3: The External Force Acts on the Center of the Curvilinear Hole
When,  then,
then,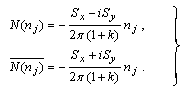 | (5.13) |
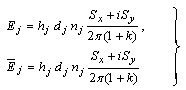 | (5.14) |
and,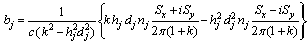 | (5.15) |
Hence Eq.(4.26) reduce to,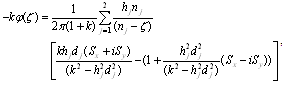 | , (5.16) |
And the second function given by,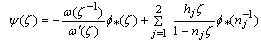 | (5.17) |
where,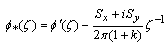 | (5.18) |
The last application gives the solution of the second fundamental boundary value problem when the heat is flowing in the negative direction of 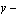 axis and the force acts on the centre of the curvilinear hole. For
axis and the force acts on the centre of the curvilinear hole. For 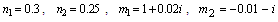 ,
, 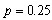 , the stress components
, the stress components  are obtained in large forms calculated by computer and illustrated in the following two cases :(i) When the study is in the normal plate, we have the following shapes for the stress components, see Fig.(20) and Fig.(21).(ii) In the thermoelasticity plate, we have the following shapes for the stress components by using the substitutions
are obtained in large forms calculated by computer and illustrated in the following two cases :(i) When the study is in the normal plate, we have the following shapes for the stress components, see Fig.(20) and Fig.(21).(ii) In the thermoelasticity plate, we have the following shapes for the stress components by using the substitutions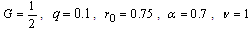 , see Fig.(22) and Fig.(23)..
, see Fig.(22) and Fig.(23)..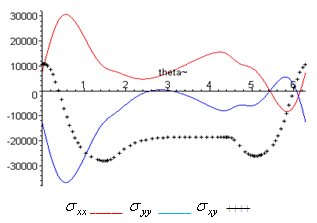 | Figure (20) |
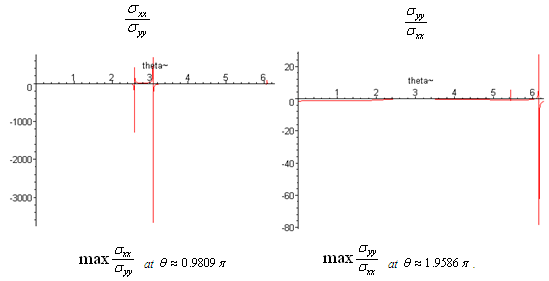
 has positive values at
has positive values at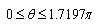 .
. .has positive values at
.has positive values at 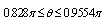 and.
and. 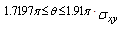 has positive values at
has positive values at  and
and 
 | Figure (21) |
 | Figure (22) |
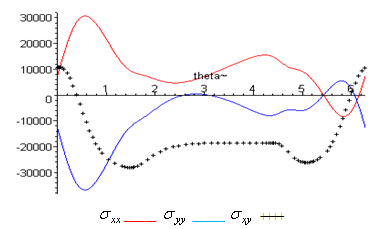
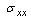 has positive values at
has positive values at 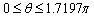 .
.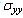 has positive values at
has positive values at 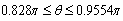 and
and 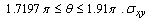 has positive values at
has positive values at 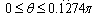 and
and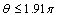 .
.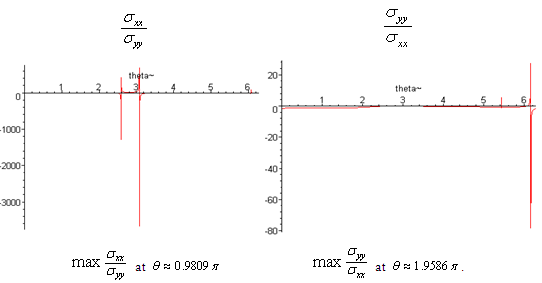 | Figure (23) |
6. Conclusions
From the previous discussion S we have the following result(i) The solution of the boundary value problems for isotropic homogeneous infinite elastic media in  plane reduce to obtain the two complex potential functions, Gaursat functions, in
plane reduce to obtain the two complex potential functions, Gaursat functions, in 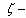 plane by using conformal mapping.(ii) The conformal mapping
plane by using conformal mapping.(ii) The conformal mapping , where, for
, where, for  mapped infinite region to out side a unit circle
mapped infinite region to out side a unit circle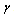 .(iii) When we applied the conformal mapping
.(iii) When we applied the conformal mapping  the boundary value problems reduce to the integro-differentail equation with discontinuous kernel.(iv) Cauchy method is the best method to solving the integro-differentail equation with Cauchy kernel and obtaining the two complex functions
the boundary value problems reduce to the integro-differentail equation with discontinuous kernel.(iv) Cauchy method is the best method to solving the integro-differentail equation with Cauchy kernel and obtaining the two complex functions 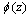 and
and 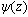 directly.(v) The components of stress
directly.(v) The components of stress 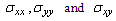 is completely determine and plotting after obtaining the two complex functions.(vi) As a main result of inserting the effect of uniform flow of heat in the negative of
is completely determine and plotting after obtaining the two complex functions.(vi) As a main result of inserting the effect of uniform flow of heat in the negative of 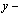 direction we have, see figures (12-23)
direction we have, see figures (12-23) 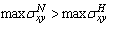 | (6.1) |
and,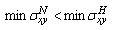 | (6.2) |
where,  represent the shear components of stress at normal state, while
represent the shear components of stress at normal state, while  represent the shear components of stress after inserting the effect of heating.(vii) If we denote to the angle that appears the maximum value of
represent the shear components of stress after inserting the effect of heating.(vii) If we denote to the angle that appears the maximum value of  in normal state by
in normal state by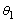 , and the angle that appears the maximum value of
, and the angle that appears the maximum value of  after inserting the effect of heating by
after inserting the effect of heating by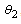 , we note
, we note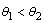 | (6.3) |
(viii) If we denote to the angle that appears the maximum value of  in normal state by
in normal state by , and the angle that appears the maximum value of
, and the angle that appears the maximum value of 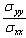 after inserting the effect of heating by
after inserting the effect of heating by , we note
, we note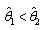 | (6.4) |
(ix) All of the previous works in this paper is considered as special cases from this study.
References
| [1] | F.D.Gakhov, Boundary value problems, Pergamon 1966. |
| [2] | P. G. Ciarlet, M. H. Schultz, and R. S. Varga, Numerical methods of high-order accuracy for nonlinear boundary value problems I. One dimensional problem, Numer. Math., Vol. 9 , 1967. |
| [3] | A. Zebib, A Chebyshev method for the solution of boundary value problems, J. Comput. Phys.Vol. 53, 1984. |
| [4] | S.Saito, M.Yamamto, Boundary value problems of quasilinear ordinary differential systems on a finite interval. Math. Japon. Vol. 34 ,1989. |
| [5] | D. Colton, R. Kress, Integral Equation Methods in Scattering Theory, John Wiley, New York, 1983. |
| [6] | M. A. Abdou, First and second fundamental problems for an elastic infinite plate with a curbilinear hole. Alex. Eng. J.Vol. 33, 1994. |
| [7] | M. A. Abdou, Fundamental problems for infinite plate with a curvilinear hole having infinite poles. Appl. Math. Comput.,Vol.93, 2002. |
| [8] | M. A. Abdou and A.K. Khamis, On a problem of an infinite plate with a curvilinear hole having three poles and arbitrary shape. Bull. Call.Math.Soc, Vol.29, 2000. |
| [9] | M.A. Abdou and E.A. Khar-Eldin, An infinite plate weakened by a hole having arbitrary shape. J. Comp. Appl. Math.,Vol. 56, 1994. |
| [10] | N. Noda, R.B. Hetnarski, Y. Tanigawa, Thermal Stress, Taylor and Francis, 2003. |
| [11] | R.B. Hetnarski, J. Ignaczak, Mathematical Theory of Elasticity, Taylor and Francis, 2004. |
| [12] | H. Parkus, Thermoelasticity, Spring-Verlag, 1976. |
| [13] | G. Ya. Popov, Contact Problems for a Linearly Deformable Foundation, Kiev, Odessa, 1988. |
| [14] | N.I. Muskhelishvili, Some Basic Problems of Mathematical Theory of Elasticity, Holland, 1953. |
| [15] | I.H. El-Sirafy, M.A. Abdou, First and second fundamental problems of infinite plate with a curvilinear hole, J. Math. Phys. Sci.Vol. 18,1984. |
| [16] | H. England, A Complex Variables Method in Elasticity, Dover publications, Inc., New-Youk, 1971. |
| [17] | A.I. Fedotov, Quadrature-difference methods for solving linear and nonlinear singular integro-differential equations, J. Nonlinear Analysis, Vol. 71, 2009. |
| [18] | A. Hanyga, M. Seredyńska, Positivity of Green's functions for a class of partial integro-differential equations including viscoelasticity, J. Wave Motion, Vol. 47, 2010. |
| [19] | V.V. Bavula, The group of automorphisms of the algebra of polynomial integro-differential operators, J. Algebra, Vol.348, 2011. |
| [20] | M.A. AL-Jawary, L.C.Wrobel, Numerical solution of two-dimensional mixed problems with variable coefficients by the boundary-domain integral and integro-differential equation methods, Engineering Analysis with Boundary Elements, Vol.35, 2011. |

 for the boundary value problem in the thermoelasticity plane are obtained. Many special cases of the conformal mapping and three applications for different cases are discussed and many main results derived from the work.
for the boundary value problem in the thermoelasticity plane are obtained. Many special cases of the conformal mapping and three applications for different cases are discussed and many main results derived from the work.
 by means of a general rational mapping
by means of a general rational mapping 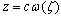 where,
where,  doesn't vanish or become infinite outside the unit circle. In thermoelastic problems for elastic media, the first and second boundary value problems are equivalent to finding two analytic functions
doesn't vanish or become infinite outside the unit circle. In thermoelastic problems for elastic media, the first and second boundary value problems are equivalent to finding two analytic functions 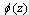 and
and  of one complex argument
of one complex argument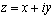 . These functions must satisfy the boundary conditions,
. These functions must satisfy the boundary conditions,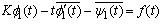
 denotes the affix of a point on the boundary. In terms of
denotes the affix of a point on the boundary. In terms of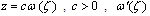 , does not vanish or become infinite for
, does not vanish or become infinite for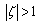 , the infinite region mapped to outside a unit circle
, the infinite region mapped to outside a unit circle .For the first fundamental boundary value problem or it called the stress boundary value problem we have
.For the first fundamental boundary value problem or it called the stress boundary value problem we have  and
and 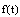 is a given function of stress. While for
is a given function of stress. While for  and
and 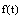 is a given function of displacement which called the thermal conductivity then eq.(1.1) called the second fundamental boundary value problems or the displacement boundary value problems. The books written by Noda et al.[10], Hetnarski and Ignaczak[11], Parkus[12] and Popov[13] contain many different methods to solve the problems in the theory of elasticity in one, two and three dimensions.The complex potential functions
is a given function of displacement which called the thermal conductivity then eq.(1.1) called the second fundamental boundary value problems or the displacement boundary value problems. The books written by Noda et al.[10], Hetnarski and Ignaczak[11], Parkus[12] and Popov[13] contain many different methods to solve the problems in the theory of elasticity in one, two and three dimensions.The complex potential functions 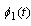 and
and 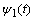 take the following form, see Parkus [12]
take the following form, see Parkus [12]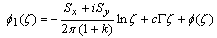
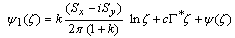
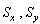 are the components of the resultant vector of all external forces acting on the boundary and
are the components of the resultant vector of all external forces acting on the boundary and 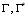 are complex constants. Generally the two complex functions
are complex constants. Generally the two complex functions  and
and  are single value analytic functions within the region outside the unit circle
are single value analytic functions within the region outside the unit circle  and
and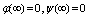 .In [14], Muskhelishvili used the rational mapping,
.In [14], Muskhelishvili used the rational mapping,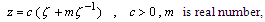
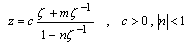
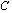 confrmally mapped on the domain outside a unit circle.The rational mapping,
confrmally mapped on the domain outside a unit circle.The rational mapping,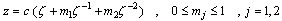
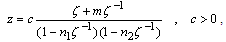
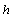 with a curvilinear hole
with a curvilinear hole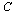 , where the origin lie inside the hole is conformally mapped on the domain outside a unit circle
, where the origin lie inside the hole is conformally mapped on the domain outside a unit circle 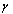 by means of a rational mapping,
by means of a rational mapping,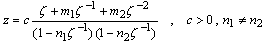
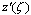 does not vanish or become infinite outside the unit circle
does not vanish or become infinite outside the unit circle 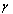 . If a temperature distribution
. If a temperature distribution 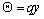 is following uniformly in the direction of the negative
is following uniformly in the direction of the negative 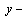 axis, where the increasing a temperature distribution
axis, where the increasing a temperature distribution 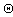 is assumed to be constant a cross the thickness of the plate, i.e.
is assumed to be constant a cross the thickness of the plate, i.e.  , and
, and 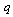 is the constant temperature gradient. The uniform flow of heat is distributed by the presence of an insulated curvilinear hole
is the constant temperature gradient. The uniform flow of heat is distributed by the presence of an insulated curvilinear hole .The heat equation satisfies the relation,
.The heat equation satisfies the relation, 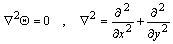
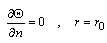

 is the unit vector perpendicular to the surface.Neglecting the variation of the strain and the stress with respect to the thickness of the plate, the thermoelastic potential
is the unit vector perpendicular to the surface.Neglecting the variation of the strain and the stress with respect to the thickness of the plate, the thermoelastic potential 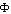 satisfies the formula, see Parkus [12]
satisfies the formula, see Parkus [12]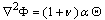
 is a scalar which present the coefficient of the thermal expansion and
is a scalar which present the coefficient of the thermal expansion and  is Poisson’s ratio. Assume the force of the plate is free of applied loads.In this case, the formula (1.1) for the first and second boundary value problems respectively take the following form,
is Poisson’s ratio. Assume the force of the plate is free of applied loads.In this case, the formula (1.1) for the first and second boundary value problems respectively take the following form,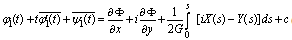
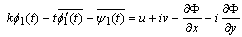
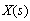 and
and 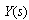 are prescribed on the boundary of the plane
are prescribed on the boundary of the plane  is the length measured from an arbitrary point,
is the length measured from an arbitrary point, 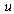 and
and 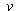 are the displacement components,
are the displacement components, 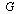 is the shear modulus. Also, here the applied stresses
is the shear modulus. Also, here the applied stresses 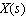 and
and 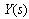 must satisfy the following, see Parkus [12]
must satisfy the following, see Parkus [12]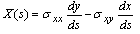
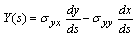
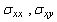 and
and 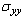 are the components of stresses which are given by the following relations,
are the components of stresses which are given by the following relations,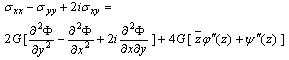
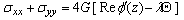
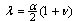 is the coefficient of heat transfer.The rational mapping
is the coefficient of heat transfer.The rational mapping 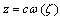 maps the boundary
maps the boundary 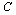 of the given region occupied by the middle plane of the plate in the
of the given region occupied by the middle plane of the plate in the 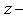 plane onto the unit circle
plane onto the unit circle  in the
in the  plane. Curvilinear coordinates
plane. Curvilinear coordinates  are thus introduce into the
are thus introduce into the 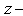 plane which are the maps of the polar conditions in the
plane which are the maps of the polar conditions in the  plane as given by
plane as given by 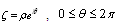 . By using the transformation
. By using the transformation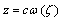 , Eq.(1.1) reduce to,
, Eq.(1.1) reduce to,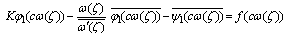
 plane.
plane. in
in 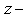 plane onto the domain of outside unit circle in
plane onto the domain of outside unit circle in 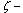 plane under the condition
plane under the condition 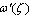 does not vanish or become infinite outside the unit circle
does not vanish or become infinite outside the unit circle . The following graphs give the different shapes of the rational mapping (2.1).
. The following graphs give the different shapes of the rational mapping (2.1). 









 and
and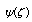 . Moreover, the three stress components
. Moreover, the three stress components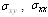 , and
, and 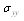 will be complete determined.
will be complete determined.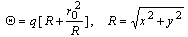
 in polar coordinates the thermoelastic potential function take the form,
in polar coordinates the thermoelastic potential function take the form,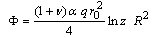
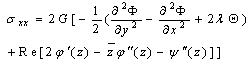
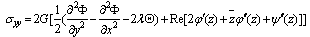
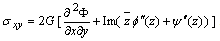
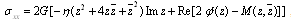
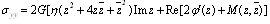
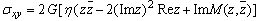
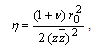
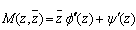
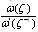 in the form,
in the form,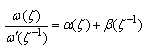
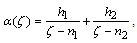
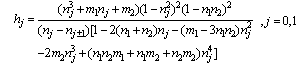
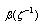 is a regular function for
is a regular function for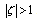 .
.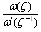 has a singularity at
has a singularity at 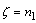 and
and .Using Eq.(1.2) and Eq.(1.3) in Eq.(2.11), we get
.Using Eq.(1.2) and Eq.(1.3) in Eq.(2.11), we get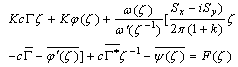
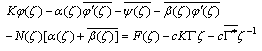
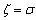 , we get
, we get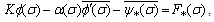
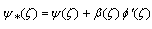
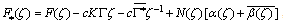
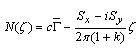
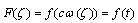
 with its derivatives must satisfy
with its derivatives must satisfy  condition. Our aim is to determine the functions
condition. Our aim is to determine the functions 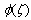 and
and 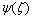 for the various boundary value problems. For this multiply both side of Eq.(4.16) by
for the various boundary value problems. For this multiply both side of Eq.(4.16) by 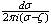 where
where 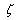 is any point the interior of
is any point the interior of  and integral over the circle, we obtain
and integral over the circle, we obtain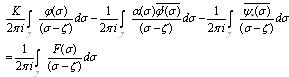
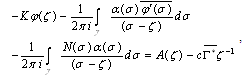
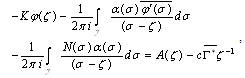
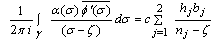
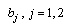 are complex constants.Also,
are complex constants.Also,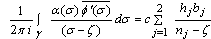
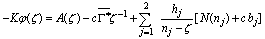
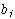 , differentiating Eq.(4.26) with respect to
, differentiating Eq.(4.26) with respect to 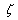 and substituting in Eq.(4.24), to get
and substituting in Eq.(4.24), to get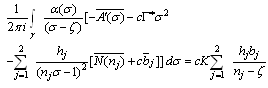
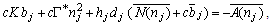
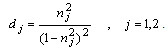
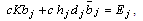
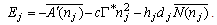
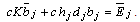
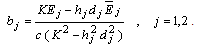
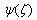 we have form Eq.(4.17) after substituting the expression of
we have form Eq.(4.17) after substituting the expression of  and
and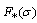 , and taking the complex conjugate of the resulting equation after using the expression of
, and taking the complex conjugate of the resulting equation after using the expression of 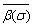 to yields,
to yields,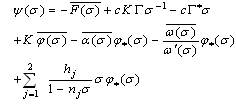
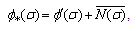
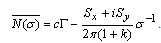
 where
where  is any point in the interior of
is any point in the interior of 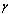 and integrating over the unit circle, then using the properties of Cauchy integral and calculate sum residue, we obtain
and integrating over the unit circle, then using the properties of Cauchy integral and calculate sum residue, we obtain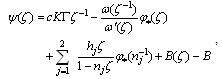
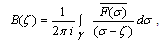
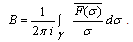
 we have,
we have,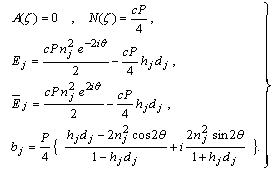
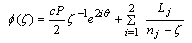
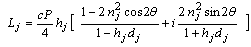
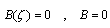
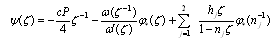
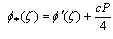
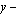 axis. This plate is weakened by a curvilinear hole C which is free from stress.For
axis. This plate is weakened by a curvilinear hole C which is free from stress.For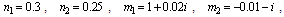
 , the stress components
, the stress components and
and 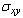 are obtained in large forms calculated by computer and illustrated in the following two cases :(i) When the study is in the normal plate, we have the following shapes for the stress components, see Fig.(12) and Fig.(13).(ii) In the thermoelasticity plate, we have the following shapes for the stress components by using the substitutions
are obtained in large forms calculated by computer and illustrated in the following two cases :(i) When the study is in the normal plate, we have the following shapes for the stress components, see Fig.(12) and Fig.(13).(ii) In the thermoelasticity plate, we have the following shapes for the stress components by using the substitutions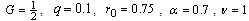 , see Fig.(14) and Fig.(15).
, see Fig.(14) and Fig.(15).
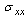 has positive values at
has positive values at 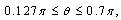
 has positive values at
has positive values at 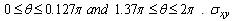 has positive values at
has positive values at 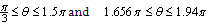 .
.

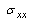 has positive values at
has positive values at 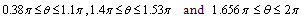 .
. 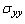 has positive values at
has positive values at 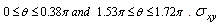 has positive values at
has positive values at 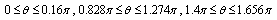 and
and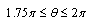 .
.
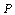
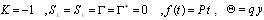 .Then,
.Then,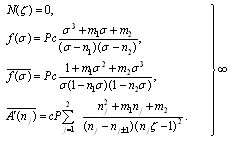
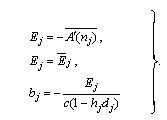
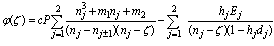
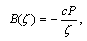
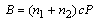
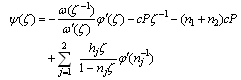
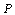 .For
.For 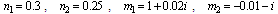
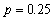 , the stress components
, the stress components 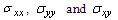 are obtained in large forms calculated by computer and illustrated in the following two cases :
are obtained in large forms calculated by computer and illustrated in the following two cases :
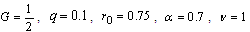 , see Fig.(18) and Fig.(19).
, see Fig.(18) and Fig.(19).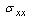 has positive values at
has positive values at 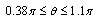
 .
. 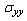 has positive values at
has positive values at 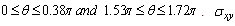 has positive values at
has positive values at 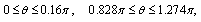
 and
and  .
.

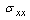 has positive values at
has positive values at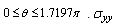 has positive values at
has positive values at .
.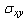 has positive values at
has positive values at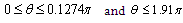 .
.
 then,
then,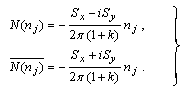
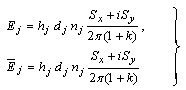
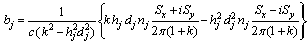
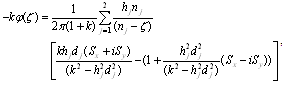
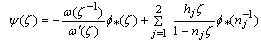
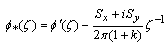
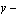 axis and the force acts on the centre of the curvilinear hole. For
axis and the force acts on the centre of the curvilinear hole. For 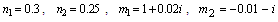 ,
, 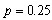 , the stress components
, the stress components  are obtained in large forms calculated by computer and illustrated in the following two cases :(i) When the study is in the normal plate, we have the following shapes for the stress components, see Fig.(20) and Fig.(21).(ii) In the thermoelasticity plate, we have the following shapes for the stress components by using the substitutions
are obtained in large forms calculated by computer and illustrated in the following two cases :(i) When the study is in the normal plate, we have the following shapes for the stress components, see Fig.(20) and Fig.(21).(ii) In the thermoelasticity plate, we have the following shapes for the stress components by using the substitutions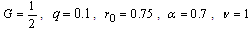 , see Fig.(22) and Fig.(23)..
, see Fig.(22) and Fig.(23)..
 has positive values at
has positive values at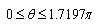 .
. .has positive values at
.has positive values at 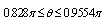 and.
and. 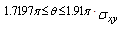 has positive values at
has positive values at 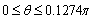 and
and 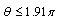


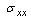 has positive values at
has positive values at 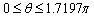 .
.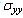 has positive values at
has positive values at 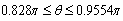 and
and 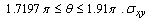 has positive values at
has positive values at 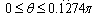 and
and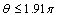 .
.
 plane reduce to obtain the two complex potential functions, Gaursat functions, in
plane reduce to obtain the two complex potential functions, Gaursat functions, in 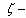 plane by using conformal mapping.(ii) The conformal mapping
plane by using conformal mapping.(ii) The conformal mapping , where, for
, where, for  mapped infinite region to out side a unit circle
mapped infinite region to out side a unit circle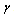 .(iii) When we applied the conformal mapping
.(iii) When we applied the conformal mapping  the boundary value problems reduce to the integro-differentail equation with discontinuous kernel.(iv) Cauchy method is the best method to solving the integro-differentail equation with Cauchy kernel and obtaining the two complex functions
the boundary value problems reduce to the integro-differentail equation with discontinuous kernel.(iv) Cauchy method is the best method to solving the integro-differentail equation with Cauchy kernel and obtaining the two complex functions 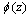 and
and 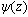 directly.(v) The components of stress
directly.(v) The components of stress 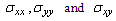 is completely determine and plotting after obtaining the two complex functions.(vi) As a main result of inserting the effect of uniform flow of heat in the negative of
is completely determine and plotting after obtaining the two complex functions.(vi) As a main result of inserting the effect of uniform flow of heat in the negative of 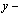 direction we have, see figures (12-23)
direction we have, see figures (12-23) 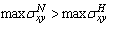
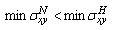
 represent the shear components of stress at normal state, while
represent the shear components of stress at normal state, while  represent the shear components of stress after inserting the effect of heating.(vii) If we denote to the angle that appears the maximum value of
represent the shear components of stress after inserting the effect of heating.(vii) If we denote to the angle that appears the maximum value of  in normal state by
in normal state by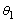 , and the angle that appears the maximum value of
, and the angle that appears the maximum value of  after inserting the effect of heating by
after inserting the effect of heating by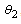 , we note
, we note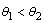
 in normal state by
in normal state by , and the angle that appears the maximum value of
, and the angle that appears the maximum value of 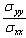 after inserting the effect of heating by
after inserting the effect of heating by , we note
, we note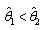
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML