-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Fluid Dynamics
p-ISSN: 2168-4707 e-ISSN: 2168-4715
2012; 2(1): 5-13
doi: 10.5923/j.ajfd.20120201.02
A Reliable Method for Boundary Layer Due to an Exponentially Stretching Continuous Surface
Qasem M. Al-Mdallal 1, Muhammed I. Syam 1, P. Donald Ariel 2
1Department of Mathematical Sciences, College of Science, United Arab Emirates University, P.O. Box 17551, Al-Ain, United Arab Emirates
2Department of Mathematical Sciences, Trinity Western University, 7600 Glover Road, Langley, BC, Canada, V2Y 1Y1
Correspondence to: Qasem M. Al-Mdallal , Department of Mathematical Sciences, College of Science, United Arab Emirates University, P.O. Box 17551, Al-Ain, United Arab Emirates.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this paper we applied the extended homotopy perturbation method (EHPM) to discuss the steady plane flow in the boundary layers on an exponentially stretching continuous surface. The EHPM calculates the solution automatically adjusting the scaling factor of the independent similarity variable normal to the plate. The results obtained by the EHPM are in excellent agreement with the exact numerical solution. Moreover the asymptotic solution, valid for large suction parameter is developed which matches well with the exact solution even for moderate values of the suction parameter.
Keywords: Homotopy perturbation method, Extended homotopy perturbation method, exponentially stretching continuous surface, Ackroyd’s method, Asymptotic solution
Cite this paper: Qasem M. Al-Mdallal , Muhammed I. Syam , P. Donald Ariel , "A Reliable Method for Boundary Layer Due to an Exponentially Stretching Continuous Surface", American Journal of Fluid Dynamics, Vol. 2 No. 1, 2012, pp. 5-13. doi: 10.5923/j.ajfd.20120201.02.
Article Outline
1. Introduction
- The investigation of steady, laminar boundary layer in a Newtonian fluid past a stretching sheet has attracted many researchers due to its applications in industry and engineering, see[5,15,30]. Examples of such applications are the aerodynamic extrusion of plastic sheets, the boundary layer along a liquid film condensation process, the cooling process of metallic plate in a cooling bath and glass and polymer industries.The history of stretching flow problem dates back to the pioneering work of Sakadias[28] and[29] who studied the laminar boundary layer flow of a viscous, incompressible fluid caused by a moving rigid surface. The work of Sakadias was generalized by Crane[12] who assumed the velocity of the sheet to vary linearly as the distance from the slit and arrived at a closed form analytical solution. Following the footsteps of Crane, Sakadias model has been extended and generalized so that the velocity of the surface is assumed to be a general function of the distance from a fixed origin, where the surface was stretched out, see for example [10,3,13,11,19-21,2,31,17,25]. Recently great attention is paid to the problem of the boundary layer flow due to an exponentially stretching sheet without suction; see [22-24,26,16,4,27]. However, to the authors knowledge, Elbashbeshy[14] was the first who had discussed the boundary layer flow due to an exponentially stretching sheet with suction. The aim of present paper is to implement the extended homotopy perturbation method (EHPM) (see [6-8]) to obtain the analytical solution to the problem of a boundary layer flow over an exponential stretching continuous sheet with suction. It should be noted that this problem without taking the suction into account has been discussed using different numerical techniques such as: HAM[25], similarity solution[22], RungeKuttaFehlberg method with shooting technique[26].This paper is organized as follows: In Section 2, We describe the mathematical model. In Section 3, we present the extended homotopy perturbation method in the context of the present problem. The validation of the method and numerical results are presented in Section 4.
2. Formulation of the Problem
- Consider the two-dimensional viscous incompressible flow bounded by a stretching sheet in which the x-axis is taken along the sheet in the direction of the motion and y-axis is perpendicular to it. In this case, if we assume that
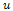 and
and 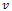 are the velocities in the
are the velocities in the 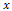 and
and 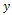 directions, respectively; the flow will be governed by the following equations:
directions, respectively; the flow will be governed by the following equations: 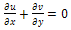 | (1) |
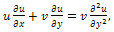 | (2) |
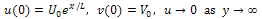 | (3) |
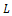 is a constant represents the characteristic length of the sheet. Introducing the following similarity transformations
is a constant represents the characteristic length of the sheet. Introducing the following similarity transformations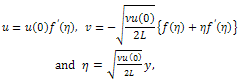 | (4) |
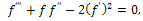 | (5) |
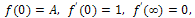 | (6) |
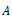 is a constant which represents the dimensionless suction velocity.
is a constant which represents the dimensionless suction velocity. 3. Method of Solution
- The following is a brief derivation of the algorithm used to solve and to obtain an analytical solution for BVP (5)-(6). This algorithm is based on the extended homotopy perturbation method (EHPM) developed by[6], which is an extension to the well-known homotopy perturbation method (HPM) due to He[18].We firstly stretch the independent variable
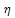 by means of a scaling parameter,
by means of a scaling parameter, 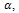 using the following transformation
using the following transformation 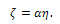 | (7) |
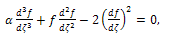 | (8) |
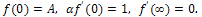 | (9) |
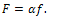 | (10) |
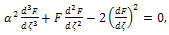 | (11) |
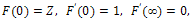 | (12) |
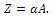 | (13) |
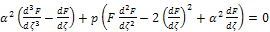 | (14) |
 , one obtains
, one obtains 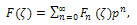 | (15) |
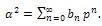 | (16) |
 on both sides, we obtain the following system of equations: For n=0:
on both sides, we obtain the following system of equations: For n=0: 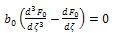 | (17) |
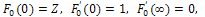 | (18) |
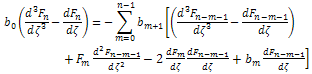 | (19) |
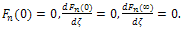 | (20) |
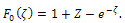 | (21) |
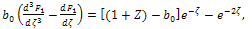 | (22) |
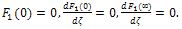 | (23) |
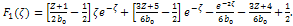 | (24) |
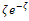 in equation (24) must be zero. This is based on the Lighthill principle, namely, that the perturbation solution at any stage is no more singular than at the preceding stage. This leads to
in equation (24) must be zero. This is based on the Lighthill principle, namely, that the perturbation solution at any stage is no more singular than at the preceding stage. This leads to 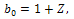 | (25) |
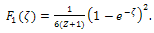 | (26) |
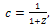 | (27) |
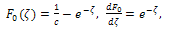 | (28) |
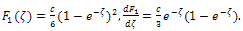 | (29) |
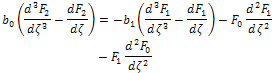 | (30) |
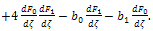 | (31) |
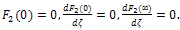 | (32) |
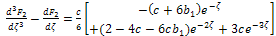 | (33) |
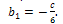 | (34) |
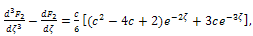 | (35) |
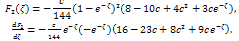 | (36) |
4. Convergence Discussion
- Tables (1)-(2) show the evaluated values of bn and F”(0) for the first few terms of expansion at arbitrary value of Z. It is clearly seen that every new term after
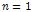 in the perturbation solution leads to two extra terms of
in the perturbation solution leads to two extra terms of 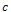 both
both 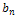 and F”(0). Note that the expressions for these two important parameters, bn and F”(0), are simple and elegant. The perturbation series (15) and (16) are convergent for all values of z≥0.The accuracy and the convergence to the solution depends strongly on the number of terms. Therefore, an obvious question arises regarding the number of terms after which the perturbation solution must be terminated. Herein, we decided to terminate the solution when the sum of the series for α2 and
and F”(0). Note that the expressions for these two important parameters, bn and F”(0), are simple and elegant. The perturbation series (15) and (16) are convergent for all values of z≥0.The accuracy and the convergence to the solution depends strongly on the number of terms. Therefore, an obvious question arises regarding the number of terms after which the perturbation solution must be terminated. Herein, we decided to terminate the solution when the sum of the series for α2 and 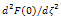 met a prescribed tolerance criterion. Below the solutions for α2 and
met a prescribed tolerance criterion. Below the solutions for α2 and 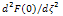 are given when the perturbation solution was terminated after twelve terms.
are given when the perturbation solution was terminated after twelve terms.
|
|
|
|
|
|
|
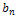 decays only by a ratio of 1/3. Thus if a tolerance of, say, 10-8 is sought then in order to achieve it roughly 17 terms will be needed. We can achieve the said accuracy by various means. Ariel [6] used the Shanks transformation for computing the axisymmetric flow past a stretching sheet within the abovementioned accuracy and found that eight erms of the perturbation solution were sufficient. Another attractive alternative is to use the Padé approximants. In the present work we have used the latter technique. For each value of
decays only by a ratio of 1/3. Thus if a tolerance of, say, 10-8 is sought then in order to achieve it roughly 17 terms will be needed. We can achieve the said accuracy by various means. Ariel [6] used the Shanks transformation for computing the axisymmetric flow past a stretching sheet within the abovementioned accuracy and found that eight erms of the perturbation solution were sufficient. Another attractive alternative is to use the Padé approximants. In the present work we have used the latter technique. For each value of 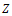 the power series in the perturbation expansions (15) and (16) were rendered into the corresponding Padé rational approximants in which the degree of the denominator was either equal or one more than that of the numerator.
the power series in the perturbation expansions (15) and (16) were rendered into the corresponding Padé rational approximants in which the degree of the denominator was either equal or one more than that of the numerator. 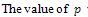 was then set to unity to get the required values of α2 and
was then set to unity to get the required values of α2 and 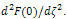 . The technique proved to be at least as powerful as the Shanks’ transformation. It is evident from the results presented in the Tables 3 through 7, where the values are given (i) directly without using the Padé approximant, and (ii) after applying the Padé approximants. The improvement in the solution is rather obvious.
. The technique proved to be at least as powerful as the Shanks’ transformation. It is evident from the results presented in the Tables 3 through 7, where the values are given (i) directly without using the Padé approximant, and (ii) after applying the Padé approximants. The improvement in the solution is rather obvious.5. A Numerical Solution
- In this section, we will present the essentials of a numerical scheme based on the Ackroyd’s method[1] for solving the BVP (8)-(9). Firstly, we write this solution as a series involving exponential functions, i.e.
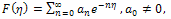 | (37) |
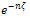 on both sides, we obtain the following recurrence relation for αn:
on both sides, we obtain the following recurrence relation for αn: 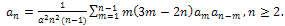 | (38) |
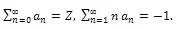 | (39) |
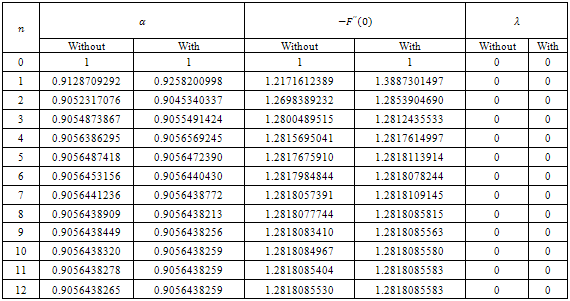
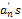 are expressed in terms of α1 and α2, therefore, the two equations in (39) enable us to determine these two unknowns, for a given value of Z which means that the solution F in (37) is completely determined. The value of A is, on the other hand, determined post priori by using equation (13). In Table 8, the values of the various parameters of interest for the present problem, (α2,-F″(0), A) are presented using the EHPM and the numerical scheme described above. The numerical results listed in the table are believed to be accurate to the last recorded digit.
are expressed in terms of α1 and α2, therefore, the two equations in (39) enable us to determine these two unknowns, for a given value of Z which means that the solution F in (37) is completely determined. The value of A is, on the other hand, determined post priori by using equation (13). In Table 8, the values of the various parameters of interest for the present problem, (α2,-F″(0), A) are presented using the EHPM and the numerical scheme described above. The numerical results listed in the table are believed to be accurate to the last recorded digit. 6. An Asymptotic Solution for Large Suction
- In this section we implement the Ackroyd’s method[1] to construct an asymptotic solution for large Z. For this purpose, we introduce the following new parameter
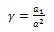 | (40) |
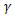 as
as 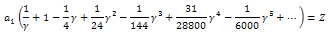 | (41) |
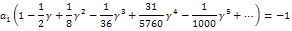 | (42) |
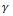
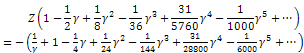 | (43) |
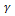 in a series of 1/Z, i.e.
in a series of 1/Z, i.e. 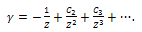 | (44) |
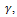 , then substituting for
, then substituting for 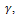 from equation (44), and equating like powers of Z on both sides, one can obtain the following constants
from equation (44), and equating like powers of Z on both sides, one can obtain the following constants 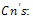 :
: 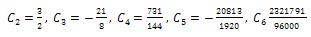 | (45) |
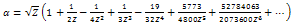 | (46) |
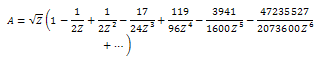 | (47) |
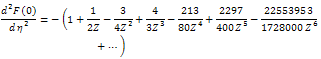 | (48) |
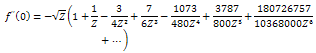 | (49) |
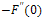 are listed for different values of
are listed for different values of 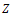 using (i) exact numerical solution obtained by the Ackroyd’s method, (ii) EHPM after applying the Padé approximation, and (iii) asymptotic solution for large Z.The velocity components in the mainstream and transverse directions respectively are presented for different values of Z in Figures (1) and (2), respectively. It is clearly seen that as Z is increased, the usual features of suction manifest themselves - a boundary layer starts forming near the stretching sheet resulting into a rapid decay of the mainstream velocity and a rapid approach to the asymptotic value for the transverse velocity, as the suction is increased.
using (i) exact numerical solution obtained by the Ackroyd’s method, (ii) EHPM after applying the Padé approximation, and (iii) asymptotic solution for large Z.The velocity components in the mainstream and transverse directions respectively are presented for different values of Z in Figures (1) and (2), respectively. It is clearly seen that as Z is increased, the usual features of suction manifest themselves - a boundary layer starts forming near the stretching sheet resulting into a rapid decay of the mainstream velocity and a rapid approach to the asymptotic value for the transverse velocity, as the suction is increased.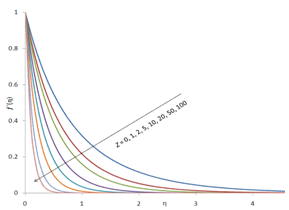 | Figure 1. Illustrating the behavior of 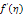 the dimensionless mainstream velocity with the dimensionless mainstream velocity with  the dimensionless distance from the sheet, for various values of Z, a dimensionless measure of the suction velocity the dimensionless distance from the sheet, for various values of Z, a dimensionless measure of the suction velocity |
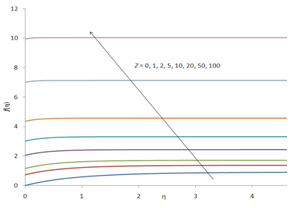 | Figure 2. Illustrating the behavior of  the dimensionless transverse velocity with the dimensionless transverse velocity with  the dimensionless distance from the sheet, for various values of Z, a dimensionless measure of the suction velocity. the dimensionless distance from the sheet, for various values of Z, a dimensionless measure of the suction velocity. |
7. Conclusions
- In this paper we applied the extended homotopy perturbation method (EHPM) to investigate the steady plane boundary layer flow past an exponentially stretching porous surface. This method calculates, in addition to the velocity distribution, the scaling factor of the flow α which leads to much simpler and more elegant analytical solution in that the values of the critical parameters can be conveniently listed. It is also shown that the convergence of the perturbation solution can be considerably accelerated by applying the Pade’ approximation. There is a complete agreement in the solutions generated by the numerical scheme and the EHPM. Finally an asymptotic solution for large Z (or A) is given, which is significantly different than the traditional asymptotic solutions which as a rule include the secular terms. Our solution is free of the secular terms and is remarkably accurate in that it can be accepted even for moderate values of A.
References
| [1] | Ackroyd J.A.D., A Series Method for the Solution of Laminar Boundary Layers on Moving Surfaces, ZAMP, 29, 1978, 729-741. |
| [2] | Ali M.E., Magyari E., Unsteady fluid and heat flow induced by a submerged stretching surface while its steady motion is slowed down gradually, Int J Heat Mass Transfer, 50, 2007, 188–195. |
| [3] | Ali M.E., On thermal previous termboundary layer on anext term power law stretched previous termsurfacenext term with suction or injection, Int. J. Heat Fluid Fl., 16, 1995, 280–290. |
| [4] | Al-Odat MQ., Damseh RA., Al-Azab TA., Thermal boundary layer on an exponentially stretching continuous surface in the presence of magnetic field effect, Int. J. Appl. Mech. Eng. 11(2), 2006, 289–299. |
| [5] | Altan T., Oh S., Gegel H., Mzetal Forming Fundamentals and Applications, American Society of Mzetals, Mzetals Park, OH, 1979. |
| [6] | Ariel P.D., Extended Homotopy Perturbation Method and Computation of Flow past a Stretching Sheet, Comp. Math. Appl., 58, 2009, 2402-2409. |
| [7] | Al-Mdallal Q.A., Syam M.I., Ariel P.D., Extended homotopy perturbation method and the axisymmetric flow past a porous stretching sheet (2011), International Journal for Numerical Methods in Fluids (In press). |
| [8] | Al-Mdallal Q.A., Syam M.I., Ariel P.D., The Extended Homotopy Perturbation Method and Boundary Layer Flow due to Condensation and Natural Convection on a porous Vertical Plate (2011), Journal of Computer Mathematics (InPress). |
| [9] | Ariel P.D., Hayat T., Asghar S., Homotopy Perturbation Method and Axisymmetric Flow over a Stretching Sheet, Int. J. Nonlinear Sci. Num. Sim., 7, 2006, 399-406. |
| [10] | Banks W.H.H., Similarity solutions of the previous termboundary-layernext termequations for previous termastretchingnext term wall, J. Mech. Theor. Appl., 2 1983, 375–392. |
| [11] | Cortell R., Viscous flow and heat transfer over a nonlinearly stretching sheet, Appl Math Comput, 184, 2007, 864–873. |
| [12] | Crane L.J., Flow past a Stretching Plate, ZAMP, 21, 1970, 645-647. |
| [13] | Cortell R., Flow and heat transfer of an electrically conducting fluid of second grade over a stretching sheet subject to suction and to a transverse magnetic field, Int J Heat Mass Transfer, 49, 2006, 1851–1856. |
| [14] | Elbahbeshy E.M.A., Heat transfer over an exponentially stretching continuous surface with suction, Arch. Mech., 53(6), 2001, 643–651. |
| [15] | Fisher E.G., Extrusion of Plastics, Wiley, New York, 1976. |
| [16] | Khan S.K., Sanjayanand E., Viscoelastic boundary layer flow and heat transfer over an exponential stretching sheet, International Journal of Heat and Mass Transfer, 48(8), 2005, 1534-1542. |
| [17] | Hayat T., Abbas Z., Javed T., Mixed convection flow of a micro-polar fluid over a nonlinearly stretching sheet, PhysLett A, 372, 2008, 637–647. |
| [18] | He J.H., Homotopy perturbation technique. Comput. Methods Appl. Mech. Eng., 178, 1999, 257-262. |
| [19] | Kumari M., Nath G., Analytical solution of unsteady three-dimensional MHD boundary layer flow and heat transfer due to impulsively stretched plane surface, Commun Nonlinear SciNumerSimulat, 14, 2009, 3339–3350. |
| [20] | Liao S.J., Series solutions of unsteady boundary-layer flows over a stretching flat plate, Stud Appl Math, 117, 2006, 2529–2539. |
| [21] | Liao S.J., An analytical solution of unsteady boundary layer flows caused by an impulsively stretched plate, Commun Nonlinear SciNumerSimulat, 11, 2006, 326–339. |
| [22] | Magyari E., Keller B, Heat and Mass Transfer in the boundary layers on an exponentially stretching continuous surface. J Phys D ApplPhys, 32, 1999, 577–585. |
| [23] | Sajida M., Hayat T., Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheetstar, International Communications in Heat and Mass Transfer, 35(3), 2008, 347-356. |
| [24] | Sanjayanand E., Khan S.J., On heat and mass transfer in a viscoelastic boundary layer flow over an exponentially stretching sheet, International Journal of Thermal Sciences, 45(8), 2006, 819-828. |
| [25] | Sajid M. and Hayat T., Influence of thermal radiation on the boundary layer flow due to an exponentially stretching sheet, IntCommn Heat Mass Transfer, 35, 2008, 347–356. |
| [26] | Pal D., Mixed convection heat transfer in the boundary layers on an exponentially stretching surface with magnetic field, Applied Mathematics and Computation Volume 217, Issue 6, 15 November 2010, Pages 2356-2369. |
| [27] | Partha M.K., Murthy P.V.S.N., Rajasekhar G.P., Effect of viscous dissipation on the mixed convection heat transfer from an exponentially stretching surface, Heat Mass Transfer, 41, 2005, 360–366 |
| [28] | Sakiadis B.C., Boundary Layer Behavior on Continuous Solid Surface, AIChEJ., 7, 1961, 26-28. |
| [29] | Sakiadis B.C., Boundary Layer Behavior on Continuous Solid Surface, AIChEJ., 7, 1961, 221-225. |
| [30] | Tadmor Z., Klein I., Engineering Principles of Plasticating Extrusion, Polymer Science and Engineering Series, Van Norstrand Reinhold, New York, 1970. |
| [31] | Xu H., An explicit analytic solution for connective heat transfer in an electrically conducting fluid at stretching surface with uniform free stream, Int J EngSci, 43, 2005, 859-874. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML


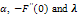 for z=2 with n, the number of terms in the perturbation solution
for z=2 with n, the number of terms in the perturbation solution
 , and
, and  for z=10 with n, the number of terms in the perturbation solution
for z=10 with n, the number of terms in the perturbation solution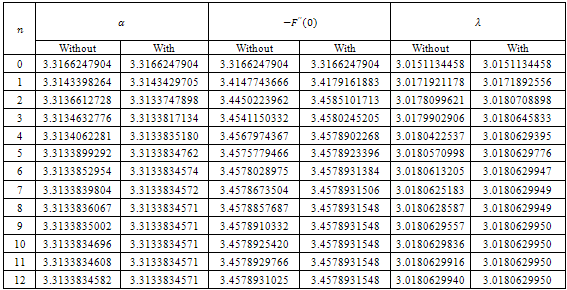
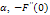 , and
, and  for z=50 with , the number of terms in the perturbation solution
for z=50 with , the number of terms in the perturbation solution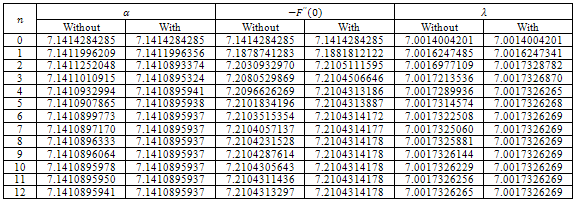
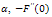 , and
, and 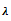 for z=100 with n, the number of terms in the perturbation solution.
for z=100 with n, the number of terms in the perturbation solution. 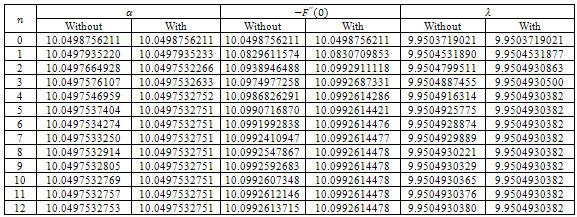
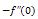 a dimensionless measure of the skin-friction at the stretching sheet with Z a parameter characterizing the flow
a dimensionless measure of the skin-friction at the stretching sheet with Z a parameter characterizing the flow 