Okedayo G. T. 1, Abah S. O. 2
1Department of Mathematical Sciences, Ondo State University of Science and Technology, Okitipupa
2Department of Mathematics, Stat. & Computer Science, Kaduna Polytechnic, Kaduna
Correspondence to: Okedayo G. T. , Department of Mathematical Sciences, Ondo State University of Science and Technology, Okitipupa.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
The objective of this study is to carry out a numerical investigation of the MHD plane stagnation flow of a temperature dependent viscosity fluid. The system of governing partial differential equations was transformed into a system of coupled nonlinear ordinary differential equations by the method of similarity transformations. These resulting equations were then solved using the classical fourth order Runge-Kutta method together with shooting techniques. The effects of the relevant thermo-physical parameters on the flow profile were investigated. The skin friction coefficient and Nusselt numbers were also determined numerically and tabulated.
Keywords:
MHD, Stagnation Point, Temperature Dependent Viscosity
Cite this paper:
Okedayo G. T. , Abah S. O. , "A Numerical Investigation of MHD Plane Stagnation Flow of Temperature Dependent Viscosity Fluid", American Journal of Fluid Dynamics, Vol. 1 No. 1, 2011, pp. 1-3. doi: 10.5923/j.ajfd.20110101.01.
1. Introduction
Stagnation point flow has become an interesting area of research among scientists and investigators due to its importance in a wide variety of applications both in industrial and scientific applications. Since the work of Crane[1], extensive research work has been carried out by many authors. For example Ramachandran et’al[7] studied the stagnation point flow towards a heated vertical plate, he considered both the arbitrary wall temperature and arbitrary surface heat flux. Ishak et.al[2] also studied the stagnation point flow but considered the case of a porous wall. Okedayo et,al[6] also carried out the analysis of plane stagnation point flow with convective boundary conditions. Aman and Ishak[3] also studied the mixed convection flows towards a stagnation point on a stretching sheet using the method of finite difference.The influence of temperature dependent viscosity flow has been studied Seddeek and Salem[4] who studied the case of a variable viscosity with magnetic field on the flow and heat transfer to a continuous moving flat plate. Why several studies has been carried out on the plane stagnation point flow the case of the stagnation point flow of a temperature dependent viscosity fluid has been much neglected which is the motivation for this study.Hence the objective of this study is to investigate the effect of various thermo-physical parameters on the plane stagnation point flow of a temperature dependent viscosity fluid.
2. Mathematical Formulations
A two-dimensional body is placed in a stream of quiescent fluid. We consider heat transfer near the upstream stagnation line, where the flow is assumed to be laminar. The problem is restricted to the case of a plane plate perpendicular to the stream. It is assumed that the fluid properties are constant except for the fluid viscosity which vary as an inverse linear function of temperature as follows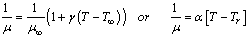 Where
Where 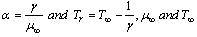 are the fluid free stream dynamic viscosity and the free stream temperature respectively.
are the fluid free stream dynamic viscosity and the free stream temperature respectively. 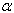 and
and 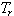 Reference state and thermal properties of the fluid. Under these assumptions the continuity, momentum and energy equations describing the flow can be written as follows.
Reference state and thermal properties of the fluid. Under these assumptions the continuity, momentum and energy equations describing the flow can be written as follows.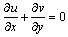 | (1) |
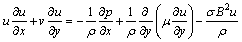 | (2) |
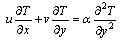 | (3) |
subject to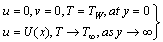 | (4) |
Where u is the velocity, T is the temperature, 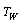 is the wall temperature,
is the wall temperature, 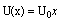 is the fluid free stream velocity, p is the pressure, B is the magnetic field,
is the fluid free stream velocity, p is the pressure, B is the magnetic field, 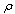 is the fluid density, is the electrical conductivity,
is the fluid density, is the electrical conductivity, 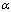 is the thermal diffusivity and (x, y) are the coordinate axes. In order to solve (1)-(4) we introduce the following similarity variables
is the thermal diffusivity and (x, y) are the coordinate axes. In order to solve (1)-(4) we introduce the following similarity variables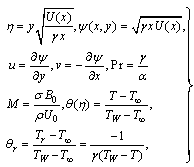 | (5) |
Substituting the above variables in equations (1)-(4), we obtain
3. Numerical Results and Discussion
The nonlinear equations (6)-(8) are solved numerically using the classical fourth order Runge-Kutta method together with the shooting technique implemented on a computer program written in Maple (14). A convenient step size was chosen to obtain the desired accuracy.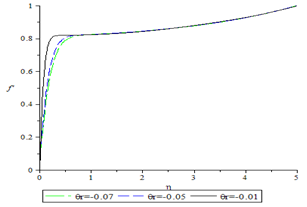 | Figure 1. Velocity profile for various values of reference temperature for M=0.4 and Pr=0.7 |
Fig.1 shows the velocity profile for various values the dimensionless reference temperature 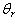 the values chosen for the reference temperature,
the values chosen for the reference temperature, 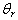 are -0.01, -0.05, and -0.07 for fixed values of the magnetic parameter, M=0.4 and Prandtl number Pr=0.7 corresponding to water. It is observed that as the dimensionless reference temperature increases the velocity profile increases, it is also observed that the velocity boundary layer thickness as the reference temperature decreases.In Fig.2, the influence of the magnetic parameter on the velocity profile is being investigated, the values chosen for M are 0.4, 0.6, and 0.8 while Pr is fixed at 0.7 and
are -0.01, -0.05, and -0.07 for fixed values of the magnetic parameter, M=0.4 and Prandtl number Pr=0.7 corresponding to water. It is observed that as the dimensionless reference temperature increases the velocity profile increases, it is also observed that the velocity boundary layer thickness as the reference temperature decreases.In Fig.2, the influence of the magnetic parameter on the velocity profile is being investigated, the values chosen for M are 0.4, 0.6, and 0.8 while Pr is fixed at 0.7 and 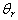 is fixed at -0.01. it is observed that as the magnetic parameter increases the velocity profile decreases.
is fixed at -0.01. it is observed that as the magnetic parameter increases the velocity profile decreases.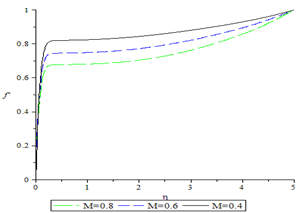 | Figure 2. Velocity profile for various values of the magnetic parameter for Pr=0.7 and 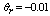 |
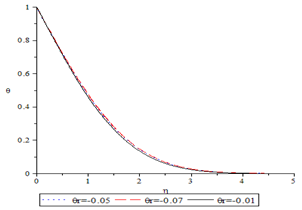 | Figure 3. Temperature profile for various values of the reference temperature for M=0.4 and Pr=0.7 |
While in Fig.3 we depict the temperature profile for various values of the reference temperature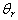 . The values chosen are -0.1, -0.5 and -0.7. While the Prandtl number and the magnetic parameters are fixed at 0.7 and 0.4 respectively. It is seen that increase in
. The values chosen are -0.1, -0.5 and -0.7. While the Prandtl number and the magnetic parameters are fixed at 0.7 and 0.4 respectively. It is seen that increase in 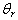 decreases the temperature profile.Similarly, in Fig.4 the influence of the magnetic parameter is been investigated, the values 0.4, 0.6, and 0.8 where used in the computation, while Pr=0.7 and
decreases the temperature profile.Similarly, in Fig.4 the influence of the magnetic parameter is been investigated, the values 0.4, 0.6, and 0.8 where used in the computation, while Pr=0.7 and 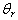 remains at -0.01. It observed that as the magnetic parameter increases the temperature profile also increases.Lastly, Fig.5 shows the effect of the Prandtl number Pr on the temperature profile. The values 0.1, 0.5 and 0.7 were used in the computation, while M and
remains at -0.01. It observed that as the magnetic parameter increases the temperature profile also increases.Lastly, Fig.5 shows the effect of the Prandtl number Pr on the temperature profile. The values 0.1, 0.5 and 0.7 were used in the computation, while M and 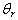 were fixed at 0.4 and -0.01 respectively. It is seen that an increase in the Prandtl number leads to a decrease in the temperature profile.
were fixed at 0.4 and -0.01 respectively. It is seen that an increase in the Prandtl number leads to a decrease in the temperature profile.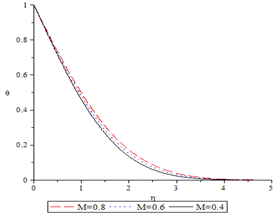 | Figure 4. Temperature profile for various values of the magnetic parameter for Pr=0.71 and 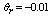 |
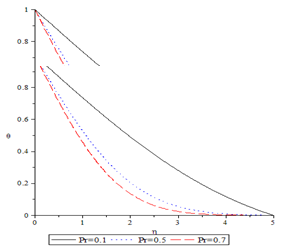 | Figure 5. Temperature profile for various values of the prandtl number, for M=0.4 and 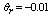 |
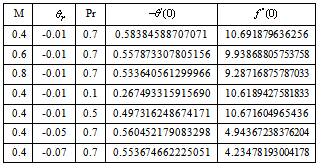
Table 1. Values Of Skin Friction And Nusselt Number For Various Thermo-Physical Parameters
 |
| |
|
Table.1 shows the values of the skin friction coefficient and heat transfer (Nusselt number) coefficients for various values of the thermo-physical parameters. From the table that both the skin friction and Nusselt numbers decreases as the Magnetic parameters increases, while they increase for increase in the Prandtl numbers, it is also observed that increase in the reference temperature leads to a decrease in both the skin friction and Nusselt numbers. The relatively large values of the skin friction and Nusselt numbers are due to the presence of the pressure gradient in plane stagnation point flow. Marinet an Tardu[5].
4. Conclusions
The problem of MHD plane stagnation point flow of a temperature dependent viscosity fluid has been carefully analysed numerically and it is observed that 1. Increase in the dimensionless reference temperature increases the velocity profile; it is also observed that the velocity boundary layer thickness as the reference temperature decreases.2. Increase in the magnetic parameter increases the velocity profile decreases.3. Increase in 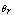 decreases the temperature profile.4. In increase in the magnetic parameter increases the temperature profile also increases.5. An increase in the Prandtl number leads to a decrease in the temperature profile.
decreases the temperature profile.4. In increase in the magnetic parameter increases the temperature profile also increases.5. An increase in the Prandtl number leads to a decrease in the temperature profile.
References
| [1] | Crane L. J. (1970) Flow past a Stretching Plate, J. Applied Math. Phys. (ZAMP), 21:645-647 |
| [2] | Ishak A., Nazar R., Pop I.(2008) Hydromagnetic Flow And Heat Transfer Adjacent To A Stretching Vertical Sheet, Heat and Mass Transfer, 44:921-927 |
| [3] | Aman F. and Ishak A.(2010) Mixed Convection Flows Toward A Stagnation Point On A Stretching Sheet. Australian J. of Basic and Aplied Sciences, 4(9). 4453-4460 |
| [4] | Seddeek M. A. and Salem A. M(2006). further results on variable viscosity with magnetic field on flow and heat transfer to a continous moving flat plate, physics letter A 353 (2006) 337-340 |
| [5] | Favre-Marinet M. and Tardu S. (2008) Convective Heat Transfer, Wiley & Sons 1st Ed. 147-150 |
| [6] | Okedayo T. Gideon, Olanrewaju P. O. and Gbadeyan J. A. MHD plane Stagnation Flow of a Temperature Dependent Viscosity Fluid (to appear) |
| [7] | Ramachandran N. T. S. Chen and B. F. Amaly, (1988) Mixed Convection In A Stagnation Flows Adjacent To A Vertical Surface. ASME J. Heat Transfer, 110, 373-377 |

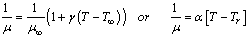 Where
Where 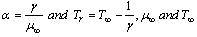 are the fluid free stream dynamic viscosity and the free stream temperature respectively.
are the fluid free stream dynamic viscosity and the free stream temperature respectively. 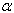 and
and 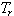 Reference state and thermal properties of the fluid. Under these assumptions the continuity, momentum and energy equations describing the flow can be written as follows.
Reference state and thermal properties of the fluid. Under these assumptions the continuity, momentum and energy equations describing the flow can be written as follows.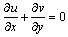
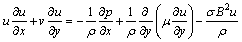
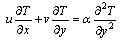
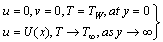
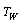 is the wall temperature,
is the wall temperature, 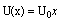 is the fluid free stream velocity, p is the pressure, B is the magnetic field,
is the fluid free stream velocity, p is the pressure, B is the magnetic field, 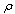 is the fluid density, is the electrical conductivity,
is the fluid density, is the electrical conductivity, 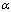 is the thermal diffusivity and (x, y) are the coordinate axes. In order to solve (1)-(4) we introduce the following similarity variables
is the thermal diffusivity and (x, y) are the coordinate axes. In order to solve (1)-(4) we introduce the following similarity variables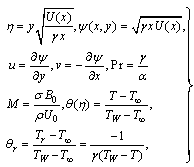

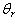 the values chosen for the reference temperature,
the values chosen for the reference temperature, 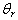 are -0.01, -0.05, and -0.07 for fixed values of the magnetic parameter, M=0.4 and Prandtl number Pr=0.7 corresponding to water. It is observed that as the dimensionless reference temperature increases the velocity profile increases, it is also observed that the velocity boundary layer thickness as the reference temperature decreases.In Fig.2, the influence of the magnetic parameter on the velocity profile is being investigated, the values chosen for M are 0.4, 0.6, and 0.8 while Pr is fixed at 0.7 and
are -0.01, -0.05, and -0.07 for fixed values of the magnetic parameter, M=0.4 and Prandtl number Pr=0.7 corresponding to water. It is observed that as the dimensionless reference temperature increases the velocity profile increases, it is also observed that the velocity boundary layer thickness as the reference temperature decreases.In Fig.2, the influence of the magnetic parameter on the velocity profile is being investigated, the values chosen for M are 0.4, 0.6, and 0.8 while Pr is fixed at 0.7 and 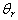 is fixed at -0.01. it is observed that as the magnetic parameter increases the velocity profile decreases.
is fixed at -0.01. it is observed that as the magnetic parameter increases the velocity profile decreases.
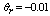

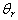 . The values chosen are -0.1, -0.5 and -0.7. While the Prandtl number and the magnetic parameters are fixed at 0.7 and 0.4 respectively. It is seen that increase in
. The values chosen are -0.1, -0.5 and -0.7. While the Prandtl number and the magnetic parameters are fixed at 0.7 and 0.4 respectively. It is seen that increase in 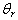 decreases the temperature profile.Similarly, in Fig.4 the influence of the magnetic parameter is been investigated, the values 0.4, 0.6, and 0.8 where used in the computation, while Pr=0.7 and
decreases the temperature profile.Similarly, in Fig.4 the influence of the magnetic parameter is been investigated, the values 0.4, 0.6, and 0.8 where used in the computation, while Pr=0.7 and 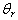 remains at -0.01. It observed that as the magnetic parameter increases the temperature profile also increases.Lastly, Fig.5 shows the effect of the Prandtl number Pr on the temperature profile. The values 0.1, 0.5 and 0.7 were used in the computation, while M and
remains at -0.01. It observed that as the magnetic parameter increases the temperature profile also increases.Lastly, Fig.5 shows the effect of the Prandtl number Pr on the temperature profile. The values 0.1, 0.5 and 0.7 were used in the computation, while M and 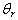 were fixed at 0.4 and -0.01 respectively. It is seen that an increase in the Prandtl number leads to a decrease in the temperature profile.
were fixed at 0.4 and -0.01 respectively. It is seen that an increase in the Prandtl number leads to a decrease in the temperature profile.
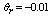

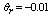
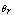 decreases the temperature profile.4. In increase in the magnetic parameter increases the temperature profile also increases.5. An increase in the Prandtl number leads to a decrease in the temperature profile.
decreases the temperature profile.4. In increase in the magnetic parameter increases the temperature profile also increases.5. An increase in the Prandtl number leads to a decrease in the temperature profile. Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-Text HTML
Full-Text HTML