-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Environmental Engineering
p-ISSN: 2166-4633 e-ISSN: 2166-465X
2025; 15(1): 1-15
doi:10.5923/j.ajee.20251501.01
Received: Jul. 16, 2025; Accepted: Aug. 9, 2025; Published: Aug. 15, 2025

Modeling and Forecasting Agrofood Supply Chain Emissions Based on VECM-ARIMA Model
Mikidady I. Selungwi 1, Erick P. Massami 2
1Department of Logistics and Transport Studies, National Institute of Transport, Dar es Salaam, Tanzania
2Department of Maritime Transport Management, National Institute of Transport, Dar es Salaam, Tanzania
Correspondence to: Erick P. Massami , Department of Maritime Transport Management, National Institute of Transport, Dar es Salaam, Tanzania.
| Email: |  |
Copyright © 2025 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Global efforts are being undertake to reduce carbon emissions in agrofood supply chain due to escalating concerns over global warming and climate change. Despite such efforts, carbon emissions continue to rise, particularly in developing countries that prioritize economic growth over environmental sustainability. This study aims to analyse the causal relationship between agrofood processing, agrofood packaging, agrofood transportation, agrofood retailing, and agrofood household consumption as exogenous variables and agrofood supply chain emissions as an endogenous variable. In addition, the study forecasts Tanzania’s agrofood supply chain emissions based on the data collected from FAO and IPCC over the period 1990-2020. The study uses the Vector Error Correction (VECM) model to examine the long-term and short-term effects between the variables whereas the Autoregressive Integrated Moving Average (ARIMA) model is used to forecast agrofood supply chain emissions from 2020 to 2030. The Johansen test of cointegration revealed the existence of both long-run and short-run relations between endogenous variable and exogeneous variables. More specifically, the findings reveal that agrofood transportation and agrofood retailing activities are dominant long-term drivers of agrofood supply chain emissions meanwhile agrofood processing activities are the major short-run influencer of agrofood supply chain emissions. In tandem, a 2030 forecast indicate a potential decline in agrofood supply chain emissions. Furthermore, the reduction of carbon emissions in agrofood supply chain can only be achieved provided all stakeholders take corrective actions including formulating and implementing green policies on agrofood supply chain, promoting agricultural resource efficiency, providing awareness training on green consumption, and using more sustainable production methods.
Keywords: Agrofood, Supply Chain Emissions, VECM Model, ARIMA Model, Forecasting Model
Cite this paper: Mikidady I. Selungwi , Erick P. Massami , Modeling and Forecasting Agrofood Supply Chain Emissions Based on VECM-ARIMA Model, American Journal of Environmental Engineering, Vol. 15 No. 1, 2025, pp. 1-15. doi: 10.5923/j.ajee.20251501.01.
Article Outline
1. Introduction
- Global efforts are being undertaken to reduce carbon emissions in agrofood supply chain due to escalating concerns over global warming and climate change. In 2015, 196 states adopted the Paris Agreement on Climate Change with the aim of limiting global warming to well below 2°C compared to pre-industrial levels [1]. This is achieved through nationally determined contributions (NDCs), where each country sets its own emission reduction goals and updates them every five years. The effectiveness of the Paris Agreement, in tandem with other environmental pollution policies, is closely linked to how each state party is responsible for reducing carbon emissions in every sector including agrofood supply chain. Globally, carbon emissions are escalating despite international efforts geared for their reduction [2]. This is particularly prevalent in developing countries that prioritize economic growth over environmental sustainability. In tandem with this view, many governments in the world have been actively implementing various strategies to curb carbon emissions. Nonetheless, the overall level of carbon emissions has not declined [3,4]. As such, reducing global CO2 emissions has become a focal objective of international policies aimed at mitigating the adverse effects of climate change. Globally, the agrofood supply chain accounts for about one-third of total human-induced emissions, but much of the research focuses on emissions from agricultural production, neglecting the downstream stages of the chain such as post-harvest handling, packaging, and consumer-level emissions.In Tanzania the agrofood supply chain which encompasses agrofood production, agrofood processing, agrofood packaging, agrofood transportation, agrofood retailing, and agrofood household consumption activities are collectively responsible for a significant share of national GHG emissions [5]. These emissions are largely attributed by inefficient logistics systems, outdated food processing technologies, limited cold chain facilities, and fossil fuel-based energy consumption. It is worth mentioning that the Tanzania’s agrofood sector is integral to both food security and economic development, contributing approximately 29% to the national GDP and employing about 65% of the population [6]. Despite its importance, the sector struggles with rising emissions linked to inefficient supply chain practices and poor energy infrastructure [7]. Regional transport challenges, such as a reliance on outdated road systems, and limited integration of green technology, further exacerbate these emissions [8]. Furthermore, less emphasis of the post-production activities of the agrofood supply chain has led to the knowledge gaps in how emissions from the non-production segments of the agrofood supply chain evolve over time [9,10].While previous studies have analysed agrofood emissions in industrialized nations, the findings cannot be easily applied to Tanzania due to context-specific issues including policy enforcement, level of investment in sustainable infrastructure and facilities, and the prevalence of informal markets. Moreover, prior studies have rarely analysed emissions in an integrated framework that accounts for interdependencies between agrofood processing, agrofood packaging, agrofood transportation, agrofood retailing, and agrofood household consumption [11]. Consequently, the general objective of this study is to develop an evaluation and forecasting model of agrofood supply chain emissions in Tanzania. The specific objectives include examining the relationships between activities related to agrofood processing, agrofood packaging, agrofood transportation, agrofood retailing, and agrofood household consumption and agrofood supply chain emissions. Additionally, the study aims to forecast agrofood supply chain emissions up to the year 2030 based on ARIMA model. The rest of this paper is organized as follows: Section 2 presents a scrutiny of the relevant studies; Section 3 presents the VECM-ARIMA modeling framework and Section 4 applies VECM-ARIMA model to evaluate and forecast agrofood supply chain emissions in Tanzania. Lastly, Section 5 gives the conclusions.
2. Scrutiny of the Relevant Studies
- A number of studies investigate agrofood supply chain emissions. Basri et al. [12] validate the significant role of global food provision while shaping the quality of the environment to achieve carbon peak targets, carbon neutrality, and promote agricultural modernization. Behvandi & Ghorbani [13] use a machine learning approach to predict GHG emissions in agri-food systems and find that on-farm energy use, pesticide manufacturing, and land use factors significantly influence GHG outputs. However, there is a lack of an integrated approach that holistically analyses emissions across multiple stages of the agrofood supply chain. Existing studies tend to isolate food system emissions into separate categories, such as transport emissions [11], pre-and post-production emissions [10], and trade-induced emissions [14], without considering how these factors interconnect within Tanzania’s agrofood system. Without a comprehensive understanding of the relationship of each of these factors and agrofood supply chain emissions, it is difficult to develop effective policies for emission reduction in agrofood supply chains.However, there are limited studies that investigate the relationship between agrofood supply chain emissions and one of these factors: agrofood processing, agrofood packaging, agrofood transportation, agrofood retailing, and agrofood household consumption.Food processing is one of the most energy-intensive stages in the agrofood supply chain, contributing significantly to GHG emissions. Activities such as pasteurization, drying, refrigeration, and packaging require substantial amounts of energy, particularly in large-scale industrial operations [15]. In Tanzania, where the food processing sector relies primarily on fossil fuel-powered electricity grids, emissions are even higher compared to nations that have adopted renewable energy solutions [11]. Studies suggest that modernizing food processing plants with energy-efficient machinery and solar or hydroelectric power sources can significantly reduce carbon emissions. However, most small and medium-sized enterprises (SMEs) in Tanzania’s agrofood industry lack the capital and infrastructure to implement such changes [14]. Despite the clear environmental impact of food processing emissions, there is limited research quantifying its contribution to Tanzania’s agrofood supply chain emissions. This study addresses this gap by providing a model that evaluates the contribution of agrofood processing activities on agrofood supply chain emissions.Food packaging plays a crucial role in protecting food products and extending shelf life, but it is also a major contributor to supply chain emissions. Most food packaging materials, particularly plastic and aluminium-based materials, have high carbon footprints due to energy-intensive production processes and end-of-life disposal challenges [16]. In Tanzania, limited recycling facilities mean that most packaging waste either ends up in landfills or is incinerated, releasing additional CO₂ and other pollutants into the atmosphere [10]. Globally, the push for sustainable packaging alternatives, such as biodegradable plastics, reusable containers, and minimal packaging designs, is gaining momentum. However, these innovations are less accessible in developing countries due to high production costs and limited consumer awareness [14]. The absence of strict regulatory policies on packaging waste further exacerbates environmental concerns in Tanzania’s food industry. While packaging emissions have been well-documented in industrialized economies, there is limited empirical research on their impact in Tanzania. This study aims to quantify agrofood packaging-related emissions and assess potential mitigation strategies, such as incentivizing sustainable packaging alternatives and expanding recycling programs.Food transportation is one of the largest contributors to food supply chain emissions, primarily due to the heavy reliance on fossil fuel-powered vehicles. Studies indicate that long-haul transportation significantly increases CO₂ emissions, especially in regions with poor infrastructure, where inefficient routes and extended travel times further raise fuel consumption [11]. Keshavarz-Ghorbani and Pasandideh [17] propose an optimization algorithm which integrates purchasing, transporting and storing decisions with the view to minimize the total costs and CO2 emissions in agro-supply chain. Accorsi et al. [18] present an optimization model that supports strategic decision-making on agriculture and food transportation issues while addressing climate stability. The findings reveal the interdependency between production, infrastructure, transportation, and environmental resources. Dwivedi et al. [19] propose an optimization model that minimizes the total transportation cost and carbon emission tax in the Indian agrofood grain supply chain. In Tanzania, the dominance of diesel-powered trucks and outdated logistics systems worsens the problem, making food transport one of the most carbon-intensive segments of the supply chain [10]. Efforts to mitigate transportation-related emissions in developed nations focus on electric freight vehicles, improved fuel efficiency, and optimized agrofood supply chains. However, electric freight vehicles remain largely inaccessible in Tanzania due to high costs, lack of charging infrastructure, and minimal policy support for green transport alternatives [15]. Additionally, the country’s heavy dependence on road transport rather than rail or waterways contributes to higher emissions per ton-km. While existing studies explore global transportation emissions, few provide insights into Tanzania’s transport logistics and inefficiencies. This study aims to fill that gap by evaluating the relationship between transportation activities and agrofood supply chain emissions, offering practical recommendations for decarbonizing food transportation in the country.The retail sector plays a critical role in food supply chain emissions, with significant contributions from refrigeration, storage, packaging, and waste generation. Large supermarkets, convenience stores, and informal market vendors all require energy-intensive cooling systems to preserve perishable foods, leading to substantial indirect CO₂ emissions [10]. In many developing countries, including Tanzania, informal food markets lack adequate refrigeration, resulting in high food spoilage rates, which in turn lead to increased methane emissions from organic waste decomposition. In addition to refrigeration, food packaging in retail contributes significantly to the supply chain’s carbon footprint. Many retailers rely on single-use plastics and non-biodegradable materials, leading to environmental pollution and increased emissions from incineration or landfill accumulation [14]. While developed countries are increasingly transitioning toward biodegradable packaging and sustainable retailing models, these solutions have yet to be fully implemented in Tanzania. Limited awareness, cost constraints, and weak regulatory enforcement continue to hinder progress in sustainable retail operations [11]. Despite its significant impact, research on Tanzania’s retail emissions is scarce. Current global studies mainly focus on formal supermarket chains, which do not represent the predominantly informal retail structures in Tanzania. This study aims to bridge that gap by evaluating the relationship between food retailing activities and agrofood supply chain emissions.Household food consumption is a significant contributor to greenhouse gas (GHG) emissions within the agrofood supply chain, particularly through energy intensive food preparation, dietary choices, and food waste generation. Studies have consistently shown that diets high in animal-based products, such as beef and dairy, have a far greater carbon footprint than plant-based diets, mainly due to methane emissions from livestock [15]. In Tanzania, the situation is further worsened by the widespread use of firewood and charcoal for cooking, which not only increases CO₂ emissions but also leads to deforestation and loss of carbon sinks [10]. Beyond energy use, food waste at the household level is another major concern. When food is discarded, it leads to unnecessary production-related emissions, while its decomposition in landfills releases methane (CH₄), a greenhouse gas 25 times more potent than CO₂. Studies indicate that developed nations have implemented food waste reduction strategies, such as portion control and redistribution programs, yet these interventions remain largely absent in Tanzania’s urban and rural settings [14]. Additionally, the lack of structured waste management systems means that much of this waste is either openly burned or left to decompose unmanaged, further contributing to emissions. Given the limited research on household emissions within Tanzania’s food supply chain, this study addresses this gap by presenting a model that evaluates the contribution of household consumption activities on agrofood supply chain emissions. The findings will help inform policies aimed at reducing household-level emissions through sustainable food consumption and waste management strategies.Despite increasing global research on greenhouse gas (GHG) emissions in the agro-food supply chain, studies focusing on Tanzania’s specific food system emissions remain scarce. While existing literature by Cui et al. [20], Crippa et al. [10], Piñero et al. [14], Jehn et al. [11], and Stöeckli et al. [16] provides valuable insights into emissions across various stages of the food supply chain, these studies primarily focus on global or industrialized economy contexts, leaving significant knowledge gaps for developing nations like Tanzania. In addition, most of prior studies are based on optimization models which focus on finding the best solution to a given agrofood supply chain problem not on forecasting time series data. More specifically, optimization models have difficulty in handling real-world complexities like uncertainty and dynamic environments. This study aims to bridge these gaps by conducting a comprehensive modeling and forecasting analysis of agrofood supply chain emissions from agrofood processing, agrofood packaging, agrofood transportation, agrofood retailing operations, and agrofood household consumption in Tanzania based on VECM-ARIMA model. The VECM-ARIMA model is a tool for time series analysis with several strengths including analyzing the short-run and long-run relationships of variables [12,21,22,23,24] and forecasting time series data. By integrating ARIMA and VECM models, this research will provide data-driven insights into key emission drivers, long-term trends, and potential policy interventions. The findings will support the development of targeted strategies for reducing emissions while enhancing supply chain efficiency in Tanzania’s agrofood sector.
3. VECM-ARIMA Modeling Framework
- A step-by-step framework for developing a Vector Error Correction (VECM) model with Autoregressive Integrated Moving Average (ARIMA) components involves identifying cointegration relationships between time series, developing ARIMA model, and integrating ARIMA model into a VECM framework.
3.1. Basic Concepts of Time Series
- A time series is a set of observations
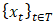 where each observation
where each observation 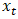 is recorded over a given time period
is recorded over a given time period 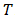 . There are two types of time series: discrete and continuous. Discrete time series result when the observations are discretely recorded (i.e. take whole number values). Continuous time series result when observations are continuously recorded over a time interval [25]. Time series are often used for forecasting future outcomes. Prior recorded observations for a time series are normally presented at daily, weekly, monthly, quarterly or annually time intervals. The time series model uses statistical tools, where historical observations gives a foundation for estimating the unknown parameters of interest [26].
. There are two types of time series: discrete and continuous. Discrete time series result when the observations are discretely recorded (i.e. take whole number values). Continuous time series result when observations are continuously recorded over a time interval [25]. Time series are often used for forecasting future outcomes. Prior recorded observations for a time series are normally presented at daily, weekly, monthly, quarterly or annually time intervals. The time series model uses statistical tools, where historical observations gives a foundation for estimating the unknown parameters of interest [26].3.1.1. Autocorrelation
- Autocorrelation (serial correlation) is the correlation of a time series and its lagged version over time. The autocorrelation coefficient
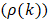 measures the correlation between a time series and a lagged version of itself. It indicates how strongly related values are at different points in time within the same series, where one basic example is that future agrofood supply chain emissions are predicted by current agrofood supply chain emissions. The autocorrelation coefficient at lag k of time series
measures the correlation between a time series and a lagged version of itself. It indicates how strongly related values are at different points in time within the same series, where one basic example is that future agrofood supply chain emissions are predicted by current agrofood supply chain emissions. The autocorrelation coefficient at lag k of time series 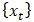 is given by equation (1).
is given by equation (1).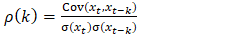 | (1) |
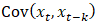 represents the variance between the time series values at time t and time t-k and measures how much these values tend to vary together;
represents the variance between the time series values at time t and time t-k and measures how much these values tend to vary together; 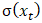 is the standard deviation of the time series values at time t; and
is the standard deviation of the time series values at time t; and 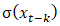 is the standard deviation of the time series values at time t-k. Similarly, the autocorrelation coefficient
is the standard deviation of the time series values at time t-k. Similarly, the autocorrelation coefficient 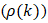 at lag k for a time series
at lag k for a time series 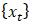 is given by equation (2).
is given by equation (2).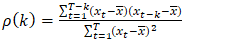 | (2) |
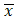 is the mean of the time series;
is the mean of the time series; 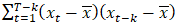 calculates the covariance between the time series values at time t and time t-k; and
calculates the covariance between the time series values at time t and time t-k; and 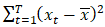 calculates the variance of the time series which measures the overall variability of the data.
calculates the variance of the time series which measures the overall variability of the data. 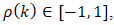 represents the strength and direction of the linear relationship. If the autocorrelation is high (close to +1 or -1), it suggests a strong correlation between past and present values, indicating patterns or dependencies in the data. One of the fundamental features of a time series that can be identified through autocorrelation is stationarity.
represents the strength and direction of the linear relationship. If the autocorrelation is high (close to +1 or -1), it suggests a strong correlation between past and present values, indicating patterns or dependencies in the data. One of the fundamental features of a time series that can be identified through autocorrelation is stationarity.3.1.2. Stationarity
- A stationary time series has statistical properties that are constant over time. This means that statistics such as the mean, variance and autocorrelation, don’t vary with time. Stationarity means that the time series does not have a trend, has a constant variance, a constant autocorrelation pattern, and no seasonal pattern. The autocorrelation function (ACF) declines to near zero rapidly for a stationary time series whereas the ACF drops slowly for a non-stationary time series. There are two fundamental types of stationary time series. Strong stationary (i.e. strict stationary) and weak stationary. A time series
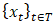 is said to be strictly stationary if the joint distribution of
is said to be strictly stationary if the joint distribution of 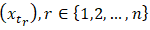 is identical to that of
is identical to that of 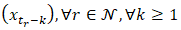 . As a result, changing the origin time by lag k has no effect on the joint distribution. On the other hand, a time seriesis said to be weakly stationary provided:
. As a result, changing the origin time by lag k has no effect on the joint distribution. On the other hand, a time seriesis said to be weakly stationary provided: 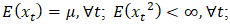
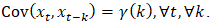 Generally, data from real-life scenarios are mostly non-stationary. However, many time series models work under the assumption that the data is stationary. Consequently, the analysis of such model becomes more complicated when working with non-stationary data. One method to transform non-stationary data to stationary is by differencing. This method eliminates trends in the data. By using a difference operator, a non-stationary time series is transformed to a stationary time series. The difference of a time series
Generally, data from real-life scenarios are mostly non-stationary. However, many time series models work under the assumption that the data is stationary. Consequently, the analysis of such model becomes more complicated when working with non-stationary data. One method to transform non-stationary data to stationary is by differencing. This method eliminates trends in the data. By using a difference operator, a non-stationary time series is transformed to a stationary time series. The difference of a time series 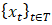 is defined by equation (3).
is defined by equation (3).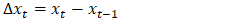 | (3) |
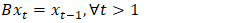 | (4) |
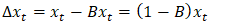 | (5) |
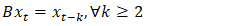 | (6) |
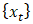 in terms of a seasonal difference operator is given by equation (7).
in terms of a seasonal difference operator is given by equation (7).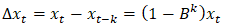 | (7) |
3.2. Statistical Tests
- The following are some commonly used statistical tests for time series.
3.2.1. Augmented Dickey-Fuller Test
- The Augmented Dickey-Fuller (ADF) is one of the methods to test whether the data of a time series is stationary or not. The method is used to detect the unit roots in the time series data. A unit root refers to a stochastic trend in a time series, which shows an unpredictable systematic pattern. It is crucial to ensure that the variables are stationary since statistical inference assumes of constant means, variances and covariances. An ADF test has the following null hypothesis (Ho) and alternative hypothesis (Ha):Ho: The time series is non-stationary,Ha: The time series is stationary.If the resulting p-value of the test is less than a specified
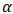 level, say
level, say 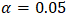 , then the null hypothesis is rejected at 5% significance level. This means that the alternative hypothesis is accepted and the time series is stationary. On the other hand, if the p-value is higher than a specified
, then the null hypothesis is rejected at 5% significance level. This means that the alternative hypothesis is accepted and the time series is stationary. On the other hand, if the p-value is higher than a specified 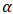 level, the null hypothesis cannot be rejected and the time series is considered non-stationary [27,28].
level, the null hypothesis cannot be rejected and the time series is considered non-stationary [27,28].3.2.2. The Kwiatkowski-Phillips-Schmidt-Shin Test
- The Kwiatkowski, Phillips, Schmidt, and Shin (KPSS) test is another method used to assess the stationarity of time series data. It has the following null hypothesis (Ho) and alternative hypothesis (Ha):Ho: The time series is stationary,Ha: The time series is non-stationary.If the p-value of the test is less than a specified
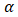 level, then the null hypothesis is rejected at
level, then the null hypothesis is rejected at 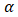 % significance level. Thu, the time series is non-stationary which suggests that differencing is required [29].
% significance level. Thu, the time series is non-stationary which suggests that differencing is required [29].3.2.3. Shapiro-Wilk Test for Normality
- The normality of a data set (i.e. residuals of VECM equation) is generally assessed by the use of a Q-Q plot, which gives a graphical visualisation of normality. If the data set scatter around the line of best fit inclined 45° with the horizontal-axis, the normality holds. However, a quantitative test is required to complement the visual inspection. The Shapiro-Wilk test is a hypothesis test that evaluates whether a data set is normally distributed. The Shapiro-Wilk test statistic (W) is computed by equation (8).
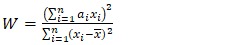 | (8) |
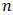 represents the number of observations;
represents the number of observations; 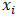 represents values of the ordered sample; and
represents values of the ordered sample; and 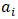 represents tabulated coefficients. The Shapiro-Wilk test has the following null hypothesis (Ho) and alternative hypothesis (Ha):Ho: The residuals are normally distributed,Ha: The residuals are not normally distributed.For a 95% confidence interval, the Shapiro-Wilk test resulting in a p-value< 0.05, indicates normalitydoes not existence among residuals. On the other hand, a p-value>0.05, indicates that the residuals are normally distributed [29].
represents tabulated coefficients. The Shapiro-Wilk test has the following null hypothesis (Ho) and alternative hypothesis (Ha):Ho: The residuals are normally distributed,Ha: The residuals are not normally distributed.For a 95% confidence interval, the Shapiro-Wilk test resulting in a p-value< 0.05, indicates normalitydoes not existence among residuals. On the other hand, a p-value>0.05, indicates that the residuals are normally distributed [29].3.3. Models for Stationary Time Series
3.3.1. White Noise Model
- White noise model is the simplest time series model. Suppose
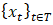 is a white noise process, which is defined as a model whose random variable is independently and identically distributed. It is worth noting that
is a white noise process, which is defined as a model whose random variable is independently and identically distributed. It is worth noting that 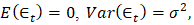
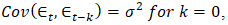
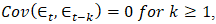 and
and 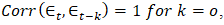
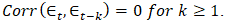
3.3.2. General Linear Model
- For the general linear model each value of
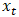 is a linear combination of both the current and preceding white noise processes and it is expressed by equation (9).
is a linear combination of both the current and preceding white noise processes and it is expressed by equation (9).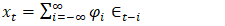 | (9) |
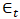 represents the white noise process and
represents the white noise process and 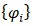 denotes a series of constants such that
denotes a series of constants such that 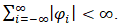
3.3.3. Autoregressive Model
- The autoregression processes are regressions on themselves. In an autoregressive model (AR(p) of order p, the model uses the p most recent values in the sequence to predict the next value. For example, an AR(1) model uses the two most recent values. An autoregressive model of order p at time t is defined by an expression given in equation (10).
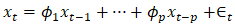 | (10) |
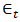 is a zero-mean white noise process with a standard deviation of
is a zero-mean white noise process with a standard deviation of 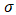 .
.3.3.4. Moving Average Model
- A moving average model of order q (referred to as MA(q) uses past forecast errors in a regression-like model, rather than using past values of the forecast variable like an autoregressive model does. In a moving average model, each value of
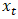 can be seen as a weighted moving average of the past few forecast errors. The model is defined by an expression given in equation (11).
can be seen as a weighted moving average of the past few forecast errors. The model is defined by an expression given in equation (11).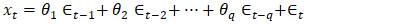 | (11) |
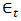 is a zero-mean white noise process with a standard deviation of
is a zero-mean white noise process with a standard deviation of 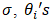 are the moving average parameters, which results in different time series patterns when changed, and q is the order of the moving average [30].
are the moving average parameters, which results in different time series patterns when changed, and q is the order of the moving average [30].3.3.5. Autoregressive Moving Average Model
- Suppose the time series
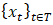 is an autoregressive moving average model of order p and q, denoted by ARMA (p, q) and defined by an expression in equation (12).
is an autoregressive moving average model of order p and q, denoted by ARMA (p, q) and defined by an expression in equation (12).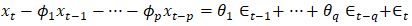 | (12) |
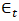 is a white noise process with a mean of zero and a standard deviation of
is a white noise process with a mean of zero and a standard deviation of 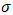 . Notably, the ARMA process incorporates both AR and MA processes. It is interesting to note that if
. Notably, the ARMA process incorporates both AR and MA processes. It is interesting to note that if 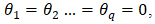 then equation (12) becomes an AR(p) process; however, if
then equation (12) becomes an AR(p) process; however, if 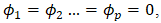 then equation (12) becomes an MA(q) model. In order to maintain a minimum order for p and q, AR(p) and MA(q) polynomials must have no common roots, where the AR(p) and MA(q) polynomials are defined by
then equation (12) becomes an MA(q) model. In order to maintain a minimum order for p and q, AR(p) and MA(q) polynomials must have no common roots, where the AR(p) and MA(q) polynomials are defined by 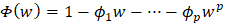 and
and 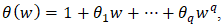 respectively.
respectively.3.3.6. Vector Autoregression Model
- Vector autoregression (VAR) is used for multivariate time series (multiple related time series). Each variable in the system is modelled as a function of its own past values and the past values of all other variables in the system. The VAR model can be used to analyse relationships and predict future values across multiple related time series. A VAR model for a system of k variables and p lags, is represented by an expression given in equation (13).
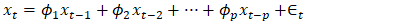 | (13) |
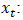 A k x 1 vector of endogenous variables at time t.
A k x 1 vector of endogenous variables at time t.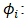 A k x k matrix of coefficients for each lag i.
A k x k matrix of coefficients for each lag i.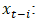 A k x 1 vector of endogenous variables at lag t-i.
A k x 1 vector of endogenous variables at lag t-i.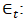 A k x 1 vector of error terms (white noise).
A k x 1 vector of error terms (white noise).3.4. VECM-ARIMA Model
- A step-by-step framework for developing a Vector Error Correction (VECM) model with Autoregressive Integrated Moving Average (ARIMA) components involves identifying cointegration relationships between time series, developing ARIMA model, and integrating ARIMA model into a VECM framework.
3.4.1. VECM Model
- A VECM model falls under the category of Vector Autoregressive (VAR) models. It is a specialized form of VAR model used when dealing with time series data that exhibit cointegration, meaning they have a long-run equilibrium relationship. A VECM models how variables deviate from their long-run equilibrium and how they adjust back to that equilibrium in the short-run. The general form of the VECM model is given by equation (14).
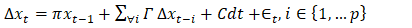 | (14) |
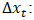 Represents the first difference of the vector of variables
Represents the first difference of the vector of variables 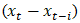 at time t. This captures the short-run dynamics and could be the first difference of the dependent variable at time t.
at time t. This captures the short-run dynamics and could be the first difference of the dependent variable at time t.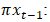 The error correction term which represents the long-run equilibrium relationship between the variables.
The error correction term which represents the long-run equilibrium relationship between the variables. 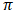 is a matrix that can be decomposed into
is a matrix that can be decomposed into 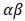 , where
, where 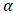 is the adjustment speed matrix and
is the adjustment speed matrix and 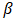 is the cointegrating vector, capturing the long-run relationships.
is the cointegrating vector, capturing the long-run relationships.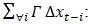 Represents the summation of lagged differences of the variables, capturing short-run dynamics and feedback effects.
Represents the summation of lagged differences of the variables, capturing short-run dynamics and feedback effects.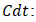 Represents deterministic terms like constant or trend.
Represents deterministic terms like constant or trend.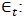 Represents the error term, assumed to be a vector of white noise with zero mean and constant covariance matrix.
Represents the error term, assumed to be a vector of white noise with zero mean and constant covariance matrix.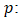 The lag order of the model. This needs to be determined through model selection criteria like Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC) etc. The sections 3.4.1.1, 3.4.1.2, and 3.4.1.3 present essential steps in VECM modeling.
The lag order of the model. This needs to be determined through model selection criteria like Akaike Information Criterion (AIC), Bayesian Information Criterion (BIC) etc. The sections 3.4.1.1, 3.4.1.2, and 3.4.1.3 present essential steps in VECM modeling.3.4.1.1. Data Pre-Processing and Stationarity
- Data collection and visualization. Gather time series data and plot them to inspect for trends, seasonality, and outliers.Stationarity testing. Apply unit root tests (e.g. ADF test) to each time series to determine if they are stationary. Non-stationary series need to be differenced to achieve stationarity.
3.4.1.2. Cointegration Analysis
- VAR model estimation. Fit a Vector Autoregression (VAR) model to the time series. Determine the optimal lag order for the VAR model using information criteria like AIC, BIC etc.Johansen test for cointegration. Perform the Johansen cointegration test to determine if the variables have a long-run equilibrium relationship. This test will identify the number of cointegrating equations (relationships).Identify cointegrating vectors. If cointegration is found, identify the cointegrating vectors, which represent the long-run relationships.
3.4.1.3. VECM Model Building
- VECM specification. Based on the cointegration results, specify the VECM model. This involves determining the number of lagged differences of the variables and the number of cointegrating equations.Error correction term. Include the error correction term(s) derived from the cointegration analysis in the VECM. This term represents the adjustment of variables towards their long-run equilibrium.
3.4.2. ARIMA Model
- The Autoregressive Integrated Moving Average (ARIMA) model integrates an AR and an MA model and thus combines differencing autoregression and moving average. It aims to describe the autocorrelations in the data. This model is denoted by ARIMA (p,d,q) where p is the order of the autoregressive (AR) part, indicating how many past values of x are used as predictors; d is the order of differencing, indicating how many times the time series needs to be differenced to be stationary; and q is the order of the moving average (MA) part, indicating how many past forecast errors are used as predictors. The general form of an ARIMA (p,d,q) model is given by equation (15).
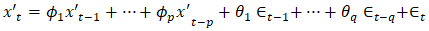 | (15) |
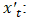 The differenced time series at time t;
The differenced time series at time t; 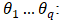 The MA coefficients;
The MA coefficients; 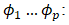 The AR coefficients; and
The AR coefficients; and 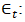 The white noise error term. Sections 3.4.2.1, 3.4.2.2, 3.4.2.3, 3.4.2.4, and 3.4.2.5 describe essential steps involved when ARIMA modeling is carried out.
The white noise error term. Sections 3.4.2.1, 3.4.2.2, 3.4.2.3, 3.4.2.4, and 3.4.2.5 describe essential steps involved when ARIMA modeling is carried out.3.4.2.1. Data Collection and Preparation
- Gather historical data on agrofood supply chain emissions from various sources (e.g. agrofood transportation); ensure data quality and address missing values or outliers; and transform the data to make it stationary (constant mean and variance over time), often by differencing.
3.4.2.2. Model Identification
- Examine autocorrelation and partial autocorrelation plots (ACF and PACF) to identify the order of the ARMA model (p, d, q).
3.4.2.3. Model Estimation and Selection
- Estimate the parameters of the chosen ARIMA model using the prepared data, and evaluate model fit using criteria like AIC or BIC to select the best model.
3.4.2.4. Forecasting
- Use the fitted ARIMA model to generate forecasts for future emission levels, the model can be used for both short-term and long-term forecasting.
3.4.2.5. Validation and Refinement
- Compare predicted emissions with actual emissions data as it becomes available. Refine the model (adjust parameters or consider adding other variables) if the forecast accuracy is not satisfactory.
3.5. Model Evaluation Measurements
- There are four different model evaluation measurements which are commonly used for evaluating and comparing different forecasting models.
3.5.1. Akaike Information Criterion
- Akaike Information Criterion (AIC) is based on a numeric value and likelihood, and aims to minimize the expression given by equation (16).
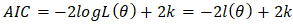 | (16) |
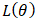 is the likelihood function of the model,
is the likelihood function of the model, 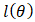 is the log-likelihood function of the model and k is the number of parameters i.e.
is the log-likelihood function of the model and k is the number of parameters i.e. 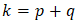 for ARMA (p, q) model. The log-likelihood function is the logarithm of the likelihood function. Since the expression is to be minimized, a numerical penalization occurs for complex models with poor likelihood. A lower AIC values indicate a better-fit model [31].Generally, the AIC works better for a large sample size as such it can potentially lead to a high degree of negative bias and overfitting when working with a small sample. To rectify this bias, a Corrected Akaike Information Criterion (AICc) is used. The AIC is a first-order estimate meanwhile AICc is the second-order AIC. The AICc is defined by an expression given by equation (17).
for ARMA (p, q) model. The log-likelihood function is the logarithm of the likelihood function. Since the expression is to be minimized, a numerical penalization occurs for complex models with poor likelihood. A lower AIC values indicate a better-fit model [31].Generally, the AIC works better for a large sample size as such it can potentially lead to a high degree of negative bias and overfitting when working with a small sample. To rectify this bias, a Corrected Akaike Information Criterion (AICc) is used. The AIC is a first-order estimate meanwhile AICc is the second-order AIC. The AICc is defined by an expression given by equation (17).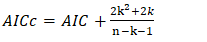 | (17) |
3.5.2. Mean Absolute Error
- The Mean Absolute Error (MAE) refers to a measure of variability in the absolute values of distances between observations and their corresponding predicted values i.e. the average magnitude of the errors. The MAE is commonly used as a measure of prediction of errors and is therefore useful when evaluating forecasting models. The MAE is defined by an expression given by equation (18).
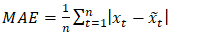 | (18) |
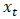 is the actual observation and
is the actual observation and 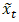 is the predicted value at time period t [26].
is the predicted value at time period t [26].3.5.3. Mean Absolute Percentage Error (MAPE)
- The Mean Absolute Percentage Error (MAPE) refers to a measure of variability in the absolute values of the ratio between the predicting errors and the observations. The MAPE is commonly used as a measure of prediction accuracy and is therefore useful when evaluating forecasting models. The MAPE is defined by an expression in equation (19).
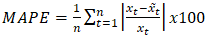 | (19) |
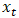 and
and 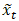 represent the actual and the forecasted value at time period t respectively.
represent the actual and the forecasted value at time period t respectively.4. Application of VECM-ARIMA Modelfor Evaluation and Forecasting Agrofood Supply Chain Emissions in Tanzania
- A VECM-ARIMA model combines the features of a VECM, which handles cointegrated time series, with the capabilities of ARIMA models for capturing autoregressive and moving average patterns within each variable. Specifically, the VECM model was applied in the analysis of the Tanzania’s agrofood supply chain emissions to understand the short-run and long-run relationships between various variables influencing carbon emissionsmeasured in kg tonnes within a supply chain. The variables that were analysed include agrofood processing activities, agrofood packaging activities, agrofood transportation, agrofood retailing activities, agrofood household consumption, and agrofood supply chain emissions. On the other hand, ARIMA model was applied to forecast the Tanzania’s agrofood supply chain emissions up to 2030 (i.e. In line with the United Nations SDGs). This allowed for identification of patterns and predicting future emission levels based on past trends. This study used secondary data retrieved from publicly accessible databases of Food and Agriculture Organization (FAO) and the Intergovernmental Panel on Climate Change (IPCC). The two sources offered historical datasets from 1990 to 2020.
4.1. Trends of Emissions and Statistical Tests of Variables in the Tanzania Agrofood Supply Chain
4.1.1. The Trend of Agrofood Supply Chain Emissions from 1990 to 2020
- Figure 1 depicts the trend of Tanzania’s agrofood supply chain emissions (kg tonnes of CO2) from 1990 to 2020.
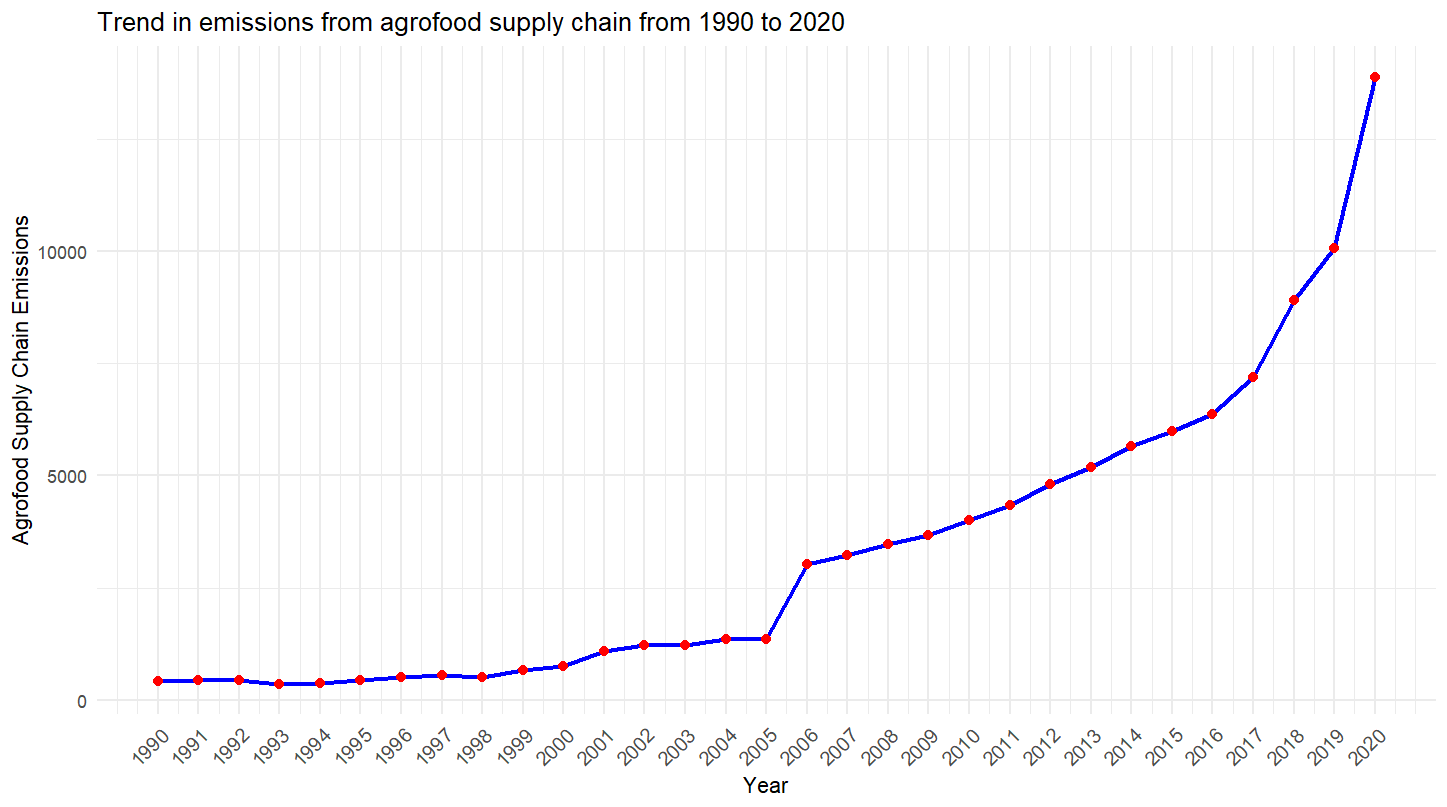 | Figure 1. The trend of Tanzania’s agrofood supply chain emissions from 1990 to 2020. (Source:Authors’ compilation from RStudio) |
4.1.2. Stationarity Test
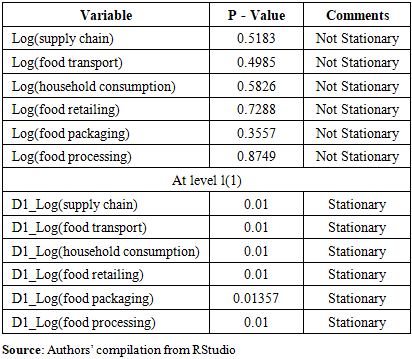
- The ADF test was applied to test whether the data of a time series is stationary or not. All six (6) variables were tested: log(supply chain), log(food processing), log(food packaging), log(food transportation), log(food retailing), and log(household consumption). The results of the test before differencing (I(0)) and after differencing (I(1)) are shown in Table 1.
|
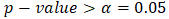 for all variables, which implies that the time series is non-stationary since the null hypothesis is not rejected. However, at level I(1) the
for all variables, which implies that the time series is non-stationary since the null hypothesis is not rejected. However, at level I(1) the 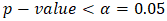 for all variables, which implies that the time series is stationary since the null hypothesis is rejected in favour of the alternative hypothesis.
for all variables, which implies that the time series is stationary since the null hypothesis is rejected in favour of the alternative hypothesis.4.1.3. Graphical Test of the Time Series Data
- If the variable in a time series data has either an upward or downward trend, it is not stationary. However, by differencing the time series may turn into stationary. Stationary data has a constant mean and variance which are independent of time. Figures 2 and 3 depict the trend of all variables at level I(0) (i.e. before differencing the time series) and level I(1) (i.e. after differencing the time series) respectively.From Figure 2 all of the variables show an upward trend. This means the mean and variance of each variable is changing over time hence the time series of each variable is not stationary at level l(0).
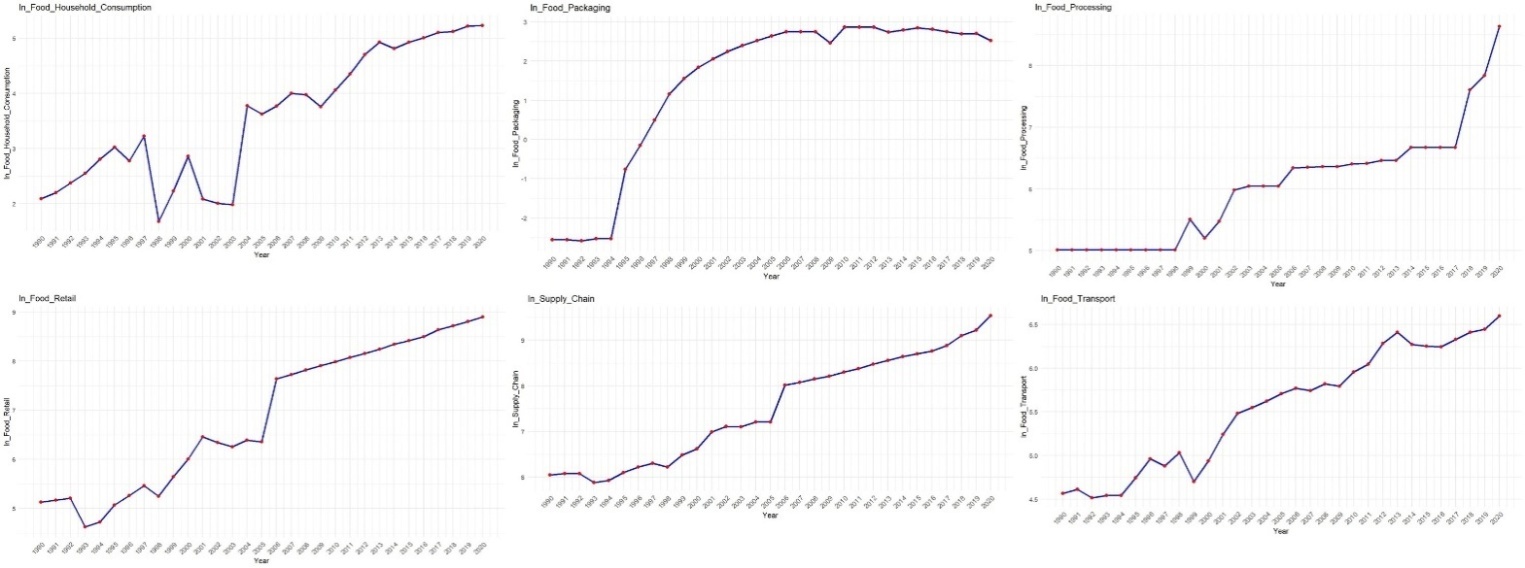 | Figure 2. Trends of variables at level l(0) (Source: Authors’ compilation from Rstudio) |
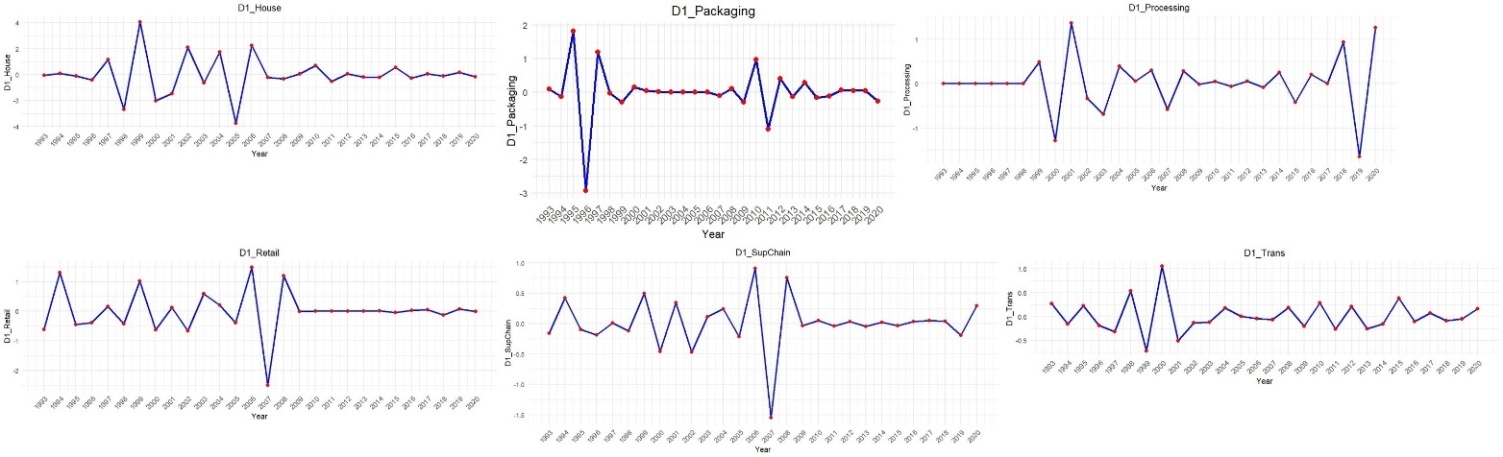 | Figure 3. Trends of variables at level l(1) (Source: Authors’ compilation from RStudio) |
4.1.4. Normality Test
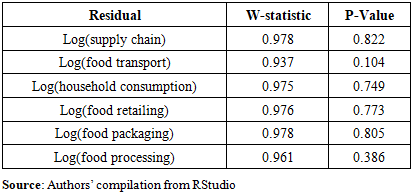
- The Shapiro-Wilk test was applied to test whether the residuals are normally distributed. All residuals for the six (6) variables were tested. These variables include log (supply chain), log(food processing), log(food packaging), log(food transportation), log(food retailing), and log(household consumption). The W-statistic values and p-values are indicated in Table 2.
|
 for all variables, the null hypothesis (Ho) is not rejected. This indicates that the residuals are normally distributed. The normality of residuals is further confirmed by the residual plots.
for all variables, the null hypothesis (Ho) is not rejected. This indicates that the residuals are normally distributed. The normality of residuals is further confirmed by the residual plots.4.1.5. Residual Plots
- Figure 4 depicts the residual plots to test the visualisation of normality for all variables.
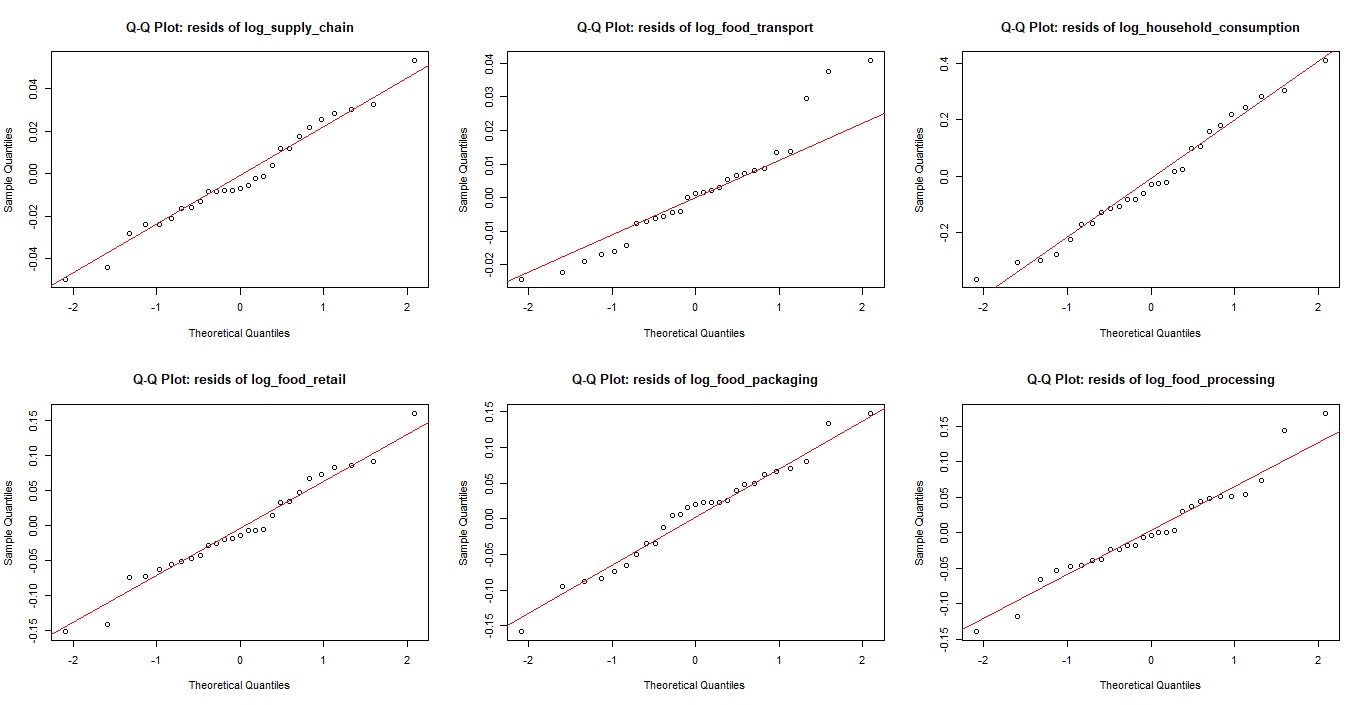 | Figure 4. Q-Q plots for normality test of variables (Source: Authors’ compilation from RStudio) |
4.1.6. Lag Order Selection
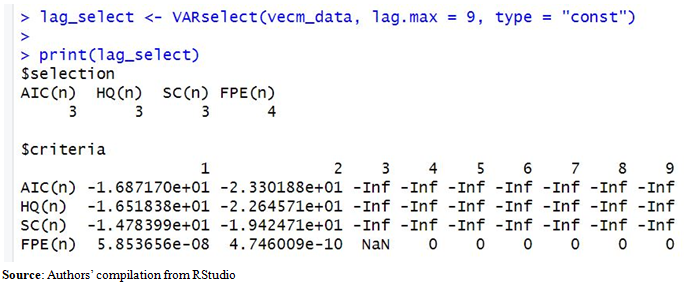
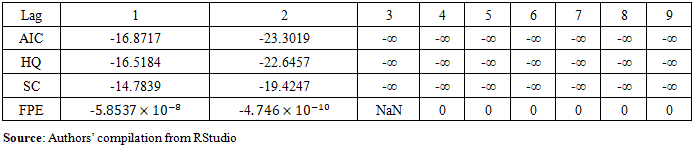
- For the determination of the maximum lag to be used in the model, the Akaike Information Criteria (AIC) was used considering its strengths over other criteria. The chosen lag should be the one with the lowest AIC and it was automatically suggested by the RStudio program. The lag selection output and optimal value are indicated in Table 3 and Table 4 respectively. From Tables 3 and 4 it is revealed that the optimal lag to be used by the model is three.
|
|
4.1.7. Cointegration Test
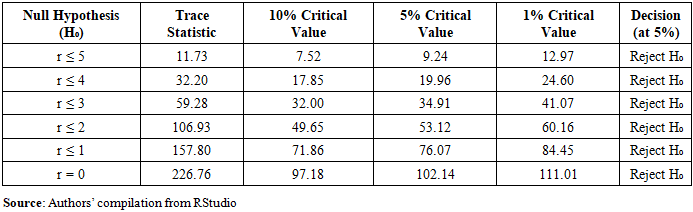
- The Johansen test was used to check if there exists a long-run and short-run relationship between the endogenous variable (agrofood supply chain emissions) and exogeneous variables (agrofood processing, agrofood packaging, agrofood transportation, agrofood retailing operations, and agrofood household consumption). The tested hypotheses were: Ho: There is no cointegration between variables, Ha: There is cointegration between variables. The tests results are presented in Table 5.
|
4.2. Analysis of Agrofood Supply Chain Emissions Based on VECM Model
- Table 5 shows that all the variables: agrofood supply chain emissions, agrofood processing, agrofood packaging, agrofood transportation, agrofood retailing operations, and agrofood household consumption are co-integrated. Thus, VECM model suits for this study.
4.2.1. Speed of Adjustment
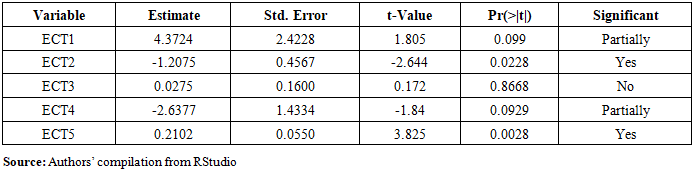
- The speed of adjustment is obtained from the Error Correction Term (ECT). The Error Correction Term (ECT) measures the deviation from long run equilibrium corrected gradually through a series of partial short run adjustments. The ECT values for the variables are presented in Table 6.
|
4.2.2. Short Run Dynamics
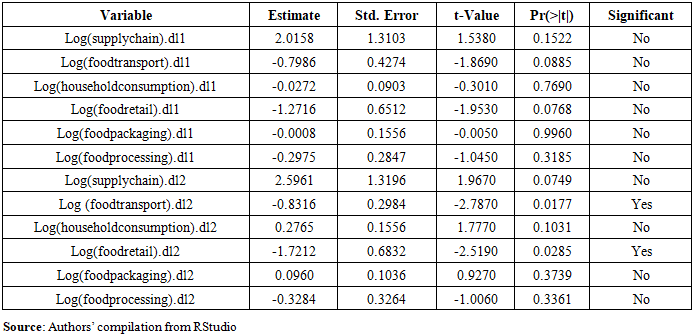
- The short run dynamics are captured by the lagged differences of emissions, which show how emissions in each sector respond to past changes in emissions from other sectors benefiting from agrofood. The results of the short-run dynamics are displayed in Table 7.
|
4.2.3. Long Run Effects
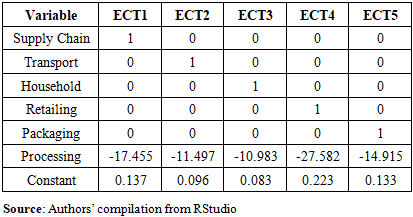
- Table 8 reveals that all sectors except agrofood processing have a unit coefficient for their respective error correction terms (ECTs). In the long run, agrofood processing emerges the most influential sector on agrofood supply chain emissions. Its adjustment coefficients are strongly negative (-17.455, -11.497, -10.983, -27.582, -14.915), implying that this sector plays a stabilizing role. Changes in agrofood processing activities significantly pull the system back to equilibrium, highlighting its prime importance in the Tanzania's agrofood chain emissions. To this end, deviations in agrofood supply chain emissions are mostly corrected by changes in agrofood processing activities. These findings align with Smith et al. [5] who emphasise that agrofood processing activities are energy-intensive users. This is concomitant with the arguments of Love et al. [15] and Jehn et al. [11] that food processing significantly contributes to GHG emissions since is one of the most energy-intensive stages in the agrofood supply chain. Thus, modernizing food processing plants with energy-efficient machinery and solar or hydroelectric power sources can significantly reduce carbon emissions. However, most SMEs in Tanzania’s agrofood industry lack capital and infrastructure to implement such changes [14]. Therefore, the government should play a key role by devising a variety of financing and fiscal schemes for SMEs.
|
4.2.4. Autocorrelation Test
- The Lagrange-multiplier was used to test the existence of autocorrelation. The two formulated hypotheses were: Ho: There is no autocorrelation present at lag order, Ha: There is autocorrelation present at lag order. The results of the Lagrange-multiplier are shown in Table 9.
|
 , the null hypothesis (Ho) is not rejected. This means that there is no significant autocorrelation in the residuals in the model, which is a good sign for model validity.
, the null hypothesis (Ho) is not rejected. This means that there is no significant autocorrelation in the residuals in the model, which is a good sign for model validity.4.3. Forecasting of Agrofood Supply Chain Emissions Using ARIMA Model
- An autoregressive integrated moving average (ARIMA) is a statistical analysis model that uses time-series data to either better understand the data set or to predict future trends which are used for analysing and forecasting time series data [32]. For the purpose of this study ARIMA model was applied to forecast and see the trend of agrofood supply chain emissions to 2030. It is worth noting that in order to achieve stationarity, the endogenous variable (i.e. agrofood supply chain emissions) was transformed using natural logarithms prior to model estimation and forecasting.The choice of using the best ARIMA model for forecasting based on the criteria of Akaike Information Criteria (AIC) was made automatically by RStudio. Table 10 reveals that ARIMA (1,0,2) was the most appropriate model for forecasting agrofood supply chain emissions.
|
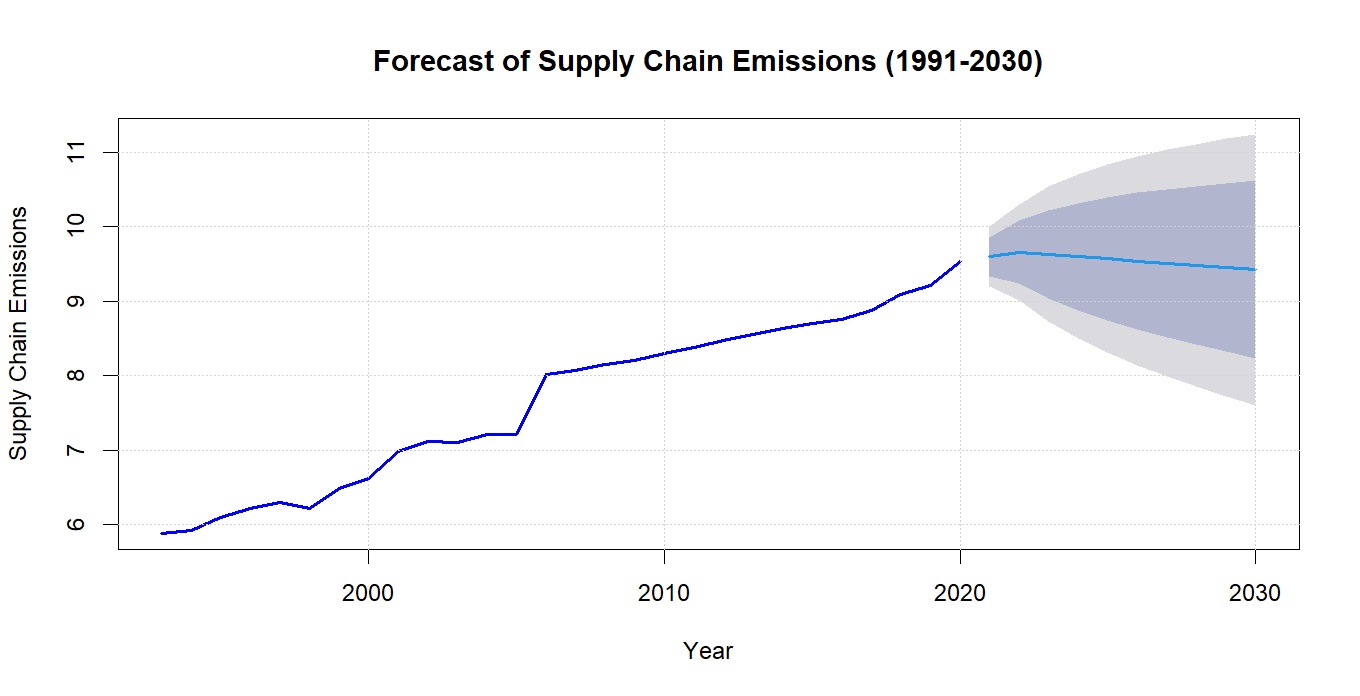 | Figure 5. ARIMA (1,0,2) forecast of agrofood supply chain emissions (Source: Authors’ compilation from RStudio) |
5. Conclusions
- The study aimed to analyse and forecast carbon emissions across the Tanzania’s agrofood supply chain emissions based on VECM-ARIMA model. The VECM model was applied to examine the short-run and long-run relationships between the research variables: agrofood processing activities, agrofood packaging activities, agrofood transportation, agrofood retailing activities, agrofood household consumption, and agrofood supply chain emissions. The ARIMA model was applied to forecast the Tanzania’s agrofood supply chain emissions based on the data collected from FAO and IPCC over the time period from 1990 to 2020. The time series data were firstly subjected to the ADF test and found to be stationary after differencing. The same results were supported by the graphical test of the time series data.The statistical tests were carried out to examine cointegration among variablesand the normality of data set. The Shapiro-Wilk test confirmed the normality for all variables. Meanwhile theJohansen test of cointegration revealed the existence of both long-run and short-run relationships between agrofood supply chain emissions (i.e. endogenous variable) and agrofood processing activities, agrofood packaging activities, agrofood transportation, agrofood retailing operations, and agrofood household consumption (i.e. exogeneous variables). More specifically, the short-run dynamics revealed that only agrofood transportation and agrofood retailing activities pose a significant influence on agrofood supply chain emissions. In the long-run, only agrofood processing activities exert a significant influence on agrofood supply chain emissions since its error correction term is strongly negative. Furthermore, the Lagrange-multiplier test revealed the non-existence of autocorrelation which confirms the model validity. On the other hand, the AIC was used to choose ARIMA (1,0,2) which provided a forecast of agrofood supply chain emissions from 2020 till 2030. The ARIMA forecasting model reveals a slightly decline of agrofood supply chain emissions up to the year 2030. This suggests that emission mitigation efforts by all stakeholders in the agrofood supply chain may be beginning to take place. Furthermore, understanding the environmental impact of agrofood sub-systems of the agrofood supply chain is crucial for informing all stakeholders about the challenges and opportunities to mitigate GHG emissions in the food sector. Specifically, the reduction of emissionsis possible provided green policies and regulations, green technology and stakeholders’ awareness towards sustainable supply chains continue to evolve. Furthermore, this study can serve as guidance for other countries where agrofood supply chain emissions are still escalating. Our future research direction is to model and forecast emissions from agri-food waste disposal systems based on VARIMA model.
Declarations
- All authors declare that they have no conflicts of interest.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML