-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Environmental Engineering
p-ISSN: 2166-4633 e-ISSN: 2166-465X
2018; 8(2): 36-43
doi:10.5923/j.ajee.20180802.03

Modelling Contaminant Dispersion in Meandering Low Wind Conditions Employing Meteorological Models
Viliam Cardoso da Silveira1, Gervásio Annes Degrazia1, Daniela Buske2, Silvia Beatriz Alves Rolim3
1Federal University of Santa Maria, Santa Maria - RS, Brazil
2Federal University of Pelotas, Pelotas - RS, Brazil
3Federal University of Rio Grande do Sul, Porto Alegre - RS, Brazil
Correspondence to: Viliam Cardoso da Silveira, Federal University of Santa Maria, Santa Maria - RS, Brazil.
| Email: |  |
Copyright © 2018 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The aim of this work is evaluating the behaviour of the pollutant plume in the region where the INEL (USA) experiment was released. The INEL diffusion experiment consists of a test series that was accomplished in a flat and uniform terrain under stable low wind atmospheric conditions. Thusly, accounting for the current understanding of the stable planetary boundary layer (PBL) turbulence pattern and characteristics (stable eddy diffusivities), a modelling system consisting of the WRF (Weather Research and Forecasting) and LES-PALM (Large-Eddy Simulation-Parallelized) model is employed to describe the dispersive effects associated with the wind meandering movements. The potential temperature profiles and heat fluxes generated by the WRF model will be used as initial conditions to the LES-PALM model. PALM is referred as a model to Large Eddy Simulation (LES) to atmospheric and oceanic fluxes that is destined to parallel computer architectures. The horizontal wind meandering generated by LES-PALM model will be used as initial conditions to the dispersion model based in the 3D-GILTT (3D Generalized Integral Laplace Transform Technique) technique that analytically solves the advection-diffusion equation. This technique of the integral transform combines a series expansion with an integration. In the expansion a trigonometric base, determined from the Sturm-Liouville auxiliary problem, is employed. The integration is made in all range of the transformed variable, making use of the orthogonality property of the base used in the expansion. The resultant ordinary differential equations system is analytically solved using the Laplace transform and diagonalization. The simulation results, generated from this modelling system are show to agree with the observed ground-level centreline concentrations of INEL experiments and also with those of other atmospheric dispersion models. The present study shows that the horizontal wind field provided by the coupling of two meteorological models (WRF and LES-PALM) can be used in a Eulerian diffusion model to properly simulate meandering enhanced dispersion of contaminants in a low wind speed stable PBL.
Keywords: Pollutants dispersion, WRF, LES, Advection-diffusion equation, 3D-GILTT Technique
Cite this paper: Viliam Cardoso da Silveira, Gervásio Annes Degrazia, Daniela Buske, Silvia Beatriz Alves Rolim, Modelling Contaminant Dispersion in Meandering Low Wind Conditions Employing Meteorological Models, American Journal of Environmental Engineering, Vol. 8 No. 2, 2018, pp. 36-43. doi: 10.5923/j.ajee.20180802.03.
Article Outline
1. Introduction
- The meandering enhanced dispersion occurring in low wind conditions (U < 1.5 m/s) [1], characterized by low frequency horizontal wind oscillations, is a relevant mechanism to describe the diffusion of atmospheric contaminants [2]. Thus, the horizontal wind meandering phenomenon is an important physical component that must be incorporated in air pollution models. These oscillations in the u and v horizontal wind components are practically independent of the atmospheric stability conditions, and are responsible for the presence of negative lobes in observed autocorrelation function (ACF) associated to the horizontal components of the wind vector ([3], [4]). This meandering ACF oscillatory behaviour makes it very difficult to establish a mean wind direction. The wind meandering phenomenon is more evident in stable conditions, but can also be present in others conditions [2]. Up to now, there is no conclusive theory available that explains the wind meandering origin. According to [5] and [6], other complementary criteria must be observed to consider the meandering occurrence, that is, the rate (in module) between the fit parameters of the autocorrelation function must be greater or equal to one. In low wind conditions, the Eulerian autocorrelation function of the horizontal wind components has a characteristic oscillatory behaviour identifying a well-defined meandering frequency. This low frequency, associated to the meandering phenomenon, can be seen in the observed meandering spectrum [6].Therefore, to describe this complex transport phenomenon characterized by the large horizontal wind oscillations, it will be used the mesoscale Weather Research and Forecasting (WRF) model coupled with the Parallelized Large-Eddy Simulation (LES-PALM) model to obtain the observed meandering horizontal wind field in the Idaho National Engineering Laboratory (INEL) experiments [7]. This modelled wind field will be employed in an Eulerian dispersion model to simulate the contaminant concentrations measured in the INEL experiments. Thusly, the aim of this study is to derive a new dispersion model based on the advection-diffusion equation, which utilizes a combination of mesoscale and LES models to describe the meandering enhanced dispersion process in distinct atmospheric stability conditions. Furthermore, the model takes into account the longitudinal diffusion term that cannot be neglected in such conditions [8]. Generally, the meandering dispersion effect in air pollution models is parameterized using Lagrangian stochastic particle diffusion models. The novel aspect shown in this work is the incorporation of dispersive effects, caused by the low frequency horizontal oscillations occurring in wind meandering phenomenon, in Eulerian dispersion models. The steady state three-dimensional advection-diffusion equation is solved by the Three-Dimensional Generalized Integral Laplace Transform Technique (3D-GILTT) [9] in which the mean wind generated from the LES-PALM is described by a power [12] and similarity [13] law. The model employs stable PBL eddy diffusivities which are used to parameterize the concentration turbulent fluxes ([10], [11]). The performance of this model is validated and evaluated through the comparison with experimental data and other different dispersion models.
2. INEL Experiments
- In the Table 1 we can see the series of INEL field experiments.
|
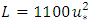 The friction velocity is calculated as [15]
The friction velocity is calculated as [15]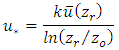 where
where 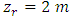 (reference height). To calculate h we use the following expression [16]
(reference height). To calculate h we use the following expression [16]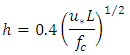 where h is the stable turbulent PBL height.
where h is the stable turbulent PBL height.3. Methods
- To describe the meandering phenomenon behaviour and to capture the strong horizontal directional variations of the wind, there were accomplished simulations with WRF model in the INEL region, where the contaminant release experiments were performed (Table 1). The potential temperature profiles and heat fluxes generated by WRF model were utilized to run the LES-PALM model [17]. The horizontal wind field simulated by LES-PALM model was used to run the dispersion model based in the solution of the advection-diffusion equation. In order to run the WRF model and provide meteorological inputs (heat fluxes and potential temperature), there were used reanalysis data of the NCEP/NCAR. The coupling between the numerical models considered 3 nested grids, being the data of the domain 3 selected to run the LES-PALM model (Figure 1). The Planetary Boundary Layer (PBL) parameterization used in WRF model was Mellor-Yamada Nakanishi Niino Scheme ([18], [19]).
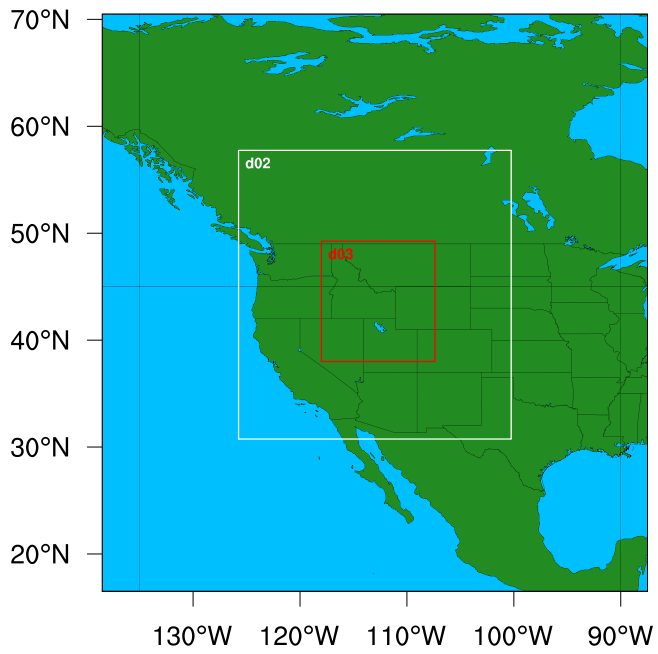 | Figure 1. The grids configuration used in the WRF model. d01, d02 and d03 are the WRF model domains |
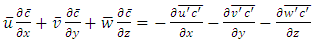 | (1) |
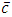 represents the mean concentration
represents the mean concentration  of a passive contaminant;
of a passive contaminant; 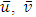 and
and 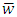 represent the mean wind components
represent the mean wind components 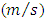 ; and the terms
; and the terms 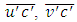 and
and 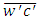 represent the concentration turbulent fluxes in x, y and z directions, respectively.In order to solve the turbulence closure problem, it is used the hypothesis of gradient transport (K theory) [21] as following
represent the concentration turbulent fluxes in x, y and z directions, respectively.In order to solve the turbulence closure problem, it is used the hypothesis of gradient transport (K theory) [21] as following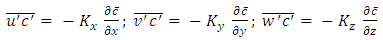 | (2) |
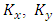 and
and 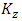 are the eddy diffusivities along x, y and z directions, respectively. Replacing Equation (2) in Equation (1) is obtained the parameterized advection-diffusion equation [22]
are the eddy diffusivities along x, y and z directions, respectively. Replacing Equation (2) in Equation (1) is obtained the parameterized advection-diffusion equation [22]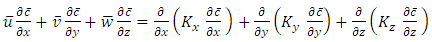 | (3) |
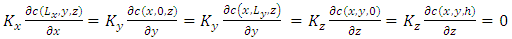 | (4) |
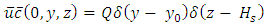 | (5) |
 is the emission rate, h is the PBL height,
is the emission rate, h is the PBL height, 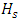 is the source height,
is the source height, 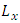 and
and 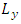 are the limits far from the source in x and y directions, respectively, and
are the limits far from the source in x and y directions, respectively, and 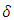 is the Dirac delta function. The horizontal mean wind components u and v are provided by
is the Dirac delta function. The horizontal mean wind components u and v are provided by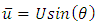 | (6) |
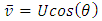 | (7) |
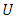 is the horizontal wind speed and
is the horizontal wind speed and 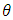 is the wind direction. Assuming the vertical mean wind component
is the wind direction. Assuming the vertical mean wind component 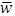 and the derivative
and the derivative 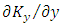 as equal to zero [23] in Equation (3), the following equation is obtained
as equal to zero [23] in Equation (3), the following equation is obtained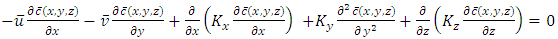 | (8) |
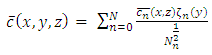 | (9) |
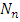 is given as
is given as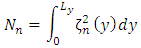 and
and 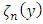 is a set of orthogonal eigenfunctions [25]
is a set of orthogonal eigenfunctions [25] 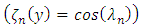 with
with 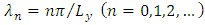 . Replacing Equation (9) in Equation (8) yields
. Replacing Equation (9) in Equation (8) yields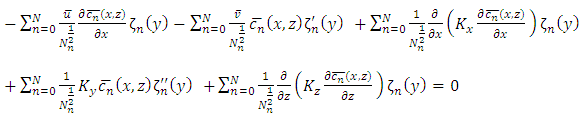 | (10) |
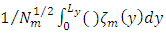 , remembering that
, remembering that 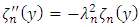 (from the associate Sturm-Liouville problem) and using the orthogonality of the eigenfunctions, one can write the Equation (10) as
(from the associate Sturm-Liouville problem) and using the orthogonality of the eigenfunctions, one can write the Equation (10) as | (11) |
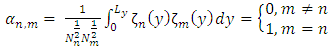 | (12) |
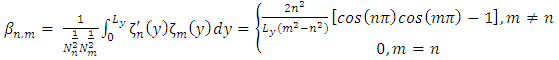 | (13) |
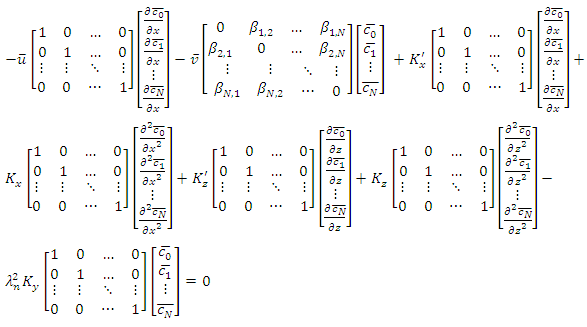 | (14) |
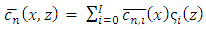 | (15) |
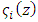 is a set of orthogonal eigenfunctions
is a set of orthogonal eigenfunctions 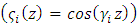 with
with 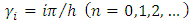 being a set of eigenvalues. Replacing Equation (15) in Equation (11), and following the same procedure adopted before, applying the integral operator
being a set of eigenvalues. Replacing Equation (15) in Equation (11), and following the same procedure adopted before, applying the integral operator 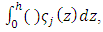 using the ortogonality of eigenfunctions, Equation (11) is written in matrix form as
using the ortogonality of eigenfunctions, Equation (11) is written in matrix form as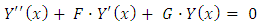 | (16) |
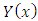 is the column vector with components
is the column vector with components 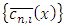 . The F matrix is given as
. The F matrix is given as 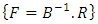 and the G matrix is
and the G matrix is 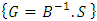 . The B, R and S matrices are written as
. The B, R and S matrices are written as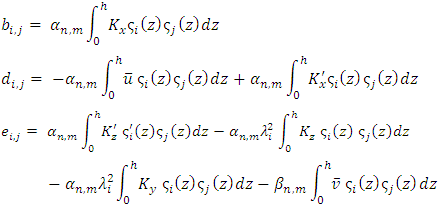 Applying the 3D-GILTT method in the source condition, one can write
Applying the 3D-GILTT method in the source condition, one can write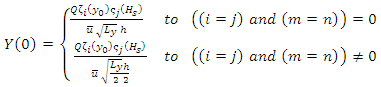 | (17) |
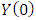 is the column vector with components
is the column vector with components 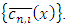 Applying an order reduction in Equation (16), we define new variables as
Applying an order reduction in Equation (16), we define new variables as 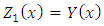 and
and 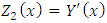 . By this procedure, the following equation in matrix form is obtained
. By this procedure, the following equation in matrix form is obtained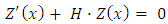 | (18) |
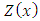 is given as
is given as 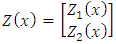 and the H matrix is written as
and the H matrix is written as 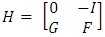 .The Equation (18) is analytically solved by using the Laplace Transform Technique and the diagonalization [24]. Applying the Laplace Transform in the x variable, transforming x in s, we have
.The Equation (18) is analytically solved by using the Laplace Transform Technique and the diagonalization [24]. Applying the Laplace Transform in the x variable, transforming x in s, we have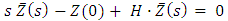 | (19) |
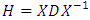 , where D is the diagonal matrix of eigenvalues of the H matrix [27]; X and
, where D is the diagonal matrix of eigenvalues of the H matrix [27]; X and 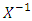 are the matrix and inverse matrix of eigenvectors, respectively [28]. After same algebraic manipulation, the solution of the Equation (19) is
are the matrix and inverse matrix of eigenvectors, respectively [28]. After same algebraic manipulation, the solution of the Equation (19) is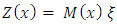 | (20) |
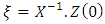 and
and 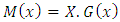 , with
, with 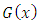 the diagonal matrix
the diagonal matrix 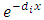 . We can write the Equation (20) in matrix form
. We can write the Equation (20) in matrix form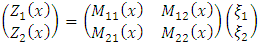 Finally, to determine
Finally, to determine 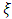 , we need to solve the following linear system by applying the boundary conditions of the solution of the Equation (18)
, we need to solve the following linear system by applying the boundary conditions of the solution of the Equation (18)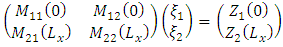 Replacing the results of the Equation (20) in Equation (15) we obtain the solution of the two-dimensional problem (2D). Replacing the results of the problem 2D (Equation (15)) in Equation (9) we obtain the three-dimensional solution of the advection-diffusion equation.Thus, employing stable PBL eddy diffusivities [10, 11] and the simulated horizontal wind field by the meteorological models in the above equations, the observed meandering effect in the dispersion of passive scalars can be described.
Replacing the results of the Equation (20) in Equation (15) we obtain the solution of the two-dimensional problem (2D). Replacing the results of the problem 2D (Equation (15)) in Equation (9) we obtain the three-dimensional solution of the advection-diffusion equation.Thus, employing stable PBL eddy diffusivities [10, 11] and the simulated horizontal wind field by the meteorological models in the above equations, the observed meandering effect in the dispersion of passive scalars can be described.4. Results and Discussion
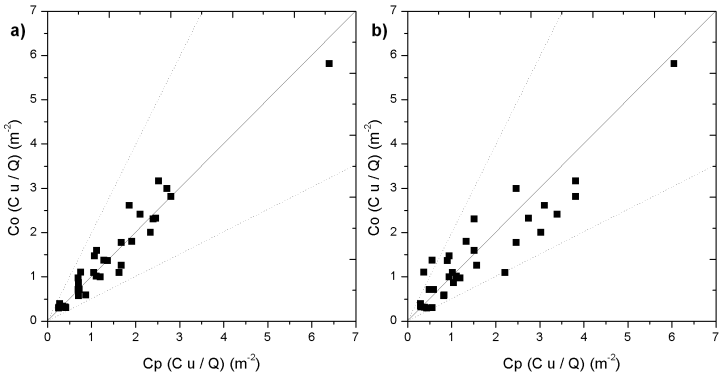
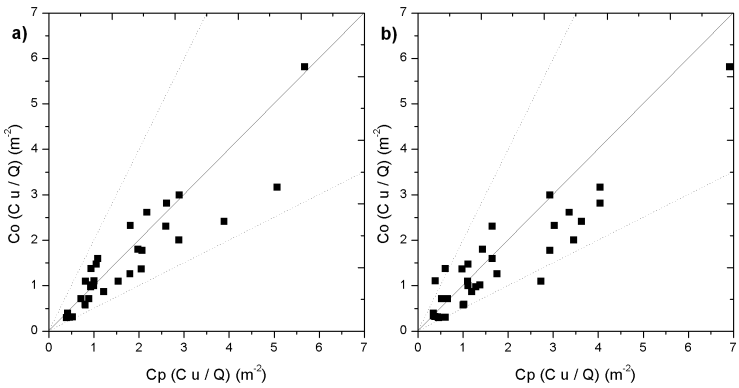
- To simplify, only the results to the test 4 are shown (Figures 2, 3, 4 and 5). Figure 2 shows the vertical profile of potential temperature simulated by WRF model to the domain 3. This profile is typical of stable atmospheric conditions. We can observe an inversion layer close to the ground. Above this inversion, we can observe a neutral layer.
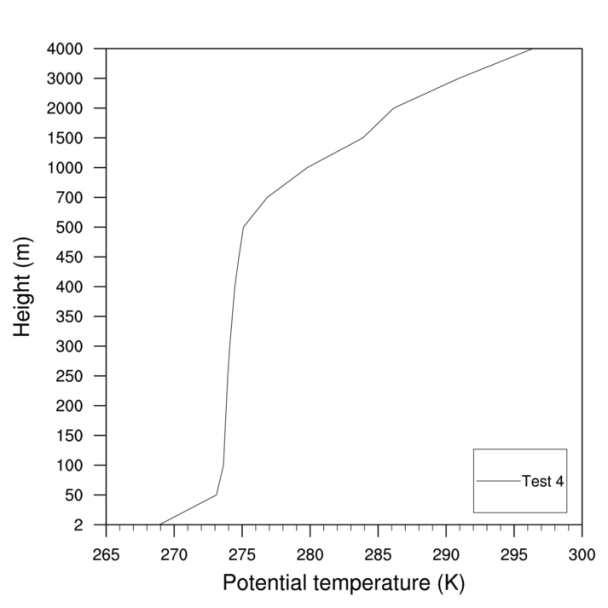 | Figure 2. Vertical profile of potential temperature simulated by WRF model |
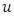 and
and 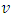 wind components simulated by the LES model. It can be seen clearly in these figures the presence of negative lobes on the horizontal wind components. These negative lobes are striking features of the existence of the meandering phenomenon in atmospheric movements [2, 4]. Therefore, the strong negative lobes exhibited in figures show that the LES-PALM model is able to reproduce the principal characteristic of the wind meandering. The rate (in module) between the adjustment parameters of the
wind components simulated by the LES model. It can be seen clearly in these figures the presence of negative lobes on the horizontal wind components. These negative lobes are striking features of the existence of the meandering phenomenon in atmospheric movements [2, 4]. Therefore, the strong negative lobes exhibited in figures show that the LES-PALM model is able to reproduce the principal characteristic of the wind meandering. The rate (in module) between the adjustment parameters of the 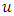 wind component proposed by Frenkiel [29] is 2.220363 and the proposed by Moor et al [4] is 2.844219. The adjustment parameters of the
wind component proposed by Frenkiel [29] is 2.220363 and the proposed by Moor et al [4] is 2.844219. The adjustment parameters of the 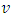 wind component calculated from the Frenkiel [29] and Moor et al [4] are 2.491916 and 3.615198, respectively.
wind component calculated from the Frenkiel [29] and Moor et al [4] are 2.491916 and 3.615198, respectively.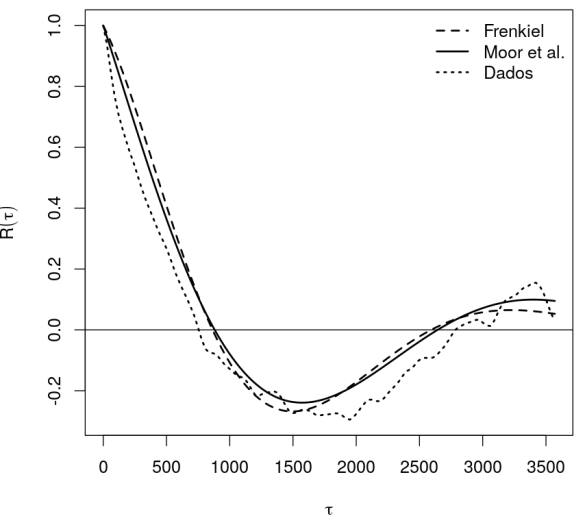 | Figure 3. Autocorrelation function calculated with the u wind component simulated by LES model |
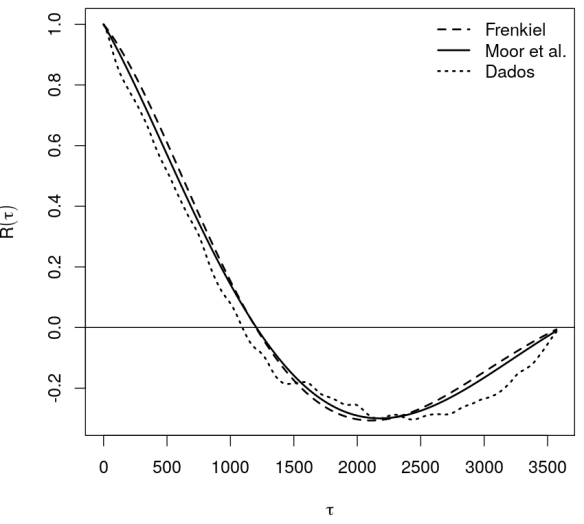 | Figure 4. Autocorrelation function calculated with the v wind component simulated by LES model |
|
5. Conclusions
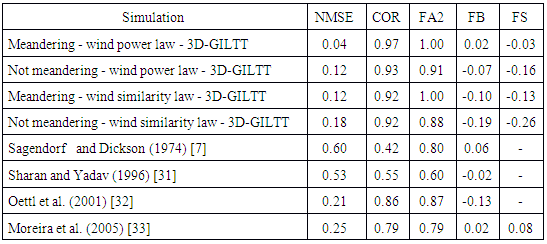
- In low wind conditions to evaluate the contaminant concentration, the air dispersion models need to consider the meandering enhanced dispersion and also the turbulent diffusion processes. In this aspect, the turbulent parameterization plays a fundamental role in dispersion models that simulate the observed contaminant concentration. Therefore, the choice of an adequate parameterization allows a better description of the turbulent transport in the PBL. In this study, an Eulerian air dispersion model based on the solution of the advection-diffusion equation (3D-GILTT), in which the simulated horizontal wind field is obtained from a meteorological modelling system (WRF and LES-PALM), is employed to simulate the contaminant concentration in low wind speed meandering situation. Its solution is obtained by applying the integral transform techniques. To represent the wind meandering effect, the horizontal wind generated from the LES-PALM is decomposed in the lateral and longitudinal directions. Concerning to the turbulent dispersion the Eulerian model uses eddy diffusivities, for stable condition, given by algebraic formulations that incorporate the physical characteristics of the energy-containing eddies. Furthermore, these eddy diffusivities describe the inhomogeneous character and the meandering effect associated to the PBL turbulence.The horizontal velocity autocorrelation function shows the characteristics of the occurrence of the wind meandering phenomenon, presenting negative lobes with the ratio of the adjustment parameters greater than or equal to one. This fact points out that the LES-PALM model reproduces in a satisfactory way the relevant features associated with the wind meandering phenomenon.The results of the simulated contaminant concentration by the Eulerian model (3D-GILTT) were compared with the observed concentrations in the INEL low wind experiments and other different turbulent diffusion models. In this aspect the results obtained by the 3D-GILTT incorporating the results of the meteorological modelling system, agree well with the experimental data, indicating that the model represents the diffusion processes correctly in low wind speed stable conditions. It is also possible to verify that 3D-GILTT results, utilizing the meandering dispersive effects, are better than those simulated by other dispersion models. Therefore, the new 3D-GILTT model incorporating the enhanced meandering dispersion, may be suitable for application in regulatory air pollution modelling.
ACKNOWLEDGEMENTS
- This study was supported by CAPES (Coordenação de Aperfeiçoamento de Pessoal de Nível Superior).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML
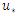 is the friction velocity, U is the mean wind speed, is the planetary boundary layer height and ym is the maximum source distance in the y direction
is the friction velocity, U is the mean wind speed, is the planetary boundary layer height and ym is the maximum source distance in the y direction