Adindu Ruth. U1, Igbokwe kelechi K1, Chigbu Timothy O.1, Ike-Amadi C. A.2
1Dept. of Physics/Electronics, Abia State Polytechnic, Aba. P.M.B 7166, Aba Nigeria
2Dept. of Chemistry, Abia State Polytechnic, Aba. P.M.B 7166, Aba Nigeria
Correspondence to: Adindu Ruth. U, Dept. of Physics/Electronics, Abia State Polytechnic, Aba. P.M.B 7166, Aba Nigeria.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
Abstract
Substantial reduction in time and cost of field measurement of infiltration are some of the benefits of using infiltration models in designing and optimizing irrigation projects, as they are adequate in predicting water infiltration to a reasonable level of accuracy. The objective of this study is to obtain the water infiltration parameters of the soils of Umudike, which could be used in simulating infiltration for these soils when designing irrigation projects, thereby saving time and cost of field measurement. Field measurements of infiltration were first made using a double ring infiltrometer. The tests lasted for 180 mins in each location. Infiltration values ranged from 4.6cm/min to 24.4cm/min. The highest value was obtained in the Forest block. Kostiakov’s infiltration model was then applied on the field data in order to determine the soils’ infiltration parameters and equations. The model empirical constants or parameters obtained were ‘m’ and ‘n'. For 'm' the values were: 0.53 for the soil of Forest block, 0.42 for Poultry block, 0.50 for P.G block, 0.41 for the soils of Staff school and Guest House. The corresponding ‘n’ values were: 1.37, 1.12, 0.37, 1.79 and 1.38. Infiltration equations: 0.41t1.38, 0.41t1.79, 0.50t0.37, 0.42t1.12 and 0.53t1.37 were determined for the locations. These were used to simulate data which were evaluated by comparing them with the field data. The two data sets showed closed relationships. This implied that the model could be used to simulate water infiltration during irrigation projects in the farms of Umudike.
Keywords:
Kostiakov, Model parameters, Infiltration, Soil, Water, Irrigation
Cite this paper: Adindu Ruth. U, Igbokwe kelechi K, Chigbu Timothy O., Ike-Amadi C. A., Application of Kostiakov’s Infiltration Model on the Soils of Umudike, Abia State - Nigeria, American Journal of Environmental Engineering, Vol. 4 No. 1, 2014, pp. 1-6. doi: 10.5923/j.ajee.20140401.01.
1. Introduction
Water infiltration into the soil is a very important issue in soil water management and water resource conservative practices. Infiltration rate describes the capacity of a soil to absorb water. Its characteristics are key variables in hydrologic analysis and modeling. It's also used in agriculture. Substantial reduction in time and cost of field measurement of infiltration can be achieved by using infiltration models[1]. These models can be used in designing and optimizing irrigation projects.[2] evaluated the Parlange’s model for four soil units, ranging from sandy loam to loam soils and found that the model was adequate in predicting water infiltration to a reasonable level of accuracy.[3] studied the performance of four different models in a Hydromorphic soil of Zango plain, Zaria Nigeria and found that[4] and[5] models provided best fit with experimental data for the soil.[6] evaluated the infiltration rates of soils under four land uses in north-eastern Mexico and noted that Modified Kostiakov’s model gave the best fit while[7],[8] and[9] stated that the values of the estimated parameters obtained by different models are soil dependent and site specific. In addition, they noted that complicated conditions and regional soil variations affects the estimated values.[10] recommended that empirical models be used to describe infiltration process.
1.1. Literature
Infiltration models can be generally classified into three groups: physically based models, semi-empirical models and empirical models[11]. Empirical models are derived from data observed either in field or in laboratory. The models of Kostiakov’s, Huggins and Monke Modified Kostiakov, etc. fall in category of empirical models. Some of the available empirical models have been quite popular and frequently used in various water resource applications all over the world, owing to their simplicity and yielding reasonably satisfactory results in most applications. For example, the wide-spread application of the Kostiakov (KT) and Modified Kostiakov (MKT) models in irrigation engineering are very important from the view point of its field applicability.
1.2. Kostiakov’s Equation
This model suggested a formula which assumes that at time t = 0, the infiltration rate is infinite and at time t = ~, the rate approaches zero[12] .This equation is given by: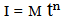 | (1) |
whereI = Cumulative infiltration rate n = Index of soil structural stabilityM = A measure of initial rate of infiltration and structural condition of the soilt = Time elapsedTaking the logs of both sides gives: 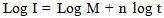 | (2) |
A plot of log I against log t gives a straight line whose slope gives the value of n, while the intercept gives the value of log M. To determine the values that best fit the equation, the values of I were calculated by substituting the values of antilogs of log M and n in equation (1) for each value obtained at any time t. ‘M’ and ‘n’ depends on soil type, vegetative cover, soil characteristics, moisture condition, rainfall intensity and soil surface conditions.
1.3. Objective
It is the objective of this study to obtain the water infiltration parameters of the soils of Umudike, which would become an input in soil water management and water resource conservative practices in this area. Also the water infiltration equations which this study shall propose could be used in simulating infiltration for these soils when designing irrigation projects, thereby saving time and cost of field measurement.
2. Materials / Method
2.1. Measurement
The infiltration capacities of Umudike soils were measured using double infiltrometer rings. The rings were driven into the ground by hammering a wooden bar placed diametrically on the rings to prevent any blowout effects around the bottoms of the rings. 2mm of sand layer was spread at the bottom of the inner and outer rings of each infiltrometer to minimize soil surface disturbance when water was poured into the compartments. Areas covered by grass were cut as low as possible with a cutlass so that the float could have free movement and care was taken not to uproot the grasses. Randomization technique was used to choose point measurements. Water from jerry-cans was poured into the infiltrometer compartments simultaneously and as quickly as possible. As soon as the jerry cans were emptied, the water level from the inner cylinder was read from the rule and the local time noted. Repeated readings were taken at intervals of 5, 10, 15, and 30, 40, 50, 60, 75, 90, 120, 150 and finally at 180 minutes. The outer cylinder compartment was refilled from time to time while maintaining the water level constantly equal. Soil samples were taken using core samplers from the surface layer to the depth of 30cm in the area outside the outer rings. These were used for the determination of the initial moisture content and bulk densities and other physical properties of the soils.
2.2. Model Application
Kostiakov’s model was then applied to the measured field data to obtain the soil infiltration parameters. The parameters were then used to predict the equations that described the cumulative infiltration of these soils. Simulated data were compared to the field data to see if the two have close agreement.
3. Results
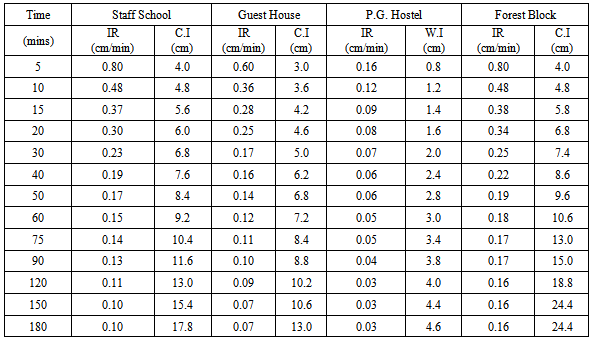
Table 1. Field measurement of Infiltration rate (IR) and Cumulative Infiltration (C.I) of Umudike Soils
 |
| |
|
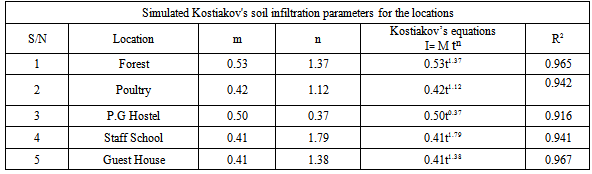
Table 2. Soils parameters and equations
 |
| |
|
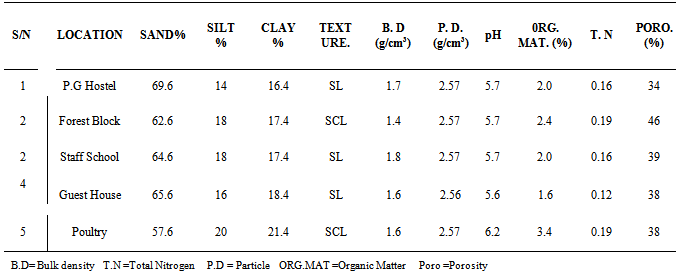
Table 3. Physical Properties of the soils of the locations
 |
| |
|
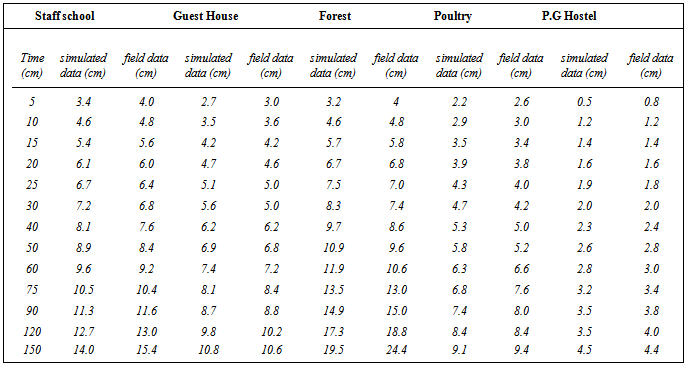
Table 4. Simulated data compared with field data
 |
| |
|
 | Figure 1. Infiltration curves of the field data |
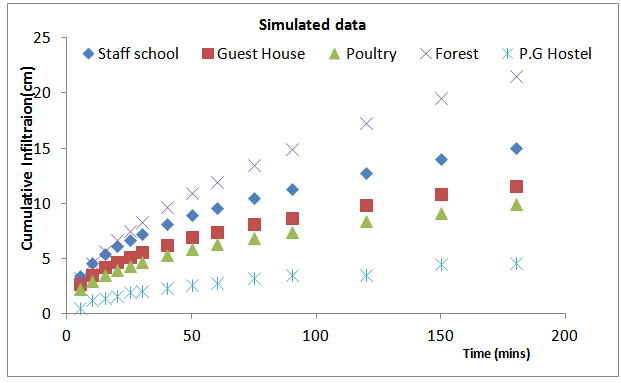 | Figure 2. Infiltration curves of the simulated data |
 | Figure 3. SImulated and field Infiltration curves for the soil of Guest House block |
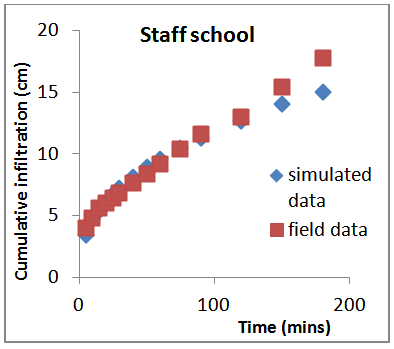 | Figure 4. SImulated and field Infiltration curves for the soil of staff school block |
3.1. Discussions
Table (1) shows the field measured cumulative infiltration depths and the infiltration rates for each location. The infiltration rate for the soil of Staff school block was 0.10cm/min while its cumulative infiltration depth was 17.8cm after 180mins. The soils of P.G and Guest House Blocks had infiltration rates of 0.03 cm/min with cumulative infiltration depth of 13.0cm and 4.6cm respectively. These were influenced by the texture, moisture content and vegetation cover of these soils. Table (2) shows the values of the estimated parameters. 'm' values ranged from 0.41 - 0.53. 'n' varied from location to location and ranged from 0.37–1.79. The infltration equations obtained for the soils were: 0.41t1.38, 0.41t1.79, 0.50t0.37, 0.42t1.12 and 0.53t1.37. This confirmed the fact that the values of the estimated parameters are soil dependent and site specific as noted by[13],[14] and[15]. Table (3) shows the physical properties of the soils, the textures of the soils are sandy loam and sandy clay loam. The bulk density ranged from 1.4 – 1.7g/cm3. The Organic Matter content and porosity of the soils are relatively high, ranging from 1.6 – 3.4. and from 34% - 46% respectively. The pH of the soils indicate acidity while the total nitrogen highest value was 0.19. Table (4) presents the Predicted cumulative infiltration. These were compared with field data. The cumulative infiltration showed a negligible difference between the field and the simulated data. Figures 1 and 2 represent the infiltration curves for the field and simulated data respectively. Figures 3 and 4 compared the simulated and field Infiltration curves for the soil of Guest House block and for the soil of staff school block. These curves were closely related, indicating that the predicted Kostiakov's equations used in simulating infiltration for the soils gave infiltration values with no significant variations from the field data, indicating that Kostiakov's model was able to simulate infiltration values that could be used for irrigation designs in this area. This result is similar to those obtained by[16] in the evaluation of some infiltration models and hydraulic parameters.[17] used same model for soils of Minna, Niger State in soil grouping of the Federal university of Technology, Minna, Nigeria. He obtained the following parameters: M =1.069, n = 0.821 for cultivated soils and M = 0.741, n = 0.760 for the fallowed soils of the same location.[18] in the evaluation of soil infiltration model coefficients obtained the infiltration equation: I = 1.0947T0.66 for Kostiakov’s model.
4. Conclusions
The objective of this study was to use Kostiakov’s model to obtain the water infiltration parameters and equations of the soils of Umudike, which could be used in simulating infiltration for these soils when designing irrigation projects, thereby saving time and cost of field measurement. Simulated infiltration could also serve an input in soil water management and water resource conservative practices in the area. Field measurements of infiltration were first made using a double ring infiltrometer in five different locations at Umudike. Infiltration rate ranged from 4.6cm/min to 24.4cm/min. Kostiakov’s infiltration model was then applied on the field data to determine the soils’ infiltration model coefficients. The coefficients obtained for 'm' were : 0.53 for the soil of Forest block, 0.42 for Poultry block, 0.50 for P.G block, 0.41 for the soils of Staff school and Guest House. The corresponding ‘n’ values ranged from 0.37-1.79. Infiltration equations obtained for the soils were: 0.41t1.38, 0.41t1.79, 0.50t0.37, 0.42t1.12 and 0.53t1.37. Simulated data were evaluated by comparing them with field data and they showed a close agreement with each other, indicating that Kostiakov’s infiltration model was capable of simulating infiltration for the soils of Umudike.
References
| [1] | Mudiare, O.J. and Adewunmi, J.K. (2000). Estimation of infiltration from field-measured sorptivity values. Nigerian Journal of soil science Research. 1:1-3. |
| [2] | Igbadun, H.E. and Idris, U.D. (2007). Performance Evaluation of infiltration Model in a Hydrmorphic oil. Nig. Jour. & Env.Res. 7:53-59. |
| [3] | Kostiakov, A. N. (1932). The dynamics of the coefficients of water percolation in soils and the necessity for studying it from a dynamic point of view for purpose of amelioration. Society of Soil Sci.,14: 17-21. |
| [4] | Rao, M.D., Raghuwanshi, N.S and Singh, R. (2006) Development of a physically 1D- infiltration model for irrigated soils. Agricultural Water Management. 85:165-174. |
| [5] | Mishra, S. and Singh, V. (2003a). Soil Conservation Service Curve Number (SCS-CN) Methodology. Kluwer Academic Publishers, Dordrecht, The Netherlands,. ISBN 1-4020-1132-6. |
| [6] | Mishra, S. Tyagi, J. Singh, V.( 2003b). Comparison of infiltration models. Journal of Hydrological Processes. 17:2629–2652. |
| [7] | Moroke, T.S., Dikinya, O. and Patrick C. (2008). Comparative Assesment of Water Infiltration of Soils under different Tillage Systems in Eastern Botswana. Physics and Chemistry of the earth. 34: 316 – 323. |
| [8] | John, J. M. and Nosa, A. E. (2009). Soil Grouping of the Federal University of Technology, Minna: Main Campus Farm using Infiltration Rate. AU J. T., 13(1): 19 – 28. |
| [9] | Parlange, J.R. (1973). Note on infiltration advance front form border irrigation. Water Resour. Res. 9:1075-1078. |
| [10] | Mbagwu, J. S. C. (1995). Testing the goodness of fit of infiltration models for highly permeable soils under different tropical soil management systems, Soil and Tillage Research, 34(3), pp, 199-205. |
| [11] | Philip, J. (1957). Theory of infiltration: The infiltration equation and its solution. Soil Science, 83(5): 345–357. |
| [12] | Singh, Yu. V. F. (1990). Derivation of infiltration equation using systems approach. Journal of Irrigation and Drainage Engineering, ASCE,116(6): 837–857. |
| [13] | Smith. R.( 1972) . The infiltration envelope: results from a theoretical infiltrometer. Journal of Hydrology. 17: 1–21. |
| [14] | Smith, R. Parlange, J.(1978). A parameter-efficient hydrologic infiltration model. Water Resources Research. 14(3): 533–538. |
| [15] | John Jiya Musa and Peter Aderemi Adeoye.(2010). Adaptability of Infiltration Equations to the Soils of the Permanent Site Farm of the Federal University of Technology, Minna, in the Guinea Savannah Zone of Nigeria. AU J.T. 14(2): 147-155. |
| [16] | Abubakar, R. and Motaileb, B. (2012). The Evaluation and Determining of Soil Infiltration Model Coefficient. Australian Jour. of Basic and Applied Sciences. 6(6):94-98. |
| [17] | Haghighi, F., Gorji M., Shorafa M. and Sarmadian F. (2010). Evaluation of some Infiltration Models and Hydraulic parameters. Spanish Journal of Agricultural Research. 8(1):210-216. |
| [18] | Navar and Synnott, (2006). River flow forecasting through conceptual models, part i-a discussion of principles. Journal of Hydrology, 10: 282–290. |
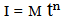
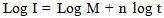




 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML


