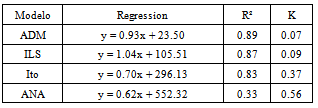-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Environmental Engineering
p-ISSN: 2166-4633 e-ISSN: 2166-465X
2013; 3(4): 147-169
doi:10.5923/j.ajee.20130304.01
Turbulent Wind Profiles and Tracer Dispersion for Eolic Park Site Evaluation
K. B. Mello1, B. E. J. Bodmann2, M. T. Vilhena2
1Departamento de Ensino, Instituto Federal do Rio Grande do Sul – Câmpus Caxias do Sul, Mario de Boni, 2250, 95012-580. Caxias do Sul, RS, Brazil
2P PROMEC & PPGMAp, Universidade Federal do Rio Grande do Sul, Av. Osvaldo Aranha 99/4, 90046-900 Porto Alegre, RS, Brazil
Correspondence to: K. B. Mello, Departamento de Ensino, Instituto Federal do Rio Grande do Sul – Câmpus Caxias do Sul, Mario de Boni, 2250, 95012-580. Caxias do Sul, RS, Brazil.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
In this work we discuss stochastic turbulent wind profiles based on the three-dimensional stochastic Langevin equation for a selection of probability density functions and a known mean wind velocity. Its solution permits to simulate tracer dispersion in turbulent regime, which is of interest in evaluating aeolian park sites for wind energy conversion. We discuss the stochastic Langevin equation together with an analytical method for solving the three-dimensional and time dependent equation which is then applied to tracer dispersion for stochastic turbulence models. The solution is obtained using the Adomian Decomposition Method, which provides a direct scheme for solving the problem without the need for linearisation and any transformation. The results of the model are compared to case studies with measured data and compared to procedures and predictions from other approaches.
Keywords: Turbulent Wind Profiles, Tracer Disperson, Langevin Equation
Cite this paper: K. B. Mello, B. E. J. Bodmann, M. T. Vilhena, Turbulent Wind Profiles and Tracer Dispersion for Eolic Park Site Evaluation, American Journal of Environmental Engineering, Vol. 3 No. 4, 2013, pp. 147-169. doi: 10.5923/j.ajee.20130304.01.
Article Outline
1. Introduction
- In recent years the Climate Change Problem raised the discussion of limiting and reducing greenhouse gas emissions caused from the burning of fossil fuels, by substitution of these limited resources with renewable and clean energy sources. One promising energy supplier among others is, as sometimes announced, “harnessing the wind”. Although, eolic energy generator technology has left its childhood already some time ago, there are still challenges to be faced in order to restrict or remove certain uncertainties related to this type of electric energy production. The incorporation of eolic energy into the total energy demand still suffers from the fact that supply of wind power depends directly on the wind conditions so that the energy to be injected into the electrical network will be strongly governed by the wind variations but not by the energy demand. In fact, this is the reason why wind energy is said to be unreliable, because of its natural fluctuations. In order to mitigate these difficulties it is of interest to study the wind conditions and its inherent variations on a short term (daily) basis, and a seasonal or long term basis, and turn more predictable the availability of eolic power for a specific site. This knowledge could give support to the management of future wind-park clusters through an additional tool that shall help to minimize or even control the aforementioned variations using probabi-lity based energy distribution plans. One of the issues addressed in the present article is related to the choice of the site for a possible installation of a wind park considering meteorological aspects as well as possible scenarios simulations and their related experimental validation. One of the possible evaluations of a site candidate may be performed using tracer experiments in order to analyse the wind conditions in the planetary boundary layer, which is typically the layer where eolic turbines are placed. Since this kind of experiments are performed only in a limited set of positions the entire wind velocity field may be reconstructed only by the use of reliable models. However, these models have to be tuned using specific meteorological parameters and conditions in the considered region and shall be subject to the local orography. Furthermore, case studies by model simulations maybe used to establish limits for the generator density using studies with data from already working wind-parks together with model simulations. To this end, existing eolic farms may be used in order to study the influence of generators on changes in the boundary layer wind profile. Such a time sequence analysis may well be performed using tracer experiments, where from the observations one may reconstruct the full space-time wind field by models. This may help to optimise the arrangement of a wind generator cluster taking into account the turbulent structure of the wind field that may in principle be modelled with and without the presence of wind generators. Recent research[11, 38] pointed out the relevance of the mutual wind turbine interaction as well as the impact of the wind flow perturbation by turbines on the atmospheric boundary layer in wind farms with extensions beyond the length scale defined by the boundary layer height. In their work the authors quantified the vertical transport kinetic energy and momentum across the boundary layer, which was found to be of the same order of magnitude as the power extracted by the forces that modelled the wind turbines. This finding was directly associated to atmospheric boundary layer turbulence, which is the focus of the present article. In references[11, 38] a model for the wind energy generators was used to simulate effects on the boundary layer. The present discussion complements the previous works in the sense that one may reconstruct the wind profile with its turbulent properties for the different stability regimes in the planetary boundary layer using data from observations instead of simulating them and tuning the model as to agree reasonably well with the experimental findings. More specifically, the measured average wind velocity field is used (see reference[27]) together with probability density functions, that depend on the stability regime in consideration, and the turbulent contribution is then determined from the nonlinear stochastic Langevin equation. This procedure may be used for analysing potential wind energy park sites or already existing ones. The choice for a Lagrangian model in comparison to an Eulerian approach resides in the fact that the latter yields average values only, whereas Lagrangian models capture the stochastic characteristics of the turbulent wind field by virtue of the employed probability density functions. The mapping of turbulent wind fields instead of mean fields is essential for opening pathways that help increasing the predictability of the wind profile in all stability regimes along the 24 hour cycle, and especially during stability changes. During changes of stability and in the unstable regime, energy of the mean field is transferred to the turbulent field that affects the gain in energy conversion by wind turbines. In the further we show how the Langevin model is solved analytically using the decomposition method which then may provide short, intermediate and long term (normalized) behaviour and permit to assess the probability of occurrence of higher or lower turbulence levels and additionally serve as a supplement for designing the afore mentioned energy response plans. Note, that natural turbulence is one of the reasons for a decrease of the efficiency of the turbines from its nominal value, and the square ratio of the turbulent velocity to the mean velocity represents a crude measure for that effect. A further aspect worth mentioning is that the average eddy size is roughly of the order of magnitude of the rotor. The stochastic character of turbulence is implemented using the appropriate Gaussian, bi-Gaussian and Gram - Chalier probability distribution for the different stabilities. Exactness of the solution is manifest in stable convergence, which we control by a Lyapunov theory inspired criterion. The most adequate probability distribution for the wind scenario of interest is indicated by a novel statistical validation index, which from comparison to experimental data selects the most significant model. Comparison to the Copenhagen and to other deterministic approaches shows the advantage of the present analytical approach even for considerably rugged land relieves. Our article is organised as follows. In section 2 we report on the state of the art of stochastic wind profile modelling, and show how a closed form solution may be obtained by Adomian’s decomposition method. In 3, we present the numerical results for three probability density functions and in section 4 we come to our conclusions.
2. Stochastic Wind Profile Modelling
- Atmospheric turbulence and tracer dispersion in the planetary boundary layer is a stochastic process and thus obeys a stochastic law which may be expressed as a set of stochastic differential equations. For a time dependent regime considered in the present work, we assume that the associated Langevin equation adequately describes atmospheric turbulence and dispersion processes, which we test by comparison to other methods in order to pin down computational errors and finally analyse for model adequacy. We are aware of the fact that up to date there do exist a variety of models and approaches to the problem, either based on numerical schemes, stochastic simulations or (semi-) analytical approaches and indicate in the further a selection of models. Numerical approaches may be found in the works of Tangerman[45], Brebbia[8], Chock et al.[17], Sharan et al.[41] and Huebner et al.[31]. There are various models that have been used effectively in the past to describe tracer dispersion[48],[42],[6],[5], and many of them make use of analytical approaches[35, 42, 43]. One also finds semi-analytical methods, where we mention the works of Parlange[39], Dike[20], Henry et al.[29], Grisogono and Oerlemans[25], Metha and Yadav[37], Carvalho et al.[13] and Carvalho and Vilhena[12]. Upon developing a model one typically faces various problems. First one has to identify a differential equation that shall represent a model or a physical law. Once the law/model is accepted as the fundamental equation one challenges the task of solving the equation in many cases approximately and analyse the error of approximation and numerical errors in order to validate its prediction against experimental data. Experimental data of a stochastic process typically spread around average values, i.e. are distributed according to probability distributions. Hence, the model shall within certain limits reproduce the experimental findings. Since the fundamental equation is already a simplification deviations may occur which in general have their origin in a model error superimposed by numerical or approximation based errors. In case of a genuine convergence criterion one may pin down the error analysis essentially to a model validation. Since in general convergence is handled by heuristic convergence criteria, a model validation is not that obvious. Thus we show with the present discussion, that our semi-analytical approach does not only yield an acceptable solution to the Langevin equation but predicts tracer concentrations closer to observed values than predictions from other models values with is also manifest in the statistical analysis. Simulation of tracer dispersion in the Planetary Boundary Layer (PBL) through a Lagrangian particle model by the use of the Langevin equation and its diffusion equation limit (random displacement equation) usually has been solved by the method of Ito calculus[24, 40]. More recently one of the authors developed the Iterative Langevin Solution (ILS) method, which solves the Langevin equation in a semi-analytical manner by the method of successive approximations, known as Picard’s iterative method. The method is principally characterised by the following steps: Application of Picard’s procedure on the Langevin equation, to be more specific, integration, linearisation of the stochastic non-linear term and iterative solution of the resultant equation, which permits to evaluate an analytical expression for the velocity. Details of this approach may be found elsewhere[13, 14, 12, 44, 15, 16]. An alternative analytical method for solving linear and non-linear differential equations was developed by Adomian[1], known as the decomposition method. The decomposition procedure permits to cast the solution into a convergent series by using the necessary number of recursions for both linear and non-linear deterministic and stochastic equations. The advantage of this method is that it provides a direct scheme for solving the problem without the need for linearisation or transformations. There exists a vast literature about applications of this method to a broad class of physical problems and we cite the works we considered relevant for the further discussion[1, 2, 3, 22, 34, 32, 19, 21]. Thus the present work extends the list of methods that solve the Langevin equation assuming Gaussian, bi-Gaussian and Gram-Chalier turbulence condition by Adomian’s approach. The variety of methods, such as the numerical solution of the Langevin equation (integrated according to the Ito calculus), analytical solution of the Langevin equation (derivation of Uhlenbeck and Ornstein[47]), Iterative Langevin Solution (ILS) and solution by decomposition (ADM)[26].
2.1. The Decomposition Method for a Stochastic Process
- A time dependent stochastic process µ is typically characterized by its time evolution, which depends on stochastic contributions, such as expectation values (En) of mean field character (E0) and higher moments (here E2), respectively. In our case we consider the Langevin equation to describe turbulence.
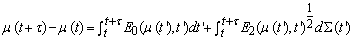 | (1) |
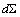 is a stochastic measure for random motion and E0 represents a drift like term, whereas E2 is a measure for diffusion intensity, which satisfy the usual Lipschitz continuity condition in order to ensure the existence of a unique strong solution. In case of a Wiener process µ(t) is Markovian, but in our case we presume that the process is an Ito process, i.e. it depends on the present and previous values, hence the integral form of mean field and fluctuation contributions. Note, that the integral form will be used further down in order to set-up the solution following Adomian’s prescription, which we resume in the following. One may rewrite the stochastic equation from above (1) as a differential equation, upon using the limit τ→ 0 and separating all terms depending on the process µ including the differential operator (LHS of equation(2)) from the noise generating term G(t) (the stochastic contribution, last term in eq. (1)).
is a stochastic measure for random motion and E0 represents a drift like term, whereas E2 is a measure for diffusion intensity, which satisfy the usual Lipschitz continuity condition in order to ensure the existence of a unique strong solution. In case of a Wiener process µ(t) is Markovian, but in our case we presume that the process is an Ito process, i.e. it depends on the present and previous values, hence the integral form of mean field and fluctuation contributions. Note, that the integral form will be used further down in order to set-up the solution following Adomian’s prescription, which we resume in the following. One may rewrite the stochastic equation from above (1) as a differential equation, upon using the limit τ→ 0 and separating all terms depending on the process µ including the differential operator (LHS of equation(2)) from the noise generating term G(t) (the stochastic contribution, last term in eq. (1)). 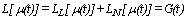 | (2) |
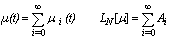 | (3) |
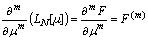 | (4) |
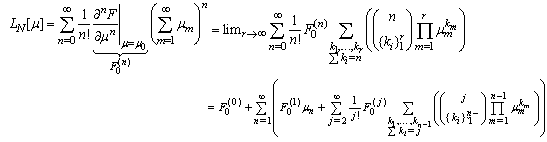 | (5) |
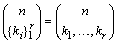 . Introducing these terms into the original differential equation permits to identify corresponding terms, that give rise to the iterative scheme in the spirit of Adomian as shown next.
. Introducing these terms into the original differential equation permits to identify corresponding terms, that give rise to the iterative scheme in the spirit of Adomian as shown next. 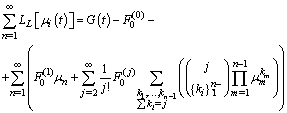 | (6) |
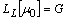
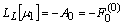
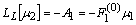
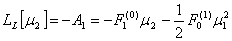 | (7) |
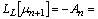
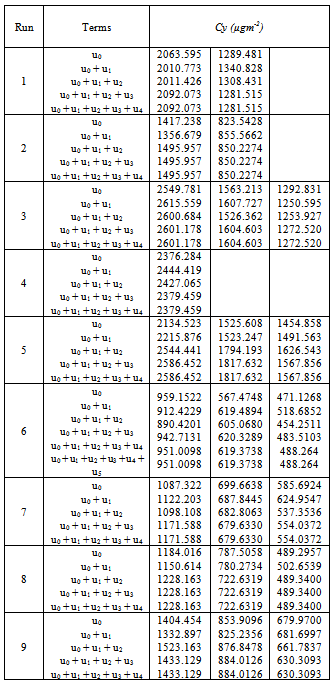
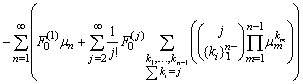 The way we have setup the iterative scheme defines the seed µ0(t) by the stochastic contribution as source term, whereas the remaining iterators are simply given by the Adomian functional polynomials as source terms of the equations to be solved. Note that in order to evaluate the i-th recursion step µi the µj with j < i are known from the previous iteration steps. Moreover, the functional expansion of the non-linear term around the function µ0 shows how the stochastic term effectively enters in the remaining terms µi with i > 0 from the non-linearity.
The way we have setup the iterative scheme defines the seed µ0(t) by the stochastic contribution as source term, whereas the remaining iterators are simply given by the Adomian functional polynomials as source terms of the equations to be solved. Note that in order to evaluate the i-th recursion step µi the µj with j < i are known from the previous iteration steps. Moreover, the functional expansion of the non-linear term around the function µ0 shows how the stochastic term effectively enters in the remaining terms µi with i > 0 from the non-linearity.2.2. A Convergent Closed Form Solution
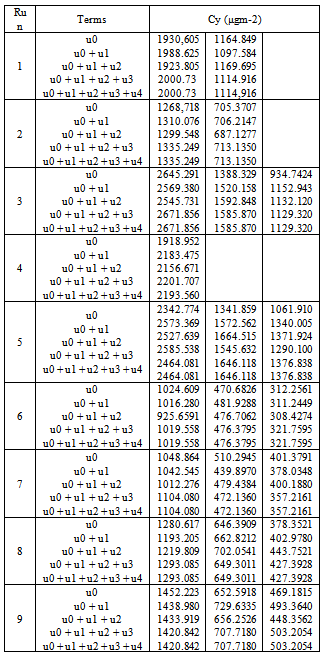
- The iteration defines a convergent series towards µ for all t in a certain domain, thus the solution
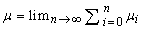 is manifest exact. Since this scheme defines an explicit analytical expressions for the µi and Ai, respectively, one arrives at a procedure which permits to solve the differential equation without linearisation in closed form. The procedure has been applied to a variety of nonlinear problems but an analytical procedure for testing convergence to the best of our knowledge has not been presented in literature, only numerical schemes may be found, see for instance refs.[32] and[4]. In general convergence is not guaranteed by the decomposition method, so that the solution shall be tested by a convenient criterion. Since standard convergence criteria do not apply for the present case due to the non-linearity and stochastic character, we present a method which is based on the reasoning of Lyapunov[9]. While Lyapunov introduced this conception in order to test the influence of variations of the initial condition on the solution, we use a similar procedure to test the stability of convergence while starting from an approximate (initial) solution µ0 (the seed of the iteration scheme). Let us denote
is manifest exact. Since this scheme defines an explicit analytical expressions for the µi and Ai, respectively, one arrives at a procedure which permits to solve the differential equation without linearisation in closed form. The procedure has been applied to a variety of nonlinear problems but an analytical procedure for testing convergence to the best of our knowledge has not been presented in literature, only numerical schemes may be found, see for instance refs.[32] and[4]. In general convergence is not guaranteed by the decomposition method, so that the solution shall be tested by a convenient criterion. Since standard convergence criteria do not apply for the present case due to the non-linearity and stochastic character, we present a method which is based on the reasoning of Lyapunov[9]. While Lyapunov introduced this conception in order to test the influence of variations of the initial condition on the solution, we use a similar procedure to test the stability of convergence while starting from an approximate (initial) solution µ0 (the seed of the iteration scheme). Let us denote 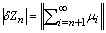 the maximum deviation of the correct from the approximate solution
the maximum deviation of the correct from the approximate solution 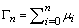 , where || ∙|| signifies the maximum norm. Then convergence occurs if there exists an n0 such that the sign of λ is negative for all n ≥ n0.
, where || ∙|| signifies the maximum norm. Then convergence occurs if there exists an n0 such that the sign of λ is negative for all n ≥ n0.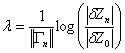 | (8) |
3. The Langevin Equation for Stochastic Turbulence
- The stochastic equation (1) may be interpreted in terms of the Langevin equation, where µ represents the turbulent velocity vector with components ui. In the Langevin equation[40] the time evolution of the turbulent velocity is driven by a dissipative term and a second term which may be understood as the gradient of a potential that depends on the fluctuations of the turbulent velocity and represents a mean field interaction of the tracer with the environment it is immersed. The last term represents the stochastic contribution due to a continuous series of particle collisions. All paragraphs must be indented.
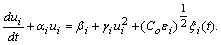 | (9) |
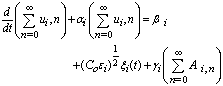 | (10) |
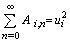 .
.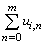 .So far we have not defined the probability density function, that characterizes the type of turbulence which is correlated to the stability of the planetary boundary layer (PBL). In the studies of turbulent dispersion the stochastic behaviour maybe classified according to stationarity or non-stationarity, according to spatial properties as homogeneity or non-homogeneity and according to the profile of the wind distribution, as Gaussian or non-Gaussian. When employing Lagrangian models one usually considers stationary and homogeneous turbulence in horizontal sheets and non-homogeneous and either Gaussian or non-Gaussian in the vertical direction depending on the stability condition. In stable or neutral conditions the velocity distribution may be considered Gaussian, whereas during convective conditions the velocity distribution is non-Gaussian because of the skewness of the turbulent velocity distribution, which has its origin in up-and down-drafts with different intensity. In the following we present the solutions for the three afore mentioned probability density functions together with their model validation against the data from the Copenhagen experiment[26].
.So far we have not defined the probability density function, that characterizes the type of turbulence which is correlated to the stability of the planetary boundary layer (PBL). In the studies of turbulent dispersion the stochastic behaviour maybe classified according to stationarity or non-stationarity, according to spatial properties as homogeneity or non-homogeneity and according to the profile of the wind distribution, as Gaussian or non-Gaussian. When employing Lagrangian models one usually considers stationary and homogeneous turbulence in horizontal sheets and non-homogeneous and either Gaussian or non-Gaussian in the vertical direction depending on the stability condition. In stable or neutral conditions the velocity distribution may be considered Gaussian, whereas during convective conditions the velocity distribution is non-Gaussian because of the skewness of the turbulent velocity distribution, which has its origin in up-and down-drafts with different intensity. In the following we present the solutions for the three afore mentioned probability density functions together with their model validation against the data from the Copenhagen experiment[26].3.1. The Copenhagen Experiment
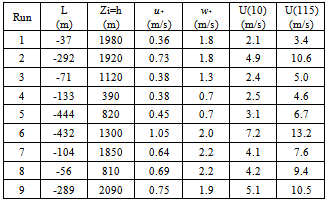
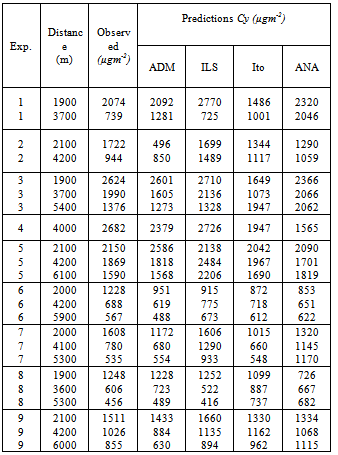
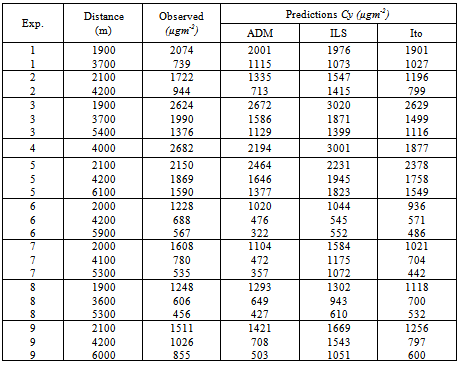
- The Copenhagen tracer experiment[26] was carried out in the northern part of Copenhagen. A tracer (SF6) was released without buoyancy from a tower at a height of 115m and collected at the ground-level positions in up to three crosswind arcs of tracer sampling units. The sampling units were positioned 2km-6km from the point of release. A total of nine tracer experiment runs were performed with instability conditions as shown in table 1. The site was mainly residential with a roughness length of 0.6m. Wind speeds at 10 and 115 meters were used to calculate the coefficient for the vertical exponential wind profile, which is used to model the wind speed.
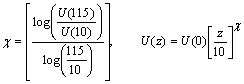 | (11) |
3.2. Solution for Gaussian Turbulence
- In the case where a Gaussian probability density function describes best the stochastic turbulence the coefficients of the Langevin equation (9) and (10) are
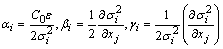 | (12) |
|
|
 | Figure 1. Lyapunov exponent λ of Adomian approach depending on the number n of terms for the 9 experiment runs |
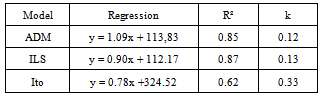
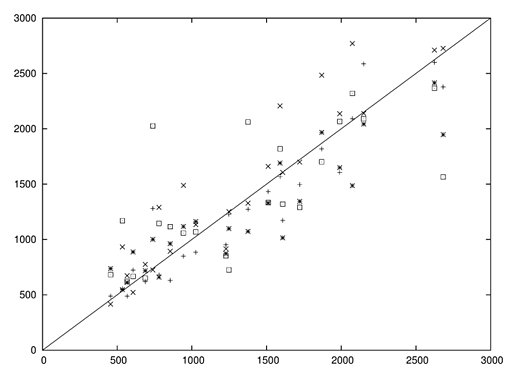 | Figure 2. Dispersion diagram of predicted (Cp) measured against measured (Co) values by by ADM (+), ILS (×) , Ito (*) e ANA (□) |
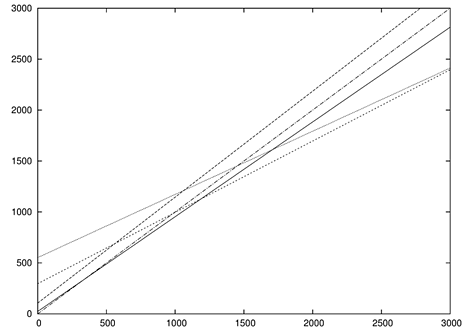 | Figure 3. Linear regression for the ADM (------), ILS (− − −). Ito (- - -) and ANA (….) with Gaussian pdf. The bisector ( -. -.-.) was added as an eye guide |
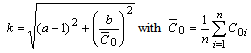 | (13) |
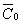 the arithmetic mean. Since both the experiment and the model are of stochastic character, fluctuations are present, but in the average model and experiment shall coincide, thus the introduced index represents a genuine model validation.
the arithmetic mean. Since both the experiment and the model are of stochastic character, fluctuations are present, but in the average model and experiment shall coincide, thus the introduced index represents a genuine model validation.3.3. Solution for bi-Gaussian Turbulence
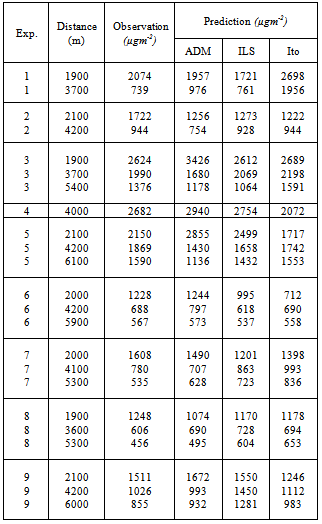
- In the convective boundary layer, the heating of the air layer close to the ground produces turbulent flux which gives origin to the so-called up- and down-drafts. This phenomenon is not symmetric but has a more intensive contribution from the up-drafts. Because of mass conservation the down-drafts occupy a larger area. As a consequence the stochastic term shall be asymmetric which excludes the Gaussian probability density as a convenient function. There is no indication for a unique probability density function so far, nevertheless the following characteristics shall be present. • The probability density shall have an enhanced tail towards higher velocities, that indicate the more energetic up-drafts, but with a smaller integral proportion than down-drafts. • The probability density shall have a pronounced maximum at negative velocities, i.e. the down-drafts. One finds typically two types of asymmetric probability density functions in the literature, the bi-Gaussian and the Gram-Chalier distribution, where the latter is represented by a truncated series of Hermite polynomials. In the further we discuss the bi-Gaussian probability density function, which contains a linear superposition of two Gaussian functions, one with maximum probability at a positive velocity, the other one at a negative value as for instance in ref.[7].The authors used a pair of Langevin equations, one for up- and one for down-drafts, each with its specific Gaussian function. In this work we condense this phenomenon in one equation, introducing a sum of two Gaussian functions with different parameters and relative weight.
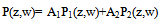 | (14) |
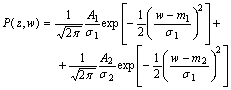 | (15) |
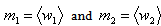 | (16) |
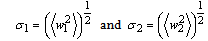 | (17) |
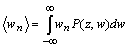 | (18) |
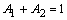 | (19) |
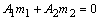 | (20) |
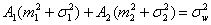 | (21) |
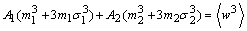 | (22) |
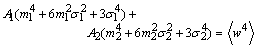 | (23) |
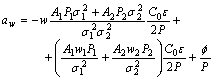 | (24) |
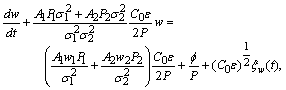 | (25) |
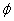 is obtained upon application of the bi-Gaussian probability density function[36]:
is obtained upon application of the bi-Gaussian probability density function[36]: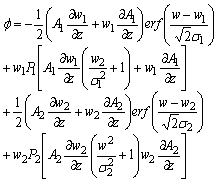 | (26) |
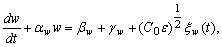 | (27) |
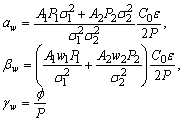 | (28) |
|
|
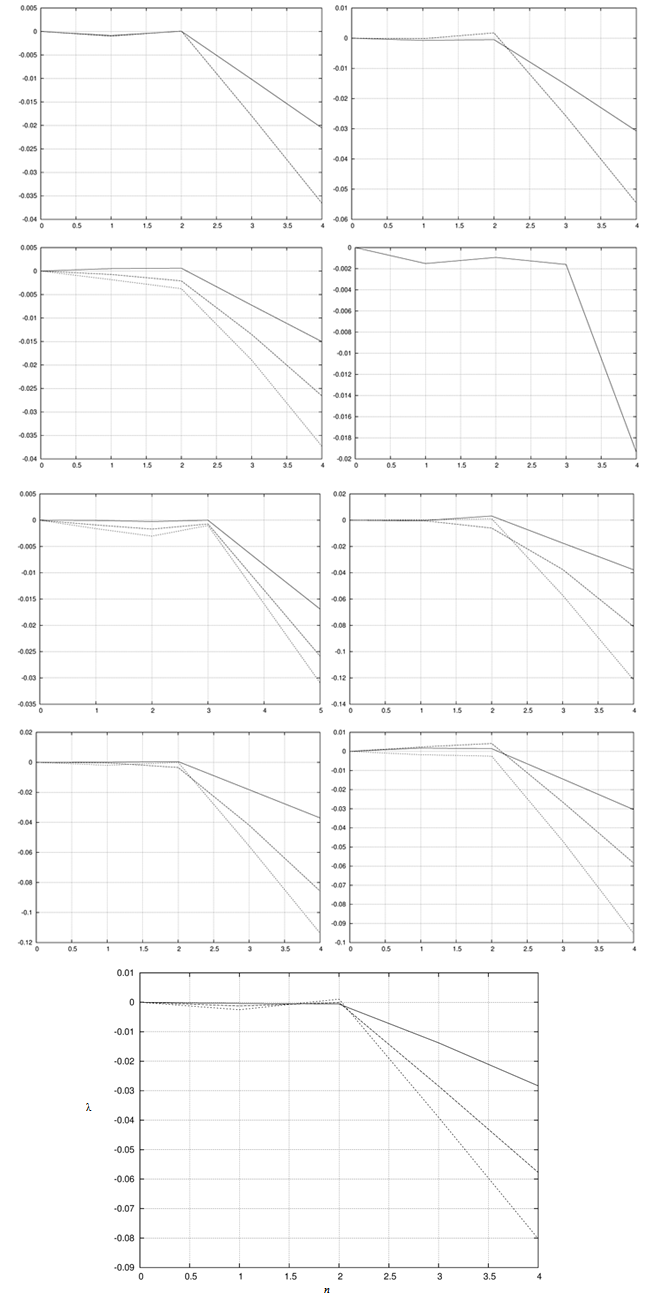 | Figure 4. Lyapunov exponent λ of the Adomian approach depending on the number n of terms for the 9 experimental runs using the bi-Gaussian pdf. |
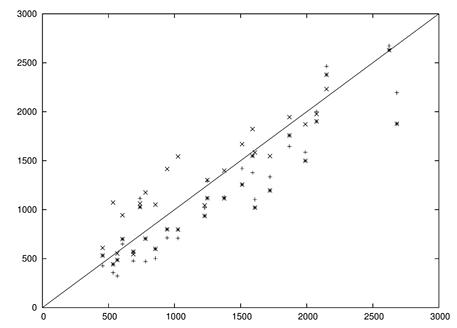 | Figure 5. Dispersion diagram of predicted (Cp) measured against measured (Co) values by by ADM (+), ILS (×) and Ito (*) for a bi-Gaussian pdf |
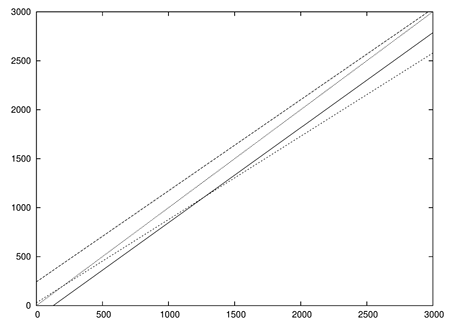 | Figure 6. Linear regression for the ADM (——), ILS (– – –) and Ito (- - - -) with a Bi-Gaussian pdf. The bisector (– · – ·) was added as an eye guide |
|
|
3.4. Solution for Gram-Chalier Turbulence
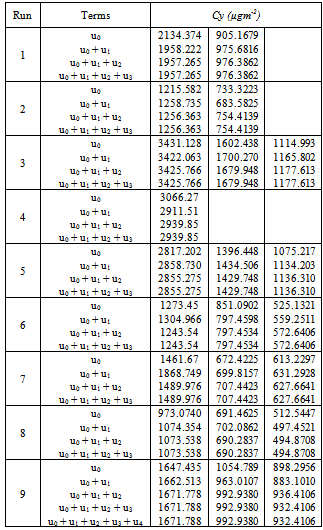
- The use of the Gram-Chalier probability density function for stochastic Lagrangian models was proposed by Ferrero and Anfossi (1998)[23] (see also the work by Jensen et al. (1997)[33]), which makes use of an expansion in Hermite polynomials. In the present discussion we use the series until the fourth term resulting in an asymmetric probability density function for the vertical turbulent velocities.
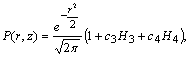 | (29) |
|
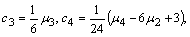 | (30) |
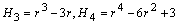 | (31) |
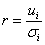 . In the case of Gaussian turbulence equation (29) recovers the normal distribution with c3 and c4 equal zero. The Gram-Charlier probability density function of the third order is obtained by the choice c4 = 0. Upon application of equation (29) in the equation of the deterministic coefficients yields,
. In the case of Gaussian turbulence equation (29) recovers the normal distribution with c3 and c4 equal zero. The Gram-Charlier probability density function of the third order is obtained by the choice c4 = 0. Upon application of equation (29) in the equation of the deterministic coefficients yields,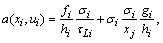 | (32) |
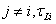 is the Lagrangian correlation time scale and
is the Lagrangian correlation time scale and 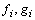 and
and 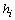 are expressions as shown below.
are expressions as shown below.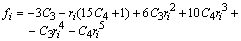 | (33) |
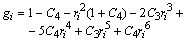 | (34) |
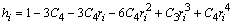 | (35) |
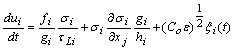 | (36) |
|
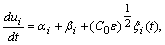 | (37) |
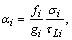 | (38) |
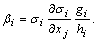 | (39) |
|
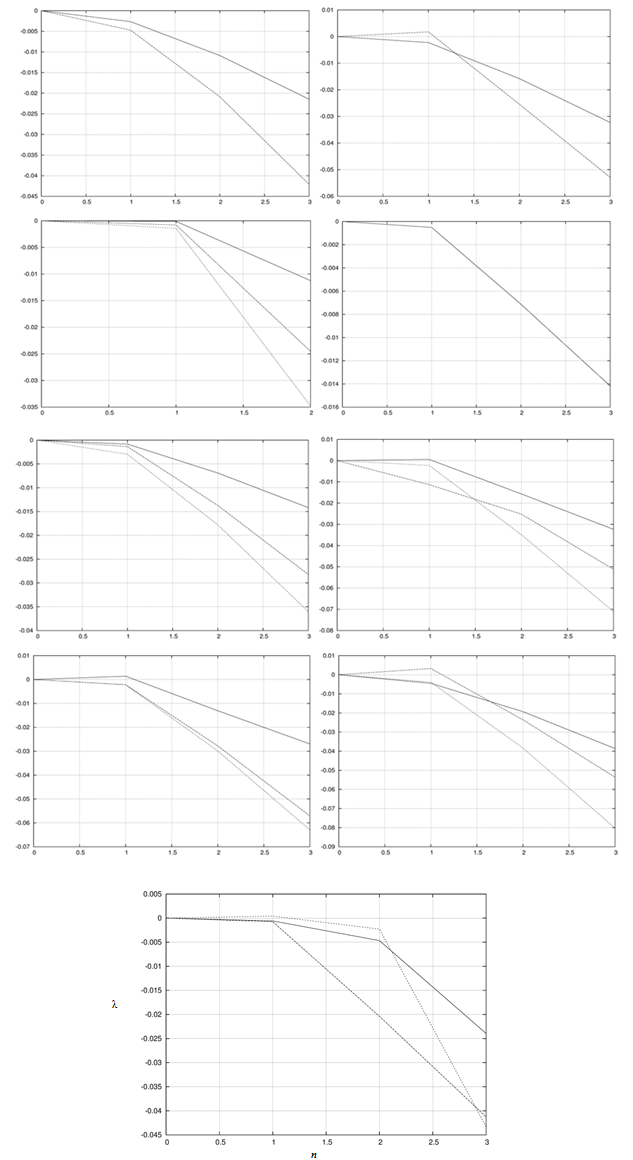 | Figure 7. Lyapunov exponent λ of the Adomian approach depending on the number of terms n for the 9 experimental runs using the Gram-Chalier pdf |
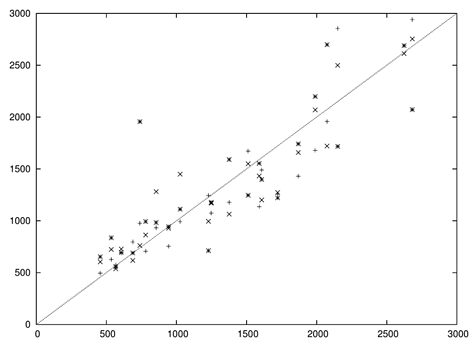 | Figure 8. Dispersion diagram of predicted (Cp) against observed values (Co) with a Gram-Chalier probability density function |
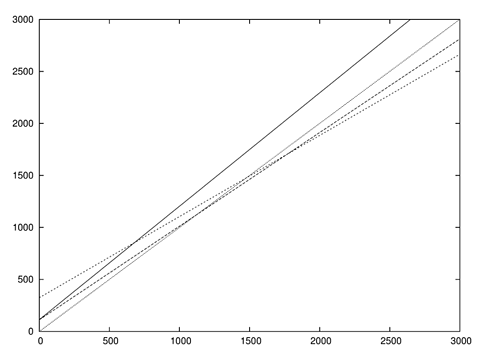 | Figure 9. Linear regression using the Gram-Chalier probability density function |
4. Conclusions
- In the present contribution we discussed an approach that is designed to simulate meteorological aspects, that are relevant in eolic park site evaluation. We showed how a realiable model for a turbulent wind profile may be determined among model candidates, that provides the full three dimensional space and time dependent turbulent wind field for an area in consideration.We showed in a general form how to construct a recursive scheme where convergence is understood. A genuine criterion was introduced based on Lyapunov’s theory, that in our case tests stability of convergence. Application of that criterion showed that in all three cases only five terms are necessary so that the approximate solution differs from the real solution by less than one percent.On the one hand, the generality of the proposed solution with respect to the considered probability density functions on the other hand the controlled convergence permits to validate the model in question. The resulting model is thus likely to simulate turbulent wind profiles close to those that could be observed in a site in question.The Gaussian density function yields within the phenomenon inherent fluctuations the best agreement between model and observation. Among the three probability distributions the Gaussian one is from the physics point of view considered the most adequate for the Copenhagen experiment. Thus the criterion to select a model among possible candidates identified the most adequate one.We believe that we have done a step into a new direction with the present contribution, that may be useful to analyse meteorological aspects as well as simulate possible scenarios, for the purpose of site evaluation, using tracer experiments. Since measurements are typically performed in a limited set of positions a calibrated model is able to reconstruct the three dimensional wind velocity field considering especially the contributions by turbulence. To the best of our knowledge up-to-date the tracer technique is not used for site evaluation, but could supply valuable information on the wind properties for a given region of interest and its time-behaviour.In this paper we presented an analytical solution of the three-dimensional stochastic Langevin equatioqn applied to tracer dispersion for Gaussian, bi-Gaussian and Gram-Chalier turbulence, respectively. The solution was obtained using the Adomian Decomposition Method (ADM) whose principal advantage relies in the fact that the non-linearity can be taken care of without linearisation or simplifications. Further, the stochastic part is absorbed in the initial term of the iteration and thus propagates through all the subsequent iteration terms. For the Langevin equation the non-trivial questions of uniqueness and convergence for the Adomian approach in stochastic problems is given since the drift and dispersion terms satisfy a Lipschitz condition.
References
| [1] | Adomian, G. “A Review of the Decomposition Method in Applied Mathematics”, J. Math. Anal. Appl., vol. 135, pp. 501-544, 1988. |
| [2] | Adomian, G. Solving Frontier Problems of Physics: The Decomposition Method, Kluwer, USA, 1994. |
| [3] | Adomian, G. “Solution of coupled non-linear partial differential equations by decomposition”, Comp. Math. Appl., vol. 31, pp. 117-120, 1996. |
| [4] | Aminataei, A., Hosseini, S.S. Applied Mathematics and Computation , vol. 1, pp. 665-669, 2007. |
| [5] | Arya, S.P. Air Pollution Meteorology and Dispersion, Oxford University Press, USA, 1999. |
| [6] | Arya, S.P. “A review of the theoretical bases of short-range atmospheric dispersion and air quality models”, , Proc. Indian Natn. Sci. Acad., vol. 69A, pp. 709-724, 2003. |
| [7] | Baerentsen, J.H., Berkowicz, R. “Monte-Carlo Simulation of Plume Diffusion in the Convective Boundary Layer”, Atmos. Environ, vol. 18, pp. 701-712, 1984. |
| [8] | Brebbia, C.A. Progress in Boundary Element Methods, Pentech Press, London, 1981. |
| [9] | Boichenko, V.A., Leonov, G.A., Reitmann, V. Dimension theory for ordinary equations, Teubner, Stuttgart, 2005. |
| [10] | Burden, R.L. Numerical analysis. 8th ed., Thomson-Brooks/Cole, Belmont, CA, 2005. |
| [11] | Calaf, M., Meneveau, C., Meyers, J. "Large eddy simulation study of fully developed wind-turbine array boundary layers”, Phys. Fluids, vol. 22, pp. 015-110, 2010. |
| [12] | Carvalho, J.C., Vilhena, M.T. “Pollutant dispersion simulation for low wind speed condition by the ILS method”, Atmos. Environm., vol. 39, pp. 6282-6288, 2005. |
| [13] | Carvalho, J.C., Nichimura, E.R. Vilhena, M.T., Moreira, D.M., Degrazia, G.A. “An iterative langevin solution for contaminant dispersion simulation using the Gram-Charlier PDF”, Environm. Mod. And Soft., vol. 20, pp. 285-289, 2005. |
| [14] | Carvalho, J.C., Vilhena, M.T., Moreira, D.M. “An alternative numerical approach to solve the Langevin equation applied to air pollution dispersion”, Water Air and Soil Pollution, vol. 163, pp. 103-118, 2005. |
| [15] | Carvalho, J.C., Vilhena, M.T., Thomson, M. “An iterative Langevin solution for turbulent dispersion in the atmosphere”, J. Comp. Appl. Math., vol. 206, pp. 534-548, 2007. |
| [16] | Carvalho, J.C., Vilhena, M.T., Moreira, D.M. “Comparison between Eulerian and Lagrangian semi-analytical models to simulate the pollutant dispersion in the PBL”. Appl. Math. Model., vol. 31, pp. 120-129, 2007. |
| [17] | Chock, D.P., Sun, P.,Winkler, S.L. “Trajectory-grid: an accurate sign preserving advection-diffusion approach for air quality modeling”, Atmos. Environ., vol. 30, no. 6, pp. 857-868, 1996. |
| [18] | Degrazia, G.A., Anfossi, D., Carvalho, J.C., Mangia, C., Tirabassi, T., Campos Velho, H.F. “Turbulence parameterization for PBL dispersion models in all stability conditions”, Atmos. Environ., vol. 34, pp. 3575-3583, 2000. |
| [19] | Dehghan, M. “The use of Adomian decomposition method for solving the one dimensional parabolic equation with non-local boundary specification”, Int. J. Comput. Math., vol. 81, pp. 25-34, 2004. |
| [20] | Dike, M.V. Perturbation Methods in Fluid Mechanics, Academic Press, USA, 1975. |
| [21] | El-Wakil, S.A., Elhanbaly, A., Abdou, M.A. “Adomian decomposition method for solving fractional non-linear differential equations”, Appl. Math. Comput., vol.182, no.1, pp. 313-324, 2006. |
| [22] | Eugene, Y. “Application of the decomposition to the solution of the reaction-convection-diffusion equation”, Appl. Math. Comput. vol. 56, pp. 1-27, 1993. |
| [23] | Ferrero, E., Anfossi, D., Tinarelli, G., Tamiazzo, M.. “Inter-comparison of Lagrangian stochastic models based on two different PDFs”, International Journal of Environment and Pollution, vol.14, pp. 225-234, 2000 |
| [24] | Gardiner, C.W. Handbook of stochastic methods for physics, chemistry and the natural sciences, Springer-Verlag, Germany, 1985. |
| [25] | Grisogono, B., Oerlemans, J. “Katabatic flow: analytic solution for gradually varying eddy diffusivities”, J. Atmos. Sci., vol. 58, pp. 3349-3354, 2001. |
| [26] | Gryning, S.E., Lyck, E. “Atmospheric dispersion from elevated source in un urban area: comparison between tracer experiments and model calculations”, J. Climate Appl. Meteor., vol. 23, pp. 651-654, 1984. |
| [27] | Gryning, S.-E., Batchvarova, E., Br¨ummer, B., Jørgensen, H., Larsen, S. “On the extension of the wind profile over homogeneous terrain beyond the surface boundary layer”. Boundary-Layer Meteorol., vol. 124, pp. 251-268, 2007. |
| [28] | Hanna, S.R. “Confidence limit for air quality models as estimated by bootstrap and jackknife re-sampling methods”, Atmos. Environm. vol. 23, pp. 1385- 1395, 1989. |
| [29] | Henry, R.C., Wand, Y.J., Gebhart, K.A. “The relationship between empirical orthogonal functions and sources of air pollution”, Atmos. Environ., vol.25A, pp. 503-509, 1991. |
| [30] | Hinze, J.O. Turbulence. Mc Graw Hill, vol. 1, CRC Press, Inc., USA, 1986. |
| [31] | Huebner, K.H.H., Dewhirst, D.L., Smith, D.E., Byrom, T.G. Finite Element Method for Engineers, J. Wiley & Sons, USA, 2001. |
| [32] | Inc, M. “On numerical solutions of partial differential equations by the decomposition method”, Kragujevac J. Math. vol. 26, pp. 153-164, 2004. |
| [33] | Jensen, A.K.V, Gryning, S.E. “A new formulation of the probability density function in a random walk model for atmospheric dispersion”. Air Pollution Modelling and its Application XII, Plenum Press, USA, pp. 429-438, 1997. |
| [34] | Laffer, P., Abbaoui, K. “Modelling of the thermic exchanges during a drilling. resolution with Adomian’s decomposition method”, Math. and Comp. Model. vol. 23, no. 10, pp. 11-14, 1996. |
| [35] | Lin, J.S., Hildemann, L.M. “Analytical solutions of the atmospheric diffusion equation with multiple sources and height-dependent wind speed and eddy diffusivities”, Atmos. Environ. vol. 30, pp. 239-254, 1997. |
| [36] | Luhar, A.K., Hibberd, M.F., Hurley, P.J. "Comparison of Closure Schemes Used to Specify the Lagrangian Stochastic Dispersion Models for Convective Conditions”, Atmos. Environ. vol. 30, pp. 1407-1418, 1996. |
| [37] | Metha, K.N., Yadav, A.K. Indian J. Pure and Appl. Math., vol. 34, pp. 963-974, 2003. |
| [38] | Meyers, J., Meneveau, C. “Optimal turbine spacing in fully developed wind farm boundary layers”, Wind Energy (online: 14 APR 2011), DOI: 10.1002/we.469, 2011. |
| [39] | Parlange, J.Y. “Theory of water movement in soils: I. One-dimensional absorption”, Soil Sci., vol. 111, no. 2, pp. 134-137, 1971. |
| [40] | Rodean, H.C. Stochastic Lagrangian models of turbulent diffusion, American Meteorological Society, USA, 1996. |
| [41] | Sharan, M., Kansa, E.J., Gupta, S. “Application of the multi-quadric method for numerical solution of elliptic partial differential equations”, Applied Mathematics and Computation, vol. 84, pp. 275-302, 1997. |
| [42] | Seinfeld, J.H., Pandis, S.N. Atmospheric Chemistry and Physics, J. Wiley & Sons, USA. |
| [43] | Sharan, M., Manish, M., Yadav, K. “Atmospheric dispersion: an overview of mathematical modelling framework”, Proc. Indian Nat. Sci. Acad. vol. 69A, no. 6, pp. 725-744, 2003. |
| [44] | Szinvelski, C.R.P., Vilhena, M.T.M.B., Carvalho, J.C., Degrazia, G.A. “Semi-analytical solution of the asymptotic langevin equation by the Picard iterative method”, Environm. Mod. And Soft. vol. 21, no. 3, pp. 406-410, 2006. |
| [45] | Tangerman, G. “Numerical simulations of air pollutant dispersion in a stratified planetary boundary layer”, Atmos. Environ. vol. 12, pp. 1365-1369, 1978. |
| [46] | Tennekes, H. Similarity relation, scaling laws and spectral dynamics, in: F.T.M. Nieuwstadt and H. Van Dop (Eds.), Atmospheric Turbulence and Air Pollution Modelling, Reidel, Dordrecht, pp. 37-68, 1982. |
| [47] | Uhlenbeck, G.E., Ornstein, L.S. “On the theory of the Brownian motion”, Phys. Rev., vol. 36, pp. 823-841, 1930. |
| [48] | Zannetti, P. Air Pollution Modelling, Southampton, Comp. Mech. Publications, UK, 1990. |
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML