-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Environmental Engineering
p-ISSN: 2166-4633 e-ISSN: 2166-465X
2013; 3(1): 56-62
doi:10.5923/j.ajee.20130301.08
Entropic Approach for Emission Rate Estimation of Area Pollutant Sources
Débora R. Roberti 1, Domenico Anfossi 2, Haroldo F. de Campos Velho 3, Gervásio A. Degrazia 1
1Department of Physics, Federal University of Santa Maria (UFSM), Santa Maria, 97105-900, Brazil
2Institute of Atmospheric Sciences and Climate (ISAC), Italian National Research Council (CNR), Turim, 10133, Italy
3Laboratory for Computing and Applied Mathematics (LAC), National Institute for Space Research (INPE), 12227-010, São José dos Campos, Brazil
Correspondence to: Débora R. Roberti , Department of Physics, Federal University of Santa Maria (UFSM), Santa Maria, 97105-900, Brazil.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The estimation of the area source pollutant strength is a relevant issue for atmospheric environment. This characterizes an inverse problem in the atmospheric pollution dispersion. In the inverse analysis, an area source domain is considered, where the strength of such area source term is assumed unknown. The inverse problem is formulated as a non-linear optimization approach, whose objective function is given by the square difference between the measured pollutant concentration and the mathematical models, associated with a regularization operator. The forward problem is addressed by a source-receptor scheme, where a regressive Lagrangian model is applied to compute the transition matrix. A quasi-Newton method is employed for minimizing the objective function. The second order maximum entropy regularization is used, and the regularization parameter is calculated by the L-curve technique. This inverse problem methodology is tested with synthetic observational data, producing good inverse solutions.
Keywords: Atmospheric Pollutant, Source Estimation, Regularized Inverse Solution, Entropic Regularization
Cite this paper: Débora R. Roberti , Domenico Anfossi , Haroldo F. de Campos Velho , Gervásio A. Degrazia , Entropic Approach for Emission Rate Estimation of Area Pollutant Sources, American Journal of Environmental Engineering, Vol. 3 No. 1, 2013, pp. 56-62. doi: 10.5923/j.ajee.20130301.08.
Article Outline
1. Introduction
- A general mathematical theory for dealing with inverse problems is due to the Russian mathematician Andrei Nikolaevich Tikhonov at 1963, introducing the regularization method as a general procedure to solve such mathematical problems. The regularization method looks for the smoothest (regular) inverse solution, where the data model would have the best fitting related to the observation data, subject to constrains. The searching for the smoothest solution is an additional information (or “a priori” information), which reads the ill-posed inverse problem a well-posed one[1]. In the mathematical implementation of the method, the inverse problem is formulated as an optimization problem with constrains (a priori information). These constrains can be added to the objective function with the help of a regularization parameter:
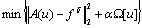 | (1) |
 the observation with δ noise level, Ω(.) the regularization operator, and α the regularization parameter.This paper is focused on the application of inverse prolem methodology for solving a problem with strong interest in meteorology and environmental science: estimation of the emission rate from the area pollutant sources. The identification of the pollution source is calculated here obtaining a regularized inverse solution.The problem for identifying the minority gas emission rate for the system ground-atmosphere is an important issue for the bio-geochemical cycle, and it has being intensively investigated. This inverse problem has been solved using regularized solutions[2], Bayes estimation[3, 4], and variational methods[5] – the latter approach coming from the data assimilation studies.In principle, we have no information about how the area pollution source emission rate is spatially distributed. Seibert[6] and other researchers have suggested a domain decomposition, where each sub-domain has different pollutant emission strength. The direct problem can be expressed as forward-time evolution problem, or even as in a backward-time pollutant diffusion problem. The choice between these approaches (forward-time or backward-time) is given by the proposed scheme that has lower computational effort. The decision is based on the number of sources and number of the measurement points. If the number of receptors is less than the number of sources, the backward-time approach should be adopted; otherwise (if the number of receptors is greater than number of sources) the forward-time approach is suggested.In this study, the direct mathematical model is described by a Lagrangian particle stochastic code. However, here the direct model is represented by the source-receptor scheme. In such approach, the measured concentration in a given receptor is calculated from the contribution of all sources by means of a transition matrix. The entries of the transition matrix are determined employing the Lagrangian code. Therefore, the direct model is represented by a matrix-vector product, instead of use the very expensive Monte Carlo Lagragian scheme for each iteration of the optimization process. This procedure reduces the computational effort (complexity) of the inverse analysis.The inverse problem is formulated as a constrained nonlinear optimization problem and solved by a quasi-Newtonian optimization algorithm. The objective function is the norm L2 (see equation (1)) of the differences between the measured concentration and the concentration computed from the mathematical model (Lagrangian code), associated to the regularization operator. The regularization operator for the objective function (1) is the entropy measure of the vector of second-differences of the unknown parameters. This constrains the class of solution candidates into a restricted set of values composed by global smooth sub-domains, similar to the second-order polynomial surface. This regularization approach has been successfully adopted to retrieve the vertical atmospheric profile from satellite data[7], and to identify the turbulent eddy diffusivity[8].The use of maximum entropy principle to reconstructing sources of inert atmospheric tracers from measurements have been independently introduced by[9] – see also[10] and[11] – an application of the Bocquet’s scheme for reconstruction of the Chernobyl accident source term is described by Davoine and Bocquet[12], for both papers the forward model is given by an Eulerian approach.In a previous study on higher entropy regularization, it was shown that Morosov’s discrepancy principle was really efficient for the problem of determining the regularization parameter[13]. Here, another method to select the regularization parameter is explored.The next section is a brief presentation of the formulation of the direct problem. This is followed by a description of the proposed inversion method, and a discussion of the numerical examples. The method is tested over a two-dimensional domain, using synthetic data corrupted with Gaussian white noise.
the observation with δ noise level, Ω(.) the regularization operator, and α the regularization parameter.This paper is focused on the application of inverse prolem methodology for solving a problem with strong interest in meteorology and environmental science: estimation of the emission rate from the area pollutant sources. The identification of the pollution source is calculated here obtaining a regularized inverse solution.The problem for identifying the minority gas emission rate for the system ground-atmosphere is an important issue for the bio-geochemical cycle, and it has being intensively investigated. This inverse problem has been solved using regularized solutions[2], Bayes estimation[3, 4], and variational methods[5] – the latter approach coming from the data assimilation studies.In principle, we have no information about how the area pollution source emission rate is spatially distributed. Seibert[6] and other researchers have suggested a domain decomposition, where each sub-domain has different pollutant emission strength. The direct problem can be expressed as forward-time evolution problem, or even as in a backward-time pollutant diffusion problem. The choice between these approaches (forward-time or backward-time) is given by the proposed scheme that has lower computational effort. The decision is based on the number of sources and number of the measurement points. If the number of receptors is less than the number of sources, the backward-time approach should be adopted; otherwise (if the number of receptors is greater than number of sources) the forward-time approach is suggested.In this study, the direct mathematical model is described by a Lagrangian particle stochastic code. However, here the direct model is represented by the source-receptor scheme. In such approach, the measured concentration in a given receptor is calculated from the contribution of all sources by means of a transition matrix. The entries of the transition matrix are determined employing the Lagrangian code. Therefore, the direct model is represented by a matrix-vector product, instead of use the very expensive Monte Carlo Lagragian scheme for each iteration of the optimization process. This procedure reduces the computational effort (complexity) of the inverse analysis.The inverse problem is formulated as a constrained nonlinear optimization problem and solved by a quasi-Newtonian optimization algorithm. The objective function is the norm L2 (see equation (1)) of the differences between the measured concentration and the concentration computed from the mathematical model (Lagrangian code), associated to the regularization operator. The regularization operator for the objective function (1) is the entropy measure of the vector of second-differences of the unknown parameters. This constrains the class of solution candidates into a restricted set of values composed by global smooth sub-domains, similar to the second-order polynomial surface. This regularization approach has been successfully adopted to retrieve the vertical atmospheric profile from satellite data[7], and to identify the turbulent eddy diffusivity[8].The use of maximum entropy principle to reconstructing sources of inert atmospheric tracers from measurements have been independently introduced by[9] – see also[10] and[11] – an application of the Bocquet’s scheme for reconstruction of the Chernobyl accident source term is described by Davoine and Bocquet[12], for both papers the forward model is given by an Eulerian approach.In a previous study on higher entropy regularization, it was shown that Morosov’s discrepancy principle was really efficient for the problem of determining the regularization parameter[13]. Here, another method to select the regularization parameter is explored.The next section is a brief presentation of the formulation of the direct problem. This is followed by a description of the proposed inversion method, and a discussion of the numerical examples. The method is tested over a two-dimensional domain, using synthetic data corrupted with Gaussian white noise.2. LAMBDA: the Lagrangian Stochastic Model
- The Lagrangian particle model LAMBDA was developed to study the transport process and pollutant diffusion, starting from the Brownian random walk modeling[14, 15]. In the LAMBDA code, full-uncoupled particle movements are assumed. Therefore, each particle trajectory can be described by the generalized three dimensional form of the Langevin equation for velocity[16]:
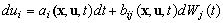 | (2a) |
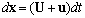 | (2b) |
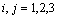 , and x is the displacement vector, U is the mean wind velocity vector, u is the Lagrangian velocity vector, ai(x,u,t) is a deterministic term and bij(x,u,t)dWj(t) is a stochastic term, and the quantity dWj(t) is the incremental Wiener process.The deterministic (drift) coefficient ai(x,u,t) is computed using a particular solution of the Fokker- Planck equation associated to the Langevin equation. The diffusion coefficient bij(x,u,t) is obtained from the Lagrangian structure function in the inertial subrange, (τK << Δt << τL), where τK is the Kolmogorov time scale and τL is the Lagrangian de-correlation time scale. These parameters can be obtained employing the Taylor statistical theory on turbulence[17].Backward integration can also be applied. This is just to identify which particle arriving in a sensor-j is coming from a source-i.The drift coefficient ai(x,u,t), for forward and backward integration is given by
, and x is the displacement vector, U is the mean wind velocity vector, u is the Lagrangian velocity vector, ai(x,u,t) is a deterministic term and bij(x,u,t)dWj(t) is a stochastic term, and the quantity dWj(t) is the incremental Wiener process.The deterministic (drift) coefficient ai(x,u,t) is computed using a particular solution of the Fokker- Planck equation associated to the Langevin equation. The diffusion coefficient bij(x,u,t) is obtained from the Lagrangian structure function in the inertial subrange, (τK << Δt << τL), where τK is the Kolmogorov time scale and τL is the Lagrangian de-correlation time scale. These parameters can be obtained employing the Taylor statistical theory on turbulence[17].Backward integration can also be applied. This is just to identify which particle arriving in a sensor-j is coming from a source-i.The drift coefficient ai(x,u,t), for forward and backward integration is given by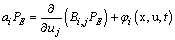 | (3a) |
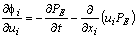 | (3b) |
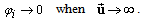 | (3c) |
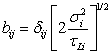 | (4) |
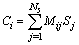 | (5) |
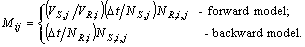 | (6) |
3. Inverse Model
- In order to set up the inverse analysis, it is assumed that the concentration obtained with a mathematic model is given by CMod(r,Q), where Q=[Q1(t), Q2(t), … , Qn(t)]T is the vector emission rate, and Qn(t) represents the emission rate of the n-th source and CExp(r) are data from measurement concentrations. The solution of an inverse problem is a function Q hat minimizes the following objective function:
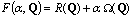 | (7) |
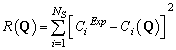 | (8) |
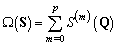 | (9a) |
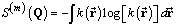 | (9b) |
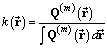 | (9c) |
3.1. Optimization Algorithm
- The optimization problem is iteratively solved by the deterministic method: quasi-Newtonian optimizer routine E04UCF[22], from the NAG Fortran Library. This routine is designed to minimize an arbitrary smooth function subject to constraints (simple bounds, linear and nonlinear constraints), using a sequential programming method. For the n-th iteration, the calculation proceeds as follows:1. Solve the direct problem for Sn and compute the objective function J(Sn).2. Compute by finite differences the gradient ∇J(Sn).3. Compute a positive-definite quasi-Newton approximation to the Hessian Hn:
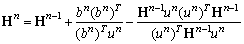 | (10) |
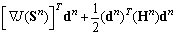 , subjected to:
, subjected to: 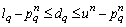 5. Set, Sn+1 = Sn + βndn where the step length βn minimizes J(Sn + βndn).6. Test the convergence; stop or return to Step 1.
5. Set, Sn+1 = Sn + βndn where the step length βn minimizes J(Sn + βndn).6. Test the convergence; stop or return to Step 1.4. Numerical Experiment
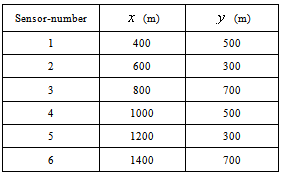
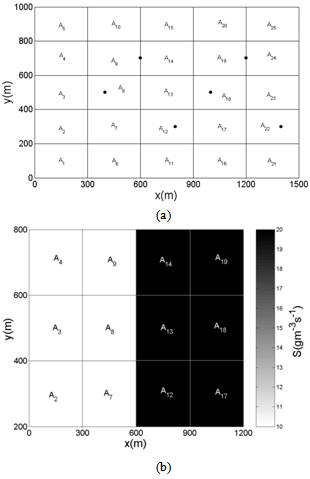
- For testing the procedure to estimate the emission rate procedure, the area pollutant sources are considered as placed in a box volume, where the horizontal domain and vertical height are given by: (1500 m 1000 m) 1000 m. There are two embedded regions R1 and R2 into a computational domain, with the following horizontal domain (600 m 600 m) for each region, and 1 m of height, and they are realising contaminants with two different emission rates. Figure 1 shows the computational scenario in a two-dimensional projection (x,y): the six sensors are placed at 10 m height and spread horizontally with the coordinates presented in Table 1. The domain is divided into sub-domains with 200 m 200 m 1 m. The emission rates for each sub-domain (SAi) are as follows,R1 = SA2 = SA3 = SA4 = SA7 = SA9 = 10 gm-3s-1 ,R2 = SA12 = SA13 = SA14 = SA17 = SA18 = SA19 = 20 gm-3s-1 .For other sub-domians: S=0. The dispersion problem is modelled by the LAMBDA backward-time code, where data from the Copenhagen experiment are used, for the period (12:33 h – 12:53 h, 19/October/1978)[23, 24] It is assumed a logarithmic vertical profile for the wind field
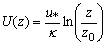 | (11) |
|
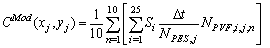 | (12) |
|
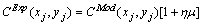 | (13) |
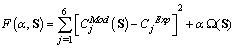 | (14) |
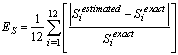 | (15) |
|
|
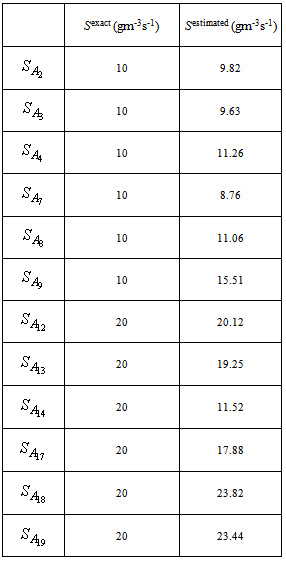
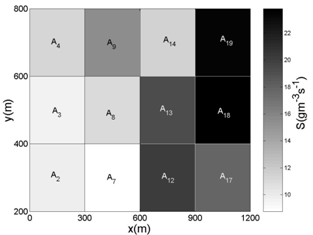 | Figure 2. Representation of the of emission rate estimation in the domain with data from Experiment-1 |
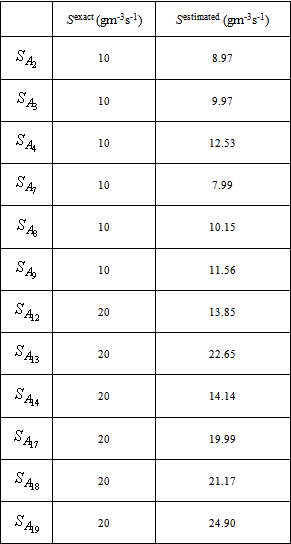
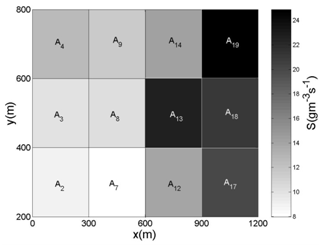 | Figure 3. Representation of the of emission rate estimation in the domain with data from Experiment-2 |
5. Conclusions
- The methodology proposed for estimating the emission rate term and localization of the source/sink was effective to produce good estimations for pollutant emission rate with second order maximum entropy. Good results were obtained even for a high level of noise, showing that the inverse model is robust related to the noise in experimental data. The determination of the regularization parameter by L-curve allowed finding an appropriated value for regularization operator, following the procedure presented by Hansen[21]. The source-receptor scheme is employed in the inverse analysis, in order to reduce the computational effort.Future works will include the application of the methodology to real gas fluxes with different types of soil covering. Further we will employ other entropic regularization operators[25], and different optimization schemes for the minimizing functional (1), using stochastic schemes and/or approaches from artificial intelligence (neural networks, or fuzzy systems).
ACKNOWLEDGEMENTS
- The authors would like to thank to the Brazilians (CNPq, FAPESP) and Italian agencies for research financial support. The first author acknowledges CNPq-Brasil (Proc. 20.0046/04-7) for the sandwich doctorate fellowship in the ISAC-CNR, Turin – Italy.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML