-
Paper Information
- Next Paper
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Environmental Engineering
p-ISSN: 2166-4633 e-ISSN: 2166-465X
2013; 3(1): 48-55
doi:10.5923/j.ajee.20130301.07
A First Order Pertubative Analysis of the Advection-Diffusion Equation for Pollutant Dispersion in the Atmospheric Boundary Layer
Cláudio C. Pellegrini 1, Daniela Buske 2, Bardo E. J. Bodmann 3, Marco T. Vilhena 3
1Depto. of Thermal and Fluid Sciences, Federal University of São João del-Rey, São João del-Rey, 36307-904, Brazil
2Department of Mathematics and Statistics, Federal University of Pelotas, Pelotas, 96010-900, Brazil
3Pos-Graduate Program in Mechanical Engineering, Federal University of Rio Grande do Sul, Porto Alegre, 90046-900, Brazil
Correspondence to: Cláudio C. Pellegrini , Depto. of Thermal and Fluid Sciences, Federal University of São João del-Rey, São João del-Rey, 36307-904, Brazil.
| Email: |  |
Copyright © 2012 Scientific & Academic Publishing. All Rights Reserved.
The present discussion focuses on the dispersion of pollution plumes in the atmospheric boundary layer. From a comparison between first order perturbation theory with equivalent findings from a spectral theory approach we identify significant contributions under certain conditions filtered out by perturbation technique. To this end we make use of the Intermediate Variable Technique and simplify the three-dimensional advection-diffusion equation according to the findings of the former. Results, where certain characteristics (diffusion, advection, turbulence) are either amplified or suppressed are compared with the complete GILTT solution.
Keywords: Pollutant Dispersion, Asymptotic Analysis, Integral Transform, Atmospheric Boundary Layer
Cite this paper: Cláudio C. Pellegrini , Daniela Buske , Bardo E. J. Bodmann , Marco T. Vilhena , A First Order Pertubative Analysis of the Advection-Diffusion Equation for Pollutant Dispersion in the Atmospheric Boundary Layer, American Journal of Environmental Engineering, Vol. 3 No. 1, 2013, pp. 48-55. doi: 10.5923/j.ajee.20130301.07.
Article Outline
1. Introduction
- Dispersion of pollution plumes in the atmospheric boundary layer (ABL) has undergone a considerable evolution from its early classification scheme according to stability to more advanced models that are based on the Monin-Obukhov similarity theory. However, the complexity more or less turbulent of the phenomenon is still manifest in parameterizations that hide physical details in phenomenological coefficients and it would be desirable to shade further light on at least some of their properties. In this sense the current discussion is an attempt to identify significant contributions from first order perturbation theory with equivalent findings from a spectral theory approach.Studies of pollutant dispersion, and in particular of its governing advection-diffusion equation (ADE), have a long tradition of being treated analytically. In fact analytical solutions are of fundamental importance in understanding and describing physical phenomena. Analytical solutions explicitly take into account all the parameters of a problem, so that their influence can reliably be investigated. It is also easy to obtain the asymptotic behaviour of the solution, which is usually more tedious to generate numerically. Moreover, in the same spirit as the Gaussian solution (the first solution of the ADE with the wind and eddy diffusivity coefficients set constant in space), the former suggest the construction of operative analytic models. Gaussian models, so named because they are based on the Gaussian solution, are forced to represent real situations by means of empirical parameters, known as "sigmas". They are fast, simple, do not require complex meteorological input, and describe the diffusive transport in an Eulerian framework, making the use of measurements easy. For these reasons they are still widely employed for regulatory applications by environmental agencies all over the world in spite of their well-known intrinsic limits.A significant number of works regarding the ADE analytical solution (mostly with a two-dimensional treatment) is available in the literature. Among them we mention the works[1-17]. However, above solutions are valid for very specialized situations: only for ground level sources, an ABL of infinite height, or specific vertical profiles for wind and eddy diffusivities. Reference[18] presented an analytical solution, called ADMM (Advection Diffusion Multilayer Method) for a limited ABL height and general wind and eddy diffusivity vertical profiles, but expressed by a stepwise function (see[19] for a complete review). The ADMM method was further associated with the Generalized Integral Transform Technique (GITT) to obtain a three-dimensional solution [20-23]. Some of the above solutions were used[17] in operational air pollution models.Finally, a general two-dimensional solution without any restrictions in the spatial function describing the wind and eddy diffusion coefficients was presented in[24-26]. The method used was the Generalized Integral Laplace Transform Technique (GILTT). That is an analytical series solution, including the solution of an associated Sturm-Liouville problem, the expansion of the pollutant concentration in a series in terms of the attained eigenfunction, replacement of this expansion in the ADE and, finally, taking of moments. This procedure leads to a set of differential ordinary equations that are analytically solved by Laplace transform technique. A complete review of the GILTT method is given in[27]. For the three-dimensional solution see[28-32]. All these analytical methods have in common the fact that three-dimensional, transient equations are not easy to treat. One way around this difficulty is to apply a first order perturbative analysis to the original problem before applying the transform technique. Recent meteorological literature contains a number of studies employing perturbation techniques, but none of them uses them to simplify the analysis via transform methods. In the literature some problems are obviously better suited for perturbation analysis due to the presence of a native small parameter, as is the case with the flow over smooth terrain (for example[33]). Regarding air pollution studies, however, very few results are found. An example is[34] that use singular perturbation techniques to obtain a new analytical solution to the 1-D transient convection-diffusion equation. The present study uses a first order perturbation technique known as IVT (Intermediate Variable Technique, briefly reviewed in what follows) to simplify the three-dimensional advection-diffusion equation. Results are compared with preceding complete GILTT results to show that the neglected terms are indeed small.
2. Perturbation Techniques
- The solution of regular problems by perturbation methods, although not always easy, is generally straightforward because the solution remains valid for the whole domain of interest. This is not the case with singular problems, thus a number of techniques were developed to deal with the mathematical difficulties arising. The most well-known are the Matched Asymptotic Expansions Technique, the Method of Multiple Scales and the Method of Strained Co-ordinates. In the analysis that follows we employ the Intermediate Variable Technique (IVT), which is less known, and thus is briefly reviewed.The IVT has its roots on Matched Asymptotic Expansions. It is based on the ideas of[35] and can also be found in[36]. When matched asymptotic expansions are used to solve boundary layer problems, a special variable (called the intermediate variable) is used to match the inner and outer solutions (in case they are only two). This is achieved through a co-ordinate stretching (or rescaling) of the kind
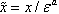 , where x is the independent variable,
, where x is the independent variable, 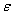 is the small parameter, a is (often but not necessarily) an integer and
is the small parameter, a is (often but not necessarily) an integer and 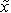 is the stretched co-ordinate. After substituting x by
is the stretched co-ordinate. After substituting x by 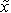 into the equations under study, a is allowed to vary and the resulting possibilities of matching are investigated. The values of a that gives such matching, shows where the boundary layers are, allowing for the construction of the inner and outer solutions that describe the whole domain of interest. The IVT is a modification of this method and is indeed implicit in the search for afore mentioned boundary layers. In IVT, no inner or outer asymptotic solutions are sought. The intermediate variable is used to define the layers where different terms dominate in the original equation and in first order approximation. The exponent a is abandoned and
into the equations under study, a is allowed to vary and the resulting possibilities of matching are investigated. The values of a that gives such matching, shows where the boundary layers are, allowing for the construction of the inner and outer solutions that describe the whole domain of interest. The IVT is a modification of this method and is indeed implicit in the search for afore mentioned boundary layers. In IVT, no inner or outer asymptotic solutions are sought. The intermediate variable is used to define the layers where different terms dominate in the original equation and in first order approximation. The exponent a is abandoned and 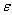 is allowed to vary continuously in the interval ]0,1] in the expression
is allowed to vary continuously in the interval ]0,1] in the expression 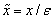 . The method thus shows the relative importance of terms in the original equation as one move from the boundaries of the problem to the far field.
. The method thus shows the relative importance of terms in the original equation as one move from the boundaries of the problem to the far field.3. Mathematical Analysis
- The time-dependent three dimensional Cartesian coordinates, advection-diffusion equations that describe the dispersion of a passive pollutant released by an elevated source on a statically neutral atmosphere are[37]:
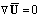 | (1) |
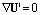 | (2) |
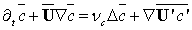 | (3) |
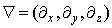 , U = (u,v,w) is the wind velocity vector with Cartesian components in the directions x, y and z, respectively, ρ is the air density and νc is the molecular diffusivity. The terms
, U = (u,v,w) is the wind velocity vector with Cartesian components in the directions x, y and z, respectively, ρ is the air density and νc is the molecular diffusivity. The terms 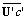 represent the turbulent fluxes of contaminants, in the longitudinal, crosswind and vertical directions.The source term is absent in eqn. (3) because it is included in the boundary conditions, which are
represent the turbulent fluxes of contaminants, in the longitudinal, crosswind and vertical directions.The source term is absent in eqn. (3) because it is included in the boundary conditions, which are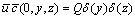 | (4) |
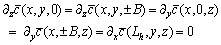 | (5) |
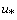 , for all turbulent velocity components and the concentration at the source
, for all turbulent velocity components and the concentration at the source 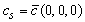 for the mean concentration. For the turbulent fluctuations of the concentration we assume
for the mean concentration. For the turbulent fluctuations of the concentration we assume 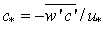 to supply with an approximate estimate. Time may be rendered dimensionless using the characteristic response time of the ABL to surface forcings, tc.To cast the space variables in dimensionless form we recognize that the atmosphere and the plume have different length scales. Thus, for the atmosphere we shall use the characteristic horizontal PBL length, Lh, for x and y, and the characteristic vertical PBL length, Lv for z but for the plume we shall use Lh for x but we apply the characteristic plume width, B, for y and z. The resulting expressions for the dimensional space variables are, thus, X1 = x/Lh, Y1 = y/Lh, Z1 = z/Lv, to be used in eqns. (1) and (2) and X2 = x/Lh, Y2 = y/B, Z2 = z/B, to be used in eqn. (3). From these relations it follows that X2 = X1, Y2 = Y1Lh /B, Z2 = Z1Lv /B. Applying all the transformations to non-dimensional coordinates and the preceding three relations to eqns. (1) to (3) yields
to supply with an approximate estimate. Time may be rendered dimensionless using the characteristic response time of the ABL to surface forcings, tc.To cast the space variables in dimensionless form we recognize that the atmosphere and the plume have different length scales. Thus, for the atmosphere we shall use the characteristic horizontal PBL length, Lh, for x and y, and the characteristic vertical PBL length, Lv for z but for the plume we shall use Lh for x but we apply the characteristic plume width, B, for y and z. The resulting expressions for the dimensional space variables are, thus, X1 = x/Lh, Y1 = y/Lh, Z1 = z/Lv, to be used in eqns. (1) and (2) and X2 = x/Lh, Y2 = y/B, Z2 = z/B, to be used in eqn. (3). From these relations it follows that X2 = X1, Y2 = Y1Lh /B, Z2 = Z1Lv /B. Applying all the transformations to non-dimensional coordinates and the preceding three relations to eqns. (1) to (3) yields 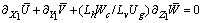 | (6) |
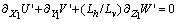 | (7) |
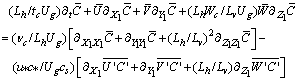 | (8) |
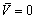 next to the surface. In this case, eqn. (6) implies that Wc must be such that LhWc/LvUg.= O(1), otherwise, ∂X1U = 0 or ∂Z1W = 0 if LhWc/LvUg.= o(1) or if o(LhWc/LvUg) = 1, respectively. The first possibility implies that there is no streamwise u velocity variation in the plume in first order approximation; the second that there is no vertical w velocity variation, respectively. Both conditions are known to be unreasonable, in the general case, for the PBL. Due to the random nature of turbulent fluctuations, the coordinate system cannot be oriented such that
next to the surface. In this case, eqn. (6) implies that Wc must be such that LhWc/LvUg.= O(1), otherwise, ∂X1U = 0 or ∂Z1W = 0 if LhWc/LvUg.= o(1) or if o(LhWc/LvUg) = 1, respectively. The first possibility implies that there is no streamwise u velocity variation in the plume in first order approximation; the second that there is no vertical w velocity variation, respectively. Both conditions are known to be unreasonable, in the general case, for the PBL. Due to the random nature of turbulent fluctuations, the coordinate system cannot be oriented such that 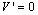 and, therefore, the above conclusion does not apply to eqn. (7). In fact, for neutral atmosphere, (Lh/Lv) = O(1)[38] holds. Substituting this relation and LhWc/LvUg.= O(1) in eqns. (6) to (8) and for convenience introducing the small parameters εt, ε*, εc*, εd results in
and, therefore, the above conclusion does not apply to eqn. (7). In fact, for neutral atmosphere, (Lh/Lv) = O(1)[38] holds. Substituting this relation and LhWc/LvUg.= O(1) in eqns. (6) to (8) and for convenience introducing the small parameters εt, ε*, εc*, εd results in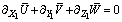 | (9) |
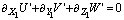 | (10) |
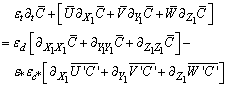 | (11) |
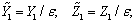 | (12) |
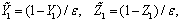 | (13) |
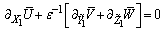 | (14) |
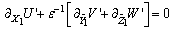 | (15) |
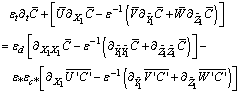 | (16) |
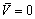 implies that the derivatives for
implies that the derivatives for 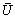 and
and 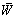 derivatives in eqn. (14) are of the same order, irrespective of the value of ε. Upon rotation it such that
derivatives in eqn. (14) are of the same order, irrespective of the value of ε. Upon rotation it such that 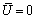 implies the
implies the 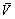 and
and 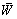 derivatives are of the same order and, thus, all terms in eqn. (14) are of the same order of magnitude. This implies that all the advective terms of eqn. (16) are of the same order of magnitude too. Again, the coordinate system cannot be rotated such that
derivatives are of the same order and, thus, all terms in eqn. (14) are of the same order of magnitude. This implies that all the advective terms of eqn. (16) are of the same order of magnitude too. Again, the coordinate system cannot be rotated such that 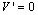 or
or 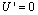 so that such a conclusion does not apply to eqn. (15). These conclusions allow us to write eqn. (16) in an order of magnitude fashion,
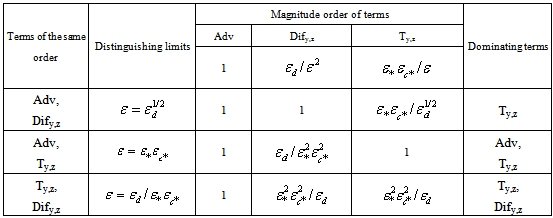
so that such a conclusion does not apply to eqn. (15). These conclusions allow us to write eqn. (16) in an order of magnitude fashion, 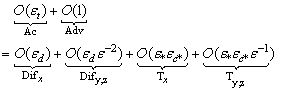 | (17) |
|
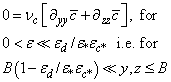 | (18) |
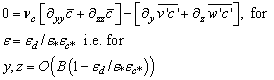 | (19) |
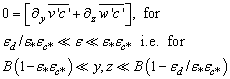 | (20) |
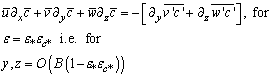 | (21) |
 | (22) |
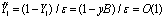 | (23) |
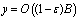 | (24) |
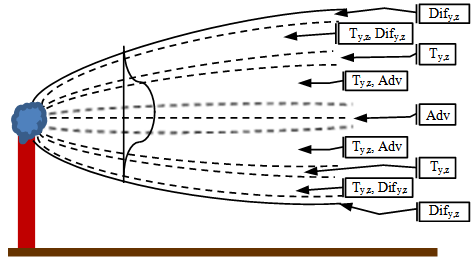 | Figure 1. Schematic drawing of the pollutant plume, showing regions of dominance of the terms in equation (3) |
4. The GILTT Method
- The ADE of air pollution in the atmosphere, eqn. (3), is essentially a statement of conservation of the suspended material and it can be written as[43]:
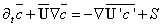 | (25) |
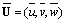 is the mean wind and S is the source term. Equation (25) has four unknown variables (the concentration and turbulent fluxes) which lead us to the well known turbulence closure problem. One of the most widely used closures for eqn. (25), is based on the gradient transport hypothesis (also called K-theory) which, in analogy with Fick’s law of molecular diffusion, assumes that turbulence causes a net movement of material following the negative gradient of material concentration at a rate which is proportional to the magnitude of the gradient[42]:
is the mean wind and S is the source term. Equation (25) has four unknown variables (the concentration and turbulent fluxes) which lead us to the well known turbulence closure problem. One of the most widely used closures for eqn. (25), is based on the gradient transport hypothesis (also called K-theory) which, in analogy with Fick’s law of molecular diffusion, assumes that turbulence causes a net movement of material following the negative gradient of material concentration at a rate which is proportional to the magnitude of the gradient[42]: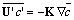 | (26) |
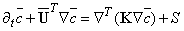 | (27) |
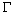 bounded by 0 < x < Lx, 0 < y < Ly and 0 < z < h and subject to the following boundary and initial conditions,
bounded by 0 < x < Lx, 0 < y < Ly and 0 < z < h and subject to the following boundary and initial conditions,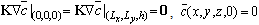 | (28) |
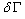 . Note, that in cases where the source is located in the domain, one still may divide the whole domain in sub-domains, where the source lies on the boundary of the sub-domains which can be solved for each sub-domain separately. Moreover, a set of different sources may be implemented as a superposition of independent problems. Since the source term location is on the boundary, in the domain this term is zero everywhere (S(r)
. Note, that in cases where the source is located in the domain, one still may divide the whole domain in sub-domains, where the source lies on the boundary of the sub-domains which can be solved for each sub-domain separately. Moreover, a set of different sources may be implemented as a superposition of independent problems. Since the source term location is on the boundary, in the domain this term is zero everywhere (S(r)  0 for r
0 for r 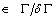 ), so that the source influence may be cast in form of a condition, where we assume that our coordinate system is oriented such that the x-axis is aligned with the mean wind direction. Since the flow crosses the plane perpendicular to the propagation (here the y-z-plane) the source condition reads:
), so that the source influence may be cast in form of a condition, where we assume that our coordinate system is oriented such that the x-axis is aligned with the mean wind direction. Since the flow crosses the plane perpendicular to the propagation (here the y-z-plane) the source condition reads: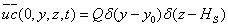 | (29) |
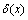 represents the Cartesian Dirac delta functional.In order to solve the problem (27) we reduce the dimensionality by one and thus cast the problem into a form already solved in[27]. To this end we apply the integral transform technique in the y variable, and expand the pollutant concentration as:
represents the Cartesian Dirac delta functional.In order to solve the problem (27) we reduce the dimensionality by one and thus cast the problem into a form already solved in[27]. To this end we apply the integral transform technique in the y variable, and expand the pollutant concentration as: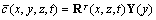 | (30) |
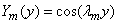 with eigenvalues
with eigenvalues 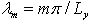 for m = 0, 1, 2, … . After substitution of eqn. (30) in eqn. (27) and taking moments, we obtain a set of M + 1 two-dimensional diffusion equations:
for m = 0, 1, 2, … . After substitution of eqn. (30) in eqn. (27) and taking moments, we obtain a set of M + 1 two-dimensional diffusion equations: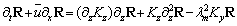 | (31) |
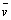 and
and 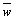 takes the null value. We neglect the diffusion component Kx because we assume that the advection is dominant in the x-direction, i.e.,
takes the null value. We neglect the diffusion component Kx because we assume that the advection is dominant in the x-direction, i.e., 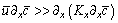 . We also consider that Ky has only dependence on the z-direction. Problem (31) is solved using Laplace transform technique and diagonalization, following the works[27][29][30]. The specific form of the eddy diffusivity determines now whether the problem (31) is a linear or non-linear one. In the linear case the K is assumed to be independent of
. We also consider that Ky has only dependence on the z-direction. Problem (31) is solved using Laplace transform technique and diagonalization, following the works[27][29][30]. The specific form of the eddy diffusivity determines now whether the problem (31) is a linear or non-linear one. In the linear case the K is assumed to be independent of 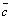 , whereas in more realistic cases, even if stationary, K may depend on the contaminant concentration and thus renders the problem non-linear. However, until now no specific law is known that links the eddy diffusivity to the concentration so that we hide this dependence using a phenomenological motivated expression for K which leaves us with a partial differential equation system in linear form, although the original phenomenon is non-linear. In[32], an example demonstrates the closed form procedure for a problem with explicit time dependence, which is novel in the literature.
, whereas in more realistic cases, even if stationary, K may depend on the contaminant concentration and thus renders the problem non-linear. However, until now no specific law is known that links the eddy diffusivity to the concentration so that we hide this dependence using a phenomenological motivated expression for K which leaves us with a partial differential equation system in linear form, although the original phenomenon is non-linear. In[32], an example demonstrates the closed form procedure for a problem with explicit time dependence, which is novel in the literature. 4. Discussion
- The reliability of each model strongly depends on the way turbulent parameters are calculated and related to the current understanding of the PBL. Following[44], during convective conditions at
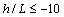 the following relation is used:
the following relation is used: 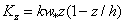 | (32) |
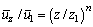 | (33) |
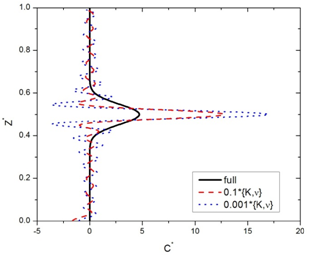 | Figure 2. Full solution of the ADE and advective dominance |
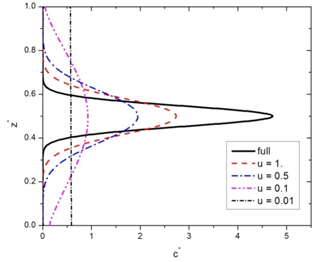 | Figure 3. Full solution of the ADE and turbulence dominance |
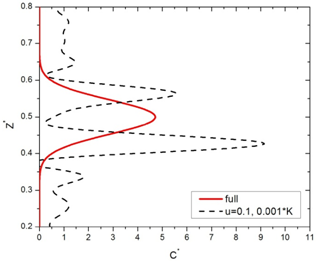 | Figure 4. Full solution of the ADE and molecular diffusion dominance |
5. Conclusions
- With the present discussion we presented a first attempt to disentangle relevant physical mechanisms that constitute the dynamics of pollutant dispersion in form of plumes. Although there are fundamental differences in the two approaches, one based on an order of magnitude analysis, i.e. small parameter expansion, the other constructed from spectral theory resulting in a solution that makes use of a parameterized turbulence model in form of phenomenological eddy diffusivity.More specifically the turbulent pollutant flow in IVT results from a perturbation order evaluation that substitutes the otherwise necessary closure, such as Fick's law among other possibilities. Therefore turbulence closure is local due to the consideration of first order terms only.The advection diffusion equation approach with its space time dependent eddy diffusivity function represents turbulent properties and is not restricted to a special regime, i.e. it is globally valid.Thus, although based on different footings, the IVT approach supplies with a qualitative hierarchy of mechanisms, that together with the spectral theory based approach allows to turn these findings semi-quantitative by fading out higher order to leading order terms in the ADE solution.The combination of IVT and GILTT provide a first step that allows to tag the mechanism profile or equivalently the dynamical profile of pollution dispersion in plumes. In future investigations we will focus on the dynamical equation for pollutant dispersion fluctuations (higher statistical moments) in order to allow for comparisons between the "local closure" from the perturbation analysis and specific limits of advection-diffusion variance. Such a procedure will open pathways to analyse compatibility of perturbative local closure with global eddy diffusivity parameterization.
ACKNOWLEDGEMENTS
- The authors wish to thank CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico), FAPERGS (Fundação de Amparo à Pesquisa do Estado do Rio Grande do Sul) and FAPEMIG (Fundação de Amparo à Pesquisa do Estado de Minas Gerais) for the partial financial support to this work.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML