A. Bakhtiari, T. Berberashvili, P. Kervalishvili
Engineering Physics faculty, Georgian Technical University, Tbilisi, Georgia
Correspondence to: A. Bakhtiari, Engineering Physics faculty, Georgian Technical University, Tbilisi, Georgia.
| Email: |  |
Copyright © 2024 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Today Regarding to the matter structure as very small size particles arrangement, their dimension change means space manipulation. There are different methods of mathematical physics that try to explain space in different orientations and physicists try to use which is suitable in their specific investigation. Therefore, not only matter study in small scale but also their physical manipulation to find a new structure are related to the space definition. On the other hand, the matter destructuring (fission) and restructuring (fusion) depends on an external energy that changes particles arrangement and somehow it can be leaded to a new structure with new physical properties. Therefore, initial matter’s particles arrangement on one hand, and manipulation by external source of energy on another hand, lead investigation to a novel dynamic space. In this work, a new space as Dynamic Fractal Space (DFS) is introduced that shows external source of energy and material in a Self-control-closed loop (SCCL) system. Hence, destructuring and restructuring of matter not only depends on external energy amount (system input), but also is correlated to the material feedback. In this regard, some other system factors such as regime of energy and matter reaction are significant. At the end, Laser-Plasma thin film case study provides a clear view of the DFS doctrine.
Keywords:
Physical properties, Fission, Fusion, Laser-Plasma, Thin film
Cite this paper: A. Bakhtiari, T. Berberashvili, P. Kervalishvili, About Dynamic Fractal Space, American Journal of Condensed Matter Physics, Vol. 13 No. 1, 2024, pp. 1-8. doi: 10.5923/j.ajcmp.20241301.01.
1. Introduction
There are two main questions for a scientist: how and how much. Answer "how" leads scientist to quality of a phenomenon as "how much" leads to quantity. Answering how much needs measuring that is guided to dimension and relativity. Hence, quantity means dimensions must be comprised by references. Obviously, there are different physical properties that should be measured. However, they are different quantities, but somehow, they are correlated together. For instance, area of a square is second exponent of its length as well as volume of a cube is third exponent of its length. Then, how many independent dimensions arises as the next question. The question leads mathematicians to Space definition. As an example, the cartesian coordinate system is the well-known example of a 3-dimensional space. A coordinate system shows a point position via dimensions on axes. But nature is dynamic, hence a space is expected to clarify a point’s new position that is leaded to mathematical structure. In other words, a structure shows character of changes. For instance, vector space is used in classical physics, Hilbert space is used in quantum mechanics, and etc [9]. Actually, a mathematical space provides general rules of changes. On the other hand, regime of changes is significant. In this regard, functions clarify regime of changes in the structure. This is the partial historic line of mathematics that has been tied to applied science. Meanwhile, applied science such as engineering physics are involved in change’s reasons. Here, energy and matter correlation are become theoretically and practically significant. Also, a space as structure and regime as function are tied to energy/matter action and reaction. In this regard, the structure and regime are expected to explain/measure changes. This is where fundamental and applied science intersection created one of the most critical rules as Energy Conservation Law and all natural and artificial structures are expected obey the law. Of course, there are phenomena without clear regime of changes in a defined space [14]. Generally, particles of every material are moving nonstop at any condition. When, small size particles tracing is not possible, then the movement is called chaotic. According to energy/ matter correlation in the space, the particles movement should be reflected on energy changes, but there is no relevant indicator [5,15]. Also, refer to Energy Conservation Law initial condition changing leads changes in the particle’s movement. Technologies associated with Nano and Micro field aim towards the manufacture of improved quality products that are suitable for devices that are lighter, faster, more reliable, more efficient and in those respects more economical for sophisticated industrial products that perform better in many ways than any other devices manufactured so far [10,12,16]. All depends on Nano or Micro scale manipulation of the matter’s structure that provides new specific physical properties. The realization of this production is achieved through processing techniques as sophisticated the devices themselves, either specially designed for this technological field or suitably altered processing for manufacturing large-scale super-finished products or miniaturized devices. Any process which related to Nano destructuring and restructuring such as Thin-Film is highly correlated to the premier matter’s structure (before destructuring) and the matter’s reaction in the process that leads to restructuring [8,11,13]. Hence, dynamic (realistic) material’s structure understanding instead of common static approach leads to the optimum technical and economic manipulation, then the best results. In this article first, natural behavior of the matter without any external manipulation is investigated and is shown a new mathematical approach is necessary. According to energy conservation law, matter observes the same way after manipulation by an external source of energy. Hence the novel mathematical space as Dynamic Fractal Space (DFS) not only explains nature behavior before any process, but also can be used for Nanoscale process designing [3,4].
2. Particles Nonstop Movement
According to Energy Conservation Law, energy is not born or disappear. Just it converts to different types. Assume a glass of water at room temperature as an isentropic system. It seems nanoparticles move chaotically, but temperature that is known as an indicator of matter small particles movement, doesn’t change. No spontaneous temperature changing in the glass of water under constant conditions represents that particles despite of chaotic movement do not fight each other or losing their energy, then it must be a harmonic motion. In other words, particles in a glass of water sense each other movement and maintain balance in the whole matter in the way of Energy Conservation Law. This scenario represents nanoparticles in a glass of water at room temperature as a unique system with the harmonic movement of particles. Therefore, it could be shown as a Self-Control Closed-Loop (SCCL) system that manages itself to observe energy conservation.Referring to SCCL principles, system auto-balance depends on feedback (figure 1). In other words, the system senses itself at the output and sends feedback to the system input, hence observes energy conservation. Feedback in the SCCL is output and input energy difference that if it is continuous in time (non-periodic without any lag), always it should be zero, and there is no auto-balance. Therefore, SCCL should be a discreet phenomenon. Hence, the paradoxical motion of particles (chaotic but harmonic) represents quantitated time in the SCCL.  | Figure 1. Self-Control Closed-Loop (SCCL) |
SCCL concept represents the role of processor (matter). In other words, different materials provide various SCCL system that regards diverse materials individuality. Consequently, if there is an external input such as initial conditions changing, not only operator (input-cause) but also the operated (material-effect) is significant.
3. Balance in Space
Basically, balance means energy conservation and leads to symmetry [19]. On the other hand, symmetry needs particles tracing in time refer to a reference in the space that not possible in a chaotic system. But, particles movement is harmonic by SCCL system. Consequently, time should be the symmetry reference in the SCCL system. Obviously, time is not a geometrical dimension such as length. Hence, looking for an appropriate space is guided to an analytic space that can be found in a topologic frame [18]. Particles movement means there must be empty places in the space. There are two common orientations for changes demonstration in the space. Classical orientations trace particles (points) in the space that here not possible. Modern orientations involved in levels of energy and probability of particles presence without regarding to the matter auto-balance concept. Hence, principles deduction shows a new space is mandatory.
4. Dynamic Fractal Space
Now, new space definition. Cluster is a free place inside a Fractal. Hence, Fractal is a set of Clusters. A Knot represents a unit of a material structure such as a molecule. Then, a Cluster can be empty or filled. Also, any mathematical structure definition needs dimensions. There are 4 dimensions to find a Fractal as XYZT. Three of them (XYZ) are geometrical dimensions and T represents time (figure 2). 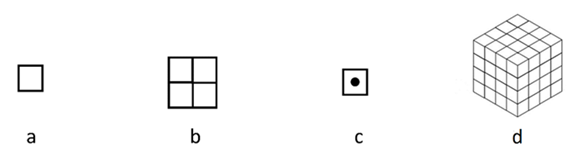 | Figure 2. (a) Cluster, (b) 2-dimensional Fractal, (c) Filled Cluster, (d) 3-dimensional Fractal |
Any Cluster in a Fractal is known by geometrical indices as Cxyz (figure 3). Hence, number of indices implies number of geometrical dimensions. For instance, Cxy is a 2-dimensional Fractal and Cxyz is a 3-dimensional Fractal.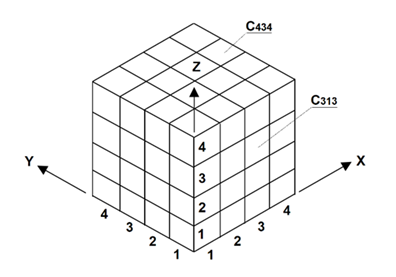 | Figure 3. Clusters and indices |
A Fractal is a set of Clusters.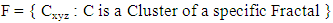 | (1) |
For instance, a 2-dimensional Fractal with 2 Clusters on any dimension will be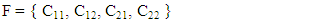 | (2) |
Consequently, as figure 4 any matter can be Fractals integrity that is called Lattice [21].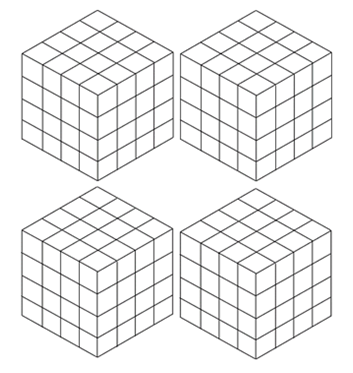 | Figure 4. Fractals and Lattices |
According to set of F (Equation 1), possible elements (Clusters) represent Tree Diagram of geometrical dimensions in a Fractal (figure 5). | Figure 5. Tree Diagram of dimensions in a Fractal represents number of elements in it |
Then, number of Clusters in a Fractal represents number of the Fractal cardinality. | (3) |
N: Number of a Fractal elements n: Number of Clusters on any dimension D: Number of dimensionsClusters of a Fractal can be empty or filled. Anyway, just 1 Knot can place in a Cluster. Then, filled Clusters and empty Clusters union in a Fractal represents all elements.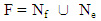 | (4) |
F: FractalN: Number of a Fractal elementsNf: Filled ClustersNe: Empty ClustersOn the other hand, a Cluster can be filled or empty. Then,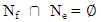 | (5) |
Nf: Filled ClustersNe: Empty ClustersAccording to matter’s Nano particle non-stop movement, a Nano particle of the matter (atom or molecule) moves Cluster to Cluster frequently that has been shown in figure 6 as an example. | Figure 6. A Nanoparticle changes it position in the Fractal. As an example, Knot changes it position from (2,2) at (a) to (1,1) after a certain time |
Hence, Filled Cluster in the Fractal is shown as figure 6 at (a) is shown as,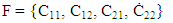 | (6) |
After specific time Knot will change its position randomly is shown as figure 6 such as (b).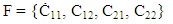 | (7) |
However, non-stop Knot position changing is not predictable, but at fixed condition (such as isentropic system) changing speed is constant. System’s status represents system’s State of Energy (SE). Therefore, if energy of the system (matter) is constant, Knots changing speed will be fixed too.A Knot movement speed implies specific time of position changing that is called Balance Period (BP). Consequently, if SE increase, Knots movement will be faster and there can be more filled Clusters in the BP. For instance, more temperature increases speed of Knots, then in the figure 6 there can be 2 filled Clusters in the BP randomly.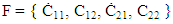 | (8) |
Every matter has specific structure that is correlated to its physical properties. Structure refers to nanoparticles (atoms or molecules) numbers and arrangement in a unit cell. Figure 7 represents 4 types of unit cells and 7 classes that represent Bravais Lattices.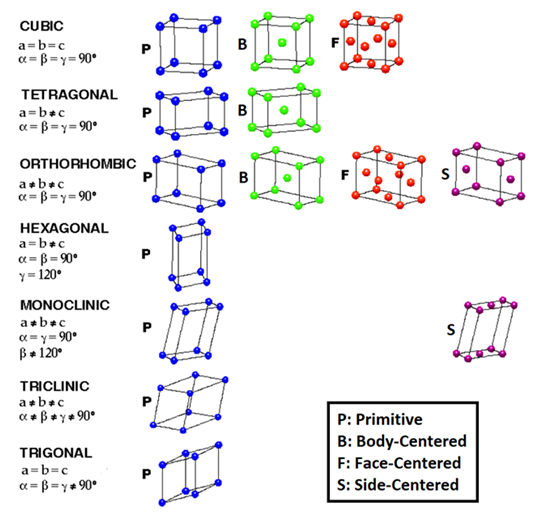 | Figure 7. Bravais Lattices |
It is clear, unit cells are similar to a Fractal. Therefore, Cluster should be sized refer to the specific material structure and its particles (atom or molecule). The r in figure 8 represents the size of Cluster.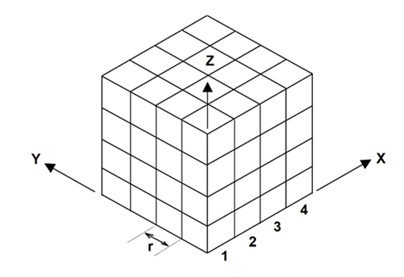 | Figure 8. Clusters must be scaled refer to material structure and the atom or molecule size |
Then, equation 3 is changed to | (9) |
N: Volumetric Fractal n: Number of Clusters on any dimension r: Unit size of a ClusterD: dimensionRefer to r in the above equation, N represents volume in 3-dimensional Fractal as well as area in 2-dimensional and length in 1-dimensional Fractal. The equation 9 refers to all Clusters with maximum D that can be 3 in the 3-dimentional space. But if the filled Clusters are in account, D cannot be an integer as 2 in 2-dimensional or 3 as 3-dimensional space. Hence, D will be a fraction. | (10) |
Dd: Dimension fraction of the matter based on filled ClustersNf: Filled Clusters n: Number of Clusters on any dimension r: Unit size of a ClusterAccording to definitions, some of Clusters are filled by Knots in a specific BP and the rest are empty which is represented by figure 9 (a) (of course, Knots positions are not fixed and they will change their position, but the figure make sensation as Fractal Dimension Fraction). On the other hand, if all Clusters at the same BP are filled, the Fractal will be same as figure 9 (b). | Figure 9. (a) fraction of 3-dimensional matter. (b) full 3-dimensional matter [2] |
Therefore, Fractal volumetric size does not change at fixed SE. According to specific Nf at certain BP and certain SE, Fractal Dimension Fraction (Dd) will be cleared. The defined space evokes Harsdorf space and Fractal Geometry [17]. But, Harsdorf space independent of time, then it cannot represent a dynamic space. Hence, this novel space is called Dynamic Fractal Space (DFS) More, investigation shows further applied orientation of DFS.
5. Adoption to Reality
According to Energy Conservation Law, energy just transform from a type to another one. Consequently, if SE change, Nf (number of filled Clusters in specific BP) will change too. In other words, SE and Nf must be Bidirectional One-One Correspondence after balance in a certain BP as has been shown in figure 10.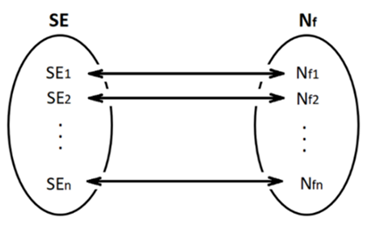 | Figure 10. Nf and SE are Bidirectional One-One Correspondence |
In this regard, connections can be described as function. Hence, function principle must be cleared. But, refer to nonpredictable character of nanoparticles movement, their tracing is impossible. Hence, the path from 1 to 2 in figure 11 is not possible.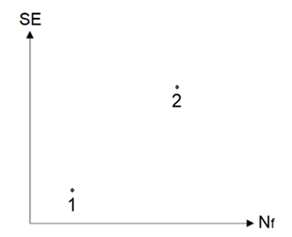 | Figure 11. Functions are not clear |
According to equation 4 a Fractal is based on Ne and Nf union. On the other hand, each Cluster has its own energy. If SE = constant, in a Fractal will be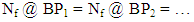 | (11) |
But if SE ≠ constant, in a Fractal will be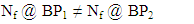 | (12) |
Matter tries to get Steady-State Balance at new SE. Hence, Nf changing will be transient until Steady-State Balance of the matter. According to Energy Conservation Law, 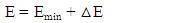 | (13) |
E: Total energy in a FractalEmin: Minimum Fractal energy at 0K△E: Energy (SE) increaseSuppose,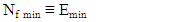 | (14) |
Then there could be an equivalence equation of E and Nf.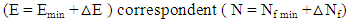 | (15) |
But, △Nf calculation is impossible, because the function is not clear. Meanwhile, a Fractal expansion or contradiction under SE changes is reality, hence n and r will be different from the ground State Fractal at 0 K. However, a Fractal’s components (Nf, n, r) changes regarding to SE changing is not clear, but dimension fraction (Dd) as the final integration of components changes must be fixed, because it is correlated to matter phase. As an example, water has 3 phases. The Fractal Ground State regards to 0K as minimum Dd. Then, maximum Dd refers to melting point (273.15 K) of the ice as 3. The rule will be iterated for liquid phase (273.15 – 373.15 K) as well as vapor. This rule refers to Dimension Conservation Law that is indicated Energy Conservation Law. Then,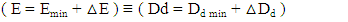 | (16) |
For instance, an ice unit structure can be a Fractal with 64 Clusters (figure 12).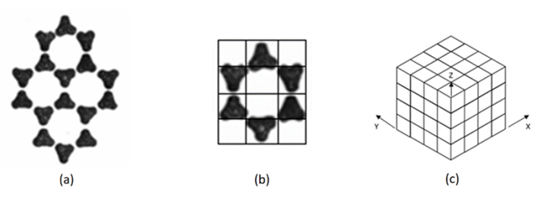 | Figure 12. (a) Ice molecular structure. (b) a unit of ice molecular Structure as a 2D Fractal. (c) 3D Fractal of the snow crystal |
There are minimum 6 Knots (Nf) in a Fractal in a BP as a minimum stable molecular structure (Fractal) of ice that has been shown in figure 13. According to equation 10, minimum Dd min of ice molecular structure in a fractal calculated 1.29248125. Dd will be different if SE increases up to maximum Dd as 3 at melting temperature. According to maximum possible Dd as 3, in the liquid phase of water Fractal components will be different, but observes all the rules.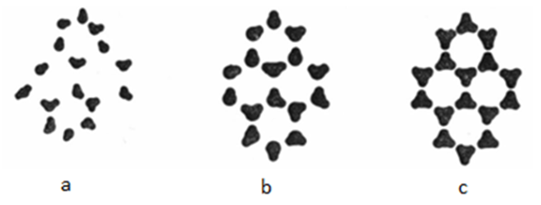 | Figure 13. Mean movement represents stable structure as gaseous in (a), liquid in (b), solid as ice in (c). all water states have the semi same structure [7] |
Consequently, figure 10 is modified to figure 14.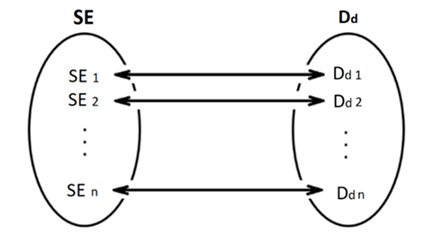 | Figure 14. Energy Conservation and Dimension Conservation correspondence |
6. Topology of Dynamic Fractal Space
The main intersection of all spaces is point. However, point is an abstract concept in mathematics, but it’s a relative identification in applied orientation depends on location. In Dynamic Fractal Space, Clusters can be assumed as points/location in the space. According to Dimension Conservation Law in Dynamic Fractal Space, Knots (filled Clusters) number of a Fractal in a BP is significant. In other words, here points relation is not distance, but distance (r) like number of filled Clusters in a Fractal (Nf) is important in Dd estimation. If SE is constant, however Knots are moving nonstop, but Dd (the main Fractal’s identification) refer to Dimension Conservation Law is constant. Then, Dd at constant SE is not time function that represent discrete character of DFS mathematics. On the other hand, a Fractal structure (Clusters arrangement) is based on Rn Metric Space as a subcategory of Topologic Space (figure 15). Hence, locations are individual Clusters in fact that could be filled or empty. Hence, despite of common mathematical spaces, location (Cluster) play the role instead of solids (Knot).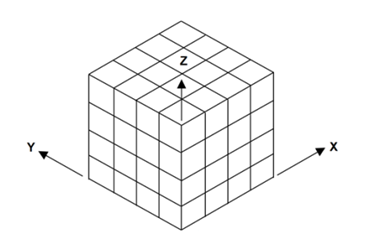 | Figure 15. Dynamic Fractal space is a lattice |
Dd depends on BP. Regarding to Knots nonstop movement, Fractal cannot be a static space. Also, through different SE, Fractal structure doesn’t change. However, the scale of the Fractal will change and there will be bigger r, but the structure will be homomorphous. All lead a Fractal to a Topologic Space. 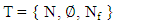 | (17) |
T: Dynamic Topology on Fractal N: Set of Clusters in a Fractal Nf: Set of filled ClustersT is a topology because,1. ∅ ∈ T2. {N} ∈ T3. Nf ⊂ N then, N ∩ Nf = Nf ∈ T4. N ∪ Nf = N ∈ T
7. Material Structure in DFS
Obviously, there is a maximum Dd for all the materials. But, minimum Dd at ground state depends on material structure. Hence, there is not specific minimum Dd for all the materials. On the other hand, △SE is related to △Dd. Maximum Dd is 3 that leads f (SE) = Dd function to no intersection with the line Dd = 3 in the figure 16. Hence, there must be a convergence function which touch the horizontal asymptote at maximum Dd = 3. Consequently, f (SE) general form should be a power function and its power should be less than 1.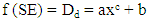 | (18) |
f (SE): Function of SE that is correlated to Ddx: represents SEa: Constant coefficient which is different for different materialsc: Power of the function which is different for different materials and c < 1b: Minimum Dd which is different for different materials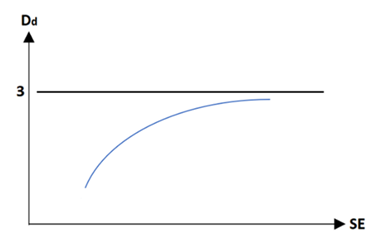 | Figure 16. Horizontal asymptote at maximum Dd |
Different materials reaction against SE changes are different. In other words, nanoparticles (Knots) movement speed of different materials in a same condition is different in a BP. Then, materials reaction to find steady-state (Balance) with different SE are different and each of them has specific characteristic function. This reaction is called Balance Rate (BR) of the material.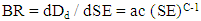 | (19) |
BR: Balance RatedDd / dSE: Dd to SE derivativea: Constant coefficient which is different for different materialsc: Power of the function which is different for different materials and c < 1Therefore, BR general graph will be power function with negative power (figure 17).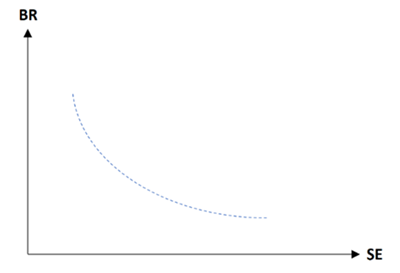 | Figure 17. BR general graph |
Practically, BR graph shows reaction speed in different cases such as heating water. If a specific volume of water is heated from 20°C to 100°C, water temperature rising will be fast at first but as much as near to 100°C, temperature rising speed will decrease.
8. Matter Destructuring/Restructuring
As a case study, Dynamic Fractal Space applied in Laser-Plasma (CWLD) thin film technology [1]. In this process, a target is destructured by laser beam to plasma plume and restructure on the substrate as a thin film. Figure 18 shows the scheme of the process.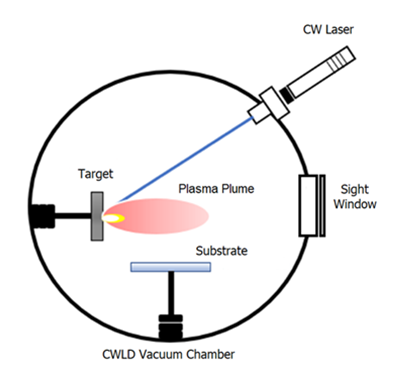 | Figure 18. CWLD process scheme |
According to SCCL concept, different operators as an external source of energy (such as laser wavelength, beam diameter, radiation angle on the target) that has been showed in figure 20 and the operated as the matter (such as different target materials and substrates) tested to find various structure of a material (figure 19).  | Figure 19. Different Operated (Targets) |
 | Figure 20. Different Operators (Laser beam) |
For instance, in different laser wavelengthes all 1W showed different responses on the same target at the same conditions that repreents the matter reaction role. Also, it represents regieme of the process operators like the other parameters. Because, regime is correlated to material reaction as the operated reaction (Nf in a BP) and material structure (r as a Cluster size). Figure 21 comprises Graphene thin film on the Silison substrate by CWLD and mechanical exfoliation.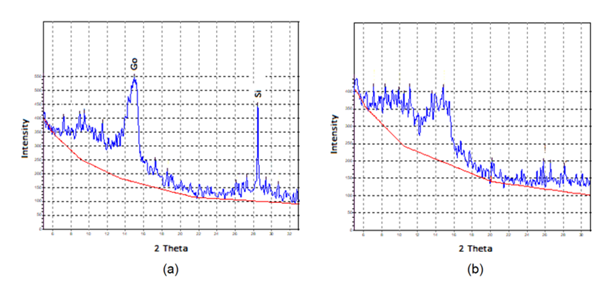 | Figure 21. (a) XRD of CWLD Graphene thin film. 2θ is 15o; FWHM is 0.0139626 radian; and d is 5.90 Å; (b) XRD of mechanical exfoliation of Graphite |
9. Conclusions
Finding the different physical properties of the matter depends on the structural features of a material that its manipulation happening just at micro-nano scale. In this regard, sometimes premier matter’s structure manipulation is inevitable that is based on destructuring (fission), then restructuring (fusion). According to principles, Energy Conservation Law matches to balance that represents the matter’s nanoparticles harmonic nonstop movement at an isentropic system. On the other hand, balance needs a symmetry reference but there is no spatial reference. However, seems a paradox, but reality proves balance. Hence, Self- Control Closed-Loop can be a suitable justification of balance without spatial reference. SCCL represents quality of the approach, but quantity orientation is necessary that leads to the novel Dynamic Fractal Space. These deductions of principles and reality must be observed any time; because of Energy Conservation Law observation. Matter structure manipulation at a predefined condition depends on the matter enforcement by an external source of energy. Therefore, new structure/physical properties are related to external energy specification (amount, intensity, and etc) and the matter reaction. In other words, the matter reaction that comes out of its nature, beside the external source of energy is significant and it cannot be neglected if a specific final structure is looking for. Hence, SCCL concept persists on the matter role (feedback) despite of external energy source (Input) beside nonsymmetric balance explanation. In destructuring and restructuring process, there are 2 main steps as before and after energy enforcement and SCCL assumes the process after energy enforcement as a Fractal approach; despite of common approaches that just final product (output) Fractal is considered. DFS as a novel mathematical and physical approach of SCCL with an applied orientation not only provides deep understanding of Nanoscale before energy enforcement, but also after that. The doctrine is highlighted in a precise technologic processing such as thin film that structure defect tolerance is limited significantly.
ACKNOWLEDGEMENTS
Thanks to Advanced Technologies GmbH and Micro & Nanoelectronics institute (IMNE) that supported us for case study.
References
| [1] | Bakhtiari, Berberashvili, Kervalishvili (2020). Phototransmitting device Tbilisi, Georgia Patent No. P 2020 7134 B. |
| [2] | Bakhtiari, Berberashvili, Kervalishvili. (2019). Clusters-Particles balance in matter by Dynamic Fractal. Batumi Shota Rustaveli State University (pp. 92-93). Batumi, Georgia: JAPMED 11. |
| [3] | Bakhtiari, Kervalishvili. (2021). Dynamic Fractal doctrine as nonlinear systems model. American journal of condensed matter physics, 11 (1): 1-6. |
| [4] | Bakhtiari, Kervalishvili. (2021). Dynamic Fractal Mathematical Model. In Innovations in Science and Technology (pp. Vol.2, Ch.2). ISBN: 978-93-5547-460-5. |
| [5] | Birmingham University. (2018). Retrieved from Nonlinear systems: https://www.birmingham.ac.uk/index.aspx. |
| [6] | Cambridge. (2023, 01 25). Retrieved from Scitechdaily: https://scitechdaily.com. |
| [7] | Eisenberg, Kauzmann. (1969). The structure and properties of water. Oxford university press. |
| [8] | Z. Gogua, P. Kervalishvili, G. Kantidze. (2011). Charge impurity scattering of electrons in quasi-two dimensional semiconductor systems. Nanotechnology Perceprtions, Vol.7, N1, 67-71. |
| [9] | Haliday. (2007). Fundamental of Physics, 8th edition, India: Winsome Books. |
| [10] | P. Kervalishvili. (1987). On the mechanism of growth of small particles of elemental boron. Soviet journal of Solid State Physica, V.29, №-4. |
| [11] | P. Kervalishvili. (2005). Semiconducting Nanostructures-Materials for Spintronics. Nanotechnoloy Perceptions, Vol.1, N.3. |
| [12] | P. Kervalishvili. (2009). Micro-Nano-Pico technologies: The main way of novel materials development. Material Science Day. Tbilisi: CNRS-TSU. |
| [13] | P. Kervalishvili. (2010). Nanostructures with controlled disorders: Quantum effects in magnetic semiconductors. Nanochemistry and nanoechnologies, 209-218. |
| [14] | LibreTexts. (2023). Chemistry. Retrieved from The Molecular Interpretation of Entropy: https://chem.libretexts.org/. |
| [15] | Linder. (2004). Thermodynamics and introductory statistical mechanics. Florida State University: A John Wiley & sons. |
| [16] | Mamalis, Markopoulos, Manolakos. (2005). Micro and Nanoprocessing techniques and applications. Nanotechnology Perceptions, Vol.1, No.1. |
| [17] | Mandelbrot. (1983). The fractal geometry of nature. H. B. Fenn and company Ltd. |
| [18] | Morris. (2019). Topolgy without tears. |
| [19] | Noether. (1918). Invariante Variationsprobleme,. Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen. |
| [20] | Pathria. (1996). Statistical mechanics. Canada: University of Waterloo. |
| [21] | Peitgen, Jurgens, Saupe. (2004). Chaos and Frcatals. Springer, ISBN: 0-387-21823-8. |
| [22] | Rydnik. (2001). ABC's of quantum mechanics. Hawaii: University of pacific. |
| [23] | Viro, Ivanov, Netsvetaev, Kharlamov. (1984). Elementary topology. American mathematical society. ISBN 978-0-8218-4506-6. |





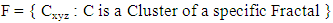
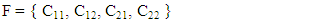


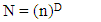
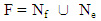
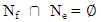

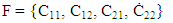
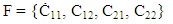
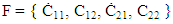



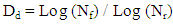



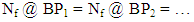
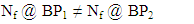
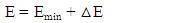
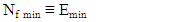
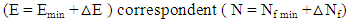
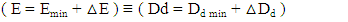




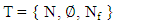
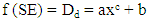

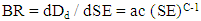





 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML