A. Bakhtiari1, 2, P. Kervalishvili1
1Georgian Technical University, Tbilisi, Georgia
2AT Advanced Technologies GmbH, Königsbrunn, Germany
Copyright © 2021 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Abstract
Atoms and molecules are known the smallest blocks of the matter. However, their substructure represent matter identification, but not sufficient to explain material physical properties like ductility, strength, work function, etc. Today matter structure (atoms or molecules arrangement) investigating is a stationary approach that particles are assumed fixed. Although particles untraceable movement is the main reason of stationary approach, but their nonregular motion is undeniable. Basically, the nonregular particles motion of the nanosystems is assumed as chaos in the common linear approach and then conducts investigations to the probability theory. But probability only focuses on the results of the random phenomenon, then the study of the reasons is disregarded. In this work, a new doctrine as Dynamic Fractal that comes out from Dynamic Topologic Space provides a new mathematical model for a lattice analysis as a system in space-time. Then, particles in the dynamic system are fractals components (in other words particles are not fragments) and they are in a harmonic movement. On the other hand, time is the main factor of any dynamic system, hence its role study is inevitable. As a matter of fact, the dynamic systematic approach by Dynamic Fractal doctrine shows a better understanding of nanomaterials structure. According to crystals strong dependency to material structure, this doctrine could be significant for crystals and crystallization analysis. Refer to crystals correlation to the crystallization process, this doctrine can provide more efficient crystals. Finally, more efficient products of industries as semiconductors, cutting machines, laser technology, watch industry, photovoltaic cells are expected.
Keywords:
Dynamic fractal, Topology, Matter structure, Nanosystem, Crystal, Lattice, Nonlinear system
Cite this paper: A. Bakhtiari, P. Kervalishvili, Dynamic Fractal Doctrine as Nonlinear Systems Model, American Journal of Condensed Matter Physics, Vol. 11 No. 1, 2021, pp. 1-6. doi: 10.5923/j.ajcmp.20211101.01.
1. Introduction
Human knowledge has plotted on phenomena quality and quantity investigation. However, quality provides the main concept of a phenomenon, but not enough without quantity. On the other hand, quantity is based on measurement and it correlates to dimensions relativity. Then, dimensions as quantity representative beside function concept as the quality representative (f(x) = y) became the base of human knowledge as a routine mathematical model. But, natural phenomena show sometimes some of them do not obey the pattern. Generally, scientists try to find a unique model of nature that explains phenomena in all scales [1]. But reality is shown different sizes as huge mass (celestial bodies), ordinary (usual world), or nanoscale (molecular or atomic) need different models [2]. Specifically, ordinary scale models cannot explain nanoscales. In the case, the most possible results estimation between all possibilities become bold as the base of probability theory. As an example, probability plus the energy level concept became the basis of the statistical thermodynamics [3,4,6]. However, probability doctrine cannot explain the process of a phenomenon occurring, but mostly sufficient. On the other hand, the ordinary scale of nature was the primitive realm of human study, hence the models of this scale became the foundation. Therefore, phenomena categorized as linear that observe the foundation, and nonlinear that do not observe it. [5]. Hence, a nonlinear phenomenon is presumed as a chaotic event that does not observe the linear approach rules. A chaos phenomenon is expected to contradict all the physical and mathematical laws. Then, if there is a nonlinear phenomenon that observes some of the rules (but not all of them), it is not chaotic instinctively. In other words, there should be a new doctrine that provides a new model. Basically, in the linear dynamic approach, matter position in space-time represent its identification. Also, it is expected a linear phenomenon observes the conservation law. However, the nonlinear phenomena do not consider space and time identification via the linear orientation [5] but they observe the energy conservation law. For instance, random motion of molecules in liquid or gas and their collision is assumed chaotic or nonregular motion [6]. But the temperature of water in a glass on the table in the room does not change spontaneously that represents energy conservation law observation.In this work, the new orientation provides a new mathematical model that not only describes particles (atoms or molecules) motion as a system but also brings up new concepts. In this doctrine, particles are not individual as fragments. Space is known as clusters for particles motion. A colony of specific number of clusters define Fractal and fractals make Lattice. Also, the energy conversion law observation goes to the Balance concept as essence of non-chaotic system. This doctrine as Dynamic Fractal defines nonlinear phenomena reason at the nanoscale by Dynamic Topologic Space concept [8].
2. Rules Review and Deduction
Reviewing the fundamentals with a glass of water on the table at room condition example will be easier to understand. But the doctrine does not restrict to the water molecular investigation. Generally, the movement of particles bases on energy conservation law. Therefore, any new theory must observe energy conservation law as well. According to the law, energy types in a system convert to each other, but the whole is constant (equation 1). Basically, particles movement categorized into three majors: 1. Ev: Vibrational2. Er: Rotational 3. Et: Transmission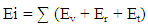 | (1) |
 | Figure 1. Nanoparticles momentum possibilities. vibrational motion in a, rotational motion in b, transitional motion in c |
Temperature is known as an indicator of matter nano particles. Therefore, no spontaneous temperature rising in the glass of water under constant conditions represents that they do not fight each other and then there must be a harmonic motion between particles. Hence, particles observe the energy conservation law. In other words, particles in a glass of water sense each other movement and maintain balance in the whole system in the way of energy conservation law.Therefore, system balance as the result of conservation law is possible only by the harmonic movement of the particles as a unique system. Hence, it is deduced a Self-Control Closed Loop (SCCL) explains particles movement and energy conversion of the nanosystem consequently (figure 2). According to the SCCL feedback role in the nanosystem Dynamic Balance keeping, time should be quantitated. Hence, particles movement in any time batch affects particles movement in the next time batch to find harmony in the system. Therefore, conservation law brings up the balance in the system.  | Figure 2. Self-Control Closed Loop |
Then, the Self-Control Closed Loop concept not only represents repetitive procedures but also shows any time batch will be a new event in the system. Hence it shows unpredictable nonlinear system concept. In short, in this doctrine particle position prediction in space-time is meaningless. But refer to energy conservation law observation, particles harmonic movements and SCCL balance should be the investigation key.
3. Balance Autopsy
According to identification by particles position in space-time through the linear approach, symmetry is the key to balance. Also, symmetry depends on the physical symmetry reference as a center or an axis. But in a nonlinear system it is meaningless; because if particle coordination is predictable, it will be linear. Dynamic Fractal doctrine via the systematic approach of SCCL is based on quantitated time. Hence, balance in a nonlinear system should be correlated to time batch. In other words, never a time batch could be in balance itself. Every time batch treats the previous time batch unbalancing, but it will be treated by the next time batch itself. Therefore, nature is always in balance seeking time batch to time batch and it is the nonstop particles movement reason.However, Self-Control Closed Loop and quantitated time approach define the quality of the Dynamic Fractal doctrine, but its quantity study is inevitable. Quantity investigation could be explained by Dynamic-Topologic space on Clusters and Knots as the Dynamic Fractal foundation.
4. Mathematical Structure of the Matter
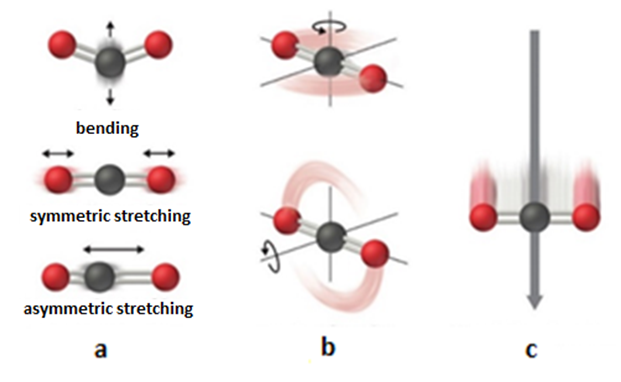
Again, the glass of water on the table could be a suitable example for the Dynamic Fractal mathematical model explanation. Particles (molecules or atoms) coordination, then their arrangement represents the structure of the matter. However, particles are not fixed but their fluctuation is limited around their position and then the stationary approach is based on average particle positions that show the main matter structure. Of course, different matter states represent a different arbitrary movement of particles, but the concept is the same. As an example, all water states have the semi same structure as are seen in short interval time photographing of water (figure 3). [9] 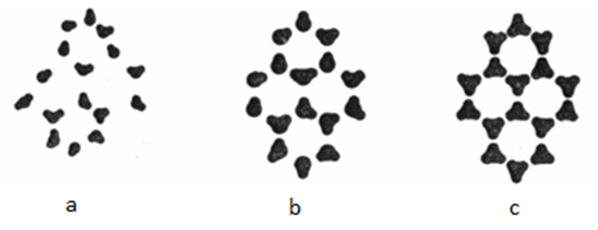 | Figure 3. Mean movement represents stable structure as gaseous in a, liquid in b, solid as ice in c [4] |
Then, the same mathematical model for all states could be acceptable. Now, a unit of a crystal (figure 4) will be a unit of Fractal.  | Figure 4. Crystal unit represents a Fractal |
Any particle in a Fractal assumes as a Knot that represents an atom or a molecule. Any Knot has its own partial space in the Fractal as a Cluster. Figure 5 shows a two-dimensional Fractal structure that could be customized in three-dimensional Fractal too.  | Figure 5. Clusters make a 2-Dimensional Fractal |
 | Figure 6. 3-Dimensional Fractal |
In summary, any Knot has its specific Cluster (in a time batch). Knots and Clusters make a Fractal and Fractals make a Lattice. In other words, Knots as fragments are not the base of investigation. Knots plus their Clusters make Fractals and Fractals in the Lattice are the foundation of the Dynamic Fractal model. Hence, according to the Fractal geometry concept, a Fractal repeats for all the Knots and Clusters in a Lattice (figure 7). [10,11]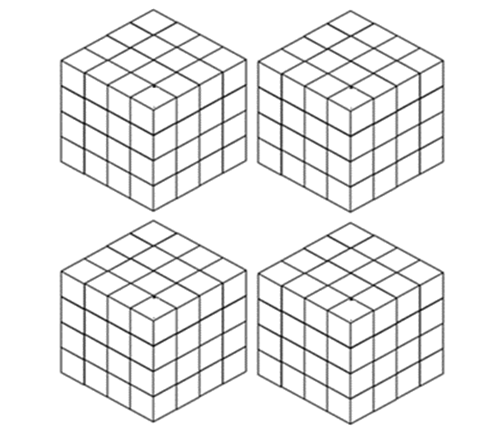 | Figure 7. Fractals make a Lattice |
Refer to the different stationary structures of different matters, Fractals sizes will be different. Anyway, Knots different presence in any time batch in Clusters of a Fractal represents the frequent motion of the particles. Hence, a Fractal is a set of Knots and Clusters and then the study goes to the set theory.Clusters are assumed as members of the set, then the set definition should be: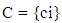 | (2) |
C: Setci: ClusterTherefore, Clusters (not Knots) are the main elements of the set. Knots presence in a time batch only separate Clusters as filled Clusters or empty Clusters. However, Knots Change their positions in a fractal frequently, but Knots number (filled Clusters) at specific standard conditions in a fractal is constant. Also, time to time batch period is constant and it is called Natural Balance Rate (NBR). It means filled Clusters in the Fractal change by the NBR and make a new pattern in every time batch to find balance. Hence, the NBR should be a symmetry reference in the nonlinear system. The set theory approach (equation 2) plus dynamic changes, nonlinearity and balance necessity conducts the investigation to Topologic Space that can be called Dynamic Topologic Space.According to a Fractal specification, Clusters are limited. Then, number of the C elements (equation 2) is clear. Hence, number of subsets is clear. On the other hand, number of filled Clusters in any time batch cannot be more than Clusters and then there are minimum and maximum possible filled Clusters in any time batch. Therefore, all possible patterns (filled Clusters) in any time batch could be subsets of the Fractal that represents a Topology on Fractal. [8,12,13]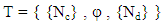 | (3) |
T: Dynamic Topology on Fractal Nc: Set of Clusters in a Fractal Nd: Set of filled Clusters It is a topology because:1. φ ∈ T2. {Nc} ∈ T3. Nc ∩ Nd = Nd ∈ T4. Nc U Nd = Nc ∈ T{Nd} represents a limited number of subsets on Dynamic Topology Space and then balance time to time must be a choice between subsets {Nd}. In other words, it is not infinite. Then, there must be a pattern for previous one to keep the balance at the next NBR regarding Self-Control Closed Loop feedback. Normally number of Clusters of a Fractal in a 3-dimensional cube (figure 6) is represented by equation (4). Then, all filled Clusters in a Fractal is represented in figure (8). 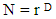 | (4) |
r: Cluster length on any sideD = 3 | Figure 8. Complete filled Clusters example |
But according to Hausdorff fraction dimension, there could be fractional dimension and then fractional space. A Fractal pattern by filled Clusters during every time batch represents a fraction of 3-dimensional space (Figure 9).  | Figure 9. Fractional filled Clusters during an NBR |
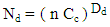 | (5) |
Nd: Number of filled Clusters in a Fractal in a NBRn: Number of Clusters in any direction in a FractalCc: Cluster unit in a Fractal is always a unitDd: Dynamic fraction Hence, Dd represents the nonlinear character of Dynamic Fractal.
5. Discussion and Achievements
According to Equation (4), Dd has a maximum as 3 and refer to equation (6) Dd should has a minimum; if there are some Knots that fill some Clusters in a Fractal. As an example, figure 5 shows a 2-dimensional stationary structure of the ice that could be expended to 3-dimentional as figure (6). In this case, minimum Dd is 1.29248125 (equation 6) that represents 6 filled Clusters (as the stationary structure of ice) in a Fractal by 64 Clusters. Hence, normally Dd is something between the minimum and maximum but constant at specific standard conditions. 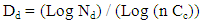 | (6) |
According to energy conservation law, when system conditions change by external energy as heating or any other type of energy, influence the number of filled Clusters in an NBR, and then Dd will change. Therefore, Dd corresponds to kinetic energy.As well as any other doctrine, Dynamic Fractal must observe energy conservation law. Then, a Fractal must obey the law. 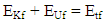 | (7) |
EKf: Kinetic energy in a FractalEUf: Potential energy in a FractalEtf: Total energy of a FractalRegards to Dd and Ekf correspondence, Etf represents maximum 3-dimensional space dimension as 3.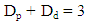 | (8) |
Dp: Potential fraction dimension of a FractalDd: Dynamic fraction dimension of a FractalDespite non-constant Etf for different materials, equation (8) shows a constant maximum space fraction for all matters in nature. It represents energy in the linear approach is based on Nd but in a nonlinear system depends on Dd. For instance, the minimum Dd of ice crystal in a fractal calculated 1.29248125 and then Dp will be 1.70751875 (equation 8). But empty correlated Clusters (Np) refer to equation (5) will be 10.66666667 that significantly different from 58 rest Clusters in a Fractal (minimum filled Clusters is 6 and total Clusters in a Fractal is 64). The energy conservation concept in a nonlinear system is clear but in a different way.According to the lattice investigation in Dynamic Fractal doctrine, crystallization could be one of the most important filed. Basically, the physical properties of matter depend on the structure that comes out from crystallization. In other words, better crystal quality provides better physical properties.Industrial crystallization or decrystallization needs an external source of energy as the laser beam, electricity, heat, etc. Hence, the external source of energy is assumed as the input of the Self-Control Closed Loop of Dynamic Fractal doctrine. On the other hand, crystallization quality depends on balance observation in the nonlinear system that refers to NBR and fractal consideration. Hence, external source pulse or flux should be matched with matter NBR and consider fractal requirement changes if the perfect crystallization is the target. Otherwise, mismatch input and Self-Control Closed Loop feedback conduct away crystal from balance and then qualified crystal. Also, unpleasant crystallization demolishing should be the same. As a case study, the doctrine has utilized in laser technology [14] for Laser wavelength and power estimation. It showed the accuracy of the doctrine in comparison to the routine methods (figure 10). 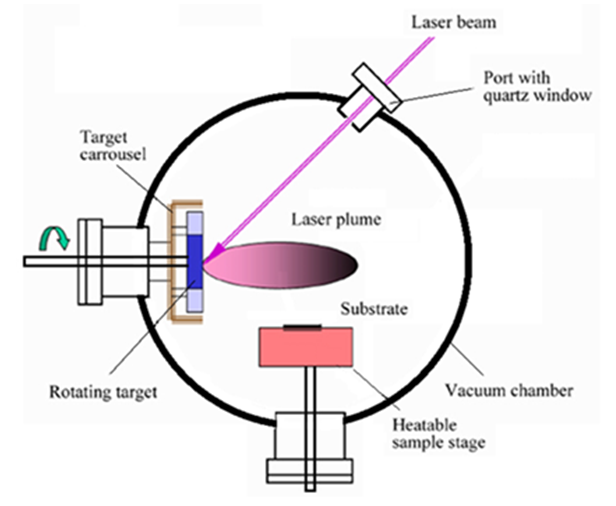 | Figure 10. Laser plume accuracy depends on laser wavelength and power |
6. Conclusions
A Simple question investigation conducted the nonlinear system into a new doctrine and deduction was the base of analysis. Scientific basics observation showed a new approach is inevitable. In this way, refer to nonlinearity of the phenomena, physical symmetry as the foundation of balance replaced by quantitated time mentality and it brought up Self-Control Closed Loop (SCCL) necessity. Then, particle tracing of the linear approach is removed. To prove the concept, the Set theory and Topology plus Hausdorff space used and refer to terminologies of mathematics, Dynamic Fractal model chose as the name of doctrine. Dynamic Fractal doctrine turns out particles in a matter are not fragments and they should assume as members of fractals. Also, SCCL time batch to time batch balance seeking shows the generator of nano the realm. As nature shows, in an artificial manipulation Natural Balance Rate (NBR) of the matter beside fractal assumption should be observed if balance is the target. In other words, any external energy to the system should be matched by NBR and fractal requirements if the perfect dynamic Lattice is the goal. On the other hand, unpleasant crystallization removal should be in the same way. Nowadays, crystal industries are seen in many applications as semiconductors (that brings different applications as electronic, communication, computer, etc), cutting machines (like the industrial diamond manufacturing), laser technology, watch industry, renewable energy (photovoltaic cells). Therefore, an efficient crystallization process brings more efficient equipment that could be possible by Dynamic Fractal doctrine.
ACKNOWLEDGEMENTS
The authors thank Hamed Hanifi from Fraunhofer institute CSP, Germany for reviewing of the paper. Also, the authors thank to Waldemar Maier from Advanced Technologies GmbH, Germany for funding the research.
References
| [1] | Kervalishvili P. On the mechanism of growth of small particles of elemental boron. Soviet journal of Solid State Physica, v. 29, №-4, 1987. |
| [2] | Bakhtiari, Berberashvili, & Kervalishvili. (2019). Clusters-Particles balance in matter by dynamic fractals. JAPMED 11 (pp. 92-93). Batumi, Georgia: Batumi Shota Rustaveli state university. |
| [3] | Chemistry. (n.d.). The Molecular Interpretation of Entropy. Retrieved from https://chem.libretexts.org/. |
| [4] | Eisenberg, & Kauzmann. (1969). The structure and properties of water. Oxfor university press. |
| [5] | Haliday, & Reznik. (8th edition). Fundamental of Physics. India: Winsome Books. |
| [6] | Linder. (2004). Thermodynamics and introductory statistical mechanics. Florida State university: A John Wiley & sons. |
| [7] | Mandelbrot. (1983). The fractal geometry of nature. H. B. Fenn and company Ltd. |
| [8] | Morris. (2019). Topolgy without tears. |
| [9] | Pathria. (1996). Statistical mechanics. Canada: University of Waterloo. |
| [10] | Peitgen, Jurgens, & Saupe. (2004). Chaos and Frcatals. Springer, ISBN: 0-387-21823-8. |
| [11] | Rydnik. (2001). ABC's of quantum mechanics. Hawaii: University of pacific. |
| [12] | University, B. (2018). Nonlinear systems. Retrieved from University of Birmingham: https://www.birmingham.ac.uk/. |
| [13] | Viro, Ivanov, Netsvetaev, & Kharlamov. (1948). Elementary topology. American mathematical society. ISBN 978-0-8218-4506-6. |
| [14] | H. Bakhtiari, T. Berberashvili, P. Kervalishvili (2018). Phototransmitting device. Patent No: P 2020 7134 B. |


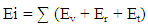







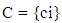
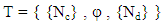
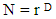


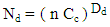
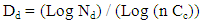
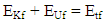
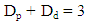

 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML