| [1] | Samara, G.A. 1976. Temperature and pressure dependence of the dielectric properties of alkaline-earth fluorides. Phys. Rev. B 13: 4529-4544. |
| [2] | Hazen, R.M. and Finger, L.W. 1981. Optical and lattice dynamical properties of simple ionic crystals. J. Appl. Crystallography 14: 234-245. |
| [3] | Song, K.S. and Williams, R.T. 1993. Alkaline Earth Fluorides. Solid-State Sciences 105: 96-122. |
| [4] | Evarestov, R.A., Murin, I.V. and Petrov, A.V. 1989. Electronic structure of fluorite-type crystals. J. Phys. Condens. Matt. 1: 6603-6609. |
| [5] | Voronin, B.M. and Volkoy, S. 2001. Ionic conductivity of fluorite type crystals CaF2, SrF2, BaF2, and SrCl2 at high temperatures. J. Phys. and Chem. of Solids 62:1349-1358. |
| [6] | Soni, S., Gupta, S.K., Talati, M. and Jha, P.K. 2011. The ground state and lattice dynamical study of ionic conductors CaF2, SrF2 and BaF2 using density functional theory. Physica B Condens. Matt. 72: 934-939. |
| [7] | Schmalzl, K. 2007. Volume and pressure dependence of ground-state and lattice-dynamical properties of BaF2 from density-functional methods. Phys. Rev. 75: 014306-014312. |
| [8] | Cadelano, E. and Cappellini, G. 2011. Electronic structure of fluorides: general trends for ground and excited state properties. Eur. Phys. J. 81: 115-120. |
| [9] | Nikiforov, A.I., Yakimov, A.I., Duarechenskii, S.A. and Chaikovskii, S.V. 2002. Barrier height and Tunneling current in Schottky diodes with embedded layers of quantum dots. J. Experimental and Theoretical Physics Letters 75: 102-106. |
| [10] | Wu, X., Qin, S. and Wu, Z. 2006. First-principles study of structural stabilities, and electronic and optical properties of CaF2 under high pressure. Phys. Rev. B73: 134103-134110. |
| [11] | Dorfman, S. M., Jiang, F., Mao, Z., Kubo, A., Prakapenka, V. and Duffy, T. S. 2010. Phase transitions and equations of state of alkaline earth fluorides CaF2, SrF2, and BaF2 to Mbar pressures. Phys. Rev. B 81: 174121-174129. |
| [12] | Hao A., Yang, X., Li, J., Xin, W., Zhang, S., Zhang, H. X. and Liu, R. 2009, First-Principles Study of Structural Stabilities, Electronic and Optical Properties of SrF2 under High Pressure. Chin. Phys. Lett. 26: 077103-077106. |
| [13] | Jiang, H., Pandey, R., Darrigan, C. and Rerat, M. 2003. First-principles study of structural, electronic and optical properties of BaF2 in its cubic, orthorhombic and hexagonal phases. J. Phys.: Condens. Matter 15: 709–718. |
| [14] | Liu, G., Wang, H., Ma, Y. and Ma, Y. 2011, Phase transition of cadmium fluoride under high pressure. Solid State Communications 151: 1899-1902. |
| [15] | Costales, A., Blanco, M.A., Pandey, R. and Recio, J.M. 2000. Theoretical characterization of the high-pressure phases of PbF2. Phys. Rev. B61: 359-362. |
| [16] | Barreda-Argueso, J.A., Lopez-Moreno,S., Sanz-Ortiz, M.N., Aguado, F., Valiente, H., Gonzalez,J., Rodrıguez, F., Romero, A.H., Munoz, A., Nataf, L. and Baudelet, F. 2013. Pressure-induced phase-transition sequence in CoF2: An experimental and first-principles study on the crystal, vibrational, and electronic properties. Phys. Rev. B88: 214108-214122. |
| [17] | Stavrou, E., Yao, Y., Goncharov, A., Konopkova, Z. and Raptis, C. 2015. High-pressure X-ray diffraction, Raman, and computational studies of MnF2. Phys. Rev. B93: 054101-054108. |
| [18] | Hoat, D.M., Rivas Silva, J.F., M´endez Blas, A. and R´ıos R´amirez, J.J. 2018. Effect of pressure on structural, electronic and optical properties of SrF2: A first principles study. Revista Mexicana de Fisica 64: 94-100. |
| [19] | Cappellini, G., Bosin, A., Serra, G., Furthmüller, J., Bechstedt, F. and Botti, S. 2020. Electronic and Optical Properties of Small Metal Fluoride Clusters. ACS Omega 22: 13268–13277. |
| [20] | Kaminskii, A., Mikaelyan, R. and Zygler, I. 1969. Spectral investigation of the stimulated radiation of Nd3+ in CaF2-YF3. Physical Status Solidi B 31: 85-86. |
| [21] | Siskos, S., Fountaine, C. and Munoz-Yague, A. 1984. Epitaxial growth of lattice-matched CaxSr1−xF2 on (100) and (110) GaAs substrates. J. Appl. Phys. 56: 1642-1646. |
| [22] | Oshita, T., Takahashi, K. and Tsutsui, K. 2009. Growth of ultra-thin fluoride heterostructures on Ge(111) for quantum devices. J. Crystal Growth. 311: 2224-2226. |
| [23] | Klimma, D. Rabe, M. Bertrama, R. Uecker, R. and Parthier, L. 2008. Phase diagram analysis and crystal growth of solid solutions Ca1−xSrxF2. J. Crystal Growth 310: 152-155. |
| [24] | Takahashi, K. and Tsutsui, K. 2013. Growth of Thin Epitaxial CaxSr1-xF2/SrF2 Layers with Low Leakage Current on Ge Substrate. Japanese J. Appl. Phys. 5: 100203-100207. |
| [25] | Suzuki, K., Cadatal-Raduban, M., Kase, M. and Ono, S. 2019. Band gap engineering of CaxSr1-xF2 and its application as filterless vacuum ultraviolet photodetectors with controllable spectra responses. Optical Materials 88: 576-579. |
| [26] | Furthmuller, J., Kachell, P. and Bechstedt, F. 2000. Extreme softening of Vander-bilt pseudopotentials. Physical Review B 61: 4576-4587. |
| [27] | Hohenberg, H. and Kohn, W. (1964), Inhomogenous electron gas. Phys. Rev. B136: 864-871. |
| [28] | Kohn, W., and Sham, L.J. 1965. Self-consistent equations including exchange and correlation effects. Phys. Rev. A 140: 1133-1138. |
| [29] | Giannozzi, P., Baroni, S., Bonini, N., Calandra, M., Car, R., Cavazzoni, C., Ceresoli, D., Chiarotti, G.L., Cococcioni, M., Dabo, I., Corso, A.D., de Gironcoli, S., Fabris, S., Fratesi, G., Gebauer, R., Gerstmann, U., Gougoussis, C., Kokalj, A., Lazzeri, M., Martin-Samos, L., Marzari, N., Mauri, F., Mazzarello, R., Paolini, S., Pasquarello, A., Paulatto, L., Sbraccia, C., Scandolo, S., Sclauzero, G., Seitsonen, A.P., Smogunov, A., Umari, P. and Wentzcovitch, R.M. 2009. QUANTUM RESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. 21: 395502-395520. |
| [30] | Perdew, J. and Wang, Y. 1992. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 45: 13244-13252. |
| [31] | Monkhorst, H.J., Pack, J.D., 1976. Special points for Brillouin-zone integrations. Phys. Rev. B 13: 5188-5192. |
| [32] | Murnaghan, F. D. 1944. The Compressibility of Media under Extreme Pressures. Proceedings of the National Academy of Sciences of the United States of America 30: 244-247. |
| [33] | Vegard, L. 1921. The constitution of mixed crystals and the space occupied by atoms. Zeitschrift fur Physik B: Condensed Matter 5: 17-26. |
| [34] | El Haj Hassan, F. and Akbarzadeh, H. 2006, First-principles elastic and bonding properties of barium chalcogenides. Comput. Mater. Sci. 35: 423-445. |
| [35] | El Haj Hassan, F., Hashemifar, S.J. and Akbarzadeh, H. 2006. Density functional study of Zn1−xMgxSeyTe1−y Quaternary semiconductor alloys. Phys. Rev. B73: 195-202. |
| [36] | Fahy, S., Chang, K.J., Louis, S.G. and Cohen, M.L. 1989. Pressure coefficients of band gaps of diamond. Phys. Rev. B 39: 7840-7847. |
| [37] | Bachelet, G.B. and Christensen, N.E. 1995. Relativistic and core relaxation effects on the energy bands of GaAs and Ge. Physical Review B 31: 879-887. |
| [38] | Onida, G., Reining, L. and Rubio, A. 2002. Electronic excitations: density-functional versus many-body Greens-function approaches. Rev. Mod. Phys.74: 601-659. |
| [39] | Boukhris, N., Meradji, H., Ghemid, S., Drablia, S. and Hassan, F.E.H. 2011. Ab initio study of the structural, electronic and thermodynamic properties of PbSe1-xSx, PbSe1-xTex and PbS1-xTex ternary alloys. Phys. Scr. 83: 065701-065709. |
| [40] | Morales-García, A., Valero, R. and Illas, F. 2017. An empirical, yet practical way to predict the band gap in solids by using density functional band structure calculations. J. Phys. Chem. 121: 18862-18866. |
| [41] | Cadelano, E. and Cappellini, G. 2011. Electronic structure of fluorides: general trends for ground and excited state properties. Eur. Phys. J. 81: 115-120. |
| [42] | West, A.R. 1999. Basic Solid State Chemistry. John Wiley and Sons, Chichester, England. 126pp. |
| [43] | Weast, R.C. 1976. Chemical Rubber Company Handbook of Chemistry and Physics, CRC Press, Boca Raton, Florida, United States. 2390pp. |
| [44] | Rubloff, G.W. 1972. Far-Ultraviolet Reflectance Spectra and the Electronic Structure of Ionic Crystals. Phys. Rev. B 5: 662-684. |


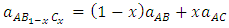
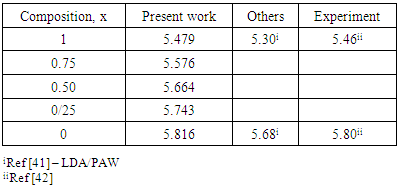
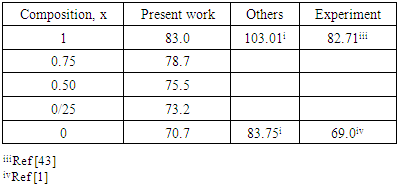
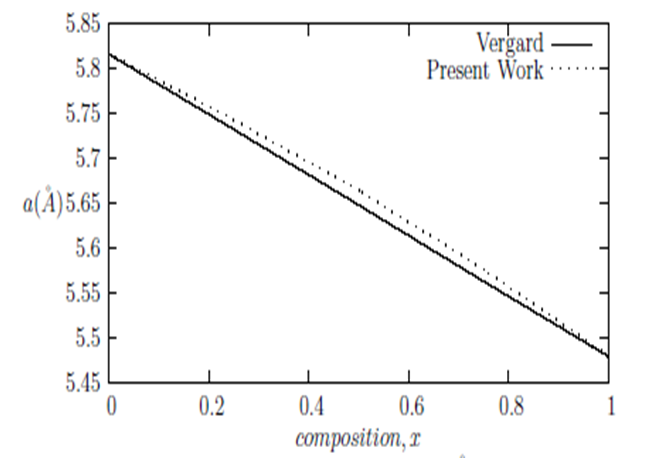
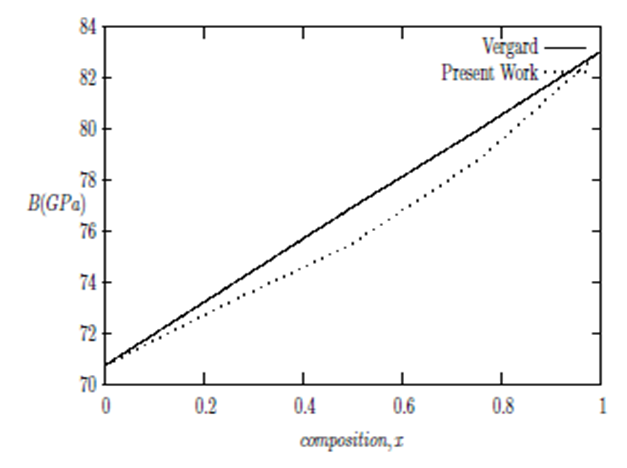
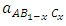 are the lattice parameters of binary compounds AB, AC and ternary alloy AB1-xCx respectively. However, the linear behaviour is not followed by many alloys and a general form is expressed by a semi-empirical quadratic relationship [34,35]. Hence, the lattice constant can be written as:
are the lattice parameters of binary compounds AB, AC and ternary alloy AB1-xCx respectively. However, the linear behaviour is not followed by many alloys and a general form is expressed by a semi-empirical quadratic relationship [34,35]. Hence, the lattice constant can be written as: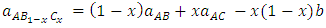
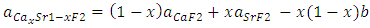
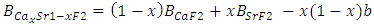
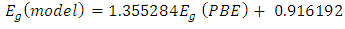
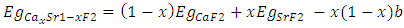
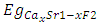 denotes the band gap energy of CaxSr1-xF2,
denotes the band gap energy of CaxSr1-xF2, 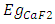 and
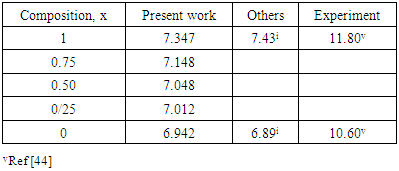
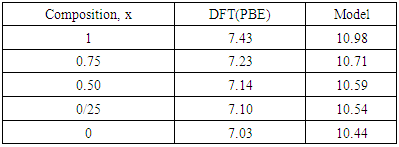
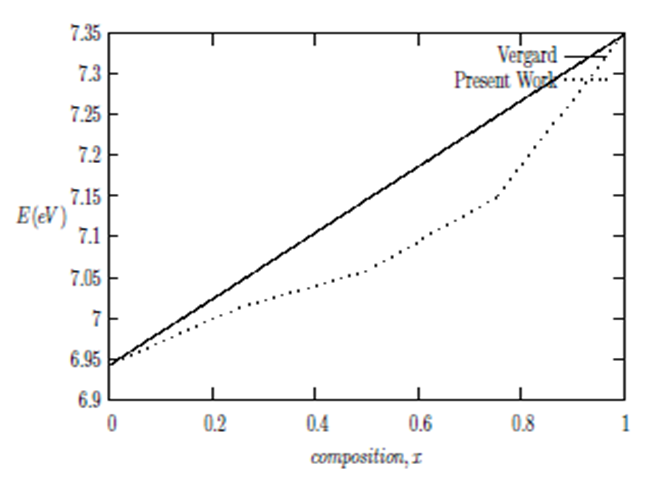
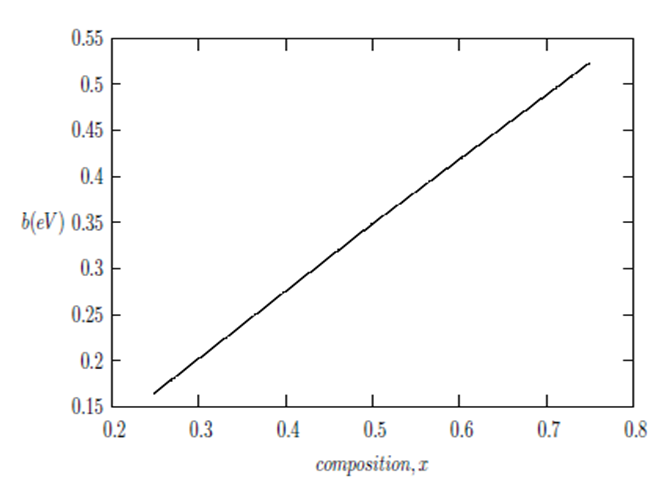
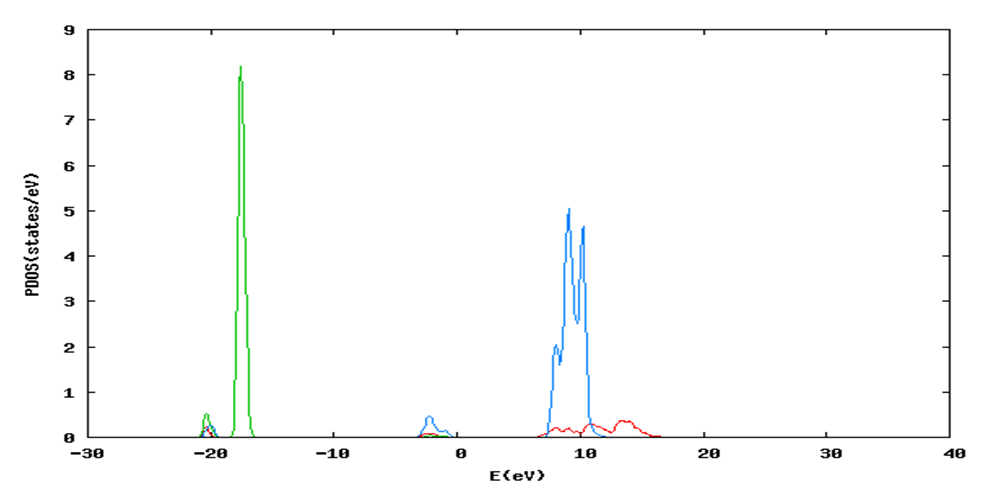
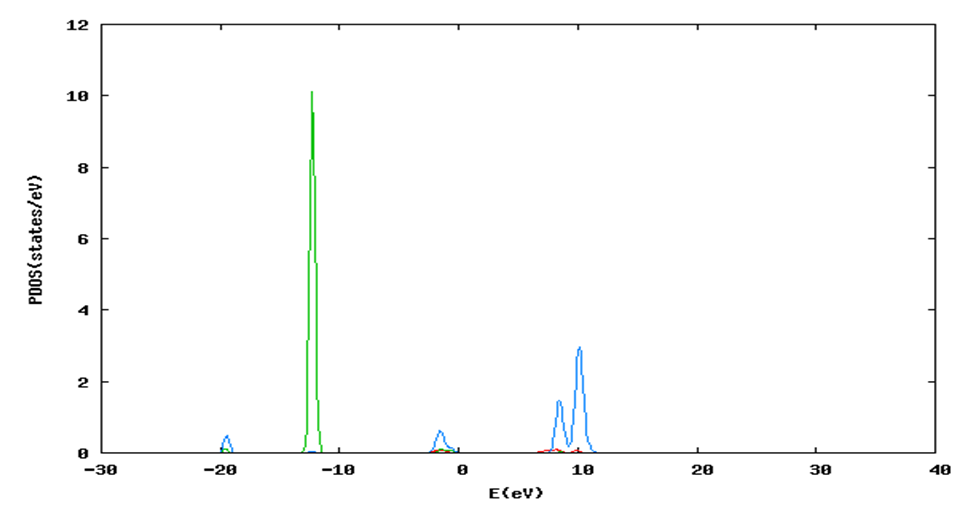
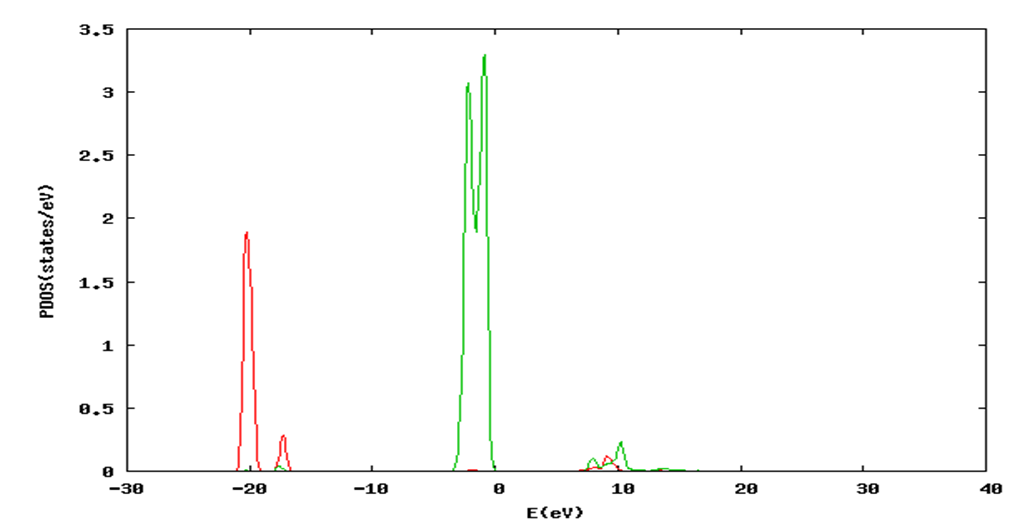
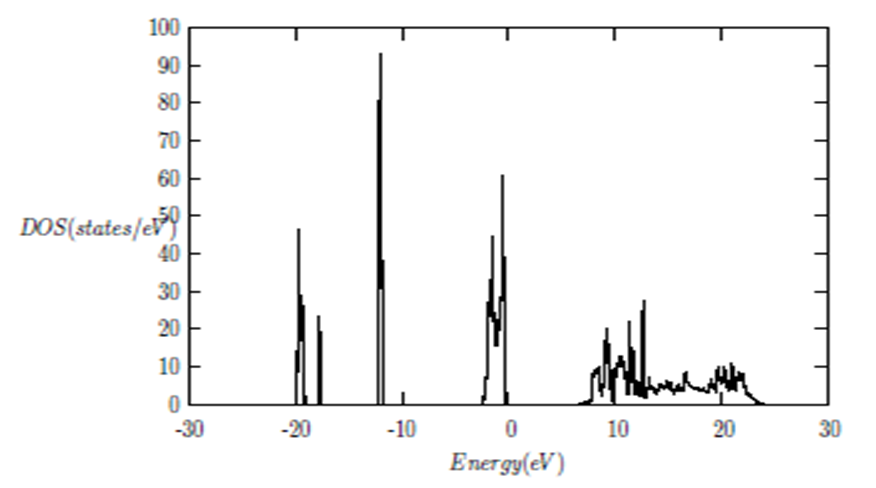
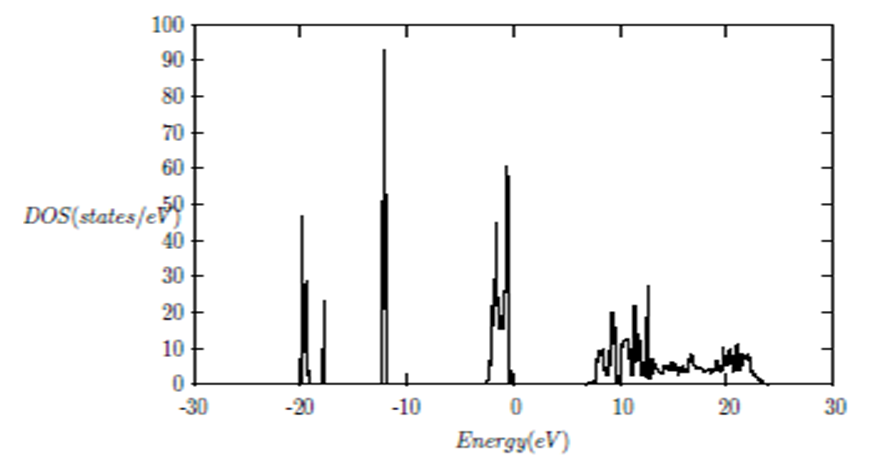
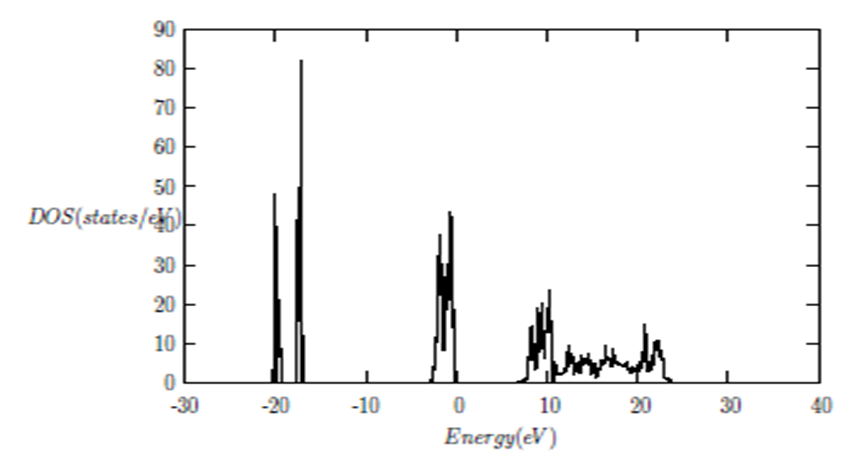
and 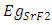 signify the band gap energy of CaF2 and SrF2, respectively while b is the band gap bowing parameter of CaxSr1-xF2.Figure 6 shows that the direct gap versus concentration, exhibit a non-linear behavior. The direct gap exhibits a downward bowing with a mean value of 0.345eV within the range of x investigated. The fundamental gap increases considerably with the Calcium composition, x. The variation of the band gap bowing in CaxSr1-xF2 with concentration is shown in Figure 7. The bowing remains linear and increases with calcium concentration.Figures 8, 9 and 10 show the partial density of states of Ca, Sr and F respectively. The red line represents s-orbitals, green line represents p-orbitals and blue line represents d-orbitals. Ca and Sr contain s, p and d orbitals while F contains only s and p orbitals. The partial density of states of the constituent elements of the alloys are used to analyze the total density of states of the alloys.The total DOS for the ternary alloys, CaxSr1−xF2 are depicted in Figures 11 and 12 at x=0.25 and 0.50 respectively. The DOS for these concentrations are very similar but the values of the peaks are different according to the composition. There are five regions. The peak at the lowest energy states, which is due to the s electrons of the fluorine, while the next two regions contain the contribution of Ca-s and Sr-s orbitals respectively. The region just below the Fermi level EF is predominately p states of F, with only a small contribution for p-Ca and p-Sr states. Above the Fermi level, the region is predominately p states of Ca and p and d states of Sr.The total DOS for the ternary alloy CaxSr1−xF2 is given in Figure 13 for the concentration x = 0.75. We observed four regions. The first region at the lowest energy states, is due to the s electrons of the fluorine, while the next region contains the contribution of Ca-s and Sr-s orbitals. The region just below the Fermi level EF is predominately p states of F, with only a small contribution for p-Ca and p-Sr states. Just above the Fermi level, the region is predominately p states of Ca and p and d states of Sr.From the DOS plots, as Ca composition increases in the alloys, the density of states of Ca-s and Ca-p orbitals decrease while the density of states of Ca-d orbitals increase. The DOS of s orbital of F increase with Ca concentration in all the alloys while that of p orbitals decrease. The DOS of s, p and d orbitals of Sr decrease with Ca composition in the alloys.The DOS for the different concentrations of all alloys indicate that the band contributions of Ca-s, Ca-p, Sr-s, Sr-p, Sr-d, and F-p orbitals gradually weaken with Ca composition but Ca-d and F-s orbitals contributions strengthen.
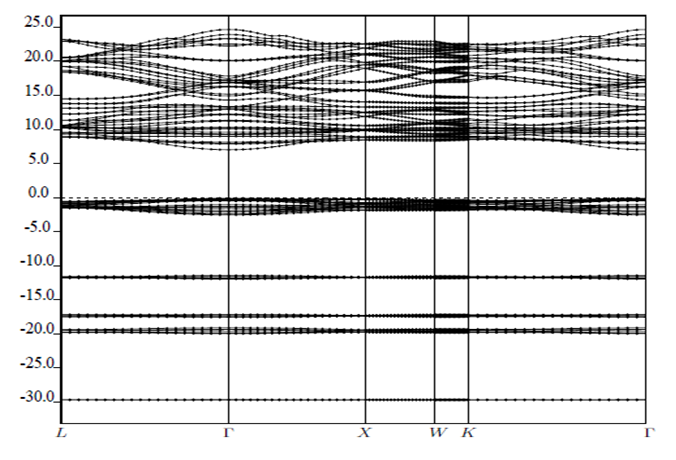
signify the band gap energy of CaF2 and SrF2, respectively while b is the band gap bowing parameter of CaxSr1-xF2.Figure 6 shows that the direct gap versus concentration, exhibit a non-linear behavior. The direct gap exhibits a downward bowing with a mean value of 0.345eV within the range of x investigated. The fundamental gap increases considerably with the Calcium composition, x. The variation of the band gap bowing in CaxSr1-xF2 with concentration is shown in Figure 7. The bowing remains linear and increases with calcium concentration.Figures 8, 9 and 10 show the partial density of states of Ca, Sr and F respectively. The red line represents s-orbitals, green line represents p-orbitals and blue line represents d-orbitals. Ca and Sr contain s, p and d orbitals while F contains only s and p orbitals. The partial density of states of the constituent elements of the alloys are used to analyze the total density of states of the alloys.The total DOS for the ternary alloys, CaxSr1−xF2 are depicted in Figures 11 and 12 at x=0.25 and 0.50 respectively. The DOS for these concentrations are very similar but the values of the peaks are different according to the composition. There are five regions. The peak at the lowest energy states, which is due to the s electrons of the fluorine, while the next two regions contain the contribution of Ca-s and Sr-s orbitals respectively. The region just below the Fermi level EF is predominately p states of F, with only a small contribution for p-Ca and p-Sr states. Above the Fermi level, the region is predominately p states of Ca and p and d states of Sr.The total DOS for the ternary alloy CaxSr1−xF2 is given in Figure 13 for the concentration x = 0.75. We observed four regions. The first region at the lowest energy states, is due to the s electrons of the fluorine, while the next region contains the contribution of Ca-s and Sr-s orbitals. The region just below the Fermi level EF is predominately p states of F, with only a small contribution for p-Ca and p-Sr states. Just above the Fermi level, the region is predominately p states of Ca and p and d states of Sr.From the DOS plots, as Ca composition increases in the alloys, the density of states of Ca-s and Ca-p orbitals decrease while the density of states of Ca-d orbitals increase. The DOS of s orbital of F increase with Ca concentration in all the alloys while that of p orbitals decrease. The DOS of s, p and d orbitals of Sr decrease with Ca composition in the alloys.The DOS for the different concentrations of all alloys indicate that the band contributions of Ca-s, Ca-p, Sr-s, Sr-p, Sr-d, and F-p orbitals gradually weaken with Ca composition but Ca-d and F-s orbitals contributions strengthen.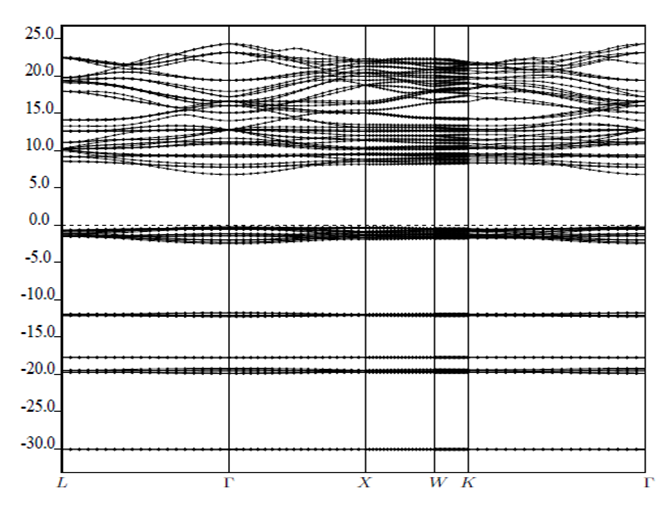
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML