1. Introduction

The phenomenon of ferroelectricity is very similar to ferromagnetism. Ferroelectric crystals are spontaneously polarized crystals with the ability to change the direction of polarization by external electric field. A ferroelectric crystal phase usually (but not necessarily) arises by means of a phase transition from the non-polar higher-temperature paraelectric phase. There are two kinds of the paraelectric phases. Their zero polarization results either from a centrosymmetric distribution of positive and negative charges in the crystal unit cell, or from thermal molecular rotation in the crystal lattice. All ferroelectrics exhibit a domain structure. As the temperature goes down, ferroelectrics typically exhibit a few ferroelectric-to-ferroelectric phase transitions. These features distinguish ferroelectrics from pyroelectrics which have neither domain structure, nor succession of phase transitions, and their polarization cannot be changed by external electric field.

Since discovered in 1920 in Rochelle salt, ferroelectricity was identified in numerous other substances and presently has important technological applications. The literature is plentiful, but usually phenomenological or technological. The available physical theory of ferroelectricity, that assumes a ferroelectric phase transition to be a critical phenomenon is invalid. We will show that a sound theory could not be developed without acceptance of the universal nucleation-and-growth molecular mechanism of solid-state phase transitions. This mechanism was put forward and described by the present author a number of times [e. g., 1-3], but had not yet entered the orbit of conventional theoretical thinking. Considering that understanding of solid-state phase transitions is a key to physics of ferroelectricity, this universal mechanism is concisely described here again.

2. Universal Nucleation-and-Growth Mechanism of Phase Transitions

2.1. History

The correct interpretation of solid-state phase transitions is vital in revealing the physical nature of ferroelectricity, as it is in the cases of ferromagnetism [1,4] and superconductivity [5]. But there was a long-standing hurdle to overcome in the way of their investigation. In 1933 a theory of phase transitions took a wrong turn when Ehrenfest misinterpreted the high peak in the calorimetric measurements of liquid helium as evidence of a new type of phase transitions. He named them asecond-order phase transitions, while the “usual” ones became first order. In spite of the rigorous proof by Justy and von Laue that the “second-order” phase transitions do not comply with thermodynamics, the suggested new phase transitions were welcomed by theoretical physicists as an opportunity to apply their knowledge of statistical mechanics.

In 1937 the research went further off course when L. Landau presented the theory of second-order phase transitions. After being unanimously accepted for many years by physical science, such phase transitions were ultimately proven to not exist [5,6]. Until that fact is accepted by modern physics, they still have to be dealt with in the areas where phase transitions play important part. Ferroelectricity is one of these areas.

2.2. First- and Second-Order Phase Transitions

Second-order phase transitions are assumed to be a process when thermal fluctuations over the crystal are intensifying with the temperature until reaching a “critical point” T_C where the crystal becomes totally unstable and the phase transition starts and completes at once. This dramatic event seemed to require changing the crystal structure instantly. However, such a macroscopic physical change at a “critical point” would be at variance with thermodynamics. Therefore, Landau made the transition to be “continuous”: any changes of the crystal structure at T_C are infinitesimal, only the crystal symmetry “jumps” sharply; the two phases cannot coexist; the temperature hysteresis is strictly zero; no heat is absorbed or emanated. These clear-cut characteristics have become instrumental in the eventual conclusion [1,5] that second-order phase transitions do not exist and made it easy to prove in any particular case that the ferroelectric phase transition is not second order.

First-order phase transitions are the ones we deal with in reality. Landau described them as exhibiting abrupt “jumps” in the state of the matter, at which latent heat is absorbed or released, symmetries of the phases are not related, and overheating or overcooling is possible. Other than listing their characteristics, no idea about the possible molecular mechanism of first-order phase transitions was offered.

Two crystal phases of a substance are independent of each other, whether their structures are similar or not. They occupy different areas in the phase diagram and can in principle be produced separately (from a liquid phase, for example) under the conditions where each is stable. Only one way of phase transition between them is in compliance with thermodynamics: an infinitesimal change of a controlling parameter (temperature, electric field, magnetic field, or pressure) gives rise to the material transfer of an infinitesimal quantity of the original phase to the new phase [5,7,8]. It is imperative to realize that no other way exists. Thus, a cooperative phase transition by instant “distortion” or “deformation” of the original crystal, or “displacement” of any its constituent particles, is not possible.

The nucleation-and-growth molecular mechanism described in next sub-sections is in compliance with the above requirements. It is the only alternative to the “second order” type. Its macroscopic indicators are: interfaces, phase coexistence, range of transition, hysteresis. Observation of any of them is sufficient to identify the transition as not “second order” and, therefore, statistical mechanics is not applicable, for there is no bulk statistics. The real (“first order”) and imagined “second order” phase transitions are antipodal and irreconcilable.

Any changes in solids are never a coordinated simultaneous movements of many particles. The real process is a molecule-by-molecule rearrangement; it is universal. The popular maneuver to justify treatment of some first-order transitions by statistical-mechanics by claiming they are “weakly first order” (or “almost,” or “close to” second order) is nonsensical: either the phase transition is localized at interfaces, or involves simultaneously all particles in the bulk. No middle is imaginable.

2.3. Nucleation in Microcavities. Hysteresis

Nucleation of the alternative phase in solid-state phase transitions differs in all respects from the theoretically-born fluctuation-based statistical picture described in the Landau and Lifshitz textbook (Section 150 in [9]). Nucleation in a given crystal is pre-determined as for its location and temperature. It would not occur at all in perfect crystals, but such crystals are extremely rare. The nucleation sites are located in specific crystal defects – microcavities and microcracks of a certain optimum size. These sites contain information on the condition (e. g., temperature) of their activation. Nucleation temperatures are not the same in different defects. A nucleus is activated only after the temperature T₀ marking the equality of free energies F1 = F2 has been passed. The nucleation lags are inevitable in both directions of phase transitions. Hysteresis is a necessary component of the phase transition mechanism. At least some finite hysteresis is inescapable. Its value is not exactly reproducible. The “ideal phase transition” (i. e., without hysteresis) cannot occur due to absence of a thermodynamic driving force ΔF. (F1 - F2 = 0 at T = T₀).

Along with the hysteresis of initiation of the new phase there is also much smaller, but consequential, hysteresis of sustaining the transition when the two phases already coexist. It will be explained in section 2.5.

2.4. Temperature of Phase Transition. Range of Transition

Temperature of phase transitions is regularly treated in scientific literature as T_C, calling it “critical temperature” (or “Curie temperature” or “critical point”) – the term designated for “critical” phenomena. This is a consequential mistake, a source of countless misinterpretations of the nature of phase transitions. Then, when the value of a measured property p shows a rapid change “in the vicinity of transition” on the experimental plots p(T), this is interpreted as a pre-transition effect. Or the plots may show p(T) not being sharp, and in some cases even rather smooth. The phase transitions look complicated. Location of the phase transition temperature becomes a subject of guessing, and the curves become a subject of mathematical delineation.

The cause of these seeming complications is that a phase transition cannot occur at T₀ due to hysteresis. It is always spread over some temperature range located after the T₀ has been passed. In that range the coexisting phases continue to be static over their bulk, while their ratio is changing by local rearrangement at the interfaces. Simply marking the correct T₀ position (it can be found by extrapolation) will erase the mystery. As for the transitions looking sharp in the plots p(T), they will not be quite sharp if recorded with a higher resolution.

2.5. Rearrangement at Contact Interface

A solid-state phase transition is intrinsically a local process. It proceeds by “molecule-by-molecule” structural rearrangement at interfaces only, while the bulk of both the original and emerged phases remain static (Fig.1). No “jumps” of macroscopic quantities or properties occur. The seeming “jumps” appearing on the experimental recordings are simply the differences between the crystal structures or their physical properties when the transition range is either narrow, or passed quickly, or both. Coexistence of the phases during phase transition is self-evident. Simple observation of simultaneously present phases is a solid proof of the nucleation-and-growth phase transition.

Figure 1. Stepwise (or edgewise) molecule-by-molecule rearrangement at the contact interface. The process is located at “kinks” on the crystal faces of the emerging phase (upper part) and proceeds by building up layer-by-layer that way, while the original phase is dissolving. No structural orientation relationship between the phases is necessary. This molecular mechanism is in accord with thermodynamics requiring only an “infinitesimal” quantity (in macroscopic terms) of the matter to be transferred at a time

The phase transition illustrated by Fig. 1 leads to the question of whether it is continuous or discontinuous. Real transitions are not discontinuous in the traditional interpretation of first-order phase transitions; they are not an instant jump of the whole crystal into a new phase. Instead, the transition is quantitatively spread over a temperature interval. But within that interval it is locally discontinuous. Every completed molecular layer requires nucleation to initiate the next layer. We call it 2-D nucleation as compared to the 3-D nucleation that initiates a new phase. The 2-D nucleation lags give rise to hysteresis, and they are also responsible for the Barkhausen effect (Section 4.10 in [1]). The hysteresis of this type is much smaller than the one described in section 2.3 but is essential, for example, in the formation of ferroelectric domain structures.

2.6. Epitaxial Type of Phase Transitions

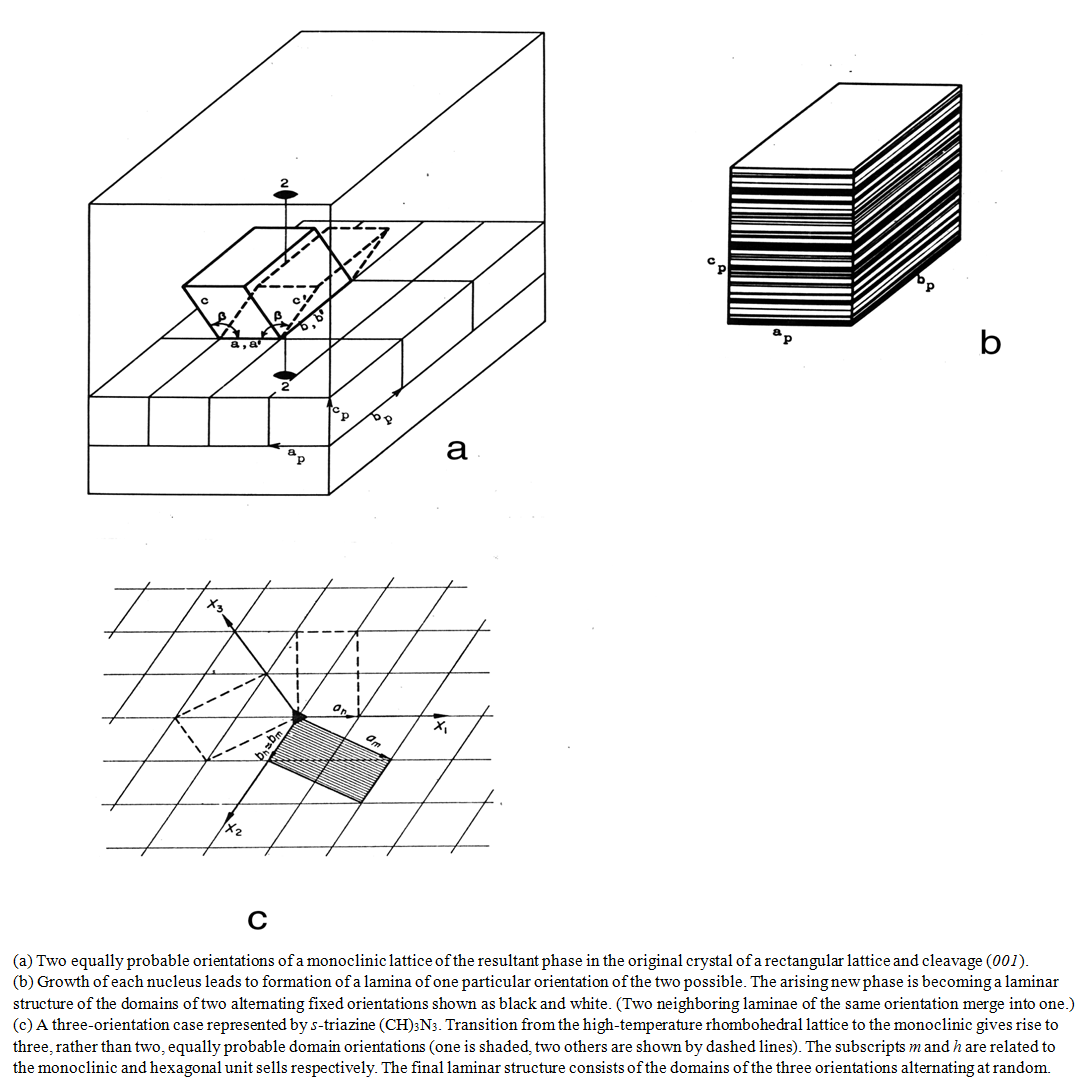
Fig. 1 illustrates a case when the crystal orientations of the phases are not related. This is because the nuclei initiating the phase transition in the crystal defects can, in principle, be oriented arbitrarily. However, a structural orientation relationship (OR) is frequently observed. That does not mean these transitions materialize by a modification or deformation of the original structure, as is still generally believed. These transitions materialize by nucleation and growth, no matter how similar the crystal structures could be. The two phases are independent of each other. The cause of the OR in these cases is oriented nucleation.

When OR is rigorous, we call the transition epitaxial. There are two circumstances when it takes place. One is in pronounced layered structures. A layered crystal consists of strongly bound, energetically advantageous two-dimensional units − molecular layers, usually appearing almost unchanged in both phases. When comparing the structures, they differ only by their layer stacking. The interlayer interaction in these crystals is relatively weak by definition. Accordingly, the divergence between the total free energies of the two structural variants is small, which is a precursor of polymorphism. Nucleation occurs in the tiny interlayer cracks. Given the close structural similarity of the layers in the two polymorphs, the nucleation is epitaxial due to the orienting effect of the “substrate” – the opposite surface of the crack (Fig. 2). The layers after the transition retain their original orientation.

Figure 2. Initial stage of phase transition in a layered crystal. Orientation of the layers is retained. (a) A microcrack: its flat shape enhances the surface interaction and is responsible for the orienting effect. (b,c) Alternatively oriented embryos of the new phase consisting of the same layers, but different layer stacking. After coming into contact, a domain structure is produced

Another case of epitaxial nucleation is when the unit cell parameters of the polymorphs are extremely close (roughly less than 1%) even in non-layered crystals. That condition is met, for example, in some order-disorder phase transitions (as observed in paramagnetic – ferromagnetic phase transition of iron [1,10]).

Epitaxial phase transitions exhibit themselves in a specific way: the OR is rigorous, the Laue X-ray patterns of the phases appear almost identical, temperature hysteresis can be small and easily missed, so is the latent heat, etc. It is the epitaxial phase transitions that are taken for “displacive”, “soft-mode”, or “second-order”. In reality they are all “first order,” having materialized by nucleation and growth. All ferroelectric phase transitions, sorted out by “displacive” and “order-disorder” in the literature, have one and the same molecular mechanism: epitaxial nucleation-and-growth.

3. “Classical Principles” of Ferroelectrics

3.1. Identifying Those Principles

The book Principles and Applications of Ferroelectrics and Related Materials by Lines and Glass (L&G), 677 pages, including 30 pages of references, first published in 1977, was re-printed in 2001 by Oxford University Press in its series Oxford Classical Texts in the Physical Sciences [11]. We will examine whether that stamp of approval by a major publisher was justified. First, it should be found what particular principles were behind the words “principles of ferroelectrics”. Then we consider if they are valid.

In a few decades after the discovery of ferroelectricity the attempts to understand the phenomenon were aimed at analyzing “ferroelectric instability” in every particular case that ferroelectricity was found. It was believed that spontaneously polarized crystals appear by displacive phase transitions of the “original” (or “prototype”) non-polar paraelectric crystal phases. The positive and negative charges in paraelectrics neutralize each other, and ferroelectric transitions represent displacements of some their atoms or molecules. However, the actual physical process of the displacements remained unknown. We find that the above “principles” by L&G are reduced to their claim that those displacements have a “soft-mode” molecular mechanism: “The microscopic breakthrough came in 1960 with the recognition of the fundamental relationship between lattice dynamics and ferroelectricity and, most importantly, of the existence of soft-mode instability at a ferroelectric transition … The great value of the soft-mode concept is that it enables us to form a reasonably unified microscopic picture of ferroelectricity … It then becomes possible to... grasp the relationship of ferroelectricity to the more general field of structural transitions and even to critical phenomena in general”. Accordingly, the book was saturated by “critical phenomena”: soft-modes, second-order phase transitions, Hamiltonians, Curie points, statistical mechanics, Landau theory, and so on. Nothing of that has the slightest relation to the real physics of ferroelectricity.

Remarkably, all those “critical phenomena” coexisted with the recognition that “most ferroelectric phase transitions are not of second order but first.” Lack of knowledge in the area of phase transitions (characteristic of the most current literature as well) made the L&G contribution to the physical sciences counterproductive.

3.2. The Soft-Mode Concept

Over the years there was a sequence of proposed mechanisms of phase transitions: displacive, martensitic, topological, soft-mode, incommensurate, scaling, quantum. None was successful [8]. The soft-mode concept was put forward in about 1960 to explain the mechanism of displacive ferroelectric transitions, but then artificially extended to the non-displacive order-disorder ferroelectric transitions and, finally, to all “structural” phase transitions. According to the theory, a structural phase transition is a cooperative distortion of the original crystal structure as a result of atomic / molecular shifts (displacements) in it. This distortion is produced by one of the “soft” (i. e., low-frequency) optical modes. That soft mode further “softens” with decreasing temperature until reaching T_C – the critical point when its wavelength becomes comparable with the crystal parameters. At that point the atomic displacements make the crystal unstable and the displacements suddenly become “frozen”, producing the alternative phase. It is to be noted that such transition, considered to be second order, is not “continuous”, as second-order phase transitions are defined to be.

The soft-mode concept was developed, tested and demonstrated by using ferroelectric BaTiO₃ as an example; even “jumps” of the physical properties at the (non-existent) Curie points were calculated. But the same BaTiO₃ was used by Landau to illustrate a continuous second-order phase transition. Evidently, at least one of the two conflicting approaches must be incorrect. Actually, both were wrong: the “first-order” nature of the BaTiO₃ phase transitions is now well established. Instead of the fixed critical points, temperature hysteresis of the transition temperatures wider than 10°C was observed.

In many experimental works on phase transitions no “good” soft-modes, properly softening toward the transition temperature, have been found. Many phase transitions were between the crystal structures so different that presenting the process as “distortion” of the original structure was unimaginable. Also, the model was inconsistent with the observations of phase transitions by moving interfaces. But the best argument against the soft-mode mechanism is the photographs of well-shaped crystals growing inside the original single crystal [1,12]. The soft-mode concept of phase transitions has not justified the hopes of its inventors. Except for some ferroelectric theories, it has fallen into oblivion.

3.3. Thirty Years After “Soft-Mode Principle”

A collection of eight articles entitled Physics of Ferroelectrics – A Modern Perspective [13] was intended to update the physical science on ferroelectricity 30 years after the 1977 L&G book. The Editors, Rabe, Ahn and Triscone, called the L&G book “classic” and a “sound foundation.” The articles were supposed to be “a complement that brings the reader from that sound foundation up to the present”. As for the physics of ferroelectricity, the following excerpts from the introductory article by K. M. Rabe and four co-authors, entitled Modern Physics of Ferroelectrics: Essential Background, tell all we need to know about the promised scientific advancement:

“The symmetry-breaking relation between the high-symmetry paraelectric structure and the ferroelectric structure is consistent with a second-order transition, and can be described with a Landau theory. Phonon spectroscopy continues to play a central role in the characterization of ferroelectric transitions. The soft-mode theory is illuminating, despite the fact that in many perovskite ferroelectrics the transition is weakly first order”.

Thus, there was no positive development in understanding of ferroelectricity. Application of the Landau theory was postulated without any justification. The “soft-mode” concept was not discarded. The science was still on the wrong critical phenomenon track. The nucleation-and-growth approach to phase transitions was still absent. The only new element was labeling many first-order phase transitions “weakly” as an excuse to justify treating them as second order. Not surprisingly, all basic facts about ferroelectrics remained explained incorrectly, or not explained at all.

3.4. I.S. Zheludev's Comprehensive Review

The earliest comprehensive review of the phenomenon of ferroelectricity belongs to I. S. Zheludev, who presented it in two 1971 volumes Physics of Crystalline Dielectrics [14] and the 1973 Russian version “Foundations of Segnetoelectricity” [15]. That pioneering work, preceding the L&G “classical” book by several years, was hardly possible to overlook; yet it was not included in their 30-page list of references. The Zheludev work, however, was more reasonable and informative as far as physics of ferroelectricity is concerned. All aspects of ferroelectricity were systematically investigated and discussed: crystallography, definition, difference from pyroelectrics, crystal structure of ferroelectrics, their stability, their domain structure, domain boundaries, dependence of spontaneous polarization on temperature, hysteresis loops of polarization, and more.

It is not to say Zheludev was always correct. For the most part he was not. His efforts were impaired by a disarray in the adjacent scientific area – phase transitions. There was a unanimous belief in the existence of second-order phase transitions, as well as in the displacive mechanism, and Zheludev did not escape it. He sorted out the ferroelectric phase transitions by first/second order and treated the formation of ferroelectrics from paraelectric phase as “displacements” and “ordering.” The universal nucleation-and-growth mechanism was only in its formulation stage at that time and certainly was unknown to Zheludev. His ultimate goal to uncover the physical origin of ferroelectricity was not achievable. But his work represented a good starting point for moving forward. He will be mentioned time and again in next sections.

4. Foundations of Ferroelectricity (Our Presentation)

4.1. On Classification of Ferroelectrics

Kittel [16] stated that ferroelectric crystals are classified into displacive and order-disorder “according to whether the transition is associated with the ordering of ions or .. the displacements of a whole sublattice of ions of one type...”. Zheludev explained that it was impossible to provide a satisfactory classification of ferroelectrics in terms of their properties, but “[that] can be made on the basis of the mechanism of the appearance of spontaneous polarization”, namely, was it by “displacements of certain ions” or by “ordering of certain structure elements”.

There was a silent problem with that classification: it was incomplete. Some ferroelectrics did not have the “Curie point,” because, as was explained by several authors, the material melts before the Curie point was reached. It was hardly a sound argument, for it tells us only about a disappearance of the ferroelectrics with rising temperature. Reverse the direction of temperature change – and we deal with formation of these ferroelectrics by melt crystallization. Therefore, one more type had to be added to the displacive and order-disorder ferroelectrics: melt-crystallized ferroelectrics. After that, to make the classification complete, the ferroelectrics crystallized from solutions should be added to the three.

The current classification of ferroelectrics is based on the lingering ignorance about solid-state phase transitions. Formation of ferroelectric crystals by two different mechanisms of phase transitions was the only base for that classification. But such mechanisms do not exist – and neither does the base. There is only one mechanism for all ferroelectrics to appear: crystallization.

4.2. Formation of Ferroelectrics

Lines and Glass stated that “the great value of the soft-mode concept is that it enables us to form a reasonably unified microscopic picture of ferroelectricity...” Instead, it rather divided ferroelectrics in two categories, since the soft-mode concept covered only the displacive, but not the order-disorder type. And it does not even count the ferroelectrics that appear from liquid phase.

Ferroelectrics do not emerge by displacements in paraelectric crystals or by ordering. Phase transitions involving a modification of the original crystal do not exist. The essence of the universal nucleation-and-growth mechanism, described in section 2, is a construction of the new crystal from the molecular material supplied by the original crystal. It is not like a renovation of an old house; it is a construction of the new one nearby by using bricks from the old house. The new house can look different; but it can also be very similar, in which case it would not mean that it appeared by a “distortion” of the old one.

The structure of the original phase in ferroelectric phase transitions, and whether it is solid or liquid, is irrelevant. The soft-mode concept did not provide the unified picture of how ferroelectricity comes into being. Crystallization does. All ferroelectrics (and antiferroelectrics too) are produced by nucleation and growth, using the original phase as a source of building material whatever it is: ordered crystal, orientation-disordered crystal, or liquid.

4.3. Distortion and Strain

According to the conventional theories, a displacive ferroelectric phase transition is distortion of the nonpolar paraelectric crystal by displacement of certain particles in its unit cell. The distortion causes strains, so they were added to the theory. Both these phenomena turn out to be fictitious after the realization that real phase transition – crystallization – does not involve systemic distortion of the ferroelectric crystals it produces. It is to be noted that the ferroelectric crystals grown from liquids cannot be thought of as distorted and strained original crystals, because the original medium was liquid phase.

4.4. Stability of Spontaneously Polarized Crystals

Spontaneously polarized crystals appear in the 10 polar symmetry classes. The question is why they appear at all, considering that a system of the mutually neutralized positive and negative electric charges, as in paraelectrc crystals, is more thermodynamical advantageous than a system of parallel dipoles in polar crystals. Therefore, Zheludev pointed out: “It is essential to understand, at least qualitatively, why the spontaneous polarization states of some crystals are thermodynamical stable” [15]. The answer, which typically escaped attention, is rooted in the fact that the interaction of electric charges alone in polar crystals does not determine their overall stability. The total contribution of all components of the crystal free energy F does.

Potential energy of atomic or intermolecular bonding always towers above other F components. This is the case even in molecular crystals where, as known, the Van der Waals' intermolecular bonding is relatively weak. As estimated by Kitaigorodskii [17], the energy of electrostatic interactions in organic crystals does not exceed 5% of the sublimation energy. Thus, the contribution of the dipole-dipole interaction to the free energy F in spontaneously polarized molecular crystals is small. The relative contribution must be even much smaller in the crystals with a chemical bonding. The part played by such a “small contributor" is not always negligible, but is not essential in the polar crystals. They are stable in spite of the disadvantage of a parallel alignment of their electric dipoles. Quite similar reason made the Heisenberg's theory of ferromagnetism unnecessary [1,4], which was an attempt to find the cause of stability of a ferromagnetic state .

4.5. Origin and Formation of Ferroelectric Domain Structures

4.5.1. The Unifying Factor

The underlying factor unifying the origin of all ferroelectrics is a very close geometrical proximity of unit cells of their polymorphs. In case of crystallization from a paraelectric phase, both ordered and disordered, this proximity makes the phase transitions epitaxial. The domains appear in certain crystallographic orientations relative to the original phase, and therefore, to each other – a necessary condition of a domain structure formation (Fig.2).

In the melt-crystallized ferroelectrics the “substrate” for oriented nucleation does not exist initially. However, in certain cases the first crystals that appear from the liquid phase, especially when they have a layered structure, can play its role.

4.5.2. Primary Cause: Multinucleation in Epitaxial Transitions

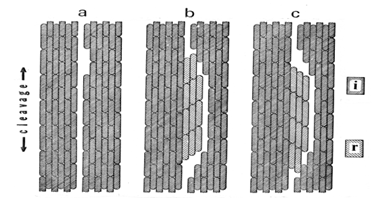
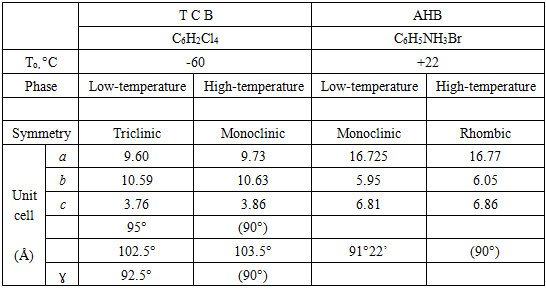
The origin of ferroelectric domain structure is a key to understanding ferroelectricity. One of the Zheludev's explanations was that “splitting into domains occurs … because the polarization, which arises at different points in a crystal at the Curie temperature is equally likely to assume any of the various crystallographically equivalent directions”. Basically, that was right idea, but in its formulation the effect, which is polarization, should be replaced by the cause, which is nucleation.

Formation of the domain structures becomes less mysterious after we realize that it is not unique to ferroelectrics. We can temporarily set aside the possible effect of polarization and look into the cases of some non-polar substances that have domain structure. Two substances presented in Table 1 are not ferroelectrics. In both cases the lower symmetry low-temperature phase is reported to appear after phase transition in two opposite orientations in approximately equal quantities. That phenomenon was interpreted as the consequence of a displacive mechanism acting in different directions in different parts of the crystal. But such mechanism does not exist. The universal nucleation-and-growth mechanism has to be invoked.

Table 1. Unit cell of the polymorphs of 1,2,4,5-tetrachlorobenzene (TCB) and aniline hydrobromide (AHB)

The very close geometrical proximity of the crystal unit cells of the polymorphs, as seen in Table 1, assures that the phase transitions are epitaxial. Analysis of the molecular packing indicated that their crystals have layered structure. Formation of the layered domain structures is almost inevitable in epitaxial transitions if the emerging phase has a lower symmetry. In practice, phase transitions in layered crystals are always multinuclear. Even a seemingly perfect single crystal of a layered structure contains multiple submicroscopic wedge-like chinks parallel to the cleavage planes. These tiny chinks act as the nucleation sites from which the layered domains of the new phase grow. As illustrated in Fig. 3, an oriented nucleus can appear with equal probability under two orientations related to one another as crystallographic twins.

Figure 3. To the formation of “twin” domain structure in epitaxial phase transitions as a result of oriented multi-nucleation of a lower-symmetry phase. The nuclei assume two or more equally probable orientations

The two crystals can be brought into coincidence with a two-fold axis perpendicular to (001). Growth of a nucleus gives rise to the formation of a laminar domain of one or the other orientation. When the sides of the adjacent domains of the same orientation meet, they merge into a single domain. Thickness of the domains varies. A layered domain structure sketched in Fig. 3b emerges with strict alternation of the orientations. Any two adjacent domains are crystallographic twins.

This mechanism is the primary cause of the domain structure in ferroelectrics; it is not related to their polarization.

4.5.3. Zigzagging by Little Mistakes

After a nucleus of ferroelectric phase appears in the layered paraelectric “matrix,” its growth gives rise to a new layered structure with almost unchanged geometrical parameters of the layers. At every stage of that growth the new layers can serve as substrates for the 2-D nucleation of subsequent layers in one or the other alternative orientation. This time the two orientations are not equally probable: the one which would continue the domain growth is more advantageous than the one starting a new domain. But their nucleation energies are so close that “mistaken” nucleation acts do occur from time to time. The result of such “zigzagging” (Fig.4) is a structure of thinner domains.

4.5.4. “Head-to-Tail” Packing

The described process of “zigzagging” is intensified by the ferroelectric polarity. It makes the “mistaken” nucleation more frequent by providing electrostatic dipole attraction (“head-to-tail”, see Fig. 4) on the sides of a domain interface.

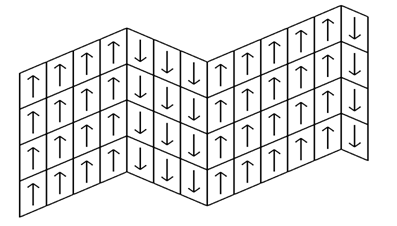Figure 4. Ziggzaging effect in formation of ferroelectric domain structure due to the 2-D nucleation errors

While the growth of the domain is still preferable, the difference between the two nucleation energies is further equalized. The very fine division of ferroelectric crystals into domains, found in experimental studies, becomes more understandable.

4.5.5. The “Wall” of Zero Thickness

The term “domain wall” was adopted by ferroelectricity from ferromagnetism. Conventional science claimed that ferromagnetic domains are separated by a thick “wall” of hundreds of lattice periods in which spins gradually turn to the new direction. The conclusion was inferred from the Heisenberg ferromagnetic theory. That theory is now proven invalid [1,4]; the ferromagnetic domain interfaces are geometrical twin boundaries. Zheludev believed in those thick ferromagnetic domain boundaries, but ferromagnetism was not the area of his expertise. Nevertheless, he arrived at the different, almost correct, conclusion that ferroelectric domain walls “should – in most cases – be of the order of the lattice constant”.

The domain boundaries – in all cases – are twin interfaces, i. e. having zero thickness. Formation of a ferroelectric crystal and its domain structure is one and the same process. The two components of that formation, as described in the previous sections, already contain the answer to what a ferroelectric domain interface is. In the multinucleation crystallization (section 4.5.2), when the sides of the adjacent domains of the same orientation meet, they merge into a single domain. If they have different orientations, they form a geometrical twin interface of zero thickness. In the zigzagging crystallization (section 4.5.3), the perfect geometrical matching during 2-D epitaxial nucleation gives rise to a perfect twin interface as well.

As for the shape and directions of the domain interfaces, they are rational crystallographic flat faces of the domain single crystals when they grow.

4.6. What Differentiates Ferroelectrics from Pyroelectrics

4.6.1. Ferroelectrics

The direction of spontaneous polarization of ferroelectrics can be changed by an external electric field E because they have domain structure. They have it, as explained in section 4.5.1, due to a very close geometrical proximity of their crystal unit cells to those of the paraelectric phase. Accordingly, their free energies are close too, F_par ≈ F_fer. The domain structure consists of multiple single crystals of identical crystal structure arranged in alternating orientation and separated by twin interfaces. The free energy F of the crystal lattice in all domains is the same until an electric field E is applied. The field E tilts the energy balance in favor of the domains with dipole moments P closer to the E direction. Every two neighboring domains now embody two competing crystal phases of slightly different F. The phases are separated by a very low potential barrier, considering that 3-D nucleation is not needed and the activation energy to move a twin interface is the lowest imaginable. A phase transition is initiated and proceeds by the molecule-by-molecule relocation at all the twin interfaces. The process is complete when the “unfavorable” domains disappear and all polarization vectors acquire the direction of the “preferred” domains. The system is now spontaneously polarized. Reversing the E direction will reverse the process of molecular rearrangement, giving rise to what is called polarization switching. Evidently, this “switching” is not instant and can sometimes be a rather slow process.

4.6.2. Pyroelectrics

The direction of spontaneous polarization in ferroelectrics can be changed because they have a domain structure. Pyroelectrics do not have the domain structure and their polarization cannot be changed. It remains to be clarified why they do not have it and why polarization cannot be changed without it.

The reason why pyroelectrics do not have their domain structure is the same reason that most crystals in nature do not have it. It is because the specific conditions for its formation, discussed in sections 4.5.1 and 4.5.2, are not satisfied. The reason why applied electric field cannot change polarization without domain structure is best illustrated with molecular crystals, where closeness of molecular packing correlates with the crystal free energy, namely, the closer packing, the lower the free energy. How close the packing can be depends on shape of the molecules. Some molecules have two or more potential packing versions of almost equal density ρ1 ≈ ρ2 ≈ ρ3…, so their free energies F1 ≈ F2 ≈ F3… . Their crystals are prone to exhibit polymorphism, and some may qualify to be ferroelectrics if they are polar and the second condition – closeness of the crystal unit sell parameters – is also satisfied. Other molecules have such a set of their closest packing that ρ1 << ρ2, ρ3 … , and, accordingly, F1 << F2, F3… . So, the system with F1 rests on the bottom of a deep potential well, so the weak driving force of applied electric field cannot extricate it from there. Pyroelectrics belong to the latter category. Also, even if F1 ≈ F2 in some cases, the system would remain pyroelectric when the crystal parameters of the phases are not very close.

5. Ferroelectric Hysteresis and Loops

5.1. Zheludev's Description

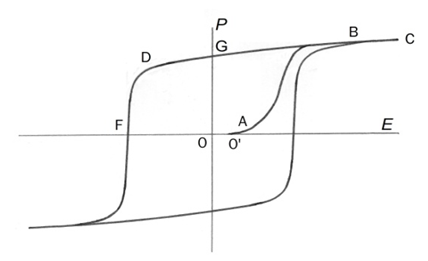
The dielectric hysteresis loops in an alternating electric field are the most prominent feature of ferroelectrics. Zheludev gave a description of such a loop (Fig. 5). Here it is in brief (translated from [15] with special attention to preserve the used terms).

Figure 5. Ferroelectric hysteresis loop P (E). P – polarization, E-applied electric field

In the region O → A, the polarization P is roughly proportional to field E; it is accompanied by an elastic (reversible) displacement of domain borders, or by no domain processes at all. Over region A → B, field E makes P grow at the expense of domain processes (emergence of domains and their growth). At point B the polarization, connected to the domains, attains saturation, and the crystal becomes a monodomain. The region B → C represents the linear relation between P and E and characterizes the induction polarization not caused by domain processes.

In lowering E from point C, the polarization, starting from point B, does not follow the path of the initial polarization. It does not return to zero at E = 0, but retains nearly all its saturation value (point D). This means that its monodomain state is preserved almost entirely in the absence of an applied field. However, when E approaches its coercivity (OF), the polarization drops precipitously, becomes zero and, reversing its polarity, reaches large values. “This means that at E values close to coercivity an intensive repolarization of the domains is going on: changing their polarity sign to the opposite.”

5.2. Discussion and Updating

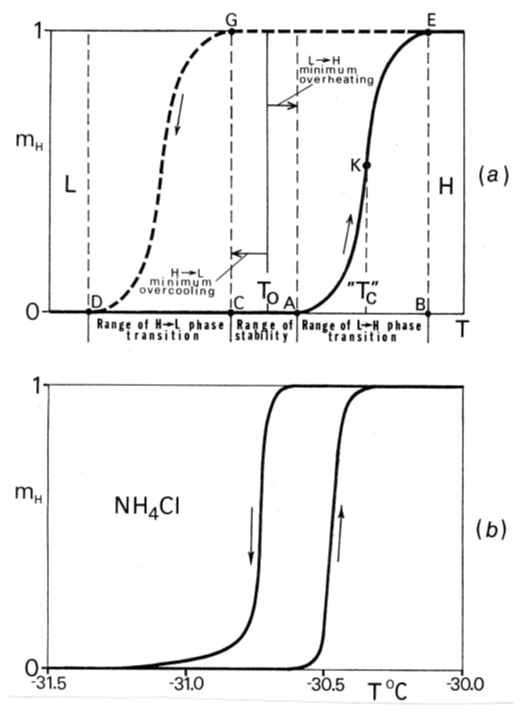
It is essential to note that the description was written exclusively in terms of the polarization changes; the structural rearrangements at the interfaces were not discerned. The cause of polarization hysteresis remained unknown. The whole domain structure was misunderstood as a single crystal with different areas (domains) of one or another direction of polarization. The term ”domain processes” was not specified. Together with the emergence of new domains and their growth, it also presumed a polarization change by domains as a whole. The main shortcoming of the whole approach was that the underlying structural rearrangements were not perceived.

The truth is that the domain structure is not a single crystal, but a conglomeration of differently spatially oriented single crystals. Therefore, rearrangement of the crystal structure between differently oriented crystals is the only way to reorganize the polarization. Structural rearrangement is the cause, and change in polarization is its effect.

It should be noted that a good understanding of the hysteresis and its loops could not be achieved without taking into account the specifics of nucleation and rearrangements at crystal interfaces in solid state. One relevant fact remained unknown in the literature as regarding the ferroelectric (and ferromagnetic) hysteresis loops: the same type of hysteresis loops has been observed in solidstate phase transitions when a physical property was measured vs. temperature T (Fig. 6). Their origin and formation is the key to explaining ferroelectric hysteresis loops. Their major characteristics are:

• They are reflecting the mass ratio of the two phases vs. T, regardless of the physical property measured;

• Nucleation lags are responsible for their formation and shape;

• Since all phase transitions in solids proceed by nucleation and growth, the hysteresis loop is an inalienable feature of any solidstate phase transition.

Figure 6. (a) (Schematic) Hysteresis loop mH(T) of a solid-state phase transition. Letters H and L denote high- and low-temperature phases. mH - mass fraction of H phase. The S-shaped curves AE and GD represent mH in the heterophase (L+H) temperature ranges of transition. Together they form a hysteresis loop DAEGD. Range of stability CA consists of two threshold lags too small to activate nucleation within. The inflection point K is not a "critical" (or Curie) point. It marks the temperature of the maximum number of activated nucleation sites; (b) (Experimental) Hysteresis loop of NH4Cl (Dinichert [15])

The similarity between ferroelectric and nonferroelectric hysteresis loops is not accidental: they all represent a process of structural phase transition by nucleation and growth under the action of a variable. In the polymorphic transitions the variable was temperature, while in ferroelectric phase transitions it is the applied electric field. The changing temperature transfers the matter across the line in a phase diagram that separates its areas of stability and instability. It is the unstable state of the matter that is the driving force of a nucleation-and-growth phase transition. Similarly, application of electric field to the (differently spatially oriented) crystalline domains destabilizes those of the unfavorable polarity, thus causing nucleation and growth at the domain interfaces. It is quite appropriate to interpret that process as an E-driven structural phase transition where quantities of the participating phases (domain mass of each orientation) are measured in the units of polarization P.

5.3. Structural Interpretation of the Loop

Now we turn to Fig. 5 again to interpret the same loop in terms of nucleation-and-growth phase transitions. First, the original crystalline object at E = 0 calls for description. It is a system of alternatively oriented spontaneously polarized single-crystal domains (they will be distinguished as right (r) and left (l) phases) separated by twin interfaces – as it emerged after temperature phase transition from paraelectric phase. Their relative mass quantities are equal; m_{r =} m_l. The applied field E initiates phase transition m_l → m_r, which proceeds by a growth of the r-phase at the expense of the l-phase at the existing interfaces. No “polarization switching” of the whole domains occurs. The transition starts from point O' rather than O due to hysteresis. Initially (O'→A) it is slow, but accelerates when the number of interfaces engaged in the process increases. After point A most interfaces are active and the dm_r/dt quickly reaches its maximum at the inflection point of the O'–A–B curve. Then, when the process nears point B, it decelerates until it becoms zero at that point. The resultant curve O'→A→B acquires the typical S-shape characteristic of the processes when two factors work in the opposite directions. In this case they are the accelerating speed of structural rearrangement and the dwindling amount of remaining matter to be rearranged.

At point B the transition is completed, all the domains becoming r-oriented. The sample is now like a single crystal, but it contains numerous potential nucleation centers, both inherited and newly formed. Increasing E from point B (line B→C) induces some reversible intra-structural changes caused by elastic deformation of the dipoles themselves, That segment does not belong to the hysteresis loop, but reminds us that the B – G part of the loop contains a small reversible component. If the field E is disconnected at that point, the polar crystal of the P = (OG) value will remain stable for the reason explained in section 4.4. Decreasing E from point B directs P along B→G→D. In sufficiently good crystals it is almost a straight line, only slightly deviated from being horizontal due to the above-mentioned elastic reversible effect. The m_r → m_l phase transition will not start at point G: the field E of negative sign must first overcome the 3-D nucleation hysteresis of that transition. A mass nucleation and growth of the l-domains after point D gives rise to the high-speed phase transition m_r→ m_l by the crystal rearrangements at all interfaces. (No polarization switching of the whole domains).

If the value of saturation polarization (point G) set to be P_max = 1, the plot in Fig. 5 can serve as a quantitative measure of the structural phase transitions between the right-oriented and left-oriented domains. The upward ordinate axis can now be marked m_r, and the downward ordinate marked m_l.

6. Parallelism with Ferromagnetism

In the article Analogies and Differences between Ferroelectrics and Ferromagnets [19] its author N. A. Spaldin maintained that “systematic comparison between the behavior of ferromagnets and ferroelectrics, does not, to our knowledge, exist in the literature.” But, using Google and the key words 'ferromagnetism ferroelectricity', it would take just minutes to find the book [1] with these words in its title where that has been done; even the hysteresis loops of polarization and magnetization were presented as a single combined “ferroic” loop.

Spaldin noted that there are many similarities between ferroelectrics and ferromagnets, but concluded that they are “superficial.” That conclusion was based on the alleged differences in the fundamental physics of spontaneous magnetization and spontaneous polarization, namely, that the former is established by the quantum-mechanical electron exchange field, while the latter resulted from a distortion of the non-polar prototype crystal phase.

The fact is, the theory of ferromagnetism in question is invalid, as is the assumption of a spontaneous polarization by crystal distortion. The ways the spontaneous ferromagnetic and ferroelectric states emerge are not different:

• Both ferromagnetic and ferroelectric crystals emerge by nucleation-and-growth phase transition from their para-phase.

• Both cases are those where the parameters of crystal unit cells of para- and ferro- phases are very close, which is a prerequisite for formation of domain structure.

• Spontaneously magnetized crystals emerge from the paramagnetic phase by epitaxial nucleation-and-growth phase transition [4], as do the spontaneously polarized crystals from the paraelectric phase.

• During those phase transitions a domain structure is formed. Its primary cause in both cases is multiple nucleation at random in different points of the para-matrix.

• The domain boundaries are twin interfaces in both cases.

• Both the magnetization and the polarization proceed exclusively by a molecule-by-molecule rearrangement at interfaces.

• The existence (i. e., thermodynamic stability) of both spontaneously polarized and magnetized states is provided by crystal field.

• The hysteresis loops of polarization in electric field, P (E), and magnetization in magnetic field, M (H), are caused by the 3-D and 2-D nucleation lags in the process of structural rearrangement between the alternatively oriented domains.

• Both hysteresis loops, P (E) and M (H), represent quantitative rates of the structural phase transitions between the domains of different spatial orientation, even though the loops are recorded in P and M units.

7. Conclusions

The fundamental physics of ferromagnetism and ferroelectricity is identical. The difference is reduced only to the saturation values of spontaneous magnetization M_S and spontaneous polarization P_S. Unlike the elementary magnetic dipole moments, which are a property of atomic spins, the electric charges of a ferroelectric dipole are spatially separated. Therefore, while M_S by itself does not appreciably depend on H, P_S depends on E to some extent due to its sensitivity to the distance between the plus and minus charges. The additional polarization induced by the field E is superimposed on that which is caused by the domain structural rearrangements and it is noticeably present on the hysteresis loops. Specifically, the saturation polarization P_S (E) continues to grow even after P of all domains is parallel. This induced polarization is strictly reversible and has nothing to do with hysteresis. Beyond that effect, the crystal structure treats the electric and magnetic dipoles equally.