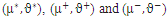-
Paper Information
- Previous Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2020; 10(1): 14-17
doi:10.5923/j.ajcmp.20201001.02

A Short Review on the Stress Field of a Screw Dislocation in a Thin Film – Substrate
Sami Youssef, Abdelfatteh Cherif, Bechir Yahmadi
Common First Year Deanship, UMM Al-Qura University, Saudi Arabia
Correspondence to: Sami Youssef, Common First Year Deanship, UMM Al-Qura University, Saudi Arabia.
| Email: |  |
Copyright © 2020 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

An analytical Fourier series analysis of the elastic field of a misfit dislocations along a thin film-substrate interface is proposed in the context of a plane strain. When the period is sufficiently large, this solution tends assymptotically towards that of an isolated dislocation in the thin film substrate system. Numerical applications are illustrated to evaluate the effect of elastic properties of the materials used as well as the effect of the film thickness and the position of the dislocation in the substrate.
Keywords: Screw dislocation, Film–substrate interface, Free surface
Cite this paper: Sami Youssef, Abdelfatteh Cherif, Bechir Yahmadi, A Short Review on the Stress Field of a Screw Dislocation in a Thin Film – Substrate, American Journal of Condensed Matter Physics, Vol. 10 No. 1, 2020, pp. 14-17. doi: 10.5923/j.ajcmp.20201001.02.
Article Outline
1. Introduction
- For about a four decades, experimental studies of epitaxial layers on monocrystalline substrate have developed considerably since the first moments of nucleation until reaching the desired thickness, which exceeds general 10 nm in silicon substrate applications (e. g) [1-2]. In parallel with these experimental studies, different theoretical models were developed to evaluate the field of dislocation stresses present in the thin-film substrate system. Since the works of Liebfried and Dietz [3] and Head [4], several other investigations have been developed Bai and Wang [5], Ogbonna [6] and Wang et al. [7]. Bonnet et al [8] have proposed a analytical solution for the stress field of a familly of misfit dislocations at the interface of a thin film – semi infinite substrate. Recently, Gharahi et al [9] have studied the interaction of a screw dislocation with a thin film–substrate interface in the anti-plane deformations of a couple stress elastic solid. They have discussed the contribution of couple stresses to the interaction force acting on the dislocation.In this paper, we develop an analytical solution of the problem of a screw dislocation interacting with a thin-film–substrate structure based on Fourrier series. The elastic field of such a dislocation is that of a periodic family of misfit dislocations periodically distributed along the semi-coherent interface. In the case of a large period, this field tends towards that of an isolated dislocation. Numerical applications are developed to show the effect of the elasticity of the medium, the thin film thickness as well as the position of the dislocation in the substrate.
2. Stress Field in a Semi – Infinite Bicristal
- The geometry of the problem and the conventions used are illustrated in Figure 1, the system of Cartesian axes
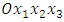 and some symbols used in the analysis. A series of misfit dislocations are periodically distributed (of period
and some symbols used in the analysis. A series of misfit dislocations are periodically distributed (of period 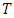 ) along the planar hetero-interface denoted (+)/(-), the thickness of the media (+) is h+, the media (-) is supposed infinite. A thin film of thickness h* is placed above the media (+).
) along the planar hetero-interface denoted (+)/(-), the thickness of the media (+) is h+, the media (-) is supposed infinite. A thin film of thickness h* is placed above the media (+). 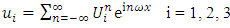 | (1) |
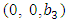 only the component
only the component 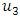 is not zero. This field sastisfy the equilibrium equation of elasticity, then the pre-exponential coefficients of expression (1) are written in the following way, leaving, for simplicity, the upper index (n) on
is not zero. This field sastisfy the equilibrium equation of elasticity, then the pre-exponential coefficients of expression (1) are written in the following way, leaving, for simplicity, the upper index (n) on 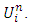
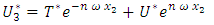 | (2a) |
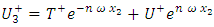 | (2b) |
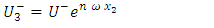 | (2c) |
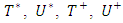 and
and 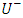 . These coefficients are the unknowns of a system of five equations with five unknowns. This system is obtained by writing the boundary conditions, linear discontinuity of the displacement field at
. These coefficients are the unknowns of a system of five equations with five unknowns. This system is obtained by writing the boundary conditions, linear discontinuity of the displacement field at 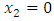 [10], continuity of the normal stresses at
[10], continuity of the normal stresses at 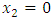 and
and  and nullity of the stresses at the level of the free surface
and nullity of the stresses at the level of the free surface 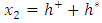 . The solutions are purely complex, they are written:
. The solutions are purely complex, they are written: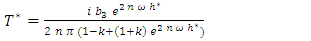 | (3) |
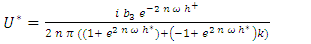 | (4) |
 | (5) |
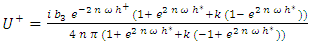 | (6) |
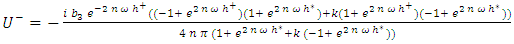 | (7) |
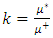 the ratio of Lamé coefficient of media (*) and (+) and
the ratio of Lamé coefficient of media (*) and (+) and 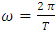 . These expressions are given when
. These expressions are given when 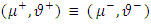 that means two elastically identical media. When the period
that means two elastically identical media. When the period 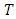 increases, the results around a misfit screw dislocation converge to those of an isolated translation screw dislocation in a substrate near a thin film.
increases, the results around a misfit screw dislocation converge to those of an isolated translation screw dislocation in a substrate near a thin film.3. Numerical Application
- Figs. 2(a,b,c,d) display, for a thin film – substrate foil (thickness of the film h* =3 nm), equistress contours related to an screw dislocation oriented along
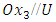 according the ratio
according the ratio 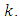 The Burgers vector
The Burgers vector 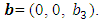 Its line position is at
Its line position is at 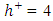 nm below the thin film. The Cartesian frame is
nm below the thin film. The Cartesian frame is 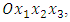 with
with 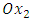 oriented towards the upper normal N to the foil. In Figs. 2(a,b,c,d), the stress fields are derived from the u field (1) and the application of Hooke’s law from isotropic elasticity theory. For a quicker convergence of the Fourier series the harmonic terms beyond 50 were reduced to their principal values so that they can be summed exactly via simple analytical functions [10]. The equistress contours correspond to σx2x2= 0 et ±50 MPa. These contours are represented in the region around the screw translation dislocation as
oriented towards the upper normal N to the foil. In Figs. 2(a,b,c,d), the stress fields are derived from the u field (1) and the application of Hooke’s law from isotropic elasticity theory. For a quicker convergence of the Fourier series the harmonic terms beyond 50 were reduced to their principal values so that they can be summed exactly via simple analytical functions [10]. The equistress contours correspond to σx2x2= 0 et ±50 MPa. These contours are represented in the region around the screw translation dislocation as 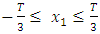 and
and 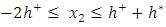 . The value of the period should reash the value
. The value of the period should reash the value 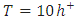 to obtain visually stable curves for a single screw translation dislocation. The test is useful to examine the validity of the proposed approach relatively to some works reported in the literature for an infinite medium [11]. The dashed line marks the position of the inteface between the film and the substrate. The internal zero stress contours meet of course the free surface of the film. Close to the core, the traction or compression regions are the same than for a dislocation in an infinite medium [11]. These contours are continuous at level
to obtain visually stable curves for a single screw translation dislocation. The test is useful to examine the validity of the proposed approach relatively to some works reported in the literature for an infinite medium [11]. The dashed line marks the position of the inteface between the film and the substrate. The internal zero stress contours meet of course the free surface of the film. Close to the core, the traction or compression regions are the same than for a dislocation in an infinite medium [11]. These contours are continuous at level 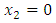 and the interface
and the interface 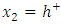 . It is interesting to note when
. It is interesting to note when 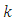 increases from 0.5 to 2, then the film becomes harder, the lobes of stress contours become wider and become more pronounced in the film.
increases from 0.5 to 2, then the film becomes harder, the lobes of stress contours become wider and become more pronounced in the film.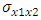 versus
versus 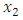 along the plane
along the plane 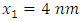 when
when 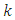 increases from 0.5 to 2. In the region
increases from 0.5 to 2. In the region 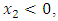 this stress and for all the values of
this stress and for all the values of 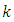 is the same than for a screw translation dislocation in an infinite medium.
is the same than for a screw translation dislocation in an infinite medium.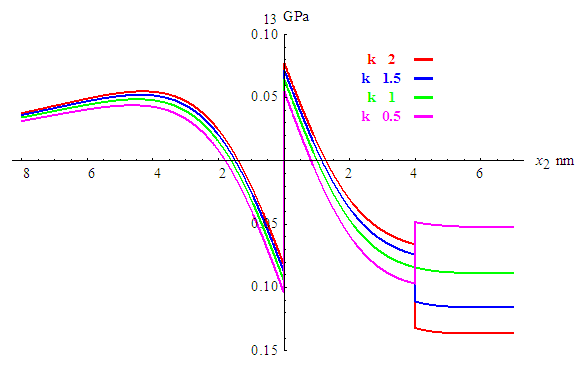 | Figure 3. Variation of stress 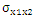 versus versus 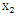 along the plane along the plane 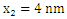 when when 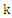 increases from 0.5 to 2 increases from 0.5 to 2 |
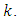 This is not the case in the region
This is not the case in the region 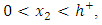 which shows a variation versus
which shows a variation versus 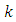 more important when
more important when 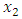 increases. The discontinuity at
increases. The discontinuity at 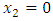 is intensive, it reaches 0.16 GPa, while at the level
is intensive, it reaches 0.16 GPa, while at the level 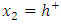 it is more lower and depends on the value of
it is more lower and depends on the value of 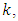 it is close to 0.048 GPa for
it is close to 0.048 GPa for 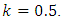 For
For 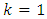 and the same level
and the same level 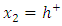 , the curve is continuous since the elastic properties for the film and the substrate are identical. Finally we propose to calculate the elastic energy
, the curve is continuous since the elastic properties for the film and the substrate are identical. Finally we propose to calculate the elastic energy 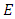 as a function of the depth of the dislocation in the substrate. A cut is first made along the interface
as a function of the depth of the dislocation in the substrate. A cut is first made along the interface 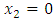 . To restore the atomic bonds, it is necessary to exert surface stress. The work of the forces of surface is calculated for the linear relative displacement [8].The integration surface extends over a length unit along
. To restore the atomic bonds, it is necessary to exert surface stress. The work of the forces of surface is calculated for the linear relative displacement [8].The integration surface extends over a length unit along 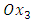 and along
and along 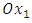 on the interval
on the interval 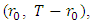 where
where 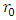 is the cutoff radius [11]. The elastic energy stored by unit of surface, noted
is the cutoff radius [11]. The elastic energy stored by unit of surface, noted 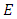 is therefore:
is therefore: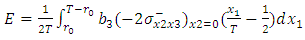 | (8) |
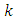 increases from 0.5 to 2. It is interesting to note that the value of energy increases as
increases from 0.5 to 2. It is interesting to note that the value of energy increases as 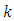 increases. This increase is due to the crowding of the substrate by the film which becomes more harder. The elastic energy tends towards an asymptotic value when the depth
increases. This increase is due to the crowding of the substrate by the film which becomes more harder. The elastic energy tends towards an asymptotic value when the depth 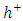 reaches 3 nm.
reaches 3 nm. | Figure 4. Variation of elastic energy with the depth of the dislocation in the substrate. 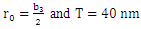 |
4. Conclusions
- In this work we present analytical solutions for the displacement and stress fields corresponding to a screw dislocation located inside a substrate near a thin-film interface. The presented solution is in the form of a Fourier series with large period. We discussed the effect of the elastic properties of two mediums on the stress field and the effect of the depth of the dislocation in the substrate on the elastic energy at nanoscale. Since the displacement field has an analytic form its nine derivatives can be easily derived analytically and therefore be useful to refine the contrast simulations of conventional TEM images of such dislocations lines.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML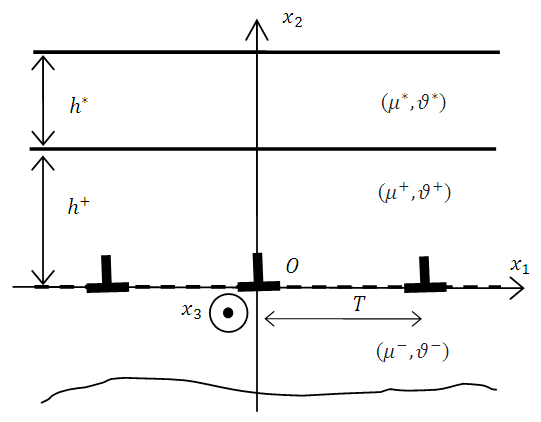
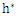 on a semi-infinite substrate. A periodic distribution of a screw dislocation of a period
on a semi-infinite substrate. A periodic distribution of a screw dislocation of a period 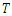 along the plane
along the plane 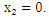 The elastic constants of Lamé and Poisson relative to the media (*), (+) and (-) are noted respectively
The elastic constants of Lamé and Poisson relative to the media (*), (+) and (-) are noted respectively