1. Critical Point and Critical Phenomenon

(a) Not a very critical point.

“Critical points” are the heart of the “critical phenomena” concept. According to Webster Dictionary, the word “critical” means tending to find fault; forming a crisis; dangerous or risky; causing anxiety. But in mathematics and physics that meaning of the word seems to be lost: “critical point” simply designates a point at which some change takes place. Thus, in case of the “critical temperature” T_C of second-order phase transitions by Landau [1], there is only change in the crystal symmetry, but not of the crystal lattice itself. And in case of a liquid – gas phase transition the critical point (T_C, p_C) in the temperature-pressure phase diagram is simply when the last traces of the liquid phase disappear. The “critical” meaning of the word arises if those changes are accompanied by singularities, such as “critical opalescence” and “heat capacity λ-anomalies”. In the absence of singularities the point loses its “critical” significance.

(b) The main property of a critical point.

From a theoretical point of view, the notion of a “critical point” appears as a feature of the cooperative process treatable by statistical mechanics. Phase transitions assumed to result from fluctuations over the bulk of the matter. In such a case, any premature or delayed phase transition cannot occur. Allowing deviations from that rigorous rule, however small, is nonsensical. Any “critical phenomenon” must occur exactly at that point, and the point should be the same when approached from the opposite sides (zero hysteresis). Even minor deviations are not acceptable. Therefore, the most important property of a “critical point” must be its positional stability. This feature provides a reliable test of whether a phase transition belongs to “critical phenomena” or not.

(c) And the reality is . . .

In solid state no example with a true “critical point” exists. Observations of the ferromagnetic phase transitions in the region of their “critical point T_C” (also called “Curie point”) is an example. As Belov [2] put it, “Many important questions connected with the behavior of materials in the region [of ferromagnetic transition] remain unsettled or in dispute. ... These include...the actual temperature behavior of the spontaneous magnetization near the Curie point, the causes of the 'smearing out' of the magnetic transition, ... the existence of 'residual' spontaneous magnetization above the Curie temperature... It even remains unsettled what we should take to be the Curie temperature, and how to determine it”.

(d) Definition of a critical phenomenon.

There are books with words “critical phenomena” in their titles, but the definition of that notion is missing. In evaluating each particular case we need to know what is behind that notion. It seems, it is always related to a phase transition. If so, is it the fact of the transition, or the singularities as such? We assume it is their combination and define it to be a phase transition driven by cooperative fluctuations and accompanied by singularities.

2. Liquid – Gas Critical Point

2.1. Why High Pressure Cannot Liquefy Gas at T > T_C

A number of definitions of a “critical point” in the reference material mention the liquid – gas critical point as an example. Yet, nobody seems to understand why it exists, namely, why sufficiently high pressure will not liquefy gas at T>T_C. To tackle the problem, it should be first noted that, logically, the only reason for that fact can be alteration of the participating particles under high temperatures. We start from the question: what makes a crystal state stable? The answer is: the ability of the particles to bond together into a low energy long-range order with short standard inter-molecular distances. It allows presenting a crystal structure as a molecular close packing [3] with the neighboring particles interlocked like gears. There are many ways for the molecules to pack together; which one prevails depends on its density: the higher it is, the lower its free energy F. The close-packing model is applicable to liquids as well. Molecular structure of a liquid is not quite chaotic. At every particular moment it consists of temporary tiny molecular clusters with molecules arranged in an imperfect "close-range" packing order where they are bonding like in a crystal state.

Liquefying gas by applying pressure is to overcome the effect of molecular thermal vibrations and rotations that kept molecules apart, squeezing them together to engage their chemical bonding. The increasing vibrations with rising temperature cause the molecules to loose their individual shape, enlarging their effective size. Ultimately, the temperature is reached (it will be marked as T_C) when their interlocking ability disappears. No matter how strongly they are now squeezed together, they are not engaging in the chemical bonding due to their inability to come close enough (and under a correct angle) to each other. The gas would not be liquefied.

As to the T_C, it is hard to see why critical opalescence would, as claimed, accompany it.

2.2. The Cause of Its Opalescence

It is always said that phase transitions in the vicinity of their critical points are accompanied by critical phenomena, or singularities, caused by fluctuations of something. For example, I. Z. Fisher [4] claimed that in the vicinity of the liquid – gas critical point a great increase of density fluctuations and the correlations of those fluctuations take place, giving rise to critical opalescence, as well as to change in the velocity and absorption of ultrasound, etc. Stanley [5] stated that critical opalescence is caused by vast fluctuations of density, and many other theoretical physicists share that view.

It should be self-evident, however, that critical opalescence would appear when the thermal fluctuations, whatever they are, increase with the rising temperature toward its critical point T_C. However, the fluctuation-based nature of the opalescence and, therefore, its "critical" status, is undermined by a simple experimental fact: the opalescence appears only upon decreasing temperature. But thermal fluctuations would not intensify with decreasing temperature.

Then, what is the nature of the observed opalescence? Answer: the phase transition gas → liquid in question starts after the temperature T₀ of the phase equilibrium (when F_liquid = F_gas) has been passed. It begins from nucleation of the liquid phase from multiple sites, producing a common fog – a system of tiny drops of liquid, which then grow and merge into the liquid phase with the gas/liquid interface. The process is not fluctuation-based. It is a nucleation-and-growth.

The observed opalescence and the related absorption/velocity effects are not singularities that allegedly accompany that “critical phenomenon”. Neither were any λ-anomalies reported. A phenomenon without singularities is not “critical”.

3. The Phenomena Commonly Deemed "Critical"

The discovery in 1932 of a “heat capacity λ-anomaly” in liquid helium phase transition (Fig. 1) was a sensational scientific event. It triggered intensive theoretical efforts over the upcoming years, as described by G. Jaeger [6]:

“The liquid-helium lambda transition became one of the most important cases in the study of critical phenomena – its true (logarithmic) nature was not understood for more than ten years … The Ehrenfest scheme [to classify phase transitions by first, second, etc. order] was then extended to include such singularities, most notably by A. Brain Pippard in 1957, with widespread acceptance. During the 1960’s these logarithmic infinities were the focus of the investigation of "scaling" by Leo Kadanoff, B. Widom and others. By the 1970s, a radically simplified binary classification of phase transitions into "first-order" and "continuous" transitions was increasingly adopted.”

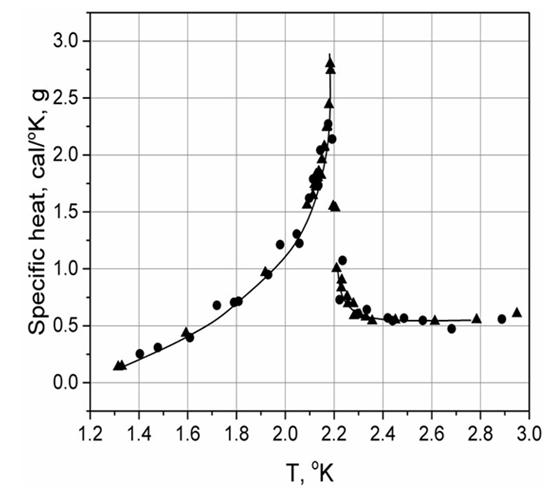Figure 1. The “λ-Anomaly” from calorimetric measurements of liquid helium phase transition. It has been interpreted as a singularity of heat capacity

The attempts to theoretically describe that “critical phenomenon” were continued. In 1982 a Nobel Prize was given to K. Wilson whose work allegedly explained the “λ-anomalies”. But it has been proven by Mnyukh and Vodyanoy [7] that all the theoretical efforts to account for the appearance and shape of the “heat capacity λ-anomaly” in liquid He are hopeless due to misinterpretation of its physical nature: it represents the latent heat of the liquid – liquid (non-"critical") phase transition, and not its heat capacity (more about it will be said in Section 6).

Which other phenomena, beside the liquid – gas “critical point” phase transition, are usually regarded “critical phenomena” in the scientific literature and among the scientific community at large? In case of solid – solid phase transitions their temperature is usually called “critical temperature” or “critical point” and marked T_C whether it involves crystal structure, ferromagnetism (where it is also called “Curie point”), ferroelectricity, superconductivity, or anything else. Does that mean all those phase transitions are “critical phenomena”? In that regard a few relevant books were examined.

● Statistical Physics, by L D Landau and E M Lifshitz [1]. Sorting out all phase transitions into first order and second order by Landau was described. The second order transitions are certainly belong to “critical phenomena”. The terms “second order” and “critical phenomenon” are probably equivalents, but such a statement in the relevant literature seems to be absent. Their equivalency is an important matter, since second-order phase transitions do not really exist. The chronological steps leading to that conclusion are given in [7]. That conclusion was made in spite of the fact that from 1934 the existence of such transitions became an unbreakable dogma. It was a result of comprehensive studies of solid-state phase transitions, initiated in 1960's, which have lead to finding their universal mechanism described in Section 4.

As for the first-order transitions, Landau did not express any interest in their unknown molecular mechanism, just calling them “usual” and listing some of their properties. One of those properties was “overheating or undercooling is possible”. In other words, they do not have a critical point and, therefore, are not a critical phenomenon. The listed properties of first-order phase transitions and those of the nucleation-and-growth (Section 4) are the same. The two concepts are identical.

● Phase Transitions, by R Brout [8]. All phase transitions are cooperative critical phenomena treatable by statistical mechanics. The theoretical goal was to justify the fact of phase transitions and account for their “singularities”. Brout rationalized that at critical points the “infinite fluctuations give rise to singularity in full energy which, in turn, give rise to the heat capacity λ-anomaly”. Theoretical models of the phase transitions, mostly Ising model, were used. In case of ferromagnetism the Ising model consists of a crystal lattice with its sites occupied by spins of two orientations, either 'up' or 'down', flipping between them arbitrarily. Due to interaction of the neighboring spins, small patches of parallel spins arise and grow as the temperature is decreasing toward the critical point T_C, at which the whole crystal somehow becomes magnetized^*.

When the real molecular mechanism of a ferromagnetic phase transitions [9,10] is invoked, it becomes evident that ferromagnetism cannot be approximated by Ising, Heisenberg, or any other theoretical model. The real mechanism is not based on fluctuations and it is not cooperative by its nature (Section 7). The theory is useless.

● Introduction to Phase Transitions and Critical Phenomena, by R. Stanley [5]. The title of the book leaves an impression that phase transitions in general are “critical phenomena”. The content of the book in many respects is similar to the book just considered. All solid-solid phase transitions are deemed to be a cooperative, treatable by the methods of statistical mechanics. The Landau theory is discussed, but it is not specified that the theory is only about second-order phase transitions. The “first order” phase transitions are not mentioned. Only two phase transitions, liquid – gas and ferromagnetic, are chosen to be analyzed. They are claimed to be similar and typical for other phase transitions, such as in ferroelectrics and superconductors.

The central premise of the similarity between the liquid – gas and ferromagnetic phase transitions is erroneous, considering that ferromagnetic phase transitions are represented by the Ising model which does not approximate reality. As already pointed out, the model represents a cooperative process, while a real ferromagnetic transition is not. A real ferromagnetic phase transition proceeds by local molecular rearrangement at the interface between coexisting phases (Section 7).

● Modern Theory of Critical Phenomena, by S K Ma [11]. The claim to be modern was based on the K. Wilson's theoretical contribution – renormalization group approach to scaling. The Wilson theory was limited by second-order phase transitions, but that fact was quickly forgotten by everyone. The critical phenomena mentioned in the book are the phase transitions: liquid-gas, ferromagnetic, antiferromagnetic, ferroelectric, in liquid He, in superconductors, in liquid and solid binary systems.

Again, the ferromagnetic case was regarded representative of all of them. The introductory chapter describes a ferromagnet from 0 K up to its phase transition to the paramagnetic phase at critical point T_C. It goes as follows. At 0 K all spins have the same direction, so the ferromagnet is magnetized to saturation. With the temperature rising, some spins become randomly oriented. Their quantity increases with temperature until all of them are disoriented at T_C and above it. Therefore, nothing happens at T_C itself, which is why the ferromagnetic – paramagnetic phase transition is called second order.

That presumed description, tailored to justify using statistical mechanics methods, reveals the main problem of the theory: it has nothing to do with reality. It suffices to note that a ferromagnetic crystal has domain structure at all temperatures from 0 K to T_C, every domain being a single crystal magnetized to saturation. There are no randomly oriented spins between 0 K and T_C. Also, there is no reason for spins of all domains to be oriented in the same way at 0 K. And there is no reason for all spins in a domain being parallel at 0 K: why, for example, not to be in a helical disposition?

4. The Universal Mechanism of Solid-Solid Phase Transitions

A time ago the common belief was that some phase transitions are “structural”, meaning representing a change of their crystal structure, and other (ferromagnetic, ferroelectric, order-disorder, normal-superconducting) are not. Those “non-structural” were declared “second order”. Then some strange "magnetostructural" phase transitions were experimentally found. Structural changes “accompanying” other non-structural transitions were recorded as well. We contrast that with the statement that all phase transitions in solids are structural and have the same nucleation-and-growth molecular mechanism. In fact, knowledge of that structural mechanism is equivalent to a basic understanding of the nature of all phase transitions and other reactions in solid state. A frequent misconception that phase transitions are accompanied by changing of the crystal structure must be reversed. It is change of crystal structure which is accompanied by the changing of its properties, whether it is ferromagnetic, ferroelectric, electric conductivity, optical, etc.

The molecular mechanism of solid-solid phase transitions was disclosed in late 1960's by the present author after the discovery of the phenomenon of crystal growth in a single crystal medium (Fig 2). It was presented in detail in [12] and its universal character was then confirmed in ensuing publications. Considering its key role in this article and that it is still far from general acceptance, its abbreviated description is given below. It is named nucleation-and-growth.

Figure 2. An example of phase transition in a transparent single crystal of p-dichlorobenzene. It is a growth of well-shaped single crystal of the new (higher-temperature) phase within the original lsingle-crystal phase. The transition started from a visible crystal defect at T > T0 by several degrees. There is no rational crystallographic orientation relationship between the original and new phases

4.1. Nucleation in Microcavities

Nucleation of the alternative phase in solid-state phase transitions differs in all respects from the theoretically-born fluctuation-based statistical picture described by Landau and Lifshitz (Section 150 in [1]). In reality the nucleation sites are located in specific crystal defects – microcavities and microcracks of a certain optimum size. Every site contains information on the actual temperature of its activation. These temperatures are not the same in different defects, but nucleation in a given crystal is predetermined as for the location of the defect and its encoded temperature. It would not occur at all in perfect crystals, but such crystals are extremely rare.

4.2. Hysteresis

Every nucleus is activated only after the temperature T₀ marking the equality of free energies of the phases,

F1 = F2, has been passed. The nucleation lags are inevitable in both directions of phase transitions. They are the only cause of hysteresis. Hysteresis is a necessary component of the phase transition mechanism. Its value is not exactly reproducible when transition was initiated by different nucleation sites. At least some finite hysteresis is inescapable. An “ideal phase transition” (i. e., without hysteresis) cannot occur, since its thermodynamic driving force ΔF = F1 - F2 = 0 at T = T₀.

Along with the hysteresis of initiation of the new phase there is also a smaller, but consequential, secondary hysteresis of sustaining the transition when the two phases already coexist.

4.3. Temperature of Phase Transition. Range of Transition

Temperature of phase transitions is regularly treated in scientific literature as T_C, calling it "critical temperature” (or “Curie temperature” or “critical point”) – the term designated for “critical” phenomena. This is a consequential mistake, a source of countless misinterpretations of the nature of phase transitions. When the value of a physical property P shows a gradual change "in the vicinity of transition" on the experimental P(T) charts, it is interpreted as a pre-transition effect. The phase transition looks complicated. Location of the phase transition temperature becomes a subject of guessing, as a quotation in Section 1(c) illustrated, and the curves become a subject of mathematical delineation and interpretation.

The cause of these seeming complications is rooted in the fact that nucleation-and-growth phase transitions are always spread over a range of transition due to the hysteresis, wide or narrow, of two levels. The hysteresis of initiation usually involves nucleation from many sites of different encoded starting temperatures. Each emerging interface is subjected to the hysteresis of sustaining that inhibits its free propagation. Their combination results in spreading the transition over a temperature range, which is located after T₀ has been passed. In the range of transition the two phases coexist, while their ratio changes by local rearrangement at their interfaces.

4.4. Rearrangement at Contact Interface

A solid-state phase transition is intrinsically a local process. It proceeds by “molecule-by-molecule” structural rearrangement at interfaces only, while the bulk of both the original and emerged phases remains static (Fig.3). No “jumps” of macroscopic quantities or properties occur. The seeming “jumps” appearing on experimental recordings are simply the differences between the crystal structures or their physical properties when the transition range is either narrow, or passed quickly, or both. Coexistence of the phases during phase transition is self-evident. Simple observation of simultaneously present phases is a solid proof of the nucleation-and-growth phase transition.

4.5. Epitaxial Type of Nucleation-and-Growth Phase Transitions

Fig. 3 illustrates a case when the crystal orientations of the phases are not related. This is because the nuclei initiating the phase transition in the crystal defects are, in principle, oriented arbitrarily. However, a structural orientation relationship is frequently observed. These transitions, usually between similar structures, materialize by nucleation and growth as well, no matter how analogous the structures could be. The cause of the orientation relationship in these cases is oriented nucleation (epitaxy). They are epitaxial phase transitions.

Figure 3. Model of stepwise (or edgewise) molecule-by-molecule rearrangement at the contact interface. The process is located at “kinks” on the crystal faces of the emerging phase (upper part) and proceeds by building it up, layer-by-layer, that way, while the original phase is dissolving. No structural orientation relationship between the phases is necessary. Every completed molecular layer requires nucleation to initiate the next layer

There are two circumstances when it takes place. One is when crystals have a pronounced layered structure. There the crystal layers in both phases are almost the same, the difference being in the layer stacking. Nucleation occurs in the tiny interlayer cracks. The nucleation is epitaxial due to the orienting effect of the “substrate” – the opposite surface of the crack. The layers after the transition retain their original orientation.

Another case of the epitaxial nucleation is when the unit cell parameters of the polymorphs are extremely close (roughly less than 1%) even in non-layered crystals. That condition is met, for example, in paramagnetic–ferromagnetic phase transition of iron (Section 7).

Epitaxial phase transitions exhibit themselves in a specific way: the original crystal orientation is preserved, the Laue X-ray patterns of the phases appear almost identical, the temperature hysteresis can be small and easily missed, so is the latent heat, etc. It is the epitaxial phase transitions that are taken for “second-order” or “weakly first-order” and improperly treated as “critical phenomena”.

4.6. On "Weakly First-Order" Phase Transitions

The nucleation-and-growth molecular mechanism is the only alternative to the “critical phenomena”. Its macroscopic indicators are: phase coexistence, interfaces, range of transition, hysteresis. Observation of any of them is sufficient to identify it, disqualifying the phase transition as being a “critical phenomenon”. This mechanism is the equivalent of the first-order transitions in the Landau first- and second-order classification. However, second-order transitions, while they would be a true critical phenomenon, do not exist [7], which is partially recognized by Ginsburg et al. [13] with the admission that they are extremely rare. In the effort to save the Landau theory and the theory of critical phenomena, the additional category – “weakly first order” phase transitions – was introduced with an arbitrary claim that they can be treated as second-order. Their features – small hysteresis, short range of transition, structural similarity – are those of the epitaxial nucleation-and-growth.

The fundamental error of that approximation is that no matter how much “weakly” the first-order transitions are, they are not a cooperative process. They are still nucleation and growth by rearrangement at interfaces. Treating them by methods of statistical mechanics is unconditionally erroneous.

5. Lambda-Transitions

5.1. Puzzle is Solved, but Not by Theory

The sharp peaks reminiscent to letter λ, recorded in heat capacity measurements over the temperature ranges of solid-state phase transitions challenged the theoretical physicists to explain their origin. The first λ-peak was observed by Simon in NH₄Cl phase transition [14]. Later on, this was repeated by many different authors and numerous other cases were also reported. Thus, more than thirty experimental λ-peaks presented as “Specific heat C_P of [substance] vs. temperature T” were reproduced in [15]. P.W. Anderson wrote [16]: “Landau, just before his death, nominated [lambda-anomalies] as the most important, yet unsolved problem in theoretical physics, and many of us agreed with him… Experimental observations of singular behavior at critical points [were] multiplied as years went on… For instance, it have been observed that magnetization of ferromagnets and antiferromagnets appeared to vanish roughly as (T_C-T)^1/3 near the Curie point, and that the λ-point had a roughly logarithmitic specific heat (T-T_C)⁰ nominally”. Feynman stated [17] that “One of the challenges of theoretical physics today is to find an exact theoretical description of the character of the specific heat near the Curie transition - an intriguing problem which has not yet been solved.”

For now this intriguing problem has been solved [12,18,7], but not by a theory based on statistical mechanics. The solution was already contained in the experimental results of the 1942 publication by Dinichert [19], but overlooked since.

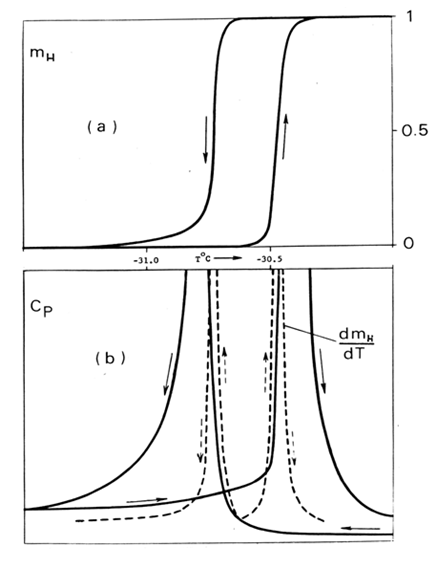
5.2. Classical Case of NH₄Cl

The canonical case of “specific heat λ-anomaly” in NH₄Cl around -30.6°C is of special significance. It was studied for years. It was the only example used by Landau in his original articles on second-order phase transitions. In every calorimetric work a sharp λ-peak was recorded (Fig. 4(b)). Neither author expressed doubts in a heat capacity nature of the peak. The case has been designated as a cooperative order-disorder transition of the lambda type. However, no one maintained that the λ-anomaly was understood.

Many of the calorimetric studies were undertaken well after 1942 when the experimental work on NH₄Cl by Dinichert [19] was published. The transition was not a cooperative nature: microphotographs revealed coexisting phases separated by interfaces. The transition was spread over a temperature range where only mass fractions m_L and m_H of the two distinct L (low-temperature) and H (high-temperature) phases were changing, producing “sigmoid”-shaped curves (Fig. 4(a)). The direct and reverse runs formed a hysteresis loop. The fact that the phase transition is first order was incontrovertible, but not identified as such.

Figure 4. Comparison of two plots representing the measurements through the range of NH4Cl phase transition, Plot ‘a’ by Dinichert represents the mass fraction mH in the two-phase L+H range of transition; mL + mH = 1. The plot ‘b’ (solid line [20]) is calorimetric λ-peaks. The two plots are shown in the same temperature scale to make it evident that shape and location of the peaks are very close to the first derivative (dashed curves) of mH. The nature of the λ-peaks and their hysteresis becomes clear, since the absorption/release of the nucleation-and-growth latent heat is proportional to dmH / dT

In Fig. 4 the Dinichert's data are compared with the calorimetric measurements (by other authors) showing “anomalies of heat capacity” (as they called the λ-peaks) and the hysteresis of the λ-peaks. Because of the hysteresis, it had to be evident at that point (but was not) that the λ-peaks cannot be a heat capacity, considering that heat capacity is a unique function of temperature. The graphs 'a' and 'b' are positioned under one another in the same temperature scale to reveal that the shape and location of the peaks are very close to first derivative of the m_H(T) (dashed curves). It remains to note that latent heat of the phase transition must be proportional to dm_H/dT. Thus, the latent heat of the first-order phase transition is found, replacing the specific heat singularity. The mystery is solved.

5.3. “λ-Anomaly” is Latent Heat of Nucleation-and-Growth

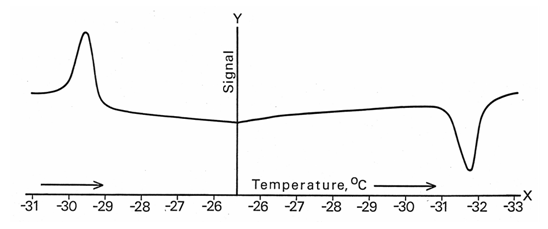
Another way to prove the latent heat nature of the λ-peak is to use differential scanning calorimetry (DSC) to record it. That technique displays endothermic and exothermic peaks of latent heat with opposite signs in the chart recordings, If the λ-peak in NH₄Cl phase transition is a latent heat, as was concluded above, the peak in a descending run must be exothermic and look downward. Our strip-chart recordings made with a Perkin-Elmer DSC-1B instrument immediately revealed that the peak acquires the opposite sign in the reverse run (Fig. 5). Its hysteresis was also unveiled.

Figure 5. The actual DSC recording of NH4Cl phase transition cycle [12], displaying temperature-ascending and descending peaks as endothermic and exothermic accordingly, thus delivering independent proof of a latent heat nature of the λ-peak. Hysteresis is seen too

6. λ-Anomaly in Liquid Helium

In Section 3 an authoritative statement was quoted about the great significance of the liquid helium “λ-transition” for the study of critical phenomena. Unfortunately for the theory of critical phenomena, the “heat capacity anomaly” used by Ehrenfest to introduce a second-order type of phase transitions does not exist. The subsequent theoretical works of many years on its shape delineation and analytic description does not have any scientific value. The consequential mistake was that the "λ-anomaly" in question (Fig. 1) is a latent heat of structural phase transition, and not a heat capacity.

It is not realistic to continue assigning a heat capacity to the λ-peak in liquid He, while the same peculiar peak in NH₄Cl and many other cases is now proven to be a latent heat. In liquid He we deal with the liquid polymorphism. At any given moment liquid consists of tiny clusters of approximately closely packed particles. A certain kind of a short-range order within the clusters is preserved. Change in the manner the particles are packed in the clusters with temperature (or pressure) is similar to polymorphic phase transitions in crystals.

In the measurements of heat effect in the liquid He phase transition an one-way adiabatic calorimetry was used. There is no doubt that an appropriate calorimeter (such as DSC) will produce the peak in cooling and heating as looking in opposite directions (as in Fig. 5), thus confirming its latent heat nature. Simultaneously, its hysteresis will be revealed too.

Surprizingly, the liquid He phase transition is not a critical phenomenon.

7. Ferromagnetic Phase Transitions

Magnetization of a ferromagnet and a ferromagnetic phase transition served to the theory of critical phenomena as the exemplary object to explore by the methods of statistical mechanics. However, the Ising and other models utilized by the theories cannot even remotely approximate the real molecular mechanism of magnetization. The real mechanism is not a cooperative statistical process of flipping spins from one direction to the other. And it is not based on spin interactions.

A detailed new explanation of spontaneous magnetization, the domain structure and the magnetization process has been presented by this author in the books [12,21] and articles [9,10]. A very realistic assumption that spin direction is fixed in the structure of its atomic carrier easily solves all problems of the current theory of ferromagnetism, eliminating its main attributes – Heisenberg theory, anisotropy energy and Bloch wall. It accounts for all its manifestations: its phase transitions, molecular mechanism, the diversity of magnetic structures, hysteresis loops, and all the rest.

Magnetization and ferromagnetic phase transitions do not occur by flipping or rotation of spins in the same structure. The source of spontaneous magnetization is crystal field that sets up the orientations of crystal particles and, therefore, the orientation of their spins. Thus, ferromagnetic phase transition and magnetization (spin reorientation) can materialize only by structural rearrangements. It proceeds by propagation of contact interfaces, where magnetic particles change their orientation by relocation, one particle at a time, in accordance with the universal stepwise mechanism of solid-state phase transitions outlined in Section 4.4.

Ferromagnetic phase transitions by moving interfaces have been observed and photographed by a number of different authors. This fact alone already reveals that the phenomenon is not of a cooperative nature and, therefore, not “critical”. The work by Novoselov et al. [22] is to be specifically mentioned. The authors were able to record a domain interface with the resolution at the molecular level. The domain interface propagated “via clear quantized jumps matching the lattice periodicity”. Also observed were “kinks” running along the interface. In other words, it was a stepwise rearrangement at the contact interface shown in (Fig. 3).

The last point to clarify is about the accompanying “singularities”. Late R.P. Feynman, a Nobel Prize Laureate, raised that problem [17]: “One of the challenges of theoretical physics today is to find an exact theoretical description of the character of the specific heat near the Curie transition - an intriguing problem which has not yet been solved. Naturally, this problem is very closely related to the shape of the magnetization curve in the same region”. The problem has been solved, but not by the theory of critical phenomena. The heat effect in question is the latent heat of the structural magnetic phase transition. It is incontrovertible: ferromagnetism and ferromagnetic phase transitions are not a critical phenomenon.

8. Ferroelectric Phase Transitions

The phenomenon of ferroelectricity is very much analogous to ferromagnetism. Electric dipoles in ferroelectrics have the same role as spins in ferromagnets do. Nevertheless, the only recognized attempt of a theoretical account for ferroelectricity, represented by the voluminous book by Lines and Glass [23], did not reflect that analogy. While ferromagnetic phase transitions are believed to occur by spin flipping in the same crystal lattice, ferroelectric phase transitions are claimed to occur by a sudden change of the crystal structure. That sudden change supposedly materialized by a displacement of electrically charged particles in the original crystal lattice. That happens at a critical temperature T_C when the amplitude of one of the crystal “soft” optical modes becomes “frozen”. The authors related the ferroelectric soft-mode phase transitions “to the more general field of structural transitions and even to critical phenomena in general”.

There are, however, fundamental inconsistencies regarding that “critical phenomena” proclamation. (1) Such an instant jump does not fit the definitions of a critical point and, even worse, the critical point does not exist at all due to the hysteresis observed experimentally. (2) The ferroelectric soft-mode phase transitions coexisted in that theory with the recognition that “most ferroelectric phase transitions are not of second order but first”. (3) The soft-mode concept per se was found invalid and disappeared from scientific literature, except when it is related to ferroelectric phase transitions.

The close parallelism of ferromagnetism and ferroelectricity is not accidental: both are the effect of the same general cause. The disposition and orientation of spins and electric dipoles are arranged by the crystal forces which combine their carriers into a crystal. This approach has been presented initially in 2001 [12], and then, in more complete form, in [9]. The origin of ferroelectrics, their classification, formation of their domain structure, their stability, difference from pyroelectrics, formation of their hysteresis loops, parallelism with ferromagnetism, and more, were presented coherently in terms of the universal nucleation-and-growth mechanism (Ferroelectric state and phase transitions, in [21], p. 117-132). Ferroelectricity and ferroelectric phase transitions are not a critical phenomenon.

9. Order – Disorder Phase Transitions

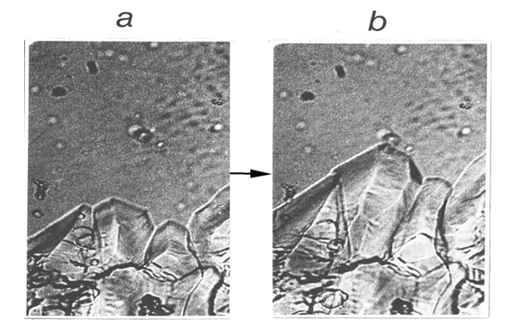
The term order – disorder denotes a kind of phase transitions when particles of the higher-temperature phase become rotating, while being arranged in a positional 3-D crystal order. The transition in NH₄Cl is one of them. For a while the common opinion was that such rotation starts in the same crystal lattice. However, phase transitions order→disorder do not occur by rotation of particles in the original crystal. The experimental results by Dinichert show transition in NH₄Cl proceeding by a gradual increasing of the quantity of one of the coexisting crystal phases at the expense of the other. The work also reveals hysteresis of the transition. All that now points to the nucleation-and-growth molecular mechanism. Phase transition in CBr₄ is another example. Observation with an optical microscope showed growing single crystals of the “disordered” phase in the medium of the original (“ordered”) crystal phase [24] (Fig. 6).

Figure 6. Order-disorder phase transition in CBr4. (a,b) Conglomeration of single crystals of “disordered” phase with rotating molecules grows within the crystal medium of the original “ordered” phase. The natural facing is evident. The two phases coexist, while all phase rearrangement occurs at the interfaces. This is nucleation-and-growth, and not a cooperative critical phenomenon

Changes of the lattice parameters in many order-disorder phase transitions are small (as, for example, in the ferromagnetic phase transition of iron), resulting in erroneously labeling them second order, which means being a critical phenomenon. That led to the following footnote in the Landau & Lifshitz book [1]: “There are claims in the literature about relation between second-order phase transitions and appearance of rotating molecules in the crystal. Such view is erroneous ...”. The real cause of that wrong classification was that those phase transitions materialize by the epitaxial kind of the nucleation-and-growth. Order – disorder phase transitions are not a critical phenomenon either.

10. Normal – Superconducting Phase Transitions

Immediately after the discovery of superconductivity in 1911 by Kamerlingh-Onnes the question of how superconducting state emerges from higher-temperature “normal” non-superconducting state arose. It had to be first established whether a superconducting phase has its individual crystal structure. Onnes was inclined to view the transition as polymorphic change. That possibility, however, was rejected in1924 by an X-ray experiment: no change in the diffraction patterns of lead was detected. The conclusion about crystallographic identity of pre-superconducting and superconducting phases was an error caused, probably, by the imperfection of the technique available at that time. It served as a basis to erroneously categorize these transitions as second order – the belief lasting up to the present time.

All superconductors known at that time are now recognized by most to exhibit first order phase transition, basically because they do not fit to be second order. The 1971-1972 articles by Ott [25-27] are to be especially mentioned, where it was reported that single crystals of lead, aluminum, zinc and gallium undergo dimensional and volume changes upon their normal – superconducting phase transitions. This alone is incontrovertible proof that they are not a critical phenomenon.

Examination of the experimental literature on “high-temperature” superconductors [7] revealed that certain structural changes resulting from normal–superconducting phase transitions do occur, even though sensitive techniques were needed to catch them. Ample evidence of that was presented in the book “Lattice Effects in High-T_C Superconductors” [28]. These changes are reported as lattice distortions, thermal expansion jumps, atomic displacements from regular lattice sites, local displacements from average crystal structure, changes of some inter-atomic distances, etc. In the following years the reports about a “structure anomaly”, “lattice distortion”, or alike, at T_C in different high-temperature superconductors continued to appear [29-32], suggesting that the phenomenon is general to all superconductors.

Structural changes in superconductors and non-superconductors alike do not occur by displacements, distortions, deformations or jumps. Notwithstanding how minute the structural changes could be, they are still macroscopic and, therefore, not allowed by thermodynamics. Any phase transition is a replacement, and not modification, of the old structure. The normal – superconducting phase transitions materialize by nucleation-and-growth. All accounts indicate that they are of the epitaxial type. They are not a critical phenomenon.

11. Non-Critical Opalescence

11.1. Misplacement of Transition Temperature Makes Opalescence Look “Critical”

The arbitrary placement of the “critical point” T_C at the top of a λ-peak turns phase transitions into extremely complicated, even mysterious phenomenon. They are perceived as starting well before the T_C and completing well after it. The pre-transition and post-transition processes in a crystal medium became a central problem of critical phenomena theory.

Realization that a phase transition proceeds over a temperature range after the equilibrium temperature T₀ has been passed (Section 4.2) eliminates the mystery. The universal nucleation-and-growth mechanism brings about a simple explanation. The peaks of light scattering form after T₀ has been passed. A sharp increase in the light scattering is caused by the mass nucleation of the new phase. Hysteresis of the peaks of light scattering has indeed been observed in the experiments.

11.2. Static Source of the Opalescence

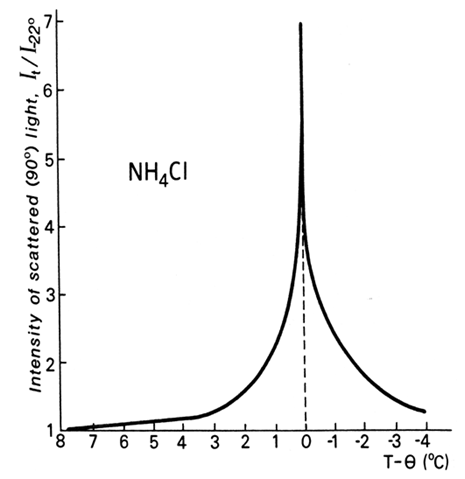
The problem of narrow peaks of light and neutron scattering that centered, as was believed, at the “critical temperature T_C” was called central peak problem. Regarding light scattering alone, extensive literature was devoted to this phenomenon called critical opalescence. A notorious “λ-anomaly” can be recognized in the central peak (Fig. 7). The significance of this phenomenon for theory of critical phenomena was expressed in the 1979 article “Quasielastic Light Scattering Near Phase Transitions” by Lyons and Fleury [33]: “Our understanding of structural phase transitions has evolved in the last decade through several stages from the simple soft mode and mean field theories to the modern coupled-mode, renormalization group and dynamic scaling ideas. Crucial to this evolution has been an increasingly detailed interpretation of the experimental data, particularly those resulting from scattering experiments”. A disconcerting circumstance, however, was that by 1979 it was already a well-proven fact that the central peaks were caused by scattering from static centers. At that stage Lyons and Fleury were compelled to suggest that the scattering centers were “long-living clusters” rather than entropy fluctuations. But failure of the dynamic theories was not recognized.

Figure 7. The apparent “critical opalescence” peak of light scattered at 90° to the primary light beam by a NH4Cl single crystal during its low-temperature (T0 = -30.6°C) phase transition (Shustin [34]). Presentation of the temperature scale as a distance from the position of the peak maximum obscures that the peak is not located at T0

The 1981 review by the same authors [35] revealed a certain evolution in representation of the subject: though the critical phenomena approach was preserved, a separate section entitled “Static and dynamic central peaks” appeared. There it was stated that the first instance of the central peak of light scattering reported for quartz by Yakovlev et al. [36] was later proven [37] to be due to “scattering from static microdomains, rather than to true critical opalescence”, and that “in most other cases confusion still persists...”. Also mentioned was K₂PO₄ where the central peak has been observed [38], but shown [39] to be “largely of static origin”. Omitted from this account was the case of NH₄Cl (Fig. 7) usually considered a valuable asset in illustrating critical phenomena: the scattering centers there also were static [40].

Other believers in critical phenomena encountered the same problem. Ginzburg et al. in their review on light scattering [41] listed more examples of the central peaks caused by static scattering centers: SrTiO₃, Pb₅Ge₃O₁₁, KH₃(SeO₃)₂. It was explained that "extraction of the part due to thermal fluctuations from the total scattering intensity is generally a rather hard task". But no evidence that such a part existed was presented.

11.3. Explanation was Ignored

The explanation of central peaks was proposed by Bartis as early as 1973 in the articles “Critical Opalescence in Ammonium Chloride” and “The Transitional Opalescence of Quartz” [40,42]. Some assumptions leading to this explanation were not quite valid. A phase transition was considered a three-step process in which only the intermediate stage was a temperature range of two-phase coexistence. But it was sufficient to advance the following idea: “To understand the increased scattering of light we focus our attention on the interface between the two crystalline forms in the intermediate stage. Inasmuch as the two forms have substantially different properties, light incident on the interface is bound to experience some scattering.”

Here is a synopsis of Bartis' reasoning. Interest in critical phenomena had led to an odd turn of events due to “the discovery of a discontinuous intermediate stage in a score of transitions previously believed to be second order”. The intermediate stage should produce a sharp rise in the scattered light that could easily be mistaken for critical opalescence. Ginzburg, and then Yakovlev et al., had made this mistake when they attributed the opalescence of quartz during its α – β transition to critical fluctuations. Even though the Ginzburg's theory predicted ~10⁴ increase in the light scattering, as was actually observed, it would be proven later that the effect had nothing do with critical fluctuations. Two forms of quartz coexist over 1°. The transitional opalescence in quartz was caused by light scattering by the interfaces.

The Bartis' account, however, was inconsistent with the orthodox theory developed over previous years. The almost self-evident solution was ignored. It was neither discussed, nor taken into account even in the subsequent publications devoted to the central peaks in quarts and NH₄Cl. The Bartis' articles were not included in the comprehensive list of about 700 references accompanying the 1981 review by Fleury and Lyons on the topic [35]. The cause of the central peaks had already been named, but the search for it was continuing. Lyons and Fleury stated [33] that further theoretical work is needed. Ginzburg et al. [41] modified the theory to include “static inhomogeneities and defects” as the primary contributors to the central peaks. The new theory involved critical fluctuations and did not mentioned nuclei and interfaces.

11.4. Sours of Light Scattering Seen in Microscope

(1) 1975. Durvasula and Gammon [43] pointed out that light scattering investigations failed to measure temperature carefully and paid little attention that the phase transitions exhibit first-order behavior. In their examination of the phase transition in KH₂AsO₄ the light scattering measurements were combined with dielectric measurements and visual monitoring of emergence of the second phase (ferroelectric domains). Both heating and cooling runs were carried out. A hysteresis loop was detected, which meant absence of the critical point.

It was found that sharp increase in light scattering starts at that same moment when the domains appear in the illuminated area of the specimen. That was a direct demonstration that the source of the light scattering responsible for the central peak was the interfaces emerging in the two-phase coexistence range. However, the leading theorists in the field would continue using vague language discussing the “static origin” of the central peaks and speculating about the nature of the “long-living clusters” or “inhomogeneities”. The nature of the “inhomogeneities” as a two-phase state had already been established, but Ginzburg et al. would suggest years later [41] that they are crystal defects.

(2) 1977. The detailed optical microscopic study of the NH₄Cl phase transition by Pique, Dolino and Vallade [44] unambiguously identified the cause of the central peak. Their results completely substantiated the interpretation by Bartis. They stressed the importance of heterophase region (which they also called “mixed state” and “coexistence state”). “During the coexistence state ... there is such an intense light scattering that...no light remains in the [primary] beam of the He-Ne laser”.

(3) 1979. A meticulous investigation of the α – β phase transitions in quartz has been carried out by Dolino [45]. Light scattering measurements were combined with optical microscopic observations. In the vicinity of the transition (~573°C) small temperature gradient was applied along the investigated quartz single crystal. A two-phase band moving from the α-end of the crystal to its β-end and in the reverse direction was observed. Dolino arrived at the conclusion that the light scattering centers were nuclei of the α-phase in the β-phase on cooling, and β-phase in α-phase on heating. The central peak resulted from light scattering by this heterophase band.

(4) The phase transition in a single crystal of β-paradichlorobenzene shown in Fig. 8 presents an opportunity to perform an imaginary experiment on light scattering. When a phase transition has the morphology like in Fig. 2, the appearance of a single crystal of the new phase would, obviously, start light scattering: this is why we can see it. This picture of phase transition is usually obscured by nucleation from multiple sites. The phase transition shown in Fig. 8 goes too quickly to reveal naturally shaped crystals of the new phase. It proceeds by moving an interface, seen as an opaque band, from left to right over the crystal. The band is a cloud of tiny crystals of the new phases. Recording of light scattering from a small area of the crystal would reveal a good "central peak" when the opaque band passes that area.

Figure 8. Single crystal of β-paradichlorobenzene in a some intermediate stage of its phase transition. In this particular case the transition proceeds by moving interface, seeing as an opaque band, from left to right. If light scattering is measured from a small area of the crystal, the recording will produce a “central peak” when the interface passes that area

11.5. Theory vs Evidence

Light scattering “central peaks” in crystal phase transitions have underwent their own transition - from best friends of critical fluctuations to their worst enemies. The 1983 articles collection “Light Scattering Near Phase Transitions” [46] reveals it best. The leading article is characteristic of all the others in the book and sufficient to illustrate the point.

The leading article was the 155-page “General Theory of Light Scattering Near Phase Transitions in Ideal Crystals” by Ginzburg, Sobyanin and Levanyuk (GSL) [13]. The authors disregarded the works on phase transitions by nucleation and growth and works on critical opalescence described in Sections 11.3 and 11.4. The theory was to be applied to second-order phase transitions, but “[they] occur, strictly speaking, only in some exceptional cases”. The predicament was resolved by a presumption that the Landau theory is applicable to “weakly” first-order transitions (Section 4.6). GSL decided that these transitions occur by “inner deformations” and nominated them to be the “order parameter”. Fluctuations of that fictitious parameter were the central idea of their theory. Thus, the theory by GSL is applicable neither to most crystal phase transitions because they are “strongly” first-order, nor to the “weakly first-order” because they are not different from "strongly" ones (see Section 4.6), nor to the “pure” second-order transitions because they are nonexistent.

But there are more to be said about the GSL work. They did not claim any more that increasing in light scattering due to critical fluctuations must be as great as 10⁴ times. Now they maintained that the effect is extremely weak and has to be extracted from the “integral intensity” caused by crystal defects. They acknowledged that “no critical region has been yet observed with confidence” with the exception of the “critical points in magnetics”. But this exception should be excluded (Section 7). GSL formulated the result of their work as follows: “The existing experimental data on the integral intensity of the thermal (molecular) light scattering near phase transition points in solids are neither reliable nor full enough to be compared with the above theoretical predictions.”

The objects, which the GSL theory was to be applied to, did not exist in reality. The light scattering by nuclei and interfaces in real phase transitions, described in previous sections, was not mentioned. The GSL work was dishonest and useless.

Such is the instructive story of the “critical opalescence” in solid-state phase transitions. The experimentally established source of the “central peaks” has been met with resistance by the prominent authors of the insolvent theories. Searching for solution of an already solved problem was continuing. Critical opalescence is still cited as a prominent feature of critical phenomena.

11.6. “λ-Anomaly” of Neutron Scattering

The central peaks of neutron scattering do not need to be discussed in detail. Their story is a carbon copy of what happened to the central peaks of light scattering.

● Original excitement over the discovery of a phenomenon that seemed to offer an intimate insight into the critical dynamics of solid-state phase transitions. The first observation of a neutron scattering central peak was reported in 1971 [47], 15 years after the first light scattering peak was reported. At that time the virtual “non-critical” cause of the light scattering peaks had already been established.

● Subsequent disappointment after finding that the neutron central peaks were a scattering from static centers.

● Search for the nature of the scattering static centers anywhere except where it has been experimentally observed in light scattering: nuclei and interfaces in the two-phase range.

● Dealing with the first-order phase transitions as if they were second-order.

● Desperate experimental search for a “dynamic” component in the “largely static” central peaks. The scope of experimentation was limited by the higher cost of the neutron scattering experiments, as well as by problems with having sufficiently intense neutron sources. As a result, the experimental data were less reliable than in light scattering, thus leaving a wider field for speculations.

● Statements that more work and time is needed to understand the origin of neutron central peaks.

Like in the light scattering, the neutron scattering was caused by nuclei and interfaces.

12. Conclusions

Over the 20^th century and up to now the theory of critical phenomena has grown into a voluminous branch of theoretical physics. Most of that time the physical nature of its objects, which are basically phase transitions, was still unknown, so the theorists analyzed their models, such as Ising model of ferromagnetic phase transition. The models were of a cooperative kind, based on ideas of thermal fluctuations, allowing them to be treated by statistical mechanics.

When the molecular mechanism of solid-state phase transitions became ultimately known, it turned out to be in a striking difference with those models. It does not involve cooperative fluctuations. It is based on the nucleation-and-growth principle. It is general to all types of phase transitions: structural, ferromagnetic, ferroelectric, order – disorder, normal – superconducting, so none is a subject of statistical mechanics. The theoretical models cannot even remotely approximate them. The theoretical models and the real mechanism are antonyms.

As for the “λ-anomalies” and the “critical opalescence” (and a host of the effects caused by the opalescence), they have been incorrectly identified and have now received simple “non-critical” explanations. To that it should be added that (a) the famous “heat capacity λ-anomaly” in liquid helium phase transition is shown to be latent heat of the structural phase transition, and (b) the classical “critical point” of liquid – gas phase transition should be striped of its rank “critical” by the reasons given in Section 2.2.

It looks like the theory of critical phenomena lacks an object it might be applied to.

Note

* While the patches are magnetized, the crystal as a whole would not.