-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2019; 9(1): 6-11
doi:10.5923/j.ajcmp.20190901.02

Theoretical Estimation of Mixing Properties of Al-Mg Binary Liquid Alloy at Different Temperatures
H. K. Limbu, G. P. Adhikari
Department of Physics, Tri-Chandra Multiple Campus, Tribhuvan University, Ghantaghar, Kathmandu, Nepal
Correspondence to: H. K. Limbu, Department of Physics, Tri-Chandra Multiple Campus, Tribhuvan University, Ghantaghar, Kathmandu, Nepal.
| Email: |  |
Copyright © 2019 The Author(s). Published by Scientific & Academic Publishing.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The Regular Solution model has been used to describe thermodynamic properties, transport properties and structural properties at different temperatures theoretically. The interaction energy is temperature dependent and played an important role to explain the properties of Al-Mg liquid alloy at different temperatures. The theoretical values of interchange energy at different temperatures are obtained by best fit parameter approximation with the help of experimental values at 1073K. The properties have been studied with the help of computed theoretical interchange energy at different temperatures using interchange energy and temperature relation. A comparison of theoretical and experimental values at 1073K shows that they are in good agreement and using this basis we have studied properties at different temperatures.
Keywords: Regular solution model, Order energy parameter, Thermodynamic properties, Transport properties, Structural properties, Different temperatures
Cite this paper: H. K. Limbu, G. P. Adhikari, Theoretical Estimation of Mixing Properties of Al-Mg Binary Liquid Alloy at Different Temperatures, American Journal of Condensed Matter Physics, Vol. 9 No. 1, 2019, pp. 6-11. doi: 10.5923/j.ajcmp.20190901.02.
Article Outline
1. Introduction
- Al-Mg has wide range of uses in industries because of its properties like comparatively less inflammable, non-toxic, non-magnetic, good mechanical strength, crack resistance, and low cost maintenance [1-3]. It is also used in automobile engines, construction and shipborne as it has light weight and excellent corrosion resistance [4-6]. We have estimated the mixing properties i.e. thermodynamic, transport and structural properties of the alloy at different temperatures using regular solution model [7]. We have the model to investigate the different properties of the alloy as atoms of Al and Mg are almost same in shape and size i.e. atomic volume of Mg/atomic volume of Al = 16.29/11.4 ≈ 1 [8] which indicates that the alloy is suitable for investigation. In thermodynamic properties, we have calculated free energy of mixing (GM), heat of mixing (HM), entropy of mixing (SM) and activity (a). In transport properties, viscosity
 and diffusion coefficient ratio (Dm/Did) have been computed. And, in structural properties the long wavelength limit (Scc(0)) and chemical short range order parameter (α1) are studied. Many researchers been working on several models to explain the mixing behavior of binary liquid alloys have been studied binary liquid alloys with different models [9-14]. And, viscosity is with the help of Moelwyn-Hughes equation [15-16]. The theoretical formulation has been presented in section (2), result and discussion in section (3) and conclusion in section (4).
and diffusion coefficient ratio (Dm/Did) have been computed. And, in structural properties the long wavelength limit (Scc(0)) and chemical short range order parameter (α1) are studied. Many researchers been working on several models to explain the mixing behavior of binary liquid alloys have been studied binary liquid alloys with different models [9-14]. And, viscosity is with the help of Moelwyn-Hughes equation [15-16]. The theoretical formulation has been presented in section (2), result and discussion in section (3) and conclusion in section (4).2. Formalism
- Regular alloys constituent atoms A and B are sufficiently similar in size and shape so they are interchangeable on the lattice. The binary liquid alloy A-B of homogenous solution consists of CA (A=Al) (≡c) mole of A and CB(B=Mg) {≡(1-c)} mole of B respectively.
2.1. Thermodynamic Properties
- The free energy of mixing
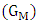 of binary liquid alloy is
of binary liquid alloy is 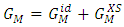 | (1) |
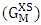 and ideal free energy of mixing
and ideal free energy of mixing 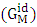 are given by
are given by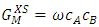 | (2) |
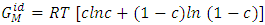 | (3) |
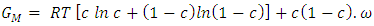 | (4) |
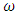 is interaction energy and R is molar gas constant. The expression for activities aA of the elements A and B
is interaction energy and R is molar gas constant. The expression for activities aA of the elements A and B 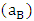 in the binary liquid alloy can be derived from the standard relations
in the binary liquid alloy can be derived from the standard relations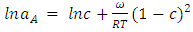 | (5) |
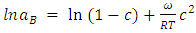 | (6) |
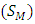 is given by
is given by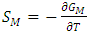 | (7) |
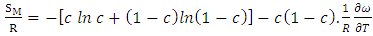 | (8) |
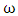 as temperature dependent has been studied by Bhatia et al. [17], Shrestha et al. [18], Alblas et al. [19]. The interchange energy
as temperature dependent has been studied by Bhatia et al. [17], Shrestha et al. [18], Alblas et al. [19]. The interchange energy 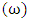 is temperature dependent.The relation for heat of mixing (HM), entropy of mixing (SM), and free energy of mixing (GM) is expressed as
is temperature dependent.The relation for heat of mixing (HM), entropy of mixing (SM), and free energy of mixing (GM) is expressed as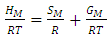 | (9) |
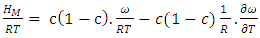 | (10) |
2.2. Transport Properties
- The relation between diffusion coefficient and concentration fluctuation derived by Singh and Sommer [20] is given as
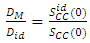 | (11) |
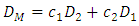 | (12) |
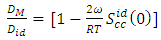 | (13) |
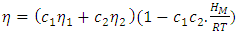 | (14) |
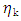 (k = 1, 2) is the viscosity of pure component K and can be calculated from Arrhenius type equation [22] as
(k = 1, 2) is the viscosity of pure component K and can be calculated from Arrhenius type equation [22] as 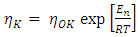 | (15) |
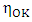 is constant (in unit of viscosity) and En is the energy of activation of viscous flow for pure metal (in unit of energy per mole).
is constant (in unit of viscosity) and En is the energy of activation of viscous flow for pure metal (in unit of energy per mole).2.3. Structural Properties
- The concentration fluctuation in the long wavelength limit (Scc(0)) [23] can be calculated as
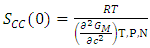 | (16) |
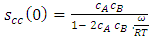 | (17) |
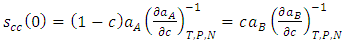 | (18) |
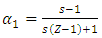 | (19) |
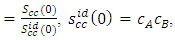 and Z is the coordination number = 10 in our investigation.
and Z is the coordination number = 10 in our investigation.2.4. Order Energy Parameter at Different Temperatures
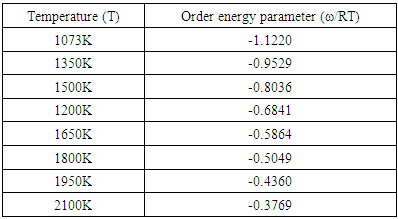
- The values of free energy of mixing (GM) of the alloy at different temperatures is computed from equation (4) using the values of order energy parameter (ω) at different temperatures from the relation [25,26]
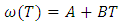 | (20) |
3. Result and Discussion
- The values of A and B is calculated using the values of ω/RT and
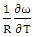 at temperature 1073K of the alloy Al-Mg in equation (20). The best fit parameters i.e. ω/RT = -1.122 and
at temperature 1073K of the alloy Al-Mg in equation (20). The best fit parameters i.e. ω/RT = -1.122 and 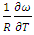 = 0.391 at temperature 1073K by the method of best fit approximation with the experimental values of the alloy from Hultgren et.al. 1973 [27] using equations (4) and (8). The theoretical values of interchange energy (ω) at different temperatures are calculated using eqation (20) which are presented in the table 1.
= 0.391 at temperature 1073K by the method of best fit approximation with the experimental values of the alloy from Hultgren et.al. 1973 [27] using equations (4) and (8). The theoretical values of interchange energy (ω) at different temperatures are calculated using eqation (20) which are presented in the table 1.
|
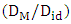 and viscosity (𝜂) at different temperatures (T) with the help of Regular solution model.
and viscosity (𝜂) at different temperatures (T) with the help of Regular solution model.3.1. Free Energy of Mixing
- The values of free energy of mixing (GM) of the alloy at temperatures 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K have been computed using the values of ω(T) in equation (4) over the entire range of concentration. The free energy of mixing (GM) of Al-Mg liquid alloy at different temperatures of study in the concentration range CAl = 0.1 to 0.9 is shown in figure (1).
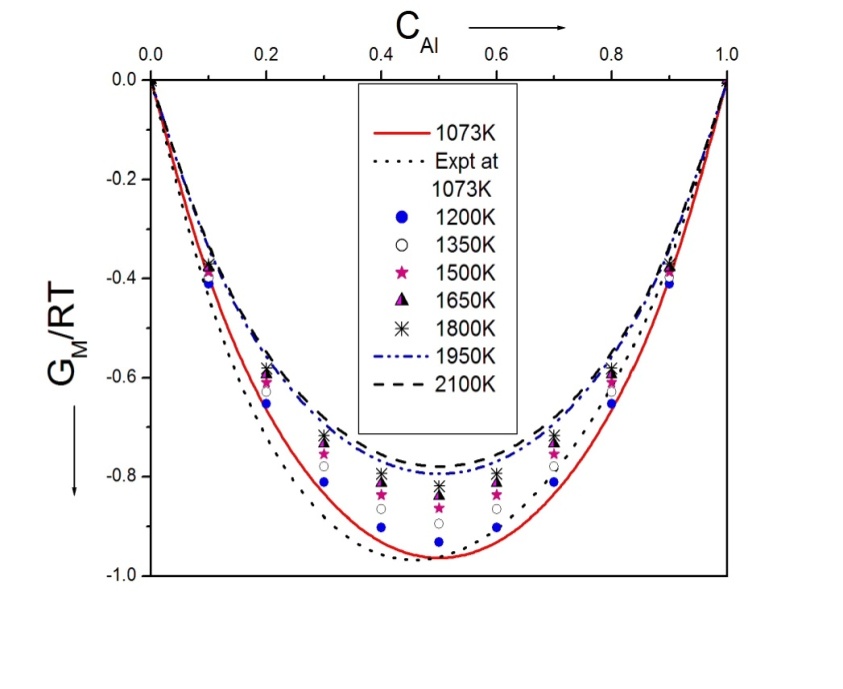 | Figure 1. Graph for (GM/RT) Versus the concentration of CAl of Al-Mg liquid alloy at temperatures 1073K, 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K |
3.2. Entropy of Mixing (SM)
- By best fit method, the theoretical value of
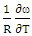 at 1073K is obtained using equation (8) with the help of experimental values of entropy of mixing (SM) is taken from Hultgren et. al. [27] i.e.
at 1073K is obtained using equation (8) with the help of experimental values of entropy of mixing (SM) is taken from Hultgren et. al. [27] i.e. 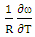 = 0.391. With the help of this theoretical value of
= 0.391. With the help of this theoretical value of 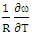 , entropy of mixing are computed at all temperatures (T) using equation (8) with the help of values of energy order parameters ω(T) at corresponding temperatures presented on the table 1.The values of SM/R are found to be positive in the entire concentration range. This explains the symmetry in entropy of mixing of Al-Mg liquid alloy. At all temperatures of study, the values of entropy of mixing remain unchanged as the theoretical value of
, entropy of mixing are computed at all temperatures (T) using equation (8) with the help of values of energy order parameters ω(T) at corresponding temperatures presented on the table 1.The values of SM/R are found to be positive in the entire concentration range. This explains the symmetry in entropy of mixing of Al-Mg liquid alloy. At all temperatures of study, the values of entropy of mixing remain unchanged as the theoretical value of 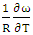 = 0.391 remains constant using equation (20).
= 0.391 remains constant using equation (20).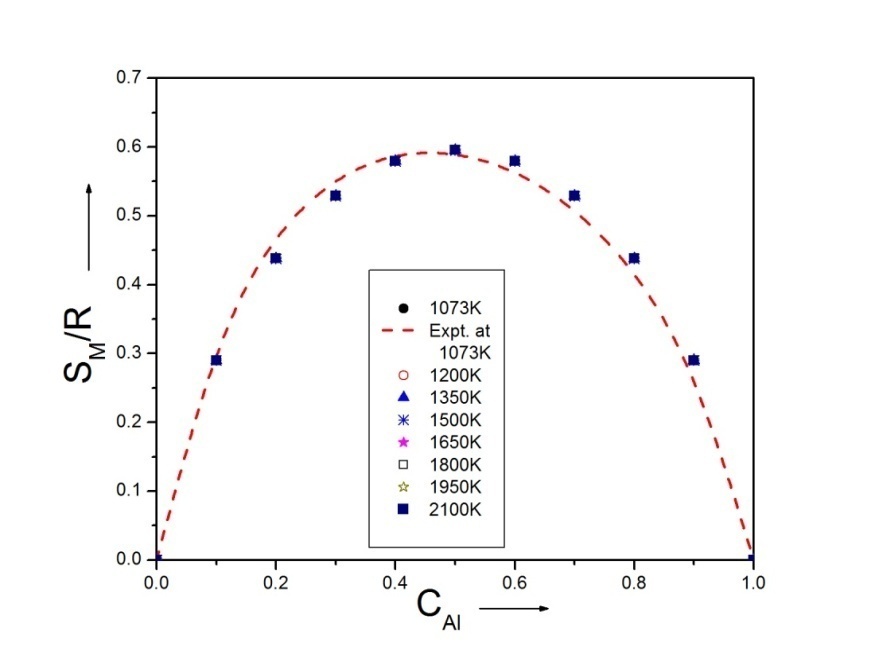 | Figure 2. Graph for SM/R versus the concentration of CAl of Al-Mg liquid alloy at temperatures 1073K, 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K |
3.3. Heat of mixing (HM)
- The heat of mixing (HM) for the alloy is calculated using equation (10) with the help of theoretical values of order energy parameter which is shown in figure 3.
 | Figure 3. Graph for HM/RT versus the concentration of CAl of Al-Mg liquid alloy at temperatures 1073K, 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K |
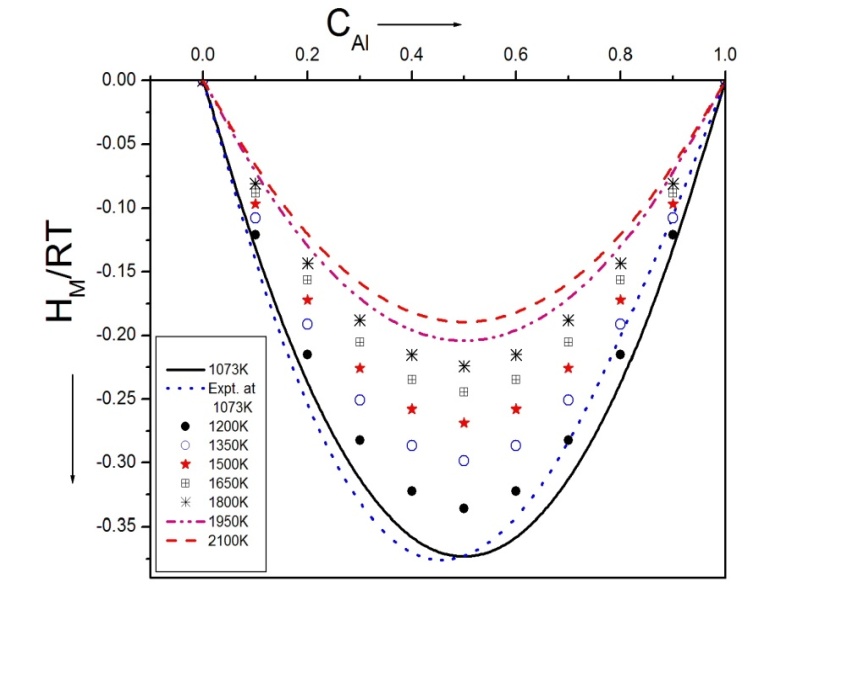
3.4. Activity
- Activity of Al and Mg atoms of the alloy is Calculated using equations (5) and (6) in entire concentration range. The activity (Ln a) versus the concentration is studied which is shown in figure 4 and figure 5.
 | Figure 4. Ln aAl versus CAl of Al-Mg liquid alloy at 1073K, 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K. |
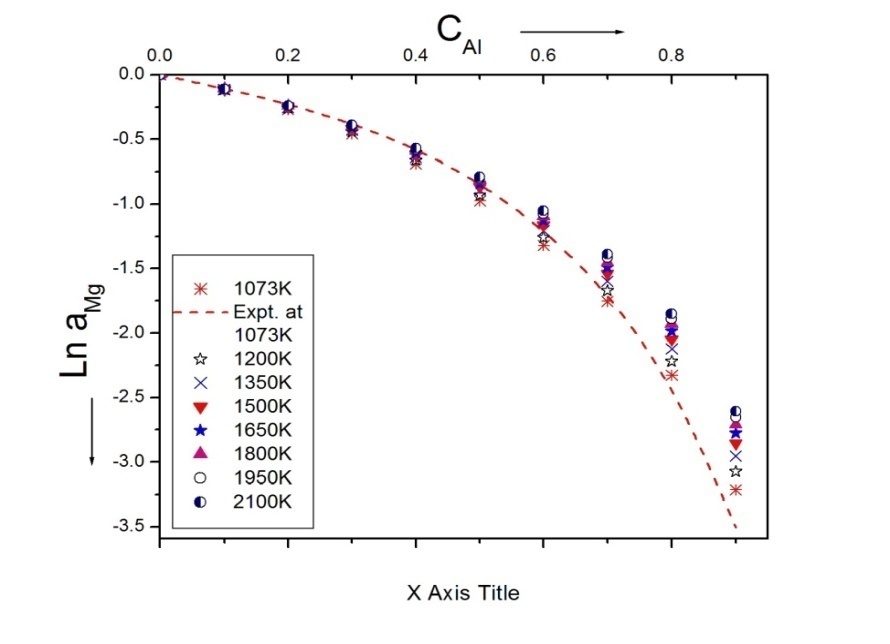 | Figure 5. Ln aMg versus CAl of Al-Mg liquid alloy at 1073K, 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K |
3.5. Transport Properties: Chemical Diffusion and Viscosity
- Equation (13) is used to calculate the diffusion coefficient
 with the help of theoretical values of order energy parameters ω(T). The investigation of the diffusion coefficient with the concentration of Al is shown in figure (6).
with the help of theoretical values of order energy parameters ω(T). The investigation of the diffusion coefficient with the concentration of Al is shown in figure (6).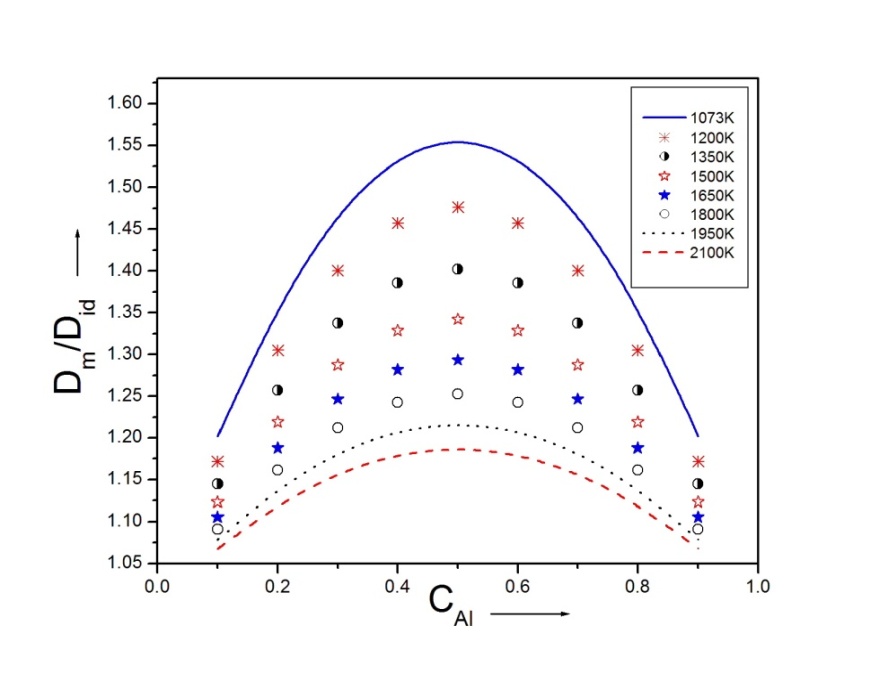 | Figure 6. Ratio of mutual and self-diffusivities,  for Al-Mg liquid alloy at temperatures 1073K, 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K versus concentration of Al for Al-Mg liquid alloy at temperatures 1073K, 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K versus concentration of Al |
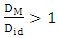 in the entire range of concentration at all temperatures (T) which shows chemical order in the alloy. The ordering tendency of the atoms in Al-Mg liquid alloys is greater about equiatomic composition as the maximum value of
in the entire range of concentration at all temperatures (T) which shows chemical order in the alloy. The ordering tendency of the atoms in Al-Mg liquid alloys is greater about equiatomic composition as the maximum value of  is at CAl = 0.5.Viscosity of the alloy is calculated using equations (14) and (15). The viscosities of pure components Al and Mg at all temperatures(T) are computed using equation (15) with the help of constants
is at CAl = 0.5.Viscosity of the alloy is calculated using equations (14) and (15). The viscosities of pure components Al and Mg at all temperatures(T) are computed using equation (15) with the help of constants  and E for the metals [22] which is used to find the viscosity of the alloy for corresponding temperatures using equation (14).
and E for the metals [22] which is used to find the viscosity of the alloy for corresponding temperatures using equation (14).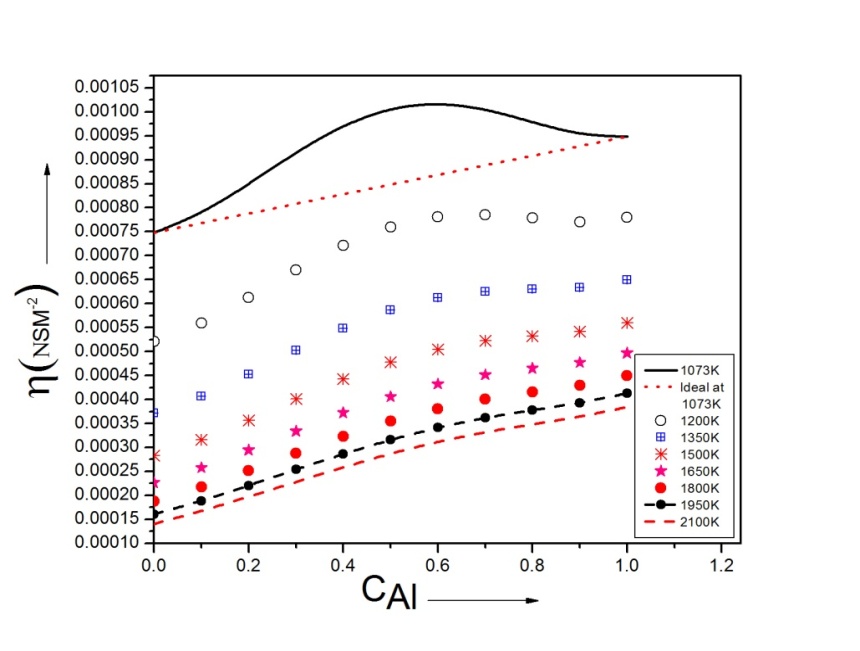 | Figure 7. Viscosity of Al-Mg liquid alloy at 1073K, 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K versus concentration of Al |
3.6. Structural Properties
- The theoretical and experimental values of concentration fluctuation in the long wavelength limit (Scc(0)) can be obtained from equations (18) and (19). The values of Short range order parameters (α1) at different temperatures are calculated from equation (19).
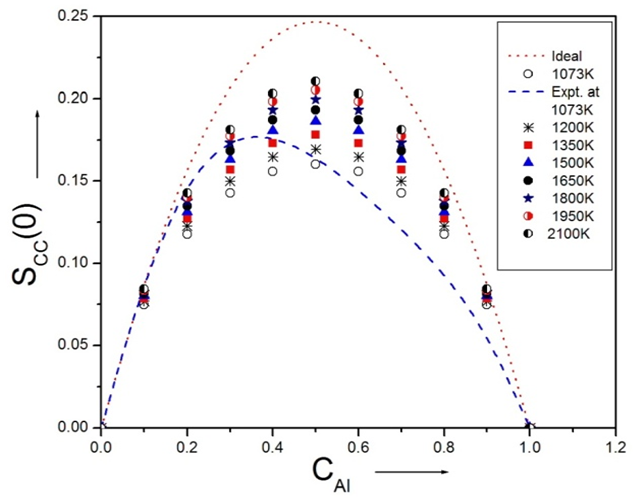 | Figure 8. Theoretical values of Concentration fluctuation of Al-Mg liquid alloy at 1073K, 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K along with experimental values at 1073K and  |
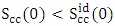 throughout the entire concentration range at all temperatures of investigation which implies that ordering is favored in the Al-Mg alloy.The theoretical values of Warren-Cowley chemical short-range order parameter (α1) [21,24] is Computed from equation (19) using the theoretical values of Scc(0). We have calculated that the Chemical short range order parameter (α1) is negative at all the concentrations which indicate ordering nature of the alloy as shown in the figure 9.
throughout the entire concentration range at all temperatures of investigation which implies that ordering is favored in the Al-Mg alloy.The theoretical values of Warren-Cowley chemical short-range order parameter (α1) [21,24] is Computed from equation (19) using the theoretical values of Scc(0). We have calculated that the Chemical short range order parameter (α1) is negative at all the concentrations which indicate ordering nature of the alloy as shown in the figure 9. | Figure 9. Chemical short range order parameter (α1) of Al-Mg liquid alloy at 1073K, 1200K, 1350K, 1500K, 1650K, 1800K, 1950K and 2100K with co-ordination number (Z)= 10 |
4. Conclusions
- - The alloy is an ordered system and interacting in nature at all temperatures of investigations.- The alloy is symmetric in nature at all temperatures.- The activity of the alloy slightly increases as the temperature increases.- Viscosity decreases as the temperature of study increases.- properties can be studied at different temperatures using temperature and interaction energy relation theoretically.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML