1. Introduction

In recent years, the ‘wonder material’ graphene has been explored intensively due to its ultrahigh room-temperature carrier mobility [1, 2] and is touted to be the next-generation electronic material to replace silicon, since silicon is approaching its performance limits.

Graphene, the well-publicized and famous two-dimensionalboron nitride (BN) allotrope, have attracted intensive research interest due to their fascinating electronic properties and extensive applications [3, 4]. Among them, Hexagonal boron nitride (h-BN) is an insulator with a large band gap [5, 6] a two-dimensional monolayer of carbon atoms arranged in a honeycomb lattice, it is the building block for other graphitic materials including one-dimensional carbon nanotubes and three-dimensional graphite. It has been theoretically investigated by several scientist for more than sixty years. For instants, Wallace calculated the electronic band structure of graphene using a tight-binding method in 1947, showing its semi-metallic nature and linear energy dispersion around the Fermi energy. [7].

Geim and Novoselov of Manchester University demonstrated that graphene could be isolated by using a remarkably simple mechanical exfoliation technique which is commonly called the Scotch tape methodin 2004 [8].

In 2005, the Manchester group [9] and Philip Kim’s group at Columbia University independently observed the quantum Hall effect in grapheme [10]. This shows the quantum Hall plateaus were found to be quantized in half-integer values which provided convincing evidence of the two-dimensional massless chiral nature of charge carriers in this system.

These early discoveries have initiated intense research activities worldwide on graphene and other two-dimensional materials. The exploding interests in graphene have been largely motivated by its remarkable electronic properties and its stable form. Due to the linear energy dispersion around the Fermi energy, the low-energy charge carriers in graphene has described by relativistic Dirac equation rather than the Schrodinger equation.

However, the high mobility of charge carriers and the ambipolar transport characteristics make graphene particularly promising for high frequency applications. It was demonstrated by Lin and his group that high frequency operation, at 100 GHz, was possible in graphene-based transistors [11] meaning that it can be integrated into a huge number of applications. The only problem with graphene is that high-quality graphene is a great conductor that does not have a band gap (a semi-metal with a zero band gap). Due to this intrinsic property, it is not possible to switch off the devices with graphene as the channel material, resulting in very poor ON/OFF ratio. Although a band gap can be introduced into graphene, but the process is extremely complex to make and will result in a loss of mobility.

In order to realize graphene’s full potential as a post-silicon electronic material, a sizable bandgap must be created [12]. Although a small bandgap can be engineered in nano-ribbons and bilayer graphene under strong electric field, but large gap has not been created at this stage sufficiently.

Mechanical properties of graphene are also extraordinary due to the strong carbon-carbon covalent bonds. The tensile strength of graphene is measured to be about 300 times greater than steel [13]. In addition, graphene can sustain a large degree of stretching and bending without structural damage. These properties together with the optical transparency make graphene very attractive in potential applications in solar cells, touch screen displays, and flexible optoelectronic devices.

The major focus of our research is to obtain the structural properties, electronic properties and elastic properties of BN for its potential applications.

2. Computational Method

All the calculations reported in this work were performed using the Quantum-ESPRESSO code [14] with the version of 5.1 which is based on density-functional theory (DFT) in which plane wave basis sets for expansion of the electronic wave function and conjugated gradient electronic minimization were used. In this package, electron-ion interactions were described using the norm-conserving or ultrasoftpseudopotentials. The exchange and correlation energies were calculated with the Perdew-Burke-Ernzerhof (PBE) form of the generalized gradient approximation (GGA) [15, 16]. Geometry optimizations were performed by the Broyden-Fletcher-Goldfarb-Shanno (BFGS) algorithm. The k-points, lattice constant and plane wave cutoff energy were thoroughly tested. In this study a k-point grid of 4x4x4 were used for the bulk properties. The optimized value for plane wave cutoff of 37 Ry used for all calculations. All the known cell parameters were fixed at the experimental value of the crystal during geometry optimizations while all the atom positions were minimized with symmetries. Where no experimental value were available the atom-atom distance was approximated by adding the covalent radii of the elements [17].

For the pseudopotential generation Brillouin Zone integrations were performed using a 8×8×1 Monkhorst and Pack special point grids using Gaussian smearing technique with a smearing width of 0.02 Ry in order to smooth the Fermi distribution. The Kohn-Sham orbitals are expanded in a plane wave basis setby obtaining the structural stability and electronic properties such as (ground state total energy, density of state (DOS) projected density of state (PDOS), magnetic moments and charge density distribution) within the DFT as implemented on the Quantum ESPRESSO package.

While dealing with the PW basis the first step was to have a details of the crystal structure for the compound of interest, therefore, our structural parameters was obtained from available literatures specifically experimental database reported in [18, 19]. Then we optimized them (relaxation calculation) using DFT-GGA by applying the Broyden-Fletcher-Goldfarb-Shannon (BFGS) algorithm [20], unless otherwaise the optimized parameters close to the experimental values was taking and employed in our calculations.

In a crystal structural optimization, one has to look for the structure with a minimum potential energy surface (PES) that is closest to the starting configuration. In practice one has to search for the ionic configuration for which all the forces are zero. A Quasi-Newton ionic relaxation within the Broyden Fletcher Goldfarb Shanno algorithm has been one of the most successful approximations within a theoretical framework for more than a decade.

In order to determine the elastic properties we consider the general deformation state, such that the number of independent components of the second, third, fourth and fifth order elastic tensors are 23, 58, 136, and 272 respectively. Conversely, there are only fourteen independent elastic constants need to be explicitly considered due to the symmetries of the atomic lattice point group of h-BN which consists of a six-fold rotational axis and six mirror planes.

The fourteen independent elastic constants of h-BN are determined by a least-squares fit to the stress-strain results from DFT based first-principles studies in two steps as implemented in Elastic code of the QE [21]. In the first step, we use a least-squares fit of five stress-strain responses.

Five relationships between stress and strain are necessary because there are five independent fifth-order elastic constants. We obtain the stress-strain relationships by simulating the following deformation states: uni-axial strain in the zigzag direction (zigzag); uni-axial strain in the armchair direction (armchair); and equibiaxial strain (biaxial). From the first step, the components of the second-order elastic constants, the third-order elastic constants, and the fourth order elastic constants are over-determined (i.e, the number of linearly independent variables are greater than the number of constrains), and the fifth-order elastic constants are well-determined (the number of linearly independent variables are equal to the number of constrains). Under such circumstances, the second step is needed: least-square solution to these over- and well- determined linear equations.

3. Results and Discussions

A Structural and Elastic Properties

I. Atomic structure

We first optimize the equilibrium lattice constant for h-BN. The total energy as a function of lattice spacing is obtained by specifying nine lattice constants varying from 3.3 Å to 4.1 Å, with full relaxations of all the atoms. A least-square fit of the energies versus lattice constants with a fourth-order polynomial function yields the equilibrium lattice constant as a = 3.731 Å. The most energetically favorable structure is set as the strain-free structure in this study and the atomic structure, as well as the conventional cell is shown in Fig. 1. Specifically, the bond length of B-N bond is 2.154 Å. The B-N-B and B-N-B angles are 120 and all atoms are within one plane. Our result of bond length is in good agreement with previous DFT calculations of A-BNNR sheet [22].

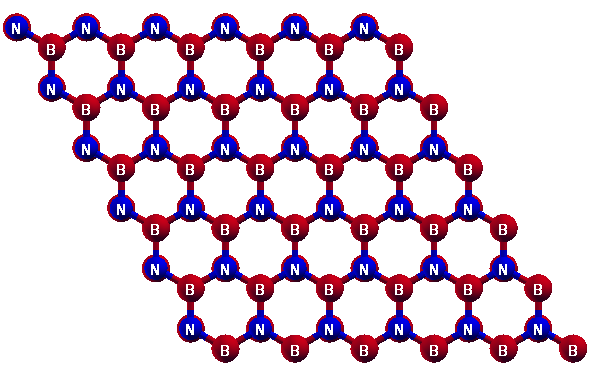Figure 1. Optimized Hexagonal Boron Nitride structure

II. X-Ray diffraction pattern

Fig. 2 below shows the calculated X-Ray diffraction pattern of the compound at 160°C. The peaks at 2θ= +24.32°, 49.60° and 74.00° (JPCD, No. 9 - 12) is attributed to hexagonal boron nitride formation. The peak at 22° corresponds to the (002) diffraction peak of h-BN which is a small angle X-ray scattering (SAXS). It has helped in phase analysis of the sample surface layers and it is also an analytical method of determining the structure of particle systems in terms of average sizes or shape. The small-angle scattering is particularly useful because of the dramatic increase in the forward scattering that occurs at phase transitions which is known as critical opalescence and because many materials, substances and biological systems possess interesting and complex features in their structure, which match the useful length scale ranges within this region. This region also provides valuable information over a wide variety of scientific and technological applications including chemical aggregation, defects in materials, surfactants colloids ferromagnetic correlations in magnetism, alloy segregation, biological membranes, [23, 24].

Variation of the incident angle allows the analysis of grade layers or multi-layer systems. Because the SAXS looks at the particle distances instead of atomic distance, the effects appears at very small scattering angles near the primary beam. This sample is more crystalline compared to other temperatures tested.

Figure 2. Calculated X-Ray of Hexagonal Boron Nitride

III. Elastic properties

Table 1 below provides the summary comparism of three different average calculated elastic properties from the three different methods, Voigt, Reus and Hill adopted by Quantum ESPRESSO. Reuss shows the smallest stable structure of 0.18739 of hexagonal boron nitride which is more stable for an excellent optical material.

Table 1. Average Elastic properties of Hexagonal Boron nitride

B Electronic Properties

I. Band Structure

From Fig 3 below the obtained band structure of Hexagonal Boron Nitride single layer which shows the (graphite-like) Band structurecan be understood in terms of sp² hybrid oriented in the direction of the bond and its orbitals constructed from these hybrids. Each B-N atoms in the lattice structure of the h-BN has one s and three p orbitals for bonding (σ and π) within the h-BN sheet. The s orbital and two in-plane p orbitals generate three sp² orbitals forming strong covalent (σ) bonds with their neighbouring B-N atoms.

The flatness of the h-BN structure can be said to come ultimately from the empty part of the π-state bonds rather than from the full part, whereas the fourth valence electron occupies a P_z orbital perpendicular to the sheet and its contributes to the delocalized electron gas which explains h-BN high conductivity. Each B atom contributes an electron to the P_z orbital to form a π band. So in total, B-N has three in plane σ orbitals which are responsible for the strength of graphene and a P_z - band perpendicular to the sheet of h-BN. The highest occupied state of this band structure is 0.101eV while the lowest unoccupied state is 4.702eV which gives the evaluated band gap as 4.601eV which confirms that this is a wide band gap semiconductor materials.

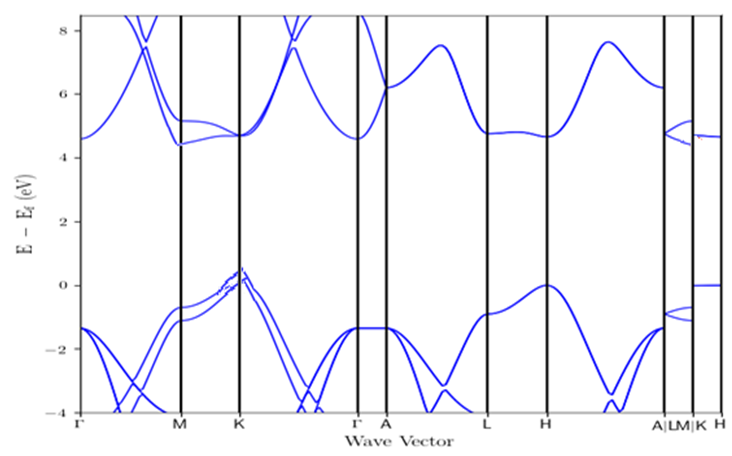Figure 3. Calculated Band Structure of Hexagonal Boron Nitride

II. Density of State

For all other configurations, almost the same band gap has been observed. To further analyze the electronic properties of the structures, density of states (DOS) have also been investigated and shown in Fig. 4 below, represents the number of electronic states available for occupancy per energy level. Here, it is observed that no electronic states are present at the Fermi level, validates the wide band semiconducting behavior of BN. It also shows that in upper valence band, the 2p states of N atoms dominate, with the maximum peak at 4.24 eV, few electronic states are present near the Fermi level, and however, there is no significant impact in the conduction band. On the contrary, 2p states of B atoms show their dominance in the conduction band with a maximum peak at -2.24 eV.

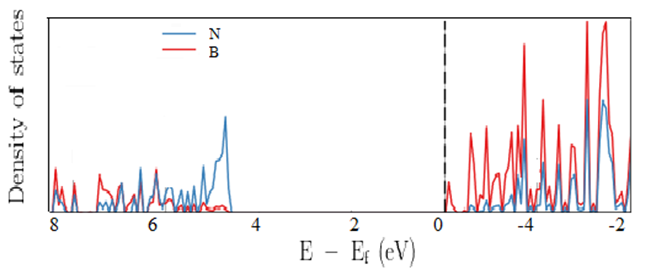Figure 4. Calculated Density of State of H-BN

III. Charge Density Distribution

In order to understand the distribution of the total electronic charge density of h-BN single layer, we calculated the electronic charge density distribution as shown in a fig. 5 below. From the result one can observe that that B-N makes the covalent bonding. It is clear that in hexagonal of BN sheet structure, B-B atoms shows a very week charge density but as we move to N-N bonding, there is the stronger charge density. Also as clear as its from the scale that the purple color shows the greater charge density, so the Nitrogen atom has the greater charge density than the Boron atoms in the sheet.

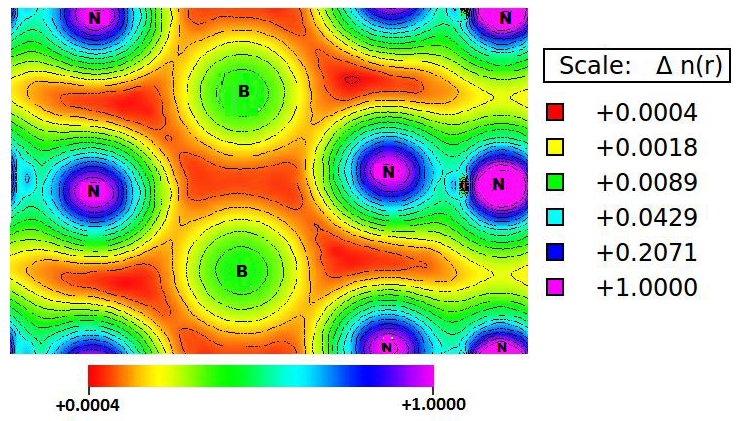Figure 5. The top view of the calculated chargedensity plot of the h-BN ssystem with colors scale n(r) indicating ranges of charge accumulation and depletionina.u

4. Conclusions

In summary, we studied the structural, electronic and elastic properties of h-BN under various strains using DFT based first principles calculations. It is observed that h-BN shows a nonlinear elastic deformation up to a definitive strain, which is 0.20881, 0.18739, and 0.20829 for Voigt, Reuss, and Hill respectively, which are large Poisson ratio compared to hexagonal graphene. We also found that the h-BN can sustain much smaller strains before the rupture. The nonlinear elasticity of h-BN was investigated. We found an accurate continuum description of the elastic properties of h-BN by explicitly determining the fourteen independent components of high order (up to fifth order) elastic constants from the fitting of the stress-strain curves obtained from DFT calculations. This data is useful to develop a continuum description which is suitable for incorporation into a finite element analysis model for its applications in large scale. The second order elastic constants including in-plane stiffness are predicted to monotonically increase with pressure while Poisson’s ratio monotonically decreases with increasing pressure.