-
Paper Information
- Next Paper
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2017; 7(3): 67-72
doi:10.5923/j.ajcmp.20170703.02

Chemical Ordering in Na-Pb and Na-Hg Liquid Alloys
Ajayi Ayodeji Akintunde, Ogunmola Enoch Debayo, Adeoye Abiodun Eyitayo
Department of Mathematical and Physical Sciences, Afe Babalola University, Ado-Ekiti, Nigeria
Correspondence to: Ogunmola Enoch Debayo, Department of Mathematical and Physical Sciences, Afe Babalola University, Ado-Ekiti, Nigeria.
| Email: |  |
Copyright © 2017 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

A simple model has been used to investigate the nature of chemical order in Na-Pb and Na-Hg liquid binary alloy at 700K and 673K respectively. The energy parameter obtained from the model was used to calculate the concentration dependent mixing properties such as Gibb’s free energy of mixing, Concentration fluctuations in the long wavelength limit and the Warren-Cowley chemical short range order parameter. Results obtained showed that both alloys are hetero-coordinated throughout the entire concentration and there is tendency for segregation and demixing to take place in the liquid alloys. We observed that Na-Hg liquid alloy is more strongly interacting binary alloy and chemically ordered than Na-Pb liquid alloy.
Keywords: Binary liquid alloy, Chemical ordering, Sodium, Theoretical study, Warren-Cowley parameter
Cite this paper: Ajayi Ayodeji Akintunde, Ogunmola Enoch Debayo, Adeoye Abiodun Eyitayo, Chemical Ordering in Na-Pb and Na-Hg Liquid Alloys, American Journal of Condensed Matter Physics, Vol. 7 No. 3, 2017, pp. 67-72. doi: 10.5923/j.ajcmp.20170703.02.
Article Outline
1. Introduction
- A number of theories have been developed by theoreticians to explain the temperature dependence of the thermodynamic properties of binary liquid alloys with a purpose of obtaining valuable microscopic information on them [1-3]. Accurate thermodynamic knowledge of the alloy mixing properties and phase diagrams of alloy systems is crucial to having a reliable theoretical result. The mixing behavior of two metals forming binary alloys is as a result of the interplay between energetic and structural adjustments of constituent elemental atoms [4]. Hetero-coordination known as the preference of unlike atoms to pair as nearest neighbors in the alloy system, form A-B pair while segregation is known as the situation where the constituent atoms in the alloy becomes self-coordinated forming A-A and B-B pairs where A and B are the constituent atoms within the binary alloy [5]. Alloys are mixture of metals and a binary alloy can be represented as AxB1-x where A and B are metals and subscripts x and 1-x are concentration of the respective metals. Na-Pb, Na-Hg, K-Pb and K-Hg are examples of binary alloys. Classification of binary alloys can be done according to the deviation of their thermodynamic functions such as chemical activity from raoulatian ideality, therefore binary alloys can be classified into two main groups; segregating (positive deviating) and heteoro-coordinating (negative deviating) alloys [6, 7]. The interest in the energetic and its effects on the alloying behavior of Na-Pb and Na-Hg stemmed from the understanding that, despite the hazards involved in the unsafe handling of Na-Pb alloy, it may still be relevant in qualitative inorganic analysis, both as reductant in acidic and alkaline media, and also as a source of sodium hydroxide for hydroxide precipitations [8]. Na-Hg has been used in organic chemistry as a powerful reducing agent, which is safer to handle than sodium itself. Na-Hg has been found to be useful in fabricating pressure-based sodium lamp [9]. It is necessary to mention that there has been a previous attempt to understand the alloying behavior of these alloys [10]. Consequently, this paper also has the purpose of complimenting earlier studies on each of Na-Pb and Na-Hg liquid alloy by studying the structural behaviour of these two Sodium-based alloy systems, mostly with, studies of concentration fluctuations and the Warren-Cowley chemical short-range order parameter (CSRO). The calculation of the structural properties using Flory’s model [11] is presented.
2. Theoretical Concepts
- In the framework of the Flory’s model, the expression for the Gibb’s free energy of mixing,
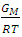 , of a binary liquid alloy is given by
, of a binary liquid alloy is given by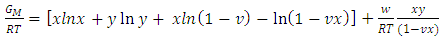 | (1) |
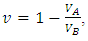 VA and VB being atomic volumes of constituents’ A and B respectively. The parameter w is the ordering energy whose value gives information on the alloying behaviour of the alloy. R is a universal gas constant.The concentration fluctuations in the long-wavelength limit, Scc(0) can be calculated from the standard relationship in terms of the Gibbs free energy of mixing
VA and VB being atomic volumes of constituents’ A and B respectively. The parameter w is the ordering energy whose value gives information on the alloying behaviour of the alloy. R is a universal gas constant.The concentration fluctuations in the long-wavelength limit, Scc(0) can be calculated from the standard relationship in terms of the Gibbs free energy of mixing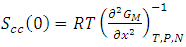 | (2) |
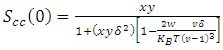 | (3) |
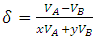 | (4) |
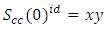 | (5) |
3. Results and Discussion
3.1. Free Energy of Mixing
- Table 1 shows the values of the fitted interaction parameter for liquid Na-Pb and Na-Hg. Eqn. (1) has been used in obtaining, the optimal value for the interaction parameter
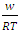 that gives agreement between experimental and theoretical Gibbs free energy. Eqn. (1) was also used to calculate the GM/RT for both systems while the experimental data were taken from the work reported by Hultgren et. al., [13]. Figure 1 and 2 shows the computed and experimental values as a function of concentration. The negative values of w in Table 1 show both alloy systems are chemically ordered, which means pairing of unlike atoms. From the results in Figure 1 and 2, it could be seen that both systems Na-Pb and Na-Hg have
that gives agreement between experimental and theoretical Gibbs free energy. Eqn. (1) was also used to calculate the GM/RT for both systems while the experimental data were taken from the work reported by Hultgren et. al., [13]. Figure 1 and 2 shows the computed and experimental values as a function of concentration. The negative values of w in Table 1 show both alloy systems are chemically ordered, which means pairing of unlike atoms. From the results in Figure 1 and 2, it could be seen that both systems Na-Pb and Na-Hg have 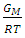 minimum values of -2.797 and -3.125 respectively. This is an indication that Na-Hg is more heterocoordinated than Na-Pb or strongly interacting binary alloy,
minimum values of -2.797 and -3.125 respectively. This is an indication that Na-Hg is more heterocoordinated than Na-Pb or strongly interacting binary alloy, 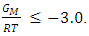
|
3.2. Concentration Fluctuations and the Warren-Cowley CSRO Parameter
- The fitted parameters were kept invariant when computing Scc(0) and the short-range order
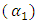 . In principle, Scc(0) can be obtained directly from small-angle diffraction experiments but the experimental procedure involved is very tedious and has not been accomplished successfully. The Scc(0) is an essential microscopic parameter which has been widely used in the study of nature of atomic order in binary liquid alloys [13, 14] and the Scc(0) with
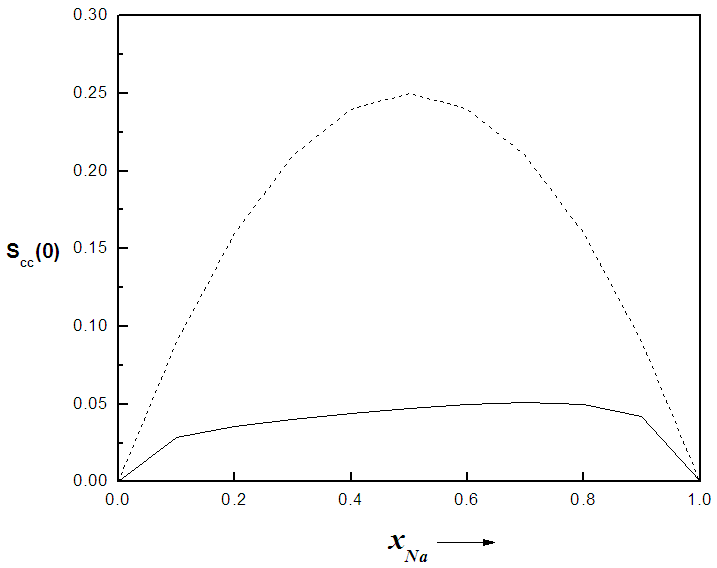
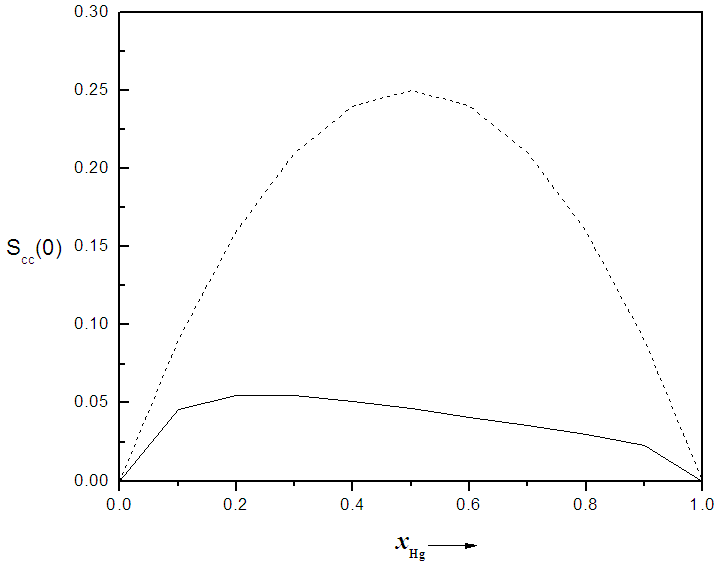
. In principle, Scc(0) can be obtained directly from small-angle diffraction experiments but the experimental procedure involved is very tedious and has not been accomplished successfully. The Scc(0) is an essential microscopic parameter which has been widely used in the study of nature of atomic order in binary liquid alloys [13, 14] and the Scc(0) with 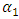 and it also formed a basis for explaining energetics in liquid alloys. Figure 3 and 4 shows the computed values of the concentration fluctuations in the long wavelength limit. Eqs. (3) and (5) has been used to compute Scc(0) and Scc(0)id respectively. The mixing behavior of liquid binary alloys can be deduced from the deviation of Scc(0) from the ideal value. Scc(0) < Scc(0)id is an evidence of chemical ordering and heterocoordination otherwise, there is tendency for segregation and demixing to take place in the liquid alloys. Fig. 3 and 4 shows heterocoordination in both alloys.
and it also formed a basis for explaining energetics in liquid alloys. Figure 3 and 4 shows the computed values of the concentration fluctuations in the long wavelength limit. Eqs. (3) and (5) has been used to compute Scc(0) and Scc(0)id respectively. The mixing behavior of liquid binary alloys can be deduced from the deviation of Scc(0) from the ideal value. Scc(0) < Scc(0)id is an evidence of chemical ordering and heterocoordination otherwise, there is tendency for segregation and demixing to take place in the liquid alloys. Fig. 3 and 4 shows heterocoordination in both alloys.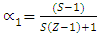 | (6) |
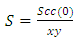 | (7) |
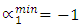 indicates complete ordering (unlike atoms pairing) while
indicates complete ordering (unlike atoms pairing) while 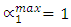 represent segregation. The degree of chemical order may be deduced from the negative values of α1. Maximum heterocoordination can be observed at xNa = 0.41 in Na-Pb and at xHg = 0.72 in Na-Hg as depicted by figures 5 and 6. α1 for Na-Pb at xNa = 0.41 is -0.30 and in the case of NaHg at xHg = 0.72 is -0.34. This reveals Na-Hg has more heterocoordination and chemical order than Na-Pb.
represent segregation. The degree of chemical order may be deduced from the negative values of α1. Maximum heterocoordination can be observed at xNa = 0.41 in Na-Pb and at xHg = 0.72 in Na-Hg as depicted by figures 5 and 6. α1 for Na-Pb at xNa = 0.41 is -0.30 and in the case of NaHg at xHg = 0.72 is -0.34. This reveals Na-Hg has more heterocoordination and chemical order than Na-Pb.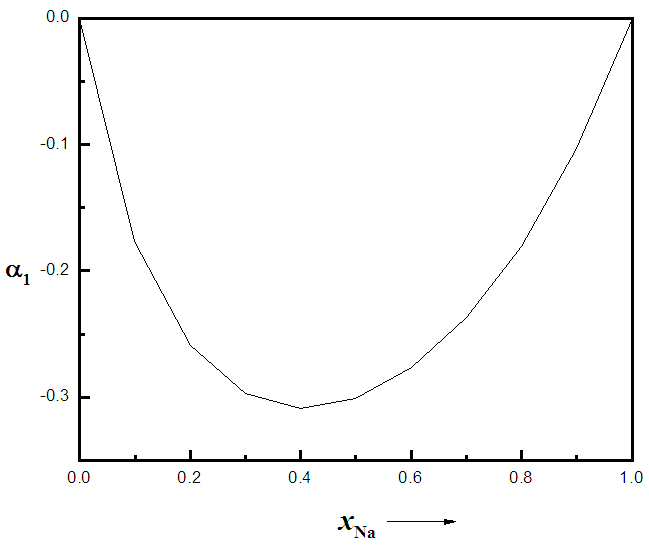 | Figure 5. Calculated Warren-Cowley CSRO parameter, α1, using eqn. (6) for Na-Pb at 700K |
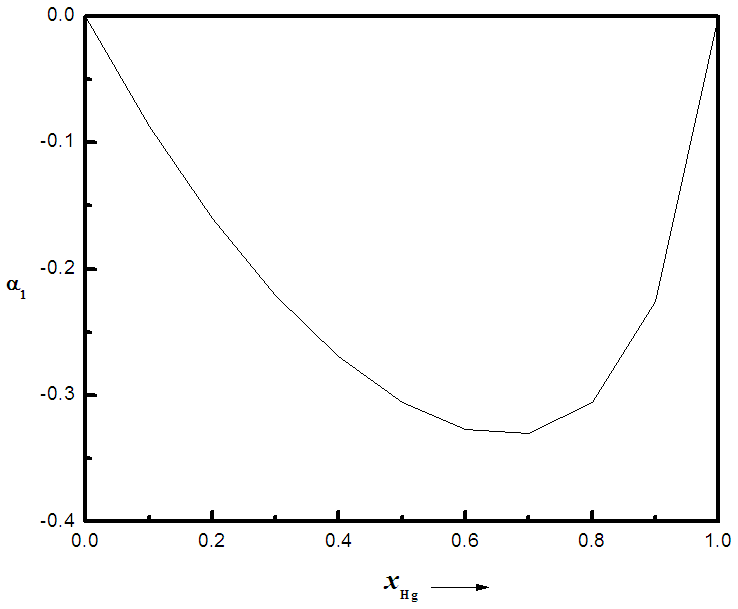 | Figure 6. Calculated Warren-Cowley CSRO parameter, α1, using eqn. (6) for Na-Hg at 673K |
4. Conclusions
- The energetics of Na-Pb and Na-Hg liquid binary alloys have been analyzed in this present study at 700K and 673K respectively. Attention has been given to their thermodynamic functions such as Gibb’s free energy of mixing, concentration fluctuations and Warren-Cowley CSRO parameter. Theoretical study of the alloying behavior of the two liquid alloys reveals hetero-coordination in both alloys throughout the entire concentration of Na in Na-Pb and Hg in Na-Hg. It has also been shown that Na-Hg alloy is a more strongly interacting binary alloy than Na-Pb.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML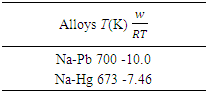
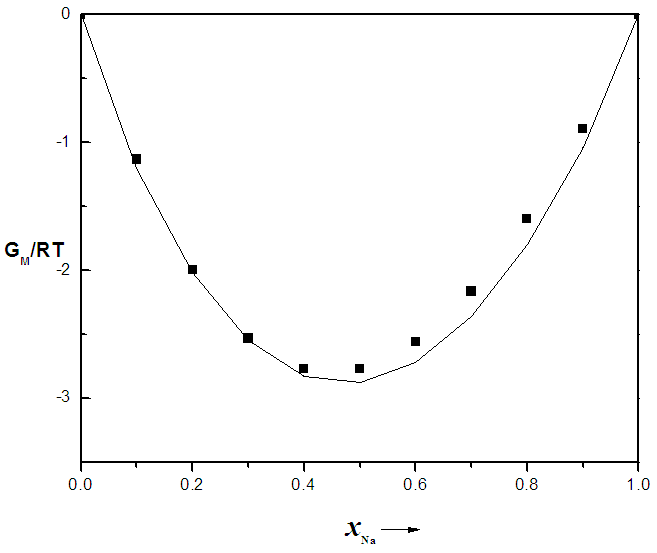
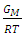 for Na-Pb liquid alloys at 700K, computed from Eqn.1. The solid line represents theoretical values and the squares represent experimental values [13], xNa is the concentration of Na in the alloy
for Na-Pb liquid alloys at 700K, computed from Eqn.1. The solid line represents theoretical values and the squares represent experimental values [13], xNa is the concentration of Na in the alloy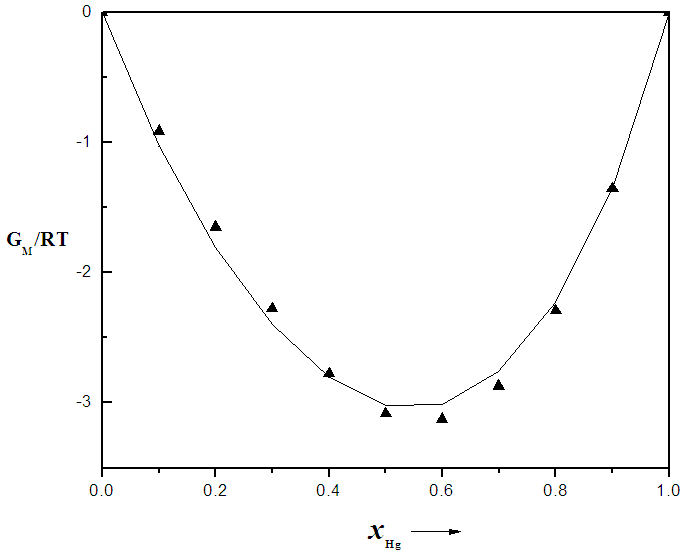
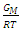 for Na-Hg liquid alloys at 673K, computed from Eqn.1. The solid line represents theoretical values and the squares represent experimental values [13]. xHg is the concentration of Hg in the alloy
for Na-Hg liquid alloys at 673K, computed from Eqn.1. The solid line represents theoretical values and the squares represent experimental values [13]. xHg is the concentration of Hg in the alloy