-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2016; 6(2): 27-35
doi:10.5923/j.ajcmp.20160602.02

Theoretical Investigation of Structural, Elastic, Electronic and Optical Properties of SnAs
Md. Afjalur Rahman, Uttam Kumar Chowdhury, T. H. Bhuyan, Md. Atikur Rahman
Department of Physics, Pabna University of Science and Technology, Pabna, Bangladesh
Correspondence to: Md. Atikur Rahman, Department of Physics, Pabna University of Science and Technology, Pabna, Bangladesh.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

The structural, elastic, electronic and optical properties of SnAs at ambient condition have been investigated by using the planewave ultrasoft pseudopotential technique which is based on the first-principles Density Functional Theory (DFT) with Generalized Gradient Approximation (GGA). The calculated structural parameters show a good agreement with the experimental and other theoretical results. The optimized lattice parameters, three independent elastic constants (C11, C12, and C44), bulk modulus (B), shear modulus (G), Young’s modulus (Y), Pugh’s ratio (G/B), Poisson’s ratio (ν) and elastic anisotropy (A) are estimated and discussed. This is the first quantitative theoretical prediction of the elastic and optical properties of SnAs compound. The electronic band structure reveals metallic conductivity and the major contribution comes from Sn-5p and As-4p states. Finally, the different optical properties such as, dielectric function, absorption, loss function, conductivity, reflectivity and refractive index of SnAs are obtained and discussed in detail. Further the reflectivity spectrum shows that the material is a perfect reflector within the energy ranges 7-13 eV.
Keywords: SnAs, Abinitio calculations, Structural, Elastic, Electronic, and Optical Properties
Cite this paper: Md. Afjalur Rahman, Uttam Kumar Chowdhury, T. H. Bhuyan, Md. Atikur Rahman, Theoretical Investigation of Structural, Elastic, Electronic and Optical Properties of SnAs, American Journal of Condensed Matter Physics, Vol. 6 No. 2, 2016, pp. 27-35. doi: 10.5923/j.ajcmp.20160602.02.
Article Outline
1. Introduction
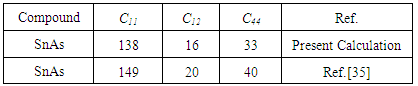
- The Rock-salt structure of superconductor has generated significant interest in scientific community over the past thirty years. The main reason for this interest is to understand the origin of superconductivity simply by different properties of the rock-salt structure of superconductors. Many studies including both theoretical and experimental have been carried out on the structural, electronic, vibrational and superconducting properties of the transition metal carbides. It has been confirmed by theoretical works [1-7] that the transition metal carbides with nine valence electrons show superconductivity while the ones with eight valence electrons are not superconductors. On the other hand, SnAs was first reported to be a superconductor [8] with critical temperature Tc in the range 3.41-3.65k as other types of materials containing non-transition metal and crystallizing in the NaCl structure. More recently, using hard X-ray photoemission spectroscopy (HAXPES), Wang et al. [9] confirmed the single valence state of Sn in the NaCl structure. Furthermore, from resistivity and heat capacity measurements, Wang et al. [9] further estimated the electron–phonon coupling parameter λ ¼ 0:62 and the critical temperature Tc¼ 3.58K. In this paper, we have made ab initio calculations of the ground state and different properties such as structural, elastic, electronic, and optical properties of SnAs in the NaCl structure by using the plane wave pseudopo- tential method within the generalized gradient approximation of the density functional scheme. To the best of our knowledge no theoretical study has yet been reported about elastic properties and optical properties of SnAs except Ref. [35]. It is well-known that the elastic properties are essential for the understanding of the macroscopic mechanical properties of SnAs crystals because they are related to various fundamental solid state and thermodynamic properties. The aim of this paper is to carry out a complete DFT-based calculation to investigate the structural, elastic, electronic and optical properties (absorption, conductivity, reflectivity, refractive index, energy-loss spectrum and dielectric function) of SnAs. Since there is no data available for the optical properties of SnAs, our study will definitely help for experimental investigation on this compound in future. The rest parts of this paper are arranged as follows: In section 2, the theoretical methods are given. The results and discussion are presented in section 3. Finally, a brief summary of our results is shown in section 4.
2. Computational Method
- The first-principles calculations have been performed using the density functional theory (DFT) based CASTEP computer program together with the generalized gradient approximation (GGA) with the PBE exchange-correlation function [10-14]. As-4S2 4P3 4S2 and Sn-5S2 5P2 are taken as valence electrons. The electromagnetic wave functions are expanded in a plane wave basis set with an energy cut-off of 400 eV. The k-point sampling of the Brillouin zone is constructed using Monkhorst-Pack scheme [15] with 10×10×10 grids in primitive cells of SnAs. The equilibrium crystal structures are obtained via geometry optimization in the Broyden-Fletcher-Goldfarb-Shanno (BFGS) minimization scheme [16]. In the geometry optimization, criteria of convergence are set to 1.0 × 10-5 eV/atom for energy, 0.03 eV/ Å for force, 1 × 10-3 Å for ionic displacement, and 0.05 GPa for stress. These parameters are carefully tasted and sufficient to lead to a well converged total energy.
3. Results and Discussion
3.1. Structural and Elastic Properties
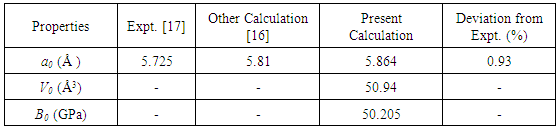
- The intermetallic SnAs compound belongs to cubic lattice of NaCl-type structure with the space group Fm-3m (225). The equilibrium lattice parameter has a value of 5.725Å [17]. The lattice constants and atomic positions have been optimized as a function of normal stress by minimizing the total energy. The optimized structure is shown in Fig.1. The calculated values of the structural properties of SnAs are presented in Table 1 along with the available experimental and other theoretical values. From Table 1, we see that our present theoretical results are very close to both experimental and other calculated results.
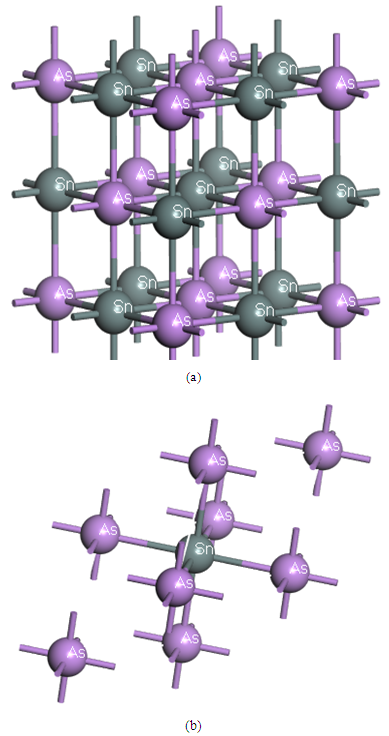 | Figure 1. The crystal structures of SnAs (a) the conventional cubic cell and (b) the primitive cell |
|
|
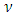 , and anisotropy factor A. They have crucial implication in engineering science. For the cubic system, the Voigt and Reuss bounds of B and G can be expressed as follows [26]:
, and anisotropy factor A. They have crucial implication in engineering science. For the cubic system, the Voigt and Reuss bounds of B and G can be expressed as follows [26]: 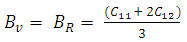 | (1) |
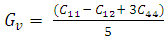 | (2) |
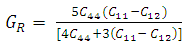 | (3) |
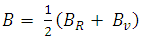 | (4) |
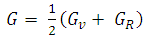 | (5) |
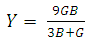 | (6) |
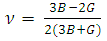 | (7) |
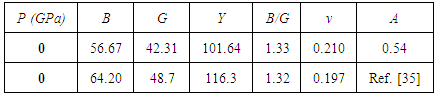
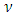 , and anisotropy factor A of SnAs are given in table 3. From Table 3, it can be seen that B > G, which indicates that the shear modulus is the prominent parameter associating with the stability of cubic SnAs.Another index to clarify the ductility and brittleness of a material is Pugh’s ratio defined as B/G [27]. A material having the ratio of B/G < 1.75 behaves in a brittle manner otherwise, it should be ductile. From Table 3, it is clear that our calculated B/G ratio is 1.33 indicates the brittleness of this compound at ambient pressure. Thus these same results of brittleness and ductility by investigating the Cauchy’s pressure and Pugh’s ratio make sure the consistency of our present study. The Young’s modulus Y, also known as the tensile modulus, is defined as the ratio between stress and strain and used to provide a measure of stiffness, i.e., the larger the value of Y, the stiffer the material. From our calculation, we have the value of Y for SnAs is 101.64GPa. So we conclude that this is a stiffer material. The Poisson’s ratio is used to reflect the stability of the material against shear and provides information about the nature of the bonding forces [28]. Bigger the Poisson’s ratio betters the plasticity. The value of ν for covalent materials is small (ν = 0.1), and for ionic materials 0.25. The value between 0.25 and 0.5 indicates that the force exists in the solid is central [29].
, and anisotropy factor A of SnAs are given in table 3. From Table 3, it can be seen that B > G, which indicates that the shear modulus is the prominent parameter associating with the stability of cubic SnAs.Another index to clarify the ductility and brittleness of a material is Pugh’s ratio defined as B/G [27]. A material having the ratio of B/G < 1.75 behaves in a brittle manner otherwise, it should be ductile. From Table 3, it is clear that our calculated B/G ratio is 1.33 indicates the brittleness of this compound at ambient pressure. Thus these same results of brittleness and ductility by investigating the Cauchy’s pressure and Pugh’s ratio make sure the consistency of our present study. The Young’s modulus Y, also known as the tensile modulus, is defined as the ratio between stress and strain and used to provide a measure of stiffness, i.e., the larger the value of Y, the stiffer the material. From our calculation, we have the value of Y for SnAs is 101.64GPa. So we conclude that this is a stiffer material. The Poisson’s ratio is used to reflect the stability of the material against shear and provides information about the nature of the bonding forces [28]. Bigger the Poisson’s ratio betters the plasticity. The value of ν for covalent materials is small (ν = 0.1), and for ionic materials 0.25. The value between 0.25 and 0.5 indicates that the force exists in the solid is central [29].
|
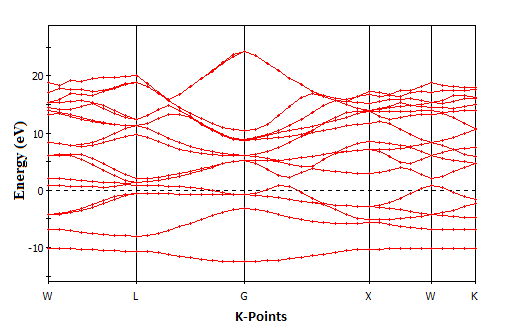 | Figure 2. Electronic band structure of SnAs |
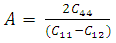 | (8) |
3.2. Electronic Properties
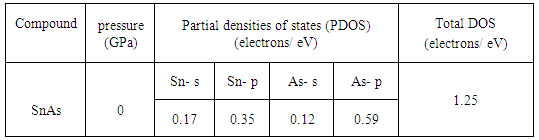
- The electronic band structure is the spectrum of the energy eigen values of a periodic system. The band structure diagram contains information about both the bonding interactions. However, the ability to understand the band structure diagram allows one to extract valuable information about a material: electronic conductivity, optical properties and stability of compound toward oxidation or reduction. In this way knowledge of the electronic band structure provides predictive insight and understanding of certain very important physical properties of solids. The calculated energy band structures at ambient pressure with the geometrically optimized structure for SnAs along high symmetry directions in the Brillouin Zone (BZ) is shown in Fig.2 in the energy range from -15ev to 30ev. The occupied valence bands of SnAs lie in the energy range from -4ev to Fermi level. Moreover, it is clear from band structure diagram that most of the bands go across the Fermi level and overlap with conduction bands. As a result, there is no band gap at the Fermi level which means SnAs material exhibits metallic behavior. In solid-state and condensed matter physics, the density of states (DOS) of a system describes the number of states per interval of energy at each energy level that are available to be occupied and it plays vital role in the analysis of the physical properties of materials. The calculated total and partial density of states (DOS) for SnAs are illustrated in Fig.3. Here we have treated Sn-5s25p2 and As-4s24p3 as valence electrons. The main density of states (DOS) can be split up into three main energy regions. In the first energy range -14.5-10ev, it is found that there is a sharp peak at 10.5ev. This peak is mainly characterized by the As-4s states with some contributions coming from other electronic states. There is hybridization between Sn-5s and As-4p states, giving rise to a strong peak at -7.19ev. In the energy range -5.5ev to 0ev; there is a high degree of hybridization of As-p states with Sn-p states, which highlight covalent interaction. The total DOS at the Fermi level for SnAs is 1.09 states per unit cell per eV. At the Fermi level, the DOS mainly originates from the hybridization between Sn-5p and As-4p states for this phase and these states are responsible for the conduction properties of SnAs compound. The partial contributions of s and p orbitals at Fermi level of both Sn and As are listed below Table 4.
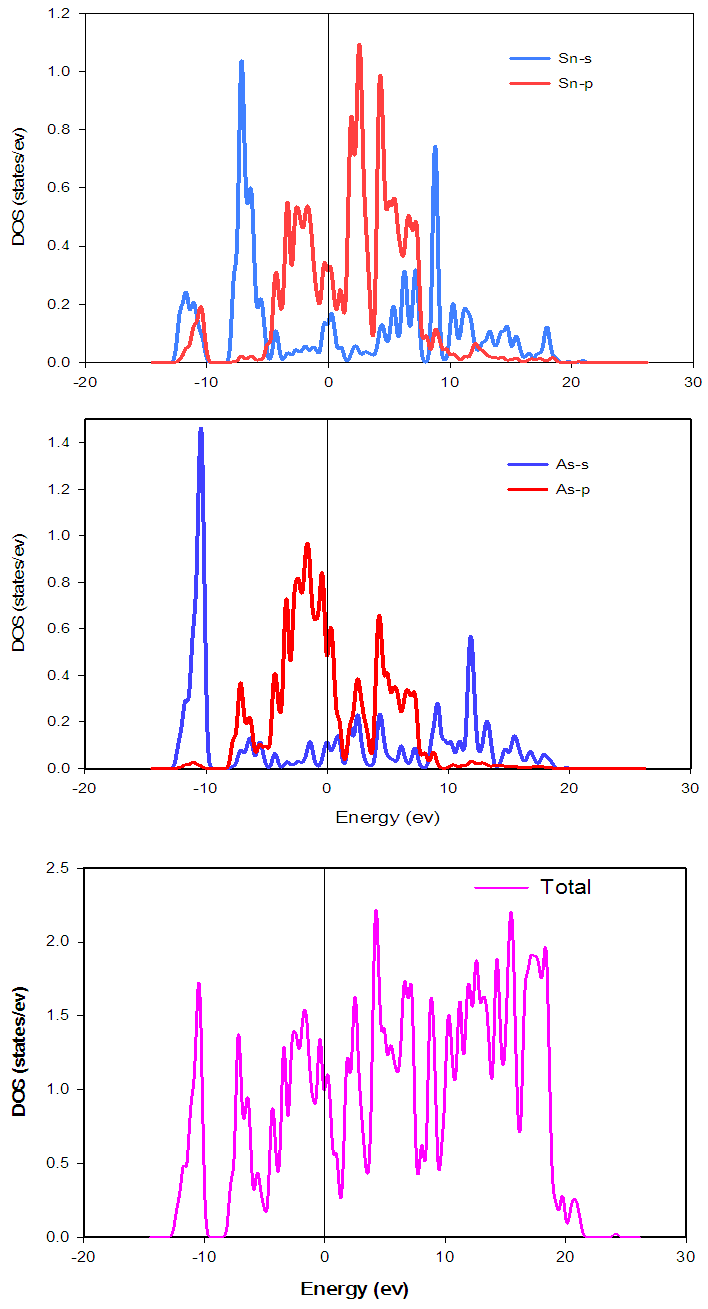 | Figure 3. Calculated partial and total density of states of SnAs |
|
3.3. Optical Properties
- The study of the optical functions of solids helps to give a better understanding of the electronic structure of different materials. The dielectric function
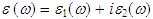 fully describes the optical properties of any homogeneous medium at all photon energies. The imaginary part
fully describes the optical properties of any homogeneous medium at all photon energies. The imaginary part 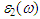 of the dielectric function is obtained from the momentum matrix elements between the occupied and the unoccupied electronic states. This is calculated directly using [31]:
of the dielectric function is obtained from the momentum matrix elements between the occupied and the unoccupied electronic states. This is calculated directly using [31]: 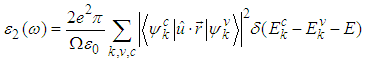 | (9) |
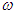 is the frequency of light, e is the electronic charge,
is the frequency of light, e is the electronic charge, 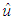 is the vector defining the polarization of the incident electric field, and
is the vector defining the polarization of the incident electric field, and 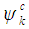 and
and 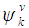 are the conduction and valence band wave functions at k, respectively. The real part of the dielectric function
are the conduction and valence band wave functions at k, respectively. The real part of the dielectric function 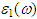 is derived from the imaginary part of the dielectric function
is derived from the imaginary part of the dielectric function 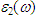 through the Kramers-Kronig relations. Other optical properties, such as refractive index, absorption spectrum, loss-function, reflectivity and conductivity (real part) are derived from equations (49) to (54) developed in Ref. [31]. Fig.4 exhibits the optical functions of SnAs calculated for photon energies up to 40eV for polarization vector [100]. We have used a 0.5eV Gaussain smearing for all calculations for the reason that this smears out the Fermi level, so that k-points will be more effective on the Fermi surface. Dielectric function is the most general property of solids, which modifies the incident electromagnetic radiation of light. It describes the polarization and absorption properties of the material. The quantity ε1(ω) represents how much a material becomes polarized when an electric field is applied due to creation of electric dipoles in the material. The quantity ε2(ω) represents absorption in a material. For a transparent material ε2(ω) is zero, but becomes nonzero when absorption begins. The real and imaginary parts of dielectric functions of SnAs as a function of photon energy is illustrated in Fig.4 (a). It is observed from Fig. 4(a) that at about 16.48 eV, the value of ε2 becomes zero and hence SnAs material becomes transparent above 16.48 eV. The value of the static dielectric constant is about 73, indicating that the compound is of promising dielectric materials. Materials with high value dielectric constant are very useful in the manufacture of high value capacitors. In optics the refractive index of an optical medium is a dimensionless number that describes how light, or any other radiation propagates through that medium. Fig.4 (b) shows the refractive index of SnAs material as function of photon energy. It is clear from the figure that the index of refraction is higher in infrared region and gradually decreased in visible and ultraviolet region. The static refractive index is found to have the value about 8.5.The absorption coefficient provides important information about optimum solar energy conversion efficiency and it indicates how far light of a specific energy (wavelength) can penetrate into the material before being absorbed. Fig.4(c) shows the absorption spectra of SnAs material for the direction [100]. It is observed that the spectra start from 0ev which reveals the metallic nature of the compound. This has also been confirmed from the band structure of SnAs compound. There are several peaks found in the absorption coefficient curve. For first absorption peak, the absorption spectrum arises sharply in the low energy region and reaches to a value of 1.9x105 cm-1. After a sharp drop of the absorption, it starts to increases drastically again up to the highest peak value of 2.1x105 cm-1 for polarization direction [100] appear at 7.5 eV and then decreases gradually with several peaks to the UV-region. This correspond shows rather good absorption coefficient in the energy range 5 to 13eV.The electron energy loss function of a material is an important optical parameter in the dielectric formalism used to describe the optical spectra and the excitations produced by swift charges in solid. The energy loss function as a function of photon energy is illustrated in Fig.4 (d). It is observed that prominent peak is found at 15.73eV, which indicates rapid reduction in the reflectance. This highest peak of energy loss spectrum is defined as bulk plasma frequency of the material, which appears at ε2 less than unity and ε1 to zero respectively [32, 34]. Hence from the energy loss spectrum it is observed that the plasma frequency is equal to15.73eV. When the incident photon frequency is higher than plasma frequency then SnAs compound will be transparent and transformed to a dielectric response.Reflectivity is the ratio of the energy of a wave reflected from a surface to the energy possessed by the wave hitting the surface. The reflectivity spectrum of SnAs as a function of photon energy is shown in Fig. 4 (e). It is noticed that reflectivity is ~0.62-0.78 in the infrared region and the value drops in the high energy region with several peaks as a result of interband transition. The large reflectivity for E<1eV indicates the characteristics of high conductance in the low energy region. This spectrum shows that the material is a perfect reflector within the energy range ~ 0-15eV. The analysis shows that SnAs material is as promising candidate for use as coating material. The photoconductivity is an optoelectronic phenomenon in which electrical conductivity a material increases due to the absorption of electromagnetic radiation. Fig.4 (f) shows the conductivity spectra as function of photon energy. It is seen that photoconductivity starts with zero photon energy due to the reason that the materials have no band gap which is evident from band structure calculation (Fig.2) and it has a higher value in the low energy region and the value gradually decreases towards the visible and ultraviolet energy range. There is no photoconductivity when the photon energy is higher than 20 eV for SnAs.
through the Kramers-Kronig relations. Other optical properties, such as refractive index, absorption spectrum, loss-function, reflectivity and conductivity (real part) are derived from equations (49) to (54) developed in Ref. [31]. Fig.4 exhibits the optical functions of SnAs calculated for photon energies up to 40eV for polarization vector [100]. We have used a 0.5eV Gaussain smearing for all calculations for the reason that this smears out the Fermi level, so that k-points will be more effective on the Fermi surface. Dielectric function is the most general property of solids, which modifies the incident electromagnetic radiation of light. It describes the polarization and absorption properties of the material. The quantity ε1(ω) represents how much a material becomes polarized when an electric field is applied due to creation of electric dipoles in the material. The quantity ε2(ω) represents absorption in a material. For a transparent material ε2(ω) is zero, but becomes nonzero when absorption begins. The real and imaginary parts of dielectric functions of SnAs as a function of photon energy is illustrated in Fig.4 (a). It is observed from Fig. 4(a) that at about 16.48 eV, the value of ε2 becomes zero and hence SnAs material becomes transparent above 16.48 eV. The value of the static dielectric constant is about 73, indicating that the compound is of promising dielectric materials. Materials with high value dielectric constant are very useful in the manufacture of high value capacitors. In optics the refractive index of an optical medium is a dimensionless number that describes how light, or any other radiation propagates through that medium. Fig.4 (b) shows the refractive index of SnAs material as function of photon energy. It is clear from the figure that the index of refraction is higher in infrared region and gradually decreased in visible and ultraviolet region. The static refractive index is found to have the value about 8.5.The absorption coefficient provides important information about optimum solar energy conversion efficiency and it indicates how far light of a specific energy (wavelength) can penetrate into the material before being absorbed. Fig.4(c) shows the absorption spectra of SnAs material for the direction [100]. It is observed that the spectra start from 0ev which reveals the metallic nature of the compound. This has also been confirmed from the band structure of SnAs compound. There are several peaks found in the absorption coefficient curve. For first absorption peak, the absorption spectrum arises sharply in the low energy region and reaches to a value of 1.9x105 cm-1. After a sharp drop of the absorption, it starts to increases drastically again up to the highest peak value of 2.1x105 cm-1 for polarization direction [100] appear at 7.5 eV and then decreases gradually with several peaks to the UV-region. This correspond shows rather good absorption coefficient in the energy range 5 to 13eV.The electron energy loss function of a material is an important optical parameter in the dielectric formalism used to describe the optical spectra and the excitations produced by swift charges in solid. The energy loss function as a function of photon energy is illustrated in Fig.4 (d). It is observed that prominent peak is found at 15.73eV, which indicates rapid reduction in the reflectance. This highest peak of energy loss spectrum is defined as bulk plasma frequency of the material, which appears at ε2 less than unity and ε1 to zero respectively [32, 34]. Hence from the energy loss spectrum it is observed that the plasma frequency is equal to15.73eV. When the incident photon frequency is higher than plasma frequency then SnAs compound will be transparent and transformed to a dielectric response.Reflectivity is the ratio of the energy of a wave reflected from a surface to the energy possessed by the wave hitting the surface. The reflectivity spectrum of SnAs as a function of photon energy is shown in Fig. 4 (e). It is noticed that reflectivity is ~0.62-0.78 in the infrared region and the value drops in the high energy region with several peaks as a result of interband transition. The large reflectivity for E<1eV indicates the characteristics of high conductance in the low energy region. This spectrum shows that the material is a perfect reflector within the energy range ~ 0-15eV. The analysis shows that SnAs material is as promising candidate for use as coating material. The photoconductivity is an optoelectronic phenomenon in which electrical conductivity a material increases due to the absorption of electromagnetic radiation. Fig.4 (f) shows the conductivity spectra as function of photon energy. It is seen that photoconductivity starts with zero photon energy due to the reason that the materials have no band gap which is evident from band structure calculation (Fig.2) and it has a higher value in the low energy region and the value gradually decreases towards the visible and ultraviolet energy range. There is no photoconductivity when the photon energy is higher than 20 eV for SnAs.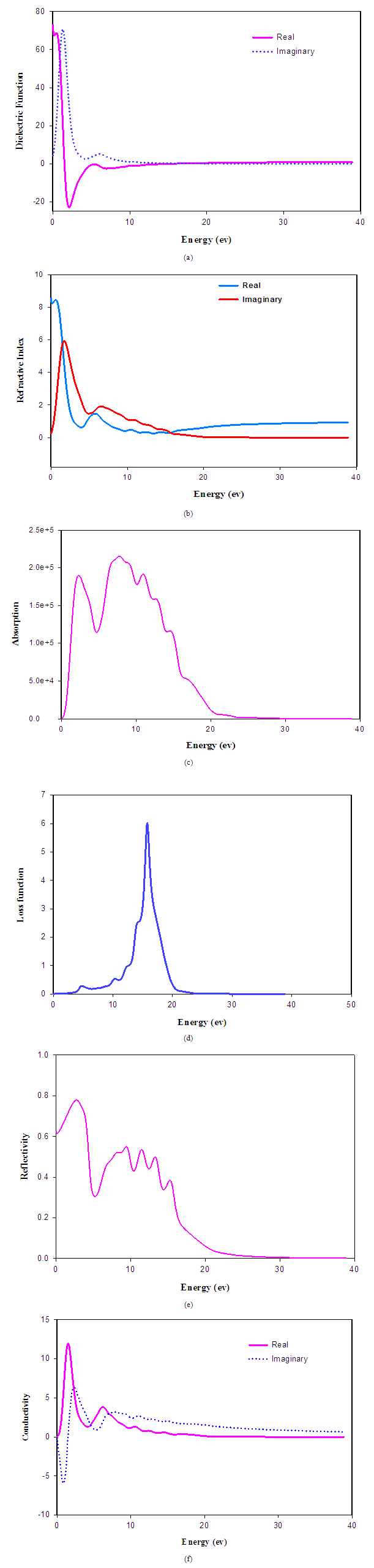 | Figure 4. The optical functions (a) dielectric function, (b) refractive index, (c) absorption, (d) loss function, (e) reflectivity and (f) conductivity of SnAs for polarization vector [100] |
4. Conclusions
- In synopsis we have implemented first-principles calculations based on density functional theory to investigate the structural, elastic, electronic and optical properties of the rock-salt superconductor SnAs. We have also evaluated the independent elastic constants, Young’s modulus, bulk modulus, shear modulus, Poisson’s ratio, compressibility and elastic anisotropy factor. The analysis shows that this compound is mechanically stable and anisotropic. Band structure and densities of states analysis suggest that the material exhibit metallic conductivity. But the negative value of the Cauchy pressure of SnAs indicates the nonmetallic behavior of this compound. It is observed that there is inconsistency in metallic vs. nonmetallic behavior from band structure diagram approach and Cauchy pressure value. The explanation for this contradiction is currently unknown and further investigation is expected in future. Further the optical properties, e.g. dielectric function, refractive index, absorption spectrum, energy loss spectrum, reflectivity and conductivity of SnAs have been analyzed first time in our study. The larger reflectivity of SnAs in the low energy region indicates suitability of the compound for use in the solar cell to remove solar heating. The present study has a great implication for future investigation on the physical and superconducting properties of others rock-salt superconductors.
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML