-
Paper Information
- Paper Submission
-
Journal Information
- About This Journal
- Editorial Board
- Current Issue
- Archive
- Author Guidelines
- Contact Us
American Journal of Condensed Matter Physics
p-ISSN: 2163-1115 e-ISSN: 2163-1123
2016; 6(1): 7-16
doi:10.5923/j.ajcmp.20160601.02

Investigations of Spectroscopic Characteristics of Virus-Like Nanobioparticles
Paata J. Kervalishvili , Tamar N. Bzhalava
Engineering Physics Department, Georgian Technical University, Tbilisi, Georgia
Correspondence to: Tamar N. Bzhalava , Engineering Physics Department, Georgian Technical University, Tbilisi, Georgia.
| Email: |  |
Copyright © 2016 Scientific & Academic Publishing. All Rights Reserved.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/

Study of spectroscopic properties of virus-like particles (VLPs), virions based on computer simulation in complement with spectroscopic experiments, in purpose of determination the spectroscopic characteristics and vibrational frequencies for identification and detection of viruses, and elaboration of model and the basis of creation the viral fingerprints database are considered. Core-shell model of virion, and electromagnetic (EM) wave scattering theory applied for single-particle study based on Maxwell’s and Helmholtz’s equations, separation of variables method and boundary conditions are considered. The geometric size, namely core-shell diameters of virion, associated with morphology of its capsid and the set of fundamental oscillation frequencies of core-shell system associated with spectral signatures of capsid, nucleic-acids (DNA/RNA) as well as whole virion, related to electrical permittivities and diameters of core-shell are proposed as the main parameters determining the spectral fingerprints of VLPs, virions. Sum Frequency Generation (SFG) spectroscopy and ultrashort pulsed lasers based spectroscopic measurement methods are considered for experimental investigation of vibrational modes of VLPs as well as for studying the nature of vibration and oscillation processes.
Keywords: Virus-like particle, Virion, Spectroscopy, Vibration frequency
Cite this paper: Paata J. Kervalishvili , Tamar N. Bzhalava , Investigations of Spectroscopic Characteristics of Virus-Like Nanobioparticles, American Journal of Condensed Matter Physics, Vol. 6 No. 1, 2016, pp. 7-16. doi: 10.5923/j.ajcmp.20160601.02.
Article Outline
1. Introduction
- Development of materials, systems and technologies with fundamentally new properties and functions requires the application of existing fundamental knowledge and elaboration of scientific methods based on new principles, which must be acquired through interdisciplinary research. In this respect, nanobioscience and nanobiotechnology offer great opportunities and possess potential to achieve the results and decision of problems facing the healthcare and environmental safety.Development of efficient and rapid detecting, scanning, measuring and imaging systems as well as diagnostic tools based on advanced technologies is of high priority of nanobioscience for its application in medicine, microbiology, environmental action and monitoring. Principal word in this direction belongs to study and design of multifunctional nanomaterials and nanoparticles, investigation of structure and processes on the atomic or molecular scales.Nanoparticles (NPs) are unique because their behaviour when measuring less than 100 nm changes from classical to quantum physics with decreasing particle size. Application of quantum-based principles in parallel to comprehension of well-known tasks of electrodynamics makes opportunity to reveal new unique properties of bioparticles at nano level.Generally, biological objects are working as mechanical machines. However, fundamentally nanobioobjects, like NPs should be functioning on the different principles. Nanoscale nanomaterials such as nanoparticles, take on novel properties and functions that differ markedly from those seen in the bulk scale. Uncommon and intriguing physical features and behaviour of ultrafine metal, semiconductor (s/c) and dielectric small particles should be similar but specific for nano-sized bioparticles. Conventional knowledge of physical and biological properties obtained by observational and theoretical means should be extended to studies of ultrafine particles of biological origin.Now it seems to be the right time to start the discussion the preliminary work, to generalize the main features of nanobioparticles, elaborate basic principles for evaluation of specific properties of interests and consider the possibility to determine the set of characteristics for creation unified database system in complement with microbiology and biochemistry based data applicable to ultrafine bioparticles, viruses.The primary focus of proposed study should be making connection between what can already be done and what is desired to be done.
2. Object of Interests
- This paper deals with the discussion of the problems concerning main physical/geometrical characteristics of ultra-sized virus-like particles (VLPs) in purpose of detection and identification of bioparticles and viruses. Nano/micro meter-sized bioobjects are targets of scientific researches in bioscience, biotechnology, medical diagnostics, environmental and epidemiological control. In a variety of bioparticles the virus-like (VLPs) particles are of main interest of diversified works dedicated to both nanoparticles and bioparticles.Due to their function and prescription (VLPs) may be classified as nature-made or “threatfull” (NVs) and artificial (AVs) particles, associated with naturally and artificially produced aerosol particles.Brief prescription of the VLPs, roles and application areas one could substantiate the idea of making the finding of the same basic physical features of NVs and AVs, and functionality principles in some qualitatively similar ways possible.It is widely known that viruses (NVs) carry out natural "genetic engineering", can transfer genetic material between different species of host; NVs are a major threat to both public health and to agricultural production as well as being responsible for a wide variety of human diseases; Viruses have been used as bio-warfare agents; Bio-aerosol (VLPs) particles transmission has the greatest impact on epidemic condition of environment and the spreading of infectious diseases. Viruses are perfectly defined organic nanoparticles which are commonly used as scaffolds or nano-vectors in materials engineering and nanotechnology. Virus-like particles (VLPs) are extensively used in genetic engineering; VLPs are biomimetic delivery vehicles that cloak nanoscale cores inside coatings of viral capsid proteins, offering the potential for protecting their contents and targeting them to particular tissues and cells. Virus-like nanoparticles (VLNPs) would be more soluble and have higher drug efficiency than current treatments. They can carry drugs directly to cancer cells to kill them, can revolutionize cancer treatment, acting not only as a safer, more specific form of cancer treatment, but also as a new imaging tool.Gold nanoparticles are used in drug and gene delivery systems, the effectiveness of nanoparticles as biomedical imaging contrast and therapeutic agents depends on their optical properties, e.g. a high-scattering cross-section is essential for cell imaging applications based on light-scattering microscopy; modification of the nanoparticle’s outer layer allows a large variety of chemical, molecular, and biological entities to be covalently or otherwise bound to it, and etc.In context of detection and identification priorities, it is proposed to study viruses (NVs), as ultra-sized particles in common physical point of view. Physical, especially spectroscopic properties of NVs by examination of physical, electrical and geometrical characteristics are considered. Viruses (NVs) among pathogenic micro-organisms are the smallest infectious agents. Most viruses are sub-microscopic, their sizes range from 20 to 300 nm, are about 1/100 the size of bacteria. Unlike most living things, viruses do not have their own metabolism and cells that divide, new viruses are assembled and reproduce inside the infected host cell, therefore cannot naturally reproduce outside a host cell [1]. Viruses can remain infectious outside their hosts for prolonged period of time, and this can lead to infections by indirect contact [2]. Extracellular infective form of a virus is called virion, a single stable entire virus particle consisting of an inner core of RNA or DNA and outer protective protein coat called a capsid [3]. Scanning and transmission electron microscopes are used to visualise virions. Virion as a (NV) particle is being considered in various medical or aerosol transmission studies, and the virion (of virus/bacteriophage) is under our close examination.Capsids are formed from identical protein subunits called capsomeres [4]. Proteins of capsids are encoded by the viral genome. Virally coded protein subunits self-assemble to form a capsid, in general, requiring the presence of the virus genome. Capsid protects the genome from lethal chemical and physical agents, as well as is involved in various viral life cycle events. An intriguing step is the capsid assembly, when capsid subunits interact with weak individual contact energies to form a globally stable icosahedral lattice; this structure is ideal for encapsidation of the viral genome and host partners and protecting its contents upon secretion, yet the unique properties of its assembly and intersubunit contacts allow the capsid to dissociate upon entering a new host cell [3]. The inside surfaces of the protein shells of many viruses are positively charged, thereby enhancing the self-assembly of capsid proteins around their oppositely charged genome [5].Shape of capsid serves as the basis for morphological distinction [6]. Main morphological virion types are: icosahedral, prolate (icosahedron elongated along the fivefold axis), helical, complex. Some species of virus envelop themselves in external lipid bilayer known as viral envelope, but in many studies are not distinguished between capsids containing external lipid membranes and those that do not, since, such lipids are often post assembly features [7].The structure of a large number of viral capsids are icosahedral or near-spherical with icosahedral symmetry. A regular icosahedron is nature's optimum method of producing a closed shell from identical sub-units. Two types of capsomeres constitute the icosahedral capsid: pentagonal at the vertices and hexagonal at the faces. There are always 12 pentagons, but the number of hexagons varies among virus groups [8]. The most virions, because of their size, have more than 60 subunits. These variations have been classified on the basis of the quasi-equivalence principle proposed by D. Caspar and A. Klug [6]. Triangulation number (T-number) is a quantitative metric for capsid size and describes the relation between the number of pentagons and hexagons i.e. their quasi-symmetry in the capsid shell. It was demonstrated that icosahedral symmetry allows for the lowest-energy configuration of particles isotropic interacting on the surface of a sphere. More explicitly, was found that the energy-per-particle is a minimum for configurations that involve 12 five-fold defects at the vertices of an icosahedron, and that these configurations are especially favourable for "magic" numbers of particles corresponding to the triangulation (T) numbers of Casper and Klug [9].Virions of helical morphology are composed of a single type of capsomer stacked around a central axis to form a helical structure, which may have a central cavity, or hollow tube. This arrangement results in rod-shaped or filamentous virions, which can be short and highly rigid, or long and very flexible. Overall, the length of a helical capsid is related to the length of the nucleic acid contained within it and the diameter is dependent on the size and arrangement of capsomers. Thus, two main medium of different structure and properties constitute the virion: capsid of protein capsomeres and nucleic acids (RNA or DNA) into the capsid. Type, number and arrangement of capsomers and length of nucleic acid are essential in defining the size of capsid designed mostly in near-symmetrical geometry, having the unique self-assemble mechanism.Conceptual framework offered by Mannige RV, Brooks CL, III [7, 10] makes geometric explanations to capsid properties - rigidity, pleomorphism, auxiliary requirements, etc., that were previously considered to be unrelatable properties of the individual virus, explains elusive species-independent evolutionary pressures on capsid design for all icosahedral capsid sizes potentially available in nature. Capsids from different classes display markedly different geometries; so they are bound to display different mechanical/physical properties. Capsid separates the genome from surrounded area and may be considered as outside surface boundary layer or thick interface with specific geometrical, mechanical and electrical properties. Phenomena occurred on inner/and outer surfaces of capsid (or within the surface layer) seems to be dominant in determining the mechanical, electrical and spectroscopic properties of ultrafine bioparticles as it takes place in metal or s/c materials. It is obvious that one of the reasons of nanoparticles properties size dependence is increase in surface area with diminishing particle size. The surface area of the particle is extremely high and about 20 percent of its atoms are present at its surface making it highly reactive, aggregating with its neighbours and associating with other molecules. Surface to volume ratio increases considerably and the surface phenomena predominate over the chemistry and physics of the bulk metal and semiconductor. Surface area of NPs plays a definite role because most chemical reactions involving solids happen at the surfaces, where the chemical bonds are incomplete and surface atoms have more energy as compared to subsurface atoms. This extra energy will be released and the surface will acquire a more stable state when the surface bonds are satisfied. Nanoscale particles with their enormous surface area are exceptionally reactive because more than a third of their chemical bonds are at their surfaces.A simple calculation shows, that the ratio of inner (core) and outer spherical volumes of small icosahedral capsid of rhinovirus (of radii 9.6 nm and 15.7 nm) is about 0,216 (data are gained from [11]), so quite a large portion (≈0.75) of volume in virion is occupied by a capsid proteins. The structure/geometry of capsids as well as chemical bonds of proteins, and processes happening in surface layer probably dominate in determination of physical/spectroscopic properties of nano-sized particles, virions.Capsid is of large enough size than the ‘‘discreteness’’ nature of protein subunits, therefore the influence of that on capsid whole geometry could probably be less significant, which allow for those capsid to be modelled as spherical/cylindrical particle of smooth inner or outer surfaces. It is necessary to note that single-particle study provides the link to multiparticle systems and is the step towards aerosol investigations based on statistical methods of estimation of physical characteristics of system. The size, shape and structure of virions are important in formation of viral aerosol particles, as well as in defining the spectroscopic properties of that. Fundamentally, aerosols are suspensions in air (or in a gas) of solid or liquid particles small enough that they will remain airborne for a prolonged period of time because of their low settling velocity, which in still air can be calculated [12] using Stokes’s law. Viral aerosol particles size varies from 20 nm to 2000μm, and in many cases, preferably small particles with diameter less then 5μm remain in air for a long period of time [13]. The lower size limit of viral airborne aerosol particles is specified by the virus size (diameter), which can be as small as 20-30 nm, while the upper limit depends on the size of particle (of different origin) with which virus is associated or bound [14]. Of course, it is essential to realize that the size of the viral aerosol particle itself does not rule the airborne particle size [14], and final size of infectious droplets also depends on humidity, temperature and other conditions of environment and aggregate processes.To sum up, we have reasonable ground for consideration at least two specifics of model: the capsid- related and the nucleic (DNA or RNA) acid-related, and for study the model of virion (icosahedral / or prolate) consider the shell-core model of spherical or cylindrical (VLPs) particles with corresponding geometric (diameters, structure, symmetry), electrical (dielectric permittivity) characteristics for investigation the spectroscopic properties in purpose to determine the signature of bio-particles and define the set of main parameters associated with fingerprints of viruses.
3. Theoretical Point of View
- For any kind of theoretical approaches and experimental measurements the size of particles or system is essential. Physical properties revealed by any system should be considered in view of particles dimension and established theories and terms. It is well known that diameter of an atom ranges from about 62 pm (He) to 520 pm (Cs), on average is 1000 times smaller then diameter of viruses. Generally, at the micrometre level are bulk materials. The mesoscopic systems are normally in the range of 100 nm (the size of a typical virus) to 1 000 nm (the size of a typical bacterium) and 100 nm is the approximate upper limit for a nanoparticle.Nanoparticles (NPs) are bridging the continuum between small molecular clusters of a few atoms and dimensions of 0.2-1 nm and macroscopic bulk materials. NPs have properties neither those of atoms and molecules or those of bulk materials but somewhat intermediate between these properties. Therefore, the theoretical approaches and principles to comprehend qualitative picture of phenomena occurred in nanostructures and nanomaterials need to be based on the reasonable combination of classical and quantum points of view [15].The fact is well-known that, any particles detecting system comprises at least two components - object of detection and facility of detection. Virus-like particles (VLPs) and electromagnetic (EM) wave, the main players of scenario are of interest of our survey and future investigations. Studying electromagnetic field and particles interaction one would consider two main parameters, namely the typical linear dimension of the system,
 , and the characteristic wavelength
, and the characteristic wavelength  of incident (EM) wave. The comparison between the two is better expressed via the dimensionless size parameter
of incident (EM) wave. The comparison between the two is better expressed via the dimensionless size parameter 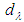 , ratio
, ratio 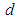 to
to  ,
,  . One can distinguish qualitative different regimes depending on radiation wavelength
. One can distinguish qualitative different regimes depending on radiation wavelength 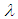 . Consideration the radiation in near optical region,
. Consideration the radiation in near optical region, 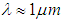 , leads to the following:a) For atomic and molecular systems,
, leads to the following:a) For atomic and molecular systems,  therefore
therefore  , and the system acts as a point, interacting with the radiation field as a dipole (or higher multipole);b) For macroscopic system, say
, and the system acts as a point, interacting with the radiation field as a dipole (or higher multipole);b) For macroscopic system, say 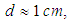 then
then 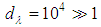 , geometric optics would apply, the photon may be regarded as a point. In cases where
, geometric optics would apply, the photon may be regarded as a point. In cases where is moderately large
is moderately large  , then the geometric optics limit would be a convenient starting point, but the corrections could be important. These limits are simple and well known.More complicated for analytical or numerical studies are systems out of the limits, when system size is comparable to the characteristic wavelength, and size parameter,
, then the geometric optics limit would be a convenient starting point, but the corrections could be important. These limits are simple and well known.More complicated for analytical or numerical studies are systems out of the limits, when system size is comparable to the characteristic wavelength, and size parameter, 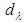 , is about 1 to 100, neither small enough for the system to be regarded as a point, nor large enough for photon to be regarded as a point, that system may be considered as mesoscopic [16], systems like microcavities, microspheres [17]. Much of our interest represents the “resonance” cases considering in scattering and diffraction theory of waves, when wavelength of radiation wave is comparable to diameter of particle,
, is about 1 to 100, neither small enough for the system to be regarded as a point, nor large enough for photon to be regarded as a point, that system may be considered as mesoscopic [16], systems like microcavities, microspheres [17]. Much of our interest represents the “resonance” cases considering in scattering and diffraction theory of waves, when wavelength of radiation wave is comparable to diameter of particle, 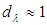 . In-depth theoretical study of scattering on single particles (especially, spherical and cylindrical symmetry) [18-24] in parallel with modelling and computing, size parameter limit for “resonance” cases seems more reasonable if it is transformed in more strict and precise form
. In-depth theoretical study of scattering on single particles (especially, spherical and cylindrical symmetry) [18-24] in parallel with modelling and computing, size parameter limit for “resonance” cases seems more reasonable if it is transformed in more strict and precise form  . Hence, for dielectric particles of complex permittivity it leads to the expression
. Hence, for dielectric particles of complex permittivity it leads to the expression  The “resonance” range is characterized by increasing the numbers of maximums and minimums in scattered field and preferable increasing of intensity in forward direction of wave propagation [23, 24], unlike the Rayleigh regime
The “resonance” range is characterized by increasing the numbers of maximums and minimums in scattered field and preferable increasing of intensity in forward direction of wave propagation [23, 24], unlike the Rayleigh regime 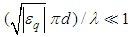 [23] characterized by symmetric distribution of scattered field in forward and backward directions. “Resonances” observed for spherical dielectric particles are called Mie resonances [22].It is known that the reduction of size and dimensionality of metals results in a drastic change in the electronic properties as the spatial length scale of the electronic motion. The quantum confinement effects appear when one dimension of a metallic material becomes comparable to the de Broglie wavelength
[23] characterized by symmetric distribution of scattered field in forward and backward directions. “Resonances” observed for spherical dielectric particles are called Mie resonances [22].It is known that the reduction of size and dimensionality of metals results in a drastic change in the electronic properties as the spatial length scale of the electronic motion. The quantum confinement effects appear when one dimension of a metallic material becomes comparable to the de Broglie wavelength 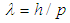 , (
, ( is Planck’s constant,
is Planck’s constant,  - the momentum). If approximate mean square speed of electrons Brownian motion in the metal assumed as
- the momentum). If approximate mean square speed of electrons Brownian motion in the metal assumed as 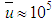 m/c, we would estimate the value of wavelength
m/c, we would estimate the value of wavelength 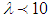 nm. The change of electronic and optical properties of a material sampled of sufficiently small size, 10 nm and less is arising. The quantum confinement effect can be observed once the diameter of the particle is of the same magnitude as the wavelength of the electron's wave function.Size dependence of properties of semiconductor (s/c) materials clearly may be presented by semi-classical model of (s/c) where electrons occupy one of two bands (valence or conduction). As an electron moves from valence band to the conduction band, it creates a positively charged hole. Together, the hole and electron are referred to as a Wannier-Mott exciton. The spatial separation of electron and its hole (in an “exciton”) is calculated using a modified Bohr model. The radius of sphere defined by the three-dimensional separation of the electron-hole pair, given by Murphy and Coffer, equals
nm. The change of electronic and optical properties of a material sampled of sufficiently small size, 10 nm and less is arising. The quantum confinement effect can be observed once the diameter of the particle is of the same magnitude as the wavelength of the electron's wave function.Size dependence of properties of semiconductor (s/c) materials clearly may be presented by semi-classical model of (s/c) where electrons occupy one of two bands (valence or conduction). As an electron moves from valence band to the conduction band, it creates a positively charged hole. Together, the hole and electron are referred to as a Wannier-Mott exciton. The spatial separation of electron and its hole (in an “exciton”) is calculated using a modified Bohr model. The radius of sphere defined by the three-dimensional separation of the electron-hole pair, given by Murphy and Coffer, equals  , where
, where  is the reduced mass of the electron-hole pair,
is the reduced mass of the electron-hole pair, 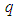 -electronic charge,
-electronic charge, 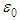 - free-space permittivity,
- free-space permittivity,  -dielectric constant of s/c. The model in a simplified picture ignores crystal anisotropies, electrons and holes with different mass behave as free particles in vacuum, nevertheless explains the bandgap difference in bulk s/c and that in a small nano-size crystal. In a bulk s/c, the bandgap is centered about the atomic energy levels with the width proportional to the nearest - neighbour interactions. The Fermi level is located between the conduction and valence bands and the optical behaviour is controlled by the levels near the band edges. The bandgap energies are lower than in smaller-size crystals where quantum confinement effects become perceptible. The increase of bandgap with decreasing crystal size is considered as the energy cost of confining the exciton within dimensions smaller than the Bohr radius. More clear interpretation is provided by the particle-in-a-box model of electron. The energy of a particle of mass
-dielectric constant of s/c. The model in a simplified picture ignores crystal anisotropies, electrons and holes with different mass behave as free particles in vacuum, nevertheless explains the bandgap difference in bulk s/c and that in a small nano-size crystal. In a bulk s/c, the bandgap is centered about the atomic energy levels with the width proportional to the nearest - neighbour interactions. The Fermi level is located between the conduction and valence bands and the optical behaviour is controlled by the levels near the band edges. The bandgap energies are lower than in smaller-size crystals where quantum confinement effects become perceptible. The increase of bandgap with decreasing crystal size is considered as the energy cost of confining the exciton within dimensions smaller than the Bohr radius. More clear interpretation is provided by the particle-in-a-box model of electron. The energy of a particle of mass  confined by one-dimensional box of dimension
confined by one-dimensional box of dimension 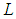 of infinite potential is given by
of infinite potential is given by 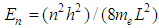 [25]. Equation implies that on decreasing the dimension
[25]. Equation implies that on decreasing the dimension  of the box, the spacing between the energy levels of the particle in the box increase. For a particle that is confined in a three-dimensional box constrained by walls of infinitely high potential energy, the allowed energy states for particle are discrete with a nonzero ground state energy. At the length of the box, which corresponds to the radius of a particle, the energy gap between the ground and the first excited state varies in proportion to
of the box, the spacing between the energy levels of the particle in the box increase. For a particle that is confined in a three-dimensional box constrained by walls of infinitely high potential energy, the allowed energy states for particle are discrete with a nonzero ground state energy. At the length of the box, which corresponds to the radius of a particle, the energy gap between the ground and the first excited state varies in proportion to  For a real nanocrystal, this means that the smaller the particle radius, the larger the energy gap to the first electronically excited state becomes. For a s/c material, there exists a size regime bounded by the onset of molecular cluster structure on the smaller side and by the Bohr radius on the larger side in which the bandgap energy varies strongly with the crystal size [25]. As relatively small changes in dimensions produce large changes in bandgap energy, the nanocrystal behaves as a tunable bandgap material, showing variable bandgap controlled by crystal size. In case of an optically allowed transition, decreasing the size relates to a blue shift in absorption and emission as has been observed in all kinds of nanocrystals. This is because the frequency and hence energy of blue light is higher than that for other parts of spectrum [25].The similar picture of size-spectrum dependence has been revealed studying the optical properties i.e., the optical resonance wavelength
For a real nanocrystal, this means that the smaller the particle radius, the larger the energy gap to the first electronically excited state becomes. For a s/c material, there exists a size regime bounded by the onset of molecular cluster structure on the smaller side and by the Bohr radius on the larger side in which the bandgap energy varies strongly with the crystal size [25]. As relatively small changes in dimensions produce large changes in bandgap energy, the nanocrystal behaves as a tunable bandgap material, showing variable bandgap controlled by crystal size. In case of an optically allowed transition, decreasing the size relates to a blue shift in absorption and emission as has been observed in all kinds of nanocrystals. This is because the frequency and hence energy of blue light is higher than that for other parts of spectrum [25].The similar picture of size-spectrum dependence has been revealed studying the optical properties i.e., the optical resonance wavelength 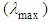 of gold nanoparticles, with increase in the nanosphere diameter from 20 to 80 nm, there is a small red shift in the
of gold nanoparticles, with increase in the nanosphere diameter from 20 to 80 nm, there is a small red shift in the 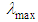 from about 520 to 550 nm [26]. This result was obtained using classical Maxwell’s electromagnetic theory and well-established theoretical tools based on the Mie theory [22] and the discrete dipole approximation (DDA) method [27]. It was clearly evident from the calculated spectra that the optical properties of nanoparticles - gold nanospheres, silica-gold nanoshells, and gold nanorods, for various nanoparticle sizes/dimensions, were highly dependent on the nanoparticle size, shape, and core-shell composition. The increase in the size results in an increase in the extinction (total) cross-section as well as the relative contribution of scattering to the extinction. Increasing the relative scattering contribution by increasing the nanoshell size or decreasing the ratio of the core/shell radii indicates the probable predominant shell-effect on scattering properties of particles. Gold nanoshells are found to have optical cross-sections comparable to and even higher than the nanospheres, and optical resonances fall favourably in the near-infrared region, nanospheres offer resonance wavelengths in the visible region [26].In our point of view it seems that increasing of “electrical” size/diameter of non-metal nanosphere which may be defined as
from about 520 to 550 nm [26]. This result was obtained using classical Maxwell’s electromagnetic theory and well-established theoretical tools based on the Mie theory [22] and the discrete dipole approximation (DDA) method [27]. It was clearly evident from the calculated spectra that the optical properties of nanoparticles - gold nanospheres, silica-gold nanoshells, and gold nanorods, for various nanoparticle sizes/dimensions, were highly dependent on the nanoparticle size, shape, and core-shell composition. The increase in the size results in an increase in the extinction (total) cross-section as well as the relative contribution of scattering to the extinction. Increasing the relative scattering contribution by increasing the nanoshell size or decreasing the ratio of the core/shell radii indicates the probable predominant shell-effect on scattering properties of particles. Gold nanoshells are found to have optical cross-sections comparable to and even higher than the nanospheres, and optical resonances fall favourably in the near-infrared region, nanospheres offer resonance wavelengths in the visible region [26].In our point of view it seems that increasing of “electrical” size/diameter of non-metal nanosphere which may be defined as 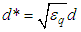 (
( is a dielectric permittivity of medium - sphere/shell) leads the “resonance” wavelength to red shift (longer scale). Simple calculation shows, that if
is a dielectric permittivity of medium - sphere/shell) leads the “resonance” wavelength to red shift (longer scale). Simple calculation shows, that if 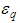 =55 for nanobioparticle with
=55 for nanobioparticle with 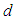 =18 nm sphere, “electrical” diameter will be equal to
=18 nm sphere, “electrical” diameter will be equal to  148,32 nm, hence “resonance” wavelength
148,32 nm, hence “resonance” wavelength  approximately falls in visible region of spectra (466 nm) instead of predictable 18 nm if size parameter
approximately falls in visible region of spectra (466 nm) instead of predictable 18 nm if size parameter 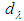 is prescribed to about 1. Value of
is prescribed to about 1. Value of 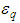 =55 is obtained for rod-shaped Tobacco Mosaic Virus (TMV) of approximately 18 nm in diameter and 280 nm in length, based on measuring of dielectrophoretic properties of TMV using time domain dielectric spectroscopy (TDDS) [28]. Data have been analysed according to the Maxwell–Wagner interfacial polarisation mechanism, for explaining and fitting the results been used the modelling virus as a long, thin rod with a homogeneous bulk permittivity of 55 [28].Wavelength dependence on “electrical” size/diameter of particle is observed in a spherical low-loss optical cavities, at wavelengths commensurate with Mie resonances, commonly referred to as whispering gallery modes (WGMs) [17, 29] or morphology-dependent resonances. WGMs are identified in Mie scattering calculations as the ripple structure, apparent in the extinction efficiency. Resonant mode can also be considered as a standing wave formed from an integer number of wavelengths around the particle circumference, referred to as the mode number,
=55 is obtained for rod-shaped Tobacco Mosaic Virus (TMV) of approximately 18 nm in diameter and 280 nm in length, based on measuring of dielectrophoretic properties of TMV using time domain dielectric spectroscopy (TDDS) [28]. Data have been analysed according to the Maxwell–Wagner interfacial polarisation mechanism, for explaining and fitting the results been used the modelling virus as a long, thin rod with a homogeneous bulk permittivity of 55 [28].Wavelength dependence on “electrical” size/diameter of particle is observed in a spherical low-loss optical cavities, at wavelengths commensurate with Mie resonances, commonly referred to as whispering gallery modes (WGMs) [17, 29] or morphology-dependent resonances. WGMs are identified in Mie scattering calculations as the ripple structure, apparent in the extinction efficiency. Resonant mode can also be considered as a standing wave formed from an integer number of wavelengths around the particle circumference, referred to as the mode number, 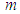 . The discreteness of wavelength of resonant modes is estimated by
. The discreteness of wavelength of resonant modes is estimated by  , where
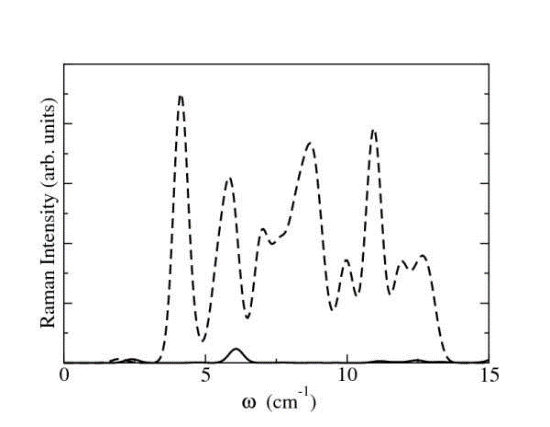
, where  is the real part of the refractive index of the particle medium [30, 31].“Electrical” size dependent tendency may be considered as probable reason of revealing the Raman active low frequency vibrational modes related to capsids of some viruses in the range of 30 GHz – 300 GHz (EHF) [32]. E.C. Dykeman and al. [33-36] calculated the Raman spectra of some viral capsids (STNV, CCMV, M13) using the atomistic displacement patterns and an empirical bond polarizability model, based on the idea that each viral capsid will have a set of unique frequencies and mode patterns due to the shape and composition of its capsid (Fig. 1).
is the real part of the refractive index of the particle medium [30, 31].“Electrical” size dependent tendency may be considered as probable reason of revealing the Raman active low frequency vibrational modes related to capsids of some viruses in the range of 30 GHz – 300 GHz (EHF) [32]. E.C. Dykeman and al. [33-36] calculated the Raman spectra of some viral capsids (STNV, CCMV, M13) using the atomistic displacement patterns and an empirical bond polarizability model, based on the idea that each viral capsid will have a set of unique frequencies and mode patterns due to the shape and composition of its capsid (Fig. 1). the VLP is considered as a scatterer of definite diameters (inner and outer) and dielectric permittivities of core and shell. In case of E-type (TM) waves, the system of algebraic equations for multipole coefficients
the VLP is considered as a scatterer of definite diameters (inner and outer) and dielectric permittivities of core and shell. In case of E-type (TM) waves, the system of algebraic equations for multipole coefficients  (corresponding the field inside the core area
(corresponding the field inside the core area  , with wave number
, with wave number 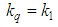 ) and
) and 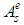 (corresponding the field outside the shell area
(corresponding the field outside the shell area  ,
,  ) are derived:
) are derived: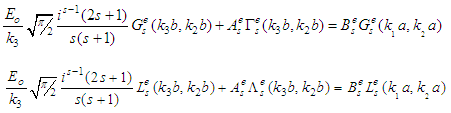 Wave numbers are specified by
Wave numbers are specified by 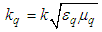 in
in 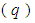 medium and by
medium and by  in free space; permeability and permittivity of free space are equal respectively
in free space; permeability and permittivity of free space are equal respectively 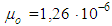 H/m,
H/m, 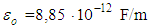 . Nonmagnetic mediums
. Nonmagnetic mediums  with complex permittivity
with complex permittivity  are considered.Assuming the incident field absence (i.e.
are considered.Assuming the incident field absence (i.e. 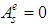 ) from system of algebraic equations we would get the equation:
) from system of algebraic equations we would get the equation: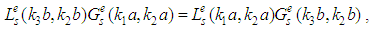 | (1) |
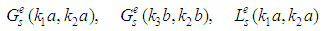 and
and  are given in analytical forms:
are given in analytical forms: 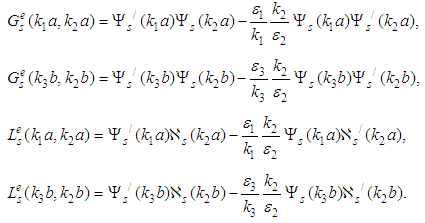 Functions used in expressions are related to the
Functions used in expressions are related to the 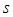 -th Riccati-Bessel and Riccati-Neumann spherical functions
-th Riccati-Bessel and Riccati-Neumann spherical functions  and
and  by formulas (“
by formulas (“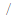 ” denotes the derivative with respect to the argument):
” denotes the derivative with respect to the argument): 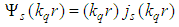 ,
,  . Assuming,
. Assuming,  and
and 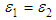 equation (1) easily may be transformed in resonant condition valid for dielectric microsphere [29]. In case of H-type waves (TE) were also derived the similar equations and corresponding expressions.The main task is finding the resonance wave vector
equation (1) easily may be transformed in resonant condition valid for dielectric microsphere [29]. In case of H-type waves (TE) were also derived the similar equations and corresponding expressions.The main task is finding the resonance wave vector 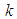 for given geometry and permittivities of core-shell. The resonance TM modes are specified by equation (1). Solution of the equation (1) if compatible appreciates eigenvalues corresponding to the eigenfrequencies of damping vibrations of system, since
for given geometry and permittivities of core-shell. The resonance TM modes are specified by equation (1). Solution of the equation (1) if compatible appreciates eigenvalues corresponding to the eigenfrequencies of damping vibrations of system, since  is complex. According to the Mie theory predictions concerning spherical particles scattering properties, eigenfrequencies of vibrations could be observed near that frequencies which correspond the maximums of intensity of particular partial scattered waves [24]. The same but more complicated frequency effects are expected for core-shell spherical particles which could be observed while studying the spectral of near and far field characteristics by estimation of EM field components as well as the total (extinction) cross section, which represents the total losses (damping) of energy from the incident beam due to both absorption and scattering, and is defined as the sum of the absorption
is complex. According to the Mie theory predictions concerning spherical particles scattering properties, eigenfrequencies of vibrations could be observed near that frequencies which correspond the maximums of intensity of particular partial scattered waves [24]. The same but more complicated frequency effects are expected for core-shell spherical particles which could be observed while studying the spectral of near and far field characteristics by estimation of EM field components as well as the total (extinction) cross section, which represents the total losses (damping) of energy from the incident beam due to both absorption and scattering, and is defined as the sum of the absorption  and scattering
and scattering 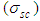 cross sections:
cross sections: 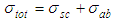 . Extinction spectra of small particles reveals some peculiarities especially if the particle is about the same size or larger than the wavelength. Extinction is preferably dominated by scattering. But absorption, which is usually manifested by absorption bands or absorption edges, can strongly affect extinction in unexpected ways: extinction may either increase or decrease with increasing absorption, and symmetric absorption bands in bulk matter may be transformed into highly asymmetric or even inverted extinction bands in small particles [18].Analysis of functions shows that decisive effect on scattering/absorption properties of VLP would be related to the values of
. Extinction spectra of small particles reveals some peculiarities especially if the particle is about the same size or larger than the wavelength. Extinction is preferably dominated by scattering. But absorption, which is usually manifested by absorption bands or absorption edges, can strongly affect extinction in unexpected ways: extinction may either increase or decrease with increasing absorption, and symmetric absorption bands in bulk matter may be transformed into highly asymmetric or even inverted extinction bands in small particles [18].Analysis of functions shows that decisive effect on scattering/absorption properties of VLP would be related to the values of  and
and  been arguments of Riccati-Bessel and Riccati-Neumann spherical functions (and derivatives), associated to the wavelength resonant modes
been arguments of Riccati-Bessel and Riccati-Neumann spherical functions (and derivatives), associated to the wavelength resonant modes 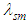 .Resonant spectra of VLPs should be strongly dependent on electrical and geometrical parameters of core-shell model. The set of wavelength resonant modes, diameters, electric permittivities of core-shell and surrounded medium could be considered as the assemblage of specific parameters of each VLP structure. The technique developed by Mie [22] is derived assuming uniform spherical particles, strictly valid only for spheres, however, easy to apply to generate a simulated spectrum from the measured size distribution and available literature optical constants. Mie theory is commonly used for modelling the optical properties of aerosols in both radiative forcing calculations and satellite data retrieval algorithms [30]. Both theoretical and simulation based outcomes would be used for comparison to the experimentally measured spectra. Modelling VLPs, study scattering characteristics of core-shell model based on rigorous solution of corresponding tasks of electrodynamics is essential for estimation of scattering and absorptive spectra experimentally measured by advanced spectroscopy or other techniques.
.Resonant spectra of VLPs should be strongly dependent on electrical and geometrical parameters of core-shell model. The set of wavelength resonant modes, diameters, electric permittivities of core-shell and surrounded medium could be considered as the assemblage of specific parameters of each VLP structure. The technique developed by Mie [22] is derived assuming uniform spherical particles, strictly valid only for spheres, however, easy to apply to generate a simulated spectrum from the measured size distribution and available literature optical constants. Mie theory is commonly used for modelling the optical properties of aerosols in both radiative forcing calculations and satellite data retrieval algorithms [30]. Both theoretical and simulation based outcomes would be used for comparison to the experimentally measured spectra. Modelling VLPs, study scattering characteristics of core-shell model based on rigorous solution of corresponding tasks of electrodynamics is essential for estimation of scattering and absorptive spectra experimentally measured by advanced spectroscopy or other techniques.4. Spectroscopic Experimental Studies
- Single-particle techniques coupled with spectroscopy have found wide applicability in the field of aerosol, colloid, environment, pharmaceutical sciences, being able to directly monitor size, phase, composition, and refractive index of medium in real-time, they can provide a route to better understand physical and chemical properties. The advanced analysis of properties of nanoparticles of any origin requires spectroscopic approaches, which permit to determine not only size and size distribution, but also their surface and subsurface properties. Spectroscopic work on nanoparticles as well as VLPs would be done with EM and associated microscopy techniques and methods of particle analysis, with conventional approaches including infrared, visible, ultraviolet and Raman spectroscopy. State of the art Raman spectroscopy overcomes many of the traditional limitations. Raman and Fourier transformation infrared (FTIR) spectroscopy are complementary in that they both measure vibrational frequencies of amino acid functional groups in proteins, but the information is derived from different interactions of electromagnetic radiation with the molecule. As a result the vibrational modes have different selection rules and non-equivalent relative intensities, and in many cases bands that are strong in the Raman spectrum are weak in the infrared and vice versa.The bonds formed between atoms have specific vibrational frequencies that correspond to the atom's masses and the strength of the bond between them. Complex molecules therefore exhibit many peaks and can be readily identified by the pattern or "fingerprint" created by those peaks. Raman scattering of light is interacted with vibrational modes of the molecule, a vibrational spectrum may be obtained allowing for identification of molecules and their functional groups. Raman scattering is strongest when vibrations cause a change in the polarizability of the electron cloud around the molecule. Therefore, the difference in energy between the incident and scattered photons is a characteristic of and provides structural information about the irradiated molecule. In experimental investigations we should keep in mind the significance of energy of light, which lies in the range of electronic and vibrational transitions in matter. The interaction of light with matter renders unique information about the structural and dynamical properties of matter. These unique spectroscopic capabilities are of great importance for the study of biological and solid-state nanostructures.The routine application of Raman spectroscopy was not possible until the advent of the laser, which provides a source of monochromatic radiation of sufficient intensity that the extremely weak inelastic scattering could be resolved.As versatile techniques with various applications to biointerfaces for studying the vibrational and spectral characteristics of VLPs, two-color sum-frequency generation (2C-SFG) nonlinear optical spectroscopy and infrared-visible sum-frequency generation (SFG) spectroscopy are preferable. SFG is more than a complementary probe to classical IR and Raman spectroscopies. It possesses specific assets, which make it a fully original tool: sensitivity to orientation, order, and symmetry; absolute intensity measurements; ultrashort temporal resolution; vibrational microscopy below the Rayleigh limit; and the possibility to study couplings between molecular levels at identical or different energy scales [46].The first experimental works done in close cooperation with colleagues of Le Laboratoire de Chimie Physique (LCP) de l´Université Paris-Sud have shown that Sum Frequency Generation (SFG) spectroscopy and ultrashort pulsed lasers based spectroscopic measurement methods are unique for investigation of vibrational modes of different viruses as well as for studying the nature of their oscillation processes and parameters of oscillation [15, 47, 48].Experimental extinction spectra of VLPs, measured simultaneously with particle size distribution allows an absolute comparison between the simulated and measured (UV/IR/Raman) spectra (scattered or absorbed), thereby providing a quantitative evaluation of errors associated with using developed theory to model spectroscopic properties of VLPs. Well adjustable simulation algorithm is the way for defining the set of resonant frequencies and spectra bands of experimental spectroscopic tools and facilities.Experimental spectroscopy-based and predicted simulation-based spectra are principal for building the library of spectra fingerprints of virions (NVs) and spectra signatures VLPs transformable in a digital and binary form suitable for analysis and detection of target (NV) agents, trace levels in complex background matrixes.Experimental data obtained by applying exquisite techniques and outcomes of theoretical or simulation models should complement each other and verify factors unforeseen in simplified approaches (surface roughness, inhomogeneity, possible anisotropy of core-shell virion areas).
5. Conclusions
- The main physical characteristics of ultrafine virus-like particles (VLPs), viruses based on single-particle level preliminary study are considered. The geometric size, namely core-shell diameters of virion, associated with morphology of capsid of virion and the set of fundamental vibrational frequencies (eigenvalues) of core-shell system associated with spectral signatures of capsid, nucleic-acids (DNA/RNA) as well as whole virion, related to electrical permittivities and diameters of core-shell are proposed as the main parameters determining the spectral fingerprints of VLPs, virions.Investigation of spectroscopic characteristics of VLPs based on core-shell model of virion, semi-classical theoretical approaches, EM wave scattering theory and computer modelling in complement with spectroscopic experimental study is proposed. Pilot experimental works shown the unique capabilities of Sum Frequency Generation (SFG) spectroscopy and ultrashort pulsed lasers based optical measurement methods for investigation of vibrational modes of different viruses and other pathogenic microorganisms as well as for studying the nature of their vibrational/oscillation processes and parameters of oscillation.Size distribution analysis and size differentiation of VLPs of any origin should be the starting stage in any scheme of VLPs detection systems. The spectroscopic-based virus identification would be considered as the next stage of virus detecting scheme if the comprehensive VLPs spectral library containing the spectral fingerprints of virions (NVs) and spectral signatures of near neighbours to the viruses created. Unified database system building on the bases of spectral library, VLPs size data in complement with bio-chemical digital images would be the purposeful way to the best collaborative work done by the scientific community. Nonlinear optics and its resonance technologies is possible direction of organization of treatment of viruses and pathogenic microorganisms in their different living media.
ACKNOWLEDGEMENTS
- The work is carrying out in Georgian Technical University supported by Shota Rustaveli National Science Foundation (SRNSF) under Grant Agreement (FR/430/3-250/13), and EU project NANOMAT-EPC (FP7-NMP-2013-CSA-7).
 Abstract
Abstract Reference
Reference Full-Text PDF
Full-Text PDF Full-text HTML
Full-text HTML