1. Introduction

The cause of spontaneous magnetization and the process of magnetization are two major problems of the theory of ferromagnetism. They are not solved correctly by the conventional theory. Their new solution has been put forward in relation to other issues [1-6], but did not attract due attention. The purpose of this article is to present the topic on its own in a consistent and detailed form in contraposition with the conventional theory. The latter is usually described as complete and impeccable. The book by Kittel [7] is a good example. His account will be used now to identify what is erroneous in it and to spot blanks. Other source for that matter is the book by Bozorth [8]. Some figures and arguments from our previous articles will be repeated for the sake of entirety.

The revised molecular mechanism of magnetization has come about from our experimental study and analysis of solid-state phase transitions as a function of temperature. An essential kind of them is ferromagnetic phase transitions, frequently referred to as "ferromagnetic ordering" in literature. Indeed, a ferromagnetic phase transition is a magnetization process with changing of the crystal structure. As far as its molecular mechanism is concern, the type of driving force (temperature) is not essential, considering that the same phase transitions could be driven by magnetic field as well. It turns out, a magnetization process with or without crystallographic change is based on the same principle, which is rearrangement of the crystal.

2. Solid-State Structural Rearrangements

The following is the general mechanism of structural rearrangements, deduced from the studies of phase transitions, presented initially by a sequence of journal articles [9-20] and then summarized in the book [1] and later by a set of articles [4-6, 21, 22].

• Rearrangements in a solid state materialize by a crystal growth involving nucleation and propagation of contact interfaces. Neither ferromagnetic phase transitions, nor ferroelectric phase transitions are excluded from this rule. Not a single sufficiently documented example exists of this process being "second order" (homogeneous, cooperative) suggested by the Landau theory.

• The nucleation differs greatly from its classical theory. It makes hysteresis inevitable. The nuclei are located in specific crystal defects − microcavities of a certain optimum size. These defects contain individual information on the condition needed to activate them (e.g., temperature, applied magnetic field) and the orientation of the resultant crystal.

• The nucleation can be epitaxial, in which case a certain orientation relationship between the initial and resultant structures is observed. It occurs in prominently layered crystals or when lattice parameters of the phases are very close. In strong epitaxial cases the contact interface becomes a twin interface.

• The interface is a rational crystallographic plane of the resultant crystal lattice. It is named contact interface owing to direct molecular contact between the two lattices without any intermediate layer. The molecular rearrangement proceeds according to stepwise (or edgewise) mechanism (Fig.1) consisting of formation of "kinks" (steps) at the flat interface and filling them, molecule-by-molecule, until the layer is complete, and building successive layers in this manner.

3. Conventional Standing on Magnetization

The following brief description of the conventional views on magnetization involves some representative excerptions from the Kittel book [7], clarifications in square brackets and comments.

"Given an internal [spin] interaction tending to line up the magnetic moments parallel to each other, we shall have a ferromagnet. Let us postulate such an interaction and call it the exchange field. The orienting effect of the exchange field is opposed by thermal agitation, and at elevated temperatures the spin order is destroyed."

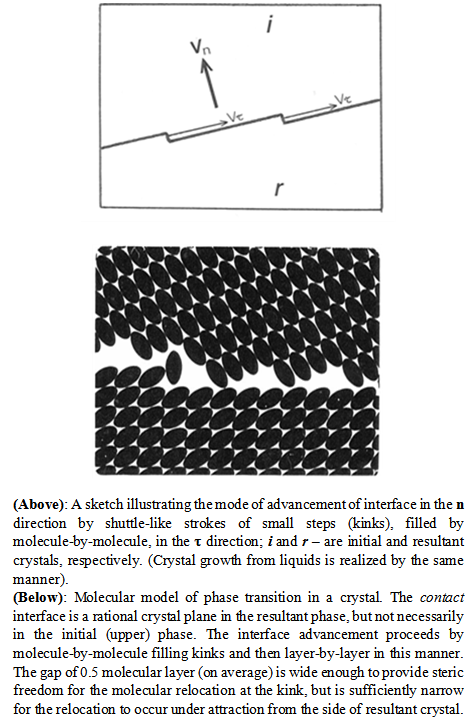Figure 1. The stepwise (or edgewise) mechanism of phase transitions and any other rearrangements in solid state

(1) The quantum-mechanical theory of spontaneous magnetization by Heisenberg was accepted (without attribution to its author) as the overall approach. (2) If the theory was valid, why was the exchange field postulated? (3) It was also postulated, implicitly, that the system of magnetic moments was an independent entity rather than a property of the crystal. In such a case, spin interaction could be the only conceivable cause of the spontaneous magnetization.

"Electronic magnetic moments of a ferromagnet are essentially all ["essentially all" or all?] lined up when regarded on a microscopic scale" [of crystal unit cells, Fig.2].

"Actual specimens [polydomain crystals that implied to be structural single crystals] are composed of a number of small regions called domains, within each of which the local magnetization is saturated. The directions of magnetization of different domains, however, need not necessarily be parallel" [Fig. 3]. The resultant magnetic moment of a polydomain crystal can be far from saturation − down to zero.

"The increase in the magnetic moment of the specimen under the action of an applied magnetic field takes place by two independent processes: (1) in weak applied fields the volume of domains which are favorably oriented with respect to the field increases at the expense of unfavorably oriented domains; (2) in strong applied fields the magnetization rotates toward the direction of the field".

Figure 2. Unit cell of ferromagnetic α-Fe crystal and its spontaneous magnetization.. The difference a (= b) - c is very small. Only recently it was shown that it is tetragonal rather than truly cubic

Figure 3. A schematic illustrating the features of domain patterns in the Fe polydomain crystals (shown is (100) plane). The broken lines help to comprehend their "rules": only interface AS is correct, not AB, AC or AD

The direction of spontaneous magnetization is called "direction of easy magnetization". The term is ambiguous in respect to an isolated domain: it is already spontaneously magnetized to saturation M_S in that direction. Evidently, it allows a possibility for the directions of spontaneous magnetization to be deviated from their "normal" position. The term acquires clear meaning when dealing with a polydomain crystal. Achieving M_S (by propagation of the domain boundaries until their disappearance), would require the lowest strength of the applied field H when it is parallel to the spontaneous magnetization of the arising crystal.

Other crystallographic directions are "hard directions" of various degrees of "hardness". In Fe, in order to magnetize a polydomain crystal in the a direction when H is not along a, the H should be stronger, since its "driving" strength is reduced to H = |H • cos (H ˆ a)|. Then, to achieve M_S to be along H, the H strength should be even higher. In that case magnetization in the a direction has been completed; there are no domain boundaries any more in the polydomain crystal. It must be remagnetized from the "easy" to a "not easy" direction − and the conventional theory does not see any alternative to a "magnetization rotation" in the crystal. The direction of spontaneous magnetization is deemed to be only "preferable", subject of changing by applied magnetic field against resistance of the crystal. A special phenomenon was introduced:

"There is an energy in a ferromagnetic crystal which directs the magnetization along certain definite crystallographic axes called directions of easy magnetization. This energy is called the magnetocrystalline or anisotropy energy."

Like in the case of the "exchange field", existence of that energy was also postulated, for its physical nature was not specified. Whether it is considered independent of the "exchange field" remains murky, but possibly not, as the two are cited to be "various contributions to the energy". Thus, the standard theory of magnetization rests on two postulated energies: of the "exchange field", arranging spins in parallel, and the "anisotropy", directing them in the crystal lattice.

The microscopic picture of domain boundaries is currently represented by a "Bloch wall" (Fig. 4), again involving the idea of spin rotation in the crystal.

Figure 4. Theoretical 180o - "Bloch wall" in a single-crystal continuum. It takes many lattice periods for the spins to gradually turn to the opposite direction. There are also "walls" of different angles of dipole rotation, e.g. "90o-walls"

"A Bloch wall in a [single] crystal is the transition layer which separates adjacent regions (domains) magnetized in different directions. The entire change in spin direction between domains does not occur in one discontinuous jump across a single atomic plain, but takes place in a gradual way over many atomic planes … In iron the thickness of the transition region is about 300 lattice constants".

Last major point in this brief description of the standard views on magnetization is origin of the domains. The phenomenon is claimed to be "a natural consequence of the various contributions to the energy − exchange, anisotropy, and magnetic − of a ferromagnetic body", and accompanied by a sketch [not shown] to illustrate that magnetic energy of a ferromagnetic single crystal is lowered by its separation into domains. There were no attempts to explain formation of the intricate domain structure like pictured in Fig. 3.

4. Questions Waiting for Answers

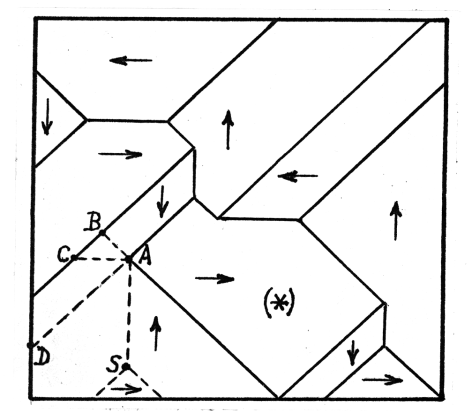
The Heisenberg's theory has been accepted owing to high prestige of its author and apparent lack of an alternative. There was, however, an authoritative skeptical voice. In contrast to Kittel and almost all other authors, presentation of ferromagnetism by R. P. Feynman [23] contained discussions of its serious weaknesses and inconsistencies. It was emphasized that while the quantum-mechanical theory by Heisenberg intended to explain the phenomenon of spontaneous magnetization by extremely strong spin interaction due to overlapping electron shells, it consistently produced the wrong sign of that interaction. Feynman concluded: "To the theoretical physicists, ferromagnetism presents a number of very interesting, unsolved, and beautiful challenges".

In the framework of the magnetization problem only, here are the major questions waiting for answers, the first one belonging to Feynman:

− "We still have the question: why is a piece of lodestone in the ground magnetized?".

− Is the cause of spontaneous magnetization the Heisenberg's electron exchange field?

− What makes spontaneously magnetized matter thermodynamically stable?

− What is the physical nature of the anisotropy (or magnetocrystalline) energy?

− How the anisotropy energy chooses and aims the spontaneous magnetization in one or another direction?

− Why does magnetization by magnetic field proceed by formation and advancement of domain boundaries, rather than by (cooperative) turning all spins simultaneously?

− Why do domain boundaries move slowly rather than by speed of magnetic waive?

− When magnetization is claimed to be "by rotation" of spins, is the rotation a cooperative (all spins together)?

− How is the peculiar domain patterns like shown in Fig. 3 formed?

− Why are the domain boundaries straight?

− How can the "Bloch wall" explain the "head to tail" attraction of elementary magnets at the domain boundaries if it is so wide as 300 lattice periods?

− How does the "Bloch wall" cover the multiple cases when the system to be magnetized is antiferromagnetic, helical or with spins being in a state of thermal agitation?

Before entering into dismantling of the standard theory, its correct part is to be recognized. That part is a description of the first magnetization stage, which is a movement of the domain boundaries until the whole polydomain crystal acquires the spin orientation of the domain having the orientation closest to (not necessarily coincident with) the H direction. All the rest − structure of polydomain crystals, origin of spontaneous magnetization, spin rotation, Bloch wall, anisotropy energy − will be challenged and replaced in the sections that follow. The first step in that direction is to reveal that the Heisenberg's theory of electron-exchange field is not valid.

5. Theoretical Predicament Ferromagnetism Cannot Exist

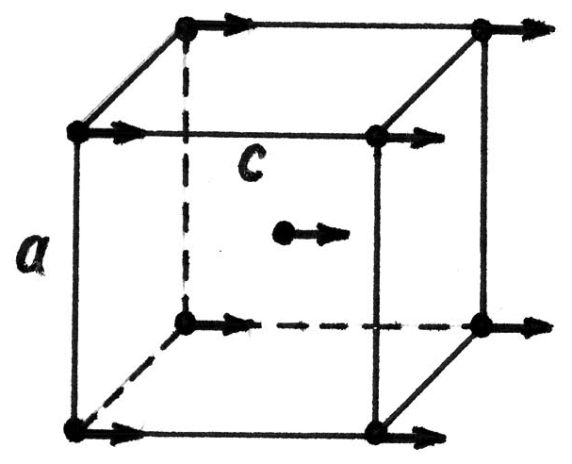
The Heisenberg's theory was an attempt to find the cause of the phenomenon of ferromagnetism narrowly interpreted as a thermodynamically stable existence of parallel spins in crystals − like that in Fig. 2. It had to be explained how that state can be stable up to the temperatures so high as 1042 K in Fe. It seemed unavoidable to conclude (incorrectly) that the force holding the elementary dipoles in parallel is their mutual interaction. In such a case, this force had to be about 10⁴ times stronger than their magnetic interaction alone. Heisenberg accepted that as a fact and developed its quantum-mechanical interpretation: it is overlapping of the electron shells that results in extremely strong electron exchange interaction, sufficient for the stable collinear spin alignment up to the observed high temperatures.

General acceptance of the Heisenberg's theory remains unshakable to the present days. The contradictions, blank areas, and vast disagreements with experiment are being ignored. Yet, there are exceptions, listed in [24], where those inconsistencies were noted. They led Feynman to state "One challenge is to understand why [ferromagnetism] exists at all". In other words, why a spontaneously magnetized state is stable?

In fact, the theory had to be rejected from the very beginning: it produced a wrong sign of the exchange forces. This means that the apparent electron-exchange field, if existed, would produce a spin repulsion of the same great strength as the attraction it had to prove. The repeated calculations consistently produced the same result, actually meant that ferromagnetism must not exist. The sign problem was carefully examined [25] and found fundamentally unavoidable in the Heisenberg model. It was suggested that the "neglect of the sign may hide important physics." (This subject is described in [4] in more detail).

The theory of electron-exchange field should be nullified not only due to its failures; it was not needed at all for explanation of ferromagnetism / spontaneous magnetization. It will be shown below that the parallel alignment of spins is set up by crystal forces, and not by spin interaction.

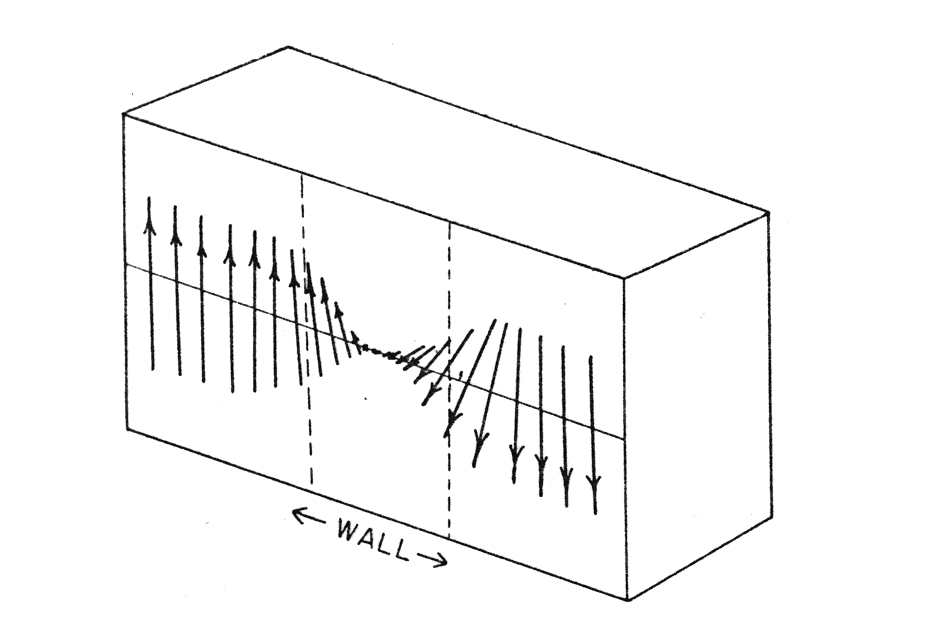
6. Tearing Down the Bloch Wall

The "Bloch wall" (Fig. 4) was a derivative of two erroneous theories, namely, the molecular / exchange field and anisotropy energy. This type of a boundary between ferromagnetic domains was not discovered experimentally, neither any credible circumstantial evidence existed. It was invented to help the Heisenberg's theory overcome a predicament: prohibitively high energy of the domain boundaries. In terms of the theory, the exchange energy between neighboring magnetic dipoles on the opposite sides of a 180^o domain boundary (i.e., when the dipoles are antiparallel) is at its maximum. A gradual change of the dipole directions over a number of lattice periods would lower that energy, but their deviation from the crystallographic "direction of easy magnetization" would have the opposite effect. The "Bloch wall" was the result of a theoretical optimization of the "exchange field" and “anisotropy" energies effects. This did not mean that the "Bloch wall" was a low energy boundary: it was only minimal under the above theoretical assumptions.

Some calculations have set the "wall" thickness from 50 to 200 nm in Fe. Kittel came up with 300 lattice spacings (~86 nm). According to Hubert [26], it is "several thousands" crystal spacings. Understanding "several" as minimum of three, this gives rise to the walls in Fe at least ten times wider than stated by Kittel. There have been no experimental data validating these numbers.

It will be revealing to compare the ~86 nm width of the "Bloch wall" with the size of domains in Fe inferred also from the standard theory. Bozorth's estimation [8], in agreement with other authors, was ~10 nm for the maximum size of a Fe crystal remaining as a single domain. This means that a larger crystal, for example, 12 nm will, or at least can, consist of two domains. But Bozorth warned us not to take the estimate "too literally". Therefore, we assume that not 12, but a 120 nm particle can consist of two, and for better illustration, a 180 nm particle of three domains. Comparison of the result with the 86 nm "Bloch walls" between them is shown in Fig. 5.

Figure 5. Inconsistence between estimates of the “Bloch wall” thickness and the dimensions of ferromagnetic domains by the theory

The result is nonsensical. Even changing one of the values under comparison by another order of magnitude (e.g., increasing the threedomain particle to 1800 nm) would not produce a satisfactory result, for even then as much as 14% of every domain will be occupied by the "walls".

As usual with artificial constructions, every particular case required a "wall" modification. For example, for the angles 180°, 109.47° and 70.53° at the domain boundaries in Ni, one has to assume three different types of the "walls". What's more, the "Bloch wall" was initially designed specifically for ferromagnetics, and not antiferromagnetics. The theory of "domain walls" became so cumbersome that an entire book [26] was needed to overview it. Unfortunately, wrong premises made that work useless.

7. Polydomain Crystal

7.1. Not a Single Crystal

The "Bloch wall" was implied to be a purely magnetic phenomenon residing in the single crystal medium, and the same idea was hidden in all relevant theories. It could even be supported by X-ray single-crystal patterns of polydomain Fe crystals. Yet, the Fe polydomain crystals are only pseudo-single crystals. They are conglomerations of single crystals (domains) of identical crystal structure differently oriented relative to one another.

During all 20^th century the structure of iron at room temperature believed to be a truly cubic. But it is shown now [1, 27] that Fe unit cell is a tetragonal pseudo-cubic, with a minute difference (a = b) - c. The arrows in Figs. 2 and 3, indicating the directions of spins, represent the directions of the lattice parameter c as well. This brings about an important revelation about a domain boundary. It is not simply a place where spins change their direction; it is the contacting place of two individual crystal lattices. While the structures of the contacting domains are identical, their different spatial orientation makes their boundary no physically different from those in phase transitions. The domain boundaries are contact interfaces, not "Bloch walls".

7.2. Formation from Paramagnetic Phase

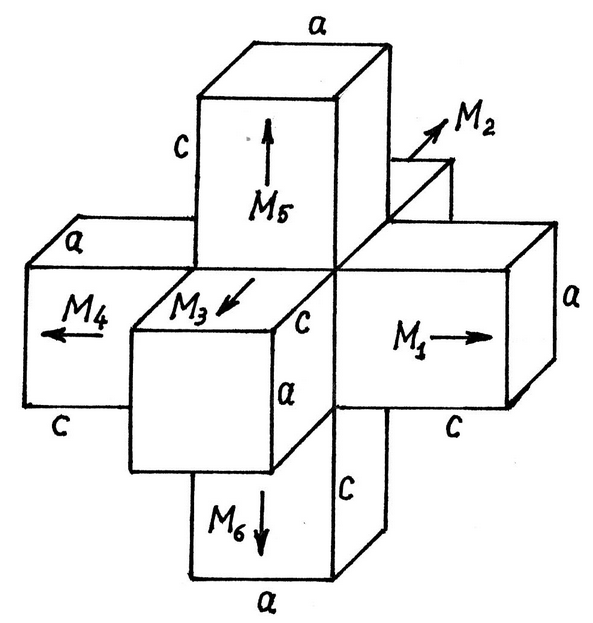
In order to describe formation of polydomain structures of the patterns as elaborate as in Fig. 3, the general mechanism of solid-state reactions outlined in Section 2 had to be invoked. That is why their formation has not been explained up to now. They are formed by epitaxial nucleation and growth.

Common solid iron is polycrystalline, consisting of randomly oriented grains separated by irregular boundaries. Every grain has a polydomain structure. Each domain is a single crystal with its own direction of the elementary magnetic dipoles (spins) along the crystal parameter c.

Let us trace the metamorphoses every grain undergoes during its paramagnetic → ferromagnetic phase transition at 770℃. Above that temperature it is a single crystal of cubic symmetry where atoms and their spins are disoriented due to thermal agitation. It is an "orientation-disordered crystal" (ODC), known in the non-magnetic world as well. Below that temperature the phase transition proceeds by multiple nucleation and growth of the normal solid phase. Because the nucleation is epitaxial, and the matrix is cubic, the nuclei appear arbitrarily in any one of six orientations (Fig. 6). When the crystals growing from those nuclei meet, there is one chance that their spins will be in parallel ("0°-boundary"), one chance - antiparallel ("180°-boundary"), and four chances - "90°-boundary". It is probable that magnetism in that phase transition comes to play only at the stage when the growing single crystals come very close to each other, so that their spins can start interacting; until then the ODC-phase between them will have a screening effect. When they ultimately meet, i.e., when the phase transition is completed, the initial domain interfaces, if not quite well organized, will be finalized already in solid state by the magnetic recrystallization [1] according to the general mechanism of all solid-state reactions (Fig. 1). It will take place to minimize free energy of the interfaces. This involves two requirements: best possible crystal packing and mutual attraction of the magnetic dipoles. The case under consideration is such that both requirements can be well satisfied: the crystal lattices on both sides will match almost perfectly to become a twin interface of zero thickness and, simultaneously, the dipoles will be arranged in a "head-to-tail" order. That is how the domain structures like one in Fig. 3 are formed.

Figure 6. Six mutual directions of spontaneous magnetization Ms that make 90° and 180° to one another in a polydomain iron crystal. While the unit cell dimensions c and a = b are very close, it is axis c which is the Ms direction. (The figure is not intended to illustrate domain boundaries)

8. Domain Interface at Molecular Level

The first observation of the stepwise (or edgewise) mode of interface propagation in a solid-state phase transition, illustrated by sketch in Fig. 1, was reported in 1966 [10]. A consonance with a crystal growth from liquid phase was specified. It was concluded that the phenomenon is a crystal growth in solid phase, in which successive crystal layers are built up by filling steps ["kinks"] one molecule at a time. The observations, however, were made only with the optical resolution not better than ~100 nm achievable at that time. It was stated that "while our technique did not allow us to observe elementary steps of growth, their existence is undoubted".

Experimental proof of that prediction had to wait for 37 years until Novoselov et al. (NGDHG) [28] recorded a domain "wall" with a high resolution attained never before. They did not see the "Bloch wall of 300 lattice periods wide", but found that the ferromagnetic domain interface propagated "via clear quantized jumps matching the lattice periodicity. The distance between the equivalent sites was measured to be 1.6 ⁺ 0.2 nm". The authors interpreted the interface movements as following the Peierls potential of the crystal lattice and believed that "the presence of a periodic atomic landscape [is] impeding movements of domain wall".

Also observed were "kinks" running along the interface. That led to speculations why the "wall" does not jump as a whole between the neighboring minimums of the Peierls potential. As a result, NGDHG stated that "further theoretical and experimental work is required to understand atomic scale [domain walls] dynamics. They did not recognize that dealt with magnetic particles rather than spins alone. The stepwise nucleation-and-growth mechanism of solid-state reactions explains all their observations.

9. Assumption: Spins Uniquely Oriented in the Structure of Their Atoms

Possibility of spin rotation within magnetic atoms is invisibly (and subconsciously) present in the current theory. It is hidden in the claims (e.g., by Bozorth [8]) that spontaneous magnetization M_s in the same crystal can be rotated by application of magnetic field H.

Let us turn to an atom of Fe. In the crystal lattice it is not simply a dot or a spherical entity. It is a non-spherical particle of which the position and orientation are set up by the forces much more powerful then the forces of H↔spin magnetic interaction. They are those of chemical crystal bonding. Orientations of the atomic particles cannot be affected by H not only in the sense that its interaction with the spins is much weaker in comparison, but because changing of particle orientations cannot occur without a complete crystal rearrangement. Therefore, claiming that spontaneous magnetization in the same crystal can be redirected by the applied magnetic field actually means spin redirection within their atoms. Our assumption is that such a possibility does not exist. Spins are uniquely oriented in the structure of their atoms.

10. The Answers

The above-formulated assumption in conjunction with the outlined in Section 2 solid-state structural rearrangements clarifies and simplifies the whole problem of magnetization and, in fact, all other major problems of ferromagnetism. By treating that assumption as a fact, here are answers to the questions listed in Section 4.

■ The cause of spontaneous magnetization. The positions and orientations of the constituent particles of any crystal are those providing overall minimum free energy to it. Since spins are permanently oriented in the atoms, with the particle orientations come certain spin orientations. If all particles are packed in parallel, the crystal turns out to be spontaneously magnetized like that in Fig. 2. An antiparallel packing of spin-carrying particles will produce the antiparallel magnetic structure. A helical packing mode will produce the helical ferromagnet … This is how unsophisticated our explanation of the spontaneous magnetization and its diversity becomes.

■ Thermodynamic stability of ferromagnets. Magnetic spin interaction in ferromagnets increases their stability in some cases and decreases in others. But its contribution to the total crystal free energy dominated by the chemical bonding is relatively small. It is the total free energy that provides stability to a ferromagnet if it is the lowest among all other structural versions.

■ Direction of spontaneous magnetization in crystal lattice. Physical nature of anisotropy energy. It is not this mysterious energy, assumed to be specific to ferromagnetic crystals, that sets up direction of spontaneous magnetization. The direction is simply reflects the orientations of particles in the crystal. The "anisotropy energy" does not need explanation of its physical nature. It is not real.

■ Magnetization by motion of domain boundaries. Orientations of spins are fixed in their particles, and the orientations of particles are fixed in the crystal lattice. Therefore, spin orientations are not changeable without reconstruction of the crystal itself. Crystal reconstruction in solid state can proceed only by atomic/molecular rearrangement at interfaces. Magnetization (changing spin directions) by motion of domain interfaces is the only way to materialize. Magnetization "by rotation" is not possible.

■ On "cooperative" spin rotation at the second stage of magnetization. No spin rotation at whatever stage is possible.

■ Domain formation and structure. For the first time formation of a domain structure in its specific details could be explained. It is done in Section 7.

■ Bloch wall. Over and above all other arguments to reject the Bloch wall model, the following two reasons are sufficient to discard it: (1) The model was based on the erroneous idea of spin rotation in a crystal medium, and (2) The model was a derivative of two defunct theories: "exchange field" and "anisotropy energy".

■ The real domain interface. Everything said below is equally applicable to both 180°-boundary and any other domain interface. The domain boundary is a structural twin interface of zero thickness. The dipoles on the opposite sides of a 180°-domain interface are either antiparallel, or their projections on the interface are antiparallel. The experimental domain patterns are entirely consistent with the crystal twin nature of the domain interfaces. The energy of a twin interface, especially with the magnetic attraction, is minimal among any imaginable crystal interfaces. The twin interfaces propagate according to the stepwise contact mechanism, which is universal for all crystal rearrangements. This mechanism is the same whatever angle happened to be between the magnetic moments of the contacting domains. Relocation of one spin carrier takes place at a "kink" on the interface, one particle at a time. Every relocation results in reorientation of one magnetic moment. Such is the universal magnetization mechanism of ferromagnets.

■ Magnetization in phase transitions. Ferromagnetic phase transitions should be interpreted as a magnetization brought about by changing of the crystal structure (not vice versa). Over all 20^th century they were classified as (and became the last resort for) the cooperative "second order" phase transitions [1, 4]. When accumulation of the experimental data has revealed that many of them were "accompanied by" structural rearrangements, the new term "magnetostructural" has come into use. The cause of that interconnection remained mysterious.

If the orientations of a spin and its carrier are uniquely bound, as argued in Section 9, the explanation becomes trivial: magnetization results from reorientation of the particles − spin carriers − upon the phase transition.

Vice versa: magnetization without reorientation of the magnetic particles is not possible. All ferromagnetic phase transitions are structural ("first order"), whether that has been detected of not yet. The term "magnetostructural" is superfluous.

This topic was considered in more detail in [4].

11. Magnetization of Antiferromagnet

Observations of magnetization of an antiferromagnet by Lavrov at al. (LKA) [29] illustrate the inability of standard science to account for them, while being in accord with our concept of magnetization.

LKA applied magnetic field to antiferromagnetic crystal and observed its rearrangement by motion of phase boundaries and kinks moving along them. While the kinks height, unlike those seen by Novoselov et al., was not elementary, the magnetization was realized by the general molecular mechanism of solid-state reactions.

In terms of the conventional science the phenomenon itself had not existed. As LKA pointed out, "the common perception [is that] magnetic field affects the orientation of spins, but has little impact on the crystal structure." But the structure did changed. The perception is erroneous: the applied magnetic field was the driving force of phase transition. While not being able to turn spins directly in the same structure, its interaction with the spins was sufficient to upset the close balance of free energies between antiferro- and ferromagnetic phases. LKA observed a structural phase transition where change of magnetization was a secondary effect.

LKA noted that "one would least expect any structural change to be induced in antiferromagnet where spins are antiparallel and give no net moment". Nevertheless, the phenomenon has took place. From the positions of the standard theory there are two reasons to see it as a contradiction. One is rooted in the belief that spins in an antiferromagnet are strongly bound together by the Heisenberg’s "exchange forces", therefore the external field H, which is weak in comparison, cannot deal separately with the parallel and antiparallel components of the spin system. The other reason is a habitual approach to phenomena as being "cooperative" even when they are clearly not. LKA dealt with antiferromagnetà ferromagnet phase transition in which the particles fill "kinks" in sequence, every second one turning its spin toward the H direction.

12. Magnetic Hysteresis Loops

The inseparable connection of a magnetization process with the underlying structural rearrangements is a guiding principle for analyzing magnetic hysteresis loops. They, in fact, are structural hysteresis loops like those observed in the temperature solid-state phase transitions and other solid state reactions. Magnetic hysteresis loops are to be interpreted as the structural rearrangements driven by application of magnetic field, while the magnetization of the matter is recorded. The structural hysteresis loops, in turn, have their roots in nucleation and its hysteresis.

This scope of the interconnected phenomena cannot be argued meaningfully in the limited frames of the present article, but the topic is presented in detail in [1, 6].

13. Conclusions

It is shown that current theories of a spontaneously magnetized state and the magnetization process of ferromagnets are invalid. Their main components − Heisenberg's electron exchange field, anisotropy energy and Bloch wall, aside from their other inconsistencies, involve an implicit idea that spins (elementary magnetic dipoles) can be directly rotated by applied magnetic field, as if they are a separate free system. That is not the case. Importance of the crystal, which the spins belong to, was overlooked.

It is demonstrated that no sophisticated theory was needed. All problems of the theory are solved at once as soon as we accept the following: the directions of spins are not changeable in the structure of atoms carrying them. Then it becomes self-evident that the spontaneous magnetization is established by the crystal field, because it holds atoms and molecules in the crystal in certain positions and orientations. The only way to reorient spins is to reorient their atoms, and the only way to reorient atoms in solid state is atom-by-atom relocation at interfaces. No spin rotation in the same structure is possible. And so on.

Any change in the state of magnetization is simply an accompanying effect of the restructuring driven by application of magnetic field. The theories of electron exchange field, anisotropy energy and Bloch wall are both invalid and superfluous.